Multi-objective and Multi-load-Conditions Topology Optimization Model for Designing Metamaterial Vibration Isolator with Customized Stiffness

Abstract

Metamaterial vibration isolation, as a promising technology for reducing and controlling vibration, can achieve mechanical properties that natural materials do not have through the microstructural design of uniformly and periodically distributed unit cells of the metamaterial isolator. However, cell patterns of existing metamaterial isolators are relatively fixed, which leads to the limited design range of three-direction stiffnesses of the isolator. Under some harsh working conditions, the internal strain will be too large for the common unit cell structure. This work develops a topology optimization model based on SIMP (solid isotropic material with penalization) method for designing metamaterial vibration isolator with customized three-direction stiffnesses. It uses the three-direction stiffnesses and strain energies as the optimization objectives. And different direction stiffnesses are calculated under different loading conditions. To simplify the design process, one unit cell with periodic boundaries and equivalent loads is optimized. The overall three-dimensional structure of the vibration isolator is eventually periodically modelled from the optimized cell structure, and its stiffnesses are compared to the customized values to verify the effectiveness of the optimization model. The load–displacement curves of the overall isolator show that the obtained stiffnesses meet well with the target stiffnesses, and the maximum deviation is only 0.12%.

1 Introduction

As an emerging reducing and controlling vibration technology, metamaterial vibration isolation technology can achieve the mechanical properties that natural materials do not have through microstructural design and optimization. When the requirements change, the metamaterial can meet the new ones only by structural adjustment, thus avoiding the complicated development process of material selection, design, verification, and so on, like traditional vibration isolators. It can greatly shorten the development process and reduce the development cost.

However, cell patterns of existing metamaterial isolators are relatively fixed, which leads to the limited design range of three-direction stiffnesses of the isolator. Under some harsh working conditions, the internal strain will be too large due to the common unit cell structure.

Among the existing optimization techniques, the topology optimization method can be considered as one of the most promising optimization tools and a research direction with the most development prospects [1, 2]. As an effective method to establish the relationship between the topological structure and mechanical properties of materials, the topology optimization method is gradually applied to the design of metamaterial structures. The investigation of topology optimization considering the stiffness optimization of mechanical structures can be traced back to the 1980s [3]. Since then, a new era of topology optimization of microstructures has been opened, and many scholars have begun to study it. Density-based topology optimization approaches were developed later [4]. Sigmund [5] proposed the transformation of the unit-cell structural design into unit-cell topological optimization design to construct macrostructural material. Zhang [6] took the material loss factor which indicates the damping characteristics of the material as the single design objective and proposed a density-based topology optimization method for designing damping composite material with high broadband damping. Fan [7] introduced the CRITIC method into the structural multi-objective topology optimization to calculate the weight coefficients of objectives.

In this work, a multi-objective and multi-load-conditions topology optimization model based on SIMP (solid isotropic material with penalization) method is developed. The method uses the three-direction stiffnesses and strain energies as the optimization objectives, and different-direction stiffnesses are calculated under different loading conditions as the constraint conditions. One unit cell is optimized by this method. The overall three-dimensional structure of the vibration isolator is eventually periodically carried out according to the optimized cell structure, and the effectiveness of the optimization model is verified by comparing its stiffnesses with the customized value.

2 Theoretical Basis

2.1 Basic Equations

Dorn [8] defined ground structure to refer to the design domain. The optimal material distribution model classifies the design domain according to the existence of materials in the ground structure. The process of topology optimization is based on the above theory to define the area with materials and the area without materials in the design domain, so as to achieve the optimal material distribution. In this study, only linear elasticity is considered and the equilibrium equation based on Newton’s second law of the domain is given as follows [9]:

$$ 0 = \nabla \cdot S + F_{V} $$

(1)

where S is the second Piola–Kirchhoff stress tensor and F_V is a body force, which represents three-direction loading in this work.

The design target value of the three-direction stiffnesses of the unit cell is the constraint condition, which is calculated as follows:

$$ K_{i} = \frac{{F_{i} }}{{avg\left( {d_{i} } \right)}} $$

(2)

where i = X, Y, Z is the three directions of the vibration isolator, F_i is the load in i-direction (Z-direction is the normal force, and the other two are shear force), d_i is the displacement of the load boundary in the i-direction, and avg means average.

Then, set the unit cell pattern and its array layout, and determine the design target value of three-direction stiffness of the unit cell according to the corresponding relationship between the unit cell stiffness and the overall stiffness of the vibration isolator. The cell patterns include but are not limited to the tetrahedron, pentahedron, hexahedron, and other polyhedrons. For example, if the hexahedron of a cuboid is used as the unit cell pattern, several units are arranged along the X, Y, and Z directions to form the vibration isolator, respectively. The design target value of the three-direction stiffnesses of the unit cell is expressed as:

$$ K_{i,cell} = \frac{o}{m \times n}K_{i,total} $$

(3)

where i = X, Y, Z is the three directions of the vibration isolator, K_{i, cell} is the design target value of i-direction stiffness of the cell, K_i,total is the design target value of i-direction stiffness of the vibration isolator, m, n and o are the number of cells in X, Y and Z directions, respectively.

2.2 Topology Optimization Model

Topology optimization based on SIMP method uses the corresponding relationship between the relative density of unit cell (design variable) and the elastic modulus in the form of the density function of the continuous variable and then transforms the discrete optimization problem into a continuous optimization problem.

In order to control the minimum structure size in the topology optimization process and eliminate the mesh dependency problems, Helmholtz equation is used to filter the design variables:

$$ \widetilde{{\rho_{e} }} - r_{\min }^{2} \nabla^{2} \widetilde{{\rho_{e} }} = \rho_{e} $$

(4)

where r_min is the parameter of filter radius, and the general value range is 1–3 times the mesh size, $\widetilde{{\rho_{e} }}$ is the filtered design variable.

The filters can make the spatial distribution of relative density smoother, but also make the gray areas (intermediate densities) in the design field more, which are unwilling for structure design. Therefore, the Heaviside equation is applied to the filtered design field:

$$ \widetilde{{\widetilde{{\rho_{e} }}}} = \frac{{\tanh \left( {\beta \left( {\widetilde{{\rho_{e} }} - \gamma_{\beta } } \right)} \right) + \tanh \left( {\beta \gamma_{\beta } } \right)}}{{\tanh \left( {\beta \left( {1 - \gamma_{\beta } } \right)} \right) + \tanh \left( {\beta \gamma_{\beta } } \right)}} $$

(5)

where $\widetilde{{\widetilde{{\rho_{e} }}}}$ is the projected design variable, $\beta$ is the projection parameter, the value range is generally 6–10, and $\gamma_{\beta }$ is the projection point, the value range is generally 0.1–0.9.

The SIMP method is adopted to solve the topology optimization problem which penalizes Young’s modulus by:

$$ E_{SIMP} = E_{0} \times \widetilde{{\widetilde{{\rho_{e} }}}}^{P} $$

(6)

where E₀ is Young's modulus of the material, and P = 6 is the penalty factor.

In structural mechanics problems, maximizing stiffness is equivalent to minimizing compliance, which is equivalent to minimizing total strain energy from the energy perspective [9]. Because the three-direction stiffnesses mentioned in Eq. (1) require three load conditions to be solved, the elastic strain energy under three load conditions of the unit cell is defined as:

$$ W_{Si} = \frac{1}{2}\sigma \left( {\rho_{e} } \right):\varepsilon $$

(7)

where i = X, Y, Z is the three directions of the unit cell, $\sigma$ and $\varepsilon$ are the stress and strain of the unit cell, respectively.

In this study, the design objective of three-direction stiffnesses is innovatively transformed into constraint conditions. With the design target value of the three-direction stiffnesses of the cell, the volume fraction of the material in the design domain, and the total strain energy of the cell as the objective function, the topology optimization model of the unit cell is established as:

$$ \left\{ \begin{gathered} {\text{find}}\qquad \rho_{e} , \quad e = 1,2,3, \ldots ,n \hfill \\ {\text{minimizing}}\quad F_{j} = \int\limits_{\Omega } {\frac{1}{2}\sigma \left( {\rho_{e} } \right):\varepsilon {\text{d}}\Omega } \hfill \\ {\text{subjected to}}\quad K_{i} \le K_{i,cell} \hfill \\ \quad \quad \quad \quad \qquad 0 \le V_{f} \le V_{0} \hfill \\ \end{gathered} \right. $$

(8)

where ρ_e is the design variable, e is the mesh unit number of the finite element mesh, n denotes the total number of finite elements for the design domain Ω, K_i is the value of the three-direction stiffnesses of the cell in the optimization process, V_f is the volume fraction of the material in the design domain, and V₀ is a constant, indicating the upbound of material volume fraction.

2.3 Implementations

The topology optimization model is implemented in COMSOL Multiphysics 5.6 with the Structure Mechanics, Optimization, and PDE modules. The computational domain is divided by quadrilateral mesh. The design variable is updated by the Optimization Solver MMA. The sensitivity of the objective function with respect to the design variables is calculated by the adjoint gradient method. The convergence criterion is expressed as:

$$ \mathop {\max }\limits_{e = 1 \ldots n} \left| {\rho_{{e_{k} }} - \rho_{{e_{k - 1} }} } \right| \le \alpha $$

(9)

where k is the current iteration step, and α is a constant, usually ranging from 10⁻⁶ to 10⁻³, which value is 10⁻⁶ in this work.

3 Case Study

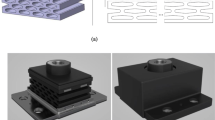
A 15 cm × 12 cm × 6 cm metamaterial vibration isolator is presented to illustrate the optimal design procedure by the multi-objective and multi-load-conditions topology optimization model based on the SIMP method mentioned in Sect. 2.2. The primitive design parameters of the metamaterial vibration isolator are shown in Table 1. The design target value of stiffness K_Z,total is 12,500 N/mm, which is main load direction, the non-load direction stiffness K_X,total is 2500 N/mm, and Y-direction stiffness has no specific requirements. Therefore, the overall structure of the vibration isolator (1 in Fig. 1a) is divided into the array layout of the unit cells (2 in Fig. 1b) of the 5 × 1 × 2 hexahedral structure.

Table 1 Primitive design parameters

Fig. 1

a An overall design dimension of vibration isolator and b the array layout of the initial unit cell

On account of the vibration, the isolator is designed for the stiffnesses mainly in X and Z directions, and the number of cells in Y-direction is 1, the three-dimensional structural design of the unit cell can be simplified to the two-dimensional plane of XZ. The design variable is the relative density of each mesh element in the design domain, the objective function is to minimize the total strain energy, and the constraints are as follows: (1) The volume fraction constraint is set to 0.6. (2) X-direction stiffness value of the unit cell shall not exceed 1000 N/mm. (3) Z-direction stiffness value of the unit cell shall not exceed 5000 N/mm. Consequently, the expression of the topology optimization model can be mathematically expressed as:

$$ \left\{ \begin{gathered} {\text{find}}\qquad \rho_{e} ,\quad e = 1,2,3, \ldots ,n \hfill \\ {\text{minimizing}}\quad F_{j} = \int\limits_{\Omega } {\frac{1}{2}\sigma \left( {\rho_{e} } \right):\varepsilon {\text{d}}\Omega } \hfill \\ {\text{subjected to}}\quad K_{X} \le 1000\,{\text{N/mm, }}K_{Z} \le 5000\,{\text{N/mm}} \hfill \\ \quad \quad \quad \quad \quad \qquad 0 \le V_{f} \le 0.6 \hfill \\ \end{gathered} \right. $$

(10)

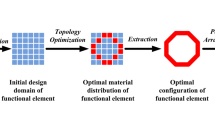
It can be seen in Fig. 2a, by using a contour of $\widetilde{{\widetilde{{\rho_{e} }}}}$ = 0.5, the two-dimensional optimal topology pattern of the unit cell is extracted from the topology optimization results. Then, modeling for two-dimensional pattern of the unit cell with 5 × 2 arrays, the two-dimensional structure of the vibration isolator is obtained. Finally, the overall three-dimensional structure of the metamaterial vibration isolator is established by extruding the two-dimensional structure in the Y-direction for 12 cm as shown in Fig. 2b.

Fig. 2

a The optimized unit cell of the metamaterial vibration isolator and b the overall three-dimensional structure of the metamaterial vibration isolator

Using the FEM of structural mechanics to analyze the overall structure of the metamaterial vibration isolator and the stiffnesses in X and Z directions, the load–displacement curves are obtained as shown in Fig. 3, and the von Mises stress is shown in Fig. 4. Through the analysis of the curve, the lateral stiffness is 2496.9 N/mm and the longitudinal stiffness is 12,497 N/mm. By comparing the stiffnesses of the metamaterial vibration isolator obtained with the target design value of the stiffnesses, the deviation between the design value of X and Z direction stiffnesses of the metamaterial vibration isolator, and the target value is calculated to be 0.124% and 0.024%, respectively.

Fig. 3

Load–displacement curves of the optimized overall metamaterial vibration isolator

Fig. 4

The distribution of von Mises stress (unit: Pa) of the metamaterial vibration isolator

4 Conclusion

In this work, a multi-objective and multi-load-conditions topology optimization model based on SIMP method is developed. The method uses three-direction stiffnesses and strain energies as the optimization objectives, and the different direction stiffnesses are calculated under different loading conditions as the constraint conditions. Innovatively, the design objective of the three-direction stiffnesses is transformed into the constraint conditions. And the overall three-dimensional structure of the metamaterial vibration isolator is eventually periodically established by the methods mentioned above, which has the advantages of withstanding high vertical load and compensating for large lateral displacement. Independent of previous engineering experience, this method can meet different application requirements that cannot be met by traditional patterns, design and obtain a new type of metamaterial vibration isolator with excellent performance, broaden the design range of three-direction stiffnesses of the metamaterial vibration isolator, and improve the vibration isolation effect of the equipment.