1 Introduction

The purpose of engineering optimization is to reduce the cost as much as possible under the condition that the structure meets the required constraints. In practical engineering problems, there are various uncertainties in the boundary conditions, geometric parameters, material properties, and working environment of the structure. And these uncertainties have a great impact on the performance of the designed structure. In this case, if the method under deterministic conditions is used to optimize the structure, the structure is often not robust enough. And the slight perturbation of design parameters may lead the deterministic optimal solution falling into the infeasible region. Thus, design optimization by taking the uncertainty into consideration has been produced one after another (Schuller and Jensen 2008).

Design optimization considering the random uncertainty includes reliability-based design optimization (RBDO) (Papadrakakis and Lagaros 2002) and robust design optimization (RDO) (Park et al. 2006). Compared with deterministic design optimization, RBDO includes structural reliability constraints or reliability-related objective functions (Yao et al. 2011; Youn et al. 2003), while RDO is a design optimization method which takes the most robust performance as the objective under the condition of considering the random uncertainty. At present, RBDO by taking the random uncertainty into consideration has attracted extensive attention in academic research and engineering applications (Chen et al. 2013; Lee et al. 2008; Liang et al. 2004; Du and Chen 2004; Elishakoff 1995). The random uncertainty is described by the probability density function (PDF), and the structural safety degree under the random uncertainty is measured by the failure probability. The structural safety model based on the failure probability is developed very well and applied widely in practical engineering. However, the PDF needs a large number of samples to be estimated accurately, and this requirement is unaffordable usually (Fan et al. 2018). Furthermore, the uncertainties of human behaviors and expertise may have an important effect on the performance of the structure, while these uncertainties cannot be considered to be random (Cremona and Gao 1997). Aiming at solving the issue of random uncertainty, the fuzzy uncertainty theory is developed (Beer and Liebscher 2008; Marano and Quaranta 2008). In the fuzzy uncertainty theory, Zadeh (1978) proposed the possibility and necessity theory based on the fuzzy uncertainty, on which fuzzy uncertainty theory is applied in engineering. Under the fuzzy uncertainty, the fuzzy variable is characterized by membership function, the safety degree of structures can be measured by the failure possibility (FP) (Tzvieli 1990). The FP investigated by Zadeh was defined as the lower bound of the fuzzy safety confidence level, which states that the structure must be safe if the membership degree of the fuzzy input is greater than the FP. Researchers have developed a variety of methods to solve the FP, and the failure possibility based design optimization (PBDO) has been also developed (Utkin et al. 1995). Mourelatos and Zhou (2005) proposed a global-local hybrid optimization method to solve PBDO. Du (2006) et al. established the formulation of PBDO using the performance measure approach (PMA), and proposed the maximal possibility search (MPS) method for inverse possibility analysis, and the PMA improves the numerical efficiency and accuracy of the optimization solution compared with the vertex combination method and the multilevel-cut method. Tang et al. (2014) proposed a possibilistic safety index (PSI)-based design optimization model (PSIBDO). The solution of PSIBDO is a double-loop nested problem of minimizing the objective function and assessing PSI; the assessing PSI is a double-loop nested optimization problem. Thus, PSIBDO is a triple-loop nested problem. To reduce the computation time, Tang proposed a design optimization method based on PMA, which is known as the target performance-based design approach (TPBDA). In the TPBDA, the assessing PSI is replaced by computing the target performance, which is only a minimization problem; thus, the triple-loop nested problem is simplified to the double-loop one, which leads to the reduction of the computational cost of optimization solution and the improvement of the computational efficiency, and furthermore, the numerical stability of the algorithm is better. Wang et al. (2017) established an optimization model of fuzzy heat conduction problem based on the interval safety possibility index. Aiming at the problem of large computational cost caused by the double-loop nested optimization model, a subinterval perturbation method based on first-order Taylor series was proposed in (Wang et al. 2017) to replace the inner nesting for improving the efficiency of design optimization.

It is worth pointing out that the performances of most structures degrade over time in engineering, the structural analysis should take the time t into consideration in many engineering cases. Therefore, it is of great significance to study the design optimization of time-dependent structures under the uncertainty. Time-dependent reliability-based design optimization (T-RBDO) under the random uncertainty has received widespread attention (Kuschel and Rackwitz 2000; Hu and Du 2015; Huang et al. 2017; Jiang et al. 2017; Fang et al. 2019). The solution of T-RBDO is a double-loop nested optimization process, in which the outer loop is the optimization of design parameters and the inner loop is time-dependent reliability analysis. The double-loop nested optimization solution of T-RBDO requires high computational cost. In order to improve the efficiency of solving T-RBDO, Kuschel and Rackwitz (2000) proposed a design optimization method in which the time-dependent reliability in T-PBDO is estimated by the crossing rate method. By defining the equivalent most probable point (MPP) of time-dependent reliability, Hu and Du (2015) extended the decoupling optimization method named as sequential optimization and reliability assessment (SORA) (Du and Chen 2004) in time-independent RBDO to solve the T-RBDO problem, and then, the time-dependent SORA (T-SORA) method was established for solving T-RBDO. In T-SORA, the solution of T-RBDO is divided into two parts: the deterministic optimization of the design parameters and the estimation of the equivalent MPP. These two parts are executed sequentially and decoupled from each other, and this decoupling strategy improves the efficiency of solving T-RBDO. Although there are abundant researches on T-RBDO under the random uncertainty, time-dependent failure possibility-based design optimization (T-PBDO) model and its solution method under the fuzzy uncertainty were rarely investigated in the existing publications. As mentioned above, it is so hard to collect enough test data to get the accurate input probability distributions in the early stages of design. And the fuzzy safety analysis can consider more sources of uncertainty, especially from human behavior and expert evaluations. It is of great significance to design the optimal time-dependent structure satisfying safety requirements under the fuzzy uncertainty. Therefore, this paper focuses on this research of T-PBDO.

At present, there are some methods to estimate the time-dependent failure possibility (TDFP) under the fuzzy uncertainty (Fan et al. 2019; Liu 2010), including double-loop optimization method (DLOM), single-loop optimization method (SLOM), and fuzzy simulation method. Similar to T-RBDO, T-PBDO is also a double-loop nested solution process. The outer loop is the optimization of the design parameters, and the inner loop is the analysis of TDFP. Therefore, it is necessary to study an efficient method to address the double-loop including the time-consuming TDFP analysis in T-PBDO. In this paper, the PMA method proposed in (Du et al. 2006) is extended to the equivalent transformation of the TDFP constraint. Meanwhile, the minimum performance target point (MPTP) is defined corresponding to the target TDFP, and an inverse TDFP analysis method is presented for solving the MPTP. Based on the MPTP through the inverse TDFP analysis, a time-dependent performance measure approach (T-PMA) for solving T-PBDO is proposed. In order to verify the accuracy and efficiency of the proposed method, the solution of the double-loop nested method (DLNM) directly solving T-PBDO is used as a comparison, in which TDFP is estimated by the single-loop optimization.

The rest of this paper is organized as follows. Section 2 reviews the definition of TDFP and the model of T-PBDO. The T-PMA is proposed to solve the T-PBDO in Section 3. Section 4 introduces case studies to verify the accuracy and efficiency of the proposed T-PMA method. Finally, conclusions are drawn in Section 5.

2 The time-dependent possibility-based design optimization model

2.1 The definition of TDFP

Suppose an n-dimensional fuzzy input vector is collected in X = [X1, X2, …, Xn]T, it is characterized by its membership function \( {\rho}_{X_i}\left({x}_i\right)\left(i=1,2,\dots, n\right) \). And it is assumed that the time-dependent performance function is Z(t) = g(X, t) with the n-dimensional fuzzy input vector X in the time domain t ∈ [t0, te] of interest. Because the time-dependent performance function Z(t) = g(X, t) is a function of the fuzzy input vector X and the time variable t, Z(t) is a time-dependent fuzzy variable, i.e., the membership function ρZ(z) of Z(t) varies with time. For the time-dependent performance function g(X, t) in the time domain t ∈ [t0, te] of interest, the structure is failed as long as there exists at least one instant t ∈ [t0, te] satisfying g(X, t) ≤ 0. Therefore, the time-dependent failure domain in the time domain t ∈ [t0, te] of interest can be denoted as F(t0, te) = {X| g(X, t) ≤ 0, ∃t ∈ [t0, te]}, and S(t0, te) = {X| g(X, t) > 0, ∀t ∈ [t0, te]} defines the corresponding time-dependent safety domain.

For time-dependent problems, the TDFP defined in Ref. (Fan et al. 2019) is the possibility of the failure occurrence in a given time domain [t0, te], which can be expressed as follows.

$$ {\pi}_f\left({t}_0,{t}_e\right)= Poss\left\{\boldsymbol{X}\in F\left({t}_0,{t}_e\right)\right\}= Sup\left\{\alpha |g\left(\boldsymbol{X}\left(\alpha \right),t\right)\le 0,\exists t\in \left[{t}_0,{t}_e\right]\right\} $$
(1)

where Poss{⋅} and Sup{⋅} are the possibility operator and the supremum operator respectively. α represents the membership level of Z(t) = g(X(α), t) and α ∈ [0, 1]. X(α) is the membership interval vector of the fuzzy input vector X under the membership level α and X(α) ∈ [XL(α), XU(α)] , where \( {\boldsymbol{X}}^U\left(\alpha \right)=\left\{{X}_1^U\left(\alpha \right),{X}_2^U\left(\alpha \right),\dots, {X}_n^U\left(\alpha \right)\right\} \) and \( {\boldsymbol{X}}^L\left(\alpha \right)=\left\{{X}_1^L\left(\alpha \right),{X}_2^L\left(\alpha \right),\dots, {X}_n^L\left(\alpha \right)\right\} \) are the upper and lower bound vectors of the membership interval of the fuzzy input vector with respect to the membership level α respectively, and \( {X}_i^U\left(\alpha \right)=\max\ {\rho}_{X_i}^{-1}\left(\alpha \right) \), \( {X}_i^L\left(\alpha \right)=\min\ {\rho}_{X_i}^{-1}\left(\alpha \right) \), \( {\rho}_{X_i}^{-1}\left(\cdot \right) \) is the inverse function of MF of \( {\rho}_{X_i}\left(\cdot \right)\ \left(i=1,2,\dots, n\right) \).

It can be seen from the above definition that the TDFP is the upper bound of membership level of time-dependent performance function under the condition of failure. That is to say, when the membership level of the time-dependent performance function is greater than the TDFP, the structure is safe in the time domain t ∈ [t0, te]. Therefore, πf (t0, te) is the maximum possibility of the structure under the fuzzy uncertainty when the failure occurs, which can be used to measure the safety degree of time-dependent structure under the fuzzy uncertainty.

The necessary and sufficient condition for the failure occurrence of the time-dependent structure is that there at least exists an instant t satisfying g(X, t) ≤ 0 in the time domain [t0, te] of interest, while \( \left\{\underset{t\in \left[{t}_0,{t}_e\right]}{\min }g\left(\boldsymbol{X},t\right)\le 0\right\} \) means that there exists at least one instant t satisfying g(X, t) ≤ 0; thus, the time-dependent failure domain can be also expressed as \( F\left({t}_0,{t}_e\right)=\left\{\boldsymbol{X}|\left\{\underset{t\in \left[{t}_0,{t}_e\right]}{\min }g\left(\boldsymbol{X},t\right)\le 0\right\}\right\} \). Let gmin(X) denote \( \underset{t\in \left[{t}_0,{t}_e\right]}{\min }g\left(\boldsymbol{X},t\right) \), then the time-dependent failure possibility πf (t0, te) can be expressed as follows.

$$ {\pi}_f\left({t}_0,{t}_e\right)= Poss\left\{{g}_{\mathrm{min}}\left(\boldsymbol{X}\right)\le 0\right\}= Sup\left\{\alpha |{g}_{\mathrm{min}}\left(\boldsymbol{X}\right)\le 0\right\} $$
(2)

For a given time interval [t0, te], the expression gmin(X) is independent of the time t. Therefore, (2) transforms the estimation of TDFP into the estimation of time-independent failure possibility of the minimum time-dependent performance function with respect to the time.

2.2 The T-PBDO model and its time-independent expression

The T-PBDO model can be formulated as follows,

$$ {\displaystyle \begin{array}{cc}\underset{d,{\boldsymbol{\mu}}_{\boldsymbol{X}}}{\min }& f\left(d,{\boldsymbol{\mu}}_{\boldsymbol{X}}\right)\\ {}s.t.& {\pi}_{fj}\left({t}_0,{t}_e\right)= Poss\left\{{g}_j\left(\boldsymbol{d},\boldsymbol{X},t\right)\le 0,\exists t\in \left[{t}_0,{t}_e\right]\right\}\le {\pi}_{fj}^{tar}\left(j=1,2,\dots, {n}_g\right)\\ {}& {\boldsymbol{d}}^L\le \boldsymbol{d}\le {\boldsymbol{d}}^U,{\boldsymbol{\mu}}_{\boldsymbol{X}}^L\le {\boldsymbol{\mu}}_{\boldsymbol{X}}\le {\boldsymbol{\mu}}_{\boldsymbol{X}}^U\end{array}} $$
(3)

where f(d, μX) represents the objective function, gj(d, X, t)(j = 1, 2, …, ng) is the time-dependent performance function of the j-th constraint, and \( {\pi}_{fj}^{tar} \) is the target TDFP corresponding to the j-th constraint. ng is the number of the TDFP constraint. d means an nd-dimensional deterministic design parameter vector with the lower bound dL and upper bound dU respectively. μX is the design parameter vector of the fuzzy input vector X, μX is usually composed of the kernel of membership function \( {\rho}_{X_i}\left({x}_i\right)\left(i=1,2,\dots, n\right) \) of each input Xi in X, and the upper and lower bound vectors of μX are \( {\boldsymbol{\mu}}_{\boldsymbol{X}}^U \) and \( {\boldsymbol{\mu}}_{\boldsymbol{X}}^L \) respectively.

According to (2), by converting the time-dependent performance function in the above optimization model into the minimum performance function, the T-PBDO model can be transformed into a time-independent design optimization model shown in the following (4).

$$ {\displaystyle \begin{array}{cc}\underset{\boldsymbol{d},{\boldsymbol{\mu}}_{\boldsymbol{X}}}{\min }& f\left(\boldsymbol{d},{\boldsymbol{\mu}}_{\boldsymbol{X}}\right)\\ {}s.t.& {\pi}_{fj}\left({t}_0,{t}_e\right)= Poss\left\{{g}_{j\min}\left(\boldsymbol{d},\boldsymbol{X}\right)\le 0\right\}\le {\pi}_{fj}^{tar}\left(j=1,2,\dots, {n}_g\right)\\ {}& {\boldsymbol{d}}^L\le \boldsymbol{d}\le {\boldsymbol{d}}^U,{\boldsymbol{\mu}}_{\boldsymbol{X}}^L\le {\boldsymbol{\mu}}_{\boldsymbol{X}}\le {\boldsymbol{\mu}}_{\boldsymbol{X}}^U\end{array}} $$
(4)

where \( {g}_{j\min}\left(\boldsymbol{d},\boldsymbol{X}\right)=\underset{t\in \left[{t}_0,{t}_e\right]}{\min }{g}_j\left(\boldsymbol{d},\boldsymbol{X},t\right)\left(j=1,2,\dots, {n}_g\right) \).

According to (3) and (4), it is shown that the T-PBDO is a double-loop nested process, the outer loop is the optimization of the design parameters, and the inner loop is the estimation of TDFP, i.e., the estimation of TDFP is embedded in each optimization cycle. At present, there are double-loop optimization method (DLOM) and single-loop optimization method (SLOM) to estimate the TDFP. The direct solution of T-PBDO is also a double-loop nested problem including minimizing the objective function and assessing the TDFP. Therefore, by coupling the DLOM or SLOM into the direct solution of T-PBDO for assessing TDFP, the direct solution of T-PBDO by combining the optimization cycle of outer design parameters with the estimation of the TDFP is a triple-loop or double-loop nested problem, which is time-consuming, especially for the problem that the performance function of the engineering structure is implicit expression and needs to call the finite element software. The method of directly solving the T-PBDO shown in (3) is the double-loop nested method (DLNM), in which TDFP is estimated by the SLOM. In the DLNM, the outer loop is the optimization of design parameters and the inner loop is the evaluation of TDFP.

3 The T-PMA for solving the T-PBDO

3.1 Equivalent transformation of TDFP constraint and its rationality proof

The key idea of the T-PMA is to replace the target TDFP constraint with a simplified equivalent constraint, which was proposed in (Du et al. 2006), i.e., the TDFP constraint \( {\pi}_{fj}= Poss\left\{{g}_{j\min}\left(\boldsymbol{d},\boldsymbol{X}\right)\le 0\right\}\le {\pi}_{fj}^{tar} \) can be replaced by the lower bound \( {g}_{j\min}^L\left(\boldsymbol{d},\boldsymbol{x}\left({\pi}_{fj}^{tar}\right)\right) \) of the minimum performance function \( {g}_{j\min}\left(\boldsymbol{d},\boldsymbol{x}\left({\pi}_{fj}^{tar}\right)\right) \) corresponding to the target TDFP \( {\pi}_{fj}^{tar} \) not less than zero, and the equivalent transformation is shown as follows.

$$ {\pi}_{fj}= Poss\left\{{g}_{j\min}\left(\boldsymbol{d},\boldsymbol{X}\right)\le 0\right\}\le {\pi}_{fj}^{tar}\iff {g}_{j\min}^L\left(\boldsymbol{d},\boldsymbol{x}\left({\pi}_{fj}^{tar}\right)\right)\ge 0 $$
(5)

where \( \boldsymbol{x}\left({\pi}_{fj}^{tar}\right) \) is the membership interval vector of the fuzzy input vector X under the membership level of the target TDFP \( {\pi}_{fj}^{tar} \). Because \( \boldsymbol{x}\left({\pi}_{fj}^{tar}\right) \) is an interval vector, the minimum performance function \( {g}_{j\min}\left(\boldsymbol{d},\boldsymbol{x}\left({\pi}_{fj}^{tar}\right)\right) \) related to \( \boldsymbol{x}\left({\pi}_{fj}^{tar}\right) \) corresponding to the j-th constraint is also an interval, and its lower bound and upper bound are denoted by \( {g}_{j\min}^L\left(\boldsymbol{d},\boldsymbol{x}\left({\pi}_{fj}^{tar}\right)\right) \) and \( {g}_{j\min}^U\Big(\boldsymbol{d},\boldsymbol{x}\left({\pi}_{fj}^{tar}\right) \) respectively.

Figure 1 shows the equivalence of the two constraints in (5). Three curves in the Fig. 1 represent three cases of the membership function of the j-th minimum performance function gjmin respectively. In Fig. 1, \( {g}_{j\min}^{ki}\left(\boldsymbol{d},\boldsymbol{x}\left({\pi}_{fj}^{tar}\right)\right)\left(k=L,U,i=a,b,c\right) \) respectively represent \( {g}_{j\min}\left(\boldsymbol{d},\boldsymbol{x}\left({\pi}_{fj}^{tar}\right)\right) \)corresponding to the k(k = L, U) boundary of the i-th(i = a, b, c) curve. And \( {\pi}_{fj}^i\left(i=a,b,c\right) \) are the TDFP of i-th(i = a, b, c) curve respectively. The equivalence of the above (5) is explained in (Du et al. 2006). In order to make it more rigorous, this study gives the proof of equivalence in (5) by using absurdity method.

Fig. 1
figure 1

The sketch of the equivalent constraint

Full size image

The following two steps are used to prove the equivalence in (5). The first step is to prove that \( {\pi}_{fj}= Poss\left\{{g}_{j\min}\left(\boldsymbol{d},\boldsymbol{X}\right)\le 0\right\}={\pi}_{fj}^{tar} \) and \( {g}_{j\min}^L\left(\boldsymbol{d},\boldsymbol{x}\left({\pi}_{fj}^{tar}\right)\right)=0 \) is equivalent, and the second step is to prove that \( {\pi}_{fj}= Poss\left\{{g}_{j\min}\left(\boldsymbol{d},\boldsymbol{X}\right)\le 0\right\}<{\pi}_{fj}^{tar} \) and \( {g}_{j\min}^L\left(\boldsymbol{d},\boldsymbol{x}\left({\pi}_{fj}^{tar}\right)\right)>0 \) is equivalent.

  • Step 1: The proof of the equivalence between \( {\pi}_{fj}= Poss\left\{{g}_{j\min}\left(\boldsymbol{d},\boldsymbol{X}\right)\le 0\right\}={\pi}_{fj}^{tar} \) and \( {g}_{j\min}^L\left(\boldsymbol{d},\boldsymbol{x}\left({\pi}_{fj}^{tar}\right)\right)=0 \)

Assuming that the target TDFP \( {\pi}_{fj}^{tar} \) constraint \( {\pi}_{fj}= Poss\left\{{g}_{j\min}\left(\boldsymbol{d},\boldsymbol{X}\right)\le 0\right\}={\pi}_{fj}^{tar} \) and the lower bound constraint of the minimum performance function \( {g}_{j\min}^L\left(\boldsymbol{d},\boldsymbol{x}\left({\pi}_{fj}^{tar}\right)\right)=0 \) are not equivalent, then one of the following two cases holds.

  • Case 1

$$ {\pi}_{fj}= Poss\left\{{g}_{j\min}\left(\boldsymbol{d},\boldsymbol{X}\right)\le 0\right\}={\pi}_{fj}^{tar}\iff {g}_{j\min}^L\left(\boldsymbol{d},\boldsymbol{x}\left({\pi}_{fj}^{tar}\right)\right)<0 $$
(6)

  • Case 2

$$ {\pi}_{fj}= Poss\left\{{g}_{j\min}\left(\boldsymbol{d},\boldsymbol{X}\right)\le 0\right\}={\pi}_{fj}^{tar}\iff {g}_{j\min}^L\left(\boldsymbol{d},\boldsymbol{x}\left({\pi}_{fj}^{tar}\right)\right)>0 $$
(7)

Case 1 and case 2 correspond to the case of curve (a) and curve (c) in Fig. 1 respectively. As shown in Fig. 1, for case 1, the inequality \( {\pi}_{fj}>{\pi}_{fj}^{tar} \) holds, and for case 2, the inequality \( {\pi}_{fj}<{\pi}_{fj}^{tar} \) holds. Obviously, (6) and (7) are contradictory to \( {\pi}_{fj}={\pi}_{fj}^{tar} \); thus, \( {\pi}_{fj}= Poss\left\{{g}_{j\min}\left(\boldsymbol{d},\boldsymbol{X}\right)\le 0\right\}={\pi}_{fj}^{tar} \) and \( {g}_{j\min}^L\left(\boldsymbol{d},\boldsymbol{x}\left({\pi}_{fj}^{tar}\right)\right)=0 \) are equivalent, that is, the following equivalent relation holds.

$$ {\pi}_{fj}= Poss\left\{{g}_{j\min}\left(\boldsymbol{d},\boldsymbol{X}\right)\le 0\right\}={\pi}_{fj}^{tar}\iff {g}_{j\min}^L\left(\boldsymbol{d},\boldsymbol{x}\left({\pi}_{fj}^{tar}\right)\right)=0 $$
(8)

  • Step 2: The proof of equivalence between \( {\pi}_{fj}= Poss\left\{{g}_{j\min}\left(\boldsymbol{d},\boldsymbol{X}\right)\le 0\right\}<{\pi}_{fj}^{tar} \) and \( {g}_{j\min}^L\left(\boldsymbol{d},\boldsymbol{x}\left({\pi}_{fj}^{tar}\right)\right)>0 \)

Similar to the step 1, it is assumed that the target TDFP \( {\pi}_{fj}^{tar} \) constraint \( {\pi}_{fj}= Poss\left\{{g}_{j\min}\left(\boldsymbol{d},\boldsymbol{X}\right)\le 0\right\}<{\pi}_{fj}^{tar} \) and the lower bound constraint of the minimum performance function \( {g}_{j\min}^L\left(\boldsymbol{d},\boldsymbol{x}\left({\pi}_{fj}^{tar}\right)\right)>0 \) are not equivalent. From the step 1, it has been proved that the equivalence between \( {\pi}_{fj}= Poss\left\{{g}_{j\min}\left(\boldsymbol{d},\boldsymbol{X}\right)\le 0\right\}={\pi}_{fj}^{tar} \) and \( {g}_{j\min}^L\left(\boldsymbol{d},\boldsymbol{x}\left({\pi}_{fj}^{tar}\right)\right)=0 \) is tenable. Therefore, from the fact that \( {\pi}_{fj}<{\pi}_{fj}^{tar} \) and \( {g}_{j\min}^L\left(\boldsymbol{d},\boldsymbol{x}\left({\pi}_{fj}^{tar}\right)\right)>0 \) are not equivalent, it can be deduced that the following condition must be true, namely,

$$ {\pi}_{fj}= Poss\left\{{g}_{j\min}\left(\boldsymbol{d},\boldsymbol{X}\right)\le 0\right\}<{\pi}_{fj}^{tar}\iff {g}_{j\min}^L\left(\boldsymbol{d},\boldsymbol{x}\left({\pi}_{fj}^{tar}\right)\right)<0 $$
(9)

Equation (9) corresponds to the case of curve (a), that is \( {\pi}_{fj}>{\pi}_{fj}^{tar} \), which is obviously contradictory to \( {\pi}_{fj}<{\pi}_{fj}^{tar} \), so we can deduce that \( {\pi}_{fj}= Poss\left\{{g}_{j\min}\left(\boldsymbol{d},\boldsymbol{X}\right)\le 0\right\}<{\pi}_{fj}^{tar} \) and \( {g}_{j\min}^L\left(\boldsymbol{d},\boldsymbol{x}\left({\pi}_{fj}^{tar}\right)\right)>0 \) are equivalent, i.e., the following equivalent relation holds.

$$ {\pi}_{fj}= Poss\left\{{g}_{j\min}\left(\boldsymbol{d},\boldsymbol{X}\right)\le 0\right\}<{\pi}_{fj}^{tar}\iff {g}_{j\min}^L\left(\boldsymbol{d},\boldsymbol{x}\left({\pi}_{fj}^{tar}\right)\right)>0 $$
(10)

Based on the conclusion of the step 1 and the step 2, the constraint equivalence shown in (5) is proved.

3.2 The T-PMA for solving the T-PBDO under the fuzzy uncertainty

For the T-PBDO model in (4), through the constraint equivalent transformation in (5), i.e., the TDFP constraint is replaced by the lower bound constraint of the minimum performance function corresponding to the target TDFP, it can be transformed into the design optimization model under the time-dependent performance measure constraint shown as follows.

$$ {\displaystyle \begin{array}{cc}\underset{d,{\boldsymbol{\mu}}_{\boldsymbol{X}}}{\min }& f\left(\boldsymbol{d},{\boldsymbol{\mu}}_{\boldsymbol{X}}\right)\\ {}s.t.& {g}_{j\min}^L\left(\boldsymbol{d},\boldsymbol{x}\left({\pi}_{fj}^{tar}\right)\right)\ge 0\left(j=1,2,\dots, {n}_g\right)\\ {}& {\boldsymbol{d}}^L\le \boldsymbol{d}\le {\boldsymbol{d}}^U,{\boldsymbol{\mu}}_{\boldsymbol{X}}^L\le {\boldsymbol{\mu}}_{\boldsymbol{X}}\le {\boldsymbol{\mu}}_{\boldsymbol{X}}^U\end{array}} $$
(11)

Equation (11) is called the optimization model based on T-PMA corresponding to the optimization model under the constraint of the target TDFP. Comparing (4) and (11), it can be seen that the complicate target TDFP constraint in (4) is transformed into the simple lower bound constraint of the minimum performance function with respect to \( {\pi}_{fj}^{tar} \) in (11), which simplifies the solution of the optimization model. In the equivalent constraint, only the minimum performance function under the necessary membership level with respect to the target TDFP \( {\pi}_{fj}^{tar} \) is needed to analyze, and this strategy can improve the numerical stability and computational efficiency of the optimization solution.

3.3 Analysis of the constraint function in T-PMA

\( {g}_{j\min}^L\left(\boldsymbol{d},\boldsymbol{x}\left({\pi}_{fj}^{tar}\right)\right) \) in the optimization model (11) is solved by the following optimization model,

$$ {\displaystyle \begin{array}{cc}\min & {g}_{j\min}\left(\boldsymbol{d},\boldsymbol{x}\left({\pi}_{fj}^{tar}\right)\right)\\ {}s.t.& \boldsymbol{x}\left({\pi}_{fj}^{tar}\right)\in \left[{\boldsymbol{x}}^L\left({\pi}_{fj}^{tar}\right),{\boldsymbol{x}}^U\left({\pi}_{fj}^{tar}\right)\right]\kern0.75em \left(j=1,2,..,{n}_g\right)\end{array}} $$
(12)

where \( {\boldsymbol{x}}^U\left({\pi}_{fj}^{tar}\right) \) and \( {\boldsymbol{x}}^L\left({\pi}_{fj}^{tar}\right) \) are the upper and lower bound vectors of the membership interval of the fuzzy input vector with respect to the target TDFP \( {\pi}_{fj}^{tar} \) respectively. The interval vector \( \boldsymbol{x}\left({\pi}_{fj}^{tar}\right)=\left\{{x}_1\left({\pi}_{fj}^{tar}\right),{x}_2\left({\pi}_{fj}^{tar}\right),\dots, {x}_n\left({\pi}_{fj}^{tar}\right)\right\} \) can be further standardized as follows.

$$ {u}_i^{(j)}=\frac{x_i\left({\pi}_{fj}^{tar}\right)-\left(\frac{x_i^L\left({\pi}_{fj}^{tar}\right)+{x}_i^U\left({\pi}_{fj}^{tar}\right)}{2}\right)}{\frac{x_i^U\left({\pi}_{fj}^{tar}\right)-{x}_i^L\left({\pi}_{fj}^{tar}\right)}{2}},\left(i=1,2,\dots, n,j=1,2,..,{n}_g\right) $$
(13)

where \( {x}_i\left({\pi}_{fj}^{tar}\right)\in \left[{x}_i^L\left({\pi}_{fj}^{tar}\right),{x}_i^U\left({\pi}_{fj}^{tar}\right)\right] \) is the membership interval variable with respect to \( {\pi}_{fj}^{tar} \) of the i-th dimension fuzzy variable. \( \frac{x_i^L\left({\pi}_{fj}^{tar}\right)+{x}_i^U\left({\pi}_{fj}^{tar}\right)}{2} \) and \( \frac{x_i^U\left({\pi}_{fj}^{tar}\right)-{x}_i^L\left({\pi}_{fj}^{tar}\right)}{2} \) are the mean value and deviation of the i-th dimension interval variable \( {x}_i\left({\pi}_{fj}^{tar}\right) \) respectively.

For the standardized variable \( {u}_i^{(j)} \) obtained by (13), it is obvious that \( {u}_i^{(j)}\in \left[-1,1\right] \) holds, i.e., \( {\left({u}_i^{(j)}\right)}^2\le 1 \). By use of the standardization in (13), (12) can be rewritten into the following form in the standardized interval space u(j).

$$ {\displaystyle \begin{array}{cc}\min & {G}_{j\min}\left(\boldsymbol{d},{\boldsymbol{u}}^{(j)}\right)\\ {}s.t.&\ {\left({u}_i^{(j)}\right)}^2\le 1\kern0.75em \left(i=1,2,\dots, n,j=1,2,..,{n}_g\right)\\ {}& {\boldsymbol{u}}^{(j)}=\left\{{u}_1^{(j)},{u}_2^{(j)},\dots, {u}_n^{(j)}\right\}\end{array}} $$
(14)

where Gjmin(d, u(j)) is the match of the j-th minimum performance function \( {g}_{j\min}\left(\boldsymbol{d},\boldsymbol{x}\left({\pi}_{fj}^{tar}\right)\right) \) in the standard interval space, and u(j) is the standard interval vector corresponding to \( \boldsymbol{x}\left({\pi}_{fj}^{tar}\right) \).

The optimization result of (14) is defined as the minimum performance target point (MPTP) corresponding to \( {\pi}_{fj}^{tar} \), and it is denoted as \( {\boldsymbol{u}}_{MPTP}^{(j)} \), namely,

$$ {\boldsymbol{u}}_{MPTP}^{(j)}=\arg \underset{{\left({u}_i^{(j)}\right)}^2\le 1}{\min }{G}_{j\min}\left(\boldsymbol{d},{\boldsymbol{u}}^{(j)}\right)\ \left(\ j=1,2,\dots, {n}_g,i=1,2,\dots, n\right) $$
(15)

Then, the time instant \( {t}_{\mathrm{min}}^{(j)} \) corresponding to \( {\boldsymbol{u}}_{MPTP}^{(j)} \) can be obtained by the following formula,

$$ {t}_{\mathrm{min}}^{(j)}=\arg \underset{t\in \left[{t}_0,{t}_e\right]}{\min }{G}_j\left(\boldsymbol{d},{\boldsymbol{u}}_{MPTP}^{(j)},t\right) $$
(16)

where \( {G}_j\left(\boldsymbol{d},{\boldsymbol{u}}_{MPTP}^{(j)},t\right) \) is the counterpart of the j-th time-dependent performance function \( {g}_j\left(\boldsymbol{d},{\boldsymbol{x}}_{MPTP}^{(j)},t\right) \) in the standard interval space, in which \( {\boldsymbol{x}}_{MPTP}^{(j)} \) is the match of \( {\boldsymbol{u}}_{MPTP}^{(j)} \) transformed by (13).

From the above analysis, the time-dependent performance measure approach (T-PMA) transforms the T-PBDO into double-loop nested optimization of (11) and (14). In an iteration process, the outer loop optimizes the design parameters, while the inner loop solves the MPTP \( {\boldsymbol{u}}_{MPTP}^{(j)} \) and the time instant \( {t}_{\mathrm{min}}^{(j)} \) corresponding to \( {\pi}_{fj}^{tar} \) under the given design parameters to judge the feasibility. Because the T-PMA avoids estimating the performance function under the unnecessary membership level except the target TDFP \( {\pi}_{fj}^{tar} \), its solving efficiency is higher than that of the direct solution of the T-PBDO. Solving the MPTP \( {\boldsymbol{u}}_{MPTP}^{(j)} \) and the corresponding time instant \( {t}_{\mathrm{min}}^{(j)} \) is the inverse process of solving the TDFP. The next subsection will give the solution of the inverse analysis of the TDFP.

3.4 An inverse analysis method of the TDFP for solving the MPTP and its corresponding time instant

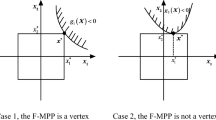
Figure 2 shows three cases of the minimum performance function minGjmin(d, u(j)) in a two-dimensional standard interval coordinate space. As shown in Fig. 2 and according to (5), if \( {g}_{j\min}^L\left(\boldsymbol{d},\boldsymbol{x}\left({\pi}_{fj}^{tar}\right)\right)=\min {G}_{j\min}\left(\boldsymbol{d},{\boldsymbol{u}}^{(j)}\right)<0 \), then \( {\pi}_{fj}>{\pi}_{fj}^{tar} \) (where πfj is the TDFP under the current design parameters), and if \( {g}_{j\min}^L\left(\boldsymbol{d},\boldsymbol{x}\left({\pi}_{fj}^{tar}\right)\right)=\min {G}_{j\min}\left(\boldsymbol{d},{\boldsymbol{u}}^{(j)}\right)\ge 0 \), then \( {\pi}_{fj}\le {\pi}_{fj}^{tar} \).

Fig. 2
figure 2

Three cases of the minimum performance function minGjmin(d, u(j)) in the standard interval space

Full size image

According to the joint analysis of (5) and (14), it can be deduced that \( {\pi}_{fj}={\pi}_{fj}^{tar} \) if \( {g}_{j\min}^L\left(\boldsymbol{d},\boldsymbol{x}\left({\pi}_{fj}^{tar}\right)\right)=\min {G}_{j\min}\left(\boldsymbol{d},{\boldsymbol{u}}^{(j)}\right)=0 \), and the optimal solution is obtained at the boundary of \( {\pi}_{fj}={\pi}_{fj}^{tar} \). Thus, the MPTP \( {\boldsymbol{u}}_{MPTP}^{(j)} \) should locate on the boundary of the standard interval space, i.e., the MPTP \( {\boldsymbol{u}}_{MPTP}^{(j)} \) is on the hypercube with side length of 2. Figure 3 gives the diagram of the MPTP in a two-dimensional standard interval coordinate space.

Fig. 3
figure 3

The diagram of the MPTP in the standard interval coordinate space

Full size image

The boundary of the hypercube with the side length of 2 can be expressed by ‖u(j)‖∞ = 1 (‖⋅‖∞ represents the infinite norm), then the optimal result of (15) can be searched in a smaller range ‖u(j)‖∞ = 1, i.e., (15) can be expressed in the form of (17).

$$ {\boldsymbol{u}}_{MPTP}^{(j)}=\arg \underset{{\left\Vert {\boldsymbol{u}}^{(j)}\right\Vert}_{\infty }=1}{\min }{G}_{j\min}\left(\boldsymbol{d},{\boldsymbol{u}}^{(j)}\right)\ \left(j=1,2,\dots, {n}_g\right) $$
(17)

Compared with (15), (17) only needs to find the MPTP on the boundary of ‖u(j)‖∞ = 1, it can improve the computational efficiency of estimating the MPTP. The inverse analysis of TDFP includes solving the MPTP and its corresponding time instant. The time instant \( {t}_{\mathrm{min}}^{(j)} \) corresponding to \( {g}_{j\min}\left(\boldsymbol{x}\right)=\underset{t\in \left[{t}_0,{t}_e\right]}{\min }{g}_j\left(\boldsymbol{x},t\right) \) changes with different input variables; thus, the estimation of \( {\boldsymbol{u}}_{MPTP}^{(j)} \) and \( {t}_{\mathrm{min}}^{(j)} \) is a double-loop optimization problem. The outer loop estimates the time instant corresponding to the MPTP, and the inner loop searches the MPTP at the given time instant.

$$ \left\{\begin{array}{l}{t}_{\mathrm{min}}^{(j)}=\arg \underset{t\in \left[{t}_0,{t}_e\right]}{\min }{G}_j\left(\boldsymbol{d},{\boldsymbol{u}}_{MPTP}^{(j)},t\right)\\ {}{\boldsymbol{u}}_{MPTP}^{(j)}=\arg \underset{{\left\Vert {\boldsymbol{u}}^{(j)}\right\Vert}_{\infty }=1}{\min }{G}_j\left(\boldsymbol{d},{\boldsymbol{u}}^{(j)},t\right)\end{array}\right. $$
(18)

It can be seen from the above formula that directly solving \( {\boldsymbol{u}}_{MPTP}^{(j)} \) and \( {t}_{\mathrm{min}}^{(j)} \) is a double loop nested optimization problem, which requires large computational cost. It is well known that the computational complexity of solving this single-loop optimization problem is extremely low compared with that of the double-loop optimization problem (Feng et al. 2019). Therefore, this process can also be replaced by the following single-loop optimization problem shown in (19).

$$ \left({\boldsymbol{u}}_{MPTP}^{(j)},{t}_{\mathrm{min}}^{(j)}\right)=\arg\ \underset{{\left\Vert {\boldsymbol{u}}^{(j)}\right\Vert}_{\infty }=1}{\overset{t\in \left[{t}_0,{t}_e\right]}{\min }}{G}_j\left(\boldsymbol{d},{\boldsymbol{u}}^{(j)},t\right)\ \left(j=1,2,\dots, {n}_g\right) $$
(19)

Combining the basic principle of T-PMA and the analysis of its constraint function, the design optimization model based on T-PMA under fuzzy uncertainty can be expressed as the following (20),

$$ {\displaystyle \begin{array}{cc}\underset{\boldsymbol{d},{\boldsymbol{\mu}}_{\boldsymbol{X}}}{\min }& f\left(\boldsymbol{d},{\boldsymbol{\mu}}_{\boldsymbol{X}}\right)\\ {}\mathrm{s}.\mathrm{t}.& {g}_j\left(\boldsymbol{d},{\boldsymbol{x}}_{MPTP}^{(j)},{t}_{\mathrm{min}}^{(j)}\right)\ge 0\left(j=1,2,\dots, {n}_g\right)\\ {}& {\boldsymbol{d}}^L\le \boldsymbol{d}\le {\boldsymbol{d}}^U,{\boldsymbol{\mu}}_{\boldsymbol{X}}^L\le {\boldsymbol{\mu}}_{\boldsymbol{X}}\le {\boldsymbol{\mu}}_{\boldsymbol{X}}^U\end{array}} $$
(20)

where \( {\boldsymbol{x}}_{MPTP}^{(j)} \) is the mapping of the MPTP \( {\boldsymbol{u}}_{MPTP}^{(j)} \) obtained in the standardized interval space corresponding to the target TDFP \( {\pi}_{fj}^{tar} \) in the original coordinate space. \( {t}_{\mathrm{min}}^{(j)} \) is the time instant corresponding to the MPTP \( {\boldsymbol{u}}_{MPTP}^{(j)} \), \( {\boldsymbol{u}}_{MPTP}^{(j)} \), and \( {t}_{\mathrm{min}}^{(j)} \) are obtained from the corresponding inverse TDFP analysis. The specific inverse TDFP analysis is realized by solving the single-loop optimization model shown in (19).

4 Case studies

In this section, a numerical and three engineering case studies are introduced and compared with DLNM to verify the feasibility and efficiency of the proposed T-PMA. The proposed T-PMA involves two major types: (a) searching the MPTP by single-loop optimization (T-PMA_SL), and (b) searching the MPTP by double-loop optimization (T-PMA_DL). The comparative analysis of T-PMA and DLNM is mainly based on T-PMA_SL. In the case studies, the membership function of the fuzzy input variable is assumed to be the normal type. The membership functions of the normal type and other common types are given in the appendix. And the optimization problems expressed by (18), (19), and (20) are solved by the active set algorithm available in the MATLAB.

4.1 Numerical case study

Suppose the T-PBDO problem with the following form,

$$ {\displaystyle \begin{array}{cc}\min &\;f\left({\boldsymbol{\mu}}_X\right)={\mu}_{X_1}+{\mu}_{X_2}\\ {}\mathrm{s}.\mathrm{t}.& Poss\left\{{g}_j\left(\boldsymbol{X},t\right)\le 0\kern1em \exists t\in \left[{t}_0,{t}_e\right]\right\}\le {\pi}_{fj}^{tar}\left(j=1,2,3\right)\\ {}& {g}_1\left(\boldsymbol{X},t\right)={X}_1^2{X}_2-5{X}_1\sin (t)+\left({X}_2+1\right){\sin}^2\left(t/8\right)-10\\ {}& {g}_2\left(\boldsymbol{X},t\right)=\frac{{\left({X}_1+{X}_2-0.1t-5\right)}^2}{30}+\frac{{\left({X}_1-{X}_2+0.2t-12\right)}^2}{120}-2\\ {}& {g}_3\left(\boldsymbol{X},t\right)=\frac{90}{{\left({X}_1+0.05t\right)}^2+8\left({X}_2+0.1t\right)-\sin t+5}-1\\ {}& 0\le {\mu}_{X_i}\le 10\left(i=1,2\right),{\pi}_{fj}^{tar}=0.1\left(j=1,2,3\right)\end{array}} $$
(21)

in which t denotes the time variable within the interval t ∈ [0, 5], and X1 and X2 are the fuzzy input variables whose membership functions are normal. The parameters of the fuzzy input variables are shown in Table 1.

Table 1 The distribution parameters of the fuzzy variables of numerical case study
Full size table

Take the initial design parameter vector as \( {\boldsymbol{\mu}}_{\boldsymbol{X}}^{(0)}=\left[{\mu}_{X_1}^{(0)},{\mu}_{X_2}^{(0)}\right]=\left[2.2,7.1\right] \), the design parameters obtained by DLNM and T-PMA (including the T-PMA_DL and the T-PMA_SL) and the TDFPs of the constraint functions under the convergence of the optimization are summarized in Table 2. The computational cost and total iteration numbers of the three methods are given in Table 3. The computational cost in Table 3 involves all the necessary calls of the constraint functions and objective functions. In this paper, the convergent condition is that the minimum values of all constraints functions is greater than 10−6 or the relative difference between the objective functions of two adjacent iterations is less than 10−6, and this convergent criterion is applicable to all the case studies. Figure 4 shows a comparison of the iterative history for DLNM and T-PMA.

Table 2 Design parameter solutions of numerical case study
Full size table
Table 3 Computational cost of numerical case study
Full size table
Fig. 4
figure 4

Constraint situations after optimal solutions

Full size image

It can be seen from Table 2 that the results of the three methods are basically consistent. The optimal results of DLNM show that the T-PMA_DL and the T-PMA_SL are accurate and effective. The difference between the T-PMA_DL and the T-PMA_SL is in solving the MPTP, while the iterative process and the optimal results of the two methods for solving T-PBDO are consistent. Compared with the T-PMA_DL, the total computational cost of calling constraint functions in the T-PMA_SL is less, which illustrates that searching the MPTP by single-loop optimization is more efficient than by double-loop optimization. Therefore, the inverse TDFP analysis method is completed by the single-loop optimization for solving the MPTP in T-PMA. The comparative analysis of T-PMA and DLNM is based on T-PMA_SL in the case studies. The computational cost of T-PMA is less than that of DLNM, and the computational time of T-PMA is 2.15 s, while the computational time of DLNM is 221.72 s, the above comparison shows the effectiveness of T-PMA. The constraint situations in the standard interval space after the convergence of the optimization estimated by T-PMA is shown in Fig. 4. From the Fig. 4, it can be seen that the minimum performance target points of the constraint functions G1min(u) and G2min(u) are on the boundary of ‖u(j)‖∞ = 1(j = 1, 2), while G3min(u) has a certain allowance. The conclusion in Fig. 4 is consistent with TDFPs of the constraint functions under the convergence of the optimization given in Table 2. The conclusion of Fig. 4 also shows the feasibility of T-PMA. The comparison of Fig. 4 shows that the total number of iterations involved in the proposed T-PMA is less than that of the DLNM, and the iteration process is faster than that of the DLNM.

The results of the case study fully verify that the equivalent transformation of the TDFP constraint in the T-PMA is accurate and effective, and since the T-PMA only needs to analyze the minimum performance function under the necessary level with respect to the target TDFP, its computational cost is much less than that of the DLNM Fig. 5.

Fig. 5
figure 5

The comparison of the iteration history

Full size image

4.2 Design optimization of a corroded bending beam

It is shown in Fig. 6 that the cross section B-B of the beam (Jiang and Lu 2020) is rectangular, and a0 and b0 represent the initial width and height of the cross section respectively. As a result of corrosion, the width and height of the cross section of the beam vary with time t. Let a(t) and b(t) respectively represent the width and height of the beam changing with the corrosion time t, and κ represents the corrosion coefficient, κ = 0.25 × 10−3m/year, then the specific expressions of a(t) and b(t) are shown as follows,

$$ a(t)={a}_0-2\kappa t\kern2.25em b(t)={b}_0-2\kappa t $$
(22)
Fig. 6
figure 6

The schematic structure of a corroded bending beam

Full size image

The center point of the bending beam is applied by the concentrated force F and \( F(t)={F}_0\sin \left(\frac{\pi t}{12}\right) \). M(t) represents the bending moment at the center point of the beam, and the time-dependent performance function can be expressed as

$$ g\left(\boldsymbol{X},t\right)={M}_u(t)-M(t)=\frac{a(t){b}^2(t){\sigma}_u}{4}-\left(\frac{F(t)L}{4}+\frac{\rho_{st}a(t)b(t){L}^2}{8}\right) $$
(23)

where Mu(t) is the ultimate bending moment, L = 5m is the length of the beam, σu is the ultimate strength, and ρst = 78.5KN/m3 is the density. In the above variables, a0, b0, σu, and F are fuzzy input variables which are denoted as X = [X1, X2, X3, X4] = [a0, b0, σu, F0]. Table 4 shows the parameters and MF types of fuzzy input variables. The T-PBDO model of the corroded bending beam is expressed as follows,

$$ {\displaystyle \begin{array}{cc}\min & f\left({\boldsymbol{\mu}}_X\right)={\mu}_{X_1}+{\mu}_{X_2}\\ {}\mathrm{s}.\mathrm{t}.& Poss\left\{g\left(\boldsymbol{X},t\right)\le 0\kern1em \exists t\in \left[{t}_0,{t}_e\right]\right\}\le {\pi}_f^{tar}\\ {}& g\left(\boldsymbol{X},t\right)=\frac{a(t){b}^2(t){\sigma}_u}{4}-\left(\frac{F(t)L}{4}+\frac{\rho_{st}a(t)b(t){L}^2}{8}\right)\\ {}& 0.01\le {\mu}_{X_1}\le \mathrm{0.2,0.01}\le {\mu}_{X_2}\le 0.1,{\pi}_f^{tar}=0.1,t\in \left[0,1\right]\end{array}} $$
(24)
Table 4 The distribution parameters of the fuzzy variables of a corroded bending beam
Full size table

Take the initial design parameter vector as \( {\boldsymbol{\mu}}_{\boldsymbol{X}}^{(0)}=\left[{\mu}_{X_1}^{(0)},{\mu}_{X_2}^{(0)}\right]=\left[0.05,0.1\right] \), the design parameters obtained by DLNM and T-PMA are summarized in Table 5. The computational cost of the number of calling functions and the number of iterations are listed in Table 6. From Table 5, one can observe that the convergent optimal solutions estimated by the proposed T-PMA can match well with that of the DLNM, which illustrates the accuracy of the T-PMA for T-PBDO. But the computational cost of calling constraint functions by DLNM is more than 105, and the computational cost of calling constraint functions by T-PMA_DL and T-PMA_SL are no more than two hundred, the computational cost of calling constraint functions by T-PMA_SL is least. Meanwhile, the proposed T-PMA requires less iteration steps than DLNM. The above analysis shows that T-PMA is more efficient than the DLNM for solving T-PBDO.

Table 5 Design parameter solutions of a corroded bending beam
Full size table
Table 6 Computational cost of a corroded bending beam
Full size table

In order to verify the numerical stability of the proposed T-PMA, the convergent optimal solutions under different initial values of the design parameter vector are given in Table 7, where \( {\boldsymbol{\mu}}_{\boldsymbol{X}}^{(0)}=\left[0.1,0.1\right] \) is in the feasible region and \( {\boldsymbol{\mu}}_{\boldsymbol{X}}^{(0)}=\left[0.07,0.08\right] \) is in the infeasible region. And the inverse TDFP analysis method is completed by the single-loop optimization for solving the MPTP in T-PMA. It can be seen from Table 7 that the DLNM and the T-PMA can obtain the convergent optimal solutions satisfying the requirement under the appropriate initial values of the design parameter vector. However, the DLNM is more sensitive to the initial value of the design variables than T-PMA, and may obtain wrong optimization solutions or even infeasible solutions. The reason is that direct solution of the T-PBDO involves a more complicated constraint than the T-PMA, which leads to poor numerical stability. Therefore, the design parameters obtained by the T-PMA are more stable, and it shows that the PMA method has wider applicability.

Table 7 Design parameter solutions under different initial values of design parameters
Full size table

4.3 A cantilever beam

As shown in Fig. 7, the left end of a cantilever beam (Shi et al. 2020) is a fixed end, and the right end is a free end. The free end of the beam is under a vertical concentrated force F1 and a horizontal concentrated force F2 changing with time. Let F1(t) and F2(t) represent the concentrated forces in the vertical and horizontal directions on the free end of the beam, then the specific expressions of F1(t) and F2(t) are shown as follows,

$$ {F}_1(t)={F}_{10}{e}^{\left(-{t}^2\right)}\kern1.25em {F}_2(t)={F}_{20}\cos \left(\pi t\right) $$
(25)
Fig. 7
figure 7

A cantilever beam

Full size image

In this case study, the optimization objective is to minimize the weight of the beam. The thickness h and width w of the cross section of the beam are deterministic design parameters, while Young’s modulus E and yield stress y are fuzzy input variables. There are two failure possibility constraint functions which respectively represent that the maximum stress is not allowed to be greater than the yield stress y and the replacement of the free end should be not greater than the allowable displacement D0 = 2.5 in. The T-PBDO of this cantilever beam is expressed as follows.

$$ {\displaystyle \begin{array}{cc}\min & f\left(\boldsymbol{d}\right)=w\times h\\ {}\mathrm{s}.\mathrm{t}.& Poss\left\{{g}_j\left(\boldsymbol{d},\boldsymbol{X},t\right)\le 0\kern1em \exists t\in \left[{t}_0,{t}_e\right]\right\}\le {\pi}_{fj}^{tar}\left(j=1,2\right)\\ {}& {g}_1\left(\boldsymbol{d},\boldsymbol{X},t\right)=y-\left(\frac{600{F}_1(t)}{w{h}^2}+\frac{600{F}_2(t)}{w^2h}\right)\\ {}& {g}_2\left(\boldsymbol{d},\boldsymbol{X},t\right)={D}_0-\frac{4{L}^3}{Ewh}\sqrt{{\left(\frac{F_1(t)}{h^2}\right)}^2+\left(\frac{F_2(t)}{w^2}\right)}\\ {}& d=\left[w,h\right],\boldsymbol{X}=\left[{X}_1,{X}_2,{X}_3,{X}_4\right]=\left[y,E,{F}_{10},{F}_{20}\right]\\ {}& w>0\;\mathrm{in},0\;\mathrm{in}<h\le 5\;\mathrm{in},{\pi}_{fj}^{tar}=0.1\left(j=1,2\right)\end{array}} $$
(26)

where L is the length of the beam which is equal to 100 in. The parameters of fuzzy input variables are listed in Table 8.

Table 8 The distribution parameters of the fuzzy variables of a cantilever beam
Full size table

In this case study, the deterministic design parameters, the fuzzy input variables, and the time variable are involved in the constraint functions. The initial design parameter vector is set to [w, h] = [2.2, 4.4] for the DLNM and the T-PMA. The design parameter solutions of DLNM and T-PMA are listed in Table 9. Table 10 shows the computational cost required by three methods, and Fig. 8 shows the iterative process of the two methods for solving the T-PBDO.

Table 9 Design parameter solutions of a cantilever beam
Full size table
Table 10 Computational cost of a cantilever beam
Full size table
Fig. 8
figure 8

Iterative process of design optimization solutions of case study 3

Full size image

It can be found from Table 9 that the design parameter solutions estimated by the three methods are similar with each other, which can demonstrate the effectiveness of the proposed T-PMA for solving T-PBDO. Compared with the DLNM method, the computational cost of calling constraint functions by T-PMA_SL is about 104 orders of magnitude less than that of the DLNM method, and the computational cost of calling objective functions by T-PMA is less than that of the DLNM method. Furthermore, the computational time of the DLNM method is 781.981 s, and that of T-PMA is no more than 3 s, which obviously improves the computational efficiency of optimal solutions. And the total iteration numbers involved in the T-PMA is 5, and the total iteration numbers of DLNM is 14. These results also show the efficiency of T-PMA for solving the T-PBDO.

4.4 A welded beam

Considering a welded beam (Shi et al. 2020) shown in Fig. 9. The left end of this beam is welded and there is a time-dependent loading \( F(t)={F}_0\sin \left(\frac{\pi t}{48}\right) \) in the right end of this beam. The fuzzy design parameters are the depth X1, the length X2, the height X3, and the thickness X4 of the welding point. Four time-dependent possibility constraint functions and one time-independent possibility constraint function are involved in this optimization, in which the four time-dependent possibility constraint functions related to the shear stress, bucking, bending stress, and displacement of free end, and the time-independent possibility constraint functions is about the restriction of welding size. The objective is to minimize the cost of welding. The fuzzy input variables are Young’s Modulus E, the length of this beam L, the shear Modulus G, the allowable displacement of free end d0, the maximum shear stress τ, the maximum normal stress σ, and the load F0. The parameters and distribution forms of fuzzy input variables are listed in Table 11. The T-PBDO of this beam is as follows,

Fig. 9
figure 9

A welded beam

Full size image
Table 11 The distribution parameters of the fuzzy variables of a welded beam
Full size table
$$ {\displaystyle \begin{array}{cc}\min & f\left({\boldsymbol{\mu}}_X\right)={c}_1{\mu}_{X_1}^2{\mu}_{X_2}+{c}_2{\mu}_{X_3}{\mu}_{X_4}\left(L+{\mu}_{X_2}\right)\\ {}\mathrm{s}.\mathrm{t}.& Poss\left\{{g}_j\left(\boldsymbol{Z},t\right)\le 0\kern1em \exists t\in \left[{t}_0,{t}_e\right]\right\}\le {\pi}_{fj}^{tar}\left(j=1,2,4,5\right)\\ {}& Poss\left\{{g}_3\left(\boldsymbol{Z}\right)\le 0\right\}\le {\pi}_{f3}^{tar}\\ {}& {g}_1\left(\boldsymbol{Z},t\right)=1-\frac{\tau \left(\boldsymbol{Z},t\right)}{\tau },{g}_2\left(\boldsymbol{Z},t\right)=1-\frac{\sigma \left(\boldsymbol{Z},t\right)}{\sigma}\\ {}& {g}_3\left(\boldsymbol{Z}\right)=1-\frac{X_1}{X_4},{g}_4\left(\boldsymbol{Z},t\right)=1-\frac{\delta \left(\boldsymbol{Z},t\right)}{d_0},{g}_5\left(\boldsymbol{Z},t\right)=\frac{P_c\left(\boldsymbol{Z}\right)}{F(t)}-1\\ {}& \boldsymbol{Z}=\left[\boldsymbol{X},\boldsymbol{P}\right],\boldsymbol{X}=\left[{X}_1,{X}_2,{X}_3,{X}_4\right],\boldsymbol{P}=\left[E,L,G,{d}_0,\tau, \sigma, {F}_0\right]\\ {}& 3.175\; mm<{\mu}_{X_1}\le 50.8\; mm,{\mu}_{X_2}\le 254\; mm,{\mu}_{X_3}\le 254\; mm,{\mu}_{X_4}\le 50.8\; mm\\ {}& {\pi}_{fj}^{tar}=0.1\left(j=1,2,3,4,5\right),\left[{t}_0,{t}_e\right]=\left[0,4\right] year\end{array}} $$
(27)

where

$$ {\displaystyle \begin{array}{l}\begin{array}{l}\begin{array}{l}\begin{array}{l}\begin{array}{l}\tau \left(\boldsymbol{Z},t\right)=\sqrt{L{\left(\boldsymbol{Z},t\right)}^2+\frac{L\left(\boldsymbol{Z},t\right)S\left(\boldsymbol{Z},t\right){X}_2}{R\left(\boldsymbol{Z}\right)}+S{\left(\boldsymbol{Z},t\right)}^2}\\ {}L\left(\boldsymbol{Z},t\right)=\frac{F(t)}{\sqrt{2}{X}_1{X}_2},S\left(\boldsymbol{Z},Y(t)\right)=\frac{M\left(\boldsymbol{Z},t\right)R\left(\boldsymbol{Z}\right)}{J\left(\boldsymbol{Z}\right)}\end{array}\\ {}M\left(\boldsymbol{Z},t\right)=F(t)\left(L+0.5{X}_2\right),\delta \left(\boldsymbol{Z},t\right)=\frac{4F(t){L}^3}{E{X}_3^3{X}_4}\end{array}\\ {}R\left(\boldsymbol{Z}\right)=0.5\sqrt{X_2^2+\left({X}_1+{X}_3\right)},J\left(\boldsymbol{Z}\right)=\sqrt{2}{X}_1{X}_2\left[\frac{X_2^2}{12}+\frac{{\left({X}_1+{X}_3\right)}^2}{4}\right]\end{array}\\ {}\sigma \left(\boldsymbol{Z},t\right)=\frac{6F(t)L}{X_3^2{X}_4},{P}_c\left(\boldsymbol{Z}\right)=\frac{4.013{X}_3{X}_4^3\sqrt{EG}}{6{L}^2}\left(1-\frac{X_3}{4L}\sqrt{\frac{E}{G}}\right)\end{array}\\ {}{c}_1=6.74135\times {10}^{-5},{c}_2=2.93585\times {10}^{-6}\end{array}} $$
(28)

Take the initial design parameter vector as \( {\boldsymbol{\mu}}_{\boldsymbol{X}}^{(0)}=\left[{\mu}_{X_1}^{(0)},{\mu}_{X_2}^{(0)},{\mu}_{X_3}^{(0)},{\mu}_{X_4}^{(0)}\right]=\left[15.2,254,254,16.2\right] \), the design parameter solutions and the computational cost estimated by DLNM and T-PMA are listed in Tables 12 and 13 shows the TDFPs of constraint functions under the convergent optimal solutions. Figure 10 shows the iterative process of DNLM and T-PMA.

Table 12 Design parameter solutions and computational cost of a welded beam
Full size table
Table 13 TDFPs of constraint functions under convergent optimal solutions
Full size table
Fig. 10
figure 10

Iterative process of design optimization solutions of a welded beam

Full size image

It can be seen from Table 12 that the design parameter solutions of the three methods are almost the same. The computational cost of calling constraint functions by T-PMA_SL and T-PMA_DL are 6770 and 82,100 respectively, while that of DLNM is about 107 orders of magnitude, and the computational cost of calling objective functions by T-PMA is less than that of DLNM, and the iteration times of T-PMA are lower than that of DLNM method. Meanwhile, the TDFPs of constraint functions under the convergent design parameters estimated by DLNM and T-PMA satisfy the required target TDFP, which further proves the feasibility of optimization solutions estimated by T-PMA. Table 12 also shows that the DLNM is not suitable in engineering application due to the large amount of computational cost. The case study results fully prove that the efficiency of the proposed T-PMA is higher than that of the DLNM and the T-PMA_SL is more efficient than T-PMA_DL.

5 Conclusion

In this paper, a time-dependent failure possibility-based design optimization model (T-PBDO) is proposed. The efficiency of solving T-PBDO directly is not acceptable in engineering application. Therefore, a time-dependent performance measure approach (T-PMA) is established to solve the T-PBDO. In the proposed method, the time-dependent failure possibility (TDFP) constraint is equivalently transformed into the time-dependent performance function constraint corresponding to the target TDFP. The minimum performance target point (MPTP) and its corresponding time instant in the performance function constraint are determined by the single-loop method of inverse TDFP analysis with respect to the target TDFP, which avoids the analysis of performance function under unnecessary membership level and improves the numerical stability and computational efficiency of solving the optimization model.

The main contributions of the work include as follows:

  1. (1)

    Establish the T-PBDO under the fuzzy uncertainty, which is of great significance to design the optimal structure in case of meeting the safety requirements.

  2. (2)

    Define the minimum performance target point (MPTP) corresponding to the target TDFP, and establishing an inverse TDFP analysis method completed by a single-loop optimization for solving the MPTP. At the same time, combining the MPTP with its corresponding time instant, the TDFP constraint is equivalently transformed into the time-dependent performance function constraint corresponding to the target TDFP, and a time-dependent performance measure approach (T-PMA) is proposed for solving T-PBDO, the proposed T-PMA avoids the analysis of constraint function under the unnecessary membership level except the target TDFP, then the computational efficiency is improved.