1 Introduction

In a possibilistic approach, reliability is the possibility that a structure under consideration can perform the intended function under specified service conditions over a given time under fuzzy uncertainty. Contrary to the reliability, failure possibility is the possibility of the failure occurrence of the system under fuzzy uncertainty (Fan et al. 2019). In real problems, the uncertainty of parameters is inevitable because the estimation of loads with time is often not accurate, deviation of material properties through environmental effects, the difference of the real elements from the specimens, errors in mathematical and physical modeling, quality of workmanship, etc. Eventually, the estimation of absolute reliability and design optimization is impossible.

Uncertainty is usually classified as random and fuzzy uncertainty based on the sources and characteristics. Random uncertainties arise from the inherent randomness in the physical properties and the system environment, and cannot be reduced, whereas fuzzy uncertainty results from a lack of knowledge and imprecision of the study variables. In this study, fuzzy uncertainty has been considered to incorporate the deterioration of input variables and consequently output quantities overtime due to environmental factors. The type of uncertainty defines the method of reliability analysis in such a way that random uncertainty possesses probability theory that requires large data to generalize the sample, whereas fuzzy uncertainty leads to possibilistic theory. The probability-based methods are well developed in analysis and design optimization of the structures that involve random uncertainties of input variables, however, it is not appropriate for problems with insufficient data. Thus, possibility-based methods treat input fuzzy variables that lack sufficient research proposed in this study to consider the propagation of the fuzzy uncertainty.

To evaluate the reliability of the structure in the presence of fuzzy uncertainty, an area ratio index of the area membership function of output performance in the safe domain to the whole area of the membership function of output performance is proposed (Shrestha and Duckstein 1997). Similar to the reliability index that is used to evaluate probability-based reliability under random uncertainty, a failure possibility index that measures the safety degree of the structure involving the fuzzy uncertainty by the possibility safety index (PSI) of the performance located in the failure domain (Fan et al. 2019).

Even though the expectation of long service of structures, the resistances deteriorate overtime because of various environmental factors. The time-dependent performance of the structures subjected to sustained load and corrosion and reliability based on probability theory is well investigated (Yu et al. 2015; Sajedi and Huang 2015; Stewart and Rosowsky 1998; Teplý et al. 1999); (Verma et al. 2014), whereas the time-dependent performance and reliability analysis of structures subjected to sustained load, corrosion, and creep and shrinkage based on possibility theory lack sufficient research. Therefore, this study is significant to predict the time-dependent performance level, the fuzziness of variables, and estimating the time-dependent reliability based on the possibility theory of the structures subjected to sustained load and environmental factors (i.e., corrosion, creep, and shrinkage).

1.1 Performance of the structure

The performance of the structure mainly depends on the input variables. The information of input variables is never certain, precise, and complete (Ranganathan 1999), i.e., uncertainty. The sources of uncertainties can be physical uncertainty, statistical uncertainty, model uncertainty, and gross errors. Due to the presence of these uncertainties of material properties, loads on the structure during its life, structural idealization model, limitation of numerical methods, and other unforeseen factors, the absolute safety of a structure is impossible (Biondini et al. 2004). Besides, the time-variant properties of the input variables lead the output performance to vary with time (Fan et al. 2019). For the structure system subjected to different loads, its time-dependent safety margin \(M_{j} \left( \cdot \right)\) generally given by

$$M_{j} (X,t) = R_{j} (X,t) - S_{j} (X,t)$$
(1)

1.1.1 Factors accelerating the failure possibility of concrete structures

1.1.1.1 Creep and shrinkage

Creep and shrinkage affect the bending stiffness and significantly increase the deflection of the reinforced concrete structures (Lluka et al. 2015; Haldar et al. 2010). The intensity of creep and shrinkage of the concrete depends on the ambient temperature and relative humidity, the dimensions of the element, the composition of the concrete, and the duration and magnitude of the loading (Fan et al. 2019) (ES EN 1992-1-1 2004).

1.1.1.2 Corrosion

Corrosion of reinforcing steel in concrete reduces the load-carrying capacity; deteriorates the diameter or effective cross-sectional area; significantly reduces bond strength; increases crack width; strongly reduced elongation of reinforcement steel (Loreto et al. 2011; Xia et al. 2013). In addition, corrosion induces internal pressure (hoop tension), which is due to increasing corrosion products with time, that easily exceeds the limited tensile strength of concrete (François et al. 2013; Hagino et al. 2013) leads to cracking and spalling of concrete cover and hence reduce the service life of the structure.

To consider the corrosion effect on the service of the structure, the corrosion initiation time can be obtained from the expression developed (Thoft-Christensen et al. 1996). The time-variant resistance of the concrete section is then determined by considering the deterioration of the reinforcing steel diameter about the corrosion initiation time. The reduction of the steel diameter is determined from the expression:

$$D_{i} \left( t \right) = \left\{ \begin{gathered} D_{i} {\text{ for }}t \le T_{i} \hfill \\ D_{i} - r_{{{\text{corr}}}} (t - T_{i} ){\text{ for }}T_{i} \le t \le T_{i} + \frac{{D_{i} }}{{r_{{{\text{corr}}}} }} \, \hfill \\ 0{\text{ for }}t \ge T_{i} + \frac{{D_{i} }}{{r_{{{\text{corr}}}} }} \, \hfill \\ \end{gathered} \right.$$
(2)

where \(D_{i} \left( t \right)\) is the \(i\,{\text{th}}\) diameter of the reinforcing bars at a time \(t\); \(D_{i}\) is the initial diameter of the \(i\,{\text{th}}\) bar before corrosion at the time \(t\); n is the number of the bars, and \(r_{{{\text{corr}}}}\) is the rate of corrosion that is given by \(0.0232i_{{{\text{corr}}}}\) in which \(1 \, \mu {\text{A}}/{\text{cm}}^{2}\) is equal to \(11.6 \, \mu {\text{m}}/{\text{year}}\).

Corrosion of embedded reinforcement not only reduces the bar diameter but also the strength of concrete and yield stress of steel with time. The reduction of concrete strength with time is given by the expression (Kliukas et al. 2015):

$$f_{{{\text{cc}}}} \left( t \right) = \alpha_{{{\text{cc}}}} k_{2} \left( t \right)f_{{{\text{ck}}}}$$
(3)

in which \(\alpha_{{{\text{cc}}}} = 1 - {{0.1M_{G} } \mathord{\left/ {\vphantom {{0.1M_{G} } {M_{E} }}} \right. \kern-0pt} {M_{E} }}\); \(k_{2} \left( t \right) = 0.85 - 1.7\rho \left( t \right)\) and \(\rho \left( t \right) = {{A_{s} \left( t \right)} \mathord{\left/ {\vphantom {{A_{s} \left( t \right)} {A_{c} }}} \right. \kern-0pt} {A_{c} }}\), where \(M_{G}\) is the bending moment caused by permanent force; \(M_{E}\) is bending moment caused by permanent and transient loads, and \(\rho \left( t \right)\) is time-dependent reinforcement ratio. However, the yield stress of the embedded reinforcement bars reduces according to the law proposed by Du et al. (2005), and its reduction is insignificant compared with the strength of the reinforcing bars.

1.2 Uncertainties of design parameters

Civil engineering structures such as buildings, bridges, transmission towers, and the like are complex and usually large. Hence, there is almost no chance to test the prototype rather than checking specific criteria on uncertain software models and limited numerical models. Due to the presence of uncertainties in materials properties, loads on the structure during its life, and structural and numerical models, the absolute safety of a structure is impossible (Ranganathan 1999).

Depending on the nature of the structure, loading, and environmental conditions, some types of uncertainties may become critical. Most of the uncertainties are associated with material properties, geometry, loads, and models due to a lack of knowledge and environmental factors (Matos 2007). For the system analysis and design, the uncertainties are classified, sorted, analyzed, and used to predict system parameters and performances. In general, the sources of uncertainties are (i) physical randomness, (ii) statistical uncertainty, (iii) model uncertainty, and (iv) gross errors. Despite the significant success of the probabilistic methods in structural reliability assessment due to randomness, many investigators (Kai-Yuan et al. 1991, 1993); [24] have indicated that epistemic uncertainty also occurs in real structures.

1.3 Methods of reliability analysis

Dealing with uncertainties in human knowledge is a difficult task within the probabilistic framework (Sexsmith 1999). The fuzzy concept has been adopted to overcome drawbacks with uncertainties in human knowledge and design parameters. The conventional reliability theory is based on the system alternating between two states, i.e., functioning or failing, and the system behavior is fully characterized in the context of probability measure assumptions. On the contrary, Kai-Yuan et al. (1991, 1995) were the pioneers to introduce the possibility and fuzzy-state assumptions to replace the probability and binary-state assumptions.

The time-dependent failure possibility (TDFP) to measure the safety degree of the structure under the fuzzy uncertainty in a given time interval (Fan et al. 2019), and the possibility of the performance is less than zero. From the definition, the TDFP is a double-loop nested optimization method (DLOM) whose computational cost is too high to solve the problems of practical engineering. To improve the computational cost, a single-loop optimization method (SLOM) has been established based on the extreme value transformation of the time-dependent performance function.

2 Basic concepts of time-dependent reliability analysis

2.1 Generation membership function for input and output parameters

Fuzzy variables can be obtained from the deterioration of material properties and cross-section dimensions, and variation of load in time due to environmental effects, and consequently, the output quantities will possess fuzziness. Fuzzy variables are generally represented by membership functions. The membership function (MF) is an appropriate mathematical description to make a subjective evaluation of different real problems. The fuzziness of variables is characterized by membership functions, which recognize the degree of belonging of the variable to the fuzzy set of study variables. However, there is no specific rule and consensus to generate membership; thus, it depends on the expertise and the availability of data. Generation of the membership functions of fuzzy variables follows a series of steps. These steps are (i) identification of fuzzy variables; (ii) determination of fuzzy interval (lower and upper limit); (iii) selection of an appropriate type of membership function; (iv) discretization of the degree of membership and the size of the variable to a reasonable figure; and (v) generation of the membership function.

However, there are numerous type of membership function triangular, trapezoidal, Gaussian, and other membership functions. Because of its simplicity, triangular membership function given in Eq. (4) has been used in this study:

$$\mu_{{\widetilde{A}}} \left( x \right) = \left\{ \begin{gathered} {{\left( {x - a} \right)} \mathord{\left/ {\vphantom {{\left( {x - a} \right)} {\left( {m - a} \right){\text{ if }}a \le x \le m}}} \right. \kern-0pt} {\left( {m - a} \right){\text{ if }}a \le x \le m}} \hfill \\ {{\left( {c - x} \right)} \mathord{\left/ {\vphantom {{\left( {c - x} \right)} {\left( {c - m} \right){\text{ if }}m \le x \le c \, }}} \right. \kern-0pt} {\left( {c - m} \right){\text{ if }}m \le x \le c \, }} \hfill \\ 0{\text{ Otherwise}} \hfill \\ \end{gathered} \right.$$
(4)

2.2 Time-dependent failure possibility

The time-dependent failure possibility is the possibility of performance less than zero under fuzzy uncertainty in a specified time interval, i.e., the maximum MF of the performance of all possible constraints at which \(f_{M}^{ - \alpha } = 0\)(Zhangchun and Zhenzhou 2014; Tang et al. 2014). In addition to the nonlinearity of material properties and failure modes, the complexity of failure possibility evaluation depends on the type of MF being selected for structure performance. The simple the selected MF, the easier the failure possibility computation, whereas the more complex the selected MF the higher the computational cost and leads to error in computational results. For instance, the Gaussian and general bell MFs can present the input variables and output quantities, which depend on the structural system, boundary conditions, loading condition, shape of whole structure or part of a structure and material properties, lead to very high computational cost, whereas the triangular MFs lead to low computational cost.

To evaluate the time-dependent reliability based on the possibilistic approach, estimation of the possibility safety index (PSI) \(\pi_{f}\) is a critical step. The PSI of the structure under fuzzy uncertainty can be obtained by the numerical algorithm shown in Eq. (5):

$$\begin{gathered} \pi_{f} = Poss\left\{ {M_{j} \left( X \right) \le 0} \right\} \hfill \\ \, = \sup \left\{ {\left. \mu \right|M_{j} \left( X \right) \le 0,j = 1,2,...,n} \right\} \hfill \\ \end{gathered}$$
(5)

where \(M_{(\alpha )}^{l}\) and \(M_{(\alpha )}^{u}\) are the lower and upper bounds of \(M_{(\alpha )}\), which is \(\alpha - {\text{cut}}\) of \(M(X,t)\); \(M_{j} (X,t)\) is the performance of a specified constraint; \(f_{M}^{ - \alpha }\) is the lower bound of \(F_{{M_{\alpha } }}\) which is \(\alpha - {\text{cut}}\) of \(F_{M}\) and \(\pi_{f}\) is the failure possibility index of the structure.

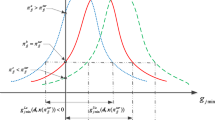
As shown in Fig. 1, the performance of the structure is less than zero, which is indicated in part \(A\) (hatched), and greater than zero is indicated in part \(B\). Any combination of input variables, output responses, and performance of different constraints in part \(A\) leads to failure of the structure, whereas in part \(B\), these combinations give reliable (safe) structure, and similarly, the interface that separates two parts \(A\) and \(B\) the combination of parameters yield \(M = 0\), at which the safety of the structure ceases or attains limit state.

Fig. 1
figure 1

The relationship between fuzzy intervals of the safety margin, membership function of performance and the failure possibility index

Full size image

Suppose that \(X = \left\{ {X_{1} ,X_{2} ,X_{3} ,...,X_{m} } \right\}\) is the fuzzy input variables with the MF of \(\mu_{{X_{i} }} \left( x \right)\)\(\left( {i = 1,2,...,m} \right)\). Assume that the time-dependent performance (TDP) of the \(j^{th}\) constraint of the structure is given by \(M_{j} (X,t)\), which is a function of the fuzzy input variables \(X\) and the time \(t\). In the system, the presence of fuzzy uncertainty of input variables (Fan et al. 2019) also propagates to the output responses. The propagation, the functional relationship of input-to-output variables, is based on the extension principle.

The TDFP analysis can be performed by fuzzy operations by modifying Eq. (5) to consider time-variant parameters and using the numerical algorithm based on possibility theory as

$$\begin{gathered} \pi_{{f_{j} t \in \left[ {t_{s} ,t_{e} } \right]}} = Poss\left\{ {M_{j} \left( t \right) \le 0} \right\} \hfill \\ \, = \sup \left\{ {\left. \mu \right|M_{j} \left( t \right) \le 0,t \in \left[ {t_{s} ,t_{e} } \right]} \right\} \hfill \\ \end{gathered}$$
(6)

where \(\pi_{{f_{j} t \in \left[ {t_{s} ,t_{e} } \right]}}\) is the TDFP at the time instant \(t \in \left[ {t_{s} ,t_{e} } \right]\); \({\text{Poss}}\left\{ \cdot \right\}\) is the possibility of the event; \(M\left( t \right)\) is the TDP of the \(j^{th}\) constraint; \(\sup \left\{ \cdot \right\}\) represents the supremum of the set and \(\mu\) is the membership degree of the performance at the time instant \(t \in [t_{s} ,t_{e} ]\).

The failure modes of the structures depend on material properties that deteriorate with time and the structural system (e.g., member arrangement and support condition, span length of the structural members, and types of load). Due to environmental factors such as corrosion, creep and shrinkage, and residual stress from improper utilization, the performance of the structure deteriorates with time. These reduced performances of the structure with time \(M(X,t)\) increase the failure possibility in time. Figure 2 shows the increment of TDFP of the structure. This shows the service life of a structure decrease with the deterioration of material properties due to corrosion, creep, and shrinkage in time that reducing the resistance of the structure. Consequently, the performance of the structure reduces over time which increases the failure possibility. To show the increment of the TDFP, the distribution of the MF of the structure performance is arranged in descending order of time because the performance reduction increase in time and failure possibility increases in time.

Fig. 2
figure 2

The relationship between TDFP and MF of the performance in the time interval

Full size image

Similar to the MF of the fuzzy variables, the value of the TDFP of the structure should satisfy the inequality \(0 \le \pi_{{f_{j} t \in [t_{s} ,t_{e} ]}} \le 1\). For boundaries of the time interval, i.e., \([t_{s} ,t_{ei} ]\) and \([t_{s} ,t_{ej} ]\) satisfy the inequality \(t_{ei} < t_{ej}\), and the time-dependent failure possibility \(\pi_{{ft \in [t_{s} ,t_{ei} ]}}\) and \(\pi_{{ft \in [t_{s} ,t_{ej} ]}}\) should satisfy the following inequality (Fan et al. 2019):

$$\pi_{{ft \in [t_{s} ,t_{ei} ]}} \le \pi_{{ft \in [t_{s} ,t_{ej} ]}} \,{\text{for }}t_{ei} < t_{ej}$$
(7)

Therefore, for every time instant \(t_{i} \in [t_{1} ,t_{2} ,t_{3,} ...,t_{n} ]\), the performance of the structure \(M(t_{i} )(i = 1,2,...,n)\) satisfies the inequality \(M(t_{1} ) < M(t_{2} ) < ,..., < M(t_{n} )\); consequently, the TDFP should satisfy the following inequality:

$$\pi_{{{\text{ft}}_{{\left( {1} \right)}} }} > \pi_{{{\text{ft}}_{{\left( {2} \right)}} }} > \pi_{{{\text{ft}}_{{\left( {3} \right)}} }} > ,...., > \pi_{{{\text{ft}}_{\left( n \right)} }}$$
(8)

where \(\pi_{{f_{j} t(i)}}\) is the failure possibility of the \(j\,{\text{th}}\) constraint at the time instant \(t(i)\); \(M_{j}^{{\text{m}}}\) is the nominal value of the \(j\,{\text{th}}\) constraint, and \([t_{1} ,t_{2} ,t_{3,} ...,t_{n} ]\) represents the descending order of the time set.

2.3 Estimation of possibilistic safety index

From the definition of failure possibility \(\pi_{f}\) expressed mathematically in Eq. (5): if the specific constraint’s performance with time satisfies the inequality \(0 \ge M_{j\left( t \right)}^{{\text{m}}}\), then \(\pi_{f\left( t \right)} = 1\), which implies complete failure (unreliable); if \(0 \le M_{j}^{l} \left( {t \in \left[ {t_{s} ,t_{e} } \right]} \right)\), then \(\pi_{{f_{j} t \in \left[ {t_{s} ,t_{e} } \right]}} = 0\) implies no failure (reliable), and if \(M_{j}^{l} \left( {t \in \left[ {t_{s} ,t_{e} } \right]} \right) \le M_{j} \left( {t \in \left[ {t_{s} ,t_{e} } \right]} \right) \le M_{j}^{{\text{m}}} \left( {t \in \left[ {t_{s} ,t_{e} } \right]} \right)\), the time-dependent failure possibility \(\pi_{{f_{j} t \in \left( {t_{s} ,t_{e} } \right)}}\) can be obtained from Eq. (9) (Tang et al. 2014):

$$\pi_{f} = \left\{ \begin{gathered} 0{\text{ if }}f_{M\left( t \right)}^{ - \alpha } \ge 0 \, \hfill \\ {\text{Poss}}\left\{ {\alpha \left| {f_{M\left( t \right)}^{ - \alpha } \le 0,\mu \in \left[ {0,1} \right]} \right.} \right\}{\text{ if 0}} \le f_{M\left( t \right)}^{ - \alpha } \le M_{j}^{m} \, \hfill \\ 1{\text{ if }}0 \ge M_{j}^{{\text{m}}} \hfill \\ \end{gathered} \right.$$
(9)

To estimate the failure possibility of the structure, the performance function should satisfy the inequality \({0} \le f_{M\left( t \right)}^{ - \alpha } \le M^{m}\) and its solution obtained from an expression:

$$f_{{M_{j} t \in \left[ {t_{s} ,t_{e} } \right]}}^{ - \alpha } = 0$$
(10)

To obtain TDFP \(\pi_{{f_{j} t \in \left[ {t_{s} ,t_{e} } \right]}}\) from Eq. (12), one should first determine the lower bound \(f_{{M_{j} t \in \left[ {t_{s} ,t_{e} } \right]}}^{ - \alpha }\) of \(F_{{M_{\mu } \left( t \right)}}\) which is \(\alpha -\)cut of \(F_{{M_{j} \left( t \right)}}\). The performance function may or may not be linear, depending on input variables and the type of constraints. For a reinforced concrete structure involving fuzzy input variables, the output variables (i.e., responses) obtained from Eq. (10) are nonlinear. For instance, flexural, shear, deflection, and crack performances of the reinforced concrete structure possess nonlinearity depending on material properties, loading type, and structure system. The nonlinearity of performance complicates the solution methods, consequently, increases computational cost.

In general, the time-dependent performance, i.e., \(M_{j} \left( t \right) = M\left( {X,t} \right)\) is a function of the fuzzy input variables \(X\) and the time \(t\). Hence, \(M_{j} \left( t \right)\) is also a fuzzy variable because of fuzzy uncertainty propagation with time through the extension principle. Eventually, the MF of the performance \(M_{j} \left( t \right)\) is also time-dependent. Similar to time-independent failure possibility (TIFP), the TDFP is the maximum failure possibility of the structure over a specified time interval \(t \in [t_{s} ,t_{e} ]\). If the membership degree of TDFP is greater than \(\pi_{{f_{j} t \in \left[ {t_{s} ,t_{e} } \right]}}\), then \(M_{j} \left( t \right)\) always could be nonnegative over the time interval \(t \in [t_{s} ,t_{e} ]\), which guarantees the reliability of the structure. For a specific time instant \(t\), we could have the time-invariant material properties, sectional dimensions, and loading. Therefore, the performance \(M_{j} \left( t \right)\) of the structure system becomes time-invariant. Thus, based on the extreme value transformation method, the minimum performance \(M_{\min } \left( X \right)\) is considered to evaluate the time-dependent failure possibility \(\pi_{f}\) at a specific time interval \(t \in [t_{s} ,t_{e} ]\). Therefore, the TDFP is equivalent to the TIFP of the minimum performance function \(\mathop {M_{\min } \left( X \right)}\limits_{{t \in [t_{s} ,t_{e} ]}}\) of \(M_{j} \left( t \right) = M\left( {Y,t} \right)\) estimated from the numerical algorithm (Fan et al. 2019):

$$\begin{gathered} \pi_{{f_{j} t \in \left[ {t_{s} ,t_{e} } \right]}} = {\text{Poss}}\left\{ {\mathop {M_{\min } \left( {X,t} \right)}\limits_{{t \in \left( {t_{s} ,t_{e} } \right)}} \le 0,\exists t \in \left[ {t_{s} ,t_{e} } \right]} \right\} \hfill \\ \, = \sup \left\{ {\mu \left| {\mathop {Min}\limits_{{t \in \left[ {t_{s} ,t_{e} } \right]}} } \right.M\left( {X,t} \right) \le 0,\mu \in \left[ {0.1} \right]} \right\} \hfill \\ \end{gathered}$$
(11)

From the time-dependent performance analysis, we would have the lower bound \(f_{{M_{j} t \in \left[ {t_{s} ,t_{e} } \right]}}^{ - \mu }\), the core value \(\overline{M} jt \in \left[ {t_{s} ,t_{e} } \right]\), and the upper bound \(f_{{M_{j} t \in \left[ {t_{s} ,t_{e} } \right]}}^{ + \mu }\) of the structural performance. To generate a triangular MF of performance obtained from Eq. (10), the lower bound and nominal value of a defined constraint are sufficient. After obtaining the lower bound of performance, whose value is less than zero at a specified time instant, and the nominal value of the performance function, the failure possibility \(\pi_{{f_{j} t \in \left[ {t_{s} ,t_{e} } \right]}}\) is computed using the algorithm by setting \(f_{{M_{j} t \in \left[ {t_{s} ,t_{e} } \right]}}^{ - \mu } = f_{{M_{j} t \in \left[ {t_{s} ,t_{e} } \right]}}^{{ - \pi_{f} }} = 0\).

2.4 Estimation of time-dependent reliability

Once the PSI is located on the membership function of the structure performance, it is easy to separate the failure and safe domain of the structure. Then, the area of failure and safe domain can be estimated using any possible mathematical applications that satisfy the equation membership function and fuzzy interval of the performance.

In this study, a single-loop optimization method (SLOM) is proposed to evaluate the time-dependent reliability (TDR) of structures. The basic step of the SLOM is shown in Fig. 3. The time-variant fuzzy reliability index can be estimated from the expression given by

$${\text{FR}}_{\left( e \right)} t \in \left[ {t_{s} ,t_{e} } \right] = \frac{{\int_{{M\left( {t,X} \right) > 0}} {\mu_{M} \left( {m\left( {t,X} \right)} \right)dx} }}{{\int {\mu_{M} \left( {m\left( {t,X} \right)} \right)dx} }}$$
(12)
Fig. 3
figure 3

The flow chart of SLOM for time-dependent fuzzy reliability analysis

Full size image

The efficiency of SLOM has been checked by SORM Tvedt’s algorithm given by

$$P_{{f_{{\left[ {t_{s,} t_{e} } \right]}} }} = A_{{1\,\left[ {t_{s,} t_{e} } \right]}} + A_{{2\left[ {t_{s,} t_{e} } \right]}} + A_{{3\left[ {t_{s,} t_{e} } \right]}}$$
(13a)
$$A_{{1\left[ {t_{s,} t_{e} } \right]}} = \Phi \left( { - \beta } \right)_{{\left[ {t_{s,} t_{e} } \right]}} \mathop \prod \limits_{j = 1}^{n - 1} \left( {1 + k_{j} \beta } \right)_{{\left[ {t_{s,} t_{e} } \right]}}^{ - 1/2}$$
(13b)
$$A_{{2\,_{{\left[ {t_{s,} t_{e} } \right]}} }} = \left[ {\beta \Phi \left( { - \beta } \right) - \phi \left( \beta \right)} \right]_{{\left[ {t_{s,} t_{e} } \right]}} \left\{ {\mathop \prod \limits_{j = 1}^{n - 1} \left( {1 + k_{j} \beta } \right)_{{\left[ {t_{s,} t_{e} } \right]}}^{ - 1/2} - \mathop \prod \limits_{j = 1}^{n - 1} \left( {1 + \left( {\beta + 1} \right)k_{j} } \right)_{{\left[ {t_{s,} t_{e} } \right]}}^{ - 1/2} } \right\}$$
(13c)
$$A_{{3_{{\left[ {t_{s,} t_{e} } \right]}} }} = \left( {\beta + 1} \right)\left[ {\beta \Phi \left( { - \beta } \right) - \phi \left( \beta \right)} \right]_{{\left[ {t_{s,} t_{e} } \right]}} \left\{ {\mathop \prod \limits_{j = 1}^{n - 1} \left( {1 + \beta k_{j} } \right)_{{\left[ {t_{s,} t_{e} } \right]}}^{ - 1/2} } \right\} - R_{e} \left\{ {\mathop \prod \limits_{j = 1}^{n - 1} \left( {1 + \left( {\beta + 1} \right)k_{j} } \right)_{{\left[ {t_{s,} t_{e} } \right]}}^{ - 1/2} } \right\}$$
(14d)

where \(P_{{f\left[ {t_{s,} t_{e} } \right]}}\) is the probability of failure of the limit-state function at specific time interval, \(\beta\) is the safety index of the specified failure mode, \(\prod\) is the summation, \(j\) indicates the jth random variable in the limit-state function, \(n\) is the total number of random variables in the limit-state function, \(k_{j}\) is the main curvature of the failure surface at the most probable point (MPP), and \(R_{e} \left\{ \cdot \right\}\) denotes the real part.

Since Eq. (14) is analytical equation, it can be implemented by following steps:

  1. 1.

    Evaluate the safety index \(\beta_{{\left[ {t_{s,} t_{e} } \right]}}\) search using HL method and locate the MPP, \(U^{ * }\)

  2. 2.

    Compute the second-order derivatives of the limit-state function, \(M\left( X \right)_{{\left[ {t_{s} ,t_{e} } \right]}}\) at \(U^{ * }\) and form the \(B_{{\left[ {t_{s} ,t_{e} } \right]}} = {{\left( {\nabla^{2} M\left( {U^{ * } } \right)} \right)_{{\left[ {t_{s} ,t_{e} } \right]}} } \mathord{\left/ {\vphantom {{\left( {\nabla^{2} M\left( {U^{ * } } \right)} \right)_{{\left[ {t_{s} ,t_{e} } \right]}} } {\left| {\nabla M\left( {U^{ * } } \right)} \right|}}} \right. \kern-0pt} {\left| {\nabla M\left( {U^{ * } } \right)} \right|}}_{{\left[ {t_{s} ,t_{e} } \right]}}\) matrix.

  3. 3.

    Calculate the orthogonal matrix \(H_{{\left[ {t_{s} ,t_{e} } \right]}} = {{\left( {\nabla M\left( {U^{ * } } \right)} \right)_{{\left[ {t_{s} ,t_{e} } \right]}} } \mathord{\left/ {\vphantom {{\left( {\nabla M\left( {U^{ * } } \right)} \right)_{{\left[ {t_{s} ,t_{e} } \right]}} } {\left| {\nabla M\left( {U^{ * } } \right)} \right|}}} \right. \kern-0pt} {\left| {\nabla M\left( {U^{ * } } \right)} \right|}}_{{\left[ {t_{s} ,t_{e} } \right]}}\)

  4. 4.

    Compute the main curvature \(k_{j}\) of the failure surface at the MPP using \(k_{{ij\left[ {t_{s} ,t_{e} } \right]}} = \left( {\overline{H} \overline{B} \overline{H} } \right)_{{ij\left[ {t_{s} ,t_{e} } \right]}} ,\left( {i,j = 1,2,...,n - 1} \right)\)

  5. 5.

    Evaluate \(A_{{1\left[ {t_{s,} t_{e} } \right]}}\), \(AS_{{1\left[ {t_{s,} t_{e} } \right]}}\), \(A_{{1\left[ {t_{s,} t_{e} } \right]}}\) and \(P_{{f\left[ {t_{s,} t_{e} } \right]}}\) using Eq. (13a)

  6. 6.

    Finally, \(FR_{\left( e \right)} t \in \left[ {t_{s} ,t_{e} } \right] = 1 - P_{{f\left[ {t_{s,} t_{e} } \right]}}\), which give the fuzzy reliability of the structure.

3 Numerical examples

To estimate the time-dependent reliability of the structures, three case studies have been carried out using SLOM as shown in Fig. 3.

Case study 1: A simply supported 500 mm × 300 mm RC beam with 50 mm concrete cover of span length 6 m subjected to the factored permanent load of \(16{\text{ kN/m}}\) including self-weight and imposed load of \(27{\text{ kN/m}}\) is provided in the building floor of salt storage. The building is located in Addis Ababa, Ethiopia whose average annual temperature \(T = 15.9 \, ^\circ C\) and the average minimum temperature and relative humidity of \({\text{RH}} = 60.7 \, \%\). Considering the kernel value of the input variables, the analysis of the beam for the time \(t = 0\) is executed. The materials of concrete grade C25/30, longitudinal reinforcement grade \(460{\text{ MPa}}\) (4 numbers of 22 mm diameter), and transverse shear reinforcement grade \(275{\text{ MPa}}\) at a center-to-center spacing of 200 mm are provided (Table 1).

Table 1 Description of fuzzy variables of reinforced concrete beam subjected to sustained load, corrosion, creep and shrinkage
Full size table

Before corrosion initiation, the structure could be subjected to the applied load and creep and shrinkage effect. The concrete cover provided as per (ES EN 1992-1-1 2004) could delay the corrosion initiation time but does not eliminate the corrosion. The corrosion initiation time, \(T_{i}\), using the baseline values of corrosion parameters mentioned in Enright and Frangopol (1998) taken as chloride diffusion coefficient \(D_{c} = 1.29{\text{ cm}}^{{2}} {\text{/year}}\), surface chloride concentration \(C_{0} = 0.10 \, \%\) weight of concrete, and critical chloride concentration \(C_{cr} = 0.04 \, \%\) weight of concrete are used for parametric studies.

The time-dependent performance of the reinforced concrete beam, the corrosion initiation time of longitudinal reinforcement is 18.41th year and shear reinforcement is 13.68th year using MatLab. In this study, a moderate corrosion rate of \(0.75\mu A/cm^{2}\) current density has been considered. The deterioration of steel diameter, and concrete strength due to corrosion are obtained using Eqs. (2) and (3), respectively.

Based on the site data, material properties, and cross-sectional dimensions, the time-variant creep coefficient and shrinkage strain model were developed using expressions provided in EC2 in Appendix B. Due to the time-variant effective modulus of concrete \(E_{ef} (t)\), creep coefficient, and shrinkage strain with time, the increment of flexure, shear force, and deflection can be determined from Eqs. (14–16), respectively:

$${{M_{{t,{\text{sh}}}} = E_{{{\text{ef}}}} (t)I(t)(1} \mathord{\left/ {\vphantom {{M_{{t,{\text{sh}}}} = E_{{{\text{ef}}}} (t)I(t)(1} {r_{{t,{\text{sh}}}} }}} \right. \kern-0pt} {r_{{t,{\text{sh}}}} }})$$
(14)
$${{V_{{t,{\text{sh}}}} = 4E_{{{\text{ef}}}} (t)I(t)(1} \mathord{\left/ {\vphantom {{V_{{t,{\text{sh}}}} = 4E_{{{\text{ef}}}} (t)I(t)(1} {r_{{t,{\text{sh}}}} }}} \right. \kern-0pt} {r_{{t,{\text{sh}}}} }})$$
(15)
$${{\delta_{{t,{\text{sh}}}} = kL^{2} (1} \mathord{\left/ {\vphantom {{\delta_{{t,{\text{sh}}}} = kL^{2} (1} {r_{{t,{\text{sh}}}} }}} \right. \kern-0pt} {r_{{t,{\text{sh}}}} }})$$
(16)

For accuracy of \(x_{u/c} (t)\), \(S_{u/c} (t)\) and \(I_{u/c} (t)\) calculation, the transformed section is being applied as per (Mosley et al. 2012), where \(E_{{c,{\text{eff}}}}\) is the long-term elastic modulus of concrete; \(x_{u}\) and \(x_{c}\) are the neutral axis for uncracked and cracked condition, respectively; \(Su\) and \(Sc\left( t \right)\) are the first moments of area of the reinforcement about the centroid of the uncracked and fully cracked sections, respectively; \(I_{u}\) and \(I_{c}\) are the second moment of area for uncracked and condition cracked condition, respectively.

Time-dependent performance of failure modes, i.e., flexure, shear, deflection, and crack had been performed for the RC beam section using Eqs. (17–20), respectively:

$$\, M_{M} \left( t \right) = A_{s} \left( t \right)f_{y} \left[ {d - 0.4x_{c} \left( t \right)} \right] - \left[ {\frac{{w_{{\text{DL + LL}}} L^{2} }}{8} + E_{c,ef} \left( t \right)I_{c} \left( t \right)\frac{1}{{r_{{t,{\text{sh}}}} }}} \right]$$
(17)
$$M_{V} \left( t \right) = \left( {V_{{{\text{Rd}},c}} \left( t \right) + V_{{{\text{Rd}},s}} \left( t \right)} \right) - \left( {\frac{{w_{{\text{DL + LL}}} L}}{2} + \frac{{4E_{{c,{\text{ef}}}} \left( t \right)I_{c} \left( t \right)}}{{r_{{t,{\text{sh}}}} L}}} \right)$$
(18)
$$M_{\Delta } \left( t \right) = \delta_{\lim } - kL^{2} \left( {{1 \mathord{\left/ {\vphantom {1 {r_{{t,{\text{Qp}}}} }}} \right. \kern-0pt} {r_{{t,{\text{Qp}}}} }} + {1 \mathord{\left/ {\vphantom {1 {r_{{t,{\text{cs}}}} }}} \right. \kern-0pt} {r_{{t,{\text{cs}}}} }}} \right)$$
(19)
$$M_{{w_{c} }} = w_{\lim } - \left\{ {\frac{{4\pi d_{c} \left( t \right)}}{{\left( {1 - v_{c} } \right)\left( {ab} \right)^{\sqrt \alpha } + \left( {1 + v_{c} } \right)\left( {ab} \right)^{\sqrt \alpha } }} + \frac{{4\pi a\left[ {\left( {1 + v_{c} } \right)b^{2} + \left( {1 - v_{c} } \right)a^{2} } \right]f_{2} }}{{\left( {b^{2} - a^{2} } \right)\left[ {\left( {1 - v_{c} } \right)\left( {a/b} \right)^{\sqrt \alpha } + \left( {1 + v_{c} } \right)\left( {b/a} \right)^{\sqrt \alpha } } \right]E_{f} }} - \frac{{2\pi bf_{t} }}{{E_{ef} }}} \right\}$$
(20)

The time-variant crack width estimation needs a rigorous procedure that is developed in Yang (2010) based on the theory of elasticity that considers the propagation crack due to the combined effect of sustained load and corrosion products also carried out in this study.

The deterioration of material properties, steel cross-section, and variation action lead to the imprecision of data, which possess fuzziness. The material properties and cross-section dimensions are considered input variables, and the failure modes and constraints are output variables. Therefore, the triangular fuzzy membership functions of input variables \(Y = \left\{ {f_{{{\text{ck}}0}} ,f_{{{\text{yo}}}} ,A_{{{\text{sto}}}} ,F} \right\}\) and output quantities \(Z = \left\{ {M,V,\delta ,w_{c} } \right\}\) have been generated and presented in Table 3.

To perform the TDR analysis, the nominal value of each constraint (see Fig. 4(a)) and the lower bound of performance \(M_{j}^{ - l} t_{i}\) of the corresponding constraint that is less than or equal to zero at a specified time interval \(t \in [t_{s} ,t_{e} ]\). From the analysis, the nominal value of flexure is \(223.73{\text{ kNm}}\), the shear force is \(126.75{\text{ kN}}\), and as per EC2 the limiting value deflection and crack width are \(24{\text{ mm}}\) and 0.3 mm. The result of the TDFP and TDR of each constraint at the specified time interval \(t \in [t_{s} ,t_{e} ]\) is presented in Table 4 using the triangular MF. The failure possibility, which is the maximum failure of all possible constraints in its design life is expressed in Eq. (21) and fuzzy reliability and Tvedt’s SORM of reinforced concrete beam and its result are represented in the last two column of Table 2.

$$\pi_{{ft \in \left[ {t_{s} ,t_{e} } \right]}} = {\text{Max}}\left\{ {\mu_{{\mathop {M_{\min } }\limits_{{t \in \left( {t_{s} ,t_{e} } \right)}} }} \left( {{\text{flexure}}} \right) \le 0,\mu_{{\mathop {M_{\min } }\limits_{{t \in \left( {t_{s} ,t_{e} } \right)}} }} \left( {{\text{shear}}} \right) \le 0,\mu_{{\mathop {M_{\min } }\limits_{{t \in \left( {t_{s} ,t_{e} } \right)}} }} \left( {{\text{deflection}}} \right) \le 0,\mu_{{\mathop {M_{\min } }\limits_{{t \in \left( {t_{s} ,t_{e} } \right)}} }} \left( {{\text{crack}}} \right) \le 0} \right\}$$
(21)
Fig. 4
figure 4

a FE result, b TDFP and TDR of RC beam subjected to sustained load, corrosion, creep and shrinkage

Full size image
Table 2 TDFP of different constraints and TDR of the RC beam subjected to sustained load, corrosion, creep and shrinkage
Full size table

The TDFP shown in Table 2 indicates the failure initiation time and the degree of failure of each constraint are different due to the functional relationship between input variables and the output performance. However, each constraint has its own MF of the performance, only the worst-case governs the failure possibility of the structure. In this insight, the RC beam structure is safe against flexure, deflection, and crack before the 20th year of its design life, whereas the structure fails against shear in the 16th year of its design life. The complete failure of the structure occurs in the 22nd year of the design life against shear force. In the possibilistic approach, the reliability expression from probability theory, i.e.,\(R = 1 - p_{f}\), is not applicable as shown in Table 2. The fuzzy reliability of the structure is obtained from Eq. (12), which is the area ratio of the safe domain to the total area of the MF of the governing failure mode. From this insight, the structure is reliable till the 16th year of its design life. For a specific time instant \(t \in [t_{s} ,t_{e} ]\), for instance [0, 30], the RC beam is completely unsafe, i.e., \(FR_{{\left( e \right)t \in \left[ {t_{s} ,t_{e} } \right]}} = 0\) as shown in Fig. 4b.

Case study 2: Consider a steel bending beam, whose length is L = 5000 mm, and its cross-section rectangular (i.e., \(b_{0} = 200{\text{ mm}}, \, h_{0} = 40{\text{ mm}}\)). This beam is subjected to dead loads (if \(\rho_{st} = 78.5{\text{ kN/m}}^{{3}}\) is the sound steel mass density and \(\rho_{{{\text{rust}}}} = 36{\text{ kN/m}}^{{3}}\) is the rust mass density (Liu and Weyers 1998), these loads are equal to \(p_{st} = \rho_{st} b_{0} h_{0}\) and \(p_{{{\text{rust}}}} = 4\rho_{{{\text{rust}}}} k^{2} t^{2}\), respectively, in N/m), and imposed point load F applied at midspan (Sudret 2008) (see Fig. 5). Before corrosion, the maximum bending moment at midspan is

$$M_{\max } = \frac{FL}{4} + \frac{{\rho_{st} b_{0} h_{0} L^{2} }}{8}$$
(22)
Fig. 5
figure 5

Corroded beam under a midspan load

Full size image

Suppose the steel has an elastic perfectly plastic constitutive law and denoting the yield stress by \(\sigma_{e}\), the ultimate bending moment of the rectangular section is

$$M_{{{\text{ult}}}} = \frac{{bh^{2} \sigma_{e} }}{4}$$
(23)

Now, assume that the steel beam corrodes in time. The corrosion phenomenon is supposed to start at \(t = 0\) and to be linear in time, meaning that the corrosion depth \(d_{c}\) all around the section increases linearly in time (\(d_{c} = kt\)). Assuming that the corroded areas have lost all mechanical stiffness, the dimensions of the sound section at any time instant \(t\) are

$$h\left( t \right) = h_{0} - 2kt; \, b\left( t \right) = b_{0} - 2kt$$
(24)

Using the above notation, the beam fails at a given point in time if \(M\left( t \right) \ge M_{{{\text{ult}}}} \left( t \right)\) (appearance of a plastic hinge at midspan). The limit-state function associated with the failure is

$$\begin{gathered} g\left( {t,X} \right) = M_{{{\text{ult}}}} \left( t \right) - M\left( t \right) \hfill \\ = \frac{{b\left( t \right)h^{2} \left( t \right)\sigma_{e} }}{4} - \left( {\frac{FL}{4} + \frac{{\rho_{st} b\left( t \right)h\left( t \right)L^{2} }}{8} + \frac{{4\rho_{rust} k^{2} t^{2} L^{2} }}{8}} \right) \hfill \\ \end{gathered}$$
(25)

where the dependency of the cross-section dimension in time has been specified in Eq. (25). The random input parameters are gathered in Table 3. The time interval under consideration is \(\left[ {0,5} \right]\) years. The corrosion kinetics is controlled by \(k = 0.25\) mm/year (Fan et al. 2019).

Table 3 Fuzzy variables of corroded bending beam variables and parameters
Full size table

Considering the deterioration of material properties and cross-sectional dimensions over time, the performance of the steel beam also deteriorates over time. The time-dependent failure possibility of the corroded steel beam is presented in Fig. 5. Similar to Example 1, the time-dependent flexural performance of the corroded beam performed just incorporating the deterioration of steel cross-section and corrosion products. Then, the TDR of the corroded steel beam carried out using triangular MF of the performance based on the single-loop optimization method (SLOM) is shown in Fig. 3. As shown in Fig. 6, the failure possibility of the corroded beam is 1 (one) at the 35th year, whereas at end of its design life, the fuzzy reliability, i.e., \(FR_{{\left( e \right)t \in \left[ {t_{s} ,t_{e} } \right]}}\), is 0.57304.

Fig. 6
figure 6

Time-dependent failure possibility and reliability of corroded steel beam

Full size image

Case study 3: A three-bar truss structure (see Fig. 7) is considered (Tang et al. 2014). The length and cross-sectional area of truss 2 are \(L = 50.8\) cm and \(A_{2}\), respectively. Truss 1 and truss 3 have the same length and cross-sectional area, i.e., √2L and \(A_{1}\). The density and elastic modulus of the material are \(\rho = 27.68{\text{ kN/m}}^{{3}}\) and \(E = 2.895 \times 10^{4} {\text{ N/mm}}^{2}\), respectively. The resultant load applied at node 4 induces the horizontal and vertical displacements at node 4. The TDR of the three-bar truss estimated from Kernel of stress and variation of input variables and output quantities are given in Table 4. The variation of members’ cross-sectional area considered for corrosion depth \(d_{c}\) all around the section in time (\(d_{c} = kt\)) and corrosion kinetics is controlled by \(k = 0.25\) mm/year as stated in Example 2.

Fig. 7
figure 7

Three-bar truss structure

Full size image
Table 4 Fuzzy variables of three-bar truss structure
Full size table

The time-dependent performance function of each constraint of the truss structure while considering the Kernel of load is given by

$$\begin{gathered} M_{1} \left( t \right) = u_{4}^{n} - \frac{{\sqrt 2 F^{n} L\cos \theta }}{{A_{1} \left( t \right)E}} \hfill \\ M_{2} \left( t \right) = v_{4}^{n} - \frac{{\sqrt 2 F^{n} L\sin \theta }}{{\left( {A_{1} \left( t \right) + \sqrt 2 A_{2} \left( t \right)} \right)E}} \hfill \\ M_{3} \left( t \right) = \sigma_{ + }^{n} \left( t \right) - \frac{\sqrt 2 }{2}\left( {\frac{{F^{n} \cos \theta }}{{A_{1} \left( t \right)}} + \frac{{F^{n} \sin \theta }}{{A_{1} \left( t \right) + \sqrt 2 A_{2} \left( t \right)}}} \right) \hfill \\ M_{4} \left( t \right) = \sigma_{ + }^{n} \left( t \right) - \frac{{\sqrt 2 F^{n} \sin \theta }}{{A_{1} \left( t \right) + \sqrt 2 A_{2} \left( t \right)}} \hfill \\ M_{5} \left( t \right) = \sigma_{ - }^{n} \left( t \right) - \frac{\sqrt 2 }{2}\left( {\frac{{F^{n} \cos \theta }}{{A_{1} \left( t \right)}} - \frac{{F^{n} \sin \theta }}{{A_{1} \left( t \right) + \sqrt 2 A_{2} \left( t \right)}}} \right) \hfill \\ \end{gathered}$$
(26)

Similar to Case studies 1 and 2, the time-dependent performance of the three-bar truss structure performed by incorporating the deterioration of the steel cross-section area due to corrosion is presented in Table 4. However, there may be numerous failure modes in the structure system as shown in Eq. (26), and only one mode may govern the system. Then, the TDR of the governing failure mode of the three-bar truss structure presented in Fig. 8 has been carried out using a single-loop optimization method (SLOM) and Tvedt’s SORM algorithm has been employed to examine the efficiency of SLOM.

Fig. 8
figure 8

Time-dependent failure possibility and reliability of the three-bar truss structure

Full size image

4 Conclusions

To evaluate the time-dependent reliability (TDR), the possibility safety index (PSI) has been applied to distinct the failure and safe domain of the structure. For a structure with performance greater than zero, failure possibility estimation is not required because failure occurs when the performance value is less than zero. The reliability of structures reduces with time by the deterioration of material properties and cross-section due to operation condition, and environmental factors such as corrosion, creep and shrinkage (concrete structures). For both concrete and steel, the majority of failure intensity has been caused by corrosion, whereas creep and shrinkage increases the action by 6.46% of the factored load in the reinforced concrete beam. Once the PSI is located on the MF of the structure performance, the area of failure and safe domain can be estimated for triangular MF. Then, the fuzzy reliability is estimated using the area ratio of the failure domain to the total area of MF. In essence, the proposed methodology prevents the exploitation of the familiar theory (i.e., failure probability) from being adopted for even fuzzy variables in uncertainty quantification. The results obtained from detail analysis indicate the SLOM is a little conservative compared with SORM Tvedt’s algorithm in such a way that their maximum-recorded percentage difference is 9.24%.