1 Introduction

Certain design applications require consideration of the nonlinear structural response, e.g., material inelasticity or buckling, to ensure the design meets specific requirements. For example, when designing structural systems for seismic excitation, the systems are intentionally permitted to undergo inelastic deformations while not exceeding specified drift limits (ASCE 2017). Although a substantial body of literature exists on the design of structural systems by topology optimization (Bendsoe and Sigmund 2004) spanning from early work by Miche (1904), to more recent advancements in methodological developments and applications (Sigmund 1994; Le et al. 2010; Asadpoure et al. 2011; Deaton and Grandhi 2014), these studies often invoke the assumption of linear elastic material response. More recently, studies have relaxed the elastic material assumption (e.g., Nakshatrala and Tortorelli 2015; Alberdi and Khandelwal 2017) explicitly considering inelastic material response. However, existing literature considering material inelasticity has focused almost entirely on continuum. In this paper, a method for the topology optimization of nonlinear structural systems composed of beam elements considering material inelasticity is presented. Material inelasticity is modeled using a hysteretic beam finite element (FE) formulation (Triantafyllou and Koumousis 2011, 2012). The objective of the topology optimization formulation is to minimize the total volume, that can be considered a proxy for the cost of the structural system, while constraining the system-level deformation.

A benefit of the hysteretic beam FE formulation, in the context of topology optimization, is that it permits the derivation of continuous and differentiable sensitivities facilitating the use of gradient-based optimization algorithms as described in detail in this paper. Similar to the established FE approach (Bathe 2006), the hysteretic FE method uses displacement interpolation functions to relate nodal degrees-of-freedom (DOF) to internal strain fields within each element. Unique to the hysteretic FE approach, however, are the addition of hysteretic DOF and associated hysteretic interpolation functions that distribute the inelastic response along the length of the element. The hysteretic DOF are governed by first-order nonlinear ordinary differential equations (ODEs), commonly referred to as evolution equations, and determine the onset of material inelasticity (Sivaselvan and Reinhorn 2000; Triantafyllou and Koumousis 2011). An additional benefit of the hysteretic FE formulation is that it offers computational efficiency, especially for transient excitation, due to the constant elastic stiffness and hysteretic matrices, which are evaluated only once at the outset of the analysis, and do not require updating throughout. Furthermore, in the context of topology optimization, this means their associated sensitivities with respect to the design variable, also only need to be evaluated for each nonlinear analysis.

Literature pertaining to nonlinearity in topology optimization has generally focused on continuum structures employing elasto-plastic or plasticity formulations. Several of these past studies have developed methods and/or analytical sensitivities for history-dependent problems for finite strain under quasi-static conditions (Tortorelli 1992; Maute et al. 1998; Yuge et al. 1999; Nakshatrala et al. 2013; Zhang et al. 2017a), transient excitation and dynamic conditions (Nakshatrala and Tortorelli 2015; Alberdi et al. 2018), and for considering both material and kinematic nonlinearities (Kleiber 1993; Tsay and Arora 1990; Schwarz et al. 2001; Wallin et al. 2016). Furthermore, recent studies have suggested combining the areas of nonlinear topology optimization of continuum structures and damage mechanics for the design of damage resistant structures (Achtziger and Bendsøe 1995; James and Waisman 2014, 2015; Alberdi and Khandelwal 2017; Li et al. 2017, 2018; Li and Khandelwal 2017). For this class of problems a damage model and local damage constraints are typically incorporated into the design problem to achieve damage resistant designs.

A few studies have considered nonlinearity for the topology optimization of frame structures. An early work by Yuge and Kikuchi (1995) studied the optimal design of frame structures considering plastic deformations. In the Yuge and Kikuchi (1995) study, two-dimensional structures were represented by a periodic microstructure where the stress field was obtained from an elasto-plastic FE analysis based on the homogenization method and plastic deformations followed plastic flow theory. In another work, Pedersen (2003) studied plasticity in topology optimization in the context of crashworthiness, where a ground structure composed of two-dimensional beam elements with rectangular solid cross sections was considered and optimized to maximize energy absorption. In the Pedersen (2003) study, plastic deformations were assumed to be concentrated at the ends of the beam elements and the plastic deformations modeled using conventional plastic flow theory. Later, Pedersen (2004) extended the method to account for distributed plasticity in the beam elements. Others have studied nonlinear elastic and hyper-elastic materials in continuum (Klarbring and Strömberg 2013; Luo et al. 2015) and discrete uniaxial truss element systems (Ramos and Paulino 2015; Zhang et al. 2017b). Multi-material design considering material nonlinearity has also been suggested for periodic structures (Swan and Kosaka 1997) and for truss structures (Zhang et al. 2018). However, the assumption of nonlinear elastic material behavior is not suitable when inelastic deformations are expected as is the case when designing structures to resist seismic ground motion.

Here we present, a method for the topology optimization of nonlinear structural systems composed of beam elements considering inelastic material behavior. As mentioned previously, the method combines topology optimization with a hysteretic FE approach to model the inelastic material behavior and as such original mathematical formulations and analytical sensitivities necessary to employ this modeling framework for the design of structural systems are presented. For this study, the ground structure approach, widely used for the topology optimization of structures is employed (Bendsoe and Sigmund 2004; Rozvany and Lewinski 2014). Nonlinear quasi-static analysis is carried out using the hysteretic beam FE model and an iterative solution scheme. As has been suggested by Kim et al. (2003) and Gömöry et al. (2009) for different applications, the hyperbolic tangent function is suggested as a suitable approximation of the signum function in the hysteretic evolution equations, to ensure these functions are continuous and differentiable everywhere. As such, analytical sensitivities with respect to the design variable were derived by direct differentiation. Numerical design examples are presented for the quasi-static case to demonstrate the utility of the method, where the objective of the design is to minimize the volume in a given domain for a given external force(s) subject to a specified system-level displacement constraint. For comparison, linear minimum compliance topology optimization problem is solved to obtain an optimal linear design solution using the optimal volume of the nonlinear design. Nonlinear analysis is performed with the linear minimum compliance design for the same level of external force and the results are compared with that of the nonlinear volume minimization design to study and illustrate the impact of explicitly considering material inelasticity in the optimization problem.

The remainder of the paper is organized as follows. Section 2 presents the overall methodology, beginning with a discussion on the nonlinear FE modeling approach in the context of beam elements. This discussion is followed by the design formulation for topology optimization of structural systems considering material inelasticity, solution schemes for the nonlinear analysis and sensitivities with respect to the design variables. Section 3 presents the numerical examples and associated results whereby the methodology is applied for the design of structural systems for static excitation including discussions of the results and observations. Lastly, in Section 4, a summary and description of the main contributions and findings are provided.

2 Methodology

The proposed method consists of three main components, specifically nonlinear structural analysis employing the hysteretic beam FE model, the optimization problem formulation, and the corresponding sensitivities to facilitate gradient-based optimization. Evaluation of the performance of a given system relies on the nonlinear static analysis employing the hysteretic beam FE model and provides the basis for the derivation of the sensitivities, hence important details of the modeling approach are described in the subsequent section for the benefit of the remainder of the paper. Herein, boldface upper and lower case font denote matrix and vector quantities, respectively.

2.1 Nonlinear beam FE model

Given the focus of this study being on the optimization of frame structures, an appropriate nonlinear beam FE model that is able to simulate inelastic behavior of beam elements is required. Here the hysteretic beam FE model suggested by Triantafyllou and Koumousis (2012) is adopted. The hysteretic FE approach is the result of efforts by various researchers to extend hysteretic models governed by first-order ODEs (Bouc 1967; Baber and Wen 1981; Baber and Noori 1985; Foliente 1995) beyond the uniaxial case toward established mechanics frameworks including an integrated hysteretic beam FE formulation (Triantafyllou and Koumousis 2011, 2012), multi-axial plasticity (Casciati 1989; Sivaselvan and Reinhorn 2000) and more recently a consistent nonlinear Timoshenko beam FE formulations (Amir et al. 2019). For a detailed derivation of the model formulations, the interested reader is referred to the aforementioned studies.

Like the conventional displacement-based FE approach (Bathe 2006), the hysteretic FE method employs displacement interpolation functions, however, there are additional hysteretic DOF and associated interpolation functions that differentiate the hysteretic FE modeling approach from conventional methods. This section summarizes the general concept and notable details of the hysteretic beam FE model. Additional details, definitions, and relationships necessary to complete the formulation can be found in Appendices Appendix and Appendix. The model employed here is based upon a two-node Euler-Bernoulli beam element with length L as illustrated in Fig. 1. The beam element has three independent displacement DOF for each node, namely longitudinal u, transverse w and rotation 𝜃; however, unique to this FE modeling approach are hysteretic DOF, z, in addition to the traditional displacement DOF. Two hysteretic DOF are considered for each node, specifically zu and zϕ corresponding to longitudinal and rotational deformations, respectively. Thus, the element displacement and hysteretic DOF vectors can be defined as:

$$ \begin{array}{@{}rcl@{}} \mathbf{d}^{el} & =& \left[ \begin{array}{ccccccc} u_{1} & w_{1} & \theta_{1} & u_{2} & w_{2} & \theta_{2} \end{array} \right]^{T} \\ \mathbf{z}^{el} & =& \left[ \begin{array}{ccccccc} z_{u1} & z_{\phi1} & z_{u2} & z_{\phi2} \end{array} \right]^{T}, \end{array} $$
(1)

where the superscripts e and l denote element-level and DOF with respect to the element local coordinates, respectively. Subscripts 1 and 2 correspond to the start and end nodes, respectively. Herein, superscripts e and l are only shown when necessary to differentiate element from system-level and local from global coordinates. Assuming a prismatic beam element, the internal stress resultants at a given point x along the length of the element are given by the following set of hysteretic laws:

$$ \begin{array}{@{}rcl@{}} P(x) & =& \alpha_{u} Ea\epsilon_{u}(x) + (1 - \alpha_{u})Eaz_{u}(x) \\ M(x) & =& \alpha_{\phi} EI\epsilon_{\phi}(x) + (1 - \alpha_{\phi})EIz_{\phi}(x), \end{array} $$
(2)

where P(x) and M(x) correspond to axial force and bending moment, respectively. The stress resultants in (2) can be viewed as the sum of two parallel components, the first component contributing to the post-elastic kinematic hardening and the second is the nonlinear component simulating the hysteretic behavior according to the hysteretic DOF (zu(x) and zϕ(x)). Variables 𝜖u(x) and 𝜖ϕ(x) are the axial strain and curvature, respectively; E, I, and a are the elastic modulus, moment of inertia, and cross-sectional area of the beam element, respectively; and αu and αϕ are the ratio of post-elastic to elastic modulus for axial and bending deformations, respectively.

Fig. 1
figure 1

Illustration of a two-node beam element and corresponding displacement and hysteretic DOF

Full size image

The hysteretic DOF evolved according to a set of nonlinear ODEs, commonly referred to as evolution equations, that for the axial deformation and curvature are expressed as:

$$ \begin{array}{@{}rcl@{}} \dot{z}_{u}(x) & =& \left( 1 - {H}_{1u}(x){H}_{2u}(x)\right)\dot{\epsilon}_{u}(x) \\ \dot{z}_{\phi}(x) & =& \left( 1 - {H}_{1\phi}(x){H}_{2\phi}(x)\right)\dot{\epsilon}_{\phi}(x), \end{array} $$
(3)

where H1u(x) and H1ϕ(x) are functions given by:

$$ {H}_{1u}(x) = \left|\frac{P^{h}(x)}{{P^{h}_{c}}}\right|^{n}, \quad {H}_{1\phi}(x) = \left|\frac{M^{h}(x)}{{M^{h}_{c}}}\right|^{n}. $$
(4)

In (4), Ph(x) is the current hysteretic axial force, \({P_{c}^{h}}\) is the hysteretic axial force capacity, Mh(x) is the current hysteretic bending moment, \({M_{c}^{h}}\) is the hysteretic bending moment capacity and n is a hysteretic parameter that controls the transition between elastic and inelastic branches. Furthermore, H2u(x) and H2ϕ(x) in Eq. 3 are heaviside functions expressed as follows:

$$ \begin{array}{@{}rcl@{}} {H}_{2u}(x) & = &\gamma \text{sgn}\left( P^{h}(x)\dot{\epsilon}_{u}(x)\right) + \beta \\ {H}_{2\phi}(x) & =& \gamma \text{sgn}\left( M^{h}(x)\dot{\epsilon}_{\phi}(x)\right) + \beta, \end{array} $$
(5)

where sgn(⋅) is the signum function and β and γ are parameters that control the relationship between the loading and unloading stiffness. Specifying the hysteretic parameters to satisfy the following constraints of β + γ = 1 and − γ ≤ β ≤ γ have been proven to result in a thermodynamically admissible model (Erlicher and Point 2004). Hence, in this study, both β and γ are set equal to 0.5 that results in the loading and unloading stiffnesses being equal in addition to satisfying the parameter constraints. To consolidate the notation into more compact expressions, the hysteretic laws shown in (2) are expressed in matrix format as:

$$ \begin{array}{@{}rcl@{}} \mathbf{m}^{el}(x) & = \mathbf{D}\boldsymbol{\epsilon}(x) + \mathbf{D}^{h}\mathbf{z}^{el}(x), \end{array} $$
(6)

where the components of mel(x) are arranged as mel(x) = [P(x) M(x)]T, and matrices D and Dh are the elastic and hysteretic rigidity matrices whose elements are functions of the material and the cross sectional properties. Similarly, the evolution equations shown in (3) are compactly expressed in matrix format as follows:

$$ \begin{array}{@{}rcl@{}} \dot{\mathbf{z}}^{el}(x) & = \left( \mathbf{I}_{2\times2} - \mathbf{S}(x) \right)\dot{\boldsymbol{\epsilon}}(x), \end{array} $$
(7)

where I is identity matrix and the matrix S(x) is defined in (8).

$$ \begin{array}{@{}rcl@{}} \mathbf{S}(x) & = \left[ \begin{array}{cccccc} H_{1u}(x)H_{2u}(x) & 0\\ 0 & H_{1\phi}(x)H_{2\phi}(x) \end{array} \right]. \end{array} $$
(8)

Following the displacement-based FE approach, the conventional cubic displacement interpolation functions are used to relate nodal displacements to the local deformation fields at a given location along the length of the element but are omitted here for brevity (see Bathe 2006). Assuming axial force is constant along the length of the element, that the bending moment varies linearly, and applying the appropriate hysteretic boundary conditions, the interpolation functions for the hysteretic DOF, zel are expressed as:

$$ \begin{array}{@{}rcl@{}} z_{u}(x) & =& \left[ \begin{array}{cccccc} 0.5 & \quad 0.5 \end{array} \right] \left[\begin{array}{cccccc} z_{u1} \\ z_{u2} \end{array} \right] \\ z_{\phi}(x) & =& \left[ \begin{array}{cccccc} 1-\frac{x}{L} & \quad \frac{x}{L} \end{array} \right] \left[\begin{array}{cccccc} z_{\phi1} \\ z_{\phi2} \end{array} \right]. \end{array} $$
(9)

The hysteretic interpolation functions shown in (9) serve to distribute the inelasticity along the length of the element. Substituting the hysteretic laws in (2), the interpolation functions and their derivatives into the variational principle of virtual work expressed for a given location x along the length of the beam element, performing the required integration by parts and enforcing the integration limits of 0 and L, the following element elastic stiffness matrix and hysteretic matrix are obtained:

$$ \begin{array}{@{}rcl@{}} \mathbf{K}^{el} & =& E\left[ \begin{array}{cccccc} \frac{\alpha_{u}a}{L} & 0 & 0 & \frac{-\alpha_{u}a}{L} & 0 & 0\\ 0 & \frac{12\alpha_{\phi} I}{L^{3}} & \frac{6\alpha_{\phi} I}{L^{2}} & 0 & -\frac{12\alpha_{\phi} I}{L^{3}} & \frac{6\alpha_{\phi} I}{L^{2}}\\ 0 & \frac{6\alpha_{\phi} I}{L^{2}} & \frac{4\alpha_{\phi} I}{L} & 0 & -\frac{6\alpha_{\phi} I}{L^{2}} & \frac{2\alpha_{\phi} I}{L}\\ \frac{-\alpha_{u}a}{L} & 0 & 0 & \frac{\alpha_{u}a}{L} & 0 & 0\\ 0 & -\frac{12\alpha_{\phi} I}{L^{3}} & -\frac{6\alpha_{\phi} I}{L^{2}} &0 & \frac{12\alpha_{\phi} I}{L^{3}} & -\frac{6\alpha_{\phi} I}{L^{2}}\\ 0 & \frac{6\alpha_{\phi} I}{L^{2}} & \frac{2\alpha_{\phi} I}{L} & 0 & -\frac{6\alpha_{\phi} I}{L^{2}} & \frac{4\alpha_{\phi} I}{L} \end{array} \right] \\ \mathbf{H}^{el} & =& E\left[ \begin{array}{cccccc} \frac{(\alpha_{u}-1)a}{2} & 0 & \frac{(\alpha_{u}-1)a}{2} & 0 \\ 0 & \frac{(\alpha_{\phi}-1)I}{L} & 0 & -\frac{(\alpha_{\phi}-1)I}{L} \\ 0 & (\alpha_{\phi}-1)I & 0 & 0 \\ -\frac{(\alpha_{u}-1)a}{2} & 0 & -\frac{(\alpha_{u}-1)a}{2} & 0\\ 0 & -\frac{(\alpha_{\phi}-1)I}{L} & 0 & \frac{(\alpha_{\phi}-1)I}{L}\\ 0 & 0 & 0 & -(\alpha_{\phi}-1)I \end{array} \right].\\ \end{array} $$
(10)

Thus, the element force deformation relationship in local coordinates can be compactly expressed as:

$$ \begin{array}{@{}rcl@{}} \mathbf{K}^{el}\mathbf{d}^{el} + \mathbf{H}^{el}\mathbf{z}^{el}= \mathbf{f}^{el}. \end{array} $$
(11)

To proceed to the solution of the system-level equations in global coordinates, both Kel and Hel must be transformed to the global coordinates system which can be accomplished according to the following expressions:

$$ \mathbf{K}^{e} = \boldsymbol{\varLambda}^{T}\mathbf{K}^{el}\boldsymbol{\varLambda}, \quad \mathbf{H}^{e} = \boldsymbol{\varLambda}^{T}\mathbf{H}^{el}, $$
(12)

where Λ is the conventional 6 × 6 transformation matrix for beam element (Bathe 2006). After performing the appropriate transformations and mapping, the global force-displacement equations are expressed as follows:

$$ \begin{array}{@{}rcl@{}} \mathbf{K}\mathbf{d} + \mathbf{H}\mathbf{z}= \mathbf{f}, \end{array} $$
(13)

where K and d are the stiffness matrix and displacement vector respectively, H and z are the hysteretic matrix and the hysteretic vector, respectively, and f is a vector of external nodal forces all in global coordinates. After assembling the global matrices, boundary conditions are imposed in the usual manner to obtain the system matrices via the typical direct stiffness assembly method. A benefit of this hysteretic FE modeling approach, in comparison with the more typical plasticity approach, is that the matrices K and H only need to be evaluated once, at the outset of the nonlinear analysis and otherwise remain constant.

The gradient-based optimization requires sensitivities of the objective function and constraints with respect to the design variables. For computational efficiency, it is preferable to use analytical sensitivities to numerical approximations and this point is one of the motivations for employing the hysteretic beam FE model. However, the exact form of the nonlinear ODEs shown in (7) includes the signum function. Hence, a mathematical approximation is introduced in order to obtain analytical sensitivities that are continuous and differentiable everywhere. Here, the hyperbolic tangent function is introduced as an approximation for the signum function according to:

$$ \begin{array}{@{}rcl@{}} {H}_{2u} & =& \gamma {\tanh}(\zeta P^{h}\dot{\epsilon_{u}}) + \beta \\ {H}_{2\phi} & =& \gamma {\tanh}(\zeta M^{h}\dot{\epsilon_{\phi}}) + \beta, \end{array} $$
(14)

where ζ is a coefficient that controls the shape of the hyperbolic tangent function in the proximity of zero. Assigning a large numerical value to ζ, closely approximates the signum function shape yet remains differentiable. In this study, a value of 50 is specified for ζ.

2.2 Optimization problem

The design problem considered here seeks to minimize the volume of the structural system subject to a system-level displacement constraint. Hence, having the nonlinear beam FE model, the volume minimization topology optimization problem considering material inelasticity subject to a system-level displacement constraint can be expressed as:

$$ \begin{array}{@{}rcl@{}} &\text{Find}: \quad & a_{1},...,a_{N} \\ &\underset{\mathbf{a}}{\text{Minimize}}: \quad & v = \sum\limits_{s=1}^{N}{a_{s}L_{s}} \\ &\text{Subject to}: \quad & \mathbf{K}\mathbf{d} + \mathbf{H}\mathbf{z}= \mathbf{f} \\ && d_{v} \leq d^{*} \\ && 0<\rho_{\min}< a \leq \rho_{\max}, \end{array} $$
(15)

where v is the volume in the domain, a is a vector of design variables representing the individual element cross-sectional areas and N is the number of elements, for a given iteration in the optimization process. Here, equilibrium of the structural system and the system-level displacement are imposed as constraints which relate the response of the system to the design variables. Nonlinear static analysis is performed to establish equilibrium of the system and to evaluate the response, which is the displacement at a specific degree of freedom, dv, here representing the system-level deformation which is constrained to a threshold value d∗. Each element’s cross-sectional area, as, is also constrained in (15) between \(\rho _{\min \limits }\) and \(\rho _{\max \limits }\). The lower limit \(\rho _{\min \limits }\) avoids singularity during the optimization process and the upper limit is based on the maximum cross sectional area available for I-shaped sections in American Institute of Steel Construction (2015). An approach for relating the cross-sectional area to other geometric properties for I-shaped cross sections suggested by Changizi and Jalalpour (2017b) is adopted in this study and the regression curves for the median range are used for the optimization process.

2.2.1 Nonlinear analysis

Nonlinear static analysis is employed to determine the unknown DOF, d and z. Each nonlinear static analysis is performed in a step-wise fashion until the specified external force value is attained. A challenge when material inelasticity is considered, is the iterative, and hence computationally expensive analysis, which is often required. For this study, a Newton solution scheme is devised for the hysteretic FE model and the nonlinear static analysis whereby for each force step, the unknowns (that is d and z) are iteratively updated until the norm of the residual vector falls below the specified tolerance. For the solution scheme, the equilibrium equations and hysteretic evolution equations are combined into a single system of nonlinear equations whereby the unknown displacement and hysteretic DOF are simultaneously updated in an iterative manner. We define a vector, \(\mathbf {x}_{i+1}^{j+1}\), which is an augmented set of unknowns containing d and z as:

$$ \begin{array}{@{}rcl@{}} \mathbf{x}_{i+1}^{j+1} = \left[ \begin{array}{cccccc} \mathbf{d}_{i+1}^{j+1} \\ \mathbf{z}_{i+1}^{j+1} \end{array} \right], \end{array} $$
(16)

where i represents the i th force-step and j represents the j th iteration of the i th force step. For a given force step, the vector of unknowns, \(\mathbf {x}_{i+1}^{j+1}\), is updated according to the following expression:

$$ \begin{array}{@{}rcl@{}} \mathbf{x}_{i+1}^{j+1} &= \mathbf{x}_{i+1}^{j} - \mathbf{J}_{v}^{-1}\mathbf{g}_{v}, \end{array} $$
(17)

where Jv and gv are the Jacobian matrix and residual vector, respectively, each subsequently defined. For a quasi-static analysis, the rate of change of the hysteretic DOF and strains are approximated using the following backward difference expressions to convert the nonlinear ODEs into a set of algebraic expressions conducive to the Newton update:

$$ \begin{array}{@{}rcl@{}} {\dot{\mathbf{z}}^{el}}_{i+1} & =& \frac{\varDelta \mathbf{z}^{el}}{\varDelta t} = \frac{\mathbf{z}^{el}_{i+1} - \mathbf{z}^{el}_{i}}{\varDelta t} \\ {\dot{\boldsymbol{\epsilon}}}_{i+1} & =& \frac{\varDelta \boldsymbol{\epsilon}}{\varDelta t} = \frac{\boldsymbol{\epsilon}_{i+1} - \boldsymbol{\epsilon}_{i}}{\varDelta t}, \end{array} $$
(18)

where Δt represents pseudo time that is, nevertheless, eliminated from the equations through algebra. Substituting (18) into (7), the following expression is obtained that relates \(\mathbf {z}_{i+1}^{el}\) to 𝜖i+ 1 for the two-node beam element:

$$ \begin{array}{@{}rcl@{}} \mathbf{z}^{el}_{i+1}& = \mathbf{z}^{el}_{i} + \left( \mathbf{I}_{2\times2} - \mathbf{S} \right)\varDelta\boldsymbol{\epsilon}, \end{array} $$
(19)

and the equilibrium equation at step i + 1 can be written as:

$$ \begin{array}{@{}rcl@{}} \mathbf{K}\mathbf{d}_{i+1}^{j} + \mathbf{H}\mathbf{z}_{i+1}^{j} = \mathbf{f}_{i+1}. \end{array} $$
(20)

Thus, the combined system of equations, which is the equilibrium (20) and the hysteretic evolution (19), is expressed compactly for the Newton update as:

$$ \begin{array}{@{}rcl@{}} \mathbf{g}_{v} & =& \mathbf{q}_{v} + \mathbf{T}_{v}\mathbf{x}_{i+1}^{j} - \mathbf{c}_{v}. \end{array} $$
(21)

The quantities qv, Tv and cv are expressed as follows:

$$ \begin{array}{@{}rcl@{}} \mathbf{q}_{v} & = &\left[\begin{array}{cccccc} \textbf{0}_{3r\times1} \\ \mathbf{g}_{z} \end{array} \right], \quad \mathbf{T}_{v} = \left[ \begin{array}{cccccc} \mathbf{K} & \mathbf{H}\\ -\mathbf{R} & \mathbf{I}_{3r\times4N} \end{array} \right] \\ \mathbf{c}_{v} & =& \left[\begin{array}{cccccc} \mathbf{f}_{i+1} \\ \mathbf{g}_{zc} \end{array} \right], \end{array} $$
(22)

where r is the number of nodes in the domain. The quantities gz, R and gzc are assembly matrices of the following element-level relations:

$$ \begin{array}{@{}rcl@{}} \mathbf{g}_{z}^{e} = \mathbf{S} \varDelta\boldsymbol{\epsilon}, \quad \mathbf{R}^{e} = \mathbf{B}\boldsymbol{\varLambda}, \quad \mathbf{g}_{zc}^{e} = \mathbf{z}_{i} - \boldsymbol{\epsilon}_{i}, \end{array} $$
(23)

where B is the strain-displacement matrix for the beam element. Lastly, the Jacobian matrix, Jv, is evaluated according to (24):

$$ \begin{array}{@{}rcl@{}} \frac{\partial{\mathbf{g}_{v}}}{\partial{\mathbf{x}_{i+1}^{j}}} = \mathbf{J}_{v} = \mathbf{T}_{v} + \mathbf{J}_{vn}, \end{array} $$
(24)

where Jvn is the part of the Jacobian matrix with complete derivation provided in Appendix Appendix. With all associated terms sufficiently defined in (16) through (24), the system of nonlinear equations can be solved for each iteration of the optimization process to determine the DOF of the system, d and z, for a specified external force, f.

2.2.2 Sensitivities

The use of gradient-based optimization necessitates sensitivities with respect to the design variable, a. The sensitivity of the objective function is obtained in a straightforward manner and is omitted here for brevity. The main challenge in deriving the sensitivities arises from the nonlinear constraint on the system-level displacement. Sensitivities for the displacement constraint were derived through direct differentiation and begins with the differentiation of the augmented vector, \(\mathbf {x}_{i+1}^{j+1}\), with respect to a and continues with the differentiation of all subsequent terms to obtain the analytical expressions for the sensitivities. The key steps of the derivation are provided here and additional details for the complete derivation are given in Appendix Appendix. The derivative of system-level displacement constraint is a component of:

$$ \begin{array}{@{}rcl@{}} \frac{\partial{\mathbf{x}_{i+1}^{j+1}}}{\partial{a}} = \left[ \begin{array}{cccccc} \frac{\partial{\mathbf{d}_{i+1}^{j+1}}}{\partial{a}} \\ \frac{\partial{\mathbf{z}_{i+1}^{j+1}}}{\partial{a}} \end{array} \right], \end{array} $$
(25)

where this derivative is obtained by differentiation of (17) according to:

$$ \begin{array}{@{}rcl@{}} \frac{\partial{\mathbf{x}_{i+1}^{j+1}}}{\partial{a}} = \frac{\partial{\mathbf{x}_{i+1}^{j}}}{\partial{a}} + \mathbf{J}_{v}^{-1}\frac{\partial{\mathbf{J}_{v}}}{\partial{a}}\mathbf{J}_{v}^{-1}\mathbf{g}_{v} - \mathbf{J}_{v}^{-1}\frac{\partial{\mathbf{g}_{v}}}{\partial{a}}, \end{array} $$
(26)

and the derivative of the Jacobian matrix, ∂Jv/∂a, is:

$$ \begin{array}{@{}rcl@{}} \frac{\partial{\mathbf{J}_{v}}}{\partial{a}} = \frac{\partial{\mathbf{T}_{v}}}{\partial{a}} + \frac{\partial{\mathbf{J}_{vn}}}{\partial{a}}. \end{array} $$
(27)

The third term in (26), ∂gv/∂a, is obtained by differentiating (21) as follows:

$$ \begin{array}{@{}rcl@{}} \frac{\partial{\mathbf{g}_{v}}}{\partial{a}} = \frac{\partial{\mathbf{q}_{v}}}{\partial{a}} + \frac{\partial{\mathbf{T}_{v}}}{\partial{a}}\mathbf{x}_{i+1}^{j} + \mathbf{T}_{v}\frac{\partial{\mathbf{x}_{i+1}^{j}}}{\partial{a}} - \frac{\partial{\mathbf{c}_{v}}}{\partial{a}}. \end{array} $$
(28)

As indicated by (28), the derivatives of the expressions in (22) for qv, Tv and cv are required and are expressed as:

$$ \begin{array}{@{}rcl@{}} \frac{\partial{\mathbf{q}_{v}}}{\partial{a}} & =& \left[\begin{array}{cccccc} \textbf{0}_{3r\times1} \\ \frac{\partial{\mathbf{g}_{z}}}{\partial{a}} \end{array} \right], \quad \frac{\partial{\mathbf{T}_{v}}}{\partial{a}} = \left[ \begin{array}{cccccc} \frac{\partial{\mathbf{K}}}{\partial{a}} & \frac{\partial{\mathbf{H}}}{\partial{a}}\\ \textbf{0}_{4N\times3r} & \textbf{0}_{4N\times4N} \end{array} \right] \\ \frac{\partial{\mathbf{c}_{v}}}{\partial{a}} & =& \left[\begin{array}{cccccc} \textbf{0}_{3r\times1} \\ \frac{\partial{\mathbf{g}_{zc}}}{\partial{a}} \end{array} \right], \end{array} $$
(29)

where ∂gz/∂a is an assembly of the following element-level derivatives:

$$ \begin{array}{@{}rcl@{}} \frac{\partial{\mathbf{g}_{z}^{e}}}{\partial{a}} & =& \frac{\partial{\mathbf{S}}}{\partial{a}} \varDelta\boldsymbol{\epsilon} + \mathbf{S} \frac{\partial{\varDelta\boldsymbol{\epsilon}}}{\partial{a}} \\ \frac{\partial{\mathbf{S}}}{\partial{a}} & = &\left[ \begin{array}{cccccc} \frac{\partial{H_{1u}}}{\partial{a}}H_{2u} + H_{1u}\frac{\partial{H_{2u}}}{\partial{a}} & 0\\ 0 & \frac{\partial{H_{1\phi}}}{\partial{a}}H_{2\phi} + H_{1\phi}\frac{\partial{H_{2\phi}}}{\partial{a}} \end{array} \right], \\ \end{array} $$
(30)

and similarly, ∂gzc/∂a is obtained using the element expression given by:

$$ \begin{array}{@{}rcl@{}} \frac{\partial{\mathbf{g}_{zc}^{e}}}{\partial{a}} = \frac{\partial{\mathbf{z}^{el}_{i}}}{\partial{a}} - \frac{\partial{\boldsymbol{\epsilon}_{i}}}{\partial{a}}, \quad \frac{\partial{\boldsymbol{\epsilon}_{i}}}{\partial{a}} = \mathbf{B}\boldsymbol{\varLambda}\frac{\partial{\mathbf{d}^{e}_{i}}}{\partial{a}}. \end{array} $$
(31)

Equations (26)–(31), and the derivative of the objective omitted, comprise the analytical sensitivities for the volume minimization design formulation.

2.3 Solution of the topology optimization process

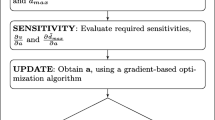
With the requisite components having been developed in the previous sections, the problem formulation described in Section 2 for the topology optimization of frame structures considering material inelasticity is applied following the process depicted by the flow diagram shown in Fig. 2. Rather than perform a single phase of optimization and then post-process the results, removing elements with areas less than the minimal constraint value, which could result in a design solution that does not satisfy the constraints, in this study multiple phases of optimization are performed to ensure the final optimized design satisfies the constraints. For each phase of optimization, the gradient-based algorithm employed is the Interior Point algorithm by way of the fmincon function in MATLAB (The MathWorks Inc. 2018) with a specified tolerance of 0.0001% on the objective function and the nonlinear constraint. Following the first phase of optimization, element areas are ranked and those with minimal area are removed from the ground structure, but without exceeding a total elements volume of 5% and an updated FE model is generated accordingly for a subsequent phase of optimization. The limit of 5% of the total volume was found to provide an adequate balance between additional computation and egregious degeneration of the solution. No difference in the final solution was observed when testing lower values for this limit, e.g., 2%. To achieve a converged design solution, subsequent phases of the optimization process (see Fig. 2), typically two or three, are performed each starting with the updated design configuration with minimal area elements having been removed. Convergence is achieved when no elements in the optimized design have minimal area, and the topology connectivity remains unchanged throughout a given phase of optimization. For each design application, the nonlinear static analysis is carried out using the iterative Newton solution scheme outlined in the previous section. The specified external force is applied in 20 equal force increments.

Fig. 2
figure 2

Flowchart for topology optimization solution scheme

Full size image

Due to the non-convex nature of the volume minimization problem, the global optima cannot be guaranteed. However, in an effort to investigate the non-convexity and gain confidence in the optimized solution, a multi-start strategy where initial values of the design variables are randomly assigned (Boese et al. 1994; Martí et al. 2016) is adopted in this study. For each numerical example, an entire optimization process was conducted for five starting cases, which is the set of specified initial cross-sectional areas, and the solution from the five optimization processes with the lowest objective function value is considered the best estimate of the global optimal design solution. For each randomized start case, the initial cross-sectional areas are established by sampling the volume for each element from a uniform distribution, from which the cross-sectional area is assigned based upon the elements location in the ground structure. One of the five starting cases assumed the initial cross-sectional area of all elements in the ground structure to be equal, referred to as uniform area.

3 Numerical examples

The utility of the proposed methodology is demonstrated through two representative numerical examples for the design of structural systems composed of beam elements. Details pertaining to the two design examples are provided in this section. As previously stated, the ground structure approach is employed in this study, whereby a dense mesh of connected elements is the initial configuration for the considered design examples. The material is assumed to be steel with Young’s modulus of 29,000 ksi and yield stress of 36 ksi. The inelastic to elastic ratios, αu and αϕ, are each set equal to 0.01, and exponent, n, for the hysteretic functions is set equal to 2. The constitutive relationship considered is illustrated by the axial stress versus axial strain, and normalized moment versus curvature relationships shown in Fig. 3. These relationships are obtained using the hysteretic laws (shown in (2)) and the entire response, that is the loading branch, unloading branch and inelastic deformations, are determined by the hysteretic variables that are governed by the hysteretic evolution equations shown in (3). Also shown in Fig. 3, for reference, is a linear elastic response.

Fig. 3
figure 3

Axial stress vs axial strain and normalized moment vs curvature relationships

Full size image

3.1 Example 1: a 4 × 2 frame structure

The first example is the design of a 4 × 2 frame structure with a lateral force applied at the top left node of the domain. The ground structure, boundary conditions and direction of applied force are shown in Fig. 4. The dimensions of the domain are Lx = 19.68 ft (6 m) and Ly = 39.4 ft (12 m).

Fig. 4
figure 4

Ground structure for the 4 × 2 frame structure under a lateral external force

Full size image

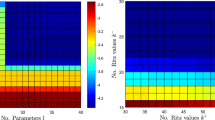
Prior to each example, the accuracy of the analytical sensitivities developed in Section 2.2.2 was evaluated by comparison with that obtained from a finite difference approximation. The sensitivity values of the displacement constraint for the 4 × 2 frame ground structure are shown in Fig. 5. As is seen from Fig. 5 the derived sensitivities from the two methods agree well with negligible error (less than 0.05%), verifying the accuracy of the analytical sensitivities obtained through the direct differentiation approach.

Fig. 5
figure 5

Comparison of the results of sensitivity analysis derived with the analytical direct differentiation method and finite difference approximation for the 4 × 2 frame ground structure

Full size image

The minimum volume design problem subject to displacement constraint is solved for the frame structure shown in Fig. 4 for a specified displacement constraint d∗ of 11.8 in., equivalent to a drift ratio of 2.5% (i.e., d∗/Ly = 0.025) and the specified external force of 500 kips. The optimized design for the d∗ = 0.025Ly by starting optimization from the uniform area distribution is shown in Fig. 6, where the thickness of the lines comprising the topologies indicates the relative size of the element area and the area values are normalized with respect to the their maximum among the designs. The numerical value adjacent to each element denote the element number. For this example, a volume of 2.3995 × 104 in.3 was required for the nonlinear optimization/design to satisfy the drift constraint.

Fig. 6
figure 6

Nonlinear minimum volume design for 2.5% system drift ratio and comparative linear design with the equivalent volume for the 4 × 2 frame structure along with the force-displacement responses for each optimized design. Numerical values adjacent to structural elements denote the element number

Full size image

In addition to the uniform area starting case, as described in Section 2.3, four randomized area starting cases were performed for each numerical example in an attempt to identify the global optima. The optimized topologies obtained for each of the randomized starting cases, including attributes of the optimized designs, and a plot of the initial randomized areas for the 4 × 2 frame structure are presented in Fig. 7. Numerical values of the initial cross-sectional areas for each starting case are tabulated and reported in Appendix Appendix. It can be seen from a comparison of the results shown in Fig. 6 with those shown in Fig. 7 that, since all designs satisfy the displacement constraint, d∗ = 11.81 in., the nonlinear design shown in Fig. 6 is comprised of the lowest volume among the five designs, and hence is considered the best solution.

Fig. 7
figure 7

Resulting nonlinear optimized designs for randomized starting cases for the 4 × 2 frame structure

Full size image

To investigate the effect of considering material nonlinearity directly in the optimization problem, the best nonlinear design shown in Fig. 6, is compared with the best design solutions from two additional optimization problems considering the same domain and external force but assuming the material to be linear elastic. Specifically, the first linear optimization problem seeks to minimize the compliance for a given volume constraint and the second linear optimization problem seeks to minimize the volume subjected to a drift displacement constraint. These linear design solutions where then evaluated using nonlinear FE analysis described in Section 2.2.1 to assess their respective performance and compare this performance with that of the best nonlinear design. Details pertaining to the two linear optimization formulations can be found in Appendix Appendix. For both the linear optimization problems, the same multi-start strategy performed for the nonlinear design problem was employed, and the solution with the lowest objective function value was considered the best linear design. Figure 6 shows a comparison of the solution from the nonlinear volume minimization problem, denoted nonlinear design, with the solution of the linear compliance minimization problem, denoted linear design, and their performance in terms of system force-displacement response when evaluated using nonlinear FE analysis. The linear design is obtained by setting the optimal volume of the nonlinear design as the volume constraint for the linear compliance problem. From Fig. 6 it can be seen that both designs share a common primary load path; however, the nonlinear design includes an additional diagonal element in comparison with the linear design and the proportioning of the individual areas differs between the two designs. For reference, the element with maximum area is from the linear compliance design solution located at element 7 with an area of 31.18 in.2. Importantly, from the system force-displacement responses shown in Fig. 6, the nonlinear design satisfies the specified constraint (11.8 in.), whereas the linear design with the same volume of material as the nonlinear design, exceeds the specified constraint when evaluated by nonlinear FE analysis, with a displacement of 15.06, equivalent to a drift ratio of 3.2%, or 27.5% larger than the response of the nonlinear optimized design.

The solution of the second linear optimization problem, that is volume minimization subject to the same displacement constraint (2.5% drift) resulted in a linear design solution with the same general topology as the other linear design shown in Fig. 6 but with a volume of 5.1767 × 103 in.3. As anticipated, this volume is considerably smaller than the optimized volume of the nonlinear design. Scaling the linear volume of 5.1767 × 103 in.3 by a factor of 4.715, without changing the proportioning of the element cross-sectional areas, results in a design based on the linear optimized topology that satisfies the drift constraint when evaluated by nonlinear quasi-static analysis. Interestingly, 4.715 × 5.1767 × 103 = 2.4408 × 104 in.3, exceeds the volume of the nonlinear design of 2.3995 × 104 in.3. These comparisons illustrate the nonlinear design offers either better performance for the same volume or lower volume for a given level of performance, by comparison with the two optimized linear designs.

A summary of the performance metrics and design attributes, for the nonlinear and linear designs, is provided in Table 1. The cross-sectional areas (in.2) for the optimized designs are reported next to each element, from which the different allocation of volume to the common load path between the nonlinear and linear designs is apparent. The lateral force resistance of the nonlinear design, at a given displacement is marginally larger than that of the linear design and hence the total energy (ET) absorbed up to the displacement constraint is larger for the nonlinear design by 1.4%. Moreover, the minimum and maximum cross-sectional areas of the nonlinear design, in comparison with the linear design, have been reduced.

Table 1 Summary of the performance metrics and design attributes of the nonlinear volume minimization optimized design and corresponding linear design for the 4 × 2 frame structure
Full size table

When considering material inelasticity, the distribution of volume differs from the linear design, where some of the volume from the main load path in the base elements (i.e., 7 and 8) for the nonlinear design is reallocated to other elements in the primary load path (i.e., 5 and 6) and to add diagonal elements, or increase the volume of the common diagonal elements (i.e., 3 and 4). The redistribution is, in part, because in the nonlinear design the moment capacity of the elements is explicitly considered and if reached, supporting diagonal elements are required to limit deformations and hence additional elements appear where unbraced elements form plastic hinges, in particular at the connecting node of elements 9 and 10.

To illustrate the importance of the diagonal elements, element 3 is removed from the nonlinear design and an additional nonlinear analysis is performed for the same specified external force. The corresponding force-displacement response for the nonlinear design with and without element 3 is shown in Fig. 8. Although element 3 constitutes only 2.35% of the total volume of the optimized structure, its importance in attaining the specified displacement constraint is significant, as its removal results in a substantial increase (68.6%) in tip displacement relative to the nonlinear design with element 3 intact and hence is not able to satisfy the displacement constraint.

Fig. 8
figure 8

Force-displacement responses of the optimized nonlinear design for 4 × 2 frame structure with and without element 3

Full size image

The objective function and displacement constraint values for each iteration throughout the entire optimization process, following the procedure shown in Fig. 2, for the best nonlinear design of the 4 × 2 frame are shown in Fig. 9. The periodic drop and rise of the objective and constraint values correspond to the beginning of each phase of optimization. As can be seen from Fig. 9, the value of dv − d∗ is approximately zero at the final phase, illustrating that the optimized nonlinear design satisfies the specified displacement constraint d∗.

Fig. 9
figure 9

Iteration histories of the objective and constraint for the nonlinear design of 4 × 2 frame structure

Full size image

Additionally, the hysteretic FE model permits assessing the cyclic response of the design and evaluating the inelastic displacements. The optimized nonlinear design was analyzed for the cyclic force history shown on the left side of Fig. 10 to obtain the system overall cyclic response shown in Fig. 10 and accordingly, the inelastic deformations can be evaluated.

Fig. 10
figure 10

Cyclic force history and cyclic response for the nonlinear design of 4 × 2 frame

Full size image

3.2 Example 2: a 3 × 2 half beam

The second design example is a 3 × 2 half beam structure under a vertical external force at the center of the full domain. The beam domain, boundary conditions, and location of the applied force are shown in Fig. 11. Due to the symmetry of the boundary conditions and loading for the full domain, a symmetric design is expected, therefore half of the domain is modeled and used in the optimization process for computational efficiency. The dimensions of the domain are Lx = 59.05 ft (18 m) and Ly = 19.68 ft (6 m). Similar to Example 1, the nonlinear minimum volume design problem subject to displacement constraint is solved for a center displacement constraint as d∗ = Lx/200 and applied external force of 250 kips.

Fig. 11
figure 11

Ground structure for the 3 × 2 half beam structure under a vertical force

Full size image

As in Example 1, the values of the sensitivities for the displacement constraint evaluated using the analytical gradients developed for the hysteretic beam FE modeling approach via the direct differentiation method are compared with numerical sensitivities obtained by finite difference approximation for the 3 × 2 half beam ground structure. For comparison, these sensitivities are plotted in Fig. 12. As with Example 1, the sensitivities agree well with negligible relative error thus providing further verification of the accuracy of the analytical sensitivities obtained through the direct differentiation approach described in Section 2.2.2.

Fig. 12
figure 12

Comparison of the results of sensitivity analysis derived with the analytical direct differentiation method and finite difference approximation for the 3 × 2 half beam ground structure

Full size image

Similar to Example 1, the nonlinear design problem is solved for multiple starting cases, including uniform and randomized starting areas. The resulting optimized topologies for uniform and randomized areas are shown in Figs. 13 and 14, respectively. Plot of the randomized initial area values for each randomized starting case and design attributes are also presented in Fig. 14. Numerical values for the randomized areas for each starting case are tabulated and reported in Appendix Appendix. Again all designs satisfy the displacement constraint of d∗ = Lx/200 = 3.54 in. so that by comparing the results shown in Fig. 13 with those shown in Fig. 14, the nonlinear design shown in Fig. 13 is comprised of the lowest volume and hence is considered the best nonlinear design solution.

Fig. 13
figure 13

Nonlinear minimum volume design for Lx/200 center displacement and the comparative linear design with the equivalent volume for the 3 × 2 half beam structure along with the force-displacement responses for each optimized design. Numerical values adjacent to the elements indicate the element number

Full size image
Fig. 14
figure 14

Resulting nonlinear optimized designs for randomized starting cases for the 3 × 2 half beam structure

Full size image

As with Example 1, the best nonlinear topology is compared with the optimized solutions from two linear topology optimization problems. Again a multi-start strategy is employed for both linear topology optimization problems and the linear design reported for each optimization problem is the one with the lowest objective function value that satisfied the constraints from among all the starting cases. These linear design solutions where then evaluated using nonlinear FE analysis described in Section 2.2.1 to assess their respective performance and compare this performance to that of the best nonlinear design. The first linear optimization problem seeks to minimize the compliance for a given volume constraint. More specifically, the linear design is obtained by setting the optimized volume of the nonlinear design as the volume constraint for the linear compliance problem for the purpose of comparison. The linear design and the associated force-displacement responses obtained from nonlinear quasi-static analysis of the nonlinear and linear designs are shown in Fig. 13. For reference the element with maximum area is located in the linear design solution (element 7). As seen from Fig. 13, the nonlinear topology obtained from the proposed methodology, shows a common primary load path with the linear design, but includes additional diagonal elements outside of this primary load path. Albeit by less of a margin than with Example 1, as expected, the nonlinear design satisfies the specified center displacement constraint, whereas the linear design when evaluated by nonlinear FE analysis slightly exceeds the constraint for this example.

The second linear optimization problem seeks to minimize the volume subjected to a drift displacement constraint. Solving the linear volume minimization design problem subject to the displacement constraint d∗ of Lx/200 resulted in a volume of 4.1016 × 103 in.3 (for details of the linear design problems, see Appendix Appendix). The topology for the linear volume minimization problem is similar to that shown in Fig. 13 and has been omitted to avoid unnecessary repetition. As expected, this volume is considerably smaller than the optimized volume of the nonlinear design. Scaling the linear volume by a factor of 2.25 results in a design, based on the linear volume minimization design, that satisfies the displacement constraint when evaluated by nonlinear quasi-static analysis. However, 2.25 times 4.1016 × 103 in.3, or 9.2286 × 103 in.3, that exceeds the volume of the nonlinear design of 9.1790 × 103 in.3. These results are consistent with those observed for the nonlinear design of the 4 × 2 frame structure in Example 1, and again illustrate that the nonlinear design either offers better performance for the same volume or lower volume for a given level of performance, by comparison with the two linear designs.

Table 2 summarizes the results and attributes for the nonlinear and comparative linear design solutions for the 3 × 2 half beam. Again the cross-sectional areas (in.2) for the optimized designs are reported next to each element, and the difference in the values of areas is shown. In the nonlinear design, the volume allocated to the primary load path (i.e., elements 2, 4, 6, 7, 8, and 10) is less than for the linear design, and a portion of volume is allocated to the supplementary supporting elements (i.e., elements 1, 3, 5, and 9), which is necessary to satisfy the specified design constraint. Again, the nonlinear design has a marginally higher force resistance for a given displacement and as such results in a larger amount of absorbed energy (ET) up to the displacement constraint, by comparison with the linear design, by 0.8%. In the nonlinear design, the minimum and maximum cross-sectional areas have been reduced relative to the linear design. Similar to Example 1, the optimized volume distribution and increase in the number of elements relative to the linear design are the main differentiating features.

Table 2 Summary of the performance metrics and design attributes of the nonlinear volume minimization optimized design and corresponding linear design for the 3 × 2 half beam structure
Full size table

The histories of the objective and displacement constraint for each iteration throughout the optimization process for the nonlinear design of the 3 × 2 half beam frame are shown in Fig. 15 following the process shown in Fig. 2. Again, in the final phase, that is, last iteration, the value of dv − d∗ is approximately zero indicating that the displacement constraint is satisfied at the final stage of optimization. As with Example 1, the periodic drop and rise of the objective and constraint values correspond to the beginning of each phase of optimization.

Fig. 15
figure 15

Iteration histories of the objective and constraint for the nonlinear design of 3 × 2 half beam structure

Full size image

As previously mentioned, the hysteretic FE modeling permits analysis of the cyclic response and evaluating the inelastic deformations of the system without any change in the formulation. For this example, the cyclic loading shown in Fig. 16 is applied to the optimized nonlinear beam design presented in Fig. 13 to obtain the cyclic response of the design and inelastic deformations.

Fig. 16
figure 16

Cyclic force history and cyclic response for the nonlinear design of 3 × 2 half beam

Full size image

4 Summary and concluding remarks

This paper contributes a method for the topology optimization of nonlinear structures based on a hysteretic beam FE model. Two beneficial features of the hysteretic FE modeling approach in the context of topology optimization are that analytical sensitivities could be derived by invoking a mathematical approximation for the signum function and the stiffness and hysteretic matrices need only to be evaluated once for each nonlinear structural analysis. As such, original analytical sensitivities and solution algorithms were presented to combine the hysteretic FE modeling approach and topology optimization.

The utility of the method was demonstrated through two numerical design examples. The optimized designs are sought while permitting material inelasticity by way of inelastic deformations in individual elements. Due to the non-convexity of the optimization problem considered in this study, multiple starting cases with randomized initial cross-sectional areas were performed and used to initiate the optimization process. For each design example presented, the uniform area starting case resulted in the best nonlinear design solution. However, it is worth noting, that sampling from a high-dimensional design space subjected to nonlinear constraints in the context of topology optimization is an ongoing research topic. The resulting nonlinear design comprised of elements along a common load path similar to the comparative linear design. However, the distribution of volume to elements in the common load path varies and additional elements are included in the nonlinear design. These elements are necessary for the design to achieve the specified displacement constraint. While the primary structural system designs are similar, these differences between the nonlinear and linear designs serve important purposes in attaining the overall design objectives. Although the optimized design from the nonlinear and linear designs share some similar features, in the context of frame structures and beam elements, the findings from this study suggest that the solution obtained from linear elastic problem formulation is not suitable if inelastic deformations are expected and that the inelastic deformations should be explicitly considered to ensure the designs compliance with the specified requirements.

For this study, the scope was restricted to planar frame structures composed of nonlinear Euler-Bernoulli beam elements to introduce the idea of hysteretic FE method for nonlinear topology optimization. As is well known, Newton type solution schemes require iterations at each step in the analysis that can significantly increase the computational cost relative to analysis of linear systems, as was observed for the numerical examples presented in this study. As such, part of ongoing research is aimed at devising a more efficient solution scheme for topology optimization employing the hysteretic finite element modeling approach. Other ongoing research is aimed at extending the suggested hysteretic FE topology optimization method to include nonlinear Timoshenko beam elements, local damage constraints, and time varying excitation for the design of frame structures whereby variation of the structural response with time is implicitly considered. Further extensions to 3D space frames and continuum structures are also possible and of interest to the authors in future work. Such extensions do however require enhancements to existing hysteretic FE beam models, including addition of transverse, rotation and torsion DOF and an appropriate yield function or development of a 3D hysteretic FE solid element.