Topology optimization framework for structures subjected to stationary stochastic dynamic loads

Abstract

The field of topology optimization has progressed substantially in recent years, with applications varying in terms of the type of structures, boundary conditions, loadings, and materials. Nevertheless, topology optimization of stochastically excited structures has received relatively little attention. Most current approaches replace the dynamic loads with either equivalent static or harmonic loads. In this study, a direct approach to problem is pursued, where the excitation is modeled as a stationary zero-mean filtered white noise. The excitation model is combined with the structural model to form an augmented representation, and the stationary covariances of the structural responses of interest are obtained by solving a Lyapunov equation. An objective function of the optimization scheme is then defined in terms of these stationary covariances. A fast large-scale solver of the Lyapunov equation is implemented for sparse matrices, and an efficient adjoint method is proposed to obtain the sensitivities of the objective function. The proposed topology optimization framework is illustrated for four examples: (i) minimization of the displacement of a mass at the free end of a cantilever beam subjected to a stochastic dynamic base excitation, (ii) minimization of tip displacement of a cantilever beam subjected to a stochastic dynamic tip load, (iii) minimization of tip displacement and acceleration of a cantilever beam subjected to a stochastic dynamic tip load, and (iv) minimization of a plate subjected to multiple stochastic dynamic loads. The results presented herein demonstrate the efficacy of the proposed approach for efficient multi-objective topology optimization of stochastically excited structures, as well as multiple input-multiple output systems.

1 Introduction

Traditional structural design methods are based on an iterative procedure that focuses on structural safety; however, such designs are generally not optimal (Xu et al. 2017a, b). In this regard, structural optimization is an important design tool that can consider various performance objectives. Within this field, topology optimization seeks to obtain optimal material layout according to a objective function subjected to given design constraints (Bendsøe and Sigmund 2003). Extensive research has been done in topology optimization to develop well-posed formulations (Bendsøe and Kikuchi 1988; Kohn and Strang 1986; Bendsøe and Sigmund 1999; Sigmund and Petersson 1998; Sigmund 2007) and solve inherent numerical problems such as mesh dependency, checkerboard patterning, islanding, and local minima (Díaz and Sigmund 1995; Sigmund and Petersson 1998).

Topology optimization has been successfully applied to solve the minimum compliance problem subjected to deterministic static loading for general structures (Bendsøe and Sigmund 2003; Talischi et al. 2012), as well as domains representing buildings (Beghini et al. 2014). It also has been applied extensively to dynamic problems, such as eigenfrequency optimization for free vibration (Olhoff 1976, 1989; Filipov et al. 2016), minimum dynamic compliance for harmonic dynamic vibration (Ma et al. 1995; Filipov et al. 2016), and strain energy optimization for transient vibration (Kang et al. 2006; Behrou and Guest 2017). The latter research usually employs time-domain solutions, which is extremely time consuming, to obtain the response of the structure and the sensitivities; some researchers have recently proposed schemes to reduce the computational time of this step using mode acceleration model reduction methods (Zhao and Wang 2016), or multiresolution approaches (Filipov et al. 2016).

Many of the most severe loads that structures withstand are stochastic in nature: earthquake, wind, snow, rain, ocean waves, jet noise, turbulence in the boundary layer, etc. (Soong and Grigoriu 1993; Li and Chen 2009). Nevertheless, structural optimization of stochastically excited structures has developed more slowly than its deterministic counterpart; for example, some work has been done in preliminary size optimization of aircraft for coupled aerodynamic structural response under stochastic gust loading (Fidkowski et al. 2008). Most of the research has been done in size optimization of buildings using Monte Carlo simulations (Balling et al. 2009); however, numerous simulations are required to obtain meaningful results, which makes this approach time prohibitive. Researchers in earthquake engineering have also considered specific ground motion records (Allahdadian and Boroomand 2016); in this case, each record is only one realization of the underlying random process. Xu et al. (2017a, b) proposed a parametric size optimization method for linear and nonlinear buildings subjected to stationary and nonstationary stochastic excitation by solving a small-scale Lyapunov equation problem.

Chun et al. (2016) proposed a reliability-based topology optimization framework for a stationary Gaussian random process excitation using a discrete representation of the excitation and solving in the time-domain; this approach provides reasonable results, but the time stepping algorithm requires considerable computational effort. Recently, researchers have proposed formulations to minimize the covariance of the displacement of a fixed point (Zhang et al. 2015; Hu et al. 2016; Zhu et al. 2017; Yang et al. 2017) or multiple points (Spencer et al. 2016; Gomez and Spencer 2017). Others (e.g., Zhang et al. 2015, Zhu et al. 2017, Yang et al. 2017) used frequency-domain solutions based on the first few frequencies and mode shapes of the structure to obtain the covariance of the displacement. The computational time increases considerably when more modes are used, and the numerical errors in the sensitivities of the mode shapes increase (Haftka and Adelman 1989). Hu et al. (2016) used an explicit time-domain solution to obtain the covariance of displacements, which provides reasonable results, but involves two time-domain analyses. In addition, all previous approaches focus on displacement response and cannot easily be generalized to multi-objective problems due to requiring additional modes to achieve adequate accuracy, or multiple input-multiple output systems. Spencer et al. (2016) and Gomez and Spencer (2017) used the Lyapunov equation to obtain the covariance of the response; however, numerical difficulties in solving the Lyapunov equation limited the size of the meshes that could be employed.

The solution of the Lyapunov equation (i.e., AX + XA^T + Q = 0) is typically obtained using the Bartels-Steward algorithm or the Hessenberg-Schur algorithm (Golub et al. 1979), both of which require the Schur factorization of the matrix A. Variations of these algorithms are implemented in typical software for scientific computing such as Matlab and Python. These methods provide good results for small dense matrices A, Q; however, two practical issues arise for large-scale systems: (i) they require $\mathbb {O}(N^{3})$ floating-point operations and (ii) $\mathbb {O}(N^{2})$ memory (Kressner 2008), both of which impose a significant constraint on the size of the problem using current computers. Several approaches have been developed that exploit the low-rank nature of the matrix Q using Krylov subspace methods (Saad 1990; Jbilou and Riquet 2006; Kressner 2008) or the matrix sign function decomposition with Newton’s iterative method (Higham 2008; Balzer 1980). These algorithms reduce the computational time and required memory; however, they fail when the symmetric part of A, i.e., A + A^T is not negative definite (Benner et al. 2008), which is the standard case for state space matrices for structural systems. The Alternating Direction Implicit (ADI) iteration algorithm was developed to solve linear systems in terms of optimal shift parameters (Wachspress 2013) and has been adapted to solve the Lyapunov and algebraic Riccati equations with low-rank matrices Q with superlinear convergence (Penzl 1999; Li and White 2002; Benner et al. 2008). This method is adopted herein to efficiently solve the Lyapunov equation with large-scale sparse matrices.

This paper proposes a new multi-objective topology optimization framework for stochastically excited structures. The performance function is given in terms of the stationary response covariances, obtained by solving a large-scale Lyapunov equation. The proposed performance function is versatile and allows optimization of the structure’s displacement, velocity, and/or acceleration, including multi-objective functions; also, an efficient adjoint method is developed to obtain the sensitivities of this performance function, which accommodates the use of gradient-based updating procedures. This paper is organized as follows: Section 2 describes the problem formulation including the state space representation of the structure and excitation, the response under stochastic excitation, and topology optimization formulation; Section 3 provides details for the solution of the optimization problem, including large-scale solution of Lyapunov equations, sensitivity analysis, and enforcing symmetry constraints; Section 4 shows numerical examples of the optimization of a cantilever beam subjected to a stochastic dynamic tip load and a cantilever beam subjected to a stochastic dynamic base excitation; Section 5 presents the conclusions of this work.

2 Problem formulation

This section formulates the topology optimization problem for structures subjected to stationary stochastic dynamic loading. First, the structural system is converted from the standard second-order differential equation into the state space representation, and the excitation is modeled as a filtered white noise. Subsequently, the covariance matrix of the stationary stochastic responses is obtained. Finally, the topology optimization framework is presented based on this formulation.

2.1 State space representation

Consider a dynamic linear system with N degrees of freedom (DOF) whose equation of motion is given by

$$ \mathbf{M}\ddot{\mathbf{u}} + \mathbf{C}\dot{\mathbf{u}} + \mathbf{Ku} = \mathbf{G f}(t) $$

(1)

where M, C, and K represent the mass, damping, and stiffness matrices, respectively; G is the load effect matrix; f(t) is the input excitation vector; and u is the displacement vector.

Defining the vector x_s as

$$ \mathbf{x}_{\text{s}} = \left[\begin{array}{ccc} \mathbf{u}^{\text{T}} && \dot{\mathbf{u}}^{\text{T}} \end{array}\right]^{\text{T}} $$

(2)

the system can be represented in the state space form by

$$ \begin{array}{cc} \dot{\mathbf{x}}_{\text{s}} = \mathbf{A}_{\text{s}} \mathbf{x}_{\text{s}} + \mathbf{B}_{\text{s}}\mathbf{f}(t) \\ \mathbf{y} = \mathbf{C}_{\text{s}} \mathbf{x}_{\text{s}} + \mathbf{D}_{\text{s}}\mathbf{f}(t) \end{array} $$

(3)

where the state matrices A_s and B_s are

$$ \mathbf{A}_{\text{s}} = \left[\begin{array}{ccc} \mathbf{0}_{N \times N} && \mathbf{I}_{N \times N} \\ -\mathbf{M}^{-1}\mathbf{K} && -\mathbf{M}^{-1}\mathbf{C} \end{array}\right], \quad \mathbf{B}_{\text{s}} = \left[\begin{array}{cc} \mathbf{0}_{N \times 1} \\ \mathbf{M}^{-1} \mathbf{G} \end{array}\right] $$

(4)

with 0 is a matrix of zeros, and I is the identity matrix, with dimensions given by the subscripts; y is the vector of output responses of interest corresponding to the matrices C_s and D_s.

2.2 Stochastic excitation

Many physical phenomena can be modeled in terms of a stochastic process (Soong and Grigoriu 1993). In this study, the excitation is assumed to be a zero-mean stationary random process modeled as a filtered white-noise with the following space state space representation

$$ \begin{array}{ll} \dot{\mathbf{x}}_{\text{f}} &= \mathbf{A}_{\text{f}} \mathbf{x}_{\text{f}} + \mathbf{B}_{\text{f}} \mathbf{w} (t) \\ \mathbf{f} &= \mathbf{C}_{\text{f}} \mathbf{x}_{\text{f}} \end{array} $$

(5)

where the matrices A_f, B_f, and C_f are based on the characteristics of the excitation; x_f is the state vector of the excitation model with N_f states; and w(t) is a vectored white noise process.

The white noise vector w(t) satisfies

$$ \mathbb{E}(\mathbf{w}(t))= 0, \quad \mathbb{E}(\mathbf{w}(t_{1})\mathbf{w}(t_{2}))= 2\pi \mathbf{S}_{0} \delta(t_{1}-t_{2}) $$

(6)

where $\mathbb {E}(\cdot )$ is the expected value operator, S₀ is the magnitude two-sided constant m × m power spectral density matrix, and δ(⋅) is the Dirac delta function.

An augmented state vector x_a can be defined as

$$ \mathbf{x}_{\text{a}} = \left[\begin{array}{ccc} \mathbf{x}_{\text{s}}^{\text{T}} && \mathbf{x}_{\text{f}}^{\text{T}} \end{array}\right]^{\text{T}} $$

(7)

yielding an augmented system whose state space representation is given by

$$ \begin{array}{ll} \dot{\mathbf{x}}_{\text{a}} &= \mathbf{A}_{\text{a}} \mathbf{x}_{\text{a}} + \mathbf{B}_{\text{a}} \mathbf{w}(t) \\ \mathbf{y} &= \mathbf{C}_{\text{a}} \mathbf{x}_{\text{a}} \end{array} $$

(8)

where the matrices A_a, B_a, and C_a are given by

$$ \begin{array}{lll} \mathbf{A}_{\text{a}} &= \left[\begin{array}{cccc} \mathbf{A}_{\text{s}} && \mathbf{B}_{\text{s}} \mathbf{C}_{\text{f}} \\ \mathbf{0}_{N_{\text{f}}\times N} && \mathbf{A}_{\text{f}} \end{array}\right], \quad \mathbf{B}_{\text{a}} = \left[\begin{array}{ccc} \mathbf{0}_{2N \times 1} \\ \mathbf{B}_{\text{f}} \end{array}\right], \\ \mathbf{C}_{\text{a}} &= \left[\begin{array}{ccc} \mathbf{C}_{\text{s}} && \mathbf{D}_{\text{s}}\mathbf{C}_{\text{f}} \end{array}\right] \end{array} $$

(9)

Note that the input of the augmented system is a vectored white noise, and the output of the augmented system is the outputs of interest for the structural system.

2.3 Structural response

The covariance matrix of the response of a linear time invariant system subjected to a white noise excitation, such as the one considered in this study, can be computed directly from Soong and Grigoriu (1993)

$$ \dot{\boldsymbol{\Gamma}}_{\mathbf{x}_{\text{a}}} =\mathbf{A}_{\text{a}} \boldsymbol{\Gamma}_{\mathbf{x}_{\text{a}}} +\boldsymbol{\Gamma}_{\mathbf{x}_{\text{a}}} \mathbf{A}_{\text{a}}^{\text{T}} + 2\pi \mathbf{B}_{\text{a}} \mathbf{S}_{0} \mathbf{B}_{\text{a}}^{\text{T}} $$

(10)

where

$$ \boldsymbol{\Gamma}_{\mathbf{x}_{\text{a}}} = \mathbb{E}((\mathbf{x}_{\text{a}}-\mathbf{\mu}_{\mathbf{x}_{\text{a}}}) (\mathbf{x}_{\text{a}}-\mathbf{\mu}_{\mathbf{x}_{\text{a}}})^{\text{T}}) = \mathbb{E}(\mathbf{x}_{\text{a}}\mathbf{x}_{\text{a}}^{\text{T}}) $$

(11)

Assuming that the input white noise has a zero mean and that $\boldsymbol {\Gamma }_{\mathbf {x}_{\text {a}}}(0)=\mathbf {0}$, then the mean value of the response is also zero, i.e., $\mathbf {\mu }_{\mathbf {x}_{\text {a}}}= \mathbf {0}$, then $\boldsymbol {\Gamma }_{\mathbf {x}_{\text {a}}} = \mathbb {E}(\mathbf {x}_{\text {a}}\mathbf {x}_{\text {a}}^{\text {T}})$. By considering the stationary part of the response, the covariance matrix becomes constant and its time derivative becomes zero, which yields the Lyapunov equation

$$ \mathbf{A}_{\text{a}} \boldsymbol{\Gamma}_{\mathbf{x}_{\text{a}}} +\boldsymbol{\Gamma}_{\mathbf{x}_{\text{a}}} \mathbf{A}_{\text{a}}^{\text{T}} + 2\pi \mathbf{B}_{\text{a}} \mathbf{S}_{0} \mathbf{B}_{\text{a}}^{\text{T}} = \mathbf{0} $$

(12)

The Lyapunov equation possesses a unique solution if the matrix A_a is Hurwitz, which means that its eigenvalues have strictly negative real parts. In the case considered herein, the eigenvalues of A_a are equal to the eigenvalues of A_s and A_g, due to the block structure of the former matrix (Strang 2003). The eigenvalues of A_s and A_g will have negative real parts if the structure and the excitation are strictly stable. Also, the matrix $2\pi \mathbf {B}_{\mathbf {a}} \mathbf {S}_{\mathbf {0}} {\mathbf {B}_{\mathbf {a}}^{\mathbf {T}}}$ is symmetric positive semi-definite, if B_a has linearly independent columns and 2πS₀ is positive definite. Finally, because of the properties of the covariance matrix, the solution of the Lyapunov equation is guaranteed to be symmetric positive semi-definite.

The covariance of the structural output y can be calculated via

$$ \boldsymbol{{\Gamma}_{y}} = \mathbb{E}(\mathbf{y y^{T}}) = \mathbf{C}_{\text{a}}\mathbb{E}(\mathbf{x}_{\text{a}} \mathbf{x}_{\text{a}}^{\text{T}}) \mathbf{C}_{\text{a}}^{\text{T}} = \mathbf{C}_{\text{a}} \boldsymbol{\Gamma}_{\mathbf{x}_{\text{a}}} \mathbf{C}_{\text{a}}^{\text{T}} $$

(13)

2.4 Topology optimization formulation

Design variables in continuous-domain topology optimization are chosen as the relative density in each element (Bendsøe and Sigmund 2003). Therefore for element n, the relative density variable is denoted by z_n, where n ∈{1,2,…, N_el}, and N_el is the total number of elements. The optimization formulation is thus given by:

Find z = [z₁, z₂,…, z_N] such that:

$$ \begin{array}{ll} \min\limits_{\mathbf{z}} & J(\mathbf{z})= \phi\left( \boldsymbol{\Gamma}_{\mathbf{x}_{\text{a}}} (\mathbf{z}), \mathbf{z} \right) \\ \text{s.t.} & g(\mathbf{z})=V(\mathbf{z})- V_{\max} \le 0\\ &\mathbf{A}_{\text{a}} \boldsymbol{\Gamma}_{\mathbf{x}_{\text{a}}} +\boldsymbol{\Gamma}_{\mathbf{x}_{\text{a}}} \mathbf{A}_{\text{a}}^{\text{T}} + 2\pi \mathbf{B}_{\text{a}} \mathbf{S}_{0} \mathbf{B}_{\text{a}}^{\text{T}} = \mathbf{0} \\ & z_{n} \in [z_{\min},z_{\max}] \text{ for} n = 1,2,\ldots,N_{\text{el}} \end{array} $$

(14)

where ϕ is a continuous differentiable positive scalar function, $\boldsymbol {\Gamma }_{\mathbf { x}_{\text {a}}}$ is the stationary covariance of the response, V is the volume, V_max is the volume constraint, and z_min and z_max are the lower and upper bounds on the density variables.

Note that the proposed performance function allows consideration of many different problems. To illustrate this point for different types of response, consider the following particular case

$$ J(\mathbf{z})= \mathbf{F}(\mathbf{z}): \boldsymbol{\Gamma}_{\mathbf{x}_{\text{a}}} (\mathbf{z}) $$

(15)

where J(z) is the objective function, : represents the double dot product between matrices or the sum of the diagonal entries of their product, F is a symmetric positive semidefinite matrix. Some examples are shown next, for which the specific matrix F is described (see the Appendix for the details of the derivations):

• 1) Covariance of the various DOFs defined by the output equation y = C_ax_a,

  $$ J= \mathbf{C}_{\text{a}} \boldsymbol{\Gamma}_{\mathbf{x}_{\text{a}}} \mathbf{C}_{\text{a}}^{\text{T}}, \quad \mathbf{F} = \mathbf{C}_{\text{a}}^{\text{T}} \mathbf{C}_{\text{a}} $$

  (16)

  For example, $\mathbf {C}_{\text {a}}=\mathbf {C_{u}} =\left [\begin {array}{cccccc} \mathbf {I}_{N\times N} && \mathbf {0}_{N\times N} && \mathbf {0}_{N\times N_{\text {f}}} \end {array}\right ]$ for displacements, $\mathbf {C}_{\text {a}}=\mathbf {C_{\dot {u}}} =\left [\begin {array}{ccccc} \mathbf {0}_{N\times N} && \mathbf {I}_{N\times N} && \mathbf {0}_{N\times N_{\text {f}}} \end {array}\right ]$ for velocities, and $\mathbf {C}_{\ddot {\mathbf {u}}} = \left [\begin {array}{ccccc} -\mathbf {M}^{-1}\mathbf {K} && -\mathbf {M}^{-1}\mathbf {C} && \mathbf {M}^{-1}\mathbf {G} \mathbf {C}_{\text {f}} \end {array}\right ]$ for accelerations. In each of these cases, all, or a selected number, of the DOFs can be employed in the objective function.

• 2) Expected value of the static compliance, based on the static case of potential energy minimization

  $$ J=\mathbb{E}(\mathbf{u}^{\text{T}} \mathbf{Ku}), \quad \mathbf{F} = \mathbf{C}_{\mathbf{ u}}^{\text{T}} \mathbf{K C_{u}} $$

  (17)

• 3) Expected value of the kinetic energy

  $$ J=\mathbb{E}(\dot{\mathbf{u}}^{\text{T}} \mathbf{M\dot{u}}), \quad \mathbf{F} = \mathbf{C}_{\dot{\mathbf{u}}}^{\text{T}} \mathbf{K C_{\dot{u}}} $$

  (18)

• 4) Linear combination of performance functions with non-negative coefficient α. For example, engineering designers may desire to perform multi-objective optimization to minimize displacements and accelerations (Xu et al. 2017a, b). In this case,

  $$ J = \mathbf{F}_{1}:\boldsymbol{\Gamma}_{\mathbf{x}_{\text{a}}} + \alpha \mathbf{F}_{2}:\boldsymbol{\Gamma}_{\mathbf{x}_{\text{a}}}, \quad \mathbf{F} = \mathbf{F}_{1}+\alpha \mathbf{F}_{2} $$

  (19)

  where $\mathbf {F}_{1} =\mathbf {C}_{\mathbf {u}}^{\text {T}} \mathbf {C}_{\mathbf {u}}$, $\mathbf {F}_{2} =\mathbf {C}_{\ddot {\mathbf {u}}}^{\text {T}}\mathbf {C}_{\ddot {\mathbf {u}}}$.

As illustrated here, the performance function is completely defined by the covariance of the response $\boldsymbol {\Gamma }_{\mathbf {x}_{\text {a}}}$, which is obtained through solution of the Lyapunov equation. Consequently, the stochastic optimization problem has been transformed into a deterministic counterpart.

A gradient-based optimization procedure is preferred, such as the method of moving asymptotes (Svanberg 1987), for which the gradient of the performance function and constraints are required. Section 3.3 provides details on how to obtain them.

3 Solution method

This section describes the numerical details for the solution of the topology optimization problem formulation for stochastic excitations. These details include the solution of the Lyapunov equation, the efficient evaluation of sensitivities, symmetry constraints to reduce problem size, and optimization details.

3.1 Material interpolation

The well-known continuous approach, based on intermediate element densities, is adopted to obtain the optimal topology (Bendsøe and Sigmund 2003). For each element n, a relative density variable z_n is chosen, where n ∈{1,2,…, N_el}. Then, Young’s modulus and density for each element are obtained by some interpolation rule; in this work, SIMP interpolation is used (Bendsøe and Sigmund 1999). However, in dynamic problems, local spurious modes may appear due to the artificially low ratios of stiffness to mass using SIMP; to overcome this problem, a modified SIMP is implemented where the elements with low relative density are penalized with a larger exponent to compute the mass (Tcherniak 2002; Du and Olhoff 2007). Du and Olhoff (2007) recommend using the penalization factor equal to p + 3 for elements with density below 0.1, and they propose corrections to ensure continuity and differentiability of the interpolation rule. Section 4.1 presents an example and further discussion of the influence of this local modes penalization on optimal topologies.

In this study, the following relationships are used

$$ \begin{array}{ll} E(z) &=[\epsilon+(1-\epsilon)z^{p}]E^{0}\\ \rho(z)&= \left\{\begin{array}{ll} z^{q}\rho^{0}, & \text{if} z\ge 0.1 \\ c_{0} z^{p + 3}\rho^{0}, & \text{if} z< 0.1 \end{array}\right. \end{array} $$

(20)

where E and ρ are Young’s modulus and density for the element with variable z, E⁰ and ρ⁰ are Young’s modulus and density for the solid material, p > 1 and q ≥ 1 are the penalization factors, 𝜖 is a small number (Talischi et al. 2012), and c₀ = 10^p+ 3−q is a coefficient to ensure continuity in density interpolation rule. Alternative interpolation rules to address this issue can be considered (Zhu et al. 2010, 2018).

3.2 Lyapunov equation solver

As seen in Section 2.3, the covariance of the response of the system can be determined from the solution of the Lyapunov equation (see (12)), which is rewritten next for simplicity

$$ \mathbf{A}_{\text{a}}\boldsymbol{\Gamma}_{\mathbf{x}_{\text{a}}}+\boldsymbol{\Gamma}_{\mathbf{x}_{\text{a}}} \mathbf{A}_{\text{a}}^{\text{T}}+\tilde{\mathbf{B}}_{\text{a}} \tilde{\mathbf{B}}_{\text{a}}^{\text{T}}=\mathbf{0} $$

(21)

where $\mathbf {A}_{\text {a}} \in \mathbb {R}^{N^{\prime }\times N^{\prime }}$ and $\tilde {\mathbf {B}}_{\text {a}} = \sqrt {2 \pi } \tilde {\mathbf {S}} \in \mathbb {R}^{N^{\prime }\times m}$ with m ≪ N^′, and $\tilde {\mathbf {S}}$ is the lower Cholesky factor of S₀. The third term of the LHS in this equation is a low-rank matrix, and the state matrix has an indefinite symmetric part; therefore, the Cholesky factor alternating direction implicit (CF-ADI) iterative algorithm is the only suitable method for the solution (Li and White 2002; Benner et al. 2008).

The CF-ADI algorithm solves for the complex matrix $\mathbf {Z} \in \mathbb {C}^{N^{\prime }\times mn}$

$$ \mathbf{Z} = \left[\begin{array}{lllllll} \mathbf{V}_{1} && \mathbf{V}_{2} && {\ldots} && \mathbf{V}_{n} \end{array}\right] $$

(22)

where the unknown matrix $\boldsymbol {\Gamma }_{\mathbf {x}_{\text {a}}}$ is given by

$$ \boldsymbol{\Gamma}_{\mathbf{x}_{\text{a}}}=\mathbf{ZZ^{H}} $$

(23)

and ^H denotes the Hermitian transpose operation.

The matrices V_i are obtained using the iterative procedure showed in the following equations

$$\begin{array}{@{}rcl@{}} \mathbf{V}_{1} &= & \sqrt{-2 \Re (p_{1})}(\mathbf{A}_{\text{a}}+p_{1} \mathbf{I})^{-1} \tilde{\mathbf{B}}_{\text{a}} \\ \mathbf{V}_{k} &= & \sqrt{\frac{\Re (p_{k})} {\Re (p_{k-1})}} [\mathbf{V}_{k-1} - (p_{k}+p^{*}_{k-1}) (\mathbf{A}_{\text{a}}+p_{k} \mathbf{I})^{-1} \mathbf{V}_{k-1}]\\ \end{array} $$

(24)

where $\mathbb {R}(\cdot )$ denotes the real part function, ^∗ denotes the complex conjugate, and $p_{i} \in \mathbb {C}^{-}$ are complex shift parameters with negative real part that satisfy

$$ \{p_{1},p_{2},\ldots,p_{l}\} = \underset{\{p_{1},\ldots,p_{l}\} \in \mathbb{C}^{-}}{\text{argmin}} \max_{t \in \sigma(\mathbf{A}_{\text{a}})} \frac{\left| r_{l}(t) \right|}{\left| r_{l}(-t) \right|} $$

(25)

with $r_{l}(t)={\prod }_{i = 1}^{l}(t-p_{i})$ and σ(A_a) denotes the spectrum of A_a. Obtaining these optimal shift parameters is a expensive task (Benner et al. 2008); therefore, in this study, an algorithm to obtain a set of sub-optimal parameters is used instead (Penzl 1999).

To assess the accuracy of the proposed solver with the traditional Bartel-Stewards algorithm, which is a built-in function in Matlab, the objective function for the same problem is computed using both approaches. A uniform rectangular domain of 6 × 12 discretized into 3200 elements is considered; this smaller problem is chosen due to the excessive computational time required for the traditional solver in larger problems. The absolute difference between the proposed approach and the standard Matlab solver for the objective function is 3.11 × 10^− 9 and the relative difference is 1.72 × 10^− 8; therefore, the proposed solver achieves an accuracy similar to the traditional solver, and in this example, it requires only 1/643 of the computational time.

The CF-ADI algorithm requires four parameters: k⁺ is the number of Ritz values using power iteration, k⁻ is the number of Ritz values using inverse iteration, l is the number of parameters, and n is the number of iterations; the accuracy and efficiency of the method depend on these parameters. To obtain appropriate values for these parameters, a numerical test was conducted for a rectangular domain of 5 × 15 discretized into 7500 elements. To assess the accuracy of the algorithm, the residual of the equation is defined as

$$ \mathbf{R}=\mathbf{A}_{\text{a}}\boldsymbol{\Gamma}_{\mathbf{x}_{\text{a}}}+\boldsymbol{\Gamma}_{\mathbf{x}_{\text{a}}} \mathbf{A}_{\text{a}}^{\text{T}}+\tilde{\mathbf{B}}_{\text{a}} \tilde{\mathbf{B}}_{\text{a}}^{\text{T}} $$

(26)

which should be a matrix of small numbers. Figure 1a shows the logarithm of the Frobenius norm of the residuals, varying the number of parameters and iterations. Figure 1b shows the logarithm of the Frobenius norm of the residual varying the number of Ritz values using power iteration and Ritz values using inverse iteration. As these figures show, the CF-ADI algorithm achieves good results for a sufficiently large number of iterations and parameters; moreover, using more Ritz values with inverse iteration improves accuracy. For a problem of this size with the largest number of iterations and parameters, a direct implementation of this solver requires a computational time of 4.9 s in a computer with processor Intel Xeon E3-1285 v6 @4.10 GHz and 32 Gb of RAM. For comparison using the same computer and the same structure, a time-domain solution of a harmonic excitation of 30 Hz with sampling frequency of 100 Hz and 1024 time steps using an efficient implementation of the Newmark method requires 3.27 s. These timing results show that a complete stochastic solution can be obtained for about the same cost as 1.5 time-history solutions of one harmonic excitation, which demonstrate the efficacy of the proposed approach.

Fig. 1

$\log \|R\|_{F}$ varying a the number of parameters l and the number of iterations n and b the number Ritz values using power iteration k⁺ and the number Ritz values using inverse iteration k⁻

3.3 Sensitivity analysis

A gradient-based optimization procedure is preferred for computational efficiency purposes; therefore, the gradient of the performance function and constraints are required. The constraints are linear, making the gradient straightforward to obtain. Because the performance function defined in (14a) depends on the covariance matrix, which is implicitly defined by (21), a direct differentiation approach would be expensive due to the large number of variables. Therefore, an adjoint method is proposed, for which the following Lagrangian function is defined with a symmetric positive semi-definite Lagrange multiplier matrix Λ

$$ \mathcal{L}(\mathbf{z},\boldsymbol{\Lambda} ) = J(\mathbf{z} ) + \boldsymbol{\Lambda} :\left( \mathbf{A}_{\text{a}} \boldsymbol{\Gamma}_{\mathbf{x}_{\text{a}}} + \boldsymbol{\Gamma}_{\mathbf{x}_{\text{a}}} \mathbf{A}_{\text{a}}^{\text{T}} + \tilde{\mathbf{B}}_{\text{a}} \tilde{\mathbf{B}}_{\text{a}}^{\text{T}}\right) $$

(27)

The corresponding adjoint equation can be solved to obtain Λ, thus eliminating the implicitly defined gradients of $\boldsymbol {{\Gamma }_{\mathbf {x}_{\text {a}}}}$,

$$ \mathbf{A}_{\text{a}}^{\text{T}}\boldsymbol{\Lambda} + \boldsymbol{\Lambda} \mathbf{A}_{\text{a}} + \frac{\partial \phi}{\partial \boldsymbol{\Gamma}_{\mathbf{x}_{\text{a}}}}=\mathbf{0} $$

(28)

The previous result is consistent with a similar approach implemented in the optimization of a control cost function (Yan et al. 2016). Equation (28) is a Lyapunov equation, which has a unique solution because $\mathbf {A}_{\text {a}}^{\text {T}}$ is Hurwitz. Finally, the sensitivity of the performance function, which is equal to the sensitivity of the Lagrangian function, is given by the following equation

$$ \begin{array}{ll} \frac{\partial J}{\partial z_{n}} = & \left( \frac{ \partial \mathbf{A}_{\text{a}}}{\partial z_{n}} \boldsymbol{\Gamma}_{\mathbf{x}_{\text{a}}} + \boldsymbol{\Gamma}_{\mathbf{x}_{\text{a}}} \frac{\partial \mathbf{A}_{\text{a}}^{\text{T}}}{\partial z_{n}} + \frac{\partial (\tilde{\mathbf{B}}_{\text{a}} \tilde{\mathbf{B}}_{\text{a}}^{\text{T}})}{\partial z_{n}} \right):\boldsymbol{\Lambda} \\ & + \frac{\partial \phi}{\partial z_{n}} \end{array} $$

(29)

For the particular case shown in (15), the previous equations reduce to

$$ \mathbf{A}_{\text{a}}^{\text{T}}\boldsymbol{\Lambda} + \boldsymbol{\Lambda} \mathbf{A}_{\text{a}} +\mathbf{F}=\mathbf{0} $$

(30)

$$ \begin{array}{ll} \frac{\partial J}{\partial z_{n}} = & \left( \frac{ \partial \mathbf{A}_{\text{a}}}{\partial z_{n}} \boldsymbol{\Gamma}_{\mathbf{x}_{\text{a}}} + \boldsymbol{\Gamma}_{\mathbf{x}_{\text{a}}} \frac{\partial \mathbf{A}_{\text{a}}^{\text{T}}}{\partial z_{n}} + \frac{\partial (\tilde{\mathbf{B}}_{\text{a}} \tilde{\mathbf{B}}_{\text{a}}^{\text{T}})}{\partial z_{n}} \right):\boldsymbol{\Lambda} \\ & + \frac{\partial \mathbf{F}}{\partial z_{n}}:\boldsymbol{\Gamma}_{\mathbf{x}_{\text{a}}} \end{array} $$

(31)

Because F is symmetric positive semi-definite, the solution of the Lyapunov equation is symmetric positive semi-definite Λ, as assumed previously. Also, note that F can be expressed as a low-rank matrix product; hence, the efficient algorithm described in Section 3.2 can be applied.

The sensitivities of the performance function require the derivatives of the matrices A_a, B_a, and F that were defined explicitly in previous sections.

Adjoint sensitivities were successfully confirmed by comparison to finite difference. To assess the efficiency of the proposed method, several runs with different number of elements were performed. Figure 2 shows the computational time for different approaches, demonstrating that the proposed approach (i.e., using the adjoint method with the CF-ADI solver) requires considerably less time.

Fig. 2

Computational time (FD, finite differences; DD, direct differentiation; AM, adjoint method with native solver; A-ADI, adjoint method with CF-ADI solver)

The detailed derivations of the results presented in this section are provided in the Appendix.

3.4 Symmetry constraints

In many problems, the domain, boundary conditions, and dynamic loadings are spatially symmetric, for example, the building subjected to a base motion in Fig. 3, and consequently, the structural response is constrained to follow symmetric and anti-symmetric modes. In the example shown in Fig. 3, the symmetry in the domain, the boundary conditions, and the loading dictates that the lateral displacement is symmetric, the vertical response is anti-symmetric, and the rotation angle response is symmetric. Therefore, using symmetry to reduce the computational burden can be done without loss of generality. Note that the proposed method does not require use of the symmetry constraint.

Fig. 3

Example of a symmetric domain with symmetric random loading

The symmetry in the response can be enforced using a constraint of the type

$$ \mathbf{u}=\mathbf{T}\tilde{\mathbf{u}} $$

(32)

where u is the vector of all DOFs, T is a transformation matrix, and $\tilde {\mathbf {u}}$ is the vector of master DOFs. Moreover, the transformation matrix and vector of all DOFs can be divided in blocks, possibly permuted due to DOF numbering, as follows

$$ \mathbf{T}=\left[\begin{array}{ll} \mathbf{I} \\ \mathbf{S} \end{array}\right], \quad \mathbf{u}=\left[\begin{array}{cc} \tilde{\mathbf{u}} \\ \mathbf{u^{c}} \end{array}\right] $$

(33)

where I is the identity matrix, S is the constraint matrix, and u^c is the vector of constrained DOFs. The constraint matrix S is a sparse matrix with exactly one non-zero entry per row and whose non-zero entries are equal to 1 or − 1, depending respectively on whether the constraint is associated with a symmetric or antisymmetric slave DOF. Therefore, the transformation matrix can be written as blocks of identity matrices, negative identity matrices, and zero matrices of consistent dimensions, possibly permuted due to DOF numbering. Similar relations are used for velocities and accelerations.

The reduced system matrices can be obtained through the following well-known relations

$$ \begin{array}{lllllll} \tilde{\mathbf{M}} &=\mathbf{T^{T} M T}, \quad & \tilde{\mathbf{C}} &=\mathbf{T^{T} C T}\\ \tilde{\mathbf{K}} &=\mathbf{T^{T} K T}, \quad & \tilde{\mathbf{G}} &=\mathbf{T^{T} G} \end{array} $$

(34)

The state space representation of this system and the augmented can be obtained using the reduced system matrices, and the Lyapunov equation can be solved to obtain the covariance of the response $\tilde {\boldsymbol {\Gamma }}_{\mathbf {x}_{\text {a}}}$. From the numerical point of view, the implementation can be done efficiently by using the previous relations, because all the matrices are highly sparse. Moreover, this transformation reduces the size of the problem to a approximately half, which results in a corresponding reduction in computation time for a given mesh size.

The covariance matrix $\boldsymbol {\Gamma }_{\mathbf {x}_{\text {a}}}$ of the initial augmented system can be recovered from the covariance matrix $\tilde {\boldsymbol {\Gamma }}_{\mathbf {x}_{\text {a}}}$ of the reduced system as follows

$$ \boldsymbol{\Gamma}_{\mathbf{x}_{\text{a}}}=\mathbb{E}({\mathbf{x}_{\text{a}}} {\mathbf{x}_{\text{a}}}^{\text{T}})=\mathbf{T}\mathbb{E}({\tilde{\mathbf{x}}_{\text{a}}} {\tilde{\mathbf{x}}_{\text{a}}}^{\text{T}})\mathbf{T}^{\text{T}}= \mathbf{T}\tilde{\boldsymbol{\Gamma}}_{\mathbf{x}_{\text{a}}}\mathbf{T}^{\text{T}} $$

(35)

Therefore, using the general form of the transformation matrix yields

$$ \boldsymbol{\Gamma}_{\mathbf{x}_{\text{a}}}=\left[\begin{array}{ll} \mathbf{I} \\ \mathbf{S} \end{array}\right] \tilde{\boldsymbol{\Gamma}}_{\mathbf{x}_{\text{a}}} \left[\begin{array}{ccc} \mathbf{I} && \mathbf{S^{T}} \end{array}\right] \implies \boldsymbol{\Gamma}_{\mathbf{x}_{\text{a}}}=\left[\begin{array}{ccc} \tilde{\boldsymbol{\Gamma}}_{\mathbf{x}_{\text{a}}} && \tilde{\boldsymbol{\Gamma}}_{\mathbf{x}_{\text{a}}}\mathbf{S^{T}} \\ \mathbf{S}\tilde{\boldsymbol{\Gamma}}_{\mathbf{x}_{\text{a}}} && \mathbf{S}\tilde{\boldsymbol{\Gamma}}_{\mathbf{x}_{\text{a}}}\mathbf{S^{T}} \end{array}\right] $$

(36)

For the case when all the constrained DOFs have a symmetric response, i.e., S = I, the cross-covariance equals the auto-covariance, and the correlation coefficient is equal to 1 for all master-constrained pairs. On the contrary, for the case when all the constrained DOFs have an anti-symmetric response, i.e., S = −I, the cross-covariance equals the negative of the auto-covariance, and the correlation coefficient is equal to -1 for all master-constrained pairs. Typically, some combination of symmetric and antisymmetric constraints is required.

3.5 Optimization details

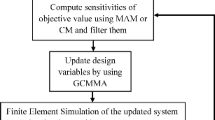
The solution of the proposed optimization problem is summarized in Fig. 4. In the initialization step, the domain is meshed, the element matrices using solid material are computed, the matrices for the excitation model are constructed, and the initial values for the design variables are chosen. Additionally, to avoid mesh dependency and numerical instabilities such as checkerboard patterns and islanding, a filter is applied to the sensitivities (Sigmund and Petersson 1998). A linear hat filter is implemented through a filter matrix that is computed in the initialization step (Talischi et al. 2012).

Fig. 4

Topology optimization flowchart for structures with stochastic dynamic loads

The remainder of the steps follow an iterative procedure. In the analysis step, the system matrices are obtained using the current values for the design variables, and then, the covariance of the response is computed by solving the Lyapunov equation. In the sensitivity step, the adjoint Lyapunov equation is solved to obtain the Lagrange multiplier and the performance function sensitivity; the constraint sensitivity is computed directly. In the update step, the new values for the design variables are obtained by using the method of moving asymptotes (Svanberg 1987; 2002). The iterative scheme is applied until the maximum change in the design variables is below a specified threshold.

4 Numerical examples

In this section, the proposed framework is illustrated through four examples: (i) minimization of the displacement of a mass at the free end of a cantilever beam subjected to a stochastic dynamic base excitation, (ii) minimization of tip displacement of a cantilever beam subjected to a stochastic dynamic tip load, (iii) minimization of tip displacement and acceleration of a cantilever beam subjected to a stochastic dynamic tip load, and (iv) minimization of a plate subjected to multiple stochastic dynamic loads.

4.1 Displacement minimization of a cantilever beam with stochastic base excitation

This example minimizes the displacement of a point mass placed at the free end of the based-excited cantilever beam that was recently considered by Yang et al. (2017). The following parameters are taken from their study. The design domain for the cantilever beam is given by a 10 m × 20 m rectangle, which is shown in Fig. 5. The solid linear elastic material has the following properties: Young’s modulus E⁰ = 10 kPa, Poisson’s ratio ν = 0.3, density $\rho ^{0} = 1 \frac {\text {kg}}{\text {m}^{3}}$, tip mass m₀ kg, and Ersatz parameter 𝜖 = 10^− 4. The domain has a uniform thickness of 1 m, and it is assumed to be in plane stress condition. The continuum domain is discretized using 80 × 160 Q4 elements. The radius of the filter is equal to 0.25. The volume of the structure is constrained to be less or equal than 0.50 of the solid domain. The damping matrix is obtained using Rayleigh damping with 5% damping ratio for the first and fourth modes. The stochastic base motion z_g(t) is modeled using a second-order Kanai-Tajimi spectrum with ω_g = 8 rad/s, ζ_g = 0.64, and S₀ = 0.019. Note that due to the large damping ratio, this excitation behaves similar to a band-limited white noise with cutoff frequency around 2 Hz.

Fig. 5

Rectangular domain geometry for cantilever plate with point mass and dynamic stochastic base excitation

Topology optimization is performed to minimize the variance of the vertical displacement of the point tip mass $\mathbb {E}(u_{\text {tip}}^{2})=\sigma _{\text {tip}}^{2}$. Figure 6a shows the optimal design for this example with m₀ = 20 kg (i.e., 20% of the allowable mass in the solid domain). Note that the optimal topology shown in Fig. 6a differs from the result obtained by Yang et al. (2017), primarily due to approximations employed in their study to facilitate the numerical solution (e.g., using first few modes approximation). An additional difference is that Yang et al. (2017) used a projection filter instead of the filter used in this study. In contrast, the solution in this study readily includes the influence of all the modes. The objective function is equal to 0.073 and the first frequency is equal to 0.265 Hz.

Fig. 6

Optimal topology for base excitation with Kanai-Tajimi spectrum with tip mass am₀ = 20 kg, bm₀ = 60 kg, and cm₀ = 160 kg; d static tip load

Finally, additional studies are performed for the same domain and excitation but varying the tip mass. Figure 6a–c shows the optimal designs for different tip masses, and Fig. 6d shows the optimal design of the domain subjected to a constant static tip load. Figure 6 illustrates that, as the tip mass increases, the optimal topology evolves toward the optimal topology corresponding to a fixed-base beam with a static tip force Moreover, for this example, if the tip mass is larger than six times the allowable mass in the solid domain, then the optimal topology is nearly identical to the static solution. This phenomenon occurs for such large masses, because the problem essentially reduces to a single DOF system. For this example, the excitation appears as a white noise to the structure as the frequencies become smaller with increasing mass; because the displacement covariance of a single DOF system subjected to a white noise is inversely proportional to the natural frequency of the structure raised to 1.5 power, minimization of the tip covariance is equivalent to maximizing the stiffness, which is the goal of static compliance minimization.

4.2 Displacement minimization of a cantilever beam with stochastic dynamic tip load

This next example explores a cantilever beam subjected to a stochastic dynamic load at the center of the free end of the beam as shown in Fig. 7. The objective is to minimize the displacement at the point of application of the force. The design domain for the cantilever beam is given by the 6 m × 12 m rectangle, which is composed of a solid linear elastic material having the following properties, which are representative of structural steel: Young’s modulus E⁰ = 210 GPa, Poisson’s ratio ν = 0.3, density $\rho ^{0} = 7500\ \frac {kg}{m^{3}}$, and Ersatz parameter 𝜖 = 10^− 4. The domain has a uniform thickness of 0.10 m, and due to its thickness, the continuum domain is assumed to be in plane stress condition. The continuum domain is discretized using 80 × 160 Q4 elements. The radius of the filter is equal to 0.20. The volume of the structure is constrained to be less or equal than 0.30 of the solid domain. The damping matrix is obtained using Rayleigh damping with 2% damping ratio for the first two modes.

Fig. 7

Rectangular domain geometry for cantilever plate with dynamic stochastic tip load

To provide a reference of comparison, the optimal topology is first obtained considering the applied tip force f(t) to be a deterministic constant (i.e., a static force). Minimization of the vertical tip displacement leads to the topology shown in Fig. 8, which is termed the reference design. The frequency response function (FRF) from the input excitation to the tip displacement, $H_{u_{\text {tip}}f}(\omega )$, is calculated as the discrete Fourier transform of the numerical impulse response function; this FRF is normalized to have a value of 1 at ω = 0 and shown in Fig. 9. The first four peaks in this FRF, corresponding to the natural frequencies of the static design, are equal to 30 Hz, 41 Hz, 55 Hz, and 75 Hz.

Fig. 8

Optimal topology for static load

Fig. 9

Normalized magnitude of the frequency response function (FRF) of the static design and magnitude of FRFs of the elliptic filters used in different designs

Next, the tip force f(t) is modeled as a band-limited white noise (BLWN), by passing a scalar white noise (WN) with power spectral density equal to S₀ through a 8-pole, low-pass elliptic filter. The filter has a cutoff frequency f_c, a peak-to-peak ripple of 0.1 dB, and stop-band attenuation of 100 dB. Subsequently, this filter is cast into the state space representation given in (5).

Topology optimization is then performed to minimize the variance of the vertical tip displacement $\mathbb {E}(u_{\text {tip}}^{2})=\sigma _{\text {tip}}^{2}$ for the cantilever beam subjected to a dynamic stochastic tip loading. The cutoff frequencies are chosen with respect to the reference structure, instead of the initial uniform design, to make a direct comparison with this optimal structure. As discussed below, when the cutoff frequency is zero (i.e., the stochastic load is just a random variable), then the static optimal design and optimal design for the stochastic load are identical. Four cases are considered as follows: (i) f_c = 7 Hz, which is below the first natural frequency of the reference design; (ii) f_c = 35 Hz, which is between the first and second natural frequencies of the reference domain; (iii) f_c = 60 Hz, which is between the second and third natural frequencies of the reference design; and (iv) f_c = ∞ Hz, (i.e., the tip force f(t) is a white noise). For case (iv), the augmented state space matrices A_a and B_a in (12) are replaced those for the structural system A_s and B_s. The magnitude of the FRF of the various elliptic filters is superimposed on the normalized FRF of the reference design in Fig. 8.

Figure 10a–d shows the optimal design for the four cases. These figures show that the optimal topology depends on the cutoff frequency. For case (i), the optimal topology matches the reference design. An additional optimization was performed using a cutoff frequency of 15 Hz; these results were also visually indistinguishable from the static design, and are thus not presented here.

Fig. 10

Optimal topologies for a BLWN with f_c = 7 Hz, b BLWN with f_c = 35 Hz, c BLWN with f_c = 60 Hz, and d white noise

To better understand why the optimal topology for a small cutoff frequency matches the reference design in this example, consider the stationary variance of the tip displacement, which is equal to the area under the curve of the power spectral density (PSD) of the tip response S_uu(ω),

$$ \sigma_{\text{tip}}^{2}= 2 {\int}_{0}^{\infty} S_{uu}(\omega) d\omega $$

(37)

The PSD of the response depends on the PSD of the input force and the FRF of the structure H_uf(ω) as follows

$$ S_{uu}(\omega) = \left|H_{uf} (\omega)\right|^{2} S_{ff}(\omega) $$

(38)

Because f(t) is a BLWN, the PSD of the response can be well-approximated as

$$ \sigma_{\text{tip}}^{2} \approx 2 S_{0} {\int}_{0}^{2\pi f_{\text{c}}} \left|H_{uf} (\omega)\right|^{2} d\omega $$

(39)

If the BLWN cutoff frequency f_c is sufficiently below the first natural frequency of the structure (i.e., the pseudo-static region), then H_uf(ω) is constant (see Fig. 11), then

$$ \sigma_{\text{tip}}^{2} \approx 4 \pi f_{\text{c}} S_{0} \left|H_{uf} (0)\right|^{2} $$

(40)

which is proportional to the square of the tip displacement due to a constant static load. Therefore, in this example, for stochastic dynamic excitation with frequency content that is well below the first natural frequency, the optimal topology can be expected to coincide with the static topology optimization case.

Fig. 11

Comparison of the FRF of the topologies obtained for different cutoff frequencies

In contrast, for large cutoff frequencies, i.e., f_c →∞, the excitation approaches a white noise, and consequently, the optimal topology coincides with the optimal topology for a pure white noise. In this particular example, the optimization was performed using cutoff frequencies of 300 Hz and 500 Hz; the results are visually indistinguishable from the white noise design and thus are not presented here.

To understand the influence of the cutoff frequency f_c in the optimal topology, the FRF of the different designs are obtained as described previously and their magnitudes are shown in Fig. 11. Note that the first frequency of the static design is represented by a large peak in the magnitude of the FRF; therefore, for f_c = 35 Hz, i.e., the cutoff is greater than the first natural frequency, the resulting topology considerably reduces the peak of the first frequency and also produces a shift of the first frequency. However, in this case, the second peak has a magnitude of the same order of the first peak of the static design, but this larger modal response does not increase the covariance because this peak is located in the stop-band of the low-pass filter. Similarly, for f_c = 60 Hz, i.e., the cutoff is greater than the third natural frequency, the resulting topology considerably reduces the peak of the first and second frequencies and also produces a shift of these frequencies. However, in this case, the third peak has shifted outside of the bandwidth of the excitation, so the larger magnitude does not increase the covariance. For the white noise excitation, the covariance of the response is the area under the magnitude of the FRF over the entire frequency domain.

Finally, Fig. 12 shows a comparison of the covariance of the tip displacement of the different designs using different excitations; the excitation cutoff frequency is shown on the x-axis, and the normalized covariance of the response is shown on the y-axis. The covariances for each cutoff frequency are normalized by the covariance of the corresponding optimal design. The different bars correspond to the designs described in the legend. As expected, the minimum covariance for each design is obtained by the case designed for the corresponding cutoff frequency. For a small cutoff frequency, the static design and the 7 Hz design perform considerably better than the other designs. For a cutoff frequency between the first and second modes of the static case, the case designed for this frequency performs better than the other designs; meanwhile, the static design yields a very large covariance, and the other dynamic designs perform better. For a cutoff frequency between the second and third modes of the static case, the case designed for this frequency performs better than the other designs; meanwhile, the first dynamic design yield a very large covariance. For a white noise, the case designed for this excitation performs best, with the other designs having poorer performance. In summary, the best performance is achieved when the excitation can be appropriately modeled in the topology optimization problem formulation.

Fig. 12

Normalized covariance of the tip displacement of the different designs using different excitations, where the covariance is normalized by the minimum covariance among the designs

4.3 Multi-objective minimization of a cantilever beam with stochastic dynamic tip load

Xu et al. (2017a) showed that interstory displacements and accelerations are often competing performance objectives; therefore; in this example, the covariance of the vertical tip displacement and acceleration of a cantilever beam subjected to a dynamic stochastic tip loading are minimized. This task is done by means of a combined performance function given by a weighted average of both responses

$$ J=\mathbb{E}(u_{\text{tip}}^{2})+\alpha \mathbb{E}(\ddot{u}_{\text{tip}}^{2}) $$

(41)

where the parameter α determines the influence of acceleration response in the performance function: small values of α correspond to displacement optimization and large values correspond to acceleration optimization. The design domain is the same 6 × 12 rectangle of Section 4.2, which is shown in Fig. 7. As in the previous example, the tip load f(t) is modeled as a band-limited white noise (BLWN).

Topology optimization is performed to minimize the multi-objective function for the following excitation cutoff frequencies: (i) f_c = 35 Hz, which is between the first and second natural frequencies of the reference domain, and (ii) f_c = 60 Hz, which is between the second and third natural frequencies of the reference design. Also, different values of the parameter α are considered for each of the two cutoff frequencies.

The stationary variance of the tip displacement and acceleration are given by the area under the curve of the PSD of the corresponding response; therefore, the objective function is given by

$$\begin{array}{@{}rcl@{}} J&=&2 {\int}_{0}^{\infty} \left( \left|H_{uf} (\omega)\right|^{2} + \alpha \left|H_{\ddot{u}f} (\omega)\right|^{2}\right) S_{ff}(\omega) d\omega \\ &=&2 {\int}_{0}^{\infty} (1 + \alpha \omega^{4}) \left|H_{uf} (\omega)\right|^{2} S_{ff}(\omega) d\omega \end{array} $$

(42)

Because f(t) is a BLWN, the objective function can be well-approximated as

$$ J \approx 2 S_{0} {\int}_{0}^{2\pi f_{\text{c}}} (1 + \alpha \omega^{4}) \left|H_{uf} (\omega)\right|^{2} d\omega $$

(43)

For small cutoff frequencies f_c, the acceleration influence in the performance function is small due to the quartic term in the integral. Therefore, for stochastic dynamic excitation with small cutoff frequency, the optimal topology can be expected to coincide with the displacement-only optimization.

Figure 13a–d shows the optimal design for f_c = 35 Hz with increasing values of α. These figures show that for this fixed cutoff frequency, the optimal topology depends on the parameter α. As seen here, when the weighting parameter is small, the optimal topology approximates the displacement only optimization α = 0, which is shown in Fig. 10b, and for larger values of α, the topology is modified considerably, with more mass being allocated to the top part of the structure.

Fig. 13

Optimal topologies for BLWN excitation with f_c = 35 Hz and multi-objective performance function (41) with aα = 10^− 8, bα = 10^− 7, cα = 10^− 6, and dα = 10^− 5

Figure 14a–d shows the optimal design for f_c = 60 Hz with increasing values of α. These figures show that for this fixed cutoff frequency, the optimal topology depends on the parameter α. As also seen here, when the weighting parameter is small, the optimal topology approximates the displacement only optimization α = 0, which is shown in Fig. 10c, and for larger values of α, the topology is modified considerably, with more mass being allocated in the top part of the structure.

Fig. 14

Optimal topologies for BLWN excitation with f_c = 60 Hz and multi-objective performance function (41) with aα = 10^− 9, bα = 10^− 8, cα = 10^− 7, and dα = 10^− 6

In both cases, the evolution of the optimal topologies can be explained by the quartic term corresponding to the acceleration response in the performance function in (43), which causes the magnitude of the acceleration FRF to increase faster than the displacement counterpart as the frequency increases (i.e., the higher modes are more important to the acceleration response, as compared to displacement response). Figure 15a–b shows the magnitudes of the FRF of the tip displacement to the excitation for all optimal designs obtained for both cutoff frequencies and different values of α in the performance function.

Fig. 15

Comparison of the FRF of the topologies for different multi-objective performance functions

Note that as α increases, the magnitude of the FRF at 0 Hz increases, indicating that the static compliance of the structure increases with α, and the first modal frequency of the structure decreases with increasing α. For the case f_c = 35 Hz, the static tip deflection of the optimal topology is increased approximately 8.4 times when α is increased from 0 to 10^− 5, which indicates that the overall system is more flexible to effectively reduce accelerations but increasing displacements. For completeness, Fig. 16a–h shows the first and second mode shapes for the optimal topologies in Figs. 13a, d and 14a, d.

Fig. 16

Mode shapes of optimal topologies shown in Figs. 13a, d and 14a, d

Finally, the Pareto optimal front is calculated to illustrate the tradeoff in the response of displacements and accelerations and plotted in Fig. 17a–b for cutoff frequencies f_c = 35 Hz and f_c = 60 Hz, respectively. This curve is a plot of the normalized standard deviation of the tip displacement versus the normalized standard deviation of the tip acceleration for different values of α. Here, the standard deviations of the tip displacements and accelerations are normalized by dividing by their corresponding minimum. The numbers shown next to each point correspond to the values of α, and note that additional values of α, whose topologies are not shown due to space limitations, are included in these curves. As expected, for small values of α, the displacement response is small but the acceleration response is large, and as the parameter α increases, the displacement response increases and the acceleration response decreases. Points below this Pareto optimal front correspond to infeasible designs and above this curve correspond to non-optimal designs. Also, the displacement response is more affected for the first cutoff frequency than for the second cutoff frequency, and the acceleration response is more affected for the second cutoff frequency than in the first cutoff frequency. This difference can be explained by the fact that the acceleration response is more dependent on higher frequencies. In summary, as the weighting parameter increases, the acceleration response is more important in the objective function, which modifies substantially the optimal topology from the displacement-only optimization; and as the cutoff frequency increases, the acceleration response becomes more important.

Fig. 17

Normalized standard deviation of displacement versus normalized standard deviation of acceleration curve for optimal designs with different objective functions (41)

4.4 Minimization of a plate with multiple stochastic dynamic loads

This example demonstrates the suitability of the proposed methodology for multiple-input multiple-output systems. The domain and loads are shown in Fig. 18, where f₁ and f₂ are different stochastic processes applied on points 1 and 2, respectively. The design domain for the cantilever beam is given by the 5 m × 5 m rectangle, which is composed of a solid linear elastic material having the following properties, which are representative of structural steel: Young’s modulus E⁰ = 210 GPa, Poisson’s ratio ν = 0.3, density $\rho ^{0} = 7500\text {} \frac {kg}{m^{3}}$, and Ersatz parameter 𝜖 = 10^− 4. The domain has a uniform thickness of 0.10 m, and due to its thickness, the continuum domain is assumed to be in plane stress condition. The continuum domain is discretized using 100 × 100 Q4 elements. The radius of the filter is equal to 0.20. The volume of the structure is constrained to be less or equal than 0.30 of the solid domain. The damping matrix is obtained using Rayleigh damping with 2% damping ratio for the first two modes. The objective function is given by

$$ J=\mathbb{E}({u_{1}^{2}})+\mathbb{E}({u_{2}^{2}}) $$

(44)

where u₁ and u₂ are the lateral and vertical displacements of points 1 and 2.

Fig. 18

Rectangular domain geometry for a plate with multiple dynamic stochastic loads

To provide a reference of comparison, the optimal topology is first obtained considering the applied forces to be deterministic constants, i.e., f₁(t) = f₂(t) = P where P is a deterministic constant. Minimization of the sum of displacements leads to the topology shown in Fig. 19a, which is termed the reference design.

Fig. 19

Optimal topologies for a static loads and b multiple BLWN excitations with correlation coefficient ρ = 0.5

The stochastic processes are modeled as correlated band-limited white noises, so that the excitation matrices are composed of independent scalar low-pass elliptic filters arranged in diagonal blocks. The cutoff frequency of both scalar filters is equal to 50 Hz. The magnitude two-sided constant power spectral density matrix is given by

$$ \mathbf{S}_{0}=\left[\begin{array}{ccc} 1 && \rho \\ \rho && 1 \end{array}\right] $$

(45)

where ρ is the correlation between the two loading processes. Note that |ρ| < 1 to assure the positive definiteness of the previous matrix. If ρ = 1, then both processes are the same, and it is treated as a single-input system. If ρ = − 1, the system is treated as a single-input, and the processes are inversely correlated, i.e., in Fig. 18, one of the loading arrows is reversed.

Figure 19b shows the optimal design for multiple stochastic dynamic loads with correlation coefficient ρ = 0.5. These figures demonstrate that for this fixed cutoff frequency, the optimal topology varies considerably when considering the forces to be stochastic.

5 Conclusions

This paper has proposed a framework for topology optimization of stochastically excited structures. The input was modeled as a filtered white noise, and the performance of the structure due to this excitation was given in terms of the covariance of the stationary structural responses. The objective function for the optimization was defined as the trace of the product of a positive semidefinite symmetric matrix and the covariance of the stationary response. The covariances were obtained by solving a large-scale Lyapunov equation using an algorithm which is efficient both in terms of memory and computational time. The objective function was shown to be general enough to represent displacement, interstory drifts, velocities, and accelerations at one or many points, making it suitable for multi-objective optimization. A volume constraint was imposed to limit the design space, and the design variables were chosen as the relative densities in each element, which were bounded to achieve physically meaningful solutions. The material properties for intermediate densities were obtained using the SIMP interpolation rule; a linear hat filter was used to avoid numerical instabilities. An efficient adjoint method to obtain the sensitivities of the performance function was proposed, which requires the solution of an adjoint Lyapunov equation, also solved using the efficient Lyapunov equation solver. Iterations were carried out using a gradient-based approach commonly employed in the topology optimization field.

The proposed framework was illustrated by conducting topology optimization of cantilever beams with different excitations and performance functions. The first example considers displacement optimization of a mass on the end of a cantilever beam with stochastic dynamic base motion. The topology obtained using the proposed approach differs from the result found in a previous study, primarily due to approximations employed in that study to achieve numerical solutions of the topology optimization problem. In the proposed approach, these approximations were not required. Local mode penalization improves the numerical behavior eliminating disconnected regions. Also, as the tip mass increases, the optimal topology evolves towards the solution obtained for a vertical static tip load.

The second example minimized the tip displacement for a cantilever beam subjected to a stochastic dynamic point force. The force was modeled as a band-limited white noise (BLWN) using an 8-pole elliptic filter with different cutoff frequencies and as a pure white noise. First, optimization was performed to minimize the covariance of the tip displacement. For cutoff frequencies well below the first natural frequency, the optimal topology coincides with the static case. For large cutoff frequencies, the excitation approaches a white noise, and consequently, the optimal topology coincides with the optimal topology obtained for a pure white noise excitation. In this example, for frequencies above 300 Hz, the optimal topology for the BLWN and the white noise was indistinguishable. The static design is outperformed by the dynamic designs when the cutoff frequency is larger than its first frequency. In general, the best performance is achieved when the excitation can be appropriately modeled in the topology optimization problem formulation.

Also, the proposed framework was employed to demonstrate the tradeoffs between minimizing tip displacement and acceleration. The cantilever beam subjected to a dynamic stochastic tip force was again examined, where the force was modeled as a band-limited white noise. For a fixed cutoff frequency, the optimal topology depends on the weighting parameter, α. For small values of α, the optimal topology is close to the displacement-only optimization, and for larger values of α, the topology is modified considerably, with more mass being allocated in the top part of the structure. The evolution of the optimal topologies with increasing values of α is due to the magnitude of the acceleration FRF that increases faster than the displacement counterpart as the frequency increases. Moreover, the static compliance increases and the first modal frequency of the structure decreases with increasing α, both of which indicate reductions in the acceleration are obtained by making the overall system more flexible. In addition, the Pareto optimal curve is introduced to explore the tradeoffs between reducing displacements and accelerations. For small values of α, the displacement response is small but the acceleration response is large, and as the parameter α increases, the displacement response increases and the acceleration response decreases. Also, as the cutoff frequency increases, the acceleration response becomes more important.

The results presented herein demonstrate the efficacy of the proposed approach for multi-objective topology optimization of stochastically excited structures. This framework can also accommodate multi-objective problems as well as multiple input-multiple output systems.

Appendix: Derivations

1.1 Performance functions

The details on how to obtain the matrix F for the performance functions described in Section 2.4 are described in this section. Initial notation is used for simplicity, the indices take values from 1, 2,…, N unless noted otherwise, and the subscript of the covariance of the response of the augmented system is dropped for simplicity.

• 1) Covariance of the various DOFs defined by the output equation y = C_ax_a, therefore $\boldsymbol {{\Gamma }_{y}} = \mathbf {C}_{\text {a}} \boldsymbol {\Gamma }_{\mathbf {x}_{\text {a}}} \mathbf {C}_{\text {a}}^{\text {T}}$

  $$\begin{array}{@{}rcl@{}} J= \mathbf{C}_{\text{a}} \boldsymbol{\Gamma}_{\mathbf{x}_{\text{a}}} \mathbf{C}_{\text{a}}^{\text{T}} & =&C_{ki} {\Gamma}_{ij} C_{kj} = C_{ki} C_{kj} {\Gamma}_{ij}\\ &=& (C^{\text{T}} C)_{ij} {\Gamma}_{ij} = (\mathbf{C}_{\text{a}}^{\text{T}} \mathbf{C}_{\text{a}}) :\boldsymbol{\Gamma}_{\mathbf{x}_{\text{a}}} \end{array} $$

  (46)
  $$ \implies \mathbf{F} = (\mathbf{C}_{\text{a}}^{\text{T}} \mathbf{C}_{\text{a}}) $$

  (47)

  F is clearly symmetric positive semi-definite.

  The following shows examples of performance functions

  $$ \begin{array}{lcl} J=\mathbb{E}({u_{p}^{2}}) & \implies & \mathbf{C}_{\text{a}} = (C_{u})_{p,:} \\ J=\mathbb{E}((u_{p}-u_{q})^{2}) & \implies & \mathbf{C}_{\text{a}} = (C_{u})_{p,:}-(C_{u})_{q,:} \\ J=\mathbb{E}({\sum}_{p} {u_{p}^{2}}) & \implies & \mathbf{C}_{\text{a}} = {\sum}_{p} (C_{u})_{p,:}\\ J=\mathbb{E}(\dot{u}_{p}^{2}) & \implies & \mathbf{C}_{\text{a}} = (C_{\dot{u}})_{p,:} \\ J=\mathbb{E}((\ddot{u}_{p}^{\text{abs}})^{2}) & \implies & \mathbf{C}_{\text{a}} = (C_{\ddot{u}})_{p,:} \end{array} $$

  (48)

  where X_p,: denotes the p th row of matrix X

• 2) expected static compliance

  $$ \begin{array}{ll} J=\mathbb{E}(\mathbf{u}^{\text{T}} \mathbf{Ku}) = \mathbb{E}(u_{i} K_{ij} u_{j}) &= K_{ij} \mathbb{E}(u_{i} u_{j}) \\ &= K_{ij} ({\Gamma}_{u})_{ij} = \mathbf{K}:\boldsymbol{{\Gamma}_{u}} \end{array} $$

  (49)

  where $\boldsymbol {{\Gamma }_{u}}=\mathbb {E}(\mathbf {uu}^{\text {T}})$ is the covariance of the displacement, then $\boldsymbol {{\Gamma }_{u}} = \mathbf {C_{u}} \boldsymbol {\Gamma }_{ \mathbf {x}_{\text {a}}} \mathbf {C}_{\mathbf {u}}^{\text {T}}$, and consequently

  $$ \begin{array}{ll} J &= K_{ij} (C_{u}{\Gamma} C_{u}^{\text{T}})_{ij} = K_{ij} (C_{u})_{ip} ({\Gamma})_{pq} (C_{u})_{jq} \\ &= (C_{u}^{\text{T}} K C_{u})_{pq} ({\Gamma})_{pq} = (\mathbf{C}_{\mathbf{u}}^{\text{T}} \mathbf{K C_{u}}):\boldsymbol{\Gamma}_{\mathbf{x}_{\text{a}}} \end{array} $$

  (50)
  $$ \implies \mathbf{F} = \mathbf{C}_{\mathbf{u}}^{\text{T}} \mathbf{K C_{u}} $$

  (51)

  Because K is symmetric positive definite, F is clearly symmetric positive semidefinite.

• 3) expected kinetic energy

  $$ \begin{array}{ll} J=\mathbb{E}(\dot{\mathbf{u}}^{\text{T}} \mathbf{M} \dot{\mathbf{u}}) = \mathbb{E}(\dot{u}_{i} M_{ij} \dot{u}_{j}) &= M_{ij} \mathbb{E}(\dot{u}_{i} \dot{u}_{j}) \\ &= M_{ij} ({\Gamma}_{\dot{u}})_{ij} = \mathbf{M}:\boldsymbol{{\Gamma}_{\dot{\mathbf{u}}}} \end{array} $$

  (52)

  where $\boldsymbol {{\Gamma }}_{\dot {\mathbf {u}}}=\mathbb {E}(\dot {\mathbf {u}}\dot {\mathbf {u}}^{\text {T}})$ is the covariance of the velocity, then $\boldsymbol {{\Gamma }}_{\dot {\mathbf {u}}} = \mathbf {C}_{\dot {\mathbf {u}}} \boldsymbol {\Gamma }_{\mathbf {x}_{\text {a}}} \mathbf {C}_{\dot {\mathbf {u}}}^{\text {T}}$, and consequently

  $$ \begin{array}{ll} J &= M_{ij} (C_{\dot{u}}{\Gamma} C_{\dot{u}}^{\text{T}})_{ij} = M_{ij} (C_{\dot{u}})_{ip} ({\Gamma})_{pq} (C_{\dot{u}})_{jq} \\ &= (C_{\dot{u}}^{\text{T}} M C_{\dot{u}})_{pq} ({\Gamma})_{pq} = (\mathbf{C}_{\dot{\mathbf{u}}}^{\text{T}} \mathbf{M C_{\dot{u}}}):\boldsymbol{\Gamma}_{\mathbf{x}_{\text{a}}} \end{array} $$

  (53)
  $$ \implies \mathbf{F} = \mathbf{C}_{\dot{\mathbf{u}}}^{\text{T}} \mathbf{M C_{\dot{u}}} $$

  (54)

  Because M is symmetric positive semidefinite, F is clearly symmetric positive semidefinite.

• 4) linear combination of previous performance functions with non-negative coefficients, i.e., the performance function is given by

  $$ J=\alpha J_{1} + \beta J_{2} $$

  (55)

  where $J_{1}=\mathbf {F}_{1}:\boldsymbol {\Gamma }_{\mathbf {x}_{\text {a}}}$ and $J_{2}=\mathbf {F}_{2}:\boldsymbol {\Gamma }_{\mathbf {x}_{\text {a}}}$, and α and β are non-negative real numbers. Then,

  $$ \begin{array}{ll} J= \alpha \mathbf{F}_{1}:\boldsymbol{\Gamma}_{\mathbf{x}_{\text{a}}} + \beta \mathbf{F}_{2}:\boldsymbol{\Gamma}_{\mathbf{x}_{\text{a}}} = (\alpha \mathbf{F}_{1}+\beta \mathbf{F}_{2}):\boldsymbol{\Gamma}_{\mathbf{x}_{\text{a}}} \end{array} $$

  (56)
  $$ \implies \mathbf{F} = \alpha \mathbf{F}_{1}+\beta \mathbf{F}_{2} $$

  (57)

  Because in this case F is a linear combination of F in the previous cases with non-negative coefficients, it is clearly symmetric positive semidefinite.

1.2 Sensitivity analysis

The details on how to obtain the sensitivity of the performance functions described in Section 3.3 are described in this section. Initial notation is used and the subscript of the covariance of the response of the augmented system is dropped for simplicity, and the indices take values from 1, 2,…, N^′ unless noted otherwise. The sensitivity of the performance function is given by

$$ \frac{\partial J}{\partial z_{n}} = \frac{\partial \phi}{\partial z_{n}} + \frac{\partial \phi}{\partial {\Gamma}_{ij}} \frac{\partial {\Gamma}_{ij}} {\partial z_{n}} $$

(58)

which requires the sensitivity of covariance matrix that is implicitly defined by (21). Differentiation to this equation yields the following equations

$$\begin{array}{@{}rcl@{}} \mathbf{A}_{\text{a}}\frac{\partial \boldsymbol{\Gamma}}{\partial z_{n}} + \frac{\partial \boldsymbol{\Gamma}}{\partial z_{n}} \mathbf{A}_{\text{a}}^{\text{T}} + \mathbf{Q}_{n} = \mathbf{0} \quad \text{ where} \\ \mathbf{Q}_{n} = \frac{\partial \mathbf{A}_{\text{a}}}{\partial z_{n}} \boldsymbol{\Gamma} + \boldsymbol{\Gamma}\frac{\partial \mathbf{A}_{\text{a}}^{\text{T}}}{\partial z_{n}} + \frac{\partial (\tilde{\mathbf{B}}_{\text{a}}\tilde{\mathbf{B}}_{\text{a}}^{\text{T}})}{\partial z_{n}} \end{array} $$

(59)

This means that the direct differentiation method requires the solution of one Lyapunov equation for each element, which makes the overall process a quartic order process. Note also, that the Q_n is not necessarily a low-rank matrix product, and consequently, the more efficient method described in Section 3.2 may not be applied.

An adjoint method is applied to make the process more efficient, in terms of the Lagrangian function expressed in (27), which is rewritten and reordered next in initial notation

$$\begin{array}{@{}rcl@{}} \mathcal{L} &=& J + {\Lambda}_{ij} (A_{\text{a},ik}{\Gamma}_{kj} +{\Gamma}_{ik} A_{\text{a},jk} + Q_{ij}) \\ &=& J + (A_{\text{a},ki}{\Lambda}_{kj} + {\Lambda}_{ik} A_{\text{a},kj}){\Gamma}_{ij} +{\Lambda}_{ij}Q_{ij} \end{array} $$

(60)

where $\mathbf {Q}=\tilde {\mathbf {B}}_{\text {a}}\tilde {\mathbf {B}}_{\text {a}}^{\text {T}}$. Differentiating the previous equation yields the following

$$\begin{array}{@{}rcl@{}} \frac{\partial \mathcal{L}}{\partial z_{n}} &= & \frac{\partial J}{\partial z_{n}} + \frac{\partial (A_{\text{a},ki}{\Lambda}_{kj} + {\Lambda}_{ik} A_{\text{a},kj})}{\partial z_{n}}{\Gamma}_{ij} \\ &&+(A_{\text{a},ki}{\Lambda}_{kj} + {\Lambda}_{ik} A_{\text{a},kj})\frac{\partial {\Gamma}_{ij}}{\partial z_{n}} +{\Lambda}_{ij} \frac{\partial Q_{ij}}{\partial z_{n}} \end{array} $$

(61)

Plugging (58) in the previous equation and reordering yields

$$\begin{array}{@{}rcl@{}} \frac{\partial \mathcal{L}}{\partial z_{n}} &=& \frac{\partial (A_{\text{a},ki}{\Lambda}_{kj} + {\Lambda}_{ik} A_{\text{a},kj})}{\partial z_{n}}{\Gamma}_{ij} + {\Lambda}_{ij} \frac{\partial Q_{ij}}{\partial z_{n}} \\ &&+\left( A_{\text{a},ki}{\Lambda}_{kj} + {\Lambda}_{ik} A_{\text{a},kj} + \frac{\partial \phi}{\partial {\Gamma}_{ij}} \right) \frac{\partial {\Gamma}_{ij}}{\partial z_{n}} +\frac{\partial \phi}{\partial z_{n}} \end{array} $$

(62)

To remove the dependence on the implicit derivative of the covariance matrix, the first factor in the third term in the RHS of the previous equation is defined as 0, that is

$$ A_{\text{a},ki}{\Lambda}_{kj} + {\Lambda}_{ik} A_{\text{a},kj}+\frac{\partial \phi}{\partial {\Gamma}_{ij}} = 0 $$

(63)

which written in abstract form yields (28). Therefore, the gradient of the performance function is given by

$$ \frac{\partial J}{\partial z_{n}} = \left( \frac{ \partial A_{\text{a},ik}}{\partial z_{n}} {\Gamma}_{kj} + {\Gamma}_{ik} \frac{ \partial A_{\text{a},jk}}{\partial z_{n}} + \frac{\partial Q_{ij}}{\partial z_{n}} \right){\Lambda}_{ij} + \frac{\partial \phi}{\partial z_{n}} $$

(64)

and the previous equation written in abstract form gives (29).

Then, the sensitivity of the performance function requires the derivatives of the matrices A_a and B_a

$$ \frac{ \partial \mathbf{A}_{\text{a}}}{\partial z_{n}} = \left[\begin{array}{cccc} \frac{ \partial \mathbf{A}_{\text{s}}}{\partial z_{n}} && \frac{ \partial \mathbf{B}_{\text{s}}}{\partial z_{n}}\mathbf{C}_{\text{f}} \\ \mathbf{0}_{N_{\text{f}} \times 2N} && \mathbf{0}_{N_{\text{f}} \times N_{\text{f}}} \end{array}\right], \quad \frac{ \partial \mathbf{B}_{\text{a}}}{\partial z_{n}} = \mathbf{0} $$

(65)

The derivative of state matrices is given by

$$ \frac{ \partial \mathbf{A}_{\text{s}}}{\partial z_{n}} = \left[\begin{array}{cccc} \mathbf{0}_{N \times N} && \mathbf{0}_{N \times N} \\ \frac{ \partial (-\mathbf{M}^{-1}\mathbf{K})}{\partial z_{n}} && \frac{ \partial (-\mathbf{M}^{-1} \mathbf{C})}{\partial z_{n}} \end{array}\right] $$

(66)

$$ \frac{ \partial \mathbf{B}_{\text{s}}}{\partial z_{n}} = \left[\begin{array}{ccc} \mathbf{0}_{N \times 1} \\ \frac{ \partial (\mathbf{M}^{-1} \mathbf{G})}{\partial z_{n}} \end{array}\right] $$

(67)

The matrices M and K are obtained using an assembly process described by

$$ \mathbf{M}(\mathbf{z}) = \underset{{n = 1}}{\overset{N_{\text{el}}}{\text{A}}} \rho(z_{n})\mathbf{M}^{0}_{n}, \quad \mathbf{K}(\mathbf{z}) = \underset{{n = 1}}{\overset{N_{\text{el}}}{\text{A}}} E(z_{n})\mathbf{K}^{0}_{n} $$

(68)

where $\mathbf {M}^{0}_{n}$ and $\mathbf {K}^{0}_{n}$ are the mass and stiffness matrices of element n with solid material. The derivatives of them are given by

$$ \frac{ \partial \mathbf{M}}{\partial z_{n}} = \frac{ \partial \rho}{\partial z}(z_{n}) \mathbf{M}^{0}_{n}, \quad \frac{ \partial \mathbf{K}}{\partial z_{n}} = \frac{ \partial E}{\partial z}(z_{n}) \mathbf{K}^{0}_{n} $$

(69)

The derivative of M^− 1 is

$$ \frac{ \partial (\mathbf{M}^{-1} )}{\partial z_{n}} = - \mathbf{M}^{-1} \frac{ \partial \mathbf{M}} {\partial z_{n}} \mathbf{M}^{-1} $$

(70)

which yields the following derivatives that appear in the state matrices

$$ \begin{array}{ll} \frac{ \partial (-\mathbf{M}^{-1} \mathbf{K})}{\partial z_{n}} = \mathbf{M}^{-1}\left( \frac{ \partial \mathbf{M}} {\partial z_{n}} \mathbf{M}^{-1} \mathbf{K} - \frac{ \partial \mathbf{K}}{\partial z_{n}}\right) \\ \frac{ \partial (-\mathbf{M}^{-1} \mathbf{C})}{\partial z_{n}} = \mathbf{M}^{-1}\left( \frac{ \partial \mathbf{M}} {\partial z_{n}} \mathbf{M}^{-1} \mathbf{C} - \frac{ \partial \mathbf{C}}{\partial z_{n}}\right) \\ \frac{ \partial (\mathbf{M}^{-1} \mathbf{G})}{\partial z_{n}} = \mathbf{M}^{-1}\left( - \frac{ \partial \mathbf{M}} {\partial z_{n}} \mathbf{M}^{-1} \mathbf{G} + \frac{ \partial \mathbf{G}}{\partial z_{n}}\right) \end{array} $$

(71)

If Rayleigh damping is used, the damping matrix is equal to

$$ \mathbf{C} = \alpha_{1} \mathbf{M} + \alpha_{2} \mathbf{K} $$

(72)

and consequently, the following derivative is given by

$$ \frac{ \partial (-\mathbf{M}^{-1} \mathbf{C})}{\partial z_{n}} = \alpha_{2} \mathbf{M}^{-1}\left( \frac{ \partial \mathbf{M}} {\partial z_{n}} \mathbf{M}^{-1} \mathbf{K} - \frac{ \partial \mathbf{K}}{\partial z_{n}}\right) $$

(73)