1 Introduction

This paper addresses topology optimization of nonlinear trusses using the ground structure (GS) approach. We consider material nonlinear behavior and concentrate on hyperelastic models, such as the ones by Hencky, Saint-Venant, Neo-Hookean and Ogden. The noteworthy feature of our approach is that we use a unified approach using the total potential energy both in the objective function and in the equilibrium solution of the nonlinear problem. We proof that the optimization formulation is convex provided that the specific strain energy is strictly convex. Moreover, in the present formulation, there is no need to compute the adjoint vector, which is a remarkable property that leads to improved computational efficiency. In addition, the sensitivity of the objective function is always non-positive. The formulation leads to a constant specific strain energy, which is a property similar to the full stress design in the linear case.

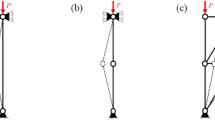
As indicated by Ringertz (1989), the deviation of the solution obtained by assuming linear structural response when the structure has nonlinear response can be significant. We verify this statement in the context of our work in topology optimization. For linear problems, each ground structure leads to a unique topology, as illustrated by Figs. 1 and 2a. However, in the nonlinear case, even if the ground structure is fixed (same), different material models may lead to different topologies. For instance, using the GS of Fig. 1 and considering the Saint Venant model, we obtain the topology of Fig. 2b for a low load level (which is the same for the linear case – c.f. Fig. 2a) or the topology of Fig. 3a for a higher load level. Thus different load levels may lead to different topologies for the same material model. Moreover, using the GS of Fig. 1 and considering the Hencky model, we obtain the topology of Fig. 3b, which is quite different from the previous one obtained with the Saint Venant model under the same load level (c.f. Fig. 3a).

Fig. 1
figure 1

Structural geometry and boundary conditions

Full size image
Fig. 2
figure 2

a Topology for linear model; b Topology for Saint Venant model considering low load level

Full size image
Fig. 3
figure 3

Topology considering high load level: a Saint Venant material model; b Hencky material model

Full size image

This paper is organized as follows. Section 2 presents related work to the present research. Section 3 presents the hyperelastic model with respect to kinematics, constitutive models of Ogden (OG), Saint Venant (SV), Neo-Hookean (NH) and Hencky (HK), principle of stationary potential energy, and linearization of the system. Section 4 addresses the optimization formulation using a nested formulation, the sensitivity analysis which precludes solution of the adjoint equation (remarkable property), proof of convexity of the objective function, and derivation of the KKT necessary conditions. Section 5 presents representative examples illustrating the effect of material model and/or structural loading level. Finally, concluding remarks are inferred in Section 6. Three appendices complement the paper.

2 Related work

The field of ground structure based topology optimization is quite vibrant. There has been substantial amount of work dealing with both linear and nonlinear structural problems (Kirsch 1989; Rozvany 1997; Bendsoe and Sigmund 2003; Ohsaki 2011), the latter being the emphasis of the present work. Specifically, here we focus on trusses with nonlinear material behavior given by hyperelastic models. Truss topology optimization is a fundamental problem of interest because it provides a natural link between optimization of discrete and continuum structures (Achtziger 1999).

Among other authors, Stricklin and Haisler (1977), Haftka and Kamat (1989), and Toklu (2004) pointed out the direct minimization of the total potential energy in order to obtain the equilibrium configuration of the structure. In the field of structural optimization, the potential energy concept has been explored in the objective function and/or constraint by several authors (Hassani and Hinton 1998; Khot and Kamat 1985; Klarbring and Strömberg 2011, 2013). In the present paper, we adopt a unified approach using the total potential energy, i.e. the total potential is used both in the objective function of the optimization problem and also to obtain the equilibrium solution. Other types of objective functions for nonlinear optimization problems can be found in Buhl et al. (2000); Kemmler et al. (2005); Sekimoto and Noguchi (2001).

The member properties regarding tension and compression behavior have a significant influence on the optimal design (Bendsoe and Sigmund 2003; Ohsaki 2011). For an overview of truss structures, the reader is referred to the review paper by Rozvany et al. (1995) and Achtziger (1997). Among others, Achtziger (1996) and Sokół (2011) have considered different behaviors in tension and compression. Particularly, Achtzlger (1996) presents two separated truss optimization formulations based on strength and stiffness, respectively.

Topology optimization for linear elastic problems consisting of compliance minimization with volume constraints are usually based on the so-called simultaneous or nested formulations. As shown by Christensen and Klarbring (2009), we obtain a non-convex problem in the simultaneous approach, and a convex problem in the nested approach. For optimization of nonlinear structures, either nested or simultaneous formulations can also be adopted (Haftka and Kamat 1989; Missoum and Gürdal 2002; Ringertz 1989). Here, we adopt a nested formulation and a strictly convex hyperelastic constitutive model in order to guarantee convexity of the optimization formulation.

3 Hyperelastic truss model

3.1 Kinematics

We adopt small deformation kinematics. In terms of notation, upper case letters are used to describe the initial undeformed position X, volume V, area A and length L. For simplicity, we assume that the strain in the truss member is uniform. According to Fig. 4:

Fig. 4
figure 4

Three-dimensional truss kinematics

Full size image
$$ L={\left\{{\left({\boldsymbol{X}}_Q-{\boldsymbol{X}}_P\right)}^T\left({\boldsymbol{X}}_Q-{\boldsymbol{X}}_P\right)\right\}}^{1/2}; $$
(1)
$$ \boldsymbol{N}=\frac{1}{L}\left({\boldsymbol{X}}_Q-{\boldsymbol{X}}_P\right); $$
(2)

The superscript T indicates transpose. With respect to the deformed configuration, the truss member undergoes nodal displacements u p and u q . The linearized stretch in the truss member i is given by

$$ {\lambda}_i=1 + \frac{{\left({\boldsymbol{N}}^{(i)}\right)}^T\left({\boldsymbol{u}}_q^{(i)}-{\boldsymbol{u}}_p^{(i)}\right)}{L_i} $$
(3)

where u (i) p and u (i) q are the nodal displacement vectors associated to the nodes p and q of the element i.

3.2 Hyperelastic constitutive models

In this work, we emphasize the Ogden (Ogden 1984) strain energy function (Ψ OG ) because of its generality and capability to reproduce a variety of hyperelastic models, especially in 1D (uniaxial strain). Such models include those by St Venant (Ψ SV ), Neo-Hookean (Ψ NH ) and Henky (Ψ HK ).

3.2.1 Ogden model

For an isotropic hyperelastic material, the strain energy per unit undeformed volume is given in terms of the principal stretches λ i as

$$ \varPsi =\varPsi \left({\lambda}_1,{\lambda}_2,{\lambda}_3\right)={\displaystyle \sum_{j=1}^M\frac{\gamma_j}{\beta_j}\left({\lambda}_1^{\beta_j}+{\lambda}_2^{\beta_j}+{\lambda}_3^{\beta_j}-3\right)} $$
(4)

where λ i denote the principal stretches and the constants γ j and β j are material parameters. For a truss member, only the principal stretch λ i  = λ is relevant. In 1D we have λ 2 = λ 3 = 1, such that Equation (4) reduces to

$$ {\varPsi}_{OG}={\varPsi}_{OG}\left(\lambda \right)={\displaystyle \sum_{j=1}^M\frac{\gamma_j}{\beta_j}\left({\lambda}^{\beta_j}-1\right)} $$
(5)

3.2.2 Other models

In the literature, we can find other hyperelastic models for uniaxial strain, such as the ones by Saint Venant (SV), Neo-Hookean (NH) and Henky (HK):

$$ {\psi}_{SV}=\frac{E_o}{8}{\left({\lambda}^2-1\right)}^2 $$
(6)
$$ {\varPsi}_{NH}=\frac{E_o}{4}\left({\lambda}^2-1-2\; \ln \left(\lambda \right)\right) $$
(7)
$$ {\varPsi}_{HK}=\frac{E_o}{2} \ln {\left(\lambda \right)}^2 $$
(8)

In the present context (uniaxial strain), the Cauchy stress is given by

$$ \sigma =\frac{\lambda }{J}\frac{\partial \varPsi }{\partial \lambda }=\frac{\partial \varPsi }{\partial \lambda } $$
(9)

where the volume ratio (Jacobian) is given by J = λ 1 λ 2 λ 3 = λ. Then, from Equation (5), we obtain

$$ \sigma \left(\lambda \right)=\frac{\partial {\varPsi}_{OG}}{\partial \lambda }={\displaystyle \sum_{j=1}^M}{\gamma}_j{\lambda}^{\beta_j-1} $$
(10)

Considering a free stress state at the undeformed configuration, σ(1) = 0, we have

$$ {\displaystyle \sum_{j=1}^M}{\gamma}_j=0 $$
(11)

The tangent modulus is given by

$$ {E}_T\left(\lambda \right)=\frac{\partial \sigma }{\partial \lambda }={\displaystyle \sum_{j=1}^M{\gamma}_j\left({\beta}_j-1\right)}{\lambda}^{\beta j-2} $$
(12)

with

$$ {E}_T(1)={E}_0={\displaystyle \sum_{j=1}^M}{\gamma}_j{\beta}_j $$
(13)

in which E 0 = Λ + 2μ, where Λ and μ are the usual Lamé constants. The tangent modulus is positive in Equation (12) (strict convexity of Ψ(λ)) if either γ j  > 0 and β j  > 1 or γ j  < 0 and β j  < 1.

In the special case of Equation (5) with M = 2, we obtain from Equations (10), (11), (12) and (13)

$$ \sigma \left(\lambda \right)={\gamma}_1\left({\lambda}^{\beta_1-1}-{\lambda}^{\beta_2-1}\right) $$
(14)
$$ \begin{array}{cc}\hfill {E}_T\left(\lambda \right)={\gamma}_1\hfill & \hfill \left[\left({\beta}_1-1\right){\lambda}^{\beta_1-2}-\left({\beta}_2-1\right){\lambda}^{\beta_2-2}\right]\hfill \end{array} $$
(15)
$$ {E}_o={\gamma}_1\left({\beta}_1-{\beta}_2\right) $$
(16)

with γ 2 = − γ 1. The tangent modulus (E T ) is positive if β 1 > 1, β 2 < 1 and γ 1 > 0 (Equation (15)). In this case, E o  > 0 (Equation (16)).

The material parameters (β 1, β 2) are obtained by solving the two nonlinear equations:

$$ {\overline{\sigma}}_t=\frac{\sigma_t}{\gamma_1^0}={\lambda}_t^{\beta_1-1}-{\lambda}_t^{\beta_2-1} $$
(17)
$$ {\overline{\sigma}}_c=\frac{\sigma_c}{\gamma_1^0}={\lambda}_c^{\beta_1-1}-{\lambda}_c^{\beta_2-1} $$
(18)

where σ t , σ c E o , λ t , λ c and γ 01 are known (specified by the user). Afterwards, the parameter γ 1 is readily computed from Equation (16). In this process, the relation \( {\sigma}_t/{\sigma}_c={\overline{\sigma}}_t/{\overline{\sigma}}_c \) is preserved. Therefore, we have the general material model given as

$$ \sigma \left(\lambda \right)=\frac{E_o}{\beta_1-{\beta}_2}\left({\lambda}^{\beta_1-1}-{\lambda}^{\beta_2-1}\right) $$
(19)

The uniaxial Cauchy stress for the Saint Venant model can be recovered from Equation (19) using (β 1 = 4; β 2 = 2):

$$ \sigma \left(\lambda \right)=\frac{E_o}{2}\left({\lambda}^3-\lambda \right) $$
(20)

Similarly, the uniaxial Cauchy stress for the Neo-Hookean model is also recovered from Equation (19) using (β 1 = 2; β 2 = 0):

$$ \sigma \left(\lambda \right)=\frac{E_o}{2}\left(\lambda -{\lambda}^{-1}\right) $$
(21)

For completeness, the uniaxial Cauchy stress for the Henky model is given by

$$ \sigma \left(\lambda \right)=\frac{\partial {\varPsi}_{HK}}{\partial \lambda }=\frac{E_0}{\lambda }1\mathrm{n}\left(\lambda \right) $$
(22)

Figure 5 illustrates the aforementioned models. Figure 5a illustrates the constitutive model given by Equation (19) in a relatively small stretch range. For comparison purpose, Fig. 5b shows the Neo-Hookean, St Venant and Henky models together with two realizations of the Ogden model (Ogden 1 and Ogden 2). Notice that, for the set of parameters chosen, the Ogden curves bound the other models.

Fig. 5
figure 5

Hyperelastic material models in uniaxial strain: a Ogden model for different parameters values; b Ogden 1 (β 1 = 2.71; β 2 = − 4.73); Ogden 2 (β 1 = 8.75; β 2 = 0.06); Neo-Hookean; Saint Venant and Hencky

Full size image

3.3 Principle of stationary potential energy

As usual, let’s denote the total potential energy of the structure by Π(u) = U(u) + Ω(u), where U(u) is the strain energy and Ω(u) is total potential of the loads, which are given by

$$ U\left(\boldsymbol{u}\right)={\displaystyle \sum_{i=1}^N{\int}_{Vi}{\varPsi}_i\left(\boldsymbol{u}\right)}dV={\displaystyle \sum_{i=1}^N{V}_i{\varPsi}_i\left(\boldsymbol{u}\right)}={\displaystyle \sum_{i=1}^N{A}_i{L}_i{\varPsi}_i\left(\boldsymbol{u}\right)} $$
(23)
$$ \varOmega \left(\boldsymbol{u}\right)=-{\boldsymbol{F}}^T\ \boldsymbol{u} $$
(24)

where Ψ i (u) is the specific strain energy function of member i, and N is the total number of members. The equilibrium of the structure is enforced by requiring Π to be stationary, i.e.

$$ \frac{\partial \prod }{\partial \boldsymbol{u}}=\frac{\partial U}{\partial \boldsymbol{u}}+\frac{\partial \varOmega }{\partial \boldsymbol{u}}=\boldsymbol{R}\left(\boldsymbol{u}\right)=\boldsymbol{T}\left(\boldsymbol{u}\right)-\boldsymbol{F}=\mathbf{0} $$
(25)

where

$$ \frac{\partial \varOmega }{\partial \boldsymbol{u}}=-\boldsymbol{F},\kern0.5em \frac{\partial U}{\partial \boldsymbol{u}}=\boldsymbol{T}\left(\boldsymbol{u}\right) $$
(26)

and the internal force vector T(u) is given as

$$ \boldsymbol{T}\left(\boldsymbol{u}\right)={\displaystyle \sum_{i=1}^N}{A}_i\ {L}_i\frac{\partial {\varPsi}_i}{\partial \boldsymbol{u}} $$
(27)

where

$$ \frac{\partial {\varPsi}_i}{\partial \boldsymbol{u}}=\frac{\partial {\varPsi}_i}{\partial {\lambda}_i}\frac{\partial {\lambda}_i}{\partial \boldsymbol{u}}={\sigma}_i\frac{\partial {\lambda}_i}{\partial \boldsymbol{u}} $$
(28)

Using Equation (3), we obtain

$$ \frac{\partial {\lambda}_i}{\partial \boldsymbol{u}}=\frac{1}{L_i}\left\{\begin{array}{c}\hfill \begin{array}{c}\hfill \begin{array}{c}\hfill \vdots \hfill \\ {}\hfill -{\boldsymbol{N}}^{(i)}\hfill \end{array}\hfill \\ {}\hfill \begin{array}{c}\hfill \hfill \\ {}\hfill \vdots \hfill \end{array}\hfill \end{array}\hfill \\ {}\hfill \begin{array}{c}\hfill \begin{array}{c}\hfill \hfill \\ {}\hfill\ {\boldsymbol{N}}^{(i)}\hfill \end{array}\hfill \\ {}\hfill \begin{array}{c}\hfill \vdots \hfill \\ {}\hfill \hfill \end{array}\hfill \end{array}\hfill \end{array}\right\}=\frac{1}{L_i}{\boldsymbol{B}}^{(i)}\kern1em \mathrm{where}\kern1em {\boldsymbol{B}}^{(i)}=\left\{\begin{array}{c}\hfill \begin{array}{c}\hfill \begin{array}{c}\hfill \vdots \hfill \\ {}\hfill -{\boldsymbol{N}}^{(i)}\hfill \end{array}\hfill \\ {}\hfill \begin{array}{c}\hfill \hfill \\ {}\hfill \vdots \hfill \end{array}\hfill \end{array}\hfill \\ {}\hfill \begin{array}{c}\hfill \begin{array}{c}\hfill \hfill \\ {}\hfill \kern0.75em {\boldsymbol{N}}^{(i)}\hfill \end{array}\hfill \\ {}\hfill \begin{array}{c}\hfill \vdots \hfill \\ {}\hfill \hfill \end{array}\hfill \end{array}\hfill \end{array}\right\}. $$
(29)

Therefore, the local internal force vector is obtained by substituting Equations (28) and (29) into (27), which is given by

$$ \boldsymbol{T}\left(\boldsymbol{u}\right)={\displaystyle \sum_{i=1}^N}{A}_{i\ }{\sigma}_i{\boldsymbol{B}}^{(i)} $$
(30)

With these hypotheses we have a nonlinear material model (NMM).

3.3.1 Linearization and solution of the nonlinear algebraic equations

The residual forces R(u) of Equation (25) can be rewritten, for an iterative step k, as follows

$$ \boldsymbol{R}\left({\boldsymbol{u}}_{k+1}\right)=\boldsymbol{R}\left({\boldsymbol{u}}_k\right)+{\boldsymbol{K}}_t\left({\boldsymbol{u}}_k\right)\varDelta {\boldsymbol{u}}_k $$
(31)

where

$$ {\boldsymbol{K}}_t\left({\boldsymbol{u}}_k\right)=\frac{\partial \boldsymbol{R}}{\partial \boldsymbol{u}}\left({\boldsymbol{u}}_k\right)=\frac{\partial \boldsymbol{T}}{\partial \boldsymbol{u}}\left({\boldsymbol{u}}_k\right) $$
(32)

The nonlinear system of equations is solved using the Newton-Raphson procedure:

$$ \boldsymbol{R}\left({\boldsymbol{u}}_{k+1}\right)=0 $$
(33)
$$ {\boldsymbol{K}}_t\left({\boldsymbol{u}}_k\right)\varDelta {\boldsymbol{u}}_k=-\boldsymbol{R}\left({\boldsymbol{u}}_k\right)=\boldsymbol{F}-\boldsymbol{T}\left({\boldsymbol{u}}_k\right) $$
(34)
$$ {\boldsymbol{u}}_{k+1}={\boldsymbol{u}}_k+\varDelta {\boldsymbol{u}}_k $$
(35)

where

$$ {\boldsymbol{K}}_t={\displaystyle \sum_{i=1}^N{\boldsymbol{K}}_{{}^t}^{(i)}} $$
(36)

in which K t is the global tangent stiffness matrix and K (i) t is the truss member tangent stiffness matrix in the global coordinates. In the beginning of the optimization process, the structural configuration tends to be more flexible than the solution been sought. Therefore the load vector is divided into increments (\( \boldsymbol{F}={\displaystyle \sum_{i=1}^{Nic}}\varDelta {\boldsymbol{F}}_i \)) and a standard incremental iterative algorithm is employed (Wriggers 2008). As the optimization progresses, the structure tends to become stiffer and thus the number of increments (Nic) for the load vector is reduced based on the change of the objective function (see Section 4).

The truss member internal force vector (t (i)) and tangent stiffness matrix (k (i) t ) for the NMM are given by

$$ {\boldsymbol{t}}^{(i)}\left({\boldsymbol{u}}^{(i)}\right)={A}_{i\ }{\sigma}_i\left({\boldsymbol{u}}^{(i)}\right)\left\{\begin{array}{c}\hfill -{\boldsymbol{N}}^{(i)}\hfill \\ {}\hfill \kern0.5em {\boldsymbol{N}}^{(i)}\hfill \end{array}\right\}\kern1em \mathrm{where}\kern1em {\boldsymbol{u}}^{(i)}=\left\{\begin{array}{c}\hfill {\boldsymbol{u}}_p^{(i)}\hfill \\ {}\hfill {\boldsymbol{u}}_q^{(i)}\hfill \end{array}\right\} $$
(37)

and (see Fig. 4)

$$ {\boldsymbol{k}}_t^{(i)}=\frac{\partial {\boldsymbol{t}}^{(i)}}{\partial {\boldsymbol{u}}^{(i)}}={\left[\begin{array}{cc}\hfill {\boldsymbol{k}}_{pp}\hfill & \hfill {\boldsymbol{k}}_{pq}\hfill \\ {}\hfill {\boldsymbol{k}}_{qp}\hfill & \hfill {\boldsymbol{k}}_{qq}\hfill \end{array}\right]}^{(i)} $$
(38)

where

$$ {\boldsymbol{k}}_{pp}={\boldsymbol{k}}_{qq}=-{\boldsymbol{k}}_{pq}=-{\boldsymbol{k}}_{qp}=\frac{A_i}{L_i}\frac{d{\sigma}_i}{d{\lambda}_i}{\boldsymbol{N}}^{(i)}{\left({\boldsymbol{N}}^{(i)}\right)}^T $$
(39)

We have used the linearized stretch (Equation (3)) to obtain the derivative of the stress σ i in relation to u (i).

4 Optimization formulation

We present the formulation and solution algorithm of topology optimization for a truss with material nonlinear behavior. The topology design consists of determining the cross sectional areas of the truss members using a ground structure (GS) approach (see Figures 6 and 7).

4.1 Nested formulations

We consider the following nested formulations for the optimization problem:

$$ \begin{array}{l}\left\{\begin{array}{cc}\hfill \underset{\boldsymbol{x}}{ \min}\mathrm{J}\left(\boldsymbol{x}\right)\hfill & \hfill \hfill \\ {}\hfill s.t.\hfill & \hfill \left\{\begin{array}{c}\hfill g\left(\boldsymbol{x}\right)={\boldsymbol{L}}^T\ \boldsymbol{x}-{V}_{max}\le 0\hfill \\ {}\hfill \kern2.5em {x}_j^{min}\le {x}_j\le {x}_j^{max},\ j=1,\dots, n\hfill \end{array}\right.\hfill \end{array}\right.\hfill \\ {}\mathrm{with}\hfill \\ {}\boldsymbol{T}\left(\boldsymbol{x},\boldsymbol{u}\left(\boldsymbol{x}\right)\right)=\boldsymbol{F}\hfill \end{array} $$
(40)

or

$$ \begin{array}{l}\left\{\begin{array}{cc}\hfill \underset{\boldsymbol{x}}{ \min}\mathrm{J}\left(\boldsymbol{x}\right)\hfill & \hfill \hfill \\ {}\hfill s.t.\hfill & \hfill \left\{\begin{array}{c}\hfill g\left(\boldsymbol{x}\right)={\boldsymbol{L}}^T\ \boldsymbol{x}-{V}_{max}\le 0\hfill \\ {}\hfill \kern2.5em {x}_j^{min}\le {x}_j\le {x}_j^{max},\ j=1,\dots, n\hfill \end{array}\right.\hfill \end{array}\right.\hfill \\ {}\mathrm{with}\hfill \\ {}\underset{\boldsymbol{u}}{ \min}\prod \left(\boldsymbol{x},\boldsymbol{u}\left(\boldsymbol{x}\right)\right)\hfill \end{array} $$
(41)

where J(x) is the objective function, x and L are the vectors of area and length, respectively, V max is the maximum material volume and x min j and \( {x}_{{}^j}^{\max } \) denote the lower and upper bounds, respectively.

There are several definitions of the objective function J(x) presented in the literature. In linear structural models the compliance J(x) = F T u is routinely used. The same approach is used in nonlinear structural models, which is called end-compliance.

In this work the objective function J(x) is based on the min-max formulation described in (Klarbring and Strömberg 2011, 2013):

$$ \underset{\boldsymbol{x}}{ \min}\mathrm{J}(x)=\underset{\boldsymbol{x}}{ \max}\left(\underset{\boldsymbol{u}}{ \min}\left(\prod \left(\boldsymbol{x},\boldsymbol{u}\left(\boldsymbol{x}\right)\right)\right)\right)=\underset{\boldsymbol{x}}{ \min}\left(-{\prod}_{\min}\left(\boldsymbol{x},\boldsymbol{u}\left(\boldsymbol{x}\right)\right)\right) $$
(42)

This objective function is obtained with the maximization of the total potential energy of the system in equilibrium, which has advantages in nonlinear problems. Some of them are low computational cost of the sensitivities (no extra adjoint equation - see next section) and achieving the same result as the compliance objective function in the linear case (J(x) = F T u). We will explore additional aspects of this approach, such as constant specific strain energy in the nonlinear case (and full stress design in linear case) and convex optimization problem for the case of strictly convex hyperelastic material (NMM). For NMM, the sum of the total potential energy and the complementary energy at the equilibrium configuration is equal to zero i.e. Π min  + Π c min  = 0 (see Appendix 1). In Appendix 2, we provide the relationship between the end-compliance, strain energy and complementary energy for the NMM formulation. To avoid singular tangent stiffness matrix in the Newton–Raphson solution (40) of the structural nonlinear equations, we prevent zero member areas by using a small lower bound area x min j (Christensen and Klarbring 2009).

4.2 Sensitivity analysis

We present sensitivities of the objective function and constraints for the optimization problem given by Equations (40) or (41) with respect to the design variables x. The constraints are linear with respect to design variables and thus the sensitivities are obtained easily. The sensitivity of the objective function is given by

$$ \frac{\partial \mathrm{J}\left(\boldsymbol{x}\right)}{\partial {x}_i}=-\frac{\partial {\varPi}_{min}\left(\boldsymbol{x},\boldsymbol{u}\left(\boldsymbol{x}\right)\right)}{\partial {x}_i}-\frac{\partial {\varPi}_{min}\left(\boldsymbol{x},\boldsymbol{u}\left(\boldsymbol{x}\right)\right)}{\partial \boldsymbol{u}}\frac{\partial \boldsymbol{u}\left(\boldsymbol{x}\right)}{\partial {x}_i} $$
(43)

Using the equilibrium condition

$$ \frac{\partial {\varPi}_{min}\left(\boldsymbol{x},\boldsymbol{u}\left(\boldsymbol{x}\right)\right)}{\partial \boldsymbol{u}}=0 $$
(44)

we obtain

$$ \frac{\partial \mathrm{J}\left(\boldsymbol{x}\right)}{\partial {x}_i}=-\frac{\partial {\varPi}_{min}\left(\boldsymbol{x},\boldsymbol{u}\left(\boldsymbol{x}\right)\right)}{\partial {x}_i}=\frac{\partial \varOmega \left(\boldsymbol{u}\left(\boldsymbol{x}\right)\right)}{\partial {x}_i}-\frac{\partial U\left(\boldsymbol{x},\boldsymbol{u}\left(\boldsymbol{x}\right)\right)}{\partial {x}_i} $$
(45)

Because Ω(u(x)) is (explicitly) independent of x (no body forces), then ∂Ω(u(x))/∂x i  = 0. Using the Equation (23) with A i  = x i , we obtain

$$ \frac{\partial \mathrm{J}\left(\boldsymbol{x}\right)}{\partial {x}_i}=-\frac{\partial U\left(\boldsymbol{x},\boldsymbol{u}\left(\boldsymbol{x}\right)\right)}{\partial {x}_i}=-{L}_i{\varPsi}_i\left(\boldsymbol{u}\left(\boldsymbol{x}\right)\right) $$
(46)

The sensitivity given by Equation (46) is always non-positive, because L i Ψ i (u(x)) ≥ 0. Observe that we do not need to calculate the adjoint equation (Khot and Kamat 1985; Klarbring and Strömberg 2011, 2013), which leads to an efficient formulation.

4.3 Convexity proof

As shown by Svanberg (1984), the nested formulation of Equations (40) and (41) is convex for the linear structural model T(x, u(x)) = K(x) u(x) and the objective function J(x) = F T u. Here, we investigate convexity of this optimization problem for the nonlinear hyperelastic structural model (T(x, u(x)) = F) and the objective function J(x) = − Π min (x, u(x)).

Because the constraint function L T x − V max  ≤ 0 is convex, we only need to study the convexity of the objective function J(x) = − Π min (x, u(x)) to prove the convexity of the optimization formulation. The derivative of Equation (46) leads to the Hessian:

$$ {H}_{ij}=\frac{\partial^2\mathrm{J}\left(\boldsymbol{x}\right)}{\partial {x}_i\ \partial {x}_j}=-\frac{\partial^2U\left(\boldsymbol{x},\boldsymbol{u}\left(\boldsymbol{x}\right)\right)}{\partial {x}_i\ \partial {x}_j}-\frac{\partial^2U\left(\boldsymbol{x},\boldsymbol{u}\left(\boldsymbol{x}\right)\right)}{\partial {x}_i\ \partial \boldsymbol{u}}\frac{\partial \boldsymbol{u}\left(\boldsymbol{x}\right)}{\partial {x}_j} $$
(47)

The first term of this equation does not depend explicitly on x j , and thus

$$ \frac{\partial^2U\left(\boldsymbol{x},\boldsymbol{u}\left(\boldsymbol{x}\right)\right)}{\partial {x}_i\ \partial {x}_j}=\frac{\partial \left({L}_k{\varPsi}_k\left(\boldsymbol{u}\left(\boldsymbol{x}\right)\right)\right)}{\partial {x}_j}=0 $$
(48)

Based on Equations (26) and (48), Equation (47) may be rewritten as

$$ \frac{\partial^2\mathrm{J}\left(\boldsymbol{x}\right)}{\partial {x}_i\ \partial {x}_j}=-\frac{\partial {\boldsymbol{T}}^T\left(\boldsymbol{x},\boldsymbol{u}\left(\boldsymbol{x}\right)\right)}{\partial {x}_i}\frac{\partial \boldsymbol{u}\left(\boldsymbol{x}\right)}{\partial {x}_j} $$
(49)

The total derivative of the internal force vector at the equilibrium configuration (T(u(x), x) = F, see Equation (25)), is given as

$$ \frac{\partial \boldsymbol{T}\left(\boldsymbol{x},\boldsymbol{u}\left(\boldsymbol{x}\right)\right)}{\partial \boldsymbol{u}}\frac{\partial \boldsymbol{u}\left(\boldsymbol{x}\right)}{\partial {x}_j}+\frac{\partial \boldsymbol{T}\left(\boldsymbol{x},\boldsymbol{u}\left(\boldsymbol{x}\right)\right)}{\partial {x}_j}=0 $$
(50)

Defining the tangent stiffness matrix as K t (x) = ∂T(x, u(x))/∂u, we have

$$ {\boldsymbol{K}}_t\left(\boldsymbol{x}\right)\frac{\partial \boldsymbol{u}\left(\boldsymbol{x}\right)}{\partial {x}_j}+\frac{\partial \boldsymbol{T}\left(\boldsymbol{x},\boldsymbol{u}\left(\boldsymbol{x}\right)\right)}{\partial {x}_j}=0 $$
(51)

and solving for ∂u/∂x j we obtain

$$ \frac{\partial \boldsymbol{u}}{\partial {x}_j}= - {\boldsymbol{K}}_t^{-1}\left(\boldsymbol{x}\right)\frac{\partial \boldsymbol{T}\left(\boldsymbol{x},\boldsymbol{u}\left(\boldsymbol{x}\right)\right)}{\partial {x}_j} $$
(52)

If this equation is inserted into Equation (49), we obtain the components of the Hessian H of J(x), as

$$ {H}_{ij}=\frac{\partial^2\mathrm{J}\left(\boldsymbol{x}\right)}{\partial {x}_i\ \partial {x}_j}=\frac{\partial {\boldsymbol{T}}^T\left(\boldsymbol{x},\boldsymbol{u}\left(\boldsymbol{x}\right)\right)}{\partial {x}_i}\ {\boldsymbol{K}}_t^{-1}\left(\boldsymbol{x}\right)\frac{\partial \boldsymbol{T}\left(\boldsymbol{x},\boldsymbol{u}\left(\boldsymbol{x}\right)\right)}{\partial {x}_j} $$
(53)

or

$$ {H}_{ij}={\overline{\boldsymbol{T}}}_i^T\left(\boldsymbol{x},\boldsymbol{u}\left(\boldsymbol{x}\right)\right)\ {\boldsymbol{K}}_t^{-1}\left(\boldsymbol{x}\right){\overline{\boldsymbol{T}}}_j\left(\boldsymbol{x},\boldsymbol{u}\left(\boldsymbol{x}\right)\right) $$
(54)

where \( {\overline{\boldsymbol{T}}}_i\left(\boldsymbol{x},\boldsymbol{u}\left(\boldsymbol{x}\right)\right)=\partial {\boldsymbol{T}}^T\left(\boldsymbol{x},\boldsymbol{u}\left(\boldsymbol{x}\right)\right)/\partial {x}_i \). In matrix format, we have:

$$ \boldsymbol{H}={\overline{\boldsymbol{T}}}^T\left(\boldsymbol{x},\boldsymbol{u}\left(\boldsymbol{x}\right)\right)\ {\boldsymbol{K}}_t^{-1}\left(\boldsymbol{x}\right)\overline{\boldsymbol{T}}\left(\boldsymbol{x},\boldsymbol{u}\left(\boldsymbol{x}\right)\right) $$
(55)

where \( \overline{\boldsymbol{T}}=\left\{{\overline{\boldsymbol{T}}}_1\ {\overline{\boldsymbol{T}}}_2\dots {\overline{\boldsymbol{T}}}_n\right\} \). In order to verify if H is positive semidefinite, we investigate if y T Hy ≥ 0, for every admissible y, i.e.

$$ {\boldsymbol{y}}^T{\overline{\boldsymbol{T}}}^T\left(\boldsymbol{x},\boldsymbol{u}\left(\boldsymbol{x}\right)\right)\ {\boldsymbol{K}}_t^{-1}\left(\boldsymbol{x}\right)\overline{\boldsymbol{T}}\left(\boldsymbol{x},\boldsymbol{u}\left(\boldsymbol{x}\right)\right)\boldsymbol{y}\ge 0 $$
(56)

or

$$ {\left(\overline{\boldsymbol{T}}\left(\boldsymbol{x},\boldsymbol{u}\left(\boldsymbol{x}\right)\right)\ \boldsymbol{y}\right)}^T{\boldsymbol{K}}_t^{-1}\left(\boldsymbol{x}\right)\left(\overline{\boldsymbol{T}}\left(\boldsymbol{x},\boldsymbol{u}\left(\boldsymbol{x}\right)\right)\ \boldsymbol{y}\right)\ge 0 $$
(57)

For this inequality to hold, the inverse of the tangent stiffness K − 1 t (x) (or K t (x)) needs to be positive definite. Therefore, in the nonlinear material model we need to have dσ(λ)dλ > 0 in Equation (39). In other words, the specific strain energy should be strictly convex to guarantee the convexity of the optimization problem based on the nonlinear material model (NMM).

4.4 KKT conditions

Because the optimization problem in Equation (40) is convex, the KKT conditions are both necessary and sufficient optimality conditions. To define them, we start with the Lagrangian

$$ \mathrm{\mathcal{L}}\left(\boldsymbol{x},\phi \right)=\mathrm{J}\left(\boldsymbol{x}\right)+\phi\ \left({\displaystyle \sum_{i=1}^n}{x}_i\ {L}_i-{V}_{max}\right) $$
(58)

Therefore (Christensen and Klarbring 2009)

$$ \frac{\partial \mathrm{\mathcal{L}}}{\partial {x}_i}\left({\boldsymbol{x}}^{*},{\phi}^{*}\right)\le 0,\kern0.5em if\ {x}_i^{*}={x}_i^{max} $$
(59)
$$ \frac{\partial \mathcal{L}}{\partial {x}_i}\left({\boldsymbol{x}}^{*},{\phi}^{*}\right)=0,\kern0.5em if\kern0.75em {x}_i^{min}<{x}_i^{*}<{x}_i^{max} $$
(60)
$$ \frac{\partial \mathrm{\mathcal{L}}}{\partial {x}_i}\left({\boldsymbol{x}}^{*},{\phi}^{*}\right)\ge 0,\kern0.5em if\ {x}_i^{*}={x}_i^{min} $$
(61)

The derivative the Lagrangian is given as

$$ \frac{\partial \mathrm{\mathcal{L}}}{\partial {x}_i}\left(\boldsymbol{x},\phi \right)=\frac{\partial \mathrm{J}\left(\boldsymbol{x}\right)}{\partial {x}_i}+\phi\ {L}_i $$
(62)

After substitution of the Equation (46) into Equation (62) and, subsequently, Equations (59) through (61), we obtain the following resulting KKT conditions at the point (x*, ϕ*):

$$ {\varPsi}_i\left(\boldsymbol{u}\left({\boldsymbol{x}}^{*}\right)\right)\ge {\phi}^{*},\kern0.5em if\kern0.5em {x}_i^{*}={x}_i^{max} $$
(63)
$$ {\varPsi}_i\left(\boldsymbol{u}\left({\boldsymbol{x}}^{*}\right)\right)={\phi}^{*},\kern0.5em if\kern0.5em {x}_i^{min}<{x}_i^{*}<{x}_i^{max} $$
(64)
$$ {\varPsi}_i\left(\boldsymbol{u}\left({\boldsymbol{x}}^{*}\right)\right)\le {\phi}^{*},\kern0.5em if\kern0.5em {x}_i^{*}={x}_i^{min} $$
(65)

Based on the Equation (64), we obtain constant specific strain energy at the optimum in the material nonlinear case when the lateral constraints are not active (Khot and Kamat 1985). In the linear case, this situation correspond to a full stress design (Christensen and Klarbring 2009): Ψ i  = σ 2 i /E o .

5 Numerical examples

We present three examples to illustrate the proposed formulation. All the examples assume material nonlinear behavior (hyperelastic models) under small displacements. The ground structures are generated by removing overlapped bars (Bendsoe and Sigmund 2003). Figure 6 illustrates the ground structure generation. In the first two examples, we illustrate dependence of the topology on the material model and, in last one, on the load level. Here we solve the nonlinear structural equilibrium problem by means of equivalent approaches:

Fig. 6
figure 6

Ground structure generation: a Level 1; b Level 2; c Full level

Full size image
  1. 1

    Direct minimization of the total potential energy (PE), Π(u) (our main approach)

  2. 2

    Solution of the nonlinear system (T(u) = F) using a Newton-Raphson (NR) method.

In the second approach, in the beginning of the nonlinear iterative process, the ground structure model may exhibit excessive flexibility. To circumvent this problem, we simply divide the load into increments during the nonlinear solution scheme (Wriggers 2008). As the optimization process progresses, we reduce the number of increments based on the change of the objective function. Figure 7 presents the optimization flowchart employed in this work.

Fig. 7
figure 7

Optimization flowchart

Full size image

In all the examples, we use convergence tolerance tol = 10− 8, αi = − 1 (η = 0.5), move limit M = 10 (x max i  − x min i ) (see Appendix 3), material modulus E o  = 70 106 kN/m 2, and parameters for strict convexity β 1 > 1 and β 2 < 1. The initial area (x 0) is defined as the ratio between the maximum volume and the sum of the length of all ground structure members. The lower and upper bounds are defined by x min = 10− 2 x 0 and x max = 104 x 0, respectively. During the iterative process, the stiffness matrix is always nonsingular because we are working with the ground structure and there are no bars of null areas. At the end of the optimization process, we interpret the topology by defining a filter that eliminates members with the ratio x i /max(x) ≤ 1 %, but keeps the members in the topology otherwise. As indicated, the filter step is applied only once, at the end of the optimization process. The intermediate nodes are not eliminated because we are not treating instability problems (geometric nonlinearities). Thus, in practical terms, the collinear bars shown in the final topology of the examples below can be replaced by a single bar. Moreover, the tension and compression bars are represented by blue and red colors, respectively, in the final topology configuration. We provide detailed information for all the parameters used in the examples in order to allow the readers to be able to reproduce the results obtained.

5.1 Example 1: Central load on simply supported square domain

In this example, we illustrate the influence of the material model on the resulting structural topology. Specifically, we compare the linear model with two nonlinear material models (see Fig. 5). The geometry, load and support conditions (two fixed supports) are shown in the Fig. 8a. In this case, we obtain 6,808 non-overlapped members using a full ground structure. We use two Ogden-based material models (Equation (19)) as illustrated by Fig. 8b. As a point of reference, Fig. 9a provides the topology for the linear model and Fig. 9b provides the normalized members areas, which are grouped in 4 sets [1, 0.94, 0.45, 0.31].

Fig. 8
figure 8

Example 1 - Full level ground structure (13×13) mesh with 6,808 non-overlapped bars (L = 6 m and V max  = 0.016 m 3): a geometry, load (P = 100 kN) and support conditions; b Ogden-based material models

Full size image
Fig. 9
figure 9

Example 1 - Linear model: a Final topology; b Member areas

Full size image

Next, we illustrate the dependence of the topology on the selected material model. The topology obtained with the material model Ogden 1 and Ogden 2 are shown in Fig. 10a and 10b, respectively. Notice that each different material model leads to a dramatically different topology, which also differs from the one for the linear case. The convexity of the nonlinear topology optimization problem is illustrated by Fig. 11a for the Ogden 1 material model. The resulting (sizing) normalized members areas are divided into 4 groups [1, 0.94, 0.51, 0.35], as illustrated by Fig. 11b.

Fig. 10
figure 10

Example 1 - Final topologies: a Material model Ogden 1; b Material model Ogden 2

Full size image
Fig. 11
figure 11

Example 1 - Material model Ogden1: a Objective function; b Normalized member areas

Full size image

Table 1 presents a summary of the data associated with the aforementioned description of Example 1. Notice that, in this specific situation, the objective function is higher for the linear case than for the nonlinear cases (see Fig. 8b) when different topologies are generated (due to the magnitude of the selected load level). The column with the max displacements (Max |u|) confirms the small displacement assumption. The range of stretches is quite narrow for all cases (c.f. Max λ i and Min λ i columns). In this example, the efficiency of the method is similar when using either the NR (with 2 load increments) or the PE approach. Moreover, for the linear case (c.f. 2nd and 3rd rows), the solution using direct minimization of the potential energy employs the same algorithm as that for nonlinear problems – thus the extra CPU cost.

Table 1 Representative parameters for Example 1 (NR denotes Newton–Raphson method and PE denotes potential energy)
Full size table

5.2 Example 2: Opposite loads in a simply supported rectangular domain

In this example, we illustrate the influence of the material model on the resulting structural topology. Specifically, we compare the linear model with a nonlinear material model (see Fig. 5). The geometry, load and support conditions (two fixed supports) are shown in Fig. 12a and the Ogden-based material model is illustrated in Fig. 12b. In this case, we have 10,098 non-overlapped connections in the ground structure.

Fig. 12
figure 12

Example 2 - Level 10 ground structure (21×11) mesh with 10,098 non-overlapped bars (L = 10m and Vmax = 0.04m3): a Geometry, load (P = 100 kN) and support conditions; b Ogden material model

Full size image

Figure 13a shows the topology for the linear case, and Fig. 13b for the nonlinear case using the Ogden model of Fig. 12b. Although both cases display small displacements (see 4th column) and stretches (c.f. Max λ i and Min λ i columns), the topologies obtained in each case are drastically distinct, as shown in Fig. 13.

Fig. 13
figure 13

Example 2 - Final topology: a Linear model; b Nonlinear model

Full size image

Table 2 summarizes the data associated with Example 2. The objective function is higher for the linear than for the nonlinear case (similar to the previous example). For the linear case, the PE energy solution is much less efficient than the standard solution (c.f. 2nd and 3rd rows), which is partially due to the case that the potential energy algorithm is quite general and not tailored to the problem. However, for the nonlinear case, the PE solution is much more efficient than the Newton Raphson (using 15 load increments) solution (c.f. 4nd and 5rd rows). As before, the column with the max displacements (Max |u|) confirms the small displacement assumption. Finally, Fig. 14 illustrates the fact that, in the beginning of the nonlinear optimization process, the ground structure exhibits excessive flexibility when compared to the behavior of the optimized structure.

Table 2 Representative parameters for Example 2 (NR denotes Newton–Raphson method and PE denotes potential energy)
Full size table
Fig. 14
figure 14

Example 2 - Nonlinear load–displacement curve at the beginning (GS curve) and at end of the optimization process

Full size image

5.3 Example 3: Top central load in a laterally constrained rectangular domain

In this example, we illustrate the influence of the load level on the resulting topology considering both linear and nonlinear material behavior (see Fig. 5). The geometry, load and support conditions are shown in Fig. 15a, and the Ogden based material model is provided in Fig. 15b. In this example, we have 3,860 non-overlapped members.

Fig. 15
figure 15

Example 3 - Level 9 ground structure (19×7) mesh with 3,860 non-overlapped bars (L = 3 m and V max  = 0.036m 3): a Geometry, load and support conditions; b Ogden material model

Full size image

Figure 16 compares the resulting topologies for the linear (Fig. 16a) and the nonlinear (Fig. 16b) models, which are identical in this case. Thus the topology for the nonlinear case considering a low load level (P = 20 kN) coincides with that for the linear case (which is independent of the load level). Figure 17 illustrates the resulting topologies for the nonlinear model considering two different load levels. In summary, Figs. 16b, 17a and 17b illustrate the resulting topologies for the nonlinear model (see Fig. 15b) considering load levels P = 20 kN (low), P = 80 kN (intermediate), and P = 160 kN (high), respectively.

Fig. 16
figure 16

Example 3 - Final topologies: a Linear model P = 80kN; b Nonlinear model P = 20kN

Full size image
Fig. 17
figure 17

Example 3 - Final topologies for nonlinear model: a P = 80 kN; b P = 160 kN

Full size image

Table 3 summarizes the data for this example. The objective function (see 2nd column) is lower for the linear case (Fig. 16a) than for the nonlinear case (Fig. 17a) under the same load level (c.f. 2nd and 6th rows wrt to J). Although the load levels are the same, the topologies are distinct, as shown by Figs. 16a and 17a. At this load level, the linear structure (0.487 kN m) is more rigid than the nonlinear one (0.593 kN m), which is the opposite situation of the previous examples. This behavior can be explained by the plot of Fig. 18, which shows that the tangent modulus for the nonlinear material in compression is lower than for the linear case (see insert in the plot). Notice that, for the nonlinear material model the PE solution is more efficient than the NR (using 1, 2 and 4 load increments, respectively, for each load case) solution. As explained previously, the PE solution for the linear case is less efficient than the approach using the direct solution of the linear system because the PE solution is general and not tailored for the linear problem. As before, the column with the max displacements (Max |u|) confirms the small displacement assumption.

Table 3 Representative parameters for Example 3 (NR denotes Newton–Raphson method and PE denotes potential energy)
Full size table
Fig. 18
figure 18

Example 3 - Material tangent modulus

Full size image

6 Concluding remarks and extensions

The unified approach for nonlinear topology optimization considering hyperelastic materials and using the ground structure approach consists of adopting the total potential energy concept both in the objective function and in the equilibrium solution of the problem. In terms of computational efficiency (for nonlinear material problems), the equilibrium solution adopting the potential energy approach makes the process either comparable or more efficient than the corresponding solution using the Newton–Raphson method. This might be due to the fact that, when minimizing the potential energy, we start the subsequent iteration using the displacement field from the previous iteration. Three examples demonstrate the features of the approach. The first two illustrate the influence of the material model on the resulting structural topology, and the last one demonstrates the influence of the load level.

Regarding the optimization formulation, the total potential energy approach has the following features:

  • The objective function is convex when the stiffness matrix is positive definite. For the hyperelastic truss model, this condition is fulfilled if the specific strain energy is strictly convex.

  • There is no need to compute the adjoint vector (see section 3.2 on sensitivities), which leads to improved computational efficiency.

  • The sensitivity of the objective function (see Equation (46)) is always non-positive.

  • The formulation leads to “constant specific strain energy” for the members in the optimum range x min j  < x j  < x max j . This behavior is similar to a “full stress design” in the linear case.

  • Under low load levels and small strains and displacements, both the hyperelastic truss model (adopted in this work) and the usual linear truss model (Christensen and Klarbring 2009) lead to the same results (as expected).

This work offers room for further extensions. For instance, multiple load cases, involving body forces, could be considered. Another interesting area for future research deals with development of more general constitutive models which allows for improved simultaneous control of material stiffness and strength.