1 Introduction

Porous structures widely exist in nature, such as in bones and sandstones. Generally, the heterogeneous materials are randomly distributed, which causes challenges in related modeling and simulation. Reconstruction of the random heterogeneous porous material model based on scanned images has attracted substantial attention (Liu and Shapiro 2015), which generates material samples sharing common characteristics such as density, porosity, stiffness, etc.

Other than reconstruction, natural materials are also widely studied for the design and optimization of engineered porous structures, which can attain superior mechanical performance by tailoring the local material distribution; see Fig. 1 for a few examples. Approaches for intentional porous structure modeling and optimization are quite diversified and a brief review is demonstrated below by distinguishing the homogeneous and heterogeneous porous structures, where the former means the uniform porosity distribution across the design domain and the latter indicates the non-uniform porosity distribution, i.e., the material structure varies from one location to another. Noted that, regardless of the homogeneity or heterogeneity, the structure of interest is deterministic which is different from the microstructures in stochastic representation.

Fig. 1
figure 1

Examples of engineered porous structures

Full size image

To build a homogeneous porous structure, a trivial approach is to select a candidate porous unit cell and spatially repeat it to form the ensemble. Hollister (Hollister et al. 2002) used cylindrical voids to model the porous unit cell of tissue scaffolds and its effective elasticity properties were empirically modeled and optimized through homogenization (Hollister and Kikuchi 1992). Fang et al. (Fang et al. 2005) characterized the effective elasticity properties of the porous unit cell with centered square channels through asymptotic homogenization, and impact of the fabrication process parameters was tested. A library of the representative porous unit cells for tissue scaffolds can be found in (Sun et al. 2005). For these aforementioned works, the porous unit cells all have the regulated geometry which can be parametrically modeled. Recently, the inverse homogenization-based topology optimization has been widely adopted to design the freeform porous unit cell, attaining superior physical properties, including elasticity properties (Sigmund 1994; Lin et al. 2004; Guest and Prévost 2006; Hollister and Lin 2007; Challis et al. 2012; Wang et al. 2014, 2016b; Vogiatzis et al. 2017a), bulk modulus (Sigmund 2000; Gibiansky and Sigmund 2000; Kang et al. 2010; Huang et al. 2011; Wang et al. 2016a), porosity (Lin et al. 2004), permeability (Guest and Prévost 2006, 2007; Hollister and Lin 2007; Challis et al. 2012; Wang et al. 2016a), and thermal expansion coefficient (Sigmund and Torquato 1997). It is widely accepted that a bigger design space is explored by enabling the local freeform material distribution. In addition, the two-scale inverse homogenization-based topology optimization has also been actively investigated, which concurrently optimizes the macrostructure and the repetitive porous unit cell (Liu et al. 2008; Niu et al. 2009; Deng et al. 2013; Huang et al. 2013; Zuo et al. 2013; Guo et al. 2015; Wang et al. 2016c). A commonality of these works is that, the porous unit cell is spatially identical and therefore, the porosity and other physical properties are spatially invariant. Hence, the overall structure is amenable for modeling, optimization, and fabrication.

The heterogeneous porosity distribution brings challenges to the porous structure modeling and optimization. A simplified approach is to use the ground structure method (Dorn et al. 1964), originally developed for truss-like structures, to design the lattice structure. The strut diameters are utilized as the optimization variables to modify the structural performance and local porosity. The heterogeneity can be further intensified by allowing the diameters approach zero (causing topological changes) (Zegard and Paulino 2014) or enable the connecting node movement (Liu and Ma 2017a). Another approach is to use predefined lattice units to repetitively form the macro structure (Liu and Ma 2017b). Similar to the ground structure method, the lattice unit densities are employed as the optimization variables, and homogenization and surrogate modeling are performed to build the empirical elastic properties. Therefore, both the lattice unit and the macrostructure can be concurrently optimized (Arabnejad Khanoki and Pasini 2012; Zhang et al. 2015; Liu et al. 2015; Cheng et al. 2017) in the case that the unit density is allowed to approach zero, which is similar to the conventional homogenization-based topology optimization method (Bendsøe and Kikuchi 1988; Bendsøe and Sigmund 2004). Prominently, the optimal design solution is physically realizable. Chen (Chen 2007) presented an adaptive change method for the repetitive lattice structure, where shape of the lattice units can be spatially varying according to the specific need. Other than the lattice structures, the spatially varying freeform porous unit cells have also been realized by the two-scale inverse homogenization-based topology optimization (Rodrigues et al. 2002; Coelho et al. 2008, 2011; Xia and Breitkopf 2014, 2015; Coelho and Rodrigues 2015; Sivapuram et al. 2016), even though the computational cost is drastically increased. Another limitation of the two-scale freeform approach is that, explicit descriptions of the local porous unit cells do not exist, and therefore, the related post-editing is extremely tedious.

For the aforementioned porous structure modeling methods, the porous units, distributed either homogeneously or heterogeneously, are placed inside the design domain based on a uniform space discretization. In other words, a fixed quadrilateral or hexahedral mesh is created first before specifying the local material distribution. This fact limits the generation of highly heterogeneous porous structures. To fix this issue, a novel approach is proposed in (Kou and Tan 2010, 2012). The Voronoi tessellation is performed to partition the design domain into a collection of sub-areas, and a local void is generated inside each sub-area by fitting in a closed B-spline curve. In this way, the overall heterogeneity can be effectively controlled by manipulating the Voronoi tessellation. Even the functionally graded Voronoi tessellation has been achieved (Kou and Tan 2012). A similar approach was adopted in (Fantini et al. 2016), where the Voronoi tessellation is processed by the Catmull-Clark algorithm to produce the smoothed internal voids. For these Voronoi-based methods, the tessellation is subjected to no optimality criteria and it is non-trivial to perform the after-tessellation optimization. Hence, this paper contributes the new method, which has the heterogeneous porous structure modeling capacity compatible to the Voronoi-based methods and more importantly, can effectively conduct the structural compliance and stress level optimization.

This proposed method employs four steps, as demonstrated below (Fig. 2):

Fig. 2
figure 2

Overview of the proposed method

Full size image

And this method shows outstanding characteristics in the following aspects:

  1. 1)

    Both the structural stiffness and stress level can be effectively optimized;

  2. 2)

    The local porosity can be explicitly controlled, e.g., both heterogeneous and functionally graded porosity distribution are achievable;

  3. 3)

    The Blinn transformation-based level set method can effectively transform the truss structure into a porous continuum.

More details will be presented in the rest of this paper.

2 Truss-like structure design with local geometry control

Truss-like structure design belongs to a discretized structure design category, where the entire structure is formed by a network of interconnected truss elements. Truss-like structure is widely employed in practice for being lightweight and stiff, e.g., lattice structures have been widely explored to infill the conventional solid mechanical parts, in order to reduce weight without drastically changing the load-bearing capacity. So far, a wide variety of methods have been developed to design truss-like structures (Stolpe 2016), including the ground structure method (Dorn et al. 1964), the density projection method (Alzahrani et al. 2015), and the non-gradient methods (Mortazavi and Toğan 2016), etc. Among them, the ground structure method attracts the most attention (Bendsøe et al. 1994; Zegard and Paulino 2014), where a ground structure composed of numerous strut elements are constructed first and later, either the strut cross-section densities or the nodal positions are optimized to achieve the optimal design. In the truss-like structure design in this work, we build a base structure as the input similar to the ground structure method, but only the nodal positions will be employed as design variables, but not the cross-section densities. Therefore, no topological changes will happen. For the reason, the porosity constraints will dynamically change if the patches merge or split, which causes oscillations in the convergence. Also, if the cross-sectional densities are considered, it may run into the well-known stress singularity phenomenon that has been widely reported in trusses (Kirsch 1990; CHENG and JIANG 1992; Cheng and Guo 1997; Rozvany 2001).

2.1 Shape optimization

The typical compliance-minimization problem is formulated in Eq. 1.

$$ {\displaystyle \begin{array}{l}\mathit{\min}.\kern0.5em {\boldsymbol{F}}^T\boldsymbol{U}\hfill \\ {}s.t.\kern0.5em \boldsymbol{K}\boldsymbol{U}=\boldsymbol{F}\hfill \\ {}\boldsymbol{K}=\sum \limits_{e=1}^N{\boldsymbol{K}}_{\boldsymbol{e}}\hfill \end{array}} $$
(1)

where K is the assembled global stiffness tensor, U is the global displacement vector, and F is the global force vector.

It is noted that:

$$ {\boldsymbol{K}}_e={{\boldsymbol{T}}_e}^T\overline{{\boldsymbol{K}}_e}\kern0.1em {\boldsymbol{T}}_e $$
(2)

where T e is the coordinate transformation tensor, \( {\overline{\boldsymbol{K}}}_{\boldsymbol{e}} \) is the stiffness tensor of strut element e in the local coordinate system, while K e is the stiffness tensor of truss element e in global coordinate system. Assembly of K e forms the global stiffness tensor K.

In case that there exist a few discrete cross-section options, e.g. different cross-section sizes or shapes, the multi-material interpolation is necessary, e.g., DMO (Discrete Material Optimization) (Stegmann and Lund 2005) is a good multi-material interpolation scheme as presented in Eq. 3:

$$ {\boldsymbol{K}}_{\boldsymbol{e}}={{\boldsymbol{T}}_{\boldsymbol{e}}}^T\left\{{\left({\rho}_{e1}\right)}^p\left[1-{\left({\rho}_{e2}\right)}^p\right]{\overline{\boldsymbol{K}}}_{\boldsymbol{e}1}+{\left({\rho}_{e2}\right)}^p\left[1-{\left({\rho}_{e1}\right)}^p\right]{\overline{\boldsymbol{K}}}_{\boldsymbol{e}2}\right\}{\boldsymbol{T}}_{\boldsymbol{e}} $$
(3)

in which \( {\overline{\boldsymbol{K}}}_{e1} \) and \( {\overline{\boldsymbol{K}}}_{e2} \) are stiffness tensors of truss element e in local coordinate system with the cross-section option 1 and 2, respectively; ρ e1 and ρ e2 are the densities related to cross-section option 1 and 2, respectively. The advantage of this multi-material interpolation scheme is that it will finally converge to either (ρ e1 = 1 , ρ e2 = 0) or (ρ e1 = 0 , ρ e2 = 1), which means a clearly identified cross-section option.

2.2 Sensitivity result

To solve this shape optimization problem, the Lagrangian is constructed as:

$$ L={\boldsymbol{F}}^T\boldsymbol{U}-\tilde{\boldsymbol{U}}\left(\boldsymbol{KU}-\boldsymbol{F}\right) $$
(4)

in which \( \overset{\sim }{\boldsymbol{U}} \) is the adjoint displacement field. Noted that, for the compliance-minimization problem, solution of the adjoint variable is \( \overset{\sim }{\boldsymbol{U}}=-\boldsymbol{U} \) (Bendsøe and Sigmund 2004).

Correspondingly, the sensitivity analysis result on the nodal coordinate is:

$$ {\displaystyle \begin{array}{c}\hfill \frac{\partial L}{\partial {x}_i}=-\sum \limits_{e=1}^n{{\boldsymbol{U}}_{\boldsymbol{e}}}^T\frac{\partial {\boldsymbol{K}}_{\boldsymbol{e}}}{\partial {x}_i}{\boldsymbol{U}}_{\boldsymbol{e}}\hfill \\ {}\hfill \kern1.2em =-\sum \limits_{e=1}^n{{\boldsymbol{U}}_{\boldsymbol{e}}}^T\left(\frac{\partial {{\boldsymbol{T}}_e}^T}{\partial {x}_i}{\overline{\boldsymbol{K}}}_{\boldsymbol{e}}{\boldsymbol{T}}_e+{{\boldsymbol{T}}_e}^T\frac{\partial {\overline{\boldsymbol{K}}}_{\boldsymbol{e}}}{\partial {x}_i}{\boldsymbol{T}}_e+{{\boldsymbol{T}}_e}^T{\overline{\boldsymbol{K}}}_{\boldsymbol{e}}\frac{\partial {\boldsymbol{T}}_e}{\partial {x}_i}\right){\boldsymbol{U}}_{\boldsymbol{e}}\hfill \end{array}} $$
(5)

where U e is the displacement vector of truss element e and x i is the ith nodal coordinate.

Then, changes of the nodal positions can be determined through Eq. 6, which ensures that the Lagrangian changes in the steepest descent direction:

$$ \frac{\partial {x}_i}{\partial t}=\sum_{e=1}^n{{\boldsymbol{U}}_{\boldsymbol{e}}}^T\frac{\partial {\boldsymbol{K}}_{\boldsymbol{e}}}{\partial {x}_i}{\boldsymbol{U}}_{\boldsymbol{e}} $$
(6)

Finally, the nodal positions are updated through Eq. 7:

$$ {x_i}^{k+1}={x_i}^k+t\frac{\partial {x}_i}{\partial t} $$
(7)

where, t is the step length and k represents the iteration number.

2.3 Local geometry control

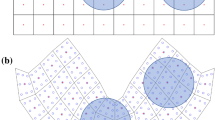
In (Xia et al. 2013), local geometry control was realized to prevent truss elements from intersection. As shown in Fig. 3, if the vertex v3 flips over the edge v1-v2, the truss elements intersect which is unreasonable in practice.

Fig. 3
figure 3

Example of truss element intersection: (a) Structure before truss element intersection, (b) Structure after truss element intersection

Full size image

Therefore, a non-intersection constraint was developed, as:

$$ {\displaystyle \begin{array}{c}\hfill {S}_j\ge \underline{S}\kern1em j=1,\dots, m\hfill \\ {}\hfill {S}_j={0.5}^{\ast}\det \left[\begin{array}{ccc}\hfill 1\hfill & \hfill 1\hfill & \hfill 1\hfill \\ {}\hfill {x}_1\hfill & \hfill {x}_2\hfill & \hfill {x}_3\hfill \\ {}\hfill {y}_1\hfill & \hfill {y}_2\hfill & \hfill {y}_3\hfill \end{array}\right]\hfill \end{array}} $$
(8)

where S j is the j th triangle grid area and it is ensured positive by counting the vertices in the contour-clockwise order. \( \underline{S} \) is the lower bound of the triangle grid area which is a small positive number to prevent the intersection. m is the number of triangular elements involved.

Inspired by this non-intersection constraint, the triangle grid areas can also be constrained with an upper bound in this work, in order to realize the local geometry control. It is:

$$ {S}_j\le \overline{S}j=1,\dots, m $$
(9)

in which \( \overline{S} \) is the upper bound of the triangle grid area. The porosity upper limit is useful for several applications, e.g., ensure the 3D printed porous structure self-support and guarantee the proper functioning of wire-wrapped sand screen.

In summary, the local porosity can be well controlled by customizing the \( \underline{S} \) and \( \overline{S} \) values.

2.4 Functionally graded porosity distribution

Inspired by Eqs. 8 and 9, the local porosities can be further controlled subjected to spatially varying bounds, by making the bound a function of the coordinates, through which functionally graded porosity distribution can be achieved. For instance, the porosities can vary in a linear pattern through Eq. 10, or in a non-linear pattern through Eq. 11, in the x-axis direction.

$$ \underline{S}=0.2+0.1x;\kern1em \overline{S}=0.3+0.1x $$
(10)
$$ \underline{S}=0.2+\sin \left(\pi x\right);\overline{S}=0.3+\sin \left(\pi x\right) $$
(11)

An example of the functionally graded porosity control is demonstrated in Fig. 4. Figure 4a presents the input base structure and the boundary condition. The truss elements have a thickness of 2.4 and the Young’s modulus of 1.3. The two bottom corners are fixed and a unit force is loaded at the top center point. Because of symmetry, only the left half of the structure is demonstrated. Fig. 4b-d presents the optimization results subjected to the \( \underline{S}=1440,2160,\mathrm{and}\ 2880 \), respectively. Then, by making the \( \underline{S} \) varying in the x-axis direction (\( \underline{S}=1440+2.4x \)), the functionally graded porosity distribution can be clearly identified in Fig. 4e.

Fig. 4
figure 4

Local geometry control

Full size image

Noted that, other than determining the porosity grading through optimization, a given grading of the porosity distribution is adopted in this work. With regards to the motivation, the structural optimization employs the mechanical properties, i.e. stiffness and stress, as the objective, but at the same time, the functionally graded porosity distribution may be related to other functional aspects, e.g. graded thermo-fluid properties, filtering properties, or bio-mechanical properties, which is prescribed when formulating the optimization problem. In fact, intentionally controlling the functionally graded porosity distribution is widely studied (Kou and Tan 2007, 2012).

3 Level set-based porous structure modeling

The truss element, according to its dimension, can then be transformed into a continuum strut represented by the implicit level set function; see below:

$$ {\displaystyle \begin{array}{l}\Phi \left({x}_0,{y}_0\right)=\min \left\{\frac{L_s}{2}-\left[\left(x-{x}_0\right) cos\theta +\left(y-{y}_0\right) sin\theta \right],\right.\hfill \\ {}\kern4.9em \frac{L_s}{2}+\left[\left(x-{x}_0\right) cos\theta +\left(y-{y}_0\right) sin\theta \right],\hfill \\ {}\kern4.9em \frac{H_s}{2}-\left[-\left(x-{x}_0\right) sin\theta +\left(y-{y}_0\right) cos\theta \right],\hfill \\ {}\kern4.9em \left.\frac{H_s}{2}+\left[-\left(x-{x}_0\right) sin\theta +\left(y-{y}_0\right) cos\theta \right]\right\}\hfill \end{array}} $$
(12)

where, L s and H s are the length and thickness of the strut, respectively; (x 0 , y 0) is the center position and θ is the orientation.

The individual struts can be combined through Boolean operations to form a complex geometry, as demonstrated below:

$$ {\displaystyle \begin{array}{l}{\Phi}_1\kern0.5em \cup \kern0.5em {\Phi}_2=\mathit{\max}\left({\Phi}_1,{\Phi}_2\right)\hfill \\ {}{\Phi}_1\kern0.5em \cap {\Phi}_2=\mathit{\min}\left({\Phi}_1,{\Phi}_2\right)\hfill \\ {}{\Phi}_1\kern0.5em \backslash \kern0.5em {\Phi}_2=\mathit{\min}\left({\Phi}_1,-{\Phi}_2\right)\hfill \end{array}} $$
(13)

In fact, topology optimization can be performed based on the input structure purely composed of Boolean operated struts, which is named the moving component method (Bell et al. 2012; Guo et al. 2014; Norato et al. 2015; Zhang et al. 2016; Guo et al. 2016), which potentially could solve the problems studied in this work .

Alternatively, we treat the structure including a large number of struts as a truss network, perform the nodal position optimization and later, restore it back to its original form. Moreover, the Boolean operators as demonstrated in Eq. 13 are not applied in this paper, because we intend to replace the sharp corners of the strut connections by smooth transitions. In this way, a subsequent shape optimization can be performed on the restored porous continuum to modify the local stress level.

To construct the porous continuum, the individual struts are combined based on the Blinn transformation (Storm et al. 2013); see below:

$$ \overline{\Phi}=\sum_{i=1}^n\exp \left({a}_i{\Phi}_i\right)-1 $$
(14)

where, a i is the Blinn factor of the i th level set function and n is the total number of struts.

An example of comparing the different operators is shown in Fig. 5.

Fig. 5
figure 5

An example of comparing the different operators

Full size image

In Eq. 14, the lattice is built based on a unified level set representation. In case that a large number of struts are involved, it will complicate the sensitivity analysis and also cause difficulties to non-sensitivity based optimization (Biyikli and To 2015), because of the non-unique matches between the a i values and the strut transition areas. To address this issue, Eq. 14 is modified into Eq. 15, where the Blinn operations are performed between each pair of struts within each triangular grid, which are later unified through union operations.

$$ {\displaystyle \begin{array}{c}\hfill \overline{\Phi}=\underset{i=1}{\overset{m}{\mathrm{U}}}\left\{\left[\exp \left({a}_{i1}{\Phi}_{i1}\right)+\exp \left({a}_{i1}{\Phi}_{i2}\right)-1\right]\cup \left[\exp \left({a}_{i2}{\Phi}_{i2}\right)+\exp \left({a}_{i2}{\Phi}_{i3}\right)-1\right]\right.\hfill \\ {}\hfill \left.\cup \left[\exp \left({a}_{i3}{\Phi}_{i3}\right)+\exp \left({a}_{i3}{\Phi}_{i1}\right)-1\right]\right\}\kern3em \hfill \end{array}} $$
(15)

In Eq. 15, m represents the number of triangular grids; in each of the triangular grid, three Blinn operations are performed and thus, a ij represents the j th Blinn factor of the i th triangular grid. Based on Eq. 15, one form of construction is performed as shown in Fig. 6b and c subjected to different a ij values, from the truss structure as demonstrated in Fig. 6a. Noted that, the smooth joints are modeled in the implicit level set representation and therefore, a printable STL file can be constructed through level set based post-processing programs (Vogiatzis et al. 2017b). This type of fillets can be well manufactured through powder bed based additive manufacturing process.

Fig. 6
figure 6

Transformation from truss into lattice (domain size: 300*312; strut thickness: 8)

Full size image

4 Local stress level optimization

Once the optimized truss structure has been transformed into a lattice model, a new optimization problem is formulated as demonstrated in Eq. 16. In this formulation, the Blinn factors are treated as the shape variables; the objective function is composed of two terms: the first one minimizes the material fraction rate (MFR) and the second term penalizes the local violations of the stress constraints.

$$ {\displaystyle \begin{array}{c}\hfill \mathit{\operatorname{Min}}.J\left(\overline{\Phi}\right)={\int}_DH\left(\overline{\Phi}\right)d\Omega +W{\int}_{D^{+}}{\left(\frac{\sigma }{\sigma_{\mathrm{lim}}}-1\right)}^2H\left(\overline{\Phi}\right)d\Omega \hfill \\ {}\hfill s.t.a\left(\boldsymbol{u},\boldsymbol{v},\overline{\Phi}\right)=l\left(\boldsymbol{v},\overline{\Phi}\right),\forall \boldsymbol{v}\in U\hfill \\ {}\hfill \mathrm{The}\kern0.5em \mathrm{notations}:{(f)}^{+}=\mathit{\max}\left(f,0\right);\hfill \\ {}\hfill a\left(\boldsymbol{u},\boldsymbol{v},\overline{\Phi}\right)={\int}_D\boldsymbol{Ae}\left(\boldsymbol{u}\right)\boldsymbol{e}\left(\boldsymbol{v}\right)H\left(\overline{\Phi}\right)d\Omega \hfill \\ {}\hfill l\left(\boldsymbol{v}\right)={\int}_{\partial \Omega}\boldsymbol{\tau} \boldsymbol{v}d\mathrm{S}\hfill \end{array}} $$
(16)

In Eq. 16, a(ᅟ) is the energy bilinear form and l(ᅟ) is the load linear form. The load linear expression does not include \( \overline{\Phi} \), because it is assumed that the area applied of boundary traction force τ is non-designable. u and v are the deformation vector and the test vector, respectively, and e(ᅟ) is the strain. U ad  = {v ∈ H 1(Ω)d| v = 0 on Γ D } is the space of kinematically admissible displacement field. The body force is ignored in this work.

To solve this problem, the Lagrange multiplier method is applied and the adjoint sensitivity result is presented in Eq. 17. Interested readers can refer to (Wang and Li 2013) for the detailed solution process.

$$ {L}^{\prime }={\int}_D\left[1+\boldsymbol{Ae}\left(\boldsymbol{u}\right)\boldsymbol{e}\left(\boldsymbol{w}\right)\right]\delta \left(\overline{\Phi}\right){\overline{\Phi}}^{\prime }d\Omega +W{\int}_{D^{+}}{\left(\frac{\sigma }{\sigma_{\mathrm{lim}}}-1\right)}^2\delta \left(\overline{\Phi}\right){\overline{\Phi}}^{\prime }d\Omega $$
(17)

where, D + represents the stress-violated area of the design domain; w is the adjoint variable which is the solution of Eq. 18.

$$ W{\int}_{D^{+}}\frac{2}{\sigma_{\mathrm{lim}}}\left(\frac{\sigma }{\sigma_{\mathrm{lim}}}-1\right){\sigma}^{\prime }H\left(\overline{\Phi}\right)d\Omega +{\int}_D\boldsymbol{Ae}\left({\boldsymbol{u}}^{\prime}\right)\boldsymbol{e}\left(\boldsymbol{w}\right)H\left(\overline{\Phi}\right)d\Omega =0 $$
(18)

The derivatives of \( \overline{\Phi} \) on the Blinn factors are calculated through:

$$ {\displaystyle \begin{array}{c}\hfill \mathrm{if}\kern0.5em \mathbf{X}\in \mathrm{triangular}\ \mathrm{grid}\kern0.5em i\kern0.5em \mathrm{and}\kern0.5em \overline{\Phi}\left(\mathbf{X}\right)=\exp \left({a}_{i1}{\Phi}_{i1}\right)+\exp \left({a}_{i1}{\Phi}_{i2}\right)-1,\hfill \\ {}\hfill \frac{\partial \overline{\Phi}\left(\mathbf{X}\right)}{\partial {a}_{i1}}=\exp \left({a}_{i1}{\Phi}_{i1}\right)\cdot {a_{i1}}^{\prime }{\Phi}_{i1}+\exp \left({a}_{i1}{\Phi}_{i2}\right)\cdot {a_{i1}}^{\prime }{\Phi}_{i2},\hfill \\ {}\hfill \mathrm{Otherwise},\frac{\partial \overline{\Phi}\left(\mathbf{X}\right)}{\partial {a}_{i1}}=0\hfill \end{array}} $$
(19)

5 Case study

For all the numerical examples, the finite element analysis is performed based on fixed quadrilateral meshes and the artificial weak material is employed for voids in order to avoid the singularity of the stiffness matrix, which is:

$$ {\boldsymbol{D}}_v={10}^{-3}\boldsymbol{D} $$
(20)

in which D v is the elasticity tensor of the void.

It is noted that, in all the numerical examples, small areas around the loading tips are neglected by the optimization algorithm to avoid the unexpectedly high stress level caused by singularity.

5.1 Case 1

The original truss structure is demonstrated in Fig. 7a, where the truss elements have the thickness of 6 and the Young’s modulus of 1.3. Two unit forces are loaded. The compliance-optimized truss structure is shown in Fig. 7b, and the transformed lattice structure is shown in Fig. 7c, where it is assumed that the coefficients a ij  = 0.4 and the Poisson’s ratio equals 0.4. The maximum stress level of the input structure is 0.126 as shown in Fig. 7d. MFR of the lattice structure is to be minimized and the stress level control is subjected to different upper limits of 0.06 and 0.07, respectively. Weight factor W of the stress level penalization term is 50 and the coefficients a i are restricted within the range of [0.05, 0.4].

Fig. 7
figure 7

Truss structure optimization and the lattice transformation

Full size image

Figure 8 demonstrates the optimization results subjected to different stress level upper limits. As shown in the results, the stress levels have been effectively constrained below the designated upper limits and a smaller upper limit leads to a larger MFR, i.e. more materials consumed. Noted that, in general, there is no guarantee that a stress constraint can be satisfied and more discussions will be presented at subsection 5.3.

Fig. 8
figure 8

Optimization results subjected to different stress-level limits

Full size image

The convergence histories are presented in Fig. 9.

Fig. 9
figure 9

Convergence histories

Full size image

5.2 Case 2

The original truss structure is demonstrated in Fig. 10a, where the truss elements have a thickness of 6 and the Young’s modulus of 1.3. Two unit forces are loaded. About the truss optimization, the local porosity control is applied, where the varying lower bounds are imposed; see Eq. 21.

$$ \underline{S}=50+0.75\left(260-y\right) $$
(21)
Fig. 10
figure 10

Truss structure optimization and the lattice transformation

Full size image

The compliance-optimized truss structure is shown in Fig. 10b, and the transformed lattice structure is shown in Fig. 10c, where it is assumed that the coefficients a ij  = 0.15 and the Poisson’s ratio is 0.4. The maximum stress level of the input structure is 0.134 as shown in Fig. 10d. MFR of the lattice structure is to be minimized and the stress level control is subjected to different upper limits of 0.05, 0.06 and 0.08, respectively. Weight factor W of the stress level penalization term is 100 and the coefficients a i are restricted within the range of [0.05, 0.4].

Figure 11 demonstrates the optimization results subjected to different stress level upper limits. Similar conclusions can be drawn as compared to the last case; more importantly, we can clearly identify the functionally graded porosity distribution.

Fig. 11
figure 11

Optimization results subjected to different stress-level limits

Full size image

The convergence histories are presented in Fig. 12.

Fig. 12
figure 12

Convergence histories

Full size image

5.3 A discussion

Even though the stress level is constrained, the optimization problem studied in this work is different from the conventional stress-related shape and topology optimization, which designs the overall material distribution to control the stress level. The proposed method conducts a two-step optimization: the stiffness is optimized first, and the stress concentrations at the interior strut joints are relieved in the second step without severely compromising the optimal stiffness achieved in step one. Therefore, the stress level may not be effectively constrained below the prescribed upper limit if the design envelop contains sharp re-entrants. This is a limitation of the proposed method.

A trial study on the L-bracket problem is demonstrated in Fig. 13. The design domain size is 300*262. The truss elements have the thickness of 6 and the Young’s modulus of 1.3. Figure 13a shows the input ground structure and Fig. 13b demonstrates the compliance minimization result where the re-entrant corner is enhanced for high stiffness. Then, the optimized truss structure is restored back into the continuum (see Fig. 13c) with the Blinn factors a ij  = 0.4 and the maximum stress level is 0.23 at the re-entrant corner (refer to Fig. 13d). For the stress optimization, the Blinn factors have the upper limit of 0.4. Figure 13e and f shows the stress optimization results with the upper limit of 0.20 and 0.19, respectively. We can see from the results that the re-entrant corners still exist since only the Blinn factors have been optimized; the stress levels have been successfully constrained below the prescribed upper limit where however, the material consumptions are significantly increased and the porosities at some local area are sacrificed. If further reducing the stress upper limit, the algorithm may fail in convergence. Hence, a main future work is to introduce more design freedom into the proposed optimization framework, i.e., allowing the moving components as conducted in MMC methodology (Guo et al. 2014) to smear out the re-entrants.

Fig. 13
figure 13

Trial solution on the L-bracket problem

Full size image

Even though there are limitations, the current method is meaningful for porous infill design, instead of competing the conventional stress-related topology optimization methods. For this type of problem, the overall shape of the part is prescribed; refer to Figs. 1 and 14 (Wu et al. 2016, 2017) for a few examples. The design objective is to create a porous infill of good mechanical properties to replace the conventional solid infill while keeping the design envelop consistent.

Fig. 14
figure 14

Examples of porous infill design

Full size image

6 Conclusion

This paper presented a new method to intentionally designing the heterogeneous porous structure, which includes two steps. First, the porous structure is established as a truss network and the connecting nodal positions are optimized to maximize the stiffness. Functionally graded porosity distribution can be realized in this step by adding spatially varying grid area constraints. Then, in the second step, the truss network is transformed into a porous continuum through a novel Blinn transformation-based level set method. And level set shape optimization is performed to minimize the material consumption while at the same time, addressing the stress level constraints.

The effectiveness of the proposed method has been proved by a few numerical examples, including a porous structure design subjected to the functionally graded porosity distribution.

This new porous structure modeling and shape optimization method brings several further research opportunities, including the applications to bone porous infill design, 3D printing part infill design, and 3D printing support structure design, where both lightweight and superior mechanical performance are important design criteria. These topics will be the main part of our future work and the manufacturability related numerical techniques (Liu and Ma 2016) will be embedded into the current algorithm.