1 Introduction

Sound reduction has gained great attention in both theoretical research and practical engineering application. In particular, active control of acoustic radiation from vibrating structures is an important issue in the design of aircrafts, ships, submarines, etc. Active structural acoustic control (ASAC) and active noise control (ANC) are considered as two main approaches and have been widely studied (Fuller et al. 1991). The former approach employs control transducers (e.g. piezoelectric patches) attached to the vibrating structure to implement a classical control strategy (Gardonio et al. 2004) or the optimal control strategy (Wang et al. 1991); while the latter generates antiphase noises to suppress the sound radiation.

It has been shown that the performance of ASAC can be significantly improved by optimizing configuration of the actuators/sensors, including their numbers, positions and sizes (Sors and Elliott 1999; Lee and Chen 1999). Therefore, many studies have been devoted to find the optimal placement of piezoelectric actuators/sensors in sound control applications. Among others, Kim et al. (1995) optimized the size, thickness and applied voltage of piezoelectric actuators embedded into a plate at specified locations to attenuate the structural sound radiation. Genetic algorithms have also been employed to optimize the locations and sizes of the piezoelectric actuators/sensors for reducing the vibration and sound level (Jha and Inman 2003). Despite of these efforts, it remains a challenging task in real world applications to treat optimal placement of discrete piezoelectric components with conventional sizing or parameter optimization formulations. For instance, it is very difficult to formulate mathematically explicit non-overlap constraints among the piezoelectric patches as their number becomes large. However, such a design problem can be suitably cast into a topology optimization problem.

Over the last two decades, several topology optimization methods have become popular (Rozvany 2001; Eschenauer and Olhoff 2001). Many studies on topology optimization of piezoelectric layers/patches for various types of smart structures (Silva and Kikuchi 1999; Kögl and Silva 2005; Kang and Tong 2008) and energy harvesters (Zheng et al. 2009; Rupp et al. 2009; Chen et al. 2010; Takezawa et al. 2013) have also been reported. Material distribution concept-based approaches are often used in topology optimization of structures incorporating piezoelectric materials. In these methods, similarly as in the solid isotropic material with penalization (SIMP) approach (Bendsøe 1989; Zhou and Rozvany 1991), artificial piezoelectric material models with penalization on piezoelectric coefficients or polarization are usually employed, see e.g. (Kögl and Silva 2005; Kang and Tong 2008). In this way, intermediate densities can be effectively suppressed to achieve crisp black and white designs.

Topology optimization of structures for mitigating sound radiation has been widely studied. Most studies focus on optimizing the distribution of stiffness (Du and Olhoff 2007; Yoon et al. 2007; Shu et al. 2011) and damping effects (Dühring et al. 2008; Zhang and Kang 2013). Several works considered topology optimization of piezoelectric layers to achieve desired active control performance for reducing the vibration level, e.g. (Wang et al. 2006). From the view point of manufacturability of fragile piezoelectric ceramics, however, it is impractical to implement piezoelectric patches with arbitrary complex shapes in engineering applications (Frecker 2003). One way to overcome this limitation is to optimize the layout of the surface electrode coverage rather than that of the piezoelectric layer itself. In fact, shape optimization for surface electrode coverage has been proved effective for maximizing the actuation displacement of the piezoelectric actuators (Nguyen et al. 2013) or finding an ideal modal sensor (Donoso and Bellido 2009a, b) in theoretical and experimental research. However, there have been few studies on topology optimization of surface electrodes of piezoelectric sensor and actuator layers for achieving the best control performance.

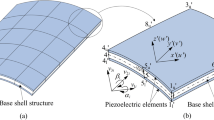
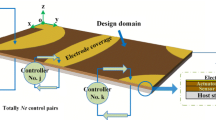
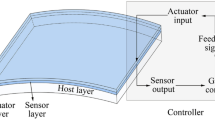
The present study aims to develop a topological design method for surface electrode coverage over the piezoelectric sensors/actuator layers of a shell structure under harmonic excitations for reducing the sound radiation. Here, the piezoelectric actuator layer and sensor layer are bonded to the top and bottom of the host structure but with opposite poling directions. The surface electrodes are designable and share the same distribution on both piezoelectric layers, as illustrated in Fig. 1. Each electrode element on the sensor is connected to a charge amplifier, and then the sensor output is converted to feedback control voltage with the constant gain velocity feedback (CGVF) control law. It is assumed that the coupling interactions of the acoustic waves exerted on the vibrating structure are so weak as can be neglected. The structure is discrete with finite element method in structural dynamic analysis, while the sound radiation analysis is performed by the boundary element method. The discretized model is characterized by a non-proportional active damping property in the global level. Thus, the complex mode superposition technique in the state space is employed for the steady-state response analysis after model reduction with real eigenvectors of the corresponding undamped system. In the optimization model, the sound pressure norm of the reference point under a specified excitation at a certain frequency or in a frequency range is to be minimized. The sensitivity analysis scheme is derived with the adjoint-variable method and the optimization problem is solved with a gradient-based mathematical programming algorithm.

Fig. 1
figure 1

Configuration of piezoelectric structures with optimal electrode coverage under active control

Full size image

The remainder of this paper is organized as follows. In Section 2, structural vibration analysis with the finite element method and sound radiation analysis with the boundary element method are described. Section 3 presents the topology optimization formulation, the sensitivity analysis scheme and numerical implementation issues. In Section 4, numerical examples are given to demonstrate the validity of the proposed method and the influences of several key factors on the optimal solution are discussed. Finally, conclusions are drawn in Section 5.

2 Vibration and sound radiation analysis of structures under piezoelectric active control

2.1 Governing equations for active control of piezoelectric laminated shells

Consider shell structures with piezoelectric sensor and actuator layers, as schematically shown in Fig. 1. The constitutive relation for the piezoelectric material is expressed by

$$\mathbf{T}=\mathbf{c}^{\mathrm{P}}:\mathbf{S}-\mathbf{e}^{\mathrm{T}}\cdot \mathbf{E} $$
(1)

Here, T and S are the mechanical stress tensor and the mechanical strain tensor, respectively; c P is the elasticity tensor of the piezoelectric material, e is the piezoelectricity tensor and E is the vector of electric field.

Only the electric potential in the thickness direction is of interest in the actuator layer and we assume that it varies linearly across the thickness. Therefore, the electric field \(\mathbf {E}^{i} \mathrm { }(i=1,2,\mathrm { ... ,N}_{\mathrm {e}} )\) for the ith actuator is

$$\mathbf{E}^{i} =\left\{ {0,0,-\frac{{\varphi}^{i} }{h_{\mathrm{a}} }} \right\}^{\mathrm{T}} (i=1, 2, ... , \mathrm{N}_{\mathrm{e}} ) $$
(2)

where Ne is the total number of piezoelectric pairs (sensor and actuator), h a is the thickness of the actuator layer, and \({\varphi }^{i} \mathrm {(i=1,2, ... ,N}_{\mathrm {e}} )\) is the applied electric voltage in the ith actuator patch. The applied voltage in the actuator layer can be written in the vector form \(\mathbf {\boldsymbol {\upvarphi } }_{\mathrm {a}} =\left \{ {{\varphi }^{1} , {\varphi }^{2} , ... , {\varphi }^{N_{\mathrm {e}} } } \right \}^{\mathrm {T}}\).

After finite element discretization, the dynamic equation of the structure subject to the harmonic external excitation \(\mathbf {f}\left (t \right )\) and piezoelectric control force f a(t) reads

$$\mathbf{M}\Ddot{\mathbf{y}}\left(t \right)+\mathbf{C}\dot{\mathbf{y}}\left(t \right)+\mathbf{Ky}\left(t \right)=\mathbf{f}\left(t \right)+\mathbf{f}_{\mathrm{a}} \left(t \right) $$
(3)

where M ∈ R n×n, C ∈ R n×n and K ∈ R n×n are the mass matrix, damping matrix and stiffness matrix of the structural model, respectively; y(t)∈R n×1, \(\Dot {\mathbf {y}}\left (t \right )\in \mathbf {R}^{n\times 1}\) and \(\Ddot {\mathbf {y}}\left (t \right )\in \mathbf {R}^{n\times 1}\) are the vectors of dynamic displacement, velocity and acceleration, respectively; n is the number of degree of freedoms. The control force f a(t) generated by the piezoelectric actuator is

$$\mathbf{f}_{\mathrm{a}} (t)=\mathbf{K}_{\mathrm{u{\upvarphi} }} \mathbf{\boldsymbol{\upvarphi} }_{\mathrm{a}} (t) $$
(4)

in which

$$\mathbf{K}_{\mathrm{u{\upvarphi} }} =\int_{\Omega_{\mathrm{a}} } {\mathbf{B}_{\mathrm{u}}^{\mathrm{T}} } \mathbf{e}^{\mathrm{T}}\mathbf{B}_{\mathrm{{\upvarphi} }} \mathrm{d}\Omega $$
(5)

Here, K uφ is the structural piezoelectric matrix for the actuator layer, B u and B φ are the strain-displacement matrix and the electric field–potential matrix, Ωa is the volume occupied by the actuator layer. The applied actuator voltage φ a(t) is determined by the CGVF control law as

$$\mathbf{\boldsymbol{\upvarphi} }_{\mathrm{a}} (t)=-\mathbf{G}_{\mathrm{a}} \mathbf{\boldsymbol{\upvarphi} }_{\mathrm{s}} (t) $$
(6)

where G a is a constant gain diagonal matrix, and φ s(t) is the output voltage of the piezoelectric sensor. In real applications, the electrode of the sensor is connected to a charge amplifier, thus the sensor charge output is converted to the voltage output φ s(t). The voltage output from the sensors has the form

$$\boldsymbol{\upvarphi}_{\mathrm{s}} (t)=\mathbf{G}_{\mathrm{s}} \mathbf{K}_{\mathrm{{\upvarphi} u}} \Dot{\mathbf{y}}(t) $$
(7)

where G s is the diagonal gain matrix (with the unit V/A) of charge amplifiers, and \(\mathbf {K}_{\mathrm {\boldsymbol {\upvarphi } u}} \mathrm {=}\int _{\Omega _{\mathrm {s}} } {\mathbf {B}_{\mathrm {\boldsymbol {\upvarphi } }}^{\mathrm {T}} } \mathbf {eB}_{\mathrm {u}} \mathrm {d}\Omega \) represents the mechanoelectronic coupling effects of the sensor layer, with Ωs denoting the volume occupied by the sensor layer. Substituting (6) and (7) into (4) gives

$$\mathbf{f}_{\mathrm{a}} (t)=-\mathbf{K}_{\mathrm{u{\upvarphi} }} \mathbf{G}_{\mathrm{a}} \mathbf{G}_{\mathrm{s}} \mathbf{K}_{\mathrm{{\upvarphi} u}} \Dot{\mathbf{y}}(t) $$
(8)

As seen in (8), the control force f a(t) is proportional to the velocity \(\Dot {\mathbf {y}}(t)\), thus it can be viewed as a damping force with the active damping matrix being

$$\mathbf{C}_{\mathrm{A}} =\mathbf{K}_{\mathrm{u{\upvarphi} }} \mathbf{G}_{\mathrm{a}} \mathbf{G}_{\mathrm{s}} \mathbf{K}_{\mathrm{{\upvarphi} u}} $$
(9)

Here, the matrix C A is not positive definite nor symmetric. This is because \(\mathbf {K}_{\mathrm {{\upvarphi } u}} \neq \mathbf {K}_{\mathrm {u{\upvarphi } }}^{\mathrm {T}} \) holds for the case that the sensor and actuator are bonded to the bottom and top surfaces respectively (Wang et al. 2001). Now the dynamic (3) can be rewritten as

$$\mathbf{M}\Ddot{\mathbf{y}}\left(t \right)\mathbf{+}\left({\mathbf{C}+\mathbf{C}_{\mathrm{A}} } \right)\Dot{\mathbf{y}}\left(t \right)\mathbf{+}\mathbf{Ky}\left(t \right)\mathbf{=}\mathbf{f}\left(t \right) $$
(10)

2.2 Structural frequency response analysis

The external harmonic excitation is given as \(\mathbf {f}\left (t \right )=\mathbf {F}\mathrm {e}^{i\omega _{\mathrm {f}} t}\) (F and ω f are the amplitude and angular frequency). Thus the steady-state displacement response \(\mathbf {y}\left (t \right )\) and velocity \(\Dot {\mathbf {y}}\left (t \right )\) can be expressed as \(\mathbf {y}\left (t \right )=\mathbf {Y}\mathrm {e}^{i\omega _{\mathrm {f}} t}\) and \(\Dot {\mathbf {y}}\left (t \right )=\mathbf {v}\mathrm {e}^{i\omega _{\mathrm {f}} t}\), where v = i ω f Y. The dynamic equation (10) can be thus rewritten as

$$\mathbf{WY}=\mathbf{F} $$
(11)

with \(\mathbf {W}\mathrm {=}-\omega _{\mathrm {f}}^{2} \mathbf {M}+i\omega _{\mathrm {f}} (\mathbf {C}+\mathbf {C}_{\mathrm {A}} )+\mathbf {K}\).

When solving this frequency response problem directly, the computation cost will grow rapidly as the number of degrees of freedom increases. For improving the computational efficiency, the structural displacement amplitude Y is first transformed into a reduced order modal space, as

$$\mathbf{Y=\boldsymbol{\Psi}\boldsymbol{\upeta}} $$
(12)

Here, the transformation matrix \(\boldsymbol {\Psi }\in \mathbf {R}^{n\times n_{\mathrm {b}} }\) consists of the first n b(n b << n) normalized real eigenvectors of the original undamped system and \(\mathbf {\upeta }\in \mathbf {R}^{n_{\mathrm {b}} \times 1}\) is the generalized response vector.

Pre-multiplying Ψ T to both sides of (10), one obtains the reduced-order dynamic equation as

$$\Tilde{\mathbf{M}}\boldsymbol{\Ddot{\upeta}}+\Tilde{\mathbf{C}}\dot{\boldsymbol{\upeta}}+\Tilde{\mathbf{K}}\boldsymbol{\upeta}=\Tilde{\mathbf{F}} $$
(13)

Here, \(\Tilde {\mathbf {M}}=\boldsymbol {\Psi }^{\mathrm {T}}\mathbf {M\Psi }\) and \(\Tilde {\mathbf {K}}=\boldsymbol {\Psi }^{\mathrm {T}}\mathbf {K}\boldsymbol {\Psi }\) are both n b×n b diagonal matrices. The reduced-order equation with the damping matrix \(\Tilde {\mathbf {C}}=\boldsymbol {\Psi }^{\mathrm {T}}\left ({\mathbf {C}+\mathbf {C}_{\mathrm {A}} } \right )\boldsymbol {\Psi }\) is not a decoupled one since the active damping matrix C A cannot be expressed as a linear combination of the original stiffness matrix K and mass matrix M.

The complex mode superposition method in the state space is considered as an efficient approach for evaluating the frequency responses of a system with non-proportional damping property. By introducing the state vector \(\mathbf {z=}\left \{ {{\begin {array}{*{20}c} \boldsymbol {\upeta } \hfill & \Dot {\boldsymbol {\upeta }} \hfill \\ \end {array} }} \right \}^{\mathrm {T}}\), the dynamic equation in the state space is written as

$$\left[ {{\begin{array}{*{20}c} {\Tilde{\mathbf{C}}} \hfill & {\Tilde{\mathbf{M}}} \hfill \\ {\Tilde{\mathbf{M}}} \hfill & \mathbf{0} \hfill \\ \end{array} }} \right]\Dot{\mathbf{z}}+\left[ {{\begin{array}{*{20}c} {\Tilde{\mathbf{K}}} \hfill & \mathbf{0} \hfill \\ \mathbf{0} \hfill & {-\Tilde{\mathbf{M}}} \hfill \\ \end{array} }} \right]\mathbf{z}=\left\{ {{\begin{array}{*{20}c} {\Tilde{\mathbf{F}}} \hfill \\ \mathbf{0} \hfill \\ \end{array} }} \right\} $$
(14)

Equation (14) can be decoupled by pre-multiplying the matrix of the generalized complex eigenvectors of the system to both sides. Thus it can be readily solved with the complex mode superposition method. The frequency response can be then obtained using the transformation given in (12). More details can be found in some other papers (Igusa et al. 1984; Kang et al. 2012).

2.3 Sound radiation analysis

We consider the sound radiation of a vibrating structure placed in an acoustic medium with an open boundary, as shown in Fig. 2. The boundary element method, in which the far-field boundary condition is satisfied automatically, is employed for predicting the sound pressure.

Fig. 2
figure 2

Exterior sound radiation problem

Full size image

For a time-harmonic linear acoustic system, the sound pressure p at any point P in the acoustic domain V satisfies the Helmholtz equation:

$$\nabla^{2}p+k^{2}p=0 $$
(15)

where k = ω f/c is the wave number. Here ω is the angular frequency of the external excitation and c the sound speed. The first step in the boundary element method is to obtain the fundamental solution of the adjoint operator.

In a three-dimensional free space, the fundament solution is ψ = e−ikR/4π R, where R denotes the distance between the field point Q and the computational point P (not necessarily located on the structural boundary). By applying the Green’s second identity to the two (15), after some manipulations (see Wu 2000), one obtains

$$p(P)=-\int_{S} {\left({i\rho_{\mathrm{A}} \omega_{f} \nu_{n} \psi +p\frac{\partial \psi }{\partial n}}\; \right)} \; \mathrm{d}S, \forall P\, \text{in}\, \mathrm{V} $$
(16)

Here, ρ A is the density of the acoustic media, and ν n is the normal velocity pointing backward acoustic domain.

The surface sound pressure p can be found from (see Wu 2000)

$$C^{0}(P)p(P)=-\int_{S} {\left({i\rho_{\mathrm{A}} \omega_{\mathrm{f}} \nu_{n} \psi +p\frac{\partial \psi }{\partial n}} \right) \mathrm{d}S, } \forall P{\kern3pt} \text{on}{\kern3pt} \mathrm{S} $$
(17)

with

$$C^{0}(P)=1-\frac{1}{4\pi }\int_{S} {\frac{\partial R}{\partial n}} \mathrm{d}S $$
(18)

The boundary of the acoustic domain (the structural surface S) is then modeled with n BN boundary nodes and N BM boundary elements. For the sake of simplicity, these nodes are placed at the same positions as the finite element nodes. Helmholtz integral (17) can then be discretized as (Wu 2000)

$$\begin{array}{@{}rcl@{}} C^{0}(P)p(P)&=&-\sum\limits_{i=1}^{N_{\text{BM}} } \left(\int_{S_{i} } \sum\limits_{l=1}^{N_{\text{BN}}^{\mathrm{e}} } {N^{l}p^{l}\frac{\partial\psi}{\partial n}\mathrm{d}S_{i}}\right.\\&&{\kern4pc}\left.+i\rho_{\mathrm{A}} \omega \int_{S_{i} } {\sum\limits_{l=1}^{N_{\text{BN}}^{\mathrm{e}} } {N^{l}{\nu_{n}^{l}} } } \psi \mathrm{ d}S_{i} \right)\\ \end{array} $$
(19)

By adopting a general direct boundary element formulation in acoustics, two ‘element coefficients’ \({h_{i}^{l}} (P)\) and \({g_{i}^{l}} (P)\) are defined as (Wu 2000)

$$\begin{array}{@{}rcl@{}} {h_{i}^{l}} (P)&=&\int_{S_{i} } {N^{l}} \frac{\partial \psi }{\partial n} \mathrm{d}S_{i} , {g_{i}^{l}} (P)\\&=&-i\omega \rho_{\mathrm{A}} \int_{S_{i} } {N^{l}} \psi \mathrm{d}S_{i} \mathrm{,} \left({l=1, 2, ..., N_{\text{BN}}^{\mathrm{e}} } \right) \end{array} $$
(20)

By assembling \({h_{i}^{l}} \) and \({g_{i}^{l}} \) into the global-level matrices \(\mathbf {H}_{\mathrm {B}} \in \mathbf {R}^{n_{\text {BN}} \times n_{\text {BN}} }\) and \(\mathbf {G}_{\mathrm {B}} \in \mathbf {R}^{n_{\text {BN}} \times n_{\text {BN}} }\), one obtains the sound pressure p S of the structural surface as

$$\left({\mathbf{C}{ }_{\mathrm{B}}+\mathbf{H}_{\mathrm{B}} } \right)\mathbf{p}_{\mathrm{S}} =\mathbf{G}_{\mathrm{B}} \mathbf{v}_{\mathrm{n}} $$
(21)

where \(\mathbf {C}_{\mathrm {B}} \in \mathbf {R}^{n_{\text {BN}} \times n_{\text {BN}} }\) is a diagonal matrix consisting of corner coefficients (C 0 in (18)). Here, nodal normal velocity vector v n in the boundary element model has the form

$$\mathbf{v}_{\mathrm{n}} =-\mathbf{N}_{\mathrm{s}} \mathbf{v}=-i\omega \mathbf{N}_{\mathrm{s}} \mathbf{Y} $$
(22)

where \(\mathbf {N}_{\mathrm {s}} =\text {diag} \left ({\mathbf {n}_{\mathrm {s}}^{1} , \mathbf {n}_{\mathrm {s}}^{1} , ..., \mathbf {n}_{\mathrm {s}}^{n_{\text {BN}} } } \right )\) is the normal velocity matrix and Y is the displacement response obtained in the structural vibration analysis. Then the sound pressure p at the specified reference point r (in the acoustic domain) can be obtained with the structural surface sound pressure p s as

$$p(r)=-\mathbf{h}_{r} \mathbf{p}_{\mathrm{s}} +\mathbf{g}_{r} \mathbf{v}_{\mathrm{n}} $$
(23)

where \(\mathbf {h}_{r} \in \mathbf {R}^{1\times n_{\text {BN}} }\) and \(\mathbf {g}_{r} \in \mathbf {R}^{1\times n_{\text {BN}} }\) are global-level vectors obtained similarly as H B and G B in (21). Substituting (22) into (23) and eliminating p s, it yields

$$p(r)=\left({-\mathbf{h}_{r} \left[ {\left({\mathbf{C}{ }_{\mathrm{B}}+\mathbf{H}_{\mathrm{B}} } \right)^{-1}\mathbf{G}_{\mathrm{B}} } \right]+\mathbf{g}_{r} } \right)\mathbf{v}_{\mathrm{n}} \equiv \mathbf{z}_{r} \mathbf{v}_{\mathrm{n}} $$
(24)

Formulating \(\mathbf {z}_{r} \in \mathbf {R}^{1\times n_{\text {BN}} }\), which reflects the geometry of the structural boundary and excitation frequency, is the most expensive step in the BEM analysis, as well as in each individual optimization iteration. However, this step needs to be performed only once at the beginning of the optimization process. The norm of the sound pressure \(\left \| {p_{r} } \right \|\) can then be determined by real and imaginary parts of sound pressure p at the reference point r as

$$\left\| {p_{r} } \right\|=\sqrt{\text{Re}\left[ {p(r)} \right]^{2}+\text{Im}\left[ {p(r)} \right]^{2}} $$
(25)

3 Topology optimization method

3.1 Problem formulation

The task of the considered optimization problem is to minimize the sound pressure at a specified reference point r with a given amount of electrode coverage in the design domain. For describing the surface electrode layout of the piezoelectric actuator and sensor layers, element-wise relative density variables \(\rho _{e} \left ({e=1, 2, ..., N_{\mathrm {e}} } \right )\) are used to indicate absence and presence of the electrode in the e th element. Thus the topology optimization problem is mathematically stated as

$$\begin{array}{@{}rcl@{}} && \underset{\boldsymbol{\uprho}}{{\min.}} f(\boldsymbol{\uprho}) \\&& {\mathrm{s.t}.\quad \left({-\omega_{\mathrm{f}}^{2} \mathbf{M}+i\omega_{\mathrm{f}} (\mathbf{C}+\mathbf{C}_{\mathrm{A}} (\boldsymbol{\uprho}))+\mathbf{K}} \right)\mathbf{Y}=\mathbf{F}}\\&& {\quad \quad p(r)=\mathbf{z}_{r} \mathbf{v}_{\mathrm{n}} \left(\mathbf{Y} \right)} \\&& {\quad \quad \sum\limits_{e=1}^{N_{\mathrm{e}} } {\rho_{e}} V_{e} -f_{\mathrm{v}} \sum\limits_{e=1}^{N_{\mathrm{e}} } {V_{e}} \le 0} \\&& \quad \quad 0 < \underline{\rho} \le \rho_{e} \le 1\quad \left({e=1,2,...,N_{\mathrm{e}} } \right)\end{array} $$
(26)

Here, \(\boldsymbol {\uprho }=\left \{ {\rho _{1} ,\rho _{2} ,...,\rho _{N_{\mathrm {e}} } } \right \}^{\mathrm {T}}\) is the vector of density design variables, whose lower bound ρ̲ is set as 10−6 in this study. The material volume constraint imposes a restriction on the total area of electrode coverage, which is necessary for limiting the complexity of the control circuit in real applications.

In problem (26), two types of objective function f(ρ) can be considered. The first is to minimize the sound pressure norm of a specified reference point r under a particular frequency excitation:

$$f(\boldsymbol{\uprho})=\left\| {p_{r} } \right\| $$
(27)

When the sound pressure in a specified excitation frequency range is of concern, the second type of objective function can be considered, which is defined as the maximum sound pressure at N p sampling points \(\omega _{\mathrm {f}}^{i} \left ({i=1,2, \mathrm {...,} N_{\mathrm {p}} } \right )\) within the frequency range (\(\omega _{\mathrm {f}}^{i}\) is usually uniformly distributed in this range):

$$f(\boldsymbol{\uprho})=\max \left({\left\| {{p_{r}^{1}} } \right\|,\left\| {{p_{r}^{2}} } \right\|, ... ,\left\| {p_{r}^{N_{\mathrm{p}} } } \right\|} \right) $$
(28)

The objective function in (28) is not a smooth one, which poses a difficulty when a gradient-based algorithm is adopted for solving the optimization problem. Therefore, an envelope function, namely KS (Kreisselmeier-Steinhauser) function is employed to approximate the maximum sound pressure in a frequency range as

$$f\left(\boldsymbol{\uprho} \right)=\text{KS}\left({\left\| {{p_{r}^{1}} } \right\|,\left\| {{p_{r}^{2}} } \right\|, ... , \left\| {p_{r}^{N_{\mathrm{p}} } } \right\|} \right)=\frac{1}{\upeta }\ln \left({\sum\limits_{i=1}^{N_{\mathrm{p}} } {\mathrm{e}^{\upeta \left\| {{p_{r}^{i}} } \right\|}} } \right) $$
(29)

Here, η denotes the aggregation parameter of the KS function and it should be given an adequate value. Since the sound pressure will not be zero at the specified reference points, (29) provides a smoothed approximation of the original objective function. In principal, a larger aggregation parameter usually leads to a more compact envelop approximation but an extremely large value may give rise to numerical instability.

The topologies of the base material layer, piezoelectric actuator and sensor layers are fixed in the design optimization (26). The electrode layers are typically very thin and we therefore neglect their stiffnesses and masses. Thus the global stiffness matrix K and mass matrix M remain unchanged during the course of optimization. The structural damping matrix C is assumed to be a proportional one with damping coefficients α and β, that is C = α M+β K.

As a usual practice in the material distribution concept-based topology optimization, we use an artificial material model with penalization on the active damping matrix C A in (26), as expressed by

$$\mathbf{C}_{\mathrm{A}} =\sum\limits_{e=1}^{N_{\mathrm{e}} } {\left({\rho_{e} } \right)^{p_{\mathrm{p}} }\mathbf{K}_{\mathrm{u{\upvarphi} }}^{\mathrm{e}} \mathbf{G}_{\mathrm{a}}^{e} \mathbf{G}_{\mathrm{s}}^{e} \mathbf{K}_{\mathrm{{\upvarphi} u}}^{\mathrm{e}} } $$
(30)

Here, p p > 1 is the penalty factor for suppressing intermediate density values by making gray elements uneconomical under a constraint on the electrode coverage area (volume constraint). Such a penalization model is only a pure numerical treatment and has no definite physical meaning. The choice of the penalty factor value for topology optimization of piezoelectric structures has been discussed in the literature (Noh and Yoon 2012; Kim et al. 2010).

3.2 Sensitivity analysis

For solving the optimization problem (26) with a gradient-based mathematical programming algorithm, the sensitivity analysis of the objective function with respect to the design variables needs to be performed. In the discrete setting, for a generic structural behavior function f(Y) (as seen in (22) and (24), the sound pressure p(r) depends on the structural displacement Y), we first introduce an adjoint vector μ to form the real-valued Lagrangian function

And the adjoint vector by solving the following adjoint equation

$$\boldsymbol{\upmu}^{\mathrm{T}} \mathbf{W}=\frac{1}{2}\left({-\frac{\partial f}{\partial \mathbf{Y}^{\mathrm{R}}}+i\frac{\partial f}{\partial \mathbf{Y}^{\mathrm{I}}}} \right), $$
(31)

Then the derivative of the function f(Y) with respect to the design variable ρ e can be obtained as (for details the readers are referred to Kang et al. (2012))

$$\begin{array}{@{}rcl@{}} \frac{\mathrm{d}f}{\mathrm{d}\rho_{e} }&=&2\text{Re}\left({\boldsymbol{\upmu}^{\mathrm{T}}\left({-\omega_{\mathrm{f}}^{2} \frac{\partial \mathbf{M}}{\partial \rho_{e} }+i \omega_{\mathrm{f}} \frac{\partial (\mathbf{C}+\mathbf{C}_{\mathrm{A}} )}{\partial \rho_{e} }+\frac{\partial \mathbf{K}}{\partial \rho_{e} }} \right)\mathbf{Y}} \right)\\ &&=2\text{Re}\left({\boldsymbol{\upmu}^{\mathrm{T}}\left({i \omega_{\mathrm{f}} p_{\mathrm{p}} \left({\rho_{e} } \right)^{\left({p_{\mathrm{1}} -1} \right)}\mathbf{K}_{\mathrm{u{\upvarphi} }}^{\mathrm{e}} G_{\mathrm{a}}^{e} G_{\mathrm{s}}^{e} \mathbf{K}_{\mathrm{{\upvarphi} u}}^{\mathrm{e}} } \right)\mathbf{Y}} \right) \\ &&\quad\times\left({e=1,2,...,N_{\mathrm{e}} } \right) \end{array} $$
(32)

where Y R and Y I denote the real and imaginary parts of the complex amplitude Y.

Specifically, for the first type of objective function \(f=\left \| {p_{r} } \right \|\), the derivatives \(\partial \left \| {p_{r} } \right \| \!/ \partial \mathbf {Y}^{\mathrm {R}}\) and \(\partial \left \| {p_{r} } \right \| \!/ \partial \mathbf {Y}^{\mathrm {I}}\) are

$$\begin{array}{@{}rcl@{}} \frac{\partial \left\| {\mathrm{P}_{r} } \right\|}{\partial \mathbf{Y}^{\mathrm{R}}}\!&=&\frac{\partial \sqrt{\text{Re}\left[ {p(r)} \right]^{2}+\text{Im}\left[ {p(r)} \right]^{2}}}{\partial \mathbf{Y}^{\mathrm{R}}} \\&&=\frac{\text{Re}\left[ {p(r)} \right]}{\left\| {\mathrm{P}_{r} } \right\|}\frac{\partial \text{Re}\left[ {p(r)} \right]}{\partial \mathbf{Y}^{\mathrm{R}}}+\frac{\text{Im}\left[ {p(r)} \right]}{\left\| {\mathrm{P}_{r} } \right\|}\frac{\partial \text{Im}\left[ {p(r)} \right]}{\partial \mathbf{Y}^{\mathrm{R}}} \\&&=\frac{1}{\left\| {\mathrm{P}_{r} } \right\|}\left({\text{Re}\left[ {p(r)} \right]\frac{\partial \text{Re}(-i\omega \mathbf{z}_{r} \mathbf{N}_{\mathrm{s}} \mathbf{Y})}{\partial \mathbf{Y}^{\mathrm{R}}}}\right.\\&&{\kern3.5pc}\left.+\text{Im}\left[ {p(r)} \right]\frac{\partial \text{Im}(-i\omega \mathbf{z}_{r} \mathbf{N}_{\mathrm{s}} \mathbf{Y})}{\partial \mathbf{Y}^{\mathrm{R}}} \right)\\&&=-\frac{1}{\left\| {\mathrm{P}_{r} } \right\|}\left(\text{Re}\left[ {p(r)} \right]\left[ {\text{Re}(i\omega \mathbf{z}_{r} \mathbf{N}_{\mathrm{s}} )^{\mathrm{T}}} \right]\right.\\&&{\kern6pt}\left.+\text{Im}\left[ {p(r)} \right]\left[ {\text{Im}(i\omega \mathbf{z}_{r} \mathbf{N}_{\mathrm{s}} )^{\mathrm{T}}} \right]\right) \end{array} $$
(33)
$$\begin{array}{@{}rcl@{}} \frac{\partial \left\| {\mathrm{P}_{r} } \right\|}{\partial \mathbf{Y}^{\mathrm{I}}}&=&\frac{\partial \sqrt{\text{Re}\left[ {p(r)} \right]^{2}+\text{Im}\left[ {p(r)} \right]^{2}}}{\partial \mathbf{Y}^{\mathrm{I}}} \\&& =\frac{1}{\left\| {\mathrm{P}_{r} } \right\|}\left(\text{Re}\left[ {p(r)} \right]\frac{\partial \text{Re}(-i\omega \mathbf{z}_{r} \mathbf{N}_{\mathrm{s}} \mathbf{Y})}{\partial \mathbf{Y}^{\mathrm{I}}}\right.\\&&{\kern6pt}\left.+\text{Im}\left[ {p(r)} \right]\frac{\partial \text{Im}(-i\omega \mathbf{z}_{r} \mathbf{N}_{\mathrm{s}} \mathbf{Y})}{\partial \mathbf{Y}^{\mathrm{I}}} \right) \\&&=\frac{1}{\left\| {\mathrm{P}_{r}} \right\|}\left(\text{Re}\left[ {p(r)} \right]\left[ {\text{Re}(\omega \mathbf{z}_{r} \mathbf{N}_{\mathrm{s}} )^{\mathrm{T}}} \right]\right.\\&&{\kern6pt}\left.+\text{Im}\left[ {p(\mathrm{r})} \right]\left[ {\text{Im}(\omega \mathbf{z}_{r} \mathbf{N}_{\mathrm{s}} )^{\mathrm{T}}} \right] \right) \end{array} $$
(34)

By substituting (33) and (34) into (31), the adjoint vector can calculated by adopting the same method for evaluating the dynamic response described in Section 2.2. Thus the derivative of the behavior function \(\left \| {p_{\mathrm {r}} } \right \|\) in (32) can be readily obtained.

For the case of the aggregated sound pressure in a specified frequency range, the derivative of the objective function becomes

$$\frac{\mathrm{d}f}{\mathrm{d}\rho_{e} }=\sum\limits_{i=1}^{N_{\mathrm{p}} } {\left({\mathrm{e}^{\eta \left\| {{p_{r}^{i}} } \right\|}\frac{\mathrm{d}\left\| {{p_{r}^{i}} } \right\|}{\mathrm{d}\rho_{e} }} \right)} \left/\vphantom{\sum\limits_{i=1}^{N_{\mathrm{p}} }}\right.\sum\limits_{i=1}^{N_{\mathrm{p}} } {\mathrm{e}^{\eta \left\| {{p_{r}^{i}} } \right\|}} $$
(35)

3.3 Optimization process

The solution of the considered topology optimization problem consists of the following steps:

  • Step 1: Initialize the design variables \(\rho _{e} \left ({e=1, 2, ..., N_{\mathrm {e}} } \right )\) and form the structural stiffness matrix K, mass matrix M and damping matrix C.

  • Step 2: Calculate z r in (24) for each excitation frequency.

  • Step 3: Form the active damping matrix C A in (30) with current design variable values ρ.

  • Step 4: Form the reduced-order dynamic (13) using the first n b eigenmodes of the undamped system.

  • Step 5: Solve the reduced-order dynamic (14) with the complex mode superposition method in the state space, calculate displacement response Y and normal velocity response v n.

  • Step 6: Calculate the sound pressure \(p\left (r \right )\) in (24) with the boundary element method.

  • Step 7: Compute the sensitivities of the sound pressure with respect to the design variables.

  • Step 8: Update the design variables with the GCMMA optimizer (Svanberg 2002).

  • Step 9: Terminate the iteration process if the relative difference of the objective function values falls below a prescribed value. Otherwise, repeat the iteration process from Step 3.

4 Numerical examples

Several numerical examples are presented to illustrate the validity of the proposed topology optimization approach as well as exploring the influences of key factors on the optimal designs. In all the examples, four-node quadrilateral Mindlin shell elements are employed in the finite element modeling of the vibrating structures, and four-node quadrilateral boundary elements are used in the sound radiation analysis. The optimization iteration will be terminated when the relative difference between the objective function values of two adjacent steps becomes less than 10−4

4.1 Example 1: Topology optimization of electrode coverage in a cantilever plate

4.1.1 Optimal solution

Firstly, we consider the topology optimization of electrode coverage for a piezoelectric cantilever plate for implementing active control, as shown in Fig. 3. The plate has geometrical dimensions a = 0.6m, b = 0.4m and t h = 6 × 10−4m for the host layer and t s = t a = 1 × 10−4m for the sensor and actuator layers. The plate is placed in a surrounding acoustic medium (air). The material properties of the host structure and the piezoelectric layers are summarized in Table 1. The mass density and sound velocity of the air are ρ air = 1.21Kg/m3 and c = 340×103m/s. A time-harmonic external force \(f(t)=F\mathrm {e}^{i\omega _{\mathrm {f}} t}\) (with F = 20 N, ω f = 2π f p and f p = 60Hz) is applied at the mid-point of the free edge. The Rayleigh’s damping coefficients of the structure are α = β = 1×10−4. The gain value of the charge amplifier is given as G s = 1 × 105V/A, and the negative feedback control gain is G a = 40.

Fig. 3
figure 3

A cantilever plate with active control under a time-harmonic load f(t) applied at the mid-point of the free edge

Full size image
Table 1 Material properties of the host layer and piezoelectric layers
Full size table

The plate is modeled by 2400 (60 × 40) uniform-sized shell elements, while the upper and bottom surfaces are discretized by 4800 uniform-sized square boundary elements for sound radiation analysis. The volume fraction ratio of the electrode in the design domain is restricted by f v = 0.5 and the initial values of the design variables are set as \(\rho _{e} =0.5 \left ({e=1,2,...,2400} \right )\). The first 60 eigenmodes are involved in the computation \(\left ({n_{\mathrm {b}} =60} \right )\). The penalty factor p p is given as 3. The objective function is the norm of sound pressure at the point 0.5m above the plate center. The optimization process converged after 75 iterations. The iteration history is given in Fig. 4, which shows that the objective function value steadily decreases from \(\left \| {p_{r} } \right \|=3.266 \text {Pa}\) in the initial design to \(\left \| {p_{r} } \right \|=1.148 \text {Pa}\) in the final optimal design. The optimal density distribution and the suggested electrode layout (with low density elements removed) are shown in Fig. 5. Figure 6 shows that the vibration level and surface sound pressure are both greatly reduced after optimization. Here, the vibration contours have a similar but not exactly identical tendency as the surface sound pressure contours. As shown in Fig. 7, the maximum control voltage applied to the actuator layer is 1.39 kV and the control voltages in the areas without electrode coverage are close to zero.

Fig. 4
figure 4

Iteration histories of objective function value \(\left \| {p_{r} } \right \|\) and volume fraction ratio f V for the cantilever plate with piezoelectric layers under active control

Full size image
Fig. 5
figure 5

Optimal solution for the cantilever plate under f P = 60 Hz excitation. aMaterial density contour; b Electrode layout (with low density elements hidden)

Full size image
Fig. 6
figure 6

Comparison of initial designs and optimal designs. aVibration amplitude contour in the initial design; b Vibration amplitude contour in the optimal design c Norm of surface sound pressure contour in the initial design; dNorm of surface sound pressure contour in the optimal design

Full size image
Fig. 7
figure 7

Actuator voltage amplitude for the optimal design

Full size image

For comparison, the optimal solution obtained by vibration analysis without model reduction is also given in Fig. 8. It is almost exactly the same as that achieved by model reduction (Fig. 5). Also, the predicted objective function values are \(\left \| {p_{r} } \right \|=3.265\, \text {Pa}\) for the initial design and \(\left \| {p_{r}} \right \|=1.144\, \text {Pa}\) for the optimal design, both of which have only less than 0.35 % differences compared with those obtained with the model reduction technique.

Fig. 8
figure 8

Optimal solution for the cantilever plate without model reduction

Full size image

The sound pressures sweep in the excitation frequency range f P = 55−65Hz for the optimal design (obtained under f P = 60Hz excitation) and the initial design with/without active control are given in Fig. 9. It is seen that the sound pressure at the reference point in the optimal design with active control is much smaller than that in the initial design (with and without control) in the range f P = 55−65Hz. However, this is not always the case, as will be further discussed in Section 4.1.4.

Fig. 9
figure 9

Sound pressure under different excitation frequencies for the optimal design and the initial design with/without control

Full size image

We now study the influence of the volume constraint on the optimal design and control effort. Four other volume fraction ratios f v = 0.1,0.3,0.7 and 0.9 are considered, and the optimal designs are given in Fig. 10. The corresponding objective function values are \(\left \| {p_{r}} \right \|=2.414, 1.441, 1.049\) and 1.019Pa, respectively. It is clear that the objective function decreases only slightly (from \(\left \| {p_{r} } \right \|=1.144 \text {Pa}\) for the case f v = 0.5 to \(\left \| {p_{r} } \right \|=1.019 \text {Pa}\) for the cases f v = 0.9) as the volume fraction ratio further increases, but at the cost of increased implementation complexity of the controller. We also examined the case without the volume constraint, but the optimization process could not achieve a stable convergence.

Fig. 10
figure 10

The optimal designs obtained with different volume fraction. a f v = 0.1; b f v = 0.3; c f v = 0.7; d f v = 0.9

Full size image

4.1.2 Influence of penalty factor

The influence of the penalty factor p p in (30) on the optimal design is discussed in this example. The same plate as previously treated is considered and the excitation frequency is fixed at f P = 105 Hz. The optimal solutions with three different penalty factors p p = 2, 3 and 5 are given in Fig. 11. It is shown that the optimal topology changes only slightly as the penalty factor p p increases. From our numerical experiences, p p = 3 is a suitable value for the penalty factor, and it will be fixed at 3 hereafter.

Fig. 11
figure 11

Optimal designs obtained with different penalty factors. a p p = 2; b p p = 3; c p p = 5

Full size image

4.1.3 Influence of excitation frequency

We now study the influence of the excitation frequency on the optimal design. Again, the reference point is located 0.5 m above the plate center. Six different excitation frequencies (f p = 26,31,42,60,85 and 130 Hz) are considered, and the corresponding optimal designs are shown in Fig. 12. As expected, as the excitation frequency increases, the optimal layout of electrode becomes spatially more complex to suppress localized vibration modes excited by the external forces.

Fig. 12
figure 12

Optimal designs in different excitation frequencies. a f p = 26 Hz; b f p = 31 Hz; c f p = 42 Hz; d f p = 60 Hz; e f p = 85 Hz; f f p = 130 Hz

Full size image

4.1.4 Optimal solution for a specified excitation frequency range

In this example, topology optimization is performed by considering harmonic excitations within the frequency range f p = 30−43 Hz. The objective function is the aggregated maximum sound pressure given in (29) with the parameter η=10. The obtained optimal topology of the electrode layer is given in Fig. 13. Obvious differences can be observed between this solution and those obtained at individual frequencies f p = 31Hz (see Fig. 12b) and f p = 42Hz (see Fig. 12c). The frequency response sweeps of the sound pressure at the reference point for the three optimal solutions and the initial design are compared in Fig. 14. As shown in the figure, the optimal design obtained under a specified frequency has the smallest sound pressure only in the vicinity of this specific frequency. On the other hand, the optimal design achieved with the aggregated objective function has a smaller peak value of the sound pressure over the whole frequency range of concern.

Fig. 13
figure 13

Optimal layout of electrode coverage for the cantilever plate excited by f P = 30−43 Hz excitation. aMaterial density contour; b Electrode layout (with low density elements hidden)

Full size image
Fig. 14
figure 14

Sound pressure under different excitation frequencies for the optimal and initial designs

Full size image

4.2 Example 2: Topology optimization of electrode coverage in a cylindrical shell

4.2.1 Optimal solution

Topology optimization of electrode coverage over the piezoelectric layers of a laminated cylindrical shell is studied. The structure has geometrical dimensions R cy = 2.3m (radius), L cy = 2.0m (length) and 𝜃 cy = 60∘ (central angle). It is excited by an exterior harmonic force \(f(t)=F\mathrm {e}^{i\omega _{\mathrm {f}} t}\) (with F = 20N, ω f = 2π f p and f p = 60 Hz) at its center, as shown in Fig. 15. The shell consists of three layers (host layer, sensor layer and actuator layer) with the thicknesses t h = 2×10−3m and t s = t a = 1 × 10−4m. The material properties are the same as in the first example. The structural damping coefficients are given as α = β = 1×10−4. The gain value of the charge amplifier is G s = 1 × 105V/A, and the negative feedback control gain is G a = 40. The structure is discretized into 3000 four-node Mindlin shell finite elements (50 elements in the axial direction and 60 elements in the circumferential direction) in the structural vibration analysis, and 6000 square boundary elements are used to discretize the upper and bottom surfaces of the structure in the sound radiation analysis. The objective function is the sound pressure norm at the reference point (0.7 m above the center point). The volume fraction ratio of the electrode in the design domain is restricted by f v = 0.4 and the initial values of the design variables are set to be \(\rho _{e} =0.4 \left ({e=1, 2, ..., 3000} \right )\). The first 60 eigenmodes \(\left ({n_{\mathrm {b}} =60} \right )\) are involved in the response and sensitivity analysis.

Fig. 15
figure 15

A four edge clamped cylindrical shell under a time-harmonic load f(t) applied at the center

Full size image

The optimization process converged after 55 iterations. The sound pressure decreases from \(\left \| {p_{r} } \right \|=5.608 \text {Pa}\) in the initial design to \(\left \| {p_{r} } \right \|=3.745 \text {Pa}\) in the optimal design. The iteration histories of the objective function and volume fraction are shown in Fig. 16, and the optimal electrode coverage are presented in Fig. 17. Figure 18 shows the actuator voltage amplitude distribution in the optimal design, which coincides well with the electrode coverage. The surface sound pressure and the structural vibration level for the initial and optimal designs are compared in Fig. 19. It is seen that the overall surface sound pressure and vibration level are both remarkably reduced. Clearly, the sound pressure at the reference point is mainly dependent on the structural vibration amplitude, but also affected by the structural geometry and the reference point location. Comparisons between the sound radiation optimization and structural vibration optimization will be discussed in the following subsection. In addition, the optimal design obtained by the vibration analysis without model reduction is given in Fig. 20, which is very similar to that obtained with the model reduction technique.

Fig. 16
figure 16

Iteration histories of objective function value \(\left \| {p_{r} } \right \|\) and volume fraction ratio f V for the cylindrical shell structure under active control

Full size image
Fig. 17
figure 17

Optimal layout of electrode coverage for minimizing sound radiation from the vibrating cylindrical shell structure. a Material density contour; b Electrode layout (with low density elements hidden)

Full size image
Fig. 18
figure 18

Actuator voltage amplitude distribution for the optimal design

Full size image
Fig. 19
figure 19

Comparison of the initial design and optimal solution for the cylindrical structure. aVibration amplitude contour in the initial design; b Vibration amplitude contour in the optimal design c Norm of surface sound pressure contour in the initial design; dNorm of surface sound pressure contour in the optimal design

Full size image
Fig. 20
figure 20

Optimal layout of electrode coverage for the cylindrical structure without model reduction

Full size image

4.2.2 Comparison of optimal solutions between dynamic optimization and sound radiation optimization

The structural dynamic topology optimization is also performed for comparison. Here, the dynamic compliance f = F T Y, which is widely used in structural dynamic optimization (Yoon 2010), is to be minimized. The excitation frequency is f p = 65Hz. The optimal density distribution and the suggested electrode coverage are shown in Fig. 21. The structural vibration contour of the optimal design is shown in Fig. 22. Further, the frequency sweeps for the dynamic compliance of the initial and optimal designs of sound radiation optimization and dynamic optimization obtained under excitation frequency f p = 65Hz is shown in Fig. 23. It can be seen that the dynamic optimization solution has the smallest dynamic compliance in the frequency range f P = 60−70 Hz. Moreover, the frequency sweeps of the concerned sound pressure for the three designs are given in Fig. 24. Clearly, the sound radiation optimization yields the best sound radiation property over the frequency range f P = 60−70 Hz.

Fig. 21
figure 21

Optimal layout of electrode coverage for structural dynamic optimization. a Material density contour; b Electrode layout (with low density elements hidden)

Full size image
Fig. 22
figure 22

Vibration amplitude contour of final topology optimization result for structural dynamic optimization

Full size image
Fig. 23
figure 23

Comparison of dynamic compliance of initial design and optimal designs obtained by sound radiation optimization and structural vibration optimization

Full size image
Fig. 24
figure 24

Comparison of sound pressure of initial design and optimal designs obtained by sound radiation optimization and structural vibration optimization

Full size image

4.2.3 Influence of reference point position

Now the structure is optimized under f P = 65 Hz excitation and control gain G c = 40, but for different locations of the reference point. The optimization results are shown in Fig. 25. When the reference point is far away from the vibrating structure, the optimal design shows only slight dependence on the reference point position (see Fig. 25a and b). This implies the structural global vibration play an important role in the optimization when the reference point is far away from the vibrating structure. However, when the reference point is close enough to the vibrating structure, the local vibrations near the reference point become dominant and thus the reference point position exerts a notable influence on the optimal topology (see Fig. 25c and d).

Fig. 25
figure 25

Optimal electrode layout obtained with different reference point positions under active control

Full size image

5 Conclusions

This paper presents an optimization formulation and numerical techniques for topological design of the surface electrodes of the piezoelectric sensors/actuator layers attached to a vibrating shell structure, with the aim to minimize the sound radiation under active control. A pseudo-density model with penalization for indicating absence and presence of surface electrode is used in the topology optimization model, and the design objective is to minimize the norm of sound pressure at a specific point under a certain excitation frequency or in a given frequency range. The finite element method is employed in the structural vibration analysis, while the boundary element method is used for the sound radiation analysis in the unbounded acoustic domain. For the CGVF control considered in this study, the overall system exhibits a non-proportional active damping property. To improve the numerical efficiency, the technique of complex mode superposition in the state space, in conjunction with a model reduction transformation, is adopted in the dynamic response analysis. In this context, the corresponding adjoint-variable sensitivity analysis scheme is derived. Several numerical examples are presented to demonstrate effectiveness of the proposed approach, and the influences of some key factors on the optimal design are also discussed.

In this study, an artificial piezoelectric material model with power-law penalization, similar as the penalized material stiffness model in the SIMP approach, is employed and the volume constraint is considered for imposing a certain restriction to the circuit complexity of the control system. It may be also interesting to explore explicit penalization of gray elements (Borrvall and Petersson 2001) and control energy constraints in the future study.