1 Introduction

In scientific and engineering fields, such as mechanical rotation, flight control systems, and high-tech fields, time delay often occurs, which in most cases causes the degradation of the system performance and even destabilizes the system. In recent decades, the time-delay system stability has been extensively studied and has attracted a lot of attentions from the researchers [1, 4, 20, 31]. Additionally, switched system is one of the current research hotspots. In Cai et al. [2], the model-based event-triggered control for uncertain discrete-time switched systems composed of stable and unstable subsystems was studied. In Zhang et al. [32], a low-cost adaptive pre-designed time tracking control strategy was proposed for nonlinear switched systems with input quantization and unknown inter-class hysteresis delay. In Swapnil and Nikita [16], the dynamics of a bimodal planar linear switched system with Hurwitz stable and unstable subsystems was studied. In the current study, the switched non-time-delay systems or time-delay non-switched systems are relatively simple, while the switched systems with time delay are more complicated [21]. It is very important to find the maximum bound of time delay to ensure the asymptotic stability of the system. The study on the time-delay switched systems has attracted great interest [3, 8, 9, 11, 29, 33].

On the other hand, due to the physical limitations of the engineering equipment in the actual system, the input saturation occurs frequently. Therefore, it is great theoretical and practical importance to design the controller to make the system stable when the input saturation occurs [22]. In recent decades, there have been many research results on the switched systems with input saturation [12, 23, 24]. In Shang and Jingcheng [17], the adaptive event-triggered robust optimal control method for discrete-time switched systems with input saturation and external disturbances was studied. In Wu and Zhang [25], a non-fragile event-triggered control method for positive switched systems with/without input saturation was proposed. In Jiang et al. [7], an adaptive neural network control scheme for a class of randomly switched systems with input saturation was studied. In Wang et al. [26], the exponential stability of the switched systems with input saturation and parameter uncertainty was studied. In Marc and Sophie [13], the anti-windup control for the discrete-time switched systems with input saturation was studied.

Due to the inherent conservativeness of the Lyapunov–Krasovskii functional (LKF) method, the researchers have been trying to find ways to reduce the conservativeness of the stability criterion. In Gu [5], an approximation to the full LKF was achieved by decomposing the integration interval and restricting arbitrary matrix functions to sectional-continuous functions. In Peet and Papachristodoulou [14], the stability analysis was transformed into a sum-of-squares problem by parametrizing arbitrary matrix functions into higher-order polynomials and using polynomial relaxation techniques. In Seuret and Gouaisbaut [18], time-delay states were projected onto Legendre polynomials to achieve exact bounding of the cross terms. In Han [6] and Yue et al. [30], by decomposing the time-delay variation interval, the conservativeness of the corresponding linear matrix inequality (LMI) conditions can be reduced. The above stability analysis methods use the time-delay variation range and the upper bound on the rate of delay change. By using these two kinds of information and introducing the triple integral term into the design of LKF, the solution space will also be enlarged, which can further reduce the conservatism of the stability analysis.

In this paper, the stability criterion and controller design for the time-delay switched systems with input saturation is investigated based on an improved LKF. Based on constructing LKF with triple integral term and making full use of delay lower bound information, the sufficient conditions for exponential stability of the system are given. A state feedback controller is designed for the input-saturated switched system. The symmetric delay rate problem is considered to accurately define the derivative of LKF, which reduces the conservatism of the system. The inverse convex method is also introduced, which can directly deal with the integration of inversely weighted convex combinations to effectively reduce the number of decision variables and obtain a less conservative stability criterion. Finally, the effectiveness of the proposed method is verified by the numerical examples .

Notations We have used some standard symbols in this paper. \(\mathbb {R}^{m \times n}\) represents the \(m\times n\) dimensional real matrix, and \(\mathbb {R}^n\) represents the n-dimensional Euclidean space. Let \(Q=\{1,2,...,2^m\}\). \(M^\textrm{T}\) and \(M^\mathrm{-1}\) show the transpose and inverse of the matrix M, respectively. \(I_n\) represents the n-dimensional identity matrix. \(M>0\) and \(M<0\) represent the positive definite and negative definite symmetric matrices, respectively. \(\dot{x}(t)\) is the derivative of the function x(t) with respect to time t. \({\lambda _{\max }}(\cdot )\) and \({\lambda _{\min }}(\cdot )\) denote the matrix minimum and maximum eigenvalues, respectively, and \(*\) denotes the symmetric terms in a symmetric matrix.

2 Problem Formulation

Consider the following time-delay switched system with input saturation:

$$\begin{aligned} \left\{ \begin{aligned}&\dot{x}(t) = {A_\sigma }x(t) + {C_\sigma }x(t - d(t)) + {B_\sigma }\mathrm{{sat}}(u(t))\\&x(\theta ) = \varphi (\theta ),\ \theta \in [ - {h_2},\ 0] \end{aligned} \right. \end{aligned}$$
(1)

where \(x(t) \in {\mathbb {R}^n}\) is the system state, \(u(t) \in {\mathbb {R}^m}\) is the system input, and \( \varphi (\theta )\) is a continuous initial function. \(\sigma (k):[0,\ \infty ) \rightarrow \mathbb {M} = \{ 1,\ 2,\ \ldots ,\ M\} \) denotes the switched signal, M denotes the modal number. And

$$\begin{aligned} \mathrm{{sat}}(u(t)) = {[\mathrm{{sat}}({u_1}(t)),\ \mathrm{{sat}}({u_1}(t)),\ \cdots ,\ \mathrm{{sat}}({u_m}(t))]^\mathrm{{T}}} \end{aligned}$$

with \( - 1 \le \mathrm{{sat}}({u_i}(t)) \le 1\). \({A_\sigma }\), \({B_\sigma }\) and \({C_\sigma }\) are constant matrices with appropriate dimensions. The time-varying delay d(t) satisfies

$$\begin{aligned}0 \le {h_1} \le d(t) \le {h_2},\ -d_{\max }< \dot{d}(t) \le {d_{\max }} < 1\end{aligned}$$

where \( h_1,\ h_2\) and \(d_{\max }\) are the positive constants.

Lemma 1

[19] (Jensen’s integral inequality) Let x be a differentiable derivative on \([\alpha ,\ \beta ] \rightarrow {\mathbb {R}^n}\). For a positive definite matrix \(R \in {\mathbb {R}^{m \times n}}\), the following inequalities hold

$$\begin{aligned} \begin{aligned}&(\beta - \alpha )\int _{\alpha } ^{\beta } {{x^\textrm{T}}(s)} Rx(s)\textrm{d}s \ge {\left( \int _\alpha ^\beta {x(s)} \textrm{d}s\right) ^\textrm{T}}R\left( \int _\alpha ^\beta {x(s)} \textrm{d}s\right) \\&\quad \frac{{{{(\beta - \alpha )}^2}}}{2}\int _\alpha ^\beta {\int _\theta ^\beta {{x^\textrm{T}}(s} } )Rx(s)\textrm{d}s\textrm{d}\theta \ge {\left( \int _\alpha ^\beta {\int _\theta ^\beta {x(s)} } \textrm{d}s\textrm{d}\theta \right) ^\textrm{T}}R\left( \int _\alpha ^\beta {\int _\theta ^\beta {x(s)} } \textrm{d}s\textrm{d}\theta \right) \end{aligned} \end{aligned}$$

where \( \alpha \) and \(\beta \) are the positive constants.

Lemma 2

[15] Let \({f_{1}},\ {f_{2 }},\ \ldots ,\ {f_N}: {R^m} \mapsto R\) have the positive values in an open subset D of \({R^m}\), and then, the \({f_i}\) mutually convex combination on D satisfies

$$\begin{aligned} \begin{aligned} \mathop {\min }\limits _{{\alpha _i} > 0,\ \sum \limits _i {{\alpha _i} = 1} } \sum \limits _i {\frac{1}{{{\alpha _i}}}} {f_i}(t) = \sum \limits _i {{f_i}(t)} + \mathop {\max }\limits _{{g_{i,j}}(t)} \sum \limits _{i \ne j} {{g_{i,j}}(t)} \end{aligned} \end{aligned}$$

then

$$\begin{aligned} \begin{aligned} \left\{ {{g_{i,j}}:{R^m} \mapsto R.\ {g_{i,j}}(t) \buildrel \Delta \over = {g_{j,i}}(t).\ \left[ {\begin{array}{*{20}{c}} {{f_i}(t)}&{}{{g_{i,j}}(t)}\\ {{g_{i,j}}(t)}&{}{{f_j}(t)} \end{array}} \right] \ge 0} \right\} \end{aligned} \end{aligned}$$

Remark 1

Lemma 2 is the inverse convex method, which can directly deal with the integration of inversely weighted convex combinations to effectively reduce the number of decision variables.

Lemma 3

[34] There are \(2^m\) diagonal matrices \(D_i\in \mathbb {R}^{m \times m}\) with elements 1 or 0, \(j \in Q\), and \(D_j^ -=I-D_j\). The scalars \(\eta _j\) satisfy \(0 \le \eta _j \le 1\) and \(\sum _{i=1}^{2^m} \eta _j =1\), and it can be concluded that

$$\begin{aligned} \begin{aligned} \sum _{j=1}^{2^m} \eta _j(D_j+D_j^ -)=I,\ j \in Q \end{aligned} \end{aligned}$$

And a bounded set is defined as

$$\begin{aligned} \begin{aligned} \mathcal {L}(H)=\{x(t) \in \mathbb {R}^n: |h_s^\textrm{T}x(t) |\le 1, s \in \{1,\ 2,\ ...,\ m \} \} \end{aligned} \end{aligned}$$

where \(h_s^\textrm{T}\) is the s-th row of \(H \in \mathbb {R}^{m \times n}\). For \( x(t) \in \mathbb {R}^n,\ K \in \mathbb {R}^{m \times n}\), if \(x(t) \in \mathcal {L}(H)\), then

$$\begin{aligned} \begin{aligned} \textrm{sat}(Kx(t)) \in \textrm{co}\{D_jKx(t)+D_j^ -Hx(t),\ j \in Q \} \end{aligned} \end{aligned}$$

where \(\textrm{co}\{\cdot \}\) denotes the convex hull.

Definition 1

[27] If there exist positive constants c and \(\lambda \) such that for any initial condition x(0), the solution of the system satisfies

$$\begin{aligned} \begin{aligned} \left\| {{x(t)}} \right\| \le c{e^{ - \lambda (t - {t_0})}}\left\| {{x(0)}} \right\| ,\ \forall t \ge {t_0} \end{aligned} \end{aligned}$$

and then the system is said to be exponentially stable with the exponential decay rate \(\lambda \).

Problem 1

Consider system (1) with \(u = 0\), a novel LKF is designed for the time-delay switched system. A less conservative stability criterion is obtained; that is, the time-delay upper bound is raised.

Problem 2

Consider system (1), a novel LKF is designed for the time-delay switched system with input saturation. A less conservative stability criterion is obtained; that is, the time-delay upper bound is raised. A state feedback controller is designed to ensure the exponential stability of the closed-loop system.

3 Main Results

Firstly, the stability of system (1) with \(u = 0\) is discussed and sufficient conditions for the exponential stability of the system are given.

Theorem 1

For given constants \({h_1}> 0,\;{h_2}> 0,\;\alpha> 0,\;\mu > 1\), if there exist matrices \({P_i}> 0,\;{R_{ji}}> 0,\;{D_{ji}}> 0,\;{Q_{ji}}> 0,\;{S_{ji}}> 0,\;{Z_i} > 0\) of appropriate dimensions satisfying

$$\begin{aligned} {\Omega _i}= & {} \left[ { \begin{array}{*{20}{c}} {{\Phi _{11}}}&{}{{\Phi _{12}}}&{}{{\Phi _{13}}}&{}{{\Phi _{14}}}&{}{{\Phi _{15}}}\\ *&{}{{\Phi _{22}}}&{}{{\Phi _{23}}}&{}{{\Phi _{24}}}&{}{{\Phi _{25}}}\\ *&{}*&{}{{\Phi _{33}}}&{}{{\Phi _{34}}}&{}{{\Phi _{35}}}\\ *&{}*&{}*&{}{{\Phi _{44}}}&{}{{\Phi _{45}}}\\ *&{}*&{}*&{}*&{}{{\Phi _{55}}} \end{array}} \right] < 0 \end{aligned}$$
(2)
$$\begin{aligned}{} & {} \left[ {\begin{array}{*{20}{c}} {{R_{1i}}}&{}{{S_{1i}}}\\ *&{}{{R_{1i}}} \end{array}} \right] > 0,\ (j=1,\ 2) \end{aligned}$$
(3)
$$\begin{aligned}{} & {} \begin{array}{l} {P_i} \le \mu {P_j},\;{Q_{1i}} \le \mu {Q_{1j}},\;{Q_{2i}} \le \mu {Q_{2j}},\;{R_{1i}} \le \mu {R_{1j}},\;{R_{2i}} \le \mu {R_{2j}},\\ \quad {D_{1i}} \le \mu {D_{1j}},\;{D_{2i}} \le \mu {D_{2j}},\;{Z_i} \le \mu {Z_j} \end{array} \end{aligned}$$
(4)

And the average dwell time \(\tau _a\) satisfies

$$\begin{aligned} \begin{aligned} \begin{array}{l} {\tau _a} > {\tau _a}^* = \frac{{\ln \mu }}{\alpha } \end{array} \end{aligned} \end{aligned}$$

where

$$\begin{aligned} {\Phi _{11}}= & {} 2\alpha {P_i} + {P_i}{A_i} + A_i^\textrm{T}{P_i} + {Q_{1i}} + {Q_{2i}} + A_i^\textrm{T}{N_i}{A_i} + {h^2_2}{Z_i} - {e^{ - 2\alpha {h_1}}}{R_{1i}},\\ {\Phi _{12}}= & {} {P_i}{C_i} + {e^{ - 2\alpha {h_1}}}{R_{1i}} - {e^{ - 2\alpha {h_1}}}{S_{1i}} + A_i^\textrm{T}{N_i}{C_i}\mathrm{{, }}\ {\Phi _{13}} = {e^{ - 2\alpha {h_1}}}{S_{1i}}\mathrm{{, }}\ {\Phi _{14}} = 0,\\ \mathrm{{ }}{\Phi _{15}}= & {} {h_2}{Z_i},\;{\Phi _{22}} = C_i^\textrm{T}{N_i}{C_i} + 2{e^{ - 2\alpha {h_1}}}{S_{1i}} - 2{e^{ - 2\alpha {h_1}}}{R_{1i}} + 2{e^{ - 2\alpha {h_2}}}{S_{2i}} - 2{e^{ - 2\alpha {h_2}}}{R_{2i}} \\{} & {} \quad - (1 - d_{\max }){e^{ - 2\alpha {h_2}}}{D_{1i}} + (1 + d_{\max }){e^{ - 2\alpha {h_2}}}{D_{2i}},\;{\Phi _{23}} = - {e^{ - 2\alpha {h_1}}}{S_{1i}} + {e^{ - 2\alpha {h_1}}}{R_{1i}},\\ \mathrm{{ }}{\Phi _{24}}= & {} - {e^{ - 2\alpha {h_2}}}{S_{2i}} + {e^{ - 2\alpha {h_2}}}{R_{2i}},\mathrm{{ }}\;{\Phi _{25}} = 0,\;{\Phi _{33}} = - {e^{ - 2\alpha {h_1}}}{Q_{1i}} - {e^{ - 2\alpha {h_1}}}{R_{1i}}\\{} & {} \quad - {e^{ - 2\alpha {h_2}}}{R_{2i}} + {e^{ - 2\alpha {h_1}}}{D_{1i}},\mathrm{{ }}\;{\Phi _{34}} = {e^{ - 2\alpha {h_2}}}{S_{2i}},\mathrm{{ }}\;{\Phi _{35}} = 0,\\ {\Phi _{44}}= & {} - {e^{ - 2\alpha {h_2}}}{R_{2i}} - {e^{ - 2\alpha {h_2}}}{Q_{2i}} - {e^{ - 2\alpha {h_2}}}{D_{2i}},\mathrm{{ }}\;{\Phi _{45}} = 0,\;{\Phi _{55}} = - {Z_i},\\ {N_i}= & {} {h^2_1}{R_{1i}} + {h^2_{12}}{R_{2i}} + \frac{{{h^4_2}}}{4}{Z_i},\;a = \min {\lambda _{\min }}({P_i}),\;\lambda = \frac{1}{2}(\alpha - \frac{{\ln \mu }}{{{\tau _a}}}),\\ b= & {} \max {\lambda _{\max }}({P_i}) + {h_1}\max {\lambda _{\max }}({Q_{1i}}) + {h_2}\max {\lambda _{\max }}({Q_{2i}}) + {h_1}\max {\lambda _{\max }}({D_{1i}}) + \\{} & {} \quad {h_2}\max {\lambda _{\max }}({D_{2i}}) + \frac{{{h^2_1}}}{2}\max {\lambda _{\max }}({R_{1i}}) +\frac{{{h^2_2}}}{2}\max {\lambda _{\max }}({R_{2i}}),\mathrm{{ }}\;{h_{12}}={h_2}-{h_1}. \end{aligned}$$

Then, the system (1) with u = 0 is exponentially stable.

Proof

We choose the following LKF

$$\begin{aligned} \begin{aligned} \begin{array}{l} {V_{\sigma (t)}}(t) = {V_1}_{\sigma (t)}(t) + {V_2}_{\sigma (t)}(t) + {V_3}_{\sigma (t)}(t) + {V_4}_{\sigma (t)}(t) + {V_5}_{\sigma (t)}(t) \end{array} \end{aligned} \end{aligned}$$
(5)

where

$$\begin{aligned}{} & {} \begin{array}{l} {V_1}_{\sigma (t)}(t) = {x^\textrm{T}}(t){P_{\sigma (t)}}x(t) \end{array} \end{aligned}$$
(6)
$$\begin{aligned}{} & {} \begin{array}{l} {V_2}_{\sigma (t)}(t) = \int _{t - {h_1}}^t {{x^\textrm{T}}(s){e^{2\alpha (s - t)}}{Q_{1\sigma (t)}}x(s)\textrm{d}s + \int _{t - {h_2}}^t {{x^\textrm{T}}(s){e^{2\alpha (s - t)}}{Q_{2\sigma (t)}}x(s)\textrm{d}s} } \end{array} \end{aligned}$$
(7)
$$\begin{aligned}{} & {} \begin{array}{l} {V_3}_{\sigma (t)}(t) = \int _{t - d(t)}^{t - {h_1}} {{x^\textrm{T}}(s){e^{2\alpha (s - t)}}{D_{1\sigma (t)}}x(s)\textrm{d}s +\int _{t - {h_2}}^{t - d(t)} {{x^\textrm{T}}(s){e^{2\alpha (s - t)}}{D_{2\sigma (t)}}x(s)\textrm{d}s} } \end{array} \end{aligned}$$
(8)
$$\begin{aligned}{} & {} \begin{array}{l} {V_4}_{\sigma (t)}(t) = {h_1} \int _{ - {h_1}}^0 {\int _{t + \theta }^t {{{\dot{x}}^\textrm{T}}(s){e^{2\alpha (s - t)}}{R_{1\sigma (t)}}\dot{x}(s)\textrm{d}s\textrm{d}\theta } }\\ \qquad \qquad \quad \quad + {h_{12}} \int _{ - {h_2}}^{ - {h_1}} {\int _{t + \theta }^t {{{\dot{x}}^\textrm{T}}(s){e^{2\alpha (s - t)}}{R_{2\sigma (t)}}\dot{x}(s)\textrm{d}s\textrm{d}\theta } } \end{array} \end{aligned}$$
(9)

and

$$\begin{aligned} \begin{aligned} \begin{array}{l} {V_5}_{\sigma (t)}(t) = \frac{{{h^2_2}}}{2} \int _{ - {h_2}}^0 {\int _\theta ^0 {\int _{t + \lambda }^t {{{\dot{x}}^\textrm{T}}(s){e^{2\alpha (s - t)}}{Z_{\sigma (t)}}\dot{x}(s)\textrm{d}s\textrm{d}\lambda \textrm{d}\theta } } } \end{array} \end{aligned} \end{aligned}$$
(10)

The derivative of (5)–(10) is

$$\begin{aligned} \begin{aligned} \begin{array}{l} {{\dot{V}}_i}(t) = {{\dot{V}}_{1i}}(t) + {{\dot{V}}_{2i}}(t) + {{\dot{V}}_{3i}}(t) + {{\dot{V}}_{4i}}(t) + {{\dot{V}}_{5i}}(t) \end{array} \end{aligned} \end{aligned}$$
(11)

where

$$\begin{aligned}{} & {} \begin{array}{l} {{\dot{V}}_{1i}}(t) = 2{x^\textrm{T}}(t){P_i}\dot{x}(t) \end{array} \end{aligned}$$
(12)
$$\begin{aligned}{} & {} \begin{array}{l} {{\dot{V}}_{2i}}(t) = - 2\alpha {V_{2i}}(t) + {x^\textrm{T}}(t){Q_{1i}}x(t) - {x^\textrm{T}}(t - {h_1}){e^{ - 2\alpha {h_1}}}{Q_{1i}}x(t - {h_1})\\ \qquad \quad \qquad + {x^\textrm{T}}(t){Q_{2i}}x(t) - {x^\textrm{T}}(t - {h_2}){e^{ - 2\alpha {h_2}}}{Q_{2i}}x(t - {h_2}) \end{array} \end{aligned}$$
(13)
$$\begin{aligned}{} & {} \begin{array}{l} {{\dot{V}}_{3i}}(t) = - 2\alpha {V_{3i}}(t) - (1 - \dot{d}(t)){x^\textrm{T}}(t - d(t)){e^{ - 2\alpha d(t)}}{\mathrm{{D}}_{1i}}x(t - d(t))\\ \qquad \quad \qquad + {x^\textrm{T}}(t - {h_1}){e^{ - 2\alpha {h_1}}}{\mathrm{{D}}_{1i}}x(t - {h_1})- {x^\textrm{T}}(t - {h_2}){e^{ - 2\alpha {h_2}}}{\mathrm{{D}}_{2i}}x(t - {h_2})\\ \qquad \quad \qquad + (1 - \dot{d}(t)){x^\textrm{T}}(t - d(t)){e^{ - 2\alpha d(t)}}{\mathrm{{D}}_{2i}}x(t - d(t)) \end{array} \end{aligned}$$
(14)
$$\begin{aligned}{} & {} \begin{array}{l} {{\dot{V}}_{4i}}(t) = - 2\alpha {V_{4i}}(t) + {h^2_1}{{\dot{x}}^\textrm{T}}(t){R_{1i}}\dot{x}(t) - {h_1} \int {{{\dot{x}}^\textrm{T}}(t){R_{1i}}\dot{x}(t)} \\ \qquad \quad \qquad - {e^{ - 2\alpha {h_1}}}{{\dot{x}}^\textrm{T}}(t - {h_1}){R_{1i}}\dot{x}(t - {h_1})\textrm{d}t+ {h^2_{12}}{{\dot{x}}^\textrm{T}}(t){R_{2i}}\dot{x}(t)\\ \qquad \quad \qquad - {h_{12}} \int {{{\dot{x}}^\textrm{T}}(t - {h_1}){R_{2i}}\dot{x}(t - {h_1})} - {e^{ - 2\alpha {h_2}}}{{\dot{x}}^\textrm{T}}(t - {h_2}){R_{2i}}\dot{x}(t - {h_2})\textrm{d}t \end{array} \end{aligned}$$
(15)

and

$$\begin{aligned} \begin{aligned} \begin{array}{l} {{\dot{V}}_{5i}}(t) = - 2\alpha {V_{5i}}(t) + \frac{{{h^4_2}}}{4}{{\dot{x}}^\textrm{T}}(t){Z_i}\dot{x}(t) - \frac{{{h^2_2}}}{2} \int _{ - {h_2}}^0 {\int _{t + \theta }^t {{{\dot{x}}^\textrm{T}}(s){e^{2\alpha (s - t)}}{Z_i}\dot{x}(s)} } \textrm{d}s\textrm{d}\theta \end{array} \end{aligned} \end{aligned}$$
(16)

Then, it can be derived

$$\begin{aligned} \begin{array}{l} {{\dot{V}}_i}(t) \le 2{x^\textrm{T}}(t){P_i}\dot{x}(t)\\ \qquad \qquad \; - 2\alpha {V_{2i}}(t) + {x^\textrm{T}}(t){Q_{1i}}x(t) - {x^\textrm{T}}(t - {h_1}){e^{ - 2\alpha {h_1}}}{Q_{1i}}x(t - {h_1})\\ \qquad \qquad \; + {x^\textrm{T}}(t){Q_{2i}}x(t) - {x^\textrm{T}}(t - {h_2}){e^{ - 2\alpha {h_2}}}{Q_{2i}}x(t - {h_2})\\ \qquad \qquad \;- 2\alpha {V_{3i}}(t) + {x^\textrm{T}}(t - {h_1}){e^{ - 2\alpha {h_1}}}{\mathrm{{D}}_{1i}}x(t - {h_1}) \\ \qquad \qquad \; - (1 - d_{\max }){x^\textrm{T}}(t - d(t)){e^{ - 2\alpha {h_2}}}{\mathrm{{D}}_{1i}}x(t - d(t))\\ \qquad \qquad \; - {x^\textrm{T}}(t - {h_2}){e^{ - 2\alpha {h_2}}}{\mathrm{{D}}_{2i}}x(t - {h_2})\\ \qquad \qquad \;+ (1 + d_{\max }){x^\textrm{T}}(t - d(t)){e^{ - 2\alpha {h_2}}}{\mathrm{{D}}_{2i}}x(t - d(t))\\ \qquad \qquad \; - 2\alpha {V_{4i}}(t) + {h^2_1}{{\dot{x}}^\textrm{T}}(t){R_{1i}}\dot{x}(t) - {h_1} \int _{t - {h_1}}^t {{{\dot{x}}^\textrm{T}}(s){e^{ - 2\alpha {h_1}}}{R_{1i}}\dot{x}(s)} \textrm{d}s\\ \qquad \qquad \; + {h^2_{12}}{{\dot{x}}^\textrm{T}}(t){R_{2i}}\dot{x}(t) - {h_{12}} \int _{t - {h_2}}^{t - {h_1}} {{{\dot{x}}^\textrm{T}}(s){e^{ - 2\alpha {h_2}}}{R_{2i}}\dot{x}(s)} \textrm{d}s\\ \qquad \qquad \; - 2\alpha {V_{5i}}(t) + \frac{{{h^4_2}}}{4}{{\dot{x}}^\textrm{T}}(t){Z_i}\dot{x}(t) - \frac{{{h^2_2}}}{2} \int _{ - {h_2}}^0 {\int _{t + \theta }^t {{{\dot{x}}^\textrm{T}}(s){Z_i}\dot{x}(s)} } \textrm{d}s\textrm{d}\theta \end{array} \end{aligned}$$
(17)

To make the stability criterion less conservative, Lemmas 1 and 2 are used to deal with the integral term,

$$\begin{aligned} \begin{aligned} \begin{array}{l} - {h_1} \int _{t - {h_1}}^t {{{\dot{x}}^\textrm{T}}(s){e^{ - 2\alpha {h_1}}}{R_{1i}}\dot{x}(s)} \textrm{d}s\\ \quad = - {h_1} \int _{t - d(t)}^t {{{\dot{x}}^\textrm{T}}(s){e^{ - 2\alpha {h_1}}}{R_{1i}}\dot{x}(s)} \textrm{d}s - {h_1}\int _{t - {h_1}}^{t - d(t)} {{{\dot{x}}^\textrm{T}}(s){e^{ - 2\alpha {h_1}}}{R_{1i}}\dot{x}(s)} \textrm{d}s\\ \quad \le - {e^{ - 2\alpha {h_1}}}\left( {\frac{{{h_1}}}{{d(t)}}{{(x(t) - x(t - d(t)))}^\textrm{T}}{R_{1i}}(x(t) - x(t - d(t))) } \right. \\ \qquad + \left. {\frac{{{h_1}}}{{{h_1} - d(t)}}{{(x(t - d(t)) - x(t - {h_1}))}^\textrm{T}}{R_{1i}}(x(t - d(t)) - x(t - {h_1}))} \right) \\ \quad = - {e^{ - 2\alpha {h_1}}}{\left[ {\begin{array}{*{20}{c}} {x(t) - x(t - d(t))}\\ {x(t - d(t)) - x(t - {h_1})} \end{array}} \right] ^\textrm{T}}\left[ {\begin{array}{*{20}{c}} {\frac{{{h_1}}}{{d(t)}}{R_{1i}}}&{}0\\ 0&{}{\frac{{{h_1}}}{{{h_1} - d(t)}}{R_{1i}}} \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {x(t) - x(t - d(t))}\\ {x(t - d(t)) - x(t - {h_1})} \end{array}} \right] \\ \quad \le - {e^{ - 2\alpha {h_1}}}{\left[ {\begin{array}{*{20}{c}} {x(t) - x(t - d(t))}\\ {x(t - d(t)) - x(t - {h_1})} \end{array}} \right] ^\textrm{T}}\left[ {\begin{array}{*{20}{c}} {{R_{1i}}}&{}{{S_{1i}}}\\ *&{}{{R_{1i}}} \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {x(t) - x(t - d(t))}\\ {x(t - d(t)) - x(t - {h_1})} \end{array}} \right] \end{array} \end{aligned} \end{aligned}$$

In the same way,

$$\begin{aligned} \begin{aligned} \begin{array}{l} - {h_{12}} \int _{t - {h_2}}^{t - {h_1}} {{{\dot{x}}^\textrm{T}}(s){e^{ - 2\alpha {h_2}}}{R_{2i}}\dot{x}(s)} \textrm{d}s\\ \quad \le - {e^{ - 2\alpha {h_2}}}{\left[ {\begin{array}{*{20}{c}} {x(t - {h_1}) - x(t - d(t))}\\ {x(t - d(t)) - x(t - {h_2})} \end{array}} \right] ^\textrm{T}}\left[ {\begin{array}{*{20}{c}} {{R_{2i}}}&{}{{S_{2i}}}\\ *&{}{{R_{2i}}} \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {x(t - {h_1}) - x(t - d(t))}\\ {x(t - d(t)) - x(t - {h_2})} \end{array}} \right] \end{array} \end{aligned} \end{aligned}$$

For the double integral, using Lemma 1, we can obtain

$$\begin{aligned} \begin{aligned} \begin{array}{l} -\frac{{{h^2_2}}}{2}\int _{ - {h_2}}^0 {\int _{t + \theta }^t {{{\dot{x}}^\textrm{T}}(s){Z_i}\dot{x}(s)} } \textrm{d}s\textrm{d}\theta \le - \int _{ - {h_2}}^0 {\int _{t + \theta }^t {{{\dot{x}}^\textrm{T}}(s)} } \textrm{d}s\textrm{d}\theta {Z_i}\int _{ - {h_2}}^0 {\int _{t + \theta }^t {{{\dot{x}}^\textrm{T}}(s)} } \textrm{d}s\textrm{d}\theta \\ \quad \le - {({h_2}x(t) - \int _{t - {h_2}}^t {x(s)} \textrm{d}s)^\textrm{T}}{Z_i}({h_2}x(t) - \int _{t - {h_2}}^t {x(s)} \textrm{d}s) \end{array} \end{aligned} \end{aligned}$$

By the above derivation, it can be concluded that

$$\begin{aligned}&{{\dot{V}}_i}(t) + 2\alpha {V_{i}}(t) \le 2{x^\textrm{T}}(t){P_i}\dot{x}(t) + 2\alpha {x^\textrm{T}}(t){P_i}x(t)\\&\qquad + {x^\textrm{T}}(t){Q_{1i}}x(t) - {x^\textrm{T}}(t - {h_1}){e^{ - 2\alpha {h_1}}}{Q_{1i}}x(t - {h_1})\\&\qquad + {x^\textrm{T}}(t){Q_{2i}}x(t) - {x^\textrm{T}}(t - {h_2}){e^{ - 2\alpha {h_2}}}{Q_{2i}}x(t - {h_2})\\&\qquad + {x^\textrm{T}}(t - {h_1}){e^{ - 2\alpha {h_1}}}{\mathrm{{D}}_{1i}}x(t - {h_1}) \\&\qquad - (1 - d_{\max }){x^\textrm{T}}(t - d(t)){e^{ - 2\alpha {h_2}}}{\mathrm{{D}}_{1i}}x(t - d(t))\\&\qquad - {x^\textrm{T}}(t - {h_2}){e^{ - 2\alpha {h_2}}}{\mathrm{{D}}_{2i}}x(t - {h_2}) \\&\qquad + (1 + d_{\max }){x^\textrm{T}}(t - d(t)){e^{ - 2\alpha {h_2}}}{\mathrm{{D}}_{2i}}x(t - d(t))\\&\qquad - {e^{ - 2\alpha {h_1}}}{\left[ {\begin{array}{*{20}{c}} {x(t) - x(t - d(t))}\\ {x(t - d(t)) - x(t - {h_1})} \end{array}} \right] ^\textrm{T}}\left[ {\begin{array}{*{20}{c}} {{R_{1i}}}&{}{{S_{1i}}}\\ *&{}{{R_{1i}}} \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {x(t) - x(t - d(t))}\\ {x(t - d(t)) - x(t - {h_1})} \end{array}} \right] \\&\qquad - {e^{ - 2\alpha {h_2}}}{\left[ {\begin{array}{*{20}{c}} {x(t - {h_1}) - x(t - d(t))}\\ {x(t - d(t)) - x(t - {h_2})} \end{array}} \right] ^\textrm{T}}\left[ {\begin{array}{*{20}{c}} {{R_{2i}}}&{}{{S_{2i}}}\\ *&{}{{R_{2i}}} \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {x(t - {h_1}) - x(t - d(t))}\\ {x(t - d(t)) - x(t - {h_2})} \end{array}} \right] \\&\qquad + {{\dot{x}}^\textrm{T}}(t)(\frac{{{h^4_2}}}{4}{Z_i} + {h^2_1}{R_{1i}} + {h^2_{12}}{R_{2i}})\dot{x}(t)\\&\qquad - {({h_2}x(t) - \int _{t - {h_2}}^t {x(s)} \textrm{d}s)^\textrm{T}}{Z_i}({h_2}x(t) - \int _{t - {h_2}}^t {x(s)} \textrm{d}s) \end{aligned}$$

Then, it can be derived

$$\begin{aligned} \begin{aligned} {\dot{V}_i}(t) + 2\alpha {V_i}(t) \le {\xi ^\textrm{T}}{\Omega _i}\xi \end{aligned} \end{aligned}$$
(18)

where

$$\begin{aligned} \begin{aligned} {\xi ^\textrm{T}} = (x(t)\mathrm{{ }},\ x(t - d(t))\mathrm{{ }},\ x(t - {h_1})\mathrm{{ }},\ x(t - {h_2})\mathrm{{ }},\ \int _{t - {h_2}}^t {x(s)} \textrm{d}s) \end{aligned} \end{aligned}$$

When \({\Omega _i} < 0\), we have \({\dot{V}_i}(t) + 2\alpha {V_i}(t) < 0\) which means

$$\begin{aligned} \begin{aligned} {V_{\sigma (t)}}({x(t)}) \le {V_{\sigma (t)}}({x({{t_k}})}){e^{ - 2\alpha (t - {t_k})}},\ t \in [{t_k},\ {t_{k + 1}}) \end{aligned} \end{aligned}$$
(19)

where \(t_k\) denotes the switched time, \({t_0}< {t_1}< {t_2}< \cdots {t_k}< {t_{k + 1}} < \cdots \).

According to condition (4), we can obtain

$$\begin{aligned} \begin{aligned} {V_{\sigma ({t_k})}}({x({{t_k}})}) \le \mu {V_{\sigma ({t_{{k^ - }}})}}({x({{t_{{k^ - }}}})}) \end{aligned} \end{aligned}$$

where \(t_{{k^ - }}\) denotes the left limit of \(t_k\).

Let \(k = {N_{\sigma ({t_0},t)}} \le t - {t_0}/{T_\alpha }\), we have

$$\begin{aligned} \begin{aligned} \begin{array}{l} V({x(t)}) \le {e^{ - 2\alpha (t - {t_k})}}\mu {V_{\sigma ({t_k}^ - )}}({x({{t_k}^ - })}) \le \ldots \le {e^{ - 2\alpha (t - {t_0})}}{\mu ^k}{V_{\sigma ({t_0})}}({x({{t_0}})})\\ \qquad \;\le {e^{ - (2\alpha - \ln \mu /{T_\alpha })(t - {t_0})}}{V_{\sigma ({t_0})}}({x({{t_0}})}) \end{array} \end{aligned} \end{aligned}$$

According to Definition 1, we can obtain

$$\begin{aligned} \begin{aligned} \left\| {{x(t)}} \right\| \le \sqrt{\frac{a}{b}} {e^{ - \lambda (t - {t_0})}}\left\| {{x(0)}} \right\| \end{aligned} \end{aligned}$$
(20)

Therefore, the system (1) with \(u = 0\) is exponentially stable. \(\square \)

Design the state feedback controller \(u(t) = {K_\sigma }x(t)\), where \({K_\sigma }\) denotes the gain of the controller. According to Lemma 3, it follows that

$$\begin{aligned} \begin{aligned} \mathrm{{sat}}(u) = \mathrm{{sat}}({K_\sigma }x) = \sum \limits _{j = 1}^{{2^m}} {{\eta _j}} ({D_j}{K_\sigma } + D_j^ - {H_\sigma })x(t)\mathrm{{ }} \end{aligned} \end{aligned}$$

Then, the following closed-loop system can be obtained

$$\begin{aligned} \begin{aligned} \left\{ \begin{array}{l} \dot{x}(t) = {A_\sigma }x(t) + {B_\sigma }\sum \limits _{j = 1}^{{2^m}} {{\eta _j}} ({D_j}{K_\sigma } + D_j^ - {H_\sigma })x(t) + {C_\sigma }x(t - d(t))\\ x(\theta ) = \varphi (\theta ),\ \theta \in [ - {h_2},\ 0] \end{array} \right. \end{aligned} \end{aligned}$$
(21)

Now, we give the sufficient conditions for the exponential stability of the time-delay switched system (21) as follows

Theorem 2

For given constants \({h_1}> 0,\;{h_2}> 0,\;\alpha> 0,\;\mu > 1\), if there exist matrices \({P_i}> 0,\;{R_{ji}}> 0,\;{\tilde{R}_{2i}}> 0,\;{D_{ji}}> 0,\;{Q_{ji}}> 0,\;{S_{ji}}> 0,\;{Z_i} > 0\) of appropriate dimensions satisfying

$$\begin{aligned} {\bar{\Omega }_i}= & {} \left[ {\begin{array}{*{20}{c}} {{{\bar{\Phi }}_{11}}}&{}{{{\bar{\Phi }}_{12}}}&{}{{{\bar{\Phi }}_{13}}}&{}{{{\bar{\Phi }}_{14}}}&{}{{{\bar{\Phi }}_{15}}}&{}{{X_i}{{{\tilde{A}}}_i}^\textrm{T} }&{}{{X_i}{{{\tilde{A}}}_i}^\textrm{T} }&{}{{X_i}{{{\tilde{A}}}_i}^\textrm{T} }\\ *&{}{{{\bar{\Phi }}_{22}}}&{}{{{\bar{\Phi }}_{23}}}&{}{{{\bar{\Phi }}_{24}}}&{}{{{\bar{\Phi }}_{25}}}&{}{{X_i}{C_i}^\textrm{T}}&{}{{X_i}{C_i}^\textrm{T}}&{}{{X_i}{C_i}^\textrm{T}}\\ *&{}*&{}{{{\bar{\Phi }}_{33}}}&{}{{{\bar{\Phi }}_{34}}}&{}{{{\bar{\Phi }}_{35}}}&{}0&{}0&{}0\\ *&{}*&{}*&{}{{{\bar{\Phi }}_{44}}}&{}{{{\bar{\Phi }}_{45}}}&{}0&{}0&{}0\\ *&{}*&{}*&{}*&{}{{{\bar{\Phi }}_{55}}}&{}0&{}0&{}0\\ *&{}*&{}*&{}*&{}*&{}{ - {{{\hat{R}}}_{1i}}}&{}0&{}0\\ *&{}*&{}*&{}*&{}*&{}*&{}{ - {{{\hat{R}}}_{2i}}}&{}0\\ *&{}*&{}*&{}*&{}*&{}*&{}*&{}{ - {{{\hat{Z}}}_i}} \end{array}} \right] < 0 \end{aligned}$$
(22)
$$\begin{aligned}{} & {} \left[ {\begin{array}{*{20}{c}} {{R_{ji}}}&{}{{S_{ji}}}\\ *&{}{{R_{ji}}} \end{array}} \right] > 0,\ (j=1,\ 2) \end{aligned}$$
(23)
$$\begin{aligned}{} & {} \left[ {\begin{array}{*{20}{c}} {{{{\tilde{R}}}_{ji}}}&{}{{X_i}}\\ *&{}{{{{\bar{R}}}_{ji}}} \end{array}} \right] > 0,\ (j=1,\ 2) \end{aligned}$$
(24)
$$\begin{aligned}{} & {} \left[ {\begin{array}{*{20}{c}} {{{{\tilde{Z}}}_i}}&{}{{X_i}}\\ *&{}{{{{\bar{Z}}}_i}} \end{array}} \right] > 0 \end{aligned}$$
(25)
$$\begin{aligned}{} & {} \begin{array}{l} {P_i} \le \mu {P_j},\;{Q_{1i}} \le \mu {Q_{1j}},\;{Q_{2i}} \le \mu {Q_{2j}},\;{R_{1i}} \le \mu {R_{1j}},\;{R_{2i}} \le \mu {R_{2j}},\\ \quad {D_{1i}} \le \mu {D_{1j}},\;{D_{2i}} \le \mu {D_{2j}},\;{Z_i} \le \mu {Z_j} \end{array} \end{aligned}$$
(26)

And the average dwell time \(\tau _a\) satisfies

$$\begin{aligned} \begin{aligned} \begin{array}{l} {\tau _a} > {\tau _a}^* = \frac{{\ln \mu }}{\alpha } \end{array} \end{aligned} \end{aligned}$$

where

$$\begin{aligned} {{\bar{\Phi }}_{11}}= & {} 2\alpha {X_i} + {A_i}{X_i} + {X_i}A_i^\textrm{T} + {{{\bar{Q}}}_{1i}} + {{{\bar{Q}}}_{2i}} + {B_i}{Y_i} + Y_i^\textrm{T}B_i^\textrm{T} + {h^2_2}{{{\bar{Z}}}_i} - {e^{ - 2\alpha {h_1}}}{{{\bar{R}}}_{1i}},\\ {{\bar{\Phi }}_{12}}= & {} {C_i}{X_i} + {e^{ - 2\alpha {h_1}}}{{{\bar{R}}}_{1i}} - {e^{ - 2\alpha {h_1}}}{{{\bar{S}}}_{1i}}\mathrm{{, }}\;{{\bar{\Phi }}_{13}} = {e^{ - 2\alpha {h_1}}}{{{\bar{S}}}_{1i}}\mathrm{{, }}\;{{\bar{\Phi }}_{14}} = 0,\mathrm{{ }}\;{{\bar{\Phi }}_{15}} = {h_2}{{{\bar{Z}}}_i},\\ {{\bar{\Phi }}_{22}}= & {} 2{e^{ - 2\alpha {h_1}}}{{{\bar{S}}}_{1i}} - 2{e^{ - 2\alpha {h_1}}}{{{\bar{R}}}_{1i}} + 2{e^{ - 2\alpha {h_2}}}{{{\bar{S}}}_{2i}} - 2{e^{ - 2\alpha {h_2}}}{{{\bar{R}}}_{2i}} - (1 - d_{\max }){e^{ - 2\alpha {h_2}}}{{{\bar{D}}}_{1i}}\\{} & {} \quad + (1 + d_{\max }){e^{ - 2\alpha {h_2}}}{{{\bar{D}}}_{2i}},\;{{\bar{\Phi }}_{23}} = - {e^{ - 2\alpha {h_1}}}{{{\bar{S}}}_{1i}} + {e^{ - 2\alpha {h_1}}}{{{\bar{R}}}_{1i}},\mathrm{{ }}\;{{\bar{\Phi }}_{24}} = - {e^{ - 2\alpha {h_2}}}{{{\bar{S}}}_{2i}} \\{} & {} \quad + {e^{ - 2\alpha {h_2}}}{{{\bar{R}}}_{2i}},\mathrm{{ }}\;{{\bar{\Phi }}_{25}} = 0, \;{{\bar{\Phi }}_{33}} = - {e^{ - 2\alpha {h_1}}}{{{\bar{Q}}}_{1i}} - {e^{ - 2\alpha {h_1}}}{{{\bar{R}}}_{1i}} - {e^{ - 2\alpha {h_2}}}{{{\bar{R}}}_{2i}} + {e^{ - 2\alpha {h_1}}}{{{\bar{D}}}_{1i}},\\ \mathrm{{ }}\;{{\bar{\Phi }}_{34}}= & {} {e^{ - 2\alpha {h_2}}}{{{\bar{S}}}_{2i}},\mathrm{{ }}\;{{\bar{\Phi }}_{35}} = 0, \;{{\bar{\Phi }}_{44}} = - {e^{ - 2\alpha {h_2}}}{{{\bar{R}}}_{2i}} - {e^{ - 2\alpha {h_2}}}{{{\bar{Q}}}_{2i}} - {e^{ - 2\alpha {h_2}}}{{{\bar{D}}}_{2i}},\mathrm{{ }}\;{{\bar{\Phi }}_{45}} = 0,\\ {{\bar{\Phi }}_{55}}= & {} - {{{\bar{Z}}}_i}, \;{\Delta _i} = \sum \limits _{j = 1}^{{2^m}} {{\eta _j}} ({D_j}{K_i} + D_j^ - {H_i}), \;{X_i} = {P_i}^{ - 1},\;{Y_i} = {\Delta _i}{X_i}\\ {{{\bar{Q}}}_{ji}}= & {} {X_i}{Q_{ji}}{X_i},\;{{{\bar{R}}}_{ji}} = {X_i}{R_{ji}}{X_i},\;{{{\bar{Z}}}_i} = {X_i}{Z_i}{X_i},\;{{{\bar{S}}}_{ji}} = {X_i}{S_{ji}}{X_i},\;{{{\bar{D}}}_{ji}} = {X_i}{D_{ji}}{X_i} \\ {{{\hat{R}}}_{1i}}= & {} { h^{ - 2}_1}{{{\tilde{R}}}_{1i}},\;{{{\hat{R}}}_{2i}} ={ h^{ - 2}_{12}}{{{\tilde{R}}}_{2i}},\;{{{\hat{Z}}}_i} = 4*{h^{ - 4}_2}{{{\tilde{Z}}}_i}.\\ b= & {} \max {\lambda _{\max }}({P_i}) + {h_1}\max {\lambda _{\max }}({Q_{1i}}) + {h_2}\max {\lambda _{\max }}({Q_{2i}}) + {h_1}\max {\lambda _{\max }}({D_{1i}}) \\{} & {} \quad + {h_2}\max {\lambda _{\max }}({D_{2i}}) + \frac{{{h^2_1}}}{2}\max {\lambda _{\max }}({R_{1i}}) + \frac{{{h^2_2}}}{2}\max {\lambda _{\max }}({R_{2i}})\\ a= & {} \min {\lambda _{\min }}({P_i}),\;\lambda = \frac{1}{2}(\alpha - \frac{{\ln \mu }}{{{\tau _a}}}). \end{aligned}$$

Then, the closed-loop system (21) is exponentially stable.

Proof

We choose the following LKF

$$\begin{aligned} \begin{aligned} \begin{array}{l} {V_{\sigma (t)}}(t) = {V_1}_{\sigma (t)}(t) + {V_2}_{\sigma (t)}(t) + {V_3}_{\sigma (t)}(t) + {V_4}_{\sigma (t)}(t) + {V_5}_{\sigma (t)}(t) \end{array} \end{aligned} \end{aligned}$$
(27)

where

$$\begin{aligned}{} & {} \begin{array}{l} {V_1}_{\sigma (t)}(t) = {x^\textrm{T}}(t){P_{\sigma (t)}}x(t) \end{array} \end{aligned}$$
(28)
$$\begin{aligned}{} & {} \begin{array}{l} {V_2}_{\sigma (t)}(t) = \int _{t - {h_1}}^t {{x^\textrm{T}}(s){e^{2\alpha (s - t)}}{Q_{1\sigma (t)}}x(s)\textrm{d}s + \int _{t - {h_2}}^t {{x^\textrm{T}}(s){e^{2\alpha (s - t)}}{Q_{2\sigma (t)}}x(s)\textrm{d}s} } \end{array} \end{aligned}$$
(29)
$$\begin{aligned}{} & {} \begin{array}{l} {V_3}_{\sigma (t)}(t) = \int _{t - d(t)}^{t - {h_1}} {{x^\textrm{T}}(s){e^{2\alpha (s - t)}}{D_{1\sigma (t)}}x(s)\textrm{d}s +\int _{t - {h_2}}^{t - d(t)} {{x^\textrm{T}}(s){e^{2\alpha (s - t)}}{D_{2\sigma (t)}}x(s)\textrm{d}s} } \end{array} \end{aligned}$$
(30)
$$\begin{aligned}{} & {} \begin{array}{l} {V_4}_{\sigma (t)}(t) = {h_1} \int _{ - {h_1}}^0 {\int _{t + \theta }^t {{{\dot{x}}^\textrm{T}}(s){e^{2\alpha (s - t)}}{R_{1\sigma (t)}}\dot{x}(s)\textrm{d}s\textrm{d}\theta } }\\ \qquad \qquad \qquad + {h_{12}}\int _{ - {h_2}}^{ - {h_1}} {\int _{t + \theta }^t {{{\dot{x}}^\textrm{T}}(s){e^{2\alpha (s - t)}}{R_{2\sigma (t)}}\dot{x}(s)\textrm{d}s\textrm{d}\theta } } \end{array} \end{aligned}$$
(31)

and

$$\begin{aligned} \begin{aligned} \begin{array}{l} {V_5}_{\sigma (t)}(t) = \frac{{{h^2_2}}}{2} \int _{ - {h_2}}^0 {\int _\theta ^0 {\int _{t + \lambda }^t {{{\dot{x}}^\textrm{T}}(s){e^{2\alpha (s - t)}}{Z_{\sigma (t)}}\dot{x}(s)\textrm{d}s\textrm{d}\lambda \textrm{d}\theta } } } \end{array} \end{aligned} \end{aligned}$$
(32)

The derivative of (27)–(32) is

$$\begin{aligned} \begin{aligned} \begin{array}{l} {{\dot{V}}_i}(t) = {{\dot{V}}_{1i}}(t) + {{\dot{V}}_{2i}}(t) + {{\dot{V}}_{3i}}(t) + {{\dot{V}}_{4i}}(t) + {{\dot{V}}_{5i}}(t) \end{array} \end{aligned} \end{aligned}$$
(33)

where

$$\begin{aligned}{} & {} \begin{array}{l} {{\dot{V}}_{1i}}(t) = 2{x^\textrm{T}}(t){P_i}\dot{x}(t) \end{array} \end{aligned}$$
(34)
$$\begin{aligned}{} & {} \begin{array}{l} {{\dot{V}}_{2i}}(t) = - 2\alpha {V_{2i}}(t) + {x^\textrm{T}}(t){Q_{1i}}x(t) - {x^\textrm{T}}(t - {h_1}){e^{ - 2\alpha {h_1}}}{Q_{1i}}x(t - {h_1})\\ \qquad \qquad \quad + {x^\textrm{T}}(t){Q_{2i}}x(t) - {x^\textrm{T}}(t - {h_2}){e^{ - 2\alpha {h_2}}}{Q_{2i}}x(t - {h_2}) \end{array}\end{aligned}$$
(35)
$$\begin{aligned}{} & {} \begin{array}{l} {{\dot{V}}_{3i}}(t) = - 2\alpha {V_{3i}}(t) - (1 - \dot{d}(t)){x^\textrm{T}}(t - d(t)){e^{ - 2\alpha d(t)}}{\mathrm{{D}}_{1i}}x(t - d(t))\\ \qquad \qquad \quad + {x^\textrm{T}}(t - {h_1}){e^{ - 2\alpha {h_1}}}{\mathrm{{D}}_{1i}}x(t - {h_1})- {x^\textrm{T}}(t - {h_2}){e^{ - 2\alpha {h_2}}}{\mathrm{{D}}_{2i}}x(t - {h_2})\\ \qquad \qquad \quad + (1 - \dot{d}(t)){x^\textrm{T}}(t - d(t)){e^{ - 2\alpha d(t)}}{\mathrm{{D}}_{2i}}x(t - d(t)) \end{array} \end{aligned}$$
(36)
$$\begin{aligned}{} & {} \begin{array}{l} {{\dot{V}}_{4i}}(t) = - 2\alpha {V_{4i}}(t) + {h^2_1}{{\dot{x}}^\textrm{T}}(t){R_{1i}}\dot{x}(t) - {h_1} \int {{{\dot{x}}^\textrm{T}}(t){R_{1i}}\dot{x}(t)} \\ \qquad \qquad \quad - {e^{ - 2\alpha {h_1}}}{{\dot{x}}^\textrm{T}}(t - {h_1}){R_{1i}}\dot{x}(t - {h_1})\textrm{d}t+ {h^2_{12}}{{\dot{x}}^\textrm{T}}(t){R_{2i}}\dot{x}(t)\\ \qquad \qquad \quad - {h_{12}} \int {{{\dot{x}}^\textrm{T}}(t - {h_1}){R_{2i}}\dot{x}(t - {h_1})} - {e^{ - 2\alpha {h_2}}}{{\dot{x}}^\textrm{T}}(t - {h_2}){R_{2i}}\dot{x}(t - {h_2})\textrm{d}t \end{array} \end{aligned}$$
(37)

and

$$\begin{aligned} \begin{aligned} \begin{array}{l} {{\dot{V}}_{5i}}(t) = - 2\alpha {V_{5i}}(t) + \frac{{{h^4_2}}}{4}{{\dot{x}}^\textrm{T}}(t){Z_i}\dot{x}(t) - \frac{{{h^2_2}}}{2} \int _{ - {h_2}}^0 {\int _{t + \theta }^t {{{\dot{x}}^\textrm{T}}(s){e^{2\alpha (s - t)}}{Z_i}\dot{x}(s)} } \textrm{d}s\textrm{d}\theta \end{array} \end{aligned}\nonumber \\ \end{aligned}$$
(38)

Then, it can be derived

$$\begin{aligned} \begin{aligned} \begin{array}{l} {{\dot{V}}_i}(t) \le 2{x^\textrm{T}}(t){P_i}\dot{x}(t)\\ \qquad \qquad \; - 2\alpha {V_{2i}}(t) + {x^\textrm{T}}(t){Q_{1i}}x(t) - {x^\textrm{T}}(t - {h_1}){e^{ - 2\alpha {h_1}}}{Q_{1i}}x(t - {h_1})\\ \qquad \qquad \; + {x^\textrm{T}}(t){Q_{2i}}x(t) - {x^\textrm{T}}(t - {h_2}){e^{ - 2\alpha {h_2}}}{Q_{2i}}x(t - {h_2})\\ \qquad \qquad \; - 2\alpha {V_{3i}}(t) + {x^\textrm{T}}(t - {h_1}){e^{ - 2\alpha {h_1}}}{\mathrm{{D}}_{1i}}x(t - {h_1}) \\ \qquad \qquad \; - (1 - d_{\max }){x^\textrm{T}}(t - d(t)){e^{ - 2\alpha {h_2}}}{\mathrm{{D}}_{1i}}x(t - d(t))\\ \qquad \qquad \; - {x^\textrm{T}}(t - {h_2}){e^{ - 2\alpha {h_2}}}{\mathrm{{D}}_{2i}}x(t - {h_2}) \\ \qquad \qquad \;+ (1 + d_{\max }){x^\textrm{T}}(t - d(t)){e^{ - 2\alpha {h_2}}}{\mathrm{{D}}_{2i}}x(t - d(t))\\ \qquad \qquad \;- 2\alpha {V_{4i}}(t) + h_1^2{{\dot{x}}^\textrm{T}}(t){R_{1i}}\dot{x}(t) - {h_1} \int _{t - {h_1}}^t {{{\dot{x}}^\textrm{T}}(s){e^{ - 2\alpha {h_1}}}{R_{1i}}\dot{x}(s)} \textrm{d}s\\ \qquad \qquad \;+ {h^2_{12}}{{\dot{x}}^\textrm{T}}(t){R_{2i}}\dot{x}(t) - {h_{12}} \int _{t - {h_2}}^{t - {h_1}} {{{\dot{x}}^\textrm{T}}(s){e^{ - 2\alpha {h_2}}}{R_{2i}}\dot{x}(s)} \textrm{d}s\\ \qquad \qquad \;- 2\alpha {V_{5i}}(t) + \frac{{{h^4_2}}}{4}{{\dot{x}}^\textrm{T}}(t){Z_i}\dot{x}(t) - \frac{{{h^2_2}}}{2} \int _{ - {h_2}}^0 {\int _{t + \theta }^t {{{\dot{x}}^\textrm{T}}(s){Z_i}\dot{x}(s)} } \textrm{d}s\textrm{d}\theta \end{array} \end{aligned} \end{aligned}$$
(39)

To make the stability criterion less conservative, Lemmas 1 and 2 are used to deal with the integral term,

$$\begin{aligned} \begin{aligned} \begin{array}{l} - {h_1} \int _{t - {h_1}}^t {{{\dot{x}}^\textrm{T}}(s){e^{ - 2\alpha {h_1}}}{R_{1i}}\dot{x}(s)} \textrm{d}s\\ \quad = - {h_1} \int _{t - d(t)}^t {{{\dot{x}}^\textrm{T}}(s){e^{ - 2\alpha {h_1}}}{R_{1i}}\dot{x}(s)} \textrm{d}s - {h_1}\int _{t - {h_1}}^{t - d(t)} {{{\dot{x}}^\textrm{T}}(s){e^{ - 2\alpha {h_1}}}{R_{1i}}\dot{x}(s)} \textrm{d}s\\ \quad \le - {e^{ - 2\alpha {h_1}}}\left( {\frac{{{h_1}}}{{d(t)}}{{(x(t) - x(t - d(t)))}^\textrm{T}}{R_{1i}}(x(t) - x(t - d(t))) } \right. \\ \qquad + \left. {\frac{{{h_1}}}{{{h_1} - d(t)}}{{(x(t - d(t)) - x(t - {h_1}))}^\textrm{T}}{R_{1i}}(x(t - d(t)) - x(t - {h_1}))} \right) \\ \quad = - {e^{ - 2\alpha {h_1}}}{\left[ {\begin{array}{*{20}{c}} {x(t) - x(t - d(t))}\\ {x(t - d(t)) - x(t - {h_1})} \end{array}} \right] ^\textrm{T}}\left[ {\begin{array}{*{20}{c}} {\frac{{{h_1}}}{{d(t)}}{R_{1i}}}&{}0\\ 0&{}{\frac{{{h_1}}}{{{h_1} - d(t)}}{R_{1i}}} \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {x(t) - x(t - d(t))}\\ {x(t - d(t)) - x(t - {h_1})} \end{array}} \right] \\ \quad \le - {e^{ - 2\alpha {h_1}}}{\left[ {\begin{array}{*{20}{c}} {x(t) - x(t - d(t))}\\ {x(t - d(t)) - x(t - {h_1})} \end{array}} \right] ^\textrm{T}}\left[ {\begin{array}{*{20}{c}} {{R_{1i}}}&{}{{S_{1i}}}\\ *&{}{{R_{1i}}} \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {x(t) - x(t - d(t))}\\ {x(t - d(t)) - x(t - {h_1})} \end{array}} \right] \end{array} \end{aligned} \end{aligned}$$

In the same way, we have

$$\begin{aligned} \begin{aligned} \begin{array}{l} - {h_{12}} \int _{t - {h_2}}^{t - {h_1}} {{{\dot{x}}^\textrm{T}}(s){e^{ - 2\alpha {h_2}}}{R_{2i}}\dot{x}(s)} \textrm{d}s\\ \quad \le - {e^{ - 2\alpha {h_2}}}{\left[ {\begin{array}{*{20}{c}} {x(t - {h_1}) - x(t - d(t))}\\ {x(t - d(t)) - x(t - {h_2})} \end{array}} \right] ^\textrm{T}}\left[ {\begin{array}{*{20}{c}} {{R_{2i}}}&{}{{S_{2i}}}\\ *&{}{{R_{2i}}} \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {x(t - {h_1}) - x(t - d(t))}\\ {x(t - d(t)) - x(t - {h_2})} \end{array}} \right] \end{array} \end{aligned} \end{aligned}$$

For the double integral, using Lemma 1, we can obtain

$$\begin{aligned} \begin{aligned} \begin{array}{l} -\frac{{{h^2_2}}}{2} \int _{ - {h_2}}^0 {\int _{t + \theta }^t {{{\dot{x}}^\textrm{T}}(s){Z_i}\dot{x}(s)} } \textrm{d}s\textrm{d}\theta \le - \int _{ - {h_2}}^0 {\int _{t + \theta }^t {{{\dot{x}}^\textrm{T}}(s)} } \textrm{d}s\textrm{d}\theta {Z_i}\int _{ - {h_2}}^0 {\int _{t + \theta }^t {{{\dot{x}}^\textrm{T}}(s)} } \textrm{d}s\textrm{d}\theta \\ \quad \le - {({h_2}x(t) - \int _{t - {h_2}}^t {x(s)} \textrm{d}s)^\textrm{T}}{Z_i}({h_2}x(t) - \int _{t - {h_2}}^t {x(s)} \textrm{d}s) \end{array} \end{aligned} \end{aligned}$$

By the above derivation, it can be concluded that

$$\begin{aligned} \begin{aligned} \begin{array}{l} {{\dot{V}}_i}(t) + 2\alpha {V_{i}}(t) \le 2{x^\textrm{T}}(t){P_i}\dot{x}(t) + 2\alpha {x^\textrm{T}}(t){P_i}x(t)\\ \quad + {x^\textrm{T}}(t){Q_{1i}}x(t) - {x^\textrm{T}}(t - {h_1}){e^{ - 2\alpha {h_1}}}{Q_{1i}}x(t - {h_1})\\ \quad + {x^\textrm{T}}(t){Q_{2i}}x(t) - {x^\textrm{T}}(t - {h_2}){e^{ - 2\alpha {h_2}}}{Q_{2i}}x(t - {h_2})\\ \quad + {x^\textrm{T}}(t - {h_1}){e^{ - 2\alpha {h_1}}}{\mathrm{{D}}_{1i}}x(t - {h_1}) \\ \quad - (1 - d_{\max }){x^\textrm{T}}(t - d(t)){e^{ - 2\alpha {h_2}}}{\mathrm{{D}}_{1i}}x(t - d(t))\\ \quad - {x^\textrm{T}}(t - {h_2}){e^{ - 2\alpha {h_2}}}{\mathrm{{D}}_{2i}}x(t - {h_2}) \\ \quad + (1 + d_{\max }){x^\textrm{T}}(t - d(t)){e^{ - 2\alpha {h_2}}}{\mathrm{{D}}_{2i}}x(t - d(t))\\ \quad - {e^{ - 2\alpha {h_1}}}{\left[ {\begin{array}{*{20}{c}} {x(t) - x(t - d(t))}\\ {x(t - d(t)) - x(t - {h_1})} \end{array}} \right] ^\textrm{T}}\left[ {\begin{array}{*{20}{c}} {{R_{1i}}}&{}{{S_{1i}}}\\ *&{}{{R_{1i}}} \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {x(t) - x(t - d(t))}\\ {x(t - d(t)) - x(t - {h_1})} \end{array}} \right] \\ \quad - {e^{ - 2\alpha {h_2}}}{\left[ {\begin{array}{*{20}{c}} {x(t - {h_1}) - x(t - d(t))}\\ {x(t - d(t)) - x(t - {h_2})} \end{array}} \right] ^\textrm{T}}\left[ {\begin{array}{*{20}{c}} {{R_{2i}}}&{}{{S_{2i}}}\\ *&{}{{R_{2i}}} \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {x(t - {h_1}) - x(t - d(t))}\\ {x(t - d(t)) - x(t - {h_2})} \end{array}} \right] \\ \quad + {{\dot{x}}^\textrm{T}}(t)(\frac{{{h^4_2}}}{4}{Z_i} + {h^2_1}{R_{1i}} + {h^2_{12}}{R_{2i}})\dot{x}(t)\\ \quad - {({h_2}x(t) - \int _{t - {h_2}}^t {x(s)} \textrm{d}s)^\textrm{T}}{Z_i}({h_2}x(t) - \int _{t - {h_2}}^t {x(s)} \textrm{d}s) \end{array} \end{aligned} \end{aligned}$$

Then, it can be derived

$$\begin{aligned} \begin{aligned}&{\dot{V}_i}(t) + 2\alpha {V_i}(t) \le {\xi ^\textrm{T}}{\Omega '_i}\xi \\ \quad {\Omega '_i}&= \left[ {\begin{array}{*{20}{c}} {{\Phi '_{11}}}&{}{{\Phi '_{12}}}&{}{{\Phi _{13}}}&{}{{\Phi _{14}}}&{}{{\Phi _{15}}}\\ *&{}{{\Phi '_{22}}}&{}{{\Phi _{23}}}&{}{{\Phi _{24}}}&{}{{\Phi _{25}}}\\ *&{}*&{}{{\Phi _{33}}}&{}{{\Phi _{34}}}&{}{{\Phi _{35}}}\\ *&{}*&{}*&{}{{\Phi _{44}}}&{}{{\Phi _{45}}}\\ *&{}*&{}*&{}*&{}{{\Phi _{55}}} \end{array}} \right] < 0 \end{aligned} \end{aligned}$$
(40)

where

$$\begin{aligned} {\Phi '_{11}}= & {} 2\alpha {P_i} + {P_i}{{{\tilde{A}}}_i} + {{{\tilde{A}}}_i}^\textrm{T}{P_i} + {Q_{1i}} + {Q_{2i}} + {{{\tilde{A}}}_i}^\textrm{T}{N_i}{{{\tilde{A}}}_i} + {h^2_2}{Z_i} - {e^{ - 2\alpha {h_1}}}{R_{1i}},\\ {\Phi '_{12}}= & {} {P_i}{C_i} + {e^{ - 2\alpha {h_1}}}{R_{1i}} - {e^{ - 2\alpha {h_1}}}{S_{1i}} + {{{\tilde{A}}}_i}^\textrm{T}{N_i}{C_i}\mathrm{{, }}\\ {\Phi '_{22}}= & {} C_i^\textrm{T}{N_i}{C_i} + 2{e^{ - 2\alpha {h_1}}}{S_{1i}} - 2{e^{ - 2\alpha {h_1}}}{R_{1i}} + 2{e^{ - 2\alpha {h_2}}}{S_{2i}} - 2{e^{ - 2\alpha {h_2}}}{R_{2i}}, \\ {\Delta _i}= & {} \sum \limits _{j = 1}^{{2^m}} {{\eta _j}} ({D_j}{K_i} + D_j^ - {H_i}), \;{{{\tilde{A}}}_i} = {A_i} + {B_i}{\Delta _i},\\ {N_i}= & {} {h^2_1}{R_{1i}} + {h^2_{12}}{R_{2i}} + \frac{{{h^4_2}}}{4}{Z_i},\\ {\xi ^\textrm{T}}= & {} (x(t)\mathrm{{ }},\ x(t - d(t))\mathrm{{ }},\ x(t - {h_1})\mathrm{{ }},\ x(t - {h_2})\mathrm{{ }},\ \int _{t - {h_2}}^t {x(s)} \textrm{d}s). \end{aligned}$$

Using the Schur complement lemma, \( {\Omega '_i} < 0 \) equals

$$\begin{aligned} {\Omega '_i}&= \left[ {\begin{array}{*{20}{c}} {{{\hat{\Phi }}_{11}}}&{}{{{\hat{\Phi }}_{12}}}&{}{{\Phi _{13}}}&{}{{\Phi _{14}}}&{}{{\Phi _{15}}}\\ *&{}{{{\hat{\Phi }}_{22}}}&{}{{\Phi _{23}}}&{}{{\Phi _{24}}}&{}{{\Phi _{25}}}\\ *&{}*&{}{{\Phi _{33}}}&{}{{\Phi _{34}}}&{}{{\Phi _{35}}}\\ *&{}*&{}*&{}{{\Phi _{44}}}&{}{{\Phi _{45}}}\\ *&{}*&{}*&{}*&{}{{\Phi _{55}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{{{\tilde{A}}}_i}^\textrm{T}{N_i}{{{\tilde{A}}}_i}}&{}{{{{\tilde{A}}}_i}^\textrm{T}{N_i}{C_i}}&{}0&{}0&{}0\\ *&{}{C_i^\textrm{T}{N_i}{C_i}}&{}0&{}0&{}0\\ *&{}*&{}0&{}0&{}0\\ *&{}*&{}*&{}0&{}0\\ *&{}*&{}*&{}*&{}0 \end{array}} \right] \nonumber \\&= \left[ {\begin{array}{*{20}{c}} {{{\hat{\Phi }}_{11}}}&{}{{{\hat{\Phi }}_{12}}}&{}{{\Phi _{13}}}&{}{{\Phi _{14}}}&{}{{\Phi _{15}}}\\ *&{}{{{\hat{\Phi }}_{22}}}&{}{{\Phi _{23}}}&{}{{\Phi _{24}}}&{}{{\Phi _{25}}}\\ *&{}*&{}{{\Phi _{33}}}&{}{{\Phi _{34}}}&{}{{\Phi _{35}}}\\ *&{}*&{}*&{}{{\Phi _{44}}}&{}{{\Phi _{45}}}\\ *&{}*&{}*&{}*&{}{{\Phi _{55}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{{{\tilde{A}}}_i}^\textrm{T}{P_i}}&{}{{{{\tilde{A}}}_i}^\textrm{T}{P_i}}&{}{{{{\tilde{A}}}_i}^\textrm{T}{P_i}}\\ {C_i^\textrm{T}{P_i}}&{}{C_i^\textrm{T}{P_i}}&{}{C_i^\textrm{T}{P_i}}\\ 0&{}0&{}0\\ 0&{}0&{}0\\ 0&{}0&{}0 \end{array}} \right] \nonumber \\&\quad \times {\left[ {\begin{array}{*{20}{c}} {H1}&{}0&{}0\\ *&{}{H12}&{}0\\ *&{}*&{}{H2} \end{array}} \right] ^{ - 1}}\left[ {\begin{array}{*{20}{c}} {{P_i} {{{\tilde{A}}}_i}}&{}{{P_i}{C_i}}&{}0&{}0&{}0\\ {{P_i} {{{\tilde{A}}}_i}}&{}{{P_i}{C_i}}&{}0&{}0&{}0\\ {{P_i} {{{\tilde{A}}}_i}}&{}{{P_i}{C_i}}&{}0&{}0&{}0 \end{array}} \right] \nonumber \\&= \left[ {\begin{array}{*{20}{c}} {{{\hat{\Phi }}_{11}}}&{}{{{\hat{\Phi }}_{12}}}&{}{{\Phi _{13}}}&{}{{\Phi _{14}}}&{}{{\Phi _{15}}}&{}{ {{{\tilde{A}}}_i}^\textrm{T}{P_i}}&{}{ {{{\tilde{A}}}_i}^\textrm{T}{P_i}}&{}{ {{{\tilde{A}}}_i}^\textrm{T}{P_i}}\\ *&{}{{{\hat{\Phi }}_{22}}}&{}{{\Phi _{23}}}&{}{{\Phi _{24}}}&{}{{\Phi _{25}}}&{}{C_i^\textrm{T}{P_i}}&{}{C_i^\textrm{T}{P_i}}&{}{C_i^\textrm{T}{P_i}}\\ *&{}*&{}{{\Phi _{33}}}&{}{{\Phi _{34}}}&{}{{\Phi _{35}}}&{}0&{}0&{}0\\ *&{}*&{}*&{}{{\Phi _{44}}}&{}{{\Phi _{45}}}&{}0&{}0&{}0\\ *&{}*&{}*&{}*&{}{{\Phi _{55}}}&{}0&{}0&{}0\\ *&{}*&{}*&{}*&{}*&{}{H1}&{}0&{}0\\ *&{}*&{}*&{}*&{}*&{}*&{}{H12}&{}0\\ *&{}*&{}*&{}*&{}*&{}*&{}*&{}{H2} \end{array}} \right] < 0 \end{aligned}$$
(41)

where

$$\begin{aligned} \begin{aligned} \begin{array}{l} {{\hat{\Phi }}_{11}} = 2\alpha {P_i} + {P_i}{A_i} + A_i^\textrm{T}{P_i} + {Q_{1i}} + {Q_{2i}} + {P_i}{B_i}{\Delta _i} + \Delta _i^\textrm{T}B_i^\textrm{T}{P_i} + {h_2}^2{Z_i} - {e^{ - 2\alpha {h_1}}}{R_{1i}},\\ {{\hat{\Phi }}_{12}} = {P_i}{C_i} + {e^{ - 2\alpha {h_1}}}{R_{1i}} - {e^{ - 2\alpha {h_1}}}{S_{1i}}\mathrm{{, }}\;{\Phi _{13}} = {e^{ - 2\alpha {h_1}}}{S_{1i}}\mathrm{{, }}\;{\Phi _{14}} = 0,\mathrm{{ }}\;{\Phi _{15}} = {h_2}{Z_i},\\ {{\hat{\Phi }}_{22}} = 2{e^{ - 2\alpha {h_1}}}{S_{1i}} - 2{e^{ - 2\alpha {h_1}}}{R_{1i}} + 2{e^{ - 2\alpha {h_2}}}{S_{2i}} - 2{e^{ - 2\alpha {h_2}}}{R_{2i}} - (1 - d_{\max }){e^{ - 2\alpha {h_2}}}{D_{1i}}\\ \qquad \quad + (1 + d_{\max }){e^{ - 2\alpha {h_2}}}{D_{2i}}, \;H12 = - {h^{- 2}_{12}}{({P_i}^{ - 1}{R_{2i}}{P_i}^{ - 1})^{ - 1}},\\ H\mathrm{{1 = }}-{h^{ - 2}_1}{({P_i}^{ - 1}{R_{1i}}{P_i}^{ - 1})^{ - 1}},\;H2 = - 4*{h^{- 4}_2}{({P_i}^{ - 1}{Z_i}{P^{ - 1}}_i)^{ - 1}}. \end{array} \end{aligned} \end{aligned}$$

For convenience, let

$$\begin{aligned} \begin{aligned}&{X_i} = {P_i}^{ - 1},\;{Y_i} = {\Delta _i}{X_i},\;{{\bar{Q}}_{ji}} = {X_i}{Q_{ji}}{X_i},\;{{\bar{R}}_{ji}} = {X_i}{R_{ji}}{X_i},\\&{{\bar{Z}}_i} = {X_i}{Z_i}{X_i},\;{{\bar{S}}_{ji}} = {X_i}{S_{ji}}{X_i},\;{{\bar{D}}_{ji}} = {X_i}{D_{ji}}{X_i} \end{aligned} \end{aligned}$$

Then, left multiplying and right multiplying inequality (41) by \(\textrm{diag }\{X_i,\ X_i,\ X_i,\ X_i,\ X_i, \ X_i, \ X_i,\ X_i\}\), we can obtain

$$\begin{aligned} \begin{aligned} \left[ {\begin{array}{*{20}{c}} {{{\bar{\Phi }}_{11}}}&{}{{{\bar{\Phi }}_{12}}}&{}{{{\bar{\Phi }}_{13}}}&{}{{{\bar{\Phi }}_{14}}}&{}{{{\bar{\Phi }}_{15}}}&{}{{X_i}{{{\tilde{A}}}_i}^\textrm{T} }&{}{{X_i}{{{\tilde{A}}}_i}^\textrm{T} }&{}{{X_i}{{{\tilde{A}}}_i}^\textrm{T} }\\ *&{}{{{\bar{\Phi }}_{22}}}&{}{{{\bar{\Phi }}_{23}}}&{}{{{\bar{\Phi }}_{24}}}&{}{{{\bar{\Phi }}_{25}}}&{}{{X_i}{C_i}^\textrm{T}}&{}{{X_i}{C_i}^\textrm{T}}&{}{{X_i}{C_i}^\textrm{T}}\\ *&{}*&{}{{{\bar{\Phi }}_{33}}}&{}{{{\bar{\Phi }}_{34}}}&{}{{{\bar{\Phi }}_{35}}}&{}0&{}0&{}0\\ *&{}*&{}*&{}{{{\bar{\Phi }}_{44}}}&{}{{{\bar{\Phi }}_{45}}}&{}0&{}0&{}0\\ *&{}*&{}*&{}*&{}{{{\bar{\Phi }}_{55}}}&{}0&{}0&{}0\\ *&{}*&{}*&{}*&{}*&{}{X_i}{H1}{X_i}&{}0&{}0\\ *&{}*&{}*&{}*&{}*&{}*&{}{X_i}{H12}{X_i}&{}0\\ *&{}*&{}*&{}*&{}*&{}*&{}*&{}{X_i}{H2}{X_i} \end{array}} \right] < 0 \end{aligned} \end{aligned}$$
(42)

Consider (24)–(25), the inequality (22) is equivalent to inequality (42). When \({\bar{\Omega }_i} < 0\), we have \({\dot{V}_i}(t) + 2\alpha {V_i}(t) < 0\) which means

$$\begin{aligned} \begin{aligned} {V_{\sigma (t)}}({x(t)}) \le {V_{\sigma (t)}}({x({{t_k}})}){e^{ - 2\alpha (t - {t_k})}},\ t \in [{t_k},\ {t_{k + 1}}) \end{aligned} \end{aligned}$$
(43)

where \(t_k\) denotes the switched time, \({t_0}< {t_1}< {t_2}< \cdots {t_k}< {t_{k + 1}} < \cdots \).

According to condition (26), we can obtain

$$\begin{aligned} \begin{aligned} {V_{\sigma ({t_k})}}({x({{t_k}})}) \le \mu {V_{\sigma ({t_{{k^ - }}})}}({x({{t_{{k^ - }}}})}) \end{aligned} \end{aligned}$$

where \(t_{{k^ - }}\) denotes the left limit of \(t_k\).

Let \(k = {N_{\sigma ({t_0},\ t)}} \le t - {t_0}/{T_\alpha }\), we have

$$\begin{aligned} \begin{aligned} \begin{array}{l} V({x(t)}) \le {e^{ - 2\alpha (t - {t_k})}}\mu {V_{\sigma ({t_k}^ - )}}({x({{t_k}^ - })}) \le \ldots \le {e^{ - 2\alpha (t - {t_0})}}{\mu ^k}{V_{\sigma ({t_0})}}({x({{t_0}})})\\ \qquad \;\le {e^{ - (2\alpha - \ln \mu /{T_\alpha })(t - {t_0})}}{V_{\sigma ({t_0})}}({x({{t_0}})}) \end{array} \end{aligned} \end{aligned}$$

According to Definition 1, we can obtain

$$\begin{aligned} \begin{aligned} \left\| {{x(t)}} \right\| \le \sqrt{\frac{a}{b}} {e^{ - \lambda (t - {t_0})}}\left\| {{x(0)}} \right\| \end{aligned} \end{aligned}$$
(44)

Therefore, the above closed-loop system (21) is exponentially stable. \(\square \)

Remark 2

Comparing with the existed results, our methods focused on utilizing time-delay information. In the design of LKF, it takes into account both the lower bound information and the rate of change of the time delay, aiming to reduce conservatism. By reducing conservatism, that is, the time-delay upper bound is raised, allowing for a wider range of time-delay signals.

4 Numerical Simulation

Consider system (1) with the following parameters

$$\begin{aligned} \begin{aligned} \begin{array}{l} {A_1} = \left[ {\begin{array}{*{20}{c}} 0&{}1\\ {17.2941}&{}0 \end{array}} \right] , \;{A_2} = \left[ {\begin{array}{*{20}{c}} 0&{}1\\ {0.2396}&{}0 \end{array}} \right] , \;{B_1} = \left[ {\begin{array}{*{20}{c}} 0\\ { - 0.1765} \end{array}} \right] , \;{B_2} = \left[ {\begin{array}{*{20}{c}} 0\\ { - 0.0052} \end{array}} \right] ,\\ \\ {C_1} = \left[ {\begin{array}{*{20}{c}} 0&{}{0.8}\\ 0&{}{0.21} \end{array}} \right] , \;{C_2} = \left[ {\begin{array}{*{20}{c}} 0&{}{0.8}\\ 0&{}{0.18} \end{array}} \right] , \;{h_1} = 0,\;\alpha = 0.5. \end{array} \end{aligned} \end{aligned}$$

Choose \(d_{\max } = 0.5\) and apply Theorem 2, we can calculate

$$\begin{aligned} \begin{aligned} \begin{array}{l} {P_1} = \left[ {\begin{array}{*{20}{c}} {0.3359}&{}{0.1852}\\ {0.1852}&{}{0.8593} \end{array}} \right] ,\;{P_2} = \left[ {\begin{array}{*{20}{c}} {0.3359}&{}{0.1852}\\ {0.1852}&{}{0.8589} \end{array}} \right] ,\\ \\ \mu = 6.9178,\; {\tau _a} > {\tau _a}^* = 3.868,\; \lambda = 0.00823. \end{array} \end{aligned} \end{aligned}$$

Then, we can obtain

$$\begin{aligned} \begin{aligned} \left\| {{x(t)}} \right\| \le 1.829{e^{ - 0.00823(t - {t_0})}}\left\| {{x(0)}} \right\| \end{aligned} \end{aligned}$$
Table 1 The \({h_2}\) for different \(d_{\max }\) and \({h_1} = 0\)
Full size table
Fig. 1
figure 1

Switched signal

Full size image
Fig. 2
figure 2

Time-delay signal

Full size image
Fig. 3
figure 3

System state with \(d_{\max }=0.5\) and \(h_2=2.300\)

Full size image
Fig. 4
figure 4

System state with \(d_{\max }=0.1\) and \(h_2=3.870\)

Full size image
Fig. 5
figure 5

System state with \(d_{\max }=0.9\) and \(h_2=1.990\)

Full size image
Fig. 6
figure 6

Control input

Full size image

It can be seen from Table 1 that the larger value of \(d_{\max }\) is, the larger the upper bound of the time-delay increases by introducing the triple integral term.

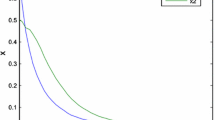
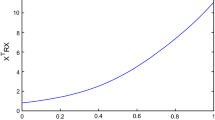
The initial value is \({x_0} = \left[ {\begin{array}{*{20}{c}} 2&{ - 2} \end{array}} \right] ^\textrm{T}\). The simulation results are as follows. The switched signal \(\sigma (t)\) of the system is shown in Fig. 1. The time-delay signal of the system is shown in Fig. 2. Figure 3 shows the system state with \(d_{\max }=0.5\), and we can see that the closed-loop system is stable. Figures 4 and 5 show the system state with \(d_{\max }=0.1\) and \(d_{\max }=0.9\), and we can see that the closed-loop system is stable. Figure 6 represents the control input, and we can see that the control input is not saturated.

5 Conclusion

In this paper, the stability criterion and controller design for the time-delay switched systems with input saturation are investigated based on an improved LKF. Based on constructing LKF with triple integral term and making full use of the delay lower bound information, the sufficient conditions for the exponential stability of the system are given. A state feedback controller is designed for the input-saturated switched system. The symmetric delay rate problem is considered to accurately define the derivative of LKF, which reduces the conservatism of the system. Finally, the effectiveness of the method is verified by the numerical examples. In future work, we will study the stability analysis for switched system with random saturation and actuator failure.