Finite-Time Stability and Boundedness of Switched Systems with Finite-Time Unstable Subsystems

Abstract

In this paper, problems covering finite-time stability and boundedness of switched systems with finite-time unstable subsystems are researched through the method of multi-Lyapunov function. On basis of the mode-dependent average dwell time method, the systems are required to meet the standards of remaining finite-time stable and finite-time bounded through the practice of designing the switching signal for finite-time stable and unstable subsystems respectively. Finally, stabilization conditions for switched linear systems based on linear matrix inequalities are presented to guarantee the finite-time stability of the closed-loop system. Numerical examples are put forward attempting to verify the efficiency through different methodologies.

1 Introduction

Switched system refers to a typical hybrid system consisting of different subsystems described by differential, difference equations and a switching law that orchestrates switching between these subsystems. In accordance with requirements from many practical applications (for example, flight control systems [24], complex dynamical network systems [24]), rapid developments of switched systems have been realized both on theoretical and practical basis in the last decades [7, 18, 21, 25, 31]. Based on Lyapunov stability of switched systems, the researches [6, 12, 13, 30] show the qualitative behavior of switched systems over an infinite time interval. In order to achieve the Lyapunov stability of switched systems, time-dependent switching law applied frequently in many researches, such as dwell time (DT) [14], average dwell time (ADT) [10] and mode-dependent average dwell time (MDADT) method [35]. These methods restrict the dwell time of each subsystem to achieve desired performance, which are widely used in various switched systems.

The aforementioned methods mainly focus on the switched systems composed by stable subsystems. However, on practical basis, the switched systems with both stable subsystems and unstable subsystems are implemented widely such as controller failures, sensor faults encountered in terms of engineering, giving rise to system models with unstable subsystems. For such switched systems, Yin et al. research the Lyapunov stability and stabilization problems in [28] through a new class of switching signal based on MDADT which gives upper bounds of dwell time for stable subsystems and the lower bounds of dwell time for unstable subsystems.

Considering of most practical applications, the main concern lies in behavior of the system over a fixed finite-time interval. For example, the system state can only be acceptable under the limitation of saturations [3]. Therefore, it is greatly meaningful to define the stability of system whose state remains within prescribed bounds in the given finite-time interval. Under this purpose, finite-time stability was studied in desirable approaches more from the view of academic in [9, 23].

In comparison with Lyapunov stability, finite-time stability (FTS) concentrates on the transient behavior of a system over a finite time interval. A great number of researches [2, 34] have delivered great attention on the light of linear matrix inequality theory. In [1, 3, 4] some conditions suitable for finite-time stability and stabilization of systems have been provided. In addition, [1, 3] have extended the concept of finite-time stability to that of finite-time boundedness. In [2, 34], authors have presented some results of finite-time stability for the systems with impulsive effects or jumps. In [8], authors introduced the concept of finite-time stability into the switched linear systems for the first time. However, it should be pointed out that the definition of finite-time stability in the above-mentioned literature is equal to the boundedness of the state within a given bound under a fixed time interval if the initial state condition is bounded by a prescribed constant. There is another kind of finite-time stability, requiring that the system be Lyapunov stable and the state converge to equilibrium point in a finite time interval, see [5, 15,16,17].

Recently, the FTS problem of switched systems composed by stable and unstable subsystems has been studied. However, these researches are mostly confined to asymptotic unstable subsystems, like [11] considering the switched systems with finite-time unstable subsystems for the first time. To achieve finite-time stability of such switched systems, they used ADT to obtain the lower bound of stable subsystems dwell time, and presented a total dwell time for all these unstable subsystems. Without the dwell time of each subsystem, the result is not convenient to be applied. Therefore, in order to reduce inconvenience, a dwell time should be required for every subsystem. Moreover, it has been shown in studies [27, 29, 36] that MDADT switching signal is more applicable in practice than ADT switching signal, and less conservative. Therefore, MDADT switching strategy used for analyzing finite-time stability of switched systems with finite-time unstable subsystems is meaningful to be implemented, promoting conduction of this research.

Considering of different effects produced by the finite-time stable systems and the finite-time unstable subsystems, we designed the switching signal for finite-time stable and unstable subsystems respectively in this paper. Sufficient conditions are presented, functioning as making the switched nonlinear systems with finite-time unstable subsystems finite-time stable. In the following section, this paper makes a further research on the problem of finite-time boundedness of switched nonlinear systems with disturbance. The FTS and FTB problems of linear systems are studied as special cases of nonlinear systems. Meanwhile, these results are offered briefly in the form of corollary. Finally, stabilization conditions of switched linear systems with finite-time unstable subsystems are given in linear matrix inequalities (LMIs).

To be specific, the structure of this paper is illustrated in the following part. In Sect. 2, necessary definitions of finite-time stability and boundedness for switched nonlinear systems are introduced, along with presentation of some problem formulations. As the significant part in this paper, Sect. 3 mainly deals with finite-time stability problem, finite-time boundedness problem and stabilization problem of switched systems with finite-time unstable subsystems. Eventually, corresponding conclusions are presented. Numerical examples are provided in Sect. 4 to demonstrate the feasibility and effectiveness of the proposed technique while the Sect. 5 points out the final conclusions.

Notations In this paper, we use $P>0$ to denote a symmetric positive definite matrix. $\lambda _{\max }(P)$ and $\lambda _{\min }(P)$ denote the maximum and minimum eigenvalues of symmetric positive definite matrix. The identity matrix of order n is denoted as $I_n$ (or I, if no confusion arises). $N^+$ denotes the positive integer.

2 Preliminary

Consider the switched nonlinear system as follows:

$$\begin{aligned} \begin{array}{l} \dot{x}(t)=f_{\sigma (t)}(x(t))\\ x(0)=x_0 \end{array} \end{aligned}$$

(1)

where $x(t)\in R^n$ is the state, $\sigma (t):[0,\infty )\rightarrow M=\{1,2,\ldots ,m\}$ is the switching signal which is a piecewise constant function depending on time t, $m\in N^+$. $f_i(\cdot )$ for any $i\in M$ is locally Lipichitz continuous, and positive integer m shows the number of the subsystems.

If $f_i(x)=A_ix$ with $A_i$ being the constant real matrices for $i\in M$, system (1) represents a switched linear system as:

$$\begin{aligned} \begin{array}{l} \dot{x}(t)=A_{\sigma (t)}x(t)\\ x(0)=x_0 \end{array} \end{aligned}$$

(2)

The system with disturbance can be described by following equations:

$$\begin{aligned} \begin{array}{l} \dot{x}(t)=f_{\sigma (t)}(x(t))+g_{\sigma (t)}(\omega (t))\\ x(0)=x_0 \end{array} \end{aligned}$$

(3)

where $\omega (t)\in R^r$ is the exogenous disturbance. $\sigma (t):[0,\infty )\rightarrow M=\{1,2,\ldots ,m\}$ is the switching signal. $f_i(\cdot )$ and $g_i(\cdot )$ are locally Lipichitz continuous for any $i\in M$.

If $f_i(x)=A_ix$, $g_i(x)=G_ix$ with $A_i$ and $G_i$ are constant real matrices, system (3) represents a class of switched linear systems with disturbance as:

$$\begin{aligned} \begin{array}{l} \dot{x}(t)=A_{\sigma (t)}x(t)+G_{\sigma (t)}\omega (t)\\ x(0)=x_0 \end{array} \end{aligned}$$

(4)

We only consider the switching signal which has a finite number of switching in any finite interval time. Based on the switching signal $\sigma (t)$, the switching sequence can be described as:

$$\begin{aligned} \{x_0;(i_0,t_0),\ldots ,(i_k,t_k),\ldots |i_k\in M,k=0,1,\ldots \} \end{aligned}$$

(5)

where $t_k$ denotes the kth switching time, and $i_kth$ subsystem is activated at $t_k$.

Assumption 1

The states of switched systems do not jump at the switching instants, i.e., the trajectory x(t) is everywhere continuous, and there are finitely many switches in every finite interval.

Assumption 2

The external disturbance $\omega (t)$ is time-varying and satisfies

$$\begin{aligned} \omega \in \varOmega =\left\{ \omega |\int _0^{T} \omega ^T(t)\omega (t) dt\le d\right\} ,d\ge 0. \end{aligned}$$

(6)

Next, some necessary definitions are reviewed. As usual, in mode-dependent average dwell time (MDADT) method, we denote $\mathscr {S}=\{1,2,\ldots ,s\}$ as the set of finite-time stable subsystems with respect to the required parameters $(c_1,c_2,T_f,R,\sigma )$, $\mathscr {U}=\{s+1,\ldots ,m\}$ denotes the set of finite-time unstable subsystems with respect to the same required parameters $(c_1,c_2,T_f,R, \sigma )$, and $\mathscr {S} \cup \mathscr {U}=M$. Based on the MDADT property, Yin et al. presented the following definitions in [28]:

Definition 1

For a switching signal $\sigma (t)$ and any $t\in [0,T]$, let $N_{\sigma p}(T,t)$ denote the switching number that the pth subsystem is activated over (t, T) and $T_p(T,t)$ denotes the total running time of the pth subsystem over the interval (t, T), $p\in \mathscr {S}$. $\sigma (t)$ is called a switching signal with slow mode-dependent average dwell time (SMDADT) $\tau _{ap}$ if there exist positive numbers $N_{0p}$ (called the mode-dependent chatter bounds) and $\tau _{ap}$ such that

$$\begin{aligned} N_{\sigma p}(T,t)\le N_{0p}+\frac{T_p(T,t)}{\tau _{ap}},\forall t\in [0,T]. \end{aligned}$$

(7)

Definition 2

For a switching signal $\sigma (t)$ and any $t\in [0,T]$, let $N_{\sigma q}(T,t)$ denote the switching number that the qth subsystem is activated over (t, T) and $T_q(T,t)$ denote the total running time of the pth subsystem over the interval (t, T), $q\in \mathscr {U}$. $\sigma (t)$ is called a switching signal with fast mode-dependent average dwell time (FMDADT) $\tau _{aq}$ if there exist positive numbers $N_{0q}$ and $\tau _{aq}$ such that

$$\begin{aligned} N_{\sigma q}(T,t)\ge N_{0q}+\frac{T_q(T,t)}{\tau _{aq}},\forall t\in [0,T]. \end{aligned}$$

(8)

Without loss of generality, we let $N_{0p}=N_{0q}=0$ as [11, 27].

Remark 1

It is easy to noticed the difference between Definitions 1 and 2. We will apply these different methods to finite-time stable subsystems and finite-time unstable subsystems respectively, like [28]. Definition 1 is called slow switching. Requiring

$$\begin{aligned} \begin{array}{c} N_{\sigma p}(T,t)\le N_{0p}+\frac{T_p(T,t)}{\tau _{ap}}\Leftrightarrow \tau _{ap}\le \frac{T_p(T,t)}{N_{\sigma p}(T,t)-N_{0p}},\\ \forall t\in [0,T]. \end{array} \end{aligned}$$

(9)

Conversely, Definition 2 requires

$$\begin{aligned} \begin{array}{c} N_{\sigma q}(T,t)\ge N_{0q}+\frac{T_q(T,t)}{\tau _{aq}}\Leftrightarrow \tau _{aq}\ge \frac{T_q(T,t)}{N_{\sigma q}(T,t)-N_{0p}},\\ \forall t\in [0,T]. \end{array} \end{aligned}$$

(10)

called fast switching.

The definition of finite-time stability and finite-time boundedness of the switched system was proposed by Amato in [3].

Definition 3

Given three positive constants $c_1$, $c_2$ and T, with $c_1<c_2$, a positive definite matrix R, and a given switching signal $\sigma (t)$, switching system (1) is said to be finite-time stable with respect to $(c_1,c_2,T,R,\sigma )$, if

$$\begin{aligned} x_0^T Rx_0\le c_1\Rightarrow x^T(t)Rx(t)\le c_2, \forall t\in (0,T]. \end{aligned}$$

(11)

Definition 4

Given four positive constants $c_1$, $c_2$, Tand d, with $c_1<c_2$, $d \ge 0$, a positive definite matrix R,and a given switching signal $\sigma (t)$, switching system (3) is said to be finite-time bounded with respect to $(c_1,c_2,T,R,\sigma ,d)$, if

$$\begin{aligned} x_0^T Rx_0\le c_1\Rightarrow x^T(t)Rx(t)\le c_2, \forall t\in (0,T],\forall \omega : \int _0^{T} \omega ^T(t)\omega (t) dt\le d. \end{aligned}$$

(12)

3 Main Results

3.1 Finite-Time Stability Analysis

First of all, we introduce a class of quasi-alternative switching signals satisfying the following conditions:

• (a) If $\sigma (t_k)\in \mathscr {S}$, then $\sigma (t_{k+1})\in M$,$\sigma (t_k)\ne \sigma (t_{k+1})$.

• (b) If $\sigma (t_k)\in \mathscr {U}$, then $\sigma (t_{k+1})\in \mathscr {S}$.

This class of switching signals implies that a switched system cannot switch from a finite-time unstable subsystem to another finite-time unstable subsystem. (If we change the condition (a) as: If $\sigma (t_k)\in \mathscr {S}$, then $\sigma (t_{k+1})\in \mathscr {U}$. The switching signal implies that finite-time stable subsystems and finite-time unstable subsystems can switch to each other alternately.)

Next, finite-time stability conditions for switched linear system (1) with finite-time unstable subsystems are given by designing quasi-alternative switching signals with MDADT property.

Theorem 1

Consider the switched nonlinear system (1), and let $\gamma _1$, $\gamma _2$, $\alpha _r>0$, $r\in M$, $\mu _p>1$, $p\in \mathscr {S}$, $0<\mu _q<1$, $q\in \mathscr {U}$ be given constants. Suppose that there are multiply Lyapunov-like functions $V_r(x(t))$ , $r \in M$ such that for $\sigma (t_k)=i$, $\sigma (t_{k+1})=j$, $i \ne j$

$$\begin{aligned} \gamma _1 (||x(t)||^2)\le & {} V_r(x(t))\le \gamma _2 (||x(t)||^2), \forall r\in M, \end{aligned}$$

(13)

$$\begin{aligned} \dot{V_r}(x(t))\le & {} \alpha _rV_r(x(t)),\forall r\in M, \end{aligned}$$

(14)

$$\begin{aligned} V_p(x(t_k))\le & {} \mu _pV_r(x(t_k^-)), \forall p\in \mathscr {S}, \forall r \in M, p\ne r, \end{aligned}$$

(15)

$$\begin{aligned} V_q(x(t_k))\le & {} \mu _qV_p(x(t_k^-)), \forall q\in \mathscr {U}, \forall p\in \mathscr {S}, \end{aligned}$$

(16)

$$\begin{aligned} \frac{\lambda _{\max }(R)\gamma _2}{\lambda _{\min }(R)\gamma _1}< & {} \frac{c_2}{c_1}e^{-\alpha _pT_f}. \end{aligned}$$

(17)

Then, the switched nonlinear systems (1) is finite-time stable with respect to $(c_1,c_2,T_f,R,\sigma )$ for any switching signal with MDADT

$$\begin{aligned} \tau _{ap} \ge \tau _{ap}^*= & {} \frac{T_f\ln \mu _p}{\ln \frac{c_2\lambda _{\max }(R)\gamma _1}{c_1\lambda _{\min }(R)\gamma _2}-\alpha _pT_f}, \end{aligned}$$

(18)

$$\begin{aligned} \tau _{aq} \le \tau _{aq}^*= & {} -\frac{\ln \mu _q}{\alpha _q} \end{aligned}$$

(19)

Proof

For any $t\in [t_k,t_{k+1}]$, we get from (14)that

$$\begin{aligned} \frac{d}{dt}e^{-\alpha _{\sigma (t_k)}t}V_{\sigma (t_k)}(x(t))= e^{-\alpha _it}(\dot{V}_{\sigma (t_k)}(x(t))-\alpha _{\sigma (t_k)}V_{\sigma (t_k)}(x(t)))\le 0. \end{aligned}$$

(20)

Integral on the interval $(t_k,t)$,

$$\begin{aligned} e^{-\alpha _{\sigma (t_k)}t}V_{\sigma (t_k)}(x(t))-e^{-\alpha _{\sigma (t_k)}t_k}V_{\sigma (t_k)}(x(t_k))\le 0\nonumber \\ V_{\sigma (t_k)}(x(t))\le e^{\alpha _{\sigma (t_k)}(t-t_k)}V_{\sigma (t_k)}(x(t_k)) \end{aligned}$$

(21)

by (15), we get

$$\begin{aligned} V_i(x(t))\le \mu _ie^{\alpha _i(t-t_k)}V_j(x(t_k^-))\nonumber \\ \sigma (t_k)=i, \sigma (t_k^-)=j, t\in (t_k,t_{k+1}) \end{aligned}$$

(22)

for $t\in [0,T_f)$,

$$\begin{aligned} V(x(t))\le&\; \mu _{\sigma (t_k)}e^{\alpha _{\sigma (t_k)}(t-t_k)}V_{\sigma (t_{k-1})}(x(t_k^-))\nonumber \\ \le&\; \mu _{\sigma (t_k)}e^{\alpha _{\sigma (t_k)}(t-t_k)}(\mu _{\sigma (t_{k-1})}e^{\alpha _{\sigma (t_k-1)}(t_k-t_{k-1})}V_{\sigma (t_k-2)}(x(t_{k-1}^-))\nonumber \\ =&\prod _p \mu _i^{N_{\sigma p}(0,t)}\prod _q \mu _i^{N_{\sigma q}(0,t)} \exp \left\{ \sum _p\alpha _pT_p(0,t)+\sum _q\alpha _qT_q(0,t)\right\} V_{\sigma (0)}(x(0))\nonumber \\ \le&\; \exp {\sum _p\left( \alpha _p+\frac{\ln \mu _p}{\tau _{ap}}\right) T_p(0,t)+\sum _q\left( \alpha _q+\frac{\ln \mu _q}{\tau _{aq}}\right) T_q(0,t)}V_{\sigma (0)}(x(0))\nonumber \\ \end{aligned}$$

(23)

by(13),we have

$$\begin{aligned} \frac{V(x(t))}{\gamma _2}\le ||x(t)||^2\le \frac{V(x(t))}{\gamma _1} \end{aligned}$$

(24)

so

$$\begin{aligned} x^T(t)Rx(t)&\le \lambda _{\max }(R)||x(t)||^2\le \lambda _{\max }(R)\frac{V(x(t))}{\gamma _1}\nonumber \\&\le \frac{\lambda _{\max }(R)}{\gamma _1}\exp \left\{ \sum _p\left( \alpha _p+\frac{\ln \mu _p}{\tau _{ap}}\right) T_p(0,t)\nonumber \right. \\&\quad \left. +\sum _q\left( \alpha _q+\frac{\ln \mu _q}{\tau _{aq}}\right) T_q(0,t)\right\} V_{\sigma (0)}(x(0)) \end{aligned}$$

(25)

$$\begin{aligned} x^T(0)Rx(0)&\ge \lambda _{\min }(R)||x(0)||^2\ge \lambda _{\min }(R)\frac{V(x(0))}{\gamma _2}\nonumber \\ V_{\sigma (0)}(x(0))&\le \frac{\gamma _2}{\lambda _{\min }(R)}x^T(0)Rx(0) \end{aligned}$$

(26)

Moreover,

$$\begin{aligned} x^T(t)Rx^T(t)&\le \frac{\lambda _{\max }(R)\gamma _2}{\lambda _{\min }(R)\gamma _1}\exp \left\{ \sum _p\left( \alpha _p+\frac{\ln \mu _p}{\tau _{ap}}\right) T_p(0,t)\nonumber \right. \\&\quad \left. +\sum _q\left( \alpha _q+\frac{\ln \mu _q}{\tau _{aq}}\right) T_q(0,t)\right\} x^T(0)Rx(0) \end{aligned}$$

(27)

by (17) and switching signal (18, 19), and notice $x^T(0)Rx(0)<c_1$, we get $x^T(t)Rx(t)<c_2$, which completes the proof of Theorem 1. $\square$

By the virtue of Theorem 1, we can give sufficient conditions under which switched linear system with finite-time unstable subsystems is finite-time stable by giving the concrete Lyapunov-like functions, like we did in [19].

Corollary 1

Consider the switched linear system (2), and let $\alpha _r>0$, $r\in M$, $\mu _p>1$, $p\in \mathscr {S}$, $0<\mu _q<1$, $q\in \mathscr {U}$ be given constants. Suppose there exists a set of matrices $P_r>0$,$r \in M$ such that

$$\begin{aligned}&A_r\overline{P}_r+\overline{P}_r A_r^T-\alpha _r\overline{P}_r\le 0, \end{aligned}$$

(28)

$$\begin{aligned}&\overline{P}_p^{-1}\le \mu _p\overline{P}_r^{-1}, \forall p\in \mathscr {S}, \forall r\in M, p\ne r, \end{aligned}$$

(29)

$$\begin{aligned}&\overline{P}_q^{-1}\le \mu _q\overline{P}_p^{-1}, \forall q\in \mathscr {U}, \forall p\in \mathscr {S}, \end{aligned}$$

(30)

and

$$\begin{aligned} \frac{\lambda _2}{\lambda _1}<\frac{c_2}{c_1}e^{-\alpha _pT_f}, \end{aligned}$$

(31)

where

$$\begin{aligned} \overline{P}_r= & {} R^{-\frac{1}{2}}P_rR^{-\frac{1}{2}}, \end{aligned}$$

(32)

$$\begin{aligned} \lambda _1= & {} \min \limits _r(\lambda _{\min }P_r), \lambda _1=\max \limits _r(\lambda _{\max }P_r), r\in M. \end{aligned}$$

(33)

Then, the switched linear systems (2) is finite-time stable with respect to $(c_1,c_2,T_f,R,\sigma )$ for any switching signal with MDADT

$$\begin{aligned} \tau _{ap}\ge & {} \tau _{ap}^*=\frac{T_f\ln \mu _p}{\ln \frac{c_2\lambda _1}{c_1\lambda _2}-\alpha _pT_f}, \end{aligned}$$

(34)

$$\begin{aligned} \tau _{aq}\le & {} \tau _{aq}^*=-\frac{\ln \mu _q}{\alpha _q}. \end{aligned}$$

(35)

Proof

Choose multiple Lyapunov-like functions

$$\begin{aligned} V(x(t))=V_{\sigma (t_k)}(x(t))=x^T\overline{P}_{\sigma (t_k)}^{-1}x \end{aligned}$$

(36)

We get from (28) that

$$\begin{aligned} \dot{V_{\sigma (t_k)}(x(t))}&=x^T(t)(A_{\sigma (t_k)}^T\overline{P}_{\sigma (t_k)}^{-1}+\overline{P}_{\sigma (t_k)}^{-1}A_{\sigma (t_k)})x(t)\nonumber \\&\le x^T(t)\alpha _{\sigma (t_k)}\overline{P}_{\sigma (t_k)}^{-1}x(t)=\alpha _{\sigma (t_k)}V_{\sigma (t_k)}(x(t)) \end{aligned}$$

(37)

By (29, 30), we get

$$\begin{aligned} V_p(x(t_k))\le & {} \mu _p V_r(x(t_k^-)), \forall p\in \mathscr {S}, \forall r\in M, p\ne r, \end{aligned}$$

(38)

$$\begin{aligned} V_q(x(t_k))\le & {} \mu _q V_p(x(t_k^-), \forall q\in \mathscr {U}, \forall p\in \mathscr {S}. \end{aligned}$$

(39)

Finally, one can conclude by Theorem 1 the switched system (2) is finite-time stable with respect to $(c_1,c_2,T_f,R,\sigma )$ for switching signal with MDADT satisfies (34, 35). $\square$

Remark 2

The theorem and corollary we presented involve some parameter such as $\alpha _r$, $\mu _p$, etc. Paper [26] had provided an approach to find these parameters.

3.2 Finite-Time Bounded Analysis

When the external disturbances are considered, finite-time boundedness of switched nonlinear systems is worthy to be discussed. In this section, we will pay attention to finite-time bounded analysis and present a sufficient condition to guarantee the switched systems finite-time boundedness.

Theorem 2

Consider switched nonlinear system (3), and let $\gamma _1$, $\gamma _2$, $\alpha _r>0$, $\rho _r>0$, $r \in M$, $\mu _p>1$, $p\in \mathscr {S}$, $0<\mu _q<1$, $q\in \mathscr {U}$ be given constants. Suppose that there are multiply Lyapunov-like functions $V_r(x(t))$, $r\in M$ such that for $\sigma (t_k)=i$, $\sigma (t_{k+1})=j$, $i\ne j$,

$$\begin{aligned} \gamma _1 (||x(t)||^2)\le & {} V_r(x(t))\le \gamma _2 (||x(t)||^2), \forall r\in M, \end{aligned}$$

(40)

$$\begin{aligned} \dot{V_r}(x(t))\le & {} \alpha _rV_r(x(t))+\rho _r\omega ^T(t)\omega (t),\forall r\in M, \end{aligned}$$

(41)

$$\begin{aligned} V_p(x(t_k))\le & {} \mu _pV_r(x(t_k^-)), \forall p\in \mathscr {S}, \forall r\in M, p\ne r, \end{aligned}$$

(42)

$$\begin{aligned} V_q(x(t_k))\le & {} \mu _qV_p(x(t_k^-)), \forall q\in \mathscr {U}, \forall p\in \mathscr {S} \end{aligned}$$

(43)

$$\begin{aligned} \frac{\gamma _2c_1}{\lambda _{\min }(R)}+\rho de^{\alpha T_f}< & {} \frac{\gamma _1c_2}{\lambda _{\max }(R)}e^{-\alpha _pT_f} \end{aligned}$$

(44)

where

$$\begin{aligned} \rho =\max \limits _r(\rho _r), \forall r\in M. \end{aligned}$$

(45)

Then, the switched nonlinear system (3) is finite-time bounded with respect to $(c_1,c_2,T_f,R,\sigma ,d)$ for any switching signal with MDADT

$$\begin{aligned} \tau _{ap} \ge \tau _{ap}^*= & {} \frac{T_f\ln \mu _p}{\ln \frac{\gamma _1c_2}{\lambda _{\max }(R)}- \ln \left( \frac{\gamma _2c_1}{\lambda _{\min }(R)}+\rho de^{\alpha T_f}\right) -\alpha _pT_f} \end{aligned}$$

(46)

$$\begin{aligned} \tau _{aq} \le \tau _{aq}^*= & {} -\frac{\ln \mu _q}{\alpha _q} \end{aligned}$$

(47)

Proof

For any $t\in [t_k,t_{k+1}]$, we get from (41) that,

$$\begin{aligned} \frac{d}{dt}e^{-\alpha _{\sigma (t_k)}t}V_{\sigma (t_k)}(x(t))&=e^{-\alpha _{\sigma (t_k)}t}(\dot{V}_{\sigma (t_k)}(x(t))-\alpha _{\sigma (t_k)}V_{\sigma (t_k)}(x(t)))\nonumber \\&\le e^{-\alpha _{\sigma (t_k)}t}\rho _{\sigma (t_k)}\omega ^T(t)\omega (t) \end{aligned}$$

(48)

Integral on the interval $(t_k,t)$,

$$\begin{aligned} e^{-\alpha _{\sigma (t_k)}t}V_{\sigma (t_k)}(x(t))-e^{-\alpha _{\sigma (t_k)}t_k}V_{\sigma (t_k)}(x(t_k))\le \rho _{\sigma (t_k)}\int _{t_k}^t e^{-\alpha _{\sigma (t_k)}s}\omega ^T(t)\omega (t)ds\nonumber \\ V_{\sigma (t_k)}(x(t))\le e^{\alpha _{\sigma (t_k)}(t-t_k)}V_{\sigma (t_k)}(x(t))+ \rho _{\sigma (t_k)}\int _{t_k}^te^{\alpha _{\sigma (t_k)}(t-s)}\omega ^T(t)\omega (t)ds.\nonumber \\ \end{aligned}$$

(49)

due to (42, 43), we have

$$\begin{aligned} V_{\sigma (t_k)}&(x(t))\\ \le&\; \mu _{\sigma (t_k)}e^{\alpha _{\sigma (t_k)}(t-t_k)}V_{\sigma (t_{k-1})}(x(t_k^-))+ \rho _{\sigma (t_k)}\int _{t_k}^te^{\alpha _{\sigma (t_k)}(t-s)}\omega ^T(s)\omega (s)ds\\ \le&\; \mu _{\sigma (t_k)}e^{\alpha _{\sigma (t_k)}(t-t_k)}(\mu _{\sigma (t_{k-1})}e^{\alpha _{\sigma (t_k-1)}(t_k-t_{k-1})}V_{\sigma (t_k-2)}(x(t_{k-1}^-))\\&+\rho _{\sigma (t_{k-1})}\int _{t_{k-1}}^{t_k}e^{\alpha _{\sigma (t_k-1)}(t_k-s)}\omega ^T(s)\omega (s)ds)\\&+\rho _{\sigma (t_k)}\int _{t_k}^te^{\alpha _{\sigma (t_k)}(t-s)}\omega ^T(s)\omega (s)ds\\ \le&\; \mu _{\sigma (t_k)}\cdots \mu _{\sigma (t_1)}e^{\alpha _{\sigma (t_k)}(t-t_k)}\cdots e^{\alpha _{\sigma (t_1)}(t_2-t_1)}e^{\alpha _{\sigma (t_0)}(t_1-t_0)}V_{\sigma (t_0)}(x(t_0))\\&+ \mu _{\sigma (t_k)}\cdots \mu _{\sigma (t_1)}e^{\alpha _{\sigma (t_k)}(t-t_k)}\cdots e^{\alpha _{\sigma (t_1)}(t_2-t_1)}\\ ~&*\rho _{\sigma (t_0)}\int _{t_0}^{t_1}e^{\alpha _{\sigma (t_0)}(t_1-s)}\omega ^T(s)\omega (s)ds\\&+ \mu _{\sigma (t_k)}\cdots \mu _{\sigma (t_2)}e^{\alpha _{\sigma (t_k)}(t-t_k)}\cdots e^{\alpha _{\sigma (t_1)}(t_3-t_2)}\\ ~&*\rho _{\sigma (t_1)}\int _{t_1}^{t_2}e^{\alpha _{\sigma (t_1)}(t_2-s)}\omega ^T(s)\omega (s)ds\\&+ \cdots + \mu _{\sigma (t_k)}e^{\alpha _{\sigma (t_k)}(t-t_k)}\rho _{\sigma (t_{k-1})}\int _{t_{k-1}}^{t_k}e^{\alpha _{\sigma (t_1)}(t_k-s)}\omega ^T(s)\omega (s)ds\\&+ \rho _{\sigma (t_k)}\int _{t_k}^te^{\alpha _{\sigma (t_k)}(t-s)}\omega ^T(s)\omega (s)ds\\ =&\prod _p\mu _p^{N_p(0,t)}\prod _q\mu _q^{N_q(0,t)}\exp \left\{ \sum _p\alpha _pT_p(0,t)+\sum _q\alpha _qT_q(0,t)\right\} V_{\sigma (t_0)}(x(t_0))\\&+ \rho \int _0^t\prod _p\mu _p^{N_p(s,t)}\prod _q\mu _q^{N_q(s,t)}e^{\alpha _{\sigma (t_k)}(t-t_k)+\cdots +\alpha _{\sigma (s)}(t_s-s)}\omega ^T(s)\omega (s)ds\\ \le&\; \prod _p\mu _p^{N_p(0,t)}\prod _q\mu _q^{N_q(0,t)}\exp \left\{ \sum _p\alpha _pT_p(0,t)+\sum _q\alpha _qT_q(0,t)\right\} V_{\sigma (t_0)}(x(t_0))\\&+ \prod _p\mu _p^{N_p(0,t)}\rho e^{\sum _p\alpha _pT_p(0,t)+\sum _q\alpha _qT_q(0,t)}\int _0^T\omega ^T(s)\omega (s)ds\\ \le&\; \prod _p\mu _p^{N_p(0,t)}\left\{ \exp \left\{ \sum _p\alpha _pT_p(0,t)+\sum _q\left( \alpha _q+\frac{\ln \mu _q}{\tau _{aq}}\right) T_q(0,t)\right\} V_{\sigma (t_0)}(x(t_0))\right. \\&\left. +\rho de^{\sum _p\alpha _pT_p(0,t)+\sum _q\alpha _qT_q(0,t)}\right\} \end{aligned}$$

By switching signal (47),

$$\begin{aligned} \sum _q\left( \alpha _q+\frac{\ln \mu _q}{\tau _{aq}}\right) T_q(0,t)<0 \end{aligned}$$

(50)

the above inequalities continue as

$$\begin{aligned} \le&\; \exp \left( \sum _p\left( \alpha _p+\frac{\ln \mu _p}{\tau _{ap}}\right) T_p(0,t)\right) \left( V_{\sigma (t_0)}(x(t_0))+\rho de^{\sum _q\alpha _qT_q(0,t)}\right) \\ \le&\; \exp \left( \sum _p\left( \alpha _p+\frac{\ln \mu _p}{\tau _{ap}}\right) T_p(0,t)\right) \left( V_{\sigma (t_0)}(x(t_0))+\rho de^{\alpha T_f}\right) \end{aligned}$$

by (40), we get

$$\begin{aligned}&\frac{V(x(t))}{\gamma _2}\le ||x(t)||^2\le \frac{V(x(t))}{\gamma _1}\\&x^T(t)Rx(t)\le \lambda _{\max }(R)||x(t)||^2\le \lambda _{\max }(R)\frac{V(x(t))}{\gamma _1}\\&x^T(0)Rx(0)\ge \lambda _{\min }(R)||x(0)||^2\ge \lambda _{\max }(R)\frac{V(x(0))}{\gamma _2}\\&V_{\sigma (0)}(x(0)\le \frac{\gamma _2}{\lambda _{\min }(R)}x^T(0)Rx(0) \end{aligned}$$

This implies

$$\begin{aligned} x^T(t)Rx(t)\le \frac{\lambda _{\max }(R)}{\gamma _1}\exp {\sum _p\left( \alpha _p+\frac{\ln \mu _p}{\tau _{ap}}\right) T_p(0,t)} \left( \frac{c_1\gamma _2}{\lambda _{\min }(R)}+\rho de^{\alpha T_f}\right) \end{aligned}$$

(51)

by (44), we have

$$\begin{aligned} \ln \frac{\gamma _1c_2}{\lambda _{\max }(R)}-\ln \left( \frac{\gamma _2c_1}{\lambda _{\min }(R)}+\rho de^{\alpha T_f}\right) -\alpha _pT_f>0. \end{aligned}$$

(52)

By switching signal (46),

$$\begin{aligned} \sum _p\left( \alpha _p+\frac{\ln \mu _p}{\tau _{ap}}\right) T_p(0,t)<\ln \left( \frac{\gamma _1c_2}{\lambda _{\max }(R)}*\frac{1}{\frac{\gamma _2c_1}{\lambda _{\min }(R)}+\rho de^{\alpha T_f}}\right) . \end{aligned}$$

(53)

Clearly, $x^T(t)Rx(t)<c_2$. This means the switched nonlinear system (3) is finite-time bounded with respect to $(c_1,c_2,T_f,R,\sigma ,d)$. $\square$

By giving concrete Lyapunov-like functions, similar result of linear switched systems can be deduced from Theorem 2, like the result we given in [19].

Corollary 2

Consider switched linear system (4), let $\alpha _r>0$, $r \in M$, $\mu _p>1$, $p\in \mathscr {S}$, $0<\mu _q<1$, $q\in \mathscr {U}$ be given constants. Suppose there exists a set of matrices $P_r>0$, $Q_r>0$, $r\in M$, such that,

$$\begin{aligned}&\begin{bmatrix} A_r\overline{P}_r+\overline{P}_r A_r^T-\alpha _r\overline{P}_r&G_rQ_r\\ *&-\gamma Q_r\\ \end{bmatrix} \le 0, \end{aligned}$$

(54)

$$\begin{aligned}&\overline{P}_p^{-1} \le \mu _p\overline{P}_r^{-1}, \forall p\in \mathscr {S}, \forall r\in M, p\ne r, \end{aligned}$$

(55)

$$\begin{aligned}&\overline{P}_q^{-1} \le \mu _q\overline{P}_p^{-1}, \forall q\in \mathscr {U}, \forall p\in \mathscr {S}, \end{aligned}$$

(56)

$$\begin{aligned}&\frac{c_1}{\lambda _1}+\frac{1}{\lambda }e^{\alpha T_f}\gamma d<\frac{c_2}{\lambda _2}e^{-\alpha _pT_f}. \end{aligned}$$

(57)

Where

$$\begin{aligned} \overline{P}_r= & {} R^{-\frac{1}{2}}P_rR^{-\frac{1}{2}}, \end{aligned}$$

(58)

$$\begin{aligned} \lambda _1= & {} \min \limits _r(\lambda _{\min }P_r), \lambda _2=\max \limits _r(\lambda _{\max }P_r), \end{aligned}$$

(59)

$$\begin{aligned} \lambda= & {} \min \limits _r(\lambda _{\min }Q_r), \alpha =\max \limits _r(\alpha _r), \forall r\in M. \end{aligned}$$

(60)

Then, the switched linear system (4) is finite-time bounded with respect to $(c_1,c_2,T_f, R,\sigma ,d)$ for any switching signal with MDADT

$$\begin{aligned} \tau _{ap}\ge & {} \tau _{ap}^*=\frac{T_f\ln \mu _p}{\ln \frac{c_2}{\lambda _2}-\ln \left( \frac{c_1}{\lambda _1}+\frac{1}{\lambda }e^{\alpha T_f}\gamma d\right) -\alpha _pT_f}, \end{aligned}$$

(61)

$$\begin{aligned} \tau _{aq}\le & {} \tau _{aq}^*=-\frac{\ln \mu _q}{\alpha _q}. \end{aligned}$$

(62)

Proof

Choose multiple Lyapunov-like functions

$$\begin{aligned} V(x(t))=V_{\sigma (t_k)}(x(t))=x^T\overline{P}_{\sigma (t_k)}^{-1}x. \end{aligned}$$

(63)

Take derivative to the both sides of the equation,

$$\begin{aligned} \dot{V}_{\sigma (t_k)}(x)&=x^T(t)(A_{\sigma (t_k)}^T\overline{P}_{\sigma (t_k)}^{-1}+\overline{P}_{\sigma (t_k)}^{-1}A_{\sigma (t_k)})x(t) +2x^T(t)\overline{P}_{\sigma (t_k)}^{-1}G_{\sigma (t_k)}\omega (t)\nonumber \\&=\begin{bmatrix} x^T(t)&\omega ^T(t)\\ \end{bmatrix} \begin{bmatrix} A_{\sigma (t_k)}^T\overline{P}_{\sigma (t_k)}^{-1}+\overline{P}_{\sigma (t_k)}^{-1}A_{\sigma (t_k)}&\quad \overline{P}_{\sigma (t_k)}^{-1}G_{\sigma (t_k)}\\ *&\quad 0\\ \end{bmatrix} \begin{bmatrix} x(t)\\ \omega (t)\\ \end{bmatrix} \end{aligned}$$

(64)

Assuming condition (54) is satisfied, then pre-multiplying and post-multiplying by the positive symmetric matrix $\begin{bmatrix} \overline{P}_{\sigma (t_k)}^{-1}&0\\ 0&\overline{Q}_{\sigma (t_k)}^{-1} \\ \end{bmatrix}$, we obtain the equivalent condition

$$\begin{aligned} \begin{bmatrix} A_{\sigma (t_k)}^T\overline{P}_{\sigma (t_k)}^{-1}+\overline{P}_{\sigma (t_k)}^{-1}A_{\sigma (t_k)}-\alpha \overline{P}_{\sigma (t_k)}^{-1}&\quad \overline{P}_{\sigma (t_k)}^{-1}G_{\sigma (t_k)}\\ *&\quad -\gamma \overline{Q}_{\sigma (t_k)}^{-1} \\ \end{bmatrix} \le 0 \end{aligned}$$

(65)

(64) leads to

$$\begin{aligned} \dot{V}_{\sigma (t_k)}(x(t))\le x^T(t)\alpha _{\sigma (t_k)}\overline{P}_{\sigma (t_k)}^{-1}x(t)+\gamma \omega ^T(t)Q_{\sigma (t_k)}^{-1}\omega (t),\nonumber \\ \dot{V}_{\sigma (t_k)}(x(t))-\alpha _{\sigma (t_k)}V_{\sigma (t_k)}(x(t))\le \gamma \omega ^T(t)Q_{\sigma (t_k)}^{-1}\omega (t). \end{aligned}$$

(66)

The following proof is similar to that of Theorem 2.We omit it there. $\square$

3.3 Finite-Time Stabilization of Switched Linear Systems

For some finite-time unstable subsystems, the feedback control algorithm guarantees that the closed-loop system can be finite-time stable. And then the theorem presented above can be applied in the closed-loop system. In this section, the problem of controller design for switched linear system with disturbances

$$\begin{aligned} \dot{x}(t)=A_{\sigma (t)}x(t)+B_{\sigma (t)}u(t)+G_{\sigma (t)}\omega (t) , \end{aligned}$$

(67)

is studied. Unlike some control methods, we don’t require all the subsystems are controllable. We assume the {$A_p,B_p$} are controllable subsystems, {$A_q,B_q$} are uncontrollable subsystems. The aim of finite-time stabilization is to design a state feedback controller

$$\begin{aligned} u(t)=K_{\sigma (t)}x(t) \end{aligned}$$

(68)

to achieve the finite-time stability of the close-loop switched linear system with MDADT switching.

Theorem 3

Let $\alpha _r>0$, $r \in M$, $\mu _p>1$, $p\in \mathscr {S}$, $0<\mu _q<1$, $q\in \mathscr {U}$, $\gamma >0$ be given constants. Suppose there exists a set of matrices $P_r>0$, $Q_r>0$, $X_r$, $r\in M$, such that

$$\begin{aligned}&\begin{bmatrix} A_r\overline{P}_r+\overline{P}_r A_r^T-\alpha _r\overline{P}_r+B_rX_r+X_r^TB_r^T&G_rQ_r\\ *&-\gamma Q_r\\ \end{bmatrix} \le 0, \end{aligned}$$

(69)

$$\begin{aligned}&\overline{P}_p^{-1} \le \mu _p\overline{P}_r^{-1}, \forall p\in \mathscr {S}, \forall r\in M, p\ne r, \end{aligned}$$

(70)

$$\begin{aligned}&\overline{P}_q^{-1} \le \mu _q\overline{P}_p^{-1}, \forall q\in \mathscr {U}, \forall p\in \mathscr {S}, \end{aligned}$$

(71)

$$\begin{aligned}&\frac{c_1}{\lambda _1}+\frac{1}{\lambda }e^{\alpha T_f}\gamma d<\frac{c_2}{\lambda _2}e^{-\alpha _pT_f}. \end{aligned}$$

(72)

Where

$$\begin{aligned} \overline{P}_r= & {} R^{-\frac{1}{2}}P_rR^{-\frac{1}{2}}, \end{aligned}$$

(73)

$$\begin{aligned} \lambda _1= & {} \min \limits _r(\lambda _{\min }P_r), \lambda _2=\max \limits _r(\lambda _{\max }P_r), \end{aligned}$$

(74)

$$\begin{aligned} \lambda= & {} \min \limits _r(\lambda _{\min }Q_r), \alpha =\max \limits _r(\alpha _r), \forall r\in M. \end{aligned}$$

(75)

Then, under the feedback controller

$$\begin{aligned} u(t)=K_{\sigma (t)}x(t)=X_{\sigma (t)}\overline{P}_{\sigma }^{-1}x(t) \end{aligned}$$

(76)

Switched system (67) is finite-time bounded with respect to $(c_1,c_2,T_f,R,\sigma ,d)$ for any switching signal with MDADT (61, 62).

Proof

Applying Corollary 2 to the closed-loop system

$$\begin{aligned} \dot{x}(t)&=A_{\sigma (t)}x(t)+B_{\sigma (t)}u(t)+G_{\sigma (t)}\omega (t)\nonumber \\&=(A_{\sigma (t)}+B_{\sigma (t)}X_{\sigma (t)}\overline{P}_{\sigma }^{-1})x(t)+G_{\sigma (t)}\omega (t) \end{aligned}$$

(77)

It is no difficult to check the result. $\square$

Remark 3

As the conditions (31, 57) are not in LMIs, we tackle them by the method mentioned used in [3], Take (57) as an example. It is guaranteed by the imposing conditions,

$$\begin{aligned}&a_rI< P_r< b_rI,\\&c_rI< Q_r,\\&\frac{c_1}{a_r}+\frac{e^{\alpha T_f}\gamma d}{c_r}<\frac{c_2}{b_r}e^{-\alpha _{p}T_f}. \end{aligned}$$

for some positive numbers $a_r,b_r,c_r$, the last inequality can be converted to an LMI using Schur complements

$$\begin{aligned} \begin{pmatrix} \frac{c_2}{b_r}e^{-\alpha T_f} &{}\quad \sqrt{c_1} &{}\quad \sqrt{e^{\alpha T_f}\gamma d}\\ \sqrt{c_1} &{}\quad \alpha _r &{}\quad 0\\ \sqrt{e^{\alpha T_f}\gamma d} &{}\quad 0 &{}\quad c_r\\ \end{pmatrix}> 0, \end{aligned}$$

and then the feasibility of these conditions can be turned into the LMIs based feasibility problem. The computational complexity increases with the increase of the size of the matrix. This is the common problem in the field of matrix computing

It should be pointed out that the new conditions in LMIs obtained are just sufficient conditions for the original conditions.

4 Numerical Examples

Example 1

Consider the finite-time stability problem for a switched nonlinear system as (1), which is consisted two subsystems as follows:

$$\begin{aligned} f_1(x(t))=(1+0.5\sin (x(t))^2)x(t), f_2(x(t))=(2+\cos (x(t))^2)x(t). \end{aligned}$$

The corresponding parameters are specified as follows:

$$\begin{aligned} c_1=1, c_2=100, T_f=1, R=I. \end{aligned}$$

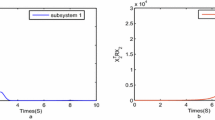
By system state Figs. 1 and 2, we can find that the first subsystem is finite-time stable and the second subsystem is finite-time unstable.

Fig. 1

$X^T{ RX}$ of first subsystem

Fig. 2

$X^T{ RX}$ of second subsystem

Choose Multi-Lyapunov-like functions as:

$$\begin{aligned} V_1=x^2, V_2=0.9x^2. \end{aligned}$$

Taking the derivative of V(x) yields

$$\begin{aligned} \dot{V}_1(x)\le 3V_1(x), \dot{V}_2(x)\le 6V_2(x) \end{aligned}$$

So by Theorem 1, we can choose $\alpha _1=3$, $\alpha _2=6$, $\mu _1=1.2$, $\mu _2=0.9$, $\gamma _1=0.8$, $\gamma _2=1.1$, the MDADT of two subsystems are obtained:

$$\begin{aligned} \tau _{a1}^*=0.1298,\tau _{a2}^*=0.0176. \end{aligned}$$

Let $\tau _{a1}=0.13$, $\tau _{a2}=0.015$, we generate the switching sequence alternating between the two subsystems. Figure 3 shows the switching signal and the value of $x^TRx$ for the switching system we considered.

Fig. 3

$X^TRX$ and switching signal

Example 2

Consider the finite-time stability problem for switched linear systems as (2) consisted of two subsystems. The corresponding subsystem matrices are given below:

$$\begin{aligned} A_1=\begin{bmatrix} 0.1&\quad 0\\ -0.5&\quad 0.5\\ \end{bmatrix}, A_2=\begin{bmatrix} 1&\quad 1\\ 1&\quad 1\\ \end{bmatrix}\\ \end{aligned}$$

Corresponding parameters are $c_1=1$, $c_2=50$, $T_f=1$, $R=I$.

It is not difficult to verify that the first subsystem is finite-time stable and the second subsystem is finite-time unstable. By using Corollary 1, if we choose $\alpha _1=1.25$, $\alpha _2=5$, $\mu _1=1.9$, $\mu _2=0.75$, the feasible solutions are obtained as follows:

$$\begin{aligned} P_1=\begin{bmatrix} 98.764&\quad 49.8608\\ 49.8608&\quad 136.68435\\ \end{bmatrix}, P_2=\begin{bmatrix} 158.6314&\quad 81.4113\\ 81.4113&\quad 215.9851\\ \end{bmatrix}. \end{aligned}$$

Moreover, we get the MDADT of two subsystems are obtained:

$$\begin{aligned} \tau _{a1}^*=0.5282, \tau _{a2}^*=0.0575. \end{aligned}$$

(78)

Let $\tau _{a1}=0.55>0.5282$, $\tau _{a2}=0.05<0.0575$, we generate the switching sequence alternating between the two subsystems. Figure 4 shows the simulation results of the value of $x^TRx$ for the switching system we considered.

Fig. 4

$X^TRX$ and switching signal

Example 3

Consider the finite-time stabilization problem of switched system (67)

$$\begin{aligned} \dot{x}(t)=A_{\sigma (t)}x(t)+B_{\sigma (t)}u(t)+G_{\sigma (t)}\omega (t). \end{aligned}$$

The corresponding subsystem matrices and parameters are specified as follows:

$$\begin{aligned}&A_1=\begin{bmatrix} 0.01&\quad 0\\ -1&\quad -3\\ \end{bmatrix},\quad B_1=\begin{bmatrix} 0\\ 0.5\\ \end{bmatrix},\quad A_2=\begin{bmatrix} 1&\quad 3\\ 0&\quad -0.25\\ \end{bmatrix},\quad B_1=\begin{bmatrix} 1\\ 0\\ \end{bmatrix},\\&G_1=G_2=I,\quad \omega (t)=\begin{bmatrix} -0.4\cos (10t+3)\\ 0.2\sin (3t)\\ \end{bmatrix},\\&c_1=5,\quad c_2=100,\quad d=1,\quad T_f=1,\quad R=I. \end{aligned}$$

By Theorem 3, we choose $\alpha _1=0.3$, $\alpha _2=0.3$, $\mu _1=1.2$, $\mu _2=0.9$, $\gamma =0.5$, then we obtain the matrix solution as:

$$\begin{aligned}&P_1=\begin{bmatrix} 145.3431&0\\ 0&39.7138\\ \end{bmatrix},\quad P_2=\begin{bmatrix} 168.0789&0\\ 0&45.7954\\ \end{bmatrix},\\&Q_1=\begin{bmatrix} 9.5608&0\\ 0&4.7065\\ \end{bmatrix},\quad Q_2=\begin{bmatrix} 4.7065&0\\ 0&7.4526\\ \end{bmatrix},\\&X_1=\begin{bmatrix} 290.6863&229.0174\\ \end{bmatrix},\quad X_2=\begin{bmatrix} -153.4567&-137.3863\\ \end{bmatrix}, \end{aligned}$$

Thus, according to the Theorem 3, under the state feedback controllers

$$\begin{aligned} u_1(t)=(2.0000,5.7667)x(t), u_2(t)=(-0.9130,-3.0000)x(t), \end{aligned}$$

and the switching signal with MDADT

$$\begin{aligned} \tau _{a1}=0.38>0.3701, \tau _{a2}=0.2<0.3512, \end{aligned}$$

close-loop system (67) is finite-time bounded with respect to $(5,100,1,1,\sigma ,1)$ (Fig. 5).

Fig. 5

$X^TRX$ and switching signal

5 Conclusions

Finite-time stability and finite-time boundedness problems of switched nonlinear systems consisting of both finite-time stable and unstable subsystems have been studied in this paper. Through an MLF approach, a class of switching signals with MDADT property has been designed to achieve the purpose. Corresponding corollaries have also been deduced for switched linear systems with finite-time unstable subsystems. For the stabilization problem, the case of linear systems has been considered in order to present controller gain matrix. The feedback controller has been designed to guarantee the closed-loop system to be finite-time stable. Corresponding future researches are still confronted with a great number of challenges. Considering of switched linear systems, implementation of Lyapunov function may lead to some conservativeness on the bound of dwell time, and the method proposed in [32] is likely to be the solution for this problem. In addition, adaptive control embraced in [22, 33] is also a prospective research problem.