A New Fault Estimation Observer Design for Nonlinear Markovian Jump Systems: An Interval Type-2 Fuzzy Method

Abstract

In this paper, we propose a new fault estimation observer for nonlinear Markovian jump systems. Following the interval type-2 fuzzy logic rules, the original system can be approximated as an interval type-2 fuzzy Markovian jump system. For such a system, we develop a new intermediate fault estimation observer, in which a variable is introduced to estimate actuator faults. Significantly, a larger design freedom can be achieved by providing the observer gain matrix in the new form. To further evaluate the proposed method, multiple fault cases are considered. The proposed method proves effective in the simultaneous fault estimation for both actuator fault and sensor fault. Furthermore, two examples are simulated to numerically verify the feasibility of the given method.

1 Introduction

Markovian jump systems (MJSs) have been widely studied, owing to their powerful ability to describe control systems subject to abrupt changes. They are usually composed of several subsystems, each of which switches according to stochastic signals that obey the Markov process. On account of Markovian switching properties, the current subsystem, which dictates the system dynamic, cannot be known precisely, but only its switching probabilities. Hence, it is more complex to analyze MJSs as compared with standard systems. In addition, the nonlinearities usually exist in the practical system modeling, however, it is difficult to deal with the nonlinearities during modeling processes, exposing a handicap. It is well-known that the type-1 fuzzy method has been popularly used since its appearance. It can describe the fuzzy variables using some selected membership functions, which requires the system states to be exactly known. Although the type-1 T–S fuzzy model provides a handy framework for the controller and observer designs, it cannot perform well in the presence of uncertainties, since their membership functions contain no uncertainty information [1]. Once, when the system states contain uncertainties, the type-1 fuzzy method fails, which, to a large extent, narrows its application scope. For this reason, the type-2 fuzzy method comes out, of which the membership functions have fuzzy properties, just to make up for the type-1 fuzzy method. Due to this, the interval type-2 fuzzy method owns stronger ability to describe the fuzzy systems, and the type-1 fuzzy method can be taken as the special case of it [2,3,4]. Recently, the researchers from control community have post their sight to the type-2 fuzzy filed, and a fruitful of results have been developed.

Based on the aforementioned discussion, a few appealing results have been reported [5,6,7,8]. Among them, the observer design turns out to be a vigorous research field, but is not fully considered. On the other hand, with an eye to the demand of the higher safety in complex systems, observer-based fault estimation methods have attract extensive attentions [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28]. To name a few, [9] proposed an observer-based fault detection filter for MJSs, which has considered the sensor saturation and randomly varying nonlinearities. Further, [10] developed another filter for MJSs subjected to non-homogeneities, enlisting the help of a fuzzy method. In [11], a reduced-order observer was designed for MJSs with the transition rates being generally uncertain, and it was then applied to estimate the actuator fault and sensor fault simultaneously. Li et al. [12] also considered the simultaneous fault estimation for MJSs, and relying on the estimated fault, a nonfragile fault-tolerant controller was proposed. Li et al. [14] achieved the fault reconstruction for MJSs by virtue of an iterative adaptive observer. On the subject of semi-MJSs. Liang et al. [15] addressed the fault estimation problem, with transition rates being assumed to be partly known. Yang and Yin [16] provided a descriptor observer based on sliding mode technique, aiming to simultaneously estimate both the actuator fault and sensor fault, and further the reduced-order structure of it was developed in [17]. Yang et al. [18] estimated both the additive and multiplicative faults for MJSs through a sliding mode observer design. For the first time, [22] considered the fault interval estimation for discrete-time MJSs, which was based on the zonotope concept. In [8], a novel mixed-triggered filter was designed for interval type-2 fuzzy nonlinear MJSs, where the packet dropout was assumed to happen. By virtue of the zonotope concept, [23] considered the interval fault detection problem for discrete-time MJSs with generally bounded transition probabilities. Kaviarasan et al. [25] investigated the mode-dependent multiple fault estimation method for time-delayed MJSs, taking the exogenous disturbance into consideration. Sun et al. [27] proposed the fast actuator fault estimation strategy for T–S fuzzy MJSs, subjected to bounded unknown input.

In view of the above-mentioned works, this paper is devoted to address the simultaneous fault estimation problem for interval type-2 fuzzy MJSs. Although there already existed rich results on the observer-based fault estimation, some pending gaps are still urgently needed to be bridged, which exactly motivates us to figure out the proposed method:

(1) The sliding mode observer-based method has been widely employed, owing to its robustness against uncertainties [28]. However, it has been found hardly to apply well in MJSs due to its stochastic switching behaviors. In addition, the sliding mode observer-based method [29] involved the design of sliding mode laws as to alleviate fault influences. Unfortunately, this will introduce the chattering phenomenon to the estimation performance, due to the sliding mode control gains being chosen large (according to the fault amplitude) and the reachability problem of sliding mode surface. However, in this paper, sliding mode laws are not required anymore, instead an intermediate variable is introduced, which can overcome the chattering issue.

(2) As for the unknown input observer-based methods [9, 30, 31], the conservatism was posed in computing the gain matrices. Specifically, in [11], the reduced-order observer was designed to estimate the fault, but some restrictive rank conditions were required to be satisfied. In [30], the gain matrices were provided to be constant before solving the observer existence conditions, which would however render these conditions unfeasible.

(3) On the subject of adaptive observer-based methods, transient responses of the fault estimation cannot be ensured well. In [12], adaptive observers were developed to achieve the fault estimation goals, where the transient responses were optimized at the cost of the estimation error convergence. As a comparison, our proposed method allows transient responses to be optimized by letting the eigenvalues of the gain matrix far away from the imaginary axis.

It is exactly the above three points that motivate us to study the fault estimation problem for a class of interval type-2 fuzzy MJSs. In this paper, a new observer structure is developed, in which the observer gain matrix is proposed in a special form. The proposed observer is proved able to simultaneously provide the estimations of the actuator fault and sensor fault. The main contributions of this paper can be summarized as follows:

(1) A new structure of fault estimation observer based on an intermediate variable is proposed to simultaneously estimate the actuator fault and sensor fault, where the existence conditions of the observer have more chance to be computed.

(2) The designed observer owns great design freedom, owing to the special form of the observer gain matrix and the introduction of slack matrix variables.

(3) The restrictive design conditions are unnecessary, such as the matching conditions using in the sliding mode observer design, implying a wider application scope.

Notations: In the paper, $\parallel x \parallel$ means the Euclidean norm of the vector x. $A>0$ implies that A is a symmetric positive definite matrix, and $\lambda _{min}(P)$ and $\lambda _{max}(P)$ are the minimum and maximum eigenvalues of matrix P. In addition, the asterisk $*$ represents the symmetric terms in a symmetric matrix.

2 Problem Statement and Preliminaries

Consider a nonlinear MJSs that can be represented by the interval type-2 fuzzy system with the following fuzzy rules as:

Rule i: If $\phi _1(x(t))$ is $\varphi _1^i$, and, ....., if $\phi _k(x(t))$ is $\varphi _k^i$, then

$$\begin{aligned}\left\{ \begin{array}{ll}\dot{x}(t)=A_i(r(t))+B_i(r(t))u(t)+D(r(t))f_a(t)\\ y(t) = C(r(t))x(t) \end{array} \right. , \end{aligned}$$

where $x(t)\in R^n$, $u(t)\in R^m$, and $y(t)\in R^p$ are the states, input and output, respectively. $f_a(t)\in R^q$ stands for the actuator fault that undermines the system. The matrices $A_i(r(t))$, $B_i(r(t))$, D(r(t)) and C(r(t)) are constant with appropriate dimension. In addition, r(t) obeys the continuous-time discrete state Markov process, which borrows values from the finite positive integer set $S=\{1,2,...,s\}$. Specifically, the jump probability from mode i at time t to mode j at time $t+h$ can be calculated by

$$\begin{aligned} \Pr (r\left( {t + h} \right) = j \vert r\left( t \right) = i)= \left\{ \begin{array}{ll} \pi _{ij} \left( t \right) h + o(h),\;j \ne i\\ 1 + \pi _{ii} \left( t \right) h + o(h),\;j = i \end{array} \right. , \end{aligned}$$

where $\pi _{ij}$ is the transition rate coming from the transition rate matrix $\Theta$, and $\pi _{ij}\ge 0$ if $i\ne j$, and $\pi _{ij}\le 0$, otherwise. When $s=3$, the transition rate matrix is in the form of

$$\begin{aligned} \Theta = \left[ {\begin{array}{*{20}{c}} {\pi _{11}}&{}{\pi _{12}}&{} {\pi _{13}}\\ {\pi _{21}}&{}{\pi _{22}}&{} {\pi _{23}}\\ {\pi _{31}}&{}{\pi _{32}}&{} {\pi _{33}}\end{array}}\right] , \end{aligned}$$

For $\pi _{ij}$, we have $\sum \nolimits _{j=1}^s\pi _{ij}=0$. Later, we note $A_i(r(t)=j)=A_{ij}$ for abbreviation. In addition, $\phi _w(x(t))$ is an interval type-2 fuzzy set of rule i corresponding to the function $\varphi _w^i(x(t))$, $w=1,2,...,k$, $i=1,2,...,r$. The firing strength of the ith rule is as follows:

$$\begin{aligned} \rho _i(x(t))=[\rho _i^L(x(t)),\rho _i^U(x(t))], \end{aligned}$$

where

$$\begin{aligned} \rho _i^L(x(t))=\vartheta _{\varphi _1^i}^L(\phi _1(x(t)))\times \vartheta _{\varphi _2^i}^L(\phi _2(x(t)))\times \vartheta _{\varphi _k^i}^L(\phi _k(x(t))), \end{aligned}$$

and

$$\begin{aligned} \rho _i^U(x(t))=\vartheta _{\varphi _1^i}^U(\phi _1(x(t)))\times \vartheta _{\varphi _2^i}^U(\phi _2(x(t)))\times \vartheta _{\varphi _k^i}^U(\phi _k(x(t))). \end{aligned}$$

It is easily seen that $\rho _i^L(x(t)) \ge 0$ and $\rho _i^U(x(t)) \ge 0$. In addition, $\vartheta _{\varphi _{w }^i}^U(\phi _{w }(x(t)))\in [0,1]$ and $\vartheta _{\varphi _{w }^i}^L(\phi _{w }(x(t)))\in [0,1]$ denote the upper and lower grades of membership governed by the corresponding membership functions, respectively. Hence, it exhibits the fact that $\vartheta _{\varphi _{w }^i}^U(\phi _{w }(x(t)))\ge \vartheta _{\varphi _{w }^i}^L(\phi _{w }(x(t)))$, thus leading to $\rho _i^U(x(t))\ge \rho _i^L(x(t))$. According to [1], the inferred interval type-2 T–S fuzzy model can be given as:

$$\begin{aligned} \left\{ \begin{array}{ll}\dot{x}(t)=\sum \limits _{i=1}^r\breve{\omega }_i(t)[A_{i}(r(t))x(t)+B_{i}(r(t))u(t)+D(r(t))f_a(t)]\\ y(t) = C(r(t))x(t) \end{array} \right. , \end{aligned}$$

where $\breve{\omega }_i(t)=\hbar ^U(x(t))\rho _i^U(x(t))+\hbar ^L(x(t))\rho _i^L(x(t))\in [0,1]$, $\sum \limits _{i=1}^r\breve{\omega _i}(t)=1$. $\hbar ^U(x(t))\in [0,1]$ and $\hbar ^L(x(t))\in [0,1]$ are nonlinear functions satisfying $\hbar ^L(x(t))+\hbar ^U(x(t))=1$.

The followings give some assumptions and lemmas, in order to facilitate the derivation of the main result.

Assumption 1

We assume that the matrix $D_j$ is of full column rank, and $rank(D_j)=rank(C_jD_j)$.

Assumption 2

The derivative of the considered actuator fault is bounded by some positive integer $\varepsilon$, that is $\Vert \dot{f_a}(t)\Vert \le \varepsilon$.

Remark 1

In fact, the assumptions in the paper do not handicap the proposed method. Assumption 1 plays a vital role in the observer design, which was also widely used in the observer design results [28, 32]. It is not difficult to satisfy for practical systems. Assumption 2 has strong generality, as the changing rate of occurred faults are with boundaries. Actually, it makes no sense to consider the infinite fault, because it cannot be suppressed at all using the effective robust control methods, such as $H_\infty$ method, sliding mode control method, etc.. Due to this, Assumption 2 exists extensively in the observer design [33, 34].

Lemma 1

(Young’s Inequality) For any $\mu _1\in R^n$ and $\mu _2\in R^n$, there exists

$$\begin{aligned} \mu _1^T\mu _2\le \frac{1}{a}\alpha ^a\Vert \mu _1\Vert ^a+\frac{1}{b}\alpha ^{-b}\Vert \mu _2\Vert ^b. \end{aligned}$$

where $\alpha >0$, $a>0$, $b>0$ and $ab=a+b$.

With an eye to the demand of the higher safety for MJSs, the observer-based fault estimation has attracted considerable attentions, since it serves as the basis of fault-tolerant control. Although some appealing results have been proposed for the fault estimation, there still exist some gaps needed to be filled. Hence, it makes sense to deal with the fault estimation problem for MJSs, and that’s what follows subsequently.

3 Fault Estimation Observer Design

In general, the considered interval type-2 fuzzy MJS can be represented as:

$$\begin{aligned} \left\{ \begin{array}{l}\dot{x}(t)=\sum \limits _{i=1}^r\breve{\omega }_i(t)[A_{ij}x(t)+B_{ij}u(t)+D_jf_a(t)]\\ y(t) = C_jx(t) \end{array} \right. , \end{aligned}$$

(1)

Define a new immediate variable $\xi (t)=f_a(t)-K_jy(t)$, where $K_j\in R^{q\times p}$ is an unknown matrix to be determined later. In this way, we have

$$\begin{aligned} {\dot{\xi }}(t)=\,&\dot{f_a}(t)-K_j\dot{y}(t)\\ =\,&\dot{f_a}(t)-K_jC_j\dot{x}(t)\\ =\,&\dot{f_a}(t)-\sum \limits _{i=1}^r\breve{\omega }_i(t)[K_jC_jA_{ij}x(t)\\&+\,K_jC_jB_{ij}u(t)+K_jC_jD_jf_a(t)]. \end{aligned}$$

(2)

According to the structures of (1) and (2), we provide the fault estimation observer as follows:

$$\begin{aligned} \left\{ \begin{array}{l}\dot{{\hat{x}}}(t)=\sum \limits _{i=1}^r\breve{\omega }_i(t)[A_{ij}{\hat{x}}(t)+B_{ij}u(t)\\ +D_j\hat{f_a}(t)+L_{ij}(y(t)-{\hat{y}}(t))]\\ \dot{{\hat{\xi }}}(t)=-\sum \limits _{i=1}^r\breve{\omega }_i(t)[K_jC_jA_{ij}{\hat{x}}(t)\\ +K_jC_jB_{ij}u(t)+K_jC_jD_j{\hat{\xi }}(t)+K_jC_jD_jK_jy(t)]\\ \hat{f}_a(t)={\hat{\xi }}(t)+K_jy(t) \end{array} \right. , \end{aligned}$$

(3)

where $\hat{f_a}(t) \in R^q$ is the estimated actuator fault, and $L_{ij}\in R^{n \times p}$ and $K_j \in R^{q \times p}$ are the unknown observer gain matrices.

Let the estimation errors be ${\tilde{x}}(t)=x(t)-{\hat{x}}(t)$, and $e_\xi (t)=\xi (t)-{\hat{\xi }}(t)$ and ${\tilde{f}}_a(t)=f_a(t)-{\hat{f}}_a(t)$. Then, subtract the first equation and second equation from (1) and (2), respectively, and one has

$$\begin{aligned} \dot{{\tilde{x}}}(t)=\,&\sum _{i=1}^r\breve{\omega }_i(t)[A_{ij}x(t)+B_{ij}u(t)\\&+\,D_jf_a(t)-A_{ij}{\hat{x}}(t)-B_{ij}u(t)\\&-D_j{\hat{f}}_a(t)-L_{ij}(y(t)-{\hat{y}}(t))]\\ =\,&\sum _{i=1}^r\breve{\omega }_i(t)[(A_{ij}-L_{ij}C_j){\tilde{x}}(t)+D_j{\tilde{f}}_a(t)],\\ \end{aligned}$$

(4)

and

$$\begin{aligned} \dot{e}_\xi (t)=\,&\dot{f}_a(t)-\sum _{i=1}^r\breve{\omega }_i(t)[K_jC_jA_{ij}x(t)+K_jC_jD_jf_a(t)\\&-K_jC_jA_{ij}{\hat{x}}(t)-K_jC_jD_j{\hat{\xi }}(t)-K_jC_jD_jK_jy(t)]\\ =\,&\dot{f}_a(t)-\sum _{i=1}^r\breve{\omega }_i(t)[K_jC_jA_{ij}{\tilde{x}}(t)+K_jC_jD_j\xi (t)\\&+\,K_jC_jD_jK_jy(t)-K_jC_jD_j{\hat{\xi }}(t)-K_jC_jD_jK_jy(t)] \\ =\,&\dot{f}_a(t)-\sum _{i=1}^r\breve{\omega }_i(t)[K_jC_jA_{ij}{\tilde{x}}(t) +K_jC_jD_je_\xi (t)] , \end{aligned}$$

(5)

by noticing $\xi (t)=f_a(t)-K_jy(t)$. It can be easily seen that

$$\begin{aligned} {\tilde{f}}_a(t)&= f_a(t)-{\hat{f}}_a(t)\\&=\xi (t)+K_jy(t)-{\hat{\xi }}(t)-K_jy(t)\\&=e_\xi (t). \end{aligned}$$

(6)

Substituting (6) into (4) yields

$$\begin{aligned} \dot{{\tilde{x}}}(t)=\sum _{i=1}^r\breve{\omega }_i(t)[(A_{ij}-L_{ij}C_j){\tilde{x}}(t)+D_je_\xi (t)]. \end{aligned}$$

(7)

In order to facilitate the observer design, we now give the matrix $K_j$ as $K_j=Q_j((C_jD_j)^TC_jD_j)^{-1}(C_jD_j)^T$, where $Q_j\in R^{q\times q}$ is an arbitrary matrix that can be determined later. According to Assumption 2, we know that $(C_jD_j)^TC_jD_j$ is invertible. Hence, substitute $K_j$ into (5), and we have

$$\begin{aligned} \dot{e}_\xi (t)=\dot{f}_a(t)-\sum _{i=1}^r\breve{\omega }_i(t)[K_jC_jA_{ij}{\tilde{x}}(t)+Q_je_\xi (t)]. \end{aligned}$$

(8)

Remark 2

From (8), we can see that the stability of (8) depends on the matrix $Q_j$. In this paper, we set $Q_j$ to be chosen according to the stability conditions of (8) instead of making it be constant. In [31], matrix $Q_j$ designed to be $Q_j=\kappa D_j^TD_j$, where $\kappa \ge 0$ is an arbitrary scalar, has more conservatism in stabilizing (8). Due to the introducing of $Q_j$, more design freedom is added to the proposed method, which leads the following stability conditions easy to find solutions.

Subsequently, the main result of the paper is shown in the following Theorem 1, which not only gives the existence conditions of the designed observer, but also provides a way to calculate the observer gain matrices $L_{ij}$ and $K_j$.

Theorem 1

For given scalar $\gamma \ge 0$, if there exist matrices $P_j \in R^{n\times n}>0$, $\Gamma _j \in R^{n\times n}>0$, and matrices $Y_{ij} \in R^{n\times p}$ and $M_j \in R^{q\times q}$ such that the following linear matrix inequality is feasible for $i=1,2,...,r$, $j=1,2,...,s$

$$\begin{aligned} \left[ {\begin{array}{*{20}{c}} {\Phi _{11}}&{}{\Phi _{12}}&{} {0}\\ {*}&{}{\Phi _{22}}&{} {\Gamma }\\ {*}&{}{*}&{} {-\gamma I_q}\end{array}}\right] <0, \end{aligned}$$

(9)

where $\Phi _{11}=P_jA_{ij}-Y_{ij}C_j+A_{ij}^TP_j-C_j^TY_{ij}^T+\sum \limits _{l=1}^s\pi _{jl}P_l$, $\Phi _{12}=P_jD_j-A_{ij}^TC_j^T\Psi _j^TM_j^T$, $\Phi _{22}=-M_j^T-M_j+\sum \limits _{l=1}^s\pi _{jl}\Gamma _l$, $\Psi _j=((C_jD_j)^TC_jD_j))^{-1}(C_jD_j)^T$, $M_j=\Gamma _jQ_j$ and $Y_{ij}=P_jL_{ij}$, then the error systems (7) and (8) can be found uniformly stable.

Proof

Consider the Lyapunov function as $V(j,t)={\tilde{x}}^T(t)P_j\tilde{x}(t)+e_\xi ^T(t)\Gamma _j e_\xi (t)$, and taking the derivative of it yields

$$\begin{aligned} {\mathcal {L}} V(j,t)=\,&\sum \limits _{i=1}^r\breve{\omega }_i(t){\tilde{x}}^T(t)[P_j(A_{ij}-L_{ij}C_j)\\&+\,(A_{ij}-L_{ij}C_j)^TP_j]{\tilde{x}}(t)\\&+\,2{\tilde{x}}^T(t)P_jD_je_\xi (t)\\&+\,2e_\xi ^T(t)\Gamma _j\dot{f}_a(t)- 2e_\xi ^T(t)\Gamma _jK_jC_jA_{ij}{\tilde{x}}(t)\\&-e_\xi ^T(t)((\Gamma _jQ_j)^T+\Gamma _jQ_j)e_\xi (t)\\&+\,{\tilde{x}}^T(t)\sum _{l=1}^s\pi _{jl}P_l{\tilde{x}}(t)+e_\xi ^T(t)\sum _{l=1}^s\pi _{jl}\Gamma _le_\xi (t). \end{aligned}$$

(10)

According to Lemma 1, we have

$$\begin{aligned} 2e_\xi (t)^T\Gamma _j\dot{f}_a(t)\le \delta \dot{f}_a^T(t)\dot{f}_a(t) +\frac{1}{\delta } e_\xi ^T(t)\Gamma _j^T\Gamma _j e_\xi (t), \end{aligned}$$

(11)

where $\delta >0$. Substituting (11) into (10) yields

$$\begin{aligned} {\mathcal {L}} V(j,t)\le&\sum _{i=1}^r\breve{\omega }_i(t){\tilde{x}}^T(t)[P_j(A_{ij}-L_{ij}C_j)\\&+\,(A_{ij}-L_{ij}C_j)^TP_j]{\tilde{x}}(t)\\&+\,2{\tilde{x}}^T(t)P_jD_je_\xi (t)-2e_\xi ^T(t)\Gamma _jK_jC_jA_{ij}{\tilde{x}}(t)\\&-e_\xi ^T(t)((\Gamma _jQ_j)^T+\Gamma _jQ_j)e_\xi (t)\\&+\,{\tilde{x}}^T(t)\sum _{l=1}^s\pi _{jl}P_l{\tilde{x}}(t)+e_\xi ^T(t)\sum _{l=1}^s\pi _{jl}\Gamma _l e_\xi (t)\\&+\,\delta \dot{f}_a^T(t)\dot{f}_a(t)+\frac{1}{\delta } e_\xi ^T(t)\Gamma _j^T\Gamma _j e_\xi (t) \end{aligned}$$

(12)

Rewrite (12) into a compact form as

$$\begin{aligned} {\mathcal {L}} V(j,t) \le&\sum _{i=1}^r\breve{\omega }_i(t)\zeta ^T(t) \left[ {\begin{array}{*{20}{c}} {{\bar{\Phi }} _{11}}&{}{{\bar{\Phi }} _{12}}\\ {*}&{}{{\bar{\Phi }} _{22}}\end{array}}\right] \zeta (t)\\&+\,\delta \dot{f}_a^T(t)\dot{f}_a(t)\\ =\,&\sum _{i=1}^r\breve{\omega }_i(t)\zeta ^T(t)\Omega _{ij}\zeta +\delta \dot{f}_a^T(t)\dot{f}_a(t) \end{aligned}$$

(13)

where $\zeta =\left[ {\begin{array}{*{20}{c}} {\tilde{x}(t)}&{e_{\xi }(t)}\end{array}}\right] ^T$, ${\bar{\Phi }}_{11}=P_j(A_{ij}-L_{ij}C_j)+(A_{ij}-L_{ij}C_j)^TP_j+\sum \limits _{l=1}^s\pi _{jl}P_l$, ${\bar{\Phi }}_{12}=P_jD_j-A_{ij}^TC_{ij}^TK_j^T\Gamma _j^T$, ${\bar{\Phi }}_{22}=\frac{1}{\delta }\Gamma _j^T\Gamma _j+\sum \limits _{l=1}^s\pi _{jl}\Gamma _l-(\Gamma _jQ_j)^T-\Gamma _jQ_j$, and $\Omega _{il}=\left[ {\begin{array}{*{20}{c}} {{\bar{\Phi }} _{11}}&{}{{\bar{\Phi }} _{12}}\\ {*}&{}{{\bar{\Phi }} _{22}}\end{array}}\right]$.

By performing Schur complement on $\Omega _{il}<0$, one obtains

$$\begin{aligned} \left[ {\begin{array}{*{20}{c}} {{\bar{\Phi }} _{11}}&{}{{\bar{\Phi }} _{12}}&{}{0}\\ {*}&{}{\sum \limits _{j=1}^s\pi _{lj}\Gamma _j-(\Gamma _jQ_j)^T-\Gamma _jQ_j}&{}{\Gamma _j^T}\\ {*}&{}{*}&{}{-\delta I_q}\end{array}}\right] <0, \end{aligned}$$

(14)

which equals to (9) by noticing $\Psi _j=((C_jD_j)^TC_jD_j))^{-1}(C_jD_j)^T$, $M_j=\Gamma _jQ_j$ and $Y_{ij}=P_jL_{ij}$. Hence, on the one hand, we have

$$\begin{aligned} {\mathcal {L}} V(j,t) \le -\sum _{i=1}^r\breve{\omega }_i(t) {\lambda _{min}(-\Omega _{ij})(\Vert \tilde{x}(t)\Vert ^2+\Vert e_\xi (t)\Vert ^2)}+\delta \varepsilon ^2. \end{aligned}$$

(15)

On the other hand, one gets

$$\begin{aligned} V(j,t)&\le \lambda _{max}(P_j)(\Vert {\tilde{x}}(t)\Vert ^2)+\lambda _{max}(\Gamma _j)\Vert e_\xi (t)\Vert ^2)\\&\le max\{\lambda _{max}(P_j),\lambda _{max}(\Gamma _j)\}(\Vert {\tilde{x}}(t)\Vert ^2+\Vert e_\xi (t)\Vert ^2), \end{aligned}$$

(16)

which implies that

$$\begin{aligned} \Vert {\tilde{x}}(t)\Vert ^2+\Vert e_\xi (t)\Vert ^2 \ge \frac{V(j,t)}{max\{\lambda _{max}(P_l),\lambda _{max}(\Gamma _l)\}}. \end{aligned}$$

(17)

Substituting (17) into (15) yields

$$\begin{aligned} {\mathcal {L}} V(j,t)\le -\beta V(j,t)+\delta \varepsilon ^2, \end{aligned}$$

(18)

where $\beta =\frac{min\{\lambda _{min}(-\Omega _{il})\}}{max\{\lambda _{max}(P_l),\lambda _{max}(\Gamma _l)\}}$.

If the pair $({\tilde{x}}(t),e_\xi (t))\in {\mathcal {W}}$, where

$$\begin{aligned} {\mathcal {W}}= & {} \left\{ (\Vert {\tilde{x}}(t)\Vert ,\Vert e_\xi (t)\Vert )\vert \lambda _{min}(P_l)\Vert {\tilde{x}}(t)\Vert ^2\right. \\&\left. +\lambda _{min}(\Gamma _l)\Vert e_\xi (t)\Vert ^2\ge \frac{\delta \varepsilon ^2}{\beta }\right\} , \end{aligned}$$

there exists ${\mathcal {L}} V(l,t)\le 0$, which ensures the uniformly bounded stability. Then, (7) and (8) converge to ${\mathcal {W}}$ at a rate greater than $e^{-\beta t}$, according to the Lyapunov stability theory and (18). This ends the proof. $\square$

Remark 3

If the actuator fault is constant, the inequality (18) becomes ${\mathcal {L}} V(j,t)\le -\beta V(j,t)$, which guarantees the mean-square exponentially stability [30]. This means, for the constant fault, the proposed observer can acquire a more accurate estimation.

Remark 4

In fact, the intermediate variable is used to generate the estimated fault with the help of the output. However, this requires the estimation of $\xi (t)$ since the output has been already known. Hence, the dynamics of the intermediate variable $\xi (t)$ is given in (2), in order to design another observer to estimate it. After estimating the intermediate variable $\xi (t)$, the estimation of the fault can be obtained by the third equation of (3).

4 Extension to Multiple Fault Estimation

In this section, the sensor fault is considered in the original system, which can also be estimated by the developed observer. A kind of interval type-2 fuzzy MJS, suffering from the sensor fault, can be written as follows:

$$\begin{aligned} \left\{ \begin{array}{ll}\dot{x}(t)=\sum \limits_{i=1}^r\breve{\omega }_i(t)[A_{ij}x(t)+B_{ij}u(t)+D_jf_a(t)]\\ y(t) = C_jx(t)+E_jf_s(t) \end{array} \right. , \end{aligned}$$

(19)

where $f_s(t) \in R^{\omega }$ is the occurred sensor fault.

Assumption 3

The derivative of the considered sensor fault $\dot{f}_s(t)$ is bounded by some positive integer $\chi$, that is $\Vert \dot{f}_s(t)\Vert \le \chi$.

Define a new variable ${\bar{x}}(t)=\left[ {\begin{array}{*{20}{c}} {x(t)}\\ {f_s(t)}\end{array}}\right]$, then system (19) can be transformed into

$$\begin{aligned} \left\{ \begin{array}{l}\dot{{\bar{x}}}(t)=\sum \limits _{i=1}^r\breve{\omega }_i(t)[{\bar{A}}_{ij}{\bar{x}}(t)+{\bar{B}}_{ij}u(t)+{\bar{D}}_jf_a(t)+{\bar{I}}\dot{f}_s(t)]\\ y(t) = {\bar{C}}_j{\bar{x}}(t) \end{array} \right. , \end{aligned}$$

(20)

where ${\bar{A}}_{ij}=\left[ {\begin{array}{*{20}{c}} {A_{ij}}&{}{0}\\ {0}&{}{0}\end{array}}\right]$ , ${\bar{B}}_{ij}=\left[ {\begin{array}{*{20}{c}} {B_{ij}}\\ {0}\end{array}}\right]$ ,${\bar{D}}_j=\left[ {\begin{array}{*{20}{c}} {D_j}\\ {0}\end{array}}\right]$, ${\bar{I}}=\left[ {\begin{array}{*{20}{c}} {0}\\ {I}\end{array}}\right]$ , and ${\bar{C}}_j=\left[ {\begin{array}{*{20}{c}} {C_j}&{E_j}\end{array}}\right]$.

Then, define a new variable ${\bar{\xi }}(t)=f_a(t)-{\bar{K}}_jy(t)$, where ${\bar{K}}_j \in R^{q \times p}$ is an unknown matrix to be determined later. Similarly, we have

$$\begin{aligned} \dot{{\bar{\xi }}}(t)=\,&\dot{f}_a(t)-\sum _{i=1}^r\breve{\omega }_i(t)[{\bar{K}}_j{\bar{C}}_j{\bar{A}}_{ij}x(t)+{\bar{K}}_j{\bar{C}}_j{\bar{B}}_{ij}u(t)\\&+\,{\bar{K}}_j{\bar{C}}_j{\bar{D}}_{j}f_a(t)+{\bar{K}}_j{\bar{C}}_j{\bar{I}}\dot{f}_s(t)]. \end{aligned}$$

(21)

According to the structures of (20) and (21), the fault estimation observer is proposed as:

$$\begin{aligned} \left\{ \begin{array}{ll}\dot{\hat{{\bar{x}}}}(t)=\sum \limits _{i=1}^r\breve{\omega }_i(t)[{\bar{A}}_{ij}\hat{{\bar{x}}}(t)+{\bar{B}}_{ij}u(t)+{\bar{D}}_j\hat{f_a}(t)\\ +\,{\bar{L}}_{ij}(y(t)-{\hat{y}}(t))]\\ \dot{\hat{{\bar{\xi }}}}(t)=-\sum _{i=1}^r\breve{\omega }_i(t)[{\bar{K}}_j{\bar{C}}_j{\bar{A}}_{ij}\hat{{\bar{x}}}(t)+{\bar{K}}_j{\bar{C}}_j{\bar{B}}_{ij}u(t)\\ +{\bar{K}}_j{\bar{C}}_j{\bar{D}}_j{\hat{\xi }}(t)+{\bar{K}}_j{\bar{C}}_j{\bar{D}}_j{\bar{K}}_jy(t)]\\ \hat{f}_a(t)=\hat{{\bar{\xi }}}(t)+{\bar{K}}_jy(t) \end{array} \right. ,\end{aligned}$$

(22)

where ${\bar{L}}_{ij}\in R^{(n+\omega )\times p}$ and ${\bar{K}}_{j}\in R^{q\times p}$ are the unknown observer gain matrices.

Define $\tilde{{\bar{x}}}(t)={\bar{x}}(t)-\hat{{\bar{x}}}(t)$ and ${\tilde{\xi }}(t)={\bar{\xi }}(t)-\hat{{\bar{\xi }}}(t)$. Then, the error dynamic systems are

$$\begin{aligned} \dot{{\tilde{x}}}(t)=\sum _{i=1}^r\breve{\omega }_i(t)[({\bar{A}}_{ij}-{\bar{L}}_{ij}{\bar{C}}_j){\tilde{\bar{x}}}(t)+{\bar{D}}_j{\tilde{\xi }}(t)+{\bar{I}}\dot{f}_s(t)], \end{aligned}$$

(23)

and

$$\begin{aligned} \dot{\tilde{{\bar{\xi }}}}(t)= \,& \dot{f}_a(t)-\sum _{i=1}^r\breve{\omega }_i(t)[{\bar{K}}_j{\bar{C}}_j{\bar{A}}_{ij}\tilde{{\bar{x}}}(t) \nonumber \\&+\,{\bar{K}}_j{\bar{C}}_j{\bar{D}}_j\tilde{{\bar{\xi }}}(t)+{\bar{K}}_j{\bar{C}}_j{\bar{I}}\dot{f}_s(t)]. \end{aligned}$$

(24)

The structure of matrix ${\bar{K}}_j$ is constructed as

$$\begin{aligned} {\bar{K}}_j={\bar{Q}}_j(({\bar{C}}_j{\bar{D}}_j)^T{\bar{C}}_j{\bar{D}}_j)^{-1}({\bar{C}}_j{\bar{D}}_j)^T, \end{aligned}$$

where ${\bar{Q}}_j\in R^{q\times q}$ is an arbitrary matrix that can be determined later. According to Assumption 2, we know that

$$\begin{aligned} {\bar{C}}_j{\bar{D}}_j=\left[ {\begin{array}{*{20}{c}} {C_{j}}&{E_j} \end{array}}\right] \left[ {\begin{array}{*{20}{c}} {D_{j}}\\ {0} \end{array}}\right] =C_jD_j \end{aligned}$$

Hence, ${\bar{C}}_j{\bar{D}}_j$ is of full column rank and $({\bar{C}}_j{\bar{D}}_j)^T{\bar{C}}_j{\bar{D}}_j$ is invertible. Substitute ${\bar{K}}_j$ into (24) and we have

$$\begin{aligned} \dot{\tilde{{\bar{\xi }}}}(t)=\dot{f}_a(t)-\sum _{i=1}^r\breve{\omega }_i(t)[{\bar{K}}_j{\bar{C}}_j{\bar{A}}_{ij}{\tilde{x}}(t) +{\bar{Q}}_j{\tilde{\xi }}(t)+{\bar{K}}_j{\bar{C}}_j{\bar{I}}\dot{f}_s(t)]. \end{aligned}$$

(25)

The following Theorem 2 is another main result of this paper, which extends the previous result to the multiple fault situation.

Theorem 2

For given scalars $\varepsilon _1,\varepsilon _2,\varepsilon _3>0$, if there exist matrices ${\bar{P}}_j\in R^{(n+\omega )\times (n+\omega )}>0$, ${\bar{\Gamma }}_j \in R^{q\times q}>0$ and matrices ${\bar{Y}}_{ij}\in R^{(n+\omega )\times p}$ and ${\bar{M}}_j \in R^{q\times q}$, the following linear matrix inequality is feasible for $i=1,2,..,r$, $j=1,2,...,s$,

$$\begin{aligned} \left[ {\begin{array}{*{20}{c}} {{\bar{\psi }}_{11}}&{}{{\bar{\psi }}_{12}}&{}{0}&{}{{\bar{P}}_j{\bar{I}}}&{}{0}\\ {*}&{}{{\bar{\psi }}_{22}}&{}{{\bar{\Gamma }}_j}&{}{0}&{}{{\bar{I}}^T{\bar{C}}_j^T{\bar{\psi }}_j^T{\bar{M}}_j^T}\\ {*}&{}{*}&{}{-\varepsilon _1I}&{}{0}&{}{0}\\ {*}&{}{*}&{}{*}&{}{-\varepsilon _2I}&{}{0}\\ {*}&{}{*}&{}{*}&{}{*}&{}{-\varepsilon _3I} \end{array}}\right] <0 \end{aligned}$$

(26)

where ${\bar{\psi }}_{11}={\bar{P}}_j{\bar{A}}_{ij}-{\bar{Y}}_{ij}{\bar{C}}_j+({\bar{P}}_j{\bar{A}}_{ij}-{\bar{Y}}_{ij}{\bar{C}}_j)^T+\sum \limits _{l=1}^s\pi _{jl}{\bar{P}}_l$, ${\bar{\psi }}_{12}={\bar{P}}_j{\bar{D}}_{j}-{\bar{A}}_{ij}^T{\bar{C}}_j^T{\bar{\psi }}_j^T{\bar{M}}_j^T$, ${\bar{\psi }}_{22}=-{\bar{M}}_j^T-{\bar{M}}_j+\sum \limits _{l=1}^s\pi _{jl}{\bar{\Gamma }}_l$, ${\bar{\Psi }}_j=(({\bar{C}}_j{\bar{D}}_j)^T{\bar{C}}_j{\bar{D}}_j)^{-1}({\bar{C}}_j{\bar{D}}_j)^T$, ${\bar{M}}_j={\bar{\Gamma }}_jQ_j$, and ${\bar{Y}}_{ij}={\bar{P}}_j{\bar{L}}_{ij}$, then, the error systems (23) and (25) are uniformly stable.

Proof

Consider the Lyapunov function as ${\bar{V}}(j,t)=\tilde{{\bar{x}}}^T(t){\bar{P}}_j \tilde{{\bar{x}}}(t)+\tilde{{\bar{\xi }}}^T(t){\bar{\Gamma }}_j\tilde{{\bar{\xi }}}(t)$, and taking the derivative of it yields

$$\begin{aligned} {\mathcal {L}} {\bar{V}}(j,t)=\,&\sum _{i=1}^r\breve{\omega }_i(t)\tilde{{\bar{x}}}^T(t)[{\bar{P}}_j({\bar{A}}_{ij}-{\bar{L}}_{ij}{\bar{C}}_j)\\&\,+({\bar{A}}_{ij}-{\bar{L}}_{ij}{\bar{C}}_j)^T{\bar{P}}_j]\tilde{{\bar{x}}}(t)\\&\,+2\tilde{{\bar{x}}}^T(t){\bar{P}}_j{\bar{D}}_j{\tilde{\xi }}(t)+2{\tilde{\xi }}^T(t){\bar{\Gamma }}_j\dot{f}_a(t)\\&\,-2{\tilde{\xi }}^T(t){\bar{\Gamma }}_j{\bar{K}}_j{\bar{C}}_j{\bar{A}}_{ij}{\tilde{x}}(t)\\&\,-{\tilde{\xi }}^T(t)({\bar{\Gamma }}_jQ_j+({\bar{\Gamma }}_jQ_j)^T){\tilde{\xi }}(t)\\&\,+\tilde{{\bar{x}}}^T(t)\sum _{l=1}^s\pi _{jl}{\bar{P}}_j\tilde{{\bar{x}}}(t)\\&\,+{\tilde{\xi }}^T(t)\sum _{l=1}^s\pi _{jl}{\bar{\Gamma }}_j{\tilde{\xi }}(t)\\&\,+2\tilde{{\bar{x}}}^T(t){\bar{P}}_j{\bar{I}}\dot{f}_s(t)-2{\tilde{\xi }}^T(t){\bar{\Gamma }}_j{\bar{K}}_j{\bar{C}}_j{\bar{I}}\dot{f}_s(t).\end{aligned}$$

(27)

According to lemma 1, we have

$$\begin{aligned}2{\tilde{\xi }}^T(t){\bar{\Gamma }}_j\dot{f}_a(t)\le \varepsilon _1\delta ^2I+\frac{1}{\varepsilon _1}{\tilde{\xi }}^T(t){\bar{\Gamma }}_j^T{\bar{\Gamma }}_j{\tilde{\xi }}(t), \end{aligned}$$

(28)

$$\begin{aligned}2\tilde{{\bar{x}}}^T(t){\bar{P}}_j{\bar{I}}\dot{f}_s(t)\le \varepsilon _2\chi ^2I+\frac{1}{\varepsilon _2}\tilde{{\bar{x}}}^T(t)({\bar{P}}_j{\bar{I}})^T{\bar{P}}_j{\bar{I}}\tilde{{\bar{x}}}(t), \end{aligned}$$

(29)

$$\begin{aligned}&-2{\tilde{\xi }}^T(t){\bar{\Gamma }}_j{\bar{K}}_j{\bar{C}}_j{\bar{I}}\dot{f}_s(t) \le \varepsilon _3\chi^2I\\ &\qquad +\frac{1}{\varepsilon _3}{\tilde{\xi }}^T(t)({\bar{\Gamma }}_j{\bar{K}}_j{\bar{C}}_j{\bar{I}})^T{\bar{\Gamma }}_j{\bar{K}}_j{\bar{C}}_j{\bar{I}}{\tilde{\xi }}(t). \end{aligned}$$

(30)

Substituting (28)–(30) into (27) yields

$$\begin{aligned} {\mathcal {L}} {\bar{V}}(j,t) \le&\sum _{i=1}^r\breve{\omega }_i(t)\tilde{{\bar{x}}}^T(t)[{\bar{P}}_j({\bar{A}}_{ij}-{\bar{L}}_{ij}{\bar{C}}_j)\\&+\,({\bar{A}}_{ij}-{\bar{L}}_{ij}{\bar{C}}_j)^T{\bar{P}}_j]\tilde{{\bar{x}}}(t)\\&+\,2\tilde{{\bar{x}}}^T(t){\bar{P}}_j{\bar{D}}_j{\tilde{\xi }}(t)\\&-2{\tilde{\xi }}^T(t){\bar{\Gamma }}_j{\bar{K}}_j{\bar{C}}_j{\bar{A}}_{ij}{\tilde{x}}(t)\\&-{\tilde{\xi }}^T(t)({\bar{\Gamma }}_jQ_j+({\bar{\Gamma }}_jQ_j)^T){\tilde{\xi }}(t)\\&+\,\tilde{{\bar{x}}}^T(t)\sum _{l=1}^s\pi _{jl}{\bar{P}}_j\tilde{{\bar{x}}}(t) +{\tilde{\xi }}^T(t)\sum _{l=1}^s\pi _{jl}{\bar{\Gamma }}_j{\tilde{\xi }}(t)\\&+\,\varepsilon _1\delta ^2I+\frac{1}{\varepsilon _1}{\tilde{\xi }}^T(t){\bar{\Gamma }}_j^T{\bar{\Gamma }}_j{\tilde{\xi }}(t)\\&+\,\varepsilon _2\chi ^2I+\frac{1}{\varepsilon _2}\tilde{{\bar{x}}}^T(t)({\bar{P}}_j{\bar{I}})^T{\bar{P}}_j{\bar{I}}\tilde{{\bar{x}}}(t)\\&+\,\varepsilon _3\chi ^2I+\frac{1}{\varepsilon _3}{\tilde{\xi }}^T(t)({\bar{\Gamma }}_j{\bar{K}}_j{\bar{C}}_j{\bar{I}})^T{\bar{\Gamma }}_j{\bar{K}}_j{\bar{C}}_j{\bar{I}}{\tilde{\xi }}(t). \end{aligned}$$

(31)

Rewrite (31) into a compact form as

$$\begin{aligned} {\mathcal {L}} {\bar{V}}(l,t) \le&\sum _{i=1}^r\breve{\omega }_{il}(t) \left[ {\begin{array}{*{20}{c}} {\tilde{{\bar{x}}}(t)}\\ {{\tilde{\xi }}(t)} \end{array}}\right] ^T{\bar{\Omega }}_{ij}\left[ {\begin{array}{*{20}{c}} {\tilde{{\bar{x}}}(t)}\\ {{\tilde{\xi }}(t)} \end{array}}\right] \\&+\,\varepsilon _1\delta ^2+\varepsilon _2\chi ^2+\varepsilon _3\chi ^2, \end{aligned}$$

(32)

where

$$\begin{aligned} {\bar{\Omega }}_{ij}= & {} \left[ {\begin{array}{*{20}{c}} { {\bar{\varrho }}_{11}}&{}{{\bar{\varrho }}_{12}}\\ {*}&{}{{\bar{\varrho }}_{22}} \end{array}}\right] , \\ {\bar{\varrho }}_{11}= & {} {\bar{P}}_j({\bar{A}}_{ij}-{\bar{L}}_{ij}{\bar{C}}_j)+({\bar{A}}_{ij}- {\bar{L}}_{ij}{\bar{C}}_j)^T{\bar{P}}_j\\&+\,\sum _{l=1}^s\pi _{jl}{\bar{P}}_j+\frac{1}{\varepsilon _2} ({\bar{P}}_j{\bar{I}})^T{\bar{P}}_j{\bar{I}}, \\ {\bar{\varrho }}_{12}= & {} {\bar{P}}_j{\bar{D}}_j-(\Gamma _j{\bar{K}}_j{\bar{C}}_j{\bar{A}}_{ij})^T, \\ {\bar{\varrho }}_{22}= & {} -{\bar{\Gamma }}_j{\bar{Q}}_j-({\bar{\Gamma }}_j{\bar{Q}}_j)^T+\sum _{l=1}^s\pi _{jl} {\bar{\Gamma }}_j\\&+\,\frac{1}{\varepsilon _1}{\bar{\Gamma }}_j^T{\bar{\Gamma }}_j+\frac{1}{\varepsilon _3} ({\bar{\Gamma }}_j{\bar{K}}_j{\bar{C}}_j{\bar{I}})^T{\bar{\Gamma }}_j{\bar{K}}_j{\bar{C}}_j{\bar{I}}. \end{aligned}$$

By performing Schur complement on $\Omega _{ij}$, one obtains $\Omega _{ij}<0$ by noticing ${\bar{\Psi }}_j=(({\bar{C}}_j{\bar{D}}_j)^T{\bar{C}}_j{\bar{D}}_j)^{-1}({\bar{C}}_j{\bar{D}}_j)^T$, ${\bar{M}}_j={\bar{\Gamma }}_j{\bar{Q}}_j$, and ${\bar{Y}}_{ij}={\bar{P}}_j{\bar{L}}_{ij}$.

By following the similar steps with the analysis in Theorem 1, we can prove that the error systems (23) and (25) are uniformly stable. This ends the proof. $\square$

Further, to better understand the whole design process, detailed algorithms are listed as follows.

(1) Solve the inequality (9) in Theorem 1 to compute $P_j$, $\Gamma _j$, $Y_{ij}$ and $M_j$, whereupon the observer gain matrix $L_{ij}$ and slack variable $Q_j$ can be worked out as $L_{ij}=P_j^{-1}Y_{ij}$ and $Q_j=\Gamma _j^{-1}M_j$.

(2) Then based on 1), another gain matrix $K_j$ can be obtained by $K_j=Q_j((C_jD_j)^TC_jD_j)^{-1}(C_jD_j)^T$.

(3) With the obtained $L_{ij}$ and $K_j$, the observer in (3) can be constructed in order to provide ${\hat{\xi }}(t)$. Hence, the estimated actuator fault can be obtained from the third equation of (3).

Remark 5

In this paper, a novel fault estimation observer is developed for interval type-2 fuzzy MJSs, by use of the intermediate variable method. With the aid of an introduced intermediate variable, the fault estimation observer is designed to estimate the actuator fault. In addition, to further discuss the extension of the proposed method, the designed observer is then proved to be applicable for the multiple fault case. It is worth saying that the proposed fault estimation observer shows some superiorities over those existing ones. For instance, a majority of existing methods employed the sliding mode observers, adaptive observers or unknown input observers to estimate faults. Specifically, the sliding mode observer cannot applied well to MJSs due to their stochastic switching natures. The adaptive observer would pose conservatism for computing the gain matrices. The unknown input observer has to involve the derivative of the output, which is factually hard to be realized for MJSs. In contrast, the proposed method applies to both the standard and switching systems and, with a special design of the gain matrix, its freedom in matrix calculations turns out to be greater than the above-mentioned ones which has been explained in Remark 6.

Remark 6

In view of the designed observer structure, a slack variable is introduced in the gain matrix design, so as to augment the freedom in gain matrix calculations. In this way, the design of $K_j$ allows the estimation error system to be transformed into (8). In addition, consider the observer error system (7), which can be robustly stable by making the pair $(A_{ij},C_j)$ observable. Then, it is obvious that the stability of (7) has a big chance to ensure the convergence of (8) for a positive variable matrix $Q_j$. In fact, these two conditions are normal, and they are easy to satisfy as well as to apply in computing gain matrices, suggesting that the proposed method has a large design freedom.

Remark 7

In traditional fault estimation methods, some restrictive conditions were required, which were however difficult to satisfy in practice. For example, the sliding mode observer and unknown input observer needed to satisfy observer matching conditions, while the reduced-order observer required the system matrices to satisfy some special rank conditions. In contrast, the proposed observer makes no demand on such restrictive preconditions anymore, which can thus undoubtedly extend its application scopes.

Remark 8

In fact, the observer design algorithm and the controller design algorithm are two different things. According to the separate principle, the algorithm of observer design has nothing to do with that of the controller design. Specifically, the controller algorithm is mainly developed to keep the system safe and reliable. In contrast, the observer algorithm in this paper is developed to estimate the actuator fault and sensor fault simultaneously. On the other hand, the core to the controller algorithm consists in seeking a suitable control gain matrix as to keep the closed-loop system stable, while the observer algorithm is devoted to design a gain matrix as to make the estimation error system stable. It is apparent that these two algorithms are totally different.

5 Simulation

5.1 Single Fault Situation

In this section, the developed fault estimation method is applied to the considered system with actuator fault. The system matrices are represented as

$$\begin{aligned}&A_{11}=\left[ {\begin{array}{*{20}{c}} {-2}&{}{0}\\ {0}&{}{-1}\end{array}}\right] ,A_{12}=\left[ {\begin{array}{*{20}{c}} {-2}&{}{0.1}\\ {0}&{}{-1}\end{array}}\right] , \\&A_{21}=\left[ {\begin{array}{*{20}{c}} {-1}&{}{0}\\ {1}&{}{-1}\end{array}}\right] ,A_{22}=\left[ {\begin{array}{*{20}{c}} {-2}&{}{1}\\ {0}&{}{-1}\end{array}}\right] ,\\&B_{11}=\left[ {\begin{array}{*{20}{c}} {-1}\\ {1}\end{array}}\right] ,B_{12}=\left[ {\begin{array}{*{20}{c}} {1}\\ {-1}\end{array}}\right] ,\\&B_{21}=\left[ {\begin{array}{*{20}{c}} {0}\\ {1}\end{array}}\right] ,B_{22}=\left[ {\begin{array}{*{20}{c}} {-1}\\ {0}\end{array}}\right] ,\\&D_{11}=\left[ {\begin{array}{*{20}{c}} {-1}\\ {1}\end{array}}\right] ,D_{12}=\left[ {\begin{array}{*{20}{c}} {-1}\\ {-1}\end{array}}\right] ,\\&D_{21}=\left[ {\begin{array}{*{20}{c}} {1}\\ {1}\end{array}}\right] ,D_{22}=\left[ {\begin{array}{*{20}{c}} {-1}\\ {0}\end{array}}\right] ,\\&C_{1}=\left[ {\begin{array}{*{20}{c}} {1}&{}{2}\\ {2}&{}{1}\end{array}}\right] ,C_{2}=\left[ {\begin{array}{*{20}{c}} {1}&{}{2}\\ {2}&{}{1}\end{array}}\right] . \end{aligned}$$

The actuator fault is set to be $f_a(t)=1$, which is constant. In addition, we set the transition rate matrix to be $\left[ {\begin{array}{*{20}{c}} {-2}&{}{2}\\ {1}&{}{-1}\end{array}}\right]$, and $\gamma =1$. In addition, $\breve{\omega }_1(t)=1-\frac{1}{e^{-(y_1+4+0.1sin(t))}}$, $\breve{\omega }_2(t)=1-\breve{\omega }_1(t)$. Substitute these parameters into Theorem 1, and we obtain

$$\begin{aligned}&L_{11}=\left[ {\begin{array}{*{20}{c}} {0.2190}&{}{-0.1218}\\ {-0.1218}&{}{0.1676}\end{array}}\right] ,L_{12}=\left[ {\begin{array}{*{20}{c}} {0.3066}&{}{-0.1706}\\ {-0.1706}&{}{0.2347}\end{array}}\right] ,\\&L_{21}=\left[ {\begin{array}{*{20}{c}} {0.2368}&{}{-0.2377}\\ {-0.2377}&{}{0.4742}\end{array}}\right] ,L_{22}=\left[ {\begin{array}{*{20}{c}} {0.3157}&{}{-0.3169}\\ {-0.3169}&{}{0.6322}\end{array}}\right] ,\\&K_{1}=\left[ {\begin{array}{*{20}{c}} {0.8779}&{0.4711}\end{array}}\right] ,K_2=\left[ {\begin{array}{*{20}{c}} {3.7973}&{2.0376}\end{array}}\right] . \end{aligned}$$

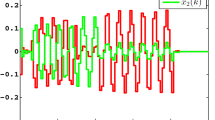
Hence, the designed observer (3) can be accomplished, and the corresponding performances are exhibited in the following Figs. 1 and 2 with the initial conditions being $x(0)=\left[ {\begin{array}{*{20}{c}} {0.2}&{0.1}\end{array}}\right] ^T$. The results reveal that the considered actuator fault can be estimated well, thus validating the proposed method.

The proposed method has shown the robustness against faults and disturbances in the estimation process. In the design process, the robustness against faults and disturbances is considered using the inequality technique, and thus the uniformly stability is closely tied to the boundaries of faults and disturbances. Especially for the incipient fault with low amplitudes, the proposed method has strong robustness, showing a good estimation performance. In order to testify the robustness of the proposed strategy, we have also examined it in the simulation, with $f_a(t)=0.8sin(0.01t)$ and $d(t)=0.05sin(t)$. Estimation results are depicted in Fig. 3, which clearly shows the robustness of the proposed method.

Fig. 1

Switching signal

Fig. 2

Actuator fault estimation

Fig. 3

Fault estimation performance with incipient fault

5.2 The Multiple Fault Situation

Based on the first simulation, now we assume that the sensor fault happens as $f_s(t)=0.01sin(t)+0.2sin(0.1t)$. By setting $\breve{\omega }_1(t)=1-\frac{1}{e^{-(y_1+4+0.1sin(t))}}$, $\breve{\omega }_2(t)=1-\breve{\omega }_1(t)$, and $\varepsilon _1=\varepsilon _2=\varepsilon _3=1$ , the observer gain matrices are calculated from Theorem 2 as

$$\begin{aligned}&L_{11}=\left[ {\begin{array}{*{20}{c}} {-8.4287}&{}{5.1785}\\ {-10.3043}&{}{16.0834}\\ {-14.2654}&{}{-2.7736}\end{array}}\right] , \\&L_{12}=\left[ {\begin{array}{*{20}{c}} {-6.0502}&{}{3.8064}\\ {-8.2632}&{}{13.3601}\\ {-12.2449}&{}{-1.5571}\end{array}}\right] ,\\&L_{21}=\left[ {\begin{array}{*{20}{c}} {7.8619}&{}{-3.1181}\\ {10.7543}&{}{-12.4733}\\ {8.8077}&{}{7.0415}\end{array}}\right] ,\\&L_{22}=\left[ {\begin{array}{*{20}{c}} {2.9507}&{}{-0.4474}\\ {4.9642}&{}{-4.6145}\\ {2.5448}&{}{4.2590}\end{array}}\right] ,\\&K_{1}=\left[ {\begin{array}{*{20}{c}} {2.5929}&{1.3913}\end{array}}\right] ,K_{2}=\left[ {\begin{array}{*{20}{c}} {20.4323}&{10.9637}\end{array}}\right] . \end{aligned}$$

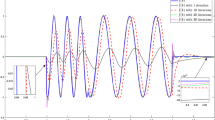
The simulation results are shown in Figs. 4 and 5, from which we can see that the proposed fault estimation method can provide accurate actuator and sensor fault estimations, thus showing the effectiveness of the proposed method.

Fig. 4

Actuator fault estimation

Fig. 5

Sensor fault estimation

5.3 Comparative Study and Comparative Analysis

To validate the above-mentioned discussions in Remarks 5-7, we also provide some comparisons from the simulation aspect. In detail, Fig. 2 shows estimation results for actuator fault and sensor fault from the proposed method, while Figs. 6 and 7 from the adaptive observer and sliding mode observer-based methods, respectively. By comparing Figs. 2 and 6, one can clearly see that the convergence of the proposed observer is much faster, implying a better transient response, as stated in Remark 6. From Figs. 2 and 7, the sliding mode observer performs poorly in the fault estimation, on account of the chattering phenomenon, which is inescapable for large fault amplitudes as stated in Remark 5.

In addition, we let the $Q_i$ to be 3, and $K_i$ tends to be constant, like the method proposed in [30]. However, we find that, in this case, the linear matrix inequalities in Theorem 1 are not feasible. However, the proposed method can always find the feasible solution due to the design of $K_i$. Hence, this reveals that the proposed method has less conservatism than the existing methods, and has much more freedom to have solution to the designed observer, as stated in Remarks 2 and 6.

Fig. 6

Fault estimation performance using the adaptive observer-based method

Fig. 7

Fault estimation performance using the sliding mode observer-based method

5.4 Practical Example

This example is brought to prove the feasibility of the proposed method for MJSs. We choose the decoupled circuit of inductively coupled power transmission system, which is composed of inductors, capacitances, resistors, Mos-tubes and diodes. The equivalent circuit can be described in Fig. 8, by letting the bridge rectifying circuit be equalled to a signal, obeying the Markov process [11]. The followings are the system matrices of the circuit.

$$\begin{aligned}&A = \left[ {\begin{array}{*{20}{c}} {\frac{{ - {R_p}{L_s}}}{{{M_{ps}}}}}&{}{\frac{{ - {L_s}}}{{{M_{ps}}}}}&{}{\frac{{ - M{R_s}}}{{{M_{ps}}}}}&{}{\frac{{ - M}}{{{M_{ps}}}}}&{}{\frac{{ - M{S_r}(t)}}{{{M_{ps}}}}}\\ {\frac{1}{{{C_p}}}}&{}0&{}0&{}0&{}0\\ {\frac{{ - {R_p}}}{{{M_{ps}}}}}&{}{\frac{{ - M}}{{{M_{ps}}}}}&{}0&{}{\frac{{ - {L_p}}}{{{M_{ps}}}}}&{}0\\ 0&{}0&{}{\frac{1}{{{C_s}}}}&{}0&{}0\\ 0&{}0&{}{\frac{{{S_r}}}{{{C_d}}}}&{}0&{}{\frac{{ - 1}}{{{C_d}{R_d}}}} \end{array}} \right] , \\&B = {\left[ {\begin{array}{*{20}{c}} {\frac{{{L_s}{S_r}(t)}}{{{L_p}{L_s} - {M^2}}}}&0&{\frac{{M{S_r}(t)}}{{{L_p}{L_s} - {M^2}}}}&0&0 \end{array}} \right] ^T},\\&{M_{ps}} = {L_p}{L_s} - {M^2},\\&C = \left[ {\begin{array}{*{20}{c}} 1&{}0&{}0&{}0&{}0\\ 0&{}1&{}1&{}0&{}0\\ 0&{}1&{}0&{}0&{}0\\ 0&{}0&{}0&{}0&{}1 \end{array}} \right] ,\\&{D} = {\left[ {\begin{array}{*{20}{c}} {\frac{{{L_s}{S_r}(t)}}{{{L_p}{L_s} - {M^2}}}}&0&{\frac{{M{S_r}(t)}}{{{L_p}{L_s} - {M^2}}}}&0&0 \end{array}} \right] ^T}. \end{aligned}$$

The signal ${S_r}(t) = \left\{ \begin{array}{l} 1,\,\,r = 1\\ - 1,\,\,\,r = 2 \end{array} \right.$ obeys a Markov process, and lead the model be a MJS. Referring to [11], the parameters are listed in Table 1 below.

Fig. 8

Sensor fault estimation

Table 1 Model Parameters for Inductively Coupled Power Transmission System

The other parameters are the same as the previous study, and especially, $\breve{\omega }_1(t)=1$. The actuator fault is set as $f_a(t) = \left\{ \begin{array}{l} 0,\,\,t\le 20\\ 2,\,\,\,t>20 \end{array} \right.$.

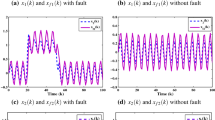
The simulation results are depicted in Figs. 9, 10, 11, and 12, which can prove the efficiency of the proposed method. The estimations of the states are provided in Figs. 9, 10, and 11, from which the estimated curves can track the real ones quickly and accurately. Figure 12 tells that the actuator fault can be estimated well using the proposed method.

Fig. 9

State estimation

Fig. 10

State estimation

Fig. 11

State estimation

Fig. 12

Actuator fault estimation

6 Conclusion

In this paper, a novel fault estimation observer is proposed for a class of MJSs. By defining a new variable, the actuator fault can be estimated without restrictive preconditions. The proposed estimation method owns large freedom owing to the special form of the observer gain matrix. The existence conditions of the designed observer is given in terms of linear matrix inequality. Two numerical examples are presented to validate the effectiveness of the proposed method. In addition, it can be seen that the convergence region of the estimation error depends on the derivative of the fault, which results in poor estimation performances for some faults with large derivatives. Then, how to figure out an effective way to ensure the asymptotic stability of the estimation error system becomes our next technical goal. What’s more, the membership function is not involved in the design process, which poses a conservatism of the proposed method. In order to improve the design freedom, the operation domain should be split, and then the membership functions can be estimated. Whereupon, a more relaxed existing condition of the observer can be obtained, which will also be our future works.