Dynamic Crosstalk Analysis in Coupled Interconnects for Ultra-Low Power Applications

Abstract

Ultra-low power circuit design has received a wide attention due to the fast growth and prominence of portable battery-operated devices with stringent power constraint. Though sub-threshold circuit operation shows huge potential toward satisfying the ultra-low power requirement, it holds challenging design issues. Of these, the increased crosstalk and delay have become serious challenges, particularly for sub-threshold interconnects as integration density increases with every scaled technology node. Consequently, in this paper an analytical approach providing closed form expressions for dynamic crosstalk in coupled interconnects under sub-threshold condition has been proposed. The proposed model is based on the sub-threshold current–voltage expression for a metal-oxide semiconductor transistor. The model determines the propagation delay and timings of the aggressor and victim drivers for the conditions when inputs are switching in-phase and out-of-phase. Subsequently, the transient analysis of dynamic crosstalk is carried out. The comparison of analytical results with SPICE shows that the model captures waveform shape, propagation delay, and timing with good accuracy, with less than 5 % error in timing estimation.

1 Introduction

The semiconductor electronics technology, as predicted by Moore, is toward dense, complex, and faster systems [9, 12]. With decreasing feature size and increasing average length of on-chip interconnections, the interconnect ground capacitance has become comparable to or larger than the input gate capacitance of the driven gate. The interconnect capacitance is therefore crucial in satisfying timing requirements. In deep submicron design, the spacing between interconnects is reduced and the thickness of the conductor is increased in order to reduce the parasitic resistance. The coupling capacitance has therefore increased significantly and has become comparable to the interconnect capacitance. The tightly coupled interconnects result in a higher probability of interaction resulting in unwanted interference which causes crosstalk [1, 7]. The crosstalk due to coupling capacitance has become extremely important in technologies below 0.18 $\upmu$m. The coupling capacitance is therefore, an important design parameter in evaluating the signal integrity of interconnects in a CMOS VLSI chip. The coupling capacitance increases the propagation delay and alters the waveform shape of the output voltage signal [11]. Consequently, the effects of the global interconnect impedance parameters particularly on delay is of great concern for the VLSI circuit designers.

Crosstalk in coupled lines can be broadly divided into two categories, viz.: (i) functional crosstalk and (ii) dynamic crosstalk. Under functional crosstalk, overshoots and undershoots are experienced on the victim (quiet) line because of switching activity on the aggressor (active) lines. Under the effect of dynamic crosstalk, noise is experienced when aggressor and victim lines switch simultaneously either in-phase or out-of-phase. Since it is common to encounter dynamic crosstalk in practice, its analysis is as important as that of functional crosstalk noise. This dynamic form of coupling causes a change in the signal propagation delay thus impacts the critical issue of timing. An accurate model for transient analysis of dynamic crosstalk is therefore important.

Low power design has also become one of the main focuses of modern VLSI circuits. The primary driving factor has been ever increasing demand for energy-constrained and battery-operated VLSI applications and biomedical devices. Sub-threshold circuits are shown to be the promising candidate for satisfying ultra-low power requirement of portable systems to ensure longer battery lifetime [8, 14]. Circuits operating in the sub-threshold regime results in ultra-low power dissipation, but significantly increase circuit propagation delay. However, reduction in power consumption outweighs the increase in delay, resulting in low power-delay product (PDP). Having a lower PDP means that sub-threshold circuit consumes lesser energy than its strong inversion counterpart when both operate with same amount of switching activities. Due to its slow performance, sub-threshold circuits are, however, limited to only certain applications where ultra-low power is the primary concern than speed [5]. Some of the applications include devices such as hearing aids, pacemakers, defibrillator, radio frequency identification (RFID), sensor nodes, and battery-operated devices such as cellular phones.

In previous works, the authors have investigated variability and speed as two important design challenges for sub-threshold circuits [3, 10]. However, there is a need to address the global interconnect performance under sub-threshold conditions because global interconnects contribute significantly to both power and speed at the nanoscale. Mathematical models in this direction if developed will be very useful for ultra-low power applications. Alternatively, there are more precise circuit models like BSIM and high level empirical models implemented in SPICE for the evaluation of integrated circuit performance. These models do not provide a closed form expression for the characteristics of the MOS transistor. However, the electrical behavior can be elucidated appropriately with the help of a relatively simpler analytical model than a highly accurate circuit simulation model. Consequently, work presented in this paper focuses on the development of analytical models providing closed form expressions for the waveform analysis and delay estimation of sub-threshold interconnect circuits in simultaneous switching coupled scenario. The accuracy of newly developed analytical expressions is also compared with SPICE. The rest of the paper is organized as follows: In Sect. 2, circuit model of MOS transistor in sub-threshold regime is presented. Analytical models for the dynamic crosstalk are proposed in Sect. 3. Results and their implications are discussed in Sect. 4. Finally, conclusions are drawn in Sect. 5.

2 MOS Transistor Model in Sub-threshold

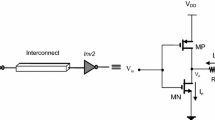
It is an important technique in VLSI to drive interconnects by buffers. Buffers have been realized using CMOS inverters. CMOS buffer and its equivalent symbolic representation are shown in Fig. 1 [6]. The n-channel drain-to-source current ($I_{n})$ of CMOS buffer in sub-threshold is governed by the expression provided in [4] which is

$$\begin{aligned} I_n =\mu _{n} C_{\mathrm{ox}}\frac{W_n}{L_n}(\mathop {\eta }\nolimits _n-1)U_{\mathrm{th}}^{2} \mathrm{e}^{\left( {\frac{V_{\mathrm{in}}-V_\mathrm{T}}{\mathop {\eta }\nolimits _n U_{\mathrm{th}}}}\right) }\left[ {1-\mathrm{e}^{\left( {-\frac{V_{\mathrm{ds}} }{U_{\mathrm{th}} }}\right) }}\right] , \end{aligned}$$

(1)

where $\mu _{n}$ is the electron mobility, $C_{\mathrm{ox}}$ is the gate-oxide capacitance per unit area, $W_{n}$ and $L_{{n}}$ are the effective channel width and channel length, respectively, $U_{\mathrm{th}}$ is the thermal voltage, $V_{\mathrm{T}}$ is the threshold voltage, $V_{\mathrm{in}}$ and $V_{\mathrm{ds}}$ are the input voltage and drain-to-source voltage, respectively, and $\mathop {\eta }\nolimits _{n}$ is the sub-threshold slope factor whose value lies between one and two.

Fig. 1

CMOS buffer driving an interconnect load and its equivalent representation

Here, the discussion digresses to identify two new regions in sub-threshold. According to [2], for large $V_{\mathrm{ds}}$, i.e., $V_{\mathrm{ds}} \ge 4U_{\mathrm{th}}$, the term $\exp \left( {-V_{\mathrm{ds}} }/{U_{\mathrm{th}}}\right)$ can be neglected in comparison to the unity. $I_{n}$ is thus independent of $V_{\mathrm{ds}}$ and the NMOS transistor (MN) is approximated by a constant current source. On the other hand, for small $V_{\mathrm{ds}}$, i.e., $V_{\mathrm{ds}} < U_{\mathrm{th}}$, $\exp \left( {{-V_{\mathrm{ds}} } {U_{\mathrm{th}}}}\right)$ becomes comparable to unity and hence cannot be neglected. Expanding the exponential term and neglecting higher order terms, $I_{n}$ becomes proportional to $V_{\mathrm{ds}}$ and MN behaves as a linear resistor. Summarizing, current in two regions can be expressed as

$$\begin{aligned} I_{n}&= B_n \mathrm{e}^{\left( {\frac{V_{\mathrm{in}} -V_\mathrm{T}}{{\eta }_n U_{\mathrm{th}}}}\right) } \qquad \qquad V_{\mathrm{ds}} \ge 4U_{\mathrm{th}}{:}\,{\hbox {sub-saturation\,region}}\nonumber \\&={\gamma }_n V_{\mathrm{ds}} \qquad \qquad \qquad \quad \; V_{\mathrm{ds}} <U_{\mathrm{th}}{:}\,{\hbox {sub-linear\,region}} \end{aligned}$$

(2)

In Eq. (2), $B_{n }$ and $\gamma _{n}$ are given as

$$\begin{aligned} B_n =\mu _n C_{\mathrm{ox}} \frac{W_n }{L_n }(\mathop {\eta }\nolimits _n -1) U_{\mathrm{th}}^2 \end{aligned}$$

(3)

$$\begin{aligned} \gamma _n =\mu _n C_{\mathrm{ox}} \frac{W_n }{L_n }(\mathop {\eta }\nolimits _n -1)U_{\mathrm{th}} \end{aligned}$$

(4)

$B_{n}$ is the drain-to-source current when $V_{\mathrm{in} }$ = $V_{\mathrm{T}}$ and $\gamma _{n }$ is the output conductance of MN in the sub-linear region. $B_{n}$ and $\gamma _{n}$ have the units of current and transconductance, respectively.

3 Proposed Analytical Model for Dynamic Crosstalk in Coupled Interconnects

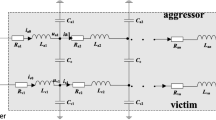
The proposed model considers CMOS gates driving two capacitively coupled lines. Sub-threshold model of a MOS transistor is used to analyze a CMOS driver. This is combined with coupled resistive-capacitive model of interconnect to derive analytical closed form expressions. Interconnect is modeled as lumped resistive-capacitive in order to emphasize the nonlinear behavior of the MOS devices. Such a representation of the composite model where two capacitively coupled lines each driven by CMOS inverter (Inv) has been shown in Fig. 2a.

Fig. 2

a Circuit model of buffer (inverter)-driven capacitively coupled interconnect lines. b Equivalent circuit of two capacitively coupled resistive-capacitive interconnections driven by CMOS buffers

The equivalent circuit for the same is shown in Fig. 2b. In this figure, $R_{1}$ ($R_{2})$ is the parasitic interconnect resistance, $C_{1}$ ($C_{2})$ is the intrinsic capacitance and includes the interconnect ground capacitance and the input gate capacitance of Inv3 (Inv4), $C_{\mathrm{c}}$ is the coupling capacitance between the wires.

The effects of coupling capacitance on the dynamic response of gate-driven coupled interconnects depend upon the switching activities at the gate inputs of these MOS transistors. The proposed analytical approach considers switching conditions as follows:

Case-I: $V_{\mathrm{in}1}$ is switching from low to high; $V_{\mathrm{in}2}$ switching from low to high. Thus, $V_{\mathrm{in}1}$ (input to Inv1) and $V_{\mathrm{in}2}$ (input to Inv2) are switching in the same direction or in-phase.

Case-II: $V_{\mathrm{in}1 }$ is switching from low to high and $V_{\mathrm{in}2}$ switches from high to low. Thus, $V_{\mathrm{in}1}$ and $V_{\mathrm{in}2}$ are switching out-of-phase. On this basis, expressions for the dynamic crosstalk have been developed and analyses of in-phase and out-of-phase switching presented.

3.1 Case-I: In-Phase Switching

The in-phase switching is an optimistic condition in terms of the effect of the coupling capacitance on the propagation delay of each CMOS inverter. It is assumed that Inv1 and Inv2 inputs transition from low to high. MN1 and MN2 are therefore the active transistors and MP1 and MP2 have been neglected in the foregoing analysis in each CMOS inverter as shown in Fig. 3. Fast ramp input is considered. An assumption of fast ramp input signal permits the condition that MN1 and MN2 operate in sub-saturation even after the completion of input transition.

Fig. 3

Equivalent circuit for the buffer-driven coupled interconnects switching simultaneously in-phase for low-to-high input transitions

The input signals driving both CMOS buffers are characterized by

$$\begin{aligned} V_{\mathrm{in} 1} =V_{\mathrm{in}2} = V_{\mathrm{DD}}\frac{t}{\tau _\mathrm{r}} \quad 0\le t \le \mathop {\tau }\nolimits _{\mathrm{r}}. \end{aligned}$$

(5)

Both the input signals are characterized by rise/fall times which are equal to $\tau _{\mathrm{r}}$. The differential equations governing the output voltage of each MOS transistor in Fig. 3 are given by

$$\begin{aligned} -\!\frac{\mathrm{d}V_1}{\mathrm{d}t}=\frac{(C_2 +C_\mathrm{c})}{C_1 C_2 +C_\mathrm{c} ( {C_1 +C_2})}I_{n_1 } +\frac{C_\mathrm{c} }{C_1 C_2+C_\mathrm{c} ( {C_1 +C_2 })}I_{n_2 }+ R_1 \frac{\mathrm{d}I_{n_1 } }{\mathrm{d}t} \end{aligned}$$

(6)

$$\begin{aligned} -\!\frac{\mathrm{d}V_2 }{\mathrm{d}t}=\frac{(C_1 +C_\mathrm{c})}{C_1 C_2 +C_\mathrm{c} ( {C_1 +C_2})}I_{n_2 } +\frac{C_\mathrm{c} }{C_1C_2 +C_\mathrm{c} ( {C_1 +C_2})}I_{n_1 } +R_2 \frac{\mathrm{d}I_{n_2}}{\mathrm{d}t} \end{aligned}$$

(7)

$I_{n_1}$ and $I_{n_2}$ being the sub-threshold currents across MN1 and MN2, respectively. For the rising ramp input, MOS transistors operate in different operating regions viz. sub- saturation and sub-linear. In order to obtain the output voltage expressions analytically, four regions of operation have been identified and discussed below.

Region-1 $(0\le t \le {\tau }_\mathrm{r})$: During this time interval, the initial conditions, i.e., at t = 0, $V_{1}$ and $V_{2}$ both are equal to $V_{\mathrm{DD}}$. The output voltages obtained are

$$\begin{aligned} V_1 \!=\! V_{\mathrm{DD}} \!-\!\mathop {\beta }\nolimits _{21} \frac{\mathop {\tau }\nolimits _\mathrm{r} \mathop {\eta }\nolimits _{n} U_{\mathrm{th}}}{V_{\mathrm{DD}} }\left[ {\mathrm{e}^{\frac{V_{\mathrm{DD}} \frac{\mathrm{t}}{\mathop {\tau }\nolimits _\mathrm{r}}\!-\!V_{\mathrm{DD}} }{\mathop {\eta }\nolimits _n U_{\mathrm{th}} }}\!-\!\mathrm{e}^{-\frac{V_{\mathrm{DD}} }{\mathop {\eta }\nolimits _n U_{\mathrm{th}} }}} \!\right] \!-\!R_1 B_{n_1 } \left[ {\mathrm{e}^{\frac{\mathrm{V}_{\mathrm{DD}} \frac{{t}}{\mathop {\tau }\nolimits _\mathrm{r} }-V_{\mathrm{DD}}}{\mathop {\eta }\nolimits _n U_{\mathrm{th}}}}\!-\!\mathrm{e}^{-\frac{V_{\mathrm{DD}}}{\mathop {\eta }\nolimits _n U_{\mathrm{th}}}}}\!\right] \nonumber \\ \end{aligned}$$

(8)

$$\begin{aligned} V_2 \!=\!V_{\mathrm{DD}} \!-\!\mathop {\beta }\nolimits _{22} \frac{\mathop {\tau }\nolimits _\mathrm{r} \mathop {\eta }\nolimits _{n} U_{\mathrm{th}}}{V_{\mathrm{DD}} }\left[ {\mathrm{e}^{\frac{\mathrm{V}_{\mathrm{DD}} \frac{{t}}{\mathop {\tau }\nolimits _\mathrm{r} }\!-\!\mathrm{V}_{\mathrm{DD}} }{\mathop {\eta }\nolimits _n U_{\mathrm{th}} }}\!-\!\mathrm{e}^{-\frac{V_{\mathrm{DD}} }{\mathop {\eta }\nolimits _{n} U_{\mathrm{th}} }}} \right] \!-\!R_2 B_{n_2 } \left[ {\mathrm{e}^{\frac{V_{\mathrm{DD}} \frac{\mathrm{t}}{\mathop {\tau }\nolimits _\mathrm{r} }\!-\!V_{\mathrm{DD}} }{\mathop {\eta }\nolimits _n U_{\mathrm{th}} }}\!-\!\mathrm{e}^{-\frac{V_{\mathrm{DD}} }{\mathop {\eta }\nolimits _n \mathrm{U}_{\mathrm{th}} }}} \right] .\nonumber \\ \end{aligned}$$

(9)

The various constants in (8) and (9) are defined as

$$\begin{aligned} \mathop {\beta }\nolimits _{21} =\frac{(C_2 +C_\mathrm{c})B_{n_1 } +C_\mathrm{c} B_{n_2} }{C_1C_2 +C_\mathrm{c} ( {C_1 +C_2})} \end{aligned}$$

(10)

$$\begin{aligned} \mathop {\beta }\nolimits _{22} =\frac{(C_1 +C_\mathrm{c} )B_{{n}_2 } +C_\mathrm{c} B_{n_1 } }{C_1 C_2 +C_\mathrm{c} ( {C_1 +C_2 })}. \end{aligned}$$

(11)

The effect of coupling can be seen in Eqs. (10) and (11). Both $\beta _{21}$ and $\beta _{22}$ include the effect of the coupling capacitance in addition to the intrinsic load capacitances. The coupling capacitance thus affects the propagation delay. This delay uncertainty in the propagation delay can be eliminated if both MN1 and MN2 have the same ratio of output current drives $( {{B_{n_1 } } /{B_{n_2 } }})$ to the corresponding intrinsic load capacitances $( {{C_1 } /{C_2 }})$. Under such situation, $\mathop {\beta }\nolimits _{21}$ and $\mathop {\beta }\nolimits _{22}$ reduce to ${B_{n_1 } }/{C_1}$ and ${B_{n_2 } } / {C_2 }$, respectively, and $C_{\mathrm{c} }$ gets eliminated from the expressions of $\mathop {\beta }\nolimits _{21}$ and $\mathop {\beta }\nolimits _{22}$. Thus, the coupling capacitance has no effect on the output voltage waveforms of $V_{1}$ and $V_{2}$. However, this condition is difficult to be realized in practical CMOS VLSI circuits. This is owing to the different geometric sizes of MOS transistors, different interconnect geometric parameters viz. interconnect width, spacing, etc. and different gate-to-source capacitances of the following fan-out logic gates. Therefore, coupling capacitance affects the output voltage and hence timing analysis under such switching environment becomes necessary. At $t\,=\,\mathop {\tau }\nolimits _\mathrm{r}$, the output voltages obtained are

$$\begin{aligned} V_1 ( {\mathop {\tau }\nolimits _\mathrm{r} })= V_{\mathrm{DD}} -\mathop {\beta }\nolimits _{21} \frac{\mathop {\tau }\nolimits _\mathrm{r} \mathop {\eta }\nolimits _n U_{\mathrm{th}} }{V_{\mathrm{DD}} }\left[ {1-\mathrm{e}^{-\frac{V_{\mathrm{DD}} }{\mathop {\eta }\nolimits _n U_{\mathrm{th}} }}} \right] - R_1 B_{n_1 } \left[ {1-\mathrm{e}^{-\frac{V_{\mathrm{DD}} }{\mathop {\eta }\nolimits _n U_{\mathrm{th}} }}} \right] \end{aligned}$$

(12)

$$\begin{aligned} V_2 ( {\mathop {\tau }\nolimits _\mathrm{r} })= V_{\mathrm{DD}} -\mathop {\beta }\nolimits _{22} \frac{\mathop {\tau }\nolimits _\mathrm{r} \mathop {\eta }\nolimits _n U_{\mathrm{th}} }{V_{\mathrm{DD}} }\left[ {1-\mathrm{e}^{-\frac{V_{\mathrm{DD}} }{\mathop {\eta }\nolimits _{n} U_{\mathrm{th}} }}} \right] -R_2 B_{n_2 } \left[ {1-\mathrm{e}^{-\frac{V_{\mathrm{DD}} }{\mathop {\eta }\nolimits _n U_{\mathrm{th}}. }}} \right] . \end{aligned}$$

(13)

Region-2 $(\mathop {\tau }\nolimits _\mathrm{r} \le t \le \zeta _{n\mathrm{sat}^1} )$: The device operating conditions are similar to the region-1. The drain-to-source currents of MN1 and MN2 are constant and given by $I_{n_1 } = B_{n_1}$ and $I_{n_2 } = B_{n_2}$. The output voltages in this region are based on the condition at $t=\mathop {\tau }\nolimits _\mathrm{r}$ and are

$$\begin{aligned} V_1 =V_1 ( {\mathop {\tau }\nolimits _\mathrm{r} })-\frac{(C_2 +C_\mathrm{c} ) B_{n_1 } +C_\mathrm{c} B_{n_2 } }{C_1 C_2 +C_\mathrm{c} ( {C_1 +C_2 })}( {t-\mathop {\tau }\nolimits _\mathrm{r} }) \end{aligned}$$

(14)

$$\begin{aligned} V_2 =V_2 ( {\mathop {\tau }\nolimits _\mathrm{r} })-\frac{(C_1 +C_\mathrm{c} )B_{n_2 } +C_\mathrm{c} B_{n_1 } }{C_1 C_2 +C_\mathrm{c} ( {C_1 +C_2 })}( {t-\mathop {\tau }\nolimits _\mathrm{r} }). \end{aligned}$$

(15)

Region-3 $(\zeta _{n\mathrm{sat}^1} \le t \le \zeta _{n\mathrm{sat}^2} )$: Depending on the geometric size of MOS transistors, it is possible that MN1 leaves the sub-saturation region and enters into sub-linear region while MN2 continues to operate in the sub-saturation. MN1 and MN2 make transition into the sub-linear region of their characteristics at times $\zeta _{n\mathrm{sat}^1}$ and $\zeta _{n\mathrm{sat}^2}$, respectively, and are not equal. In this case, the drain-to-source current of MN1 is characterized by

$$\begin{aligned} I_{n_1 } =\gamma _{n_1 } V_1 \end{aligned}$$

(16)

$\gamma _{n_1}$ is the output conductance of MN1 in the sub-linear region. The output voltages obtained in this region are

$$\begin{aligned} V_1 \!=\!-\!V_\mathrm{a} -\left[ {V_{1_{t=\zeta _{n\mathrm{sat}^1} } } \!+\!V_\mathrm{a} } \right] \mathrm{e}^{-\alpha _{{n}_1 } ( {t-\zeta _{n\mathrm{sat}^1} })} \end{aligned}$$

(17)

$$\begin{aligned} V_2 =V_{2_{{{t}}=\zeta _{n\mathrm{sat}^1} } } -V_\mathrm{b} -\frac{B_{n_2 } }{C_2 +C_\mathrm{c} }( {{t}-\zeta _{n\mathrm{sat}^1} }) \end{aligned}$$

(18)

$$\begin{aligned} \mathrm{where}\,\, V_\mathrm{a} =\frac{C_\mathrm{c} }{( {C_2 +\mathrm{C}_\mathrm{c} })\gamma _{n_1 } }B_{n_2} \end{aligned}$$

(19)

$$\begin{aligned} \alpha _{n_1 } =\frac{(C_2 +C_\mathrm{c} )}{\left[ {C_1 C_2 +C_\mathrm{c} ( {C_1 +C_2 })} \right] ( {1+\gamma _{n_1 } R_1 })}\gamma _{{n}_1 } \end{aligned}$$

(20)

$$\begin{aligned} V_\mathrm{b} =\frac{C_\mathrm{c} }{( {C_2 +C_\mathrm{c} })}( {1+\gamma _{n_1 } R_1 })\left[ {V_{1_{{t}=\zeta _{n\mathrm{sat}^1} } } +V_\mathrm{a} } \right] ( {1-\mathrm{e}^{-\alpha _{n_1 } ( {t-\zeta _{n\mathrm{sat}^1} })}}). \end{aligned}$$

(21)

Region-4 $(t>\zeta _{n\mathrm{sat}^2} )$: After $\zeta _{n\mathrm{sat}^2}$, MN1 and MN2 operate in the sub-linear region. The differential equations governing the output voltage of each MOS transistor are given by

$$\begin{aligned} -\!(C_1 +C_\mathrm{c} )( {1+\gamma _{n_1 } R_1 })\frac{\mathrm{d}V_1 }{\mathrm{d}t}+C_\mathrm{c} ( {1+\gamma _{\mathrm{n}_2 } R_2 })\frac{\mathrm{d}V_2 }{\mathrm{d}t}=\gamma _{n_1 } V_1 \end{aligned}$$

(22)

$$\begin{aligned} -\!(C_2 +C_\mathrm{c} )( {1+\gamma _{n_2 } R_2 })\frac{\mathrm{d}V_2 }{\mathrm{d}t}+C_\mathrm{c} ( {1+\gamma _{{n}_1 } R_1 })\frac{\mathrm{d}V_1 }{\mathrm{d}t}=\gamma _{n_2 } V_2 . \end{aligned}$$

(23)

Here $\gamma _{n_2 }$ is the output conductance of MN2 in the sub-linear region. The solutions of these coupled differential equations are obtained as

$$\begin{aligned} V_1&= \frac{1}{2}V_{1_{t=\zeta _{n\mathrm{sat}^2} } } \left[ {\mathrm{e}^{\frac{\chi \!-\!( {{a}_1 +b_1 })}{2}( {t\!-\!\zeta _{n\mathrm{sat}^2} })}\left( {1\!+\!\frac{b_1 \!-\!{a}_1 }{\chi }}\right) \!+\!\mathrm{e}^{-\frac{\chi \!+\!( {{a}_1 +b_1 })}{2}( {{t}\!-\!\zeta _{n\mathrm{sat}^2} })}\left( {1-\frac{b_1 -{a}_1 }{\chi }}\right) } \right] \nonumber \\&\quad -\frac{{a}_2 }{\chi }V_{2_{{t}=\zeta _{n\mathrm{sat}^2} } } \left[ {\mathrm{e}^{\frac{\chi -( {{a}_1 +\mathrm{b}_1 })}{2}( {{t}-\zeta _{n\mathrm{sat}^2} })}-\mathrm{e}^{-\frac{\chi +( {{a}_1 +b_1 })}{2}( {t-\zeta _{n\mathrm{sat}^2} })}} \right] \end{aligned}$$

(24)

$$\begin{aligned} V_2&\!=\!\frac{1}{2}V_{2_{{t}=\zeta _{n\mathrm{sat}^2} } } \left[ {\mathrm{e}^{\frac{\chi -( {{a}_1 \!+\!b_1 })}{2}( {t\!-\!\zeta _{n\mathrm{sat}^2} })}\left( {1\!+\!\frac{{a}_1 -b_1 }{\chi }}\right) \!+\!\mathrm{e}^{-\frac{\chi +( {{a}_1 +b_1 })}{2}( {t-\zeta _{n\mathrm{sat}^2} })}\left( {1-\frac{{a}_1 -b_1 }{\chi }}\right) } \right] \nonumber \\&\quad -\frac{b_2 }{\chi }V_{1_{t=\zeta _{n\mathrm{sat}^2} } } \left[ {\mathrm{e}^{\frac{\chi -( {{a}_1 +b_1 })}{2}( {t-\zeta _{n\mathrm{sat}^2} })}-\mathrm{e}^{-\frac{\chi +( {{a}_1 +b_1 })}{2}( {t-\zeta _{n\mathrm{sat}^2} })}} \right] . \end{aligned}$$

(25)

The various constants $a_{1}$, $a_{2}$, $b_{1}$, $b_{2}$, and $\chi$ are defined as

$$\begin{aligned} {a}_1 =\frac{(C_2 +C_\mathrm{c} )}{C_1 C_2 +C_\mathrm{c} ( {C_1 +C_2 })}\gamma _{n_1 } \end{aligned}$$

(26)

$$\begin{aligned} {a}_2 =\frac{C_\mathrm{c} }{C_1 C_2 +C_\mathrm{c} ( {C_1 +C_2 })}\gamma _{n_2 } \end{aligned}$$

(27)

$$\begin{aligned} b_1 =\frac{(C_1 +C_\mathrm{c} )}{C_1 C_2 +C_\mathrm{c} ( {C_1 +C_2 })}\gamma _{n_2 } \end{aligned}$$

(28)

$$\begin{aligned} b_2 =\frac{C_\mathrm{c} }{C_1 C_2 +C_\mathrm{c} ( {C_1 +C_2 })}\gamma _{n_1 } \end{aligned}$$

(29)

$$\begin{aligned} \chi =\sqrt{( {\alpha _1 -\mathop {\beta }\nolimits _1 })^2+4\alpha _2 } \mathop {\beta }\nolimits _2 \end{aligned}$$

(30)

$V_{1_{{t}=\zeta _{n\mathrm{sat}^2} } }$ and $V_{2_{{t}=\zeta _{n\mathrm{sat}^2} } }$ are initial values of $V_{1}$ and $V_{2}$ at $t = \zeta _{n\mathrm{sat}^2}$.

3.1.1 Propagation Delay of Fast Ramp Input Signal

The high-to-low propagation delays $\zeta _{1_{0.5}^n}$ and $\zeta _{2_{0.5}^n}$ of MN1 and MN2, respectively, are computed based on (14) and (15). At $t = \zeta _{1_{0.5} ^\mathrm{n}}$ and $t = \zeta _{2_{0.5}^n}$, the output voltages $V_{1}$ and $V_{2}$ both are equal to 0.5$V_{\mathrm{DD}}$, i.e.,

$$\begin{aligned} V_1 ( {\mathop {\tau }\nolimits _\mathrm{r} })-\frac{(C_2 +C_\mathrm{c} )B_{n_1 } + C_{\mathrm{c}} B_{n_2 } }{C_1 C_2 +C_\mathrm{c} ( {C_1 +{C}_2 })}( {\zeta _{1_{0.5} ^n} -\mathop {\tau }\nolimits _\mathrm{r} })=0.5V_{\mathrm{DD}} \end{aligned}$$

(31)

$$\begin{aligned} V_2 ( {\mathop {\tau }\nolimits _\mathrm{r} })-\frac{(C_1 +C_\mathrm{c} )B_{n_2 } + C_\mathrm{c} B_{n_1 } }{C_1 C_2 +C_\mathrm{c} ( {C_1 +C_2 })}( {\zeta _{2_{0.5} ^n} -\mathop {\tau }\nolimits _\mathrm{r} })=0.5V_{\mathrm{DD}}. \end{aligned}$$

(32)

Simplification of (31) and (32) gives

$$\begin{aligned} \zeta _{1_{0.5} ^n} =\mathop {\tau }\nolimits _\mathrm{r} +\frac{0.5V_{\mathrm{DD}} -R_1 B_{n_1 } ( {1-\mathrm{e}^{-V_{\mathrm{DD}} }})}{\frac{(C_2 +C_\mathrm{c} )B_{n_1 } +C_\mathrm{c} B_{n_2 } }{C_1 C_2 +C_\mathrm{c} ({C_1 +C_2 })}}-\frac{\mathop {\tau }\nolimits _\mathrm{r} ( {1-\mathrm{e}^{-V_{\mathrm{DD}} }})}{V_{\mathrm{DD}} } \end{aligned}$$

(33)

$$\begin{aligned} \zeta _{2_{0.5} ^n} =\mathop {\tau }\nolimits _\mathrm{r} +\frac{0.5V_{\mathrm{DD}} -R_2 B_{n_2 } ( {1-\mathrm{e}^{-V_{\mathrm{DD}} }})}{\frac{(C_1 +C_\mathrm{c} )B_{n_2 } +C_\mathrm{c} B_{n_1 } }{C_1 C_2 +C_\mathrm{c} ( {C_1 +C_2 })}}-\frac{\mathop {\tau }\nolimits _\mathrm{r} ( {1-\mathrm{e}^{-V_{\mathrm{DD}} }})}{V_{\mathrm{DD}} }. \end{aligned}$$

(34)

The low-to-high propagation delays can be obtained in a similar fashion. The propagation delay is the average of the high-to-low and low-to-high propagation delays. $\zeta _{n\mathrm{sat}^1}$ and $\zeta _{n\mathrm{sat}^2}$ are determined based on the boundary condition defined in Sect. 2, i.e.,

$$\begin{aligned} V_1 ( {\mathop {\tau }\nolimits _\mathrm{r} })-\frac{(C_2 +C_\mathrm{c} )B_{n_1 } +C_\mathrm{c} B_{n_2 } }{C_1 C_2 +C_\mathrm{c} ( {C_1 +C_2 })}( {\zeta _{n\mathrm{sat}^1} -\mathop {\tau }\nolimits _\mathrm{r} })=4U_{\mathrm{th}} \end{aligned}$$

(35)

$$\begin{aligned} V_{2,{t}=\zeta _{n\mathrm{sat}^1} } -V_\mathrm{b} -\frac{B_{n_2 } }{C_2 +C_\mathrm{c} }( {\zeta _{n\mathrm{sat}^2} -\zeta _{n\mathrm{sat}^1} })=4U_{\mathrm{th}} \end{aligned}$$

(36)

Equation (35) is solved to yield

$$\begin{aligned} \zeta _{n\mathrm{sat}^1} =\mathop {\tau }\nolimits _\mathrm{r} +\left[ {( {V_1 ( {\mathop {\tau }\nolimits _\mathrm{r} })-4U_{\mathrm{th}} })\times \frac{C_1 C_2 +C_\mathrm{c} ( {C_1 +C_2 })}{( {C_2 +C_\mathrm{c} })B_{n_1 } +C_\mathrm{c} B_{n_2 } }} \right] \end{aligned}$$

(37)

$\zeta _{n\mathrm{sat}^2}$ can be computed using (36) and Newton–Raphson numeric solver.

3.2 Case-II: Out-of-Phase Switching

The out-of-phase transition is a pessimistic condition in terms of the effect of the coupling capacitance on the propagation delays of CMOS inverters [13]. In this case, it is assumed that input to the aggressor driver is switching from low-to-high and input to the victim driver is switching from high-to-low as shown in Fig. 4. MN1 and MP2 are the active transistors in each inverter for the considered input conditions. The related current directions are also shown. $I_{p_2 }$ is the current that flows across MP2. The differential equations governing the output voltage of each MOS transistor shown in Fig. 4 are given by

$$\begin{aligned} -\!\!\frac{\mathrm{d}V_1 }{\mathrm{d}t}=\frac{(C_2 +C_\mathrm{c} )}{C_1 C_2 +C_\mathrm{c} ( {C_1 +C_2 })}I_{n_1 } -\frac{C_\mathrm{c} }{C_1 C_2 +C_\mathrm{c} ( {C_1 +C_2 })}I_{p_2 } +R_1 \frac{\mathrm{d}I_{n_1 } }{\mathrm{d}t} \end{aligned}$$

(38)

$$\begin{aligned} -\!\!\frac{\mathrm{d}V_2 }{\mathrm{d}t}=\frac{C_\mathrm{c} }{C_1 C_2 + C_\mathrm{c} ( {C_1 +C_2 })}I_{n_1 } -\frac{(C_1 +C_\mathrm{c} )}{C_1 C_2 +C_\mathrm{c} ( {C_1 +C_2 })}I_{p_2 } -R_2 \frac{\mathrm{d}I_{p_2 } }{\mathrm{d}t}. \end{aligned}$$

(39)

Fig. 4

Equivalent circuit for the aggressor buffer switching from low-to-high and victim buffer from high-to-low

For the opposite switching condition with fast ramp input, MOS transistors operate in different regions over different intervals of time. In order to obtain the output voltage expressions analytically, four regions of operation have been discussed below.

Region-1 $(0\le t\le \mathop {\tau }\nolimits _\mathrm{r} )$: In region-1, MN1 and MP2 operate in the sub-saturation regions. The current across MP2 is given by

$$\begin{aligned} I_{p_2 } =B_{p_2 }\mathrm{e}^{\frac{V_{\mathrm{DD}} \frac{t}{{\tau }_\mathrm{r}}-V_{\mathrm{DD}} }{{\eta }_p U_{\mathrm{th}} }} \end{aligned}$$

(40)

$B_{p_2 }$ is the source-to-drain current of MP2 when $V_{\mathrm{in}2} =V_{\mathrm{DD}}$ and $\mathop {\eta }\nolimits _p$ is its sub-threshold slope factor. The output voltages obtained are given by

$$\begin{aligned} V_1 =V_{\mathrm{DD}} -\frac{( {C_2 +C_\mathrm{c} })V_{n,1} -C_\mathrm{c} V_{p,2} }{C_1 C_2 +C_\mathrm{c} ( {C_1 +C_2 })}-R_1 B_{n_1 } \left[ {\mathrm{e}^{\frac{V_{\mathrm{DD}} \frac{t}{\mathop {\tau }\nolimits _\mathrm{r} }-V_{\mathrm{DD}} }{\mathop {\eta }\nolimits _n U_{\mathrm{th}} }}-\mathrm{e}^{-\frac{V_{\mathrm{DD}} }{\mathop {\eta }\nolimits _n U_{\mathrm{th}} }}} \right] \end{aligned}$$

(41)

$$\begin{aligned} V_2 =\frac{( {C_1 +C_\mathrm{c} })V_{\mathrm{p},2} -C_\mathrm{c} V_{n,1} }{C_1 C_2 +C_\mathrm{c} ( {C_1 +C_2 })}+R_2 B_{p_2 } \left[ {\mathrm{e}^{\frac{V_{\mathrm{DD}} \frac{t}{\mathop {\tau }\nolimits _\mathrm{r} }-V_{\mathrm{DD}} }{\mathop {\eta }\nolimits _p U_{\mathrm{th}} }}-\mathrm{e}^{-\frac{V_{\mathrm{DD}} }{\mathop {\eta }\nolimits _{p} U_{\mathrm{th}} }}} \right] \end{aligned}$$

(42)

$$\begin{aligned} \mathrm{where}\,\,V_{n,1} =\frac{B_{n_1 } \mathop {\tau }\nolimits _\mathrm{r} \mathop {\eta }\nolimits _n U_{\mathrm{th}} }{V_{\mathrm{DD}} }\left[ {\mathrm{e}^{\frac{V_{\mathrm{DD}} \frac{{t}}{\mathop {\tau }\nolimits _\mathrm{r} }-V_{\mathrm{DD}} }{\mathop {\eta }\nolimits _n U_{\mathrm{th}} }}- \mathrm{e}^{-\frac{V_{\mathrm{DD}} }{\mathop {\eta }\nolimits _n U_{\mathrm{th}} }}} \right] \end{aligned}$$

(43)

$$\begin{aligned} V_{p,2} =\frac{B_{p_2 } \mathop {\tau }\nolimits _\mathrm{r} \mathop {\eta }\nolimits _p U_{\mathrm{th}} }{V_{\mathrm{DD}} }\left[ {\mathrm{e}^{\frac{V_{\mathrm{DD}} \frac{t}{\mathop {\tau }\nolimits _\mathrm{r} }-V_{\mathrm{DD}} }{\mathop {\eta }\nolimits _p U_{\mathrm{th}} }}-e^{-\frac{V_{\mathrm{DD}} }{\mathop {\eta }\nolimits _p U_{\mathrm{th}} }}} \right] . \end{aligned}$$

(44)

The effect of coupling is observed in (41) and (42). Coupling affects $V_{1}$ and $V_{2}$ through $V_{n,1}$ and $V_{p,2}$, respectively. It may also be observed that the presence of the coupling term $V_{p,2}$ in (41) tends to decrease $V_{1}$ slowly while the coupling component $V_{\mathrm{n},1}$ causes $V_{2}$ to increase slowly in (42).

Region-2 $(\mathop {\tau }\nolimits _\mathrm{r} \le t\le \zeta _{n\mathrm{sat}^1})$: After $\mathop {\tau }\nolimits _\mathrm{r}$ both the inputs attain fixed values, equal to $V_{\mathrm{DD}}$ and ground, respectively. However, MN1 and MP2 continue to operate in the sub-saturation region. For this duration, the voltages at the output of both transistors are given by

$$\begin{aligned} V_1 =V_1 (\mathop {\tau }\nolimits _\mathrm{r} )-\frac{(C_2 +C_\mathrm{c} )B_{n_1 } -C_\mathrm{c} B_{p_2 } }{C_1 C_2 +C_\mathrm{c} ({C_1 +C_2 })}( {t-\mathop {\tau }\nolimits _\mathrm{r} }) \end{aligned}$$

(45)

$$\begin{aligned} V_2 = V_2 (\mathop {\tau }\nolimits _\mathrm{r} )+\frac{(C_1 +C_\mathrm{c} )B_{p_2 } -C_\mathrm{c} B_{n_1 } }{C_1 C_2 +C_\mathrm{c} ({C_1 +C_2 })}( {t-\mathop {\tau }\nolimits _\mathrm{r} }). \end{aligned}$$

(46)

Region-3 $(\zeta _{n\mathrm{sat}^1} \le t\le \zeta _{\mathrm{psat}^2})$: MN1 and MP2 may leave sub-saturation region at different time durations if both transistors have unequal output conductances. Here, it is assumed that MP2 makes transition into the sub-linear region at $t=\zeta _{\mathrm{psat}^2}$. In this region, therefore MN1 operates in the sub-linear region while MP2 continues to remain in the sub-saturation region. The relationship of $V_{1}$ and $V_{2}$ are given by

$$\begin{aligned} V_1 =V_{1,a} -\left[ {-V_{1_{{t}=\zeta _{n\mathrm{sat}^1} } } +V_{1,a} } \right] \mathrm{e}^{-\alpha _{n_1 } ( {t-\zeta _{n\mathrm{sat}^1} })} \end{aligned}$$

(47)

$$\begin{aligned} V_2 =V_{2_{{t}=\zeta _{n\mathrm{sat}^1} } } -V_{1,b} +\frac{B_{p_2 } }{( {C_2 +C_\mathrm{c} })}( {t-\zeta _{n\mathrm{sat}^1} }), \end{aligned}$$

(48)

$$\begin{aligned} \mathrm{where}\,\,V_{1,a} =\frac{C_\mathrm{c}}{\gamma _{n_1 } ( {C_2 +C_\mathrm{c} })}B_{p_2 } \end{aligned}$$

(49)

$$\begin{aligned} V_{1,b} =\frac{C_\mathrm{c} }{C_2 +C_\mathrm{c} }( {1+\gamma _{n_1 } R_1 })\left[ {V_{1,a} -V_{1_{{t}=\zeta _{n\mathrm{sat}^1} } } } \right] ( {1-\mathrm{e}^{-\alpha _{n_1 } ( {t-\zeta _{n\mathrm{sat}^1} })}}). \end{aligned}$$

(50)

Region-4 $(t>\zeta _{\mathrm{psat}^2} )$: In this region, MN1 and MP2 operate in the sub-linear region. The differential equations governing the output voltage of each MOS transistor are given by

$$\begin{aligned} -(C_1 +C_\mathrm{c})({1+\gamma _{{n}_1 } R_1 })\frac{\mathrm{d}V_1 }{\mathrm{d}t}+C_\mathrm{c} ( {1+\gamma _{p_2 } R_2 })\frac{\mathrm{d}V_2 }{\mathrm{d}t}=\gamma _{n_1 } V_1 \end{aligned}$$

(51)

$$\begin{aligned} -C_\mathrm{c} ( {1+\gamma _{n_1 } R_1 })\frac{\mathrm{d}V_1 }{\mathrm{d}t}+( {C_2 +C_\mathrm{c} })( {1+\gamma _{p_2 } R_2 })\frac{\mathrm{d}V_1 }{\mathrm{d}t}=\gamma _{p_2 } V_2 . \end{aligned}$$

(52)

These coupled differential equations are solved and the solution obtained is given as

$$\begin{aligned} V_1&= \frac{1}{2\chi }\mathrm{e}^{\frac{\left[ {\chi \!-\!({a}_1 \!+\!b_1 )} \right] }{2}({t-\zeta _{\mathrm{psat}^2} })}\left[ \!{\begin{array}{l} V_{1_{t=\zeta _{\mathrm{psat}^2} } } ( {\chi \!-\!{a}_1 \!+\!b_1 })\!-\!2{a}_2 V_{2_{t=\zeta _{\mathrm{psat}^2} } } \!-\!\frac{1}{( {{a}_1 b_1\! -\!{a}_2 b_2 })} \\ \left\{ {{a}_3 ( {b_1^2 -{a}_1 b_1 +b_1 \chi +2{a}_2 b_2 })-( {\chi +{a}_1 +b_1}){a}_2 b_3 } \right\} \end{array}} \!\right] \nonumber \\&+\frac{1}{{a}_1 b_1 -{a}_2 b_2 }( {{a}_3 b_1 -{a}_2 b_3 }) \end{aligned}$$

(53)

$$\begin{aligned} V_2&\!=\!\frac{1}{2\chi }\mathrm{e}^{\frac{\left[ {\chi \!-\!({a}_1 \!+\!b_1 )} \right] }{2}( {t\!-\!\zeta _{\mathrm{psat}^2} })}\left[ {\begin{array}{l} \left\{ {V_{2_{t=\zeta _{\mathrm{psat}^2} } } ( {\chi +{a}_1 -b_1 })-2\mathop {\beta }\nolimits _2 V_{1_{t=\zeta _{psat^2} } } } \right\} +\frac{1}{( {{a}_1 b_1 -{a}_2 b_2 })} \\ \left\{ {{a}_3 b_2 ( {\chi \!+\!{a}_1 \!+\!b_1 })\!-\!( {{a}_1 ^2b_3 \!-\!{a}_1 b_1 b_3 \!+\!2{a}_2 b_2 b_3 \!+\!{a}_1 b_3 \chi })} \right\} \\ \end{array}} \right] \nonumber \\&\quad +\frac{1}{{a}_1 b_1 -{a}_2 b_2 }( {{a}_1 b_3 -{a}_3 b_2 }). \end{aligned}$$

(54)

The constants $a_{3}$ and $b_{3}$ are defined as

$$\begin{aligned} {a}_3 ={a}_2 V_{\mathrm{DD}} \end{aligned}$$

(55)

$$\begin{aligned} b_3 =b_2 V_{\mathrm{DD}}. \end{aligned}$$

(56)

Here $V_{1_{{t}=\zeta _{\mathrm{psat}^2} } }$ and $V_{2_{{t}=\zeta _{\mathrm{psat}^2} } }$ are the initial values of $V_{1}$ and $V_{2}$ at $t = \zeta _{\mathrm{psat}^2}$ and $\gamma _{p_2 }$ is the output conductance of MP2 in the sub-linear region.

3.2.1 Propagation Delay of Fast Ramp Input Signal

The high-to-low $\zeta _{1_{0.5}^n}$ and low-to-high $\zeta _{2_{0.5}^p}$ propagation delays of MN1 and MP2, respectively, are computed based on Eqs. (45) and (46) and are given as

$$\begin{aligned} \zeta _{1_{0.5}^n} ={\tau }_\mathrm{r} +\frac{\left[ {V_1 ( {{\tau }_\mathrm{r} })-0.5V_{\mathrm{DD}} } \right] \left[ {C_1 C_2 +C_\mathrm{c} ( {C_1 +C_2 })} \right] }{B_{n_1 } (C_2 +C_\mathrm{c} )-C_\mathrm{c} B_{p_2 } } \end{aligned}$$

(57)

$$\begin{aligned} \zeta _{2_{0.5}^p} ={\tau }_\mathrm{r} +\frac{\left[ {0.5V_{\mathrm{DD}} -V_2 ( {{\tau }_\mathrm{r} })} \right] \left[ {C_1 C_2 + C_\mathrm{c} ( {C_1 +C_2 })} \right] }{(C_1 +C_\mathrm{c} )B_{p_2 } -C_\mathrm{c} B_{n_1 } } \end{aligned}$$

(58)

$\zeta _{n\mathrm{sat}^1}$ is calculated based on (47) and is given by

$$\begin{aligned} \zeta _{n\mathrm{sat}^1} ={\tau }_\mathrm{r} +\left[ {\left\{ {V_1 ({{\tau }_\mathrm{r} })-4U_{\mathrm{th}} } \right\} \times \frac{C_1 C_2 + C_\mathrm{c} ( {C_1 +C_2 })}{( {C_2 + C_\mathrm{c} }) B_{{n}_1 } - C_\mathrm{c} B_{p_2 } }} \right] \end{aligned}$$

(59)

$\zeta _{\mathrm{psat}^2}$ is calculated using Newton–Raphson numerical solver depending upon the condition

$$\begin{aligned} V_{2_{{t}=\zeta _{n\mathrm{sat}^1} } } - V_{1,b} +\frac{B_{p_2 } }{( {C_2 + C_\mathrm{c} })}( {\zeta _{\mathrm{psat}^2} -\zeta _{n\mathrm{sat}^1} })= V_{\mathrm{DD}} -4U_{\mathrm{th}}. \end{aligned}$$

(60)

For slow ramp input, timing analyses of in-phase and out-of-phase transitions over each of these regions are presented in Appendices 1 and 2, respectively. The proposed model is further validated and verified using SPICE simulations.

4 Results and Validation of the Proposed Model

The proposed models are validated using SPICE simulations. The rise time of the input ramp taken is 0.1 $\upmu$s. For the CMOS buffer, data of PTM 65 nm, 0.36 V, and Level-54 are used [16]. The coupled interconnects have coupling length equal to 5 mm, while interconnect width and spacing each are equal to 0.54 $\upmu$m. The comparison of output voltage waveforms generated by SPICE simulations and analytical model for Case I under fast and slow ramps has been shown in Figs. 5 and 6, respectively. For fast ramp, MN1 width ($W_{\mathrm{n}1})$ is 97.5 nm, while for slow ramp, $W_{n_1 }= 4\,\upmu$m has been taken. Furthermore, for the CMOS drivers, PMOS channel width is 2.5 times that of NMOS width. The values of parasitic impedance parameters for the two lines are extracted as detailed in Appendix 3. The wire parasitics thus obtained are: $R_{1}$ = $R_{2 }$ = 208.93$\,\Omega$, $C_{1}$ = $C_{2 }$ = 301.475 fF. The two lines are coupled through a coupling capacitance of 105.4 fF. It can be observed from the figures that the waveforms obtained from the proposed model match SPICE waveforms closely.

Fig. 5

Voltage waveforms at the output of a aggressor buffer and b victim buffer under in-phase switching for fast ramp with $W_{n_1 }$ = 97.5 nm = $W_{n_2}$, $W_{p_1 }$ = 2.5 $W_{n_1 }$ = $W_{p_2}$

Fig. 6

Voltage waveforms at the output of a aggressor buffer and b victim buffer under in-phase switching for slow ramp with $W_{n_1 }$ = 4 $\upmu$m = $W_{n_2}$, $W_{p_1 }$ = 2.5 $W_{n_1 }$ = $W_{p_2}$

Figures 7 and 8 confirm the validity of the proposed model by comparing the waveforms generated analytically and SPICE simulations under out-of-phase switching. For fast ramp, MP2 width ($W_{\mathrm{p}2})$ of 0.4 $\upmu$m has been taken, while for slow ramp, $W_{\mathrm{p}2 }$= 10 $\upmu$m has been taken. It can be observed from these figures that analytical results match SPICE simulations quite closely. Furthermore, the maximum variation between SPICE and analytical results is less than 5 %.

Fig. 7

Voltage waveforms under out-of-phase switching for fast ramp at the output of a victim buffer and b aggressor buffer with $W_{n_1}$ = 0.10 $\upmu$m, $W_{n_2 }$ = 0.16 $\upmu$m, $W_{p_1}$ = 0.24 $\upmu$m, $W_{p_2}$ = 0.4 $\upmu$m

Fig. 8

Voltage waveforms under out-of-phase switching for fast ramp at the output of a victim buffer and b aggressor buffer with $W_{n_1}$ = 4 $\upmu$m = $W_{n_2}$, $W_{p_1 }$ = 10 $\upmu$m = $W_{p_2}$

The propagation delay for the aggressor and victim buffers (${\tau }_{p_1}$ and ${\tau }_{p_2 }$, respectively) under fast ramp is analytically determined for in-phase switching and is provided in Table 1. Variable interconnect load conditions and widths for the aggressor and victim buffers have been considered. The proposed analytical model yields maximum errors in the propagation delays for the aggressor and victim drivers as 6.99 and 2.75 %, respectively, whereas the average errors involved in the same are 3.34 and 1.71 %, respectively.

Table 1 Propagation delay and error involved for in-phase switching with respect to SPICE simulation

Table 2 presents an account of the propagation delay and computational error involved as predicted by the proposed model with respect to SPICE simulations for out-of-phase switching. Variable interconnect load and asymmetric aggressor and victim driver dimensions have been considered. It can be observed that ${\tau }_{p_1 }$ obtained by the proposed model has an average error of 3.44 % and maximum error of 6.15 %. Similarly, ${\tau }_{p_2}$ predicted by the proposed analytical model results in average and maximum errors of 2 and 3.91 %, respectively. It is to be noted that delay estimates provided in Tables 1 and 2 are based on the assumption of a fast ramp input.

Table 2 Propagation delay and error involved for out-of-phase switching with respect to SPICE simulation

Table 3 compares timing of the aggressor and victim buffers with respect to SPICE simulation. Here, timing refers to the time instant when active transistors in each buffer make transition from sub-saturation to the sub-linear region of operation. Fast and slow ramps have been considered for in-phase and out-of-phase transitions. It can be seen that maximum errors in the estimation of timing for the aggressor and victim drivers under in-phase switching are 8.120 and 7.445 % while the average errors in the same are 5.197 and 4.571 %. For out-of-phase switching, the maximum and average errors predicted by the proposed analytical model are 9.827, 7.662 and 4.257, 4.613 % for the aggressor and victim drivers, respectively. Thus, transition time is also very well predicted by the proposed model.

Table 3 Aggressor and victim buffer timings along with the error involved with respect to SPICE simulation

A comparison of the propagation delay with respect to SPICE simulations is shown in Table 4 for in-phase and out-of-phase transitions. Different MOS widths are used for in-phase (slow and fast input ramps) and out-of-phase (fast input ramps) switching. The error involved in propagation delay with respect to SPICE simulations under switching conditions considered is also computed. Aggressor MOS width ($W_{n_1})$ is varied from 0.1 to 4 $\upmu$m. The propagation delay predicted by the proposed model of aggressor and victim buffers for in-phase switching exhibit maximum errors (with respect to SPICE) of 2.77 and 2.70 %, respectively. For out-of-phase switching condition, the propagation delay estimated by the proposed model has maximum errors of 8.04 and 5.65 % for MN1 and MP2, respectively. It can also be observed from Table 4 that as aggressor width is increased from 0.1 to 4 $\upmu$m, propagation delay decreases by 45.6 and 50.1 % for in-phase and out-of-phase transitions, respectively. Another observation of the analysis is that propagation delay is higher under out-of-phase switching. This is accounted for by the fact that amount of interconnect coupling capacitance is dependent upon the nature of the signal transitions [16]. If drivers are driven by signals switching in the same direction, the effective coupling capacitance is approximately zero and the total capacitance of each interconnect is approximately equal to the line-to-ground capacitance. Alternatively, if signals on each interconnect are switching in the opposite direction or out-of-phase, the effective capacitance approximately doubles to $2 \times C_\mathrm{c}$. Hence, the delay variations can be positive and negative, depending on the direction of the simultaneous transitions.

Table 4 Propagation delay with aggressor and victim buffer size and error involved with respect to SPICE simulation

5 Conclusions

In this paper, crosstalk analysis of CMOS buffer-driven interconnects for in-phase and out-of-phase switching conditions have been presented. Sub-threshold current model is used to represent MOS transistor in CMOS buffer. Comparison of the proposed models with SPICE simulations shows that the analytical results capture waveform shape, propagation delay, and timings with good accuracy. Under in-phase switching, the average error in the propagation delay with respect to SPICE is 3.34 and 1.71 % for the aggressor and victim buffers, respectively. For out-of-phase switching, average errors in the same are 3.44 and 2 %. The timing is also very well predicted by the proposed models. The average errors involved in the estimation of timing for the aggressor and victim buffers are 5.20 and 4.57 %, under in-phase switching. The average errors involved in the same for out-of-phase switching are 4.26 and 4.61 %.

The main advantage of proposed analytical approach is that it results in high accuracy without the need for computational expensive iterations and numerical methods used in circuit simulators like SPICE. The proposed model also gives physical insight of the parameters affecting the transient behavior. This is essential for the avoidance of dynamic crosstalk and circuit malfunctioning. Furthermore, the proposed model can be applied to complex CMOS logic gates, since clock distribution networks are based on inverter-like circuits which can be reduced to an equivalent inverter. The close proximity between SPICE and the proposed analytical model clearly establishes that the results of the present investigation shall be highly beneficial in designing ultra-low power VLSI circuits, which is an immediate requirement in the modern portable and biomedical applications.

Appendices

Appendix 1

1.1 Output Voltages for Slow Ramp Input Signal: In-Phase Switching

If the active device enters into sub-linear region before the completion of input transition, the input ramp signal is a slow ramp signal. The output voltages of coupled buffers in the time interval $0\le t\le \varsigma _{n_1 }$ are essentially similar to (8) and (9). At $\varsigma _{n_1 }$ instant, MN1 leaves the sub-saturation region. MN2 makes transition to sub-linear region of its characteristics at $t =\varsigma _{n_2 }$. The output voltages of each CMOS buffer in this interval are given by following expressions:

$$\begin{aligned} V_1&=V_{1_{{t}=\varsigma _{n_1 } } } \mathrm{e}^{-\alpha _{n_1 } ( {t-\varsigma _{n_1 } })}-\frac{C_\mathrm{c} B_{n_2 } {\tau }_\mathrm{r} {\eta }_n U_{\mathrm{th}} \mathrm{e}^{-\frac{V_{\mathrm{DD}} }{{\eta }_n U_{\mathrm{th}} }}}{V_{\mathrm{DD}} \left[ {C_1 C_2 +C_\mathrm{c} ( {C_1 +C_2 })} \right] +{\tau }_\mathrm{r} {\eta }_n U_{\mathrm{th}} ( {C_2 +C_\mathrm{c} })\gamma _{n_1 } }\nonumber \\&\quad \times \left[ {\mathrm{e}^{\frac{V_{\mathrm{DD}} ( {t-\varsigma _{n_1 } })}{{\tau }_\mathrm{r} {\eta }_\mathrm{n} U_{\mathrm{th}} }}-\mathrm{e}^{-\alpha _{n_1 } ( {t-\varsigma _{n_1 } })}} \right] \end{aligned}$$

(61)

$$\begin{aligned} V_2&= V_{2_{t=\varsigma _{n_1 } } } - R_2 B_{n_2 } -\frac{B_{n_2 } {\tau }_\mathrm{r} {\eta }_n U_{\mathrm{th}} ( {C_1 +C_\mathrm{c} })}{V_{\mathrm{DD}} \left[ {C_1 C_2 +C_\mathrm{c} ( {C_1 +C_2 })} \right] }\mathrm{e}^{-\frac{V_{\mathrm{DD}} }{{\eta }_n U_{\mathrm{th}} }}\left[ {\mathrm{e}^{\frac{V_{\mathrm{DD}} }{{\tau }_\mathrm{r} }( {t-\varsigma _{n_1 } })}-1} \right] \nonumber \\&\quad -\frac{C_\mathrm{c} }{C_1 C_2 +C_\mathrm{c} ( {C_1 +C_2 })}\gamma _{n_1 } \int \limits _{\varsigma _{n_1 } }^{t} {V_1 } \mathrm{d}t. \end{aligned}$$

(62)

Appendix 2

1.1 Output Voltages for Slow Ramp Input Signal: Out-of-Phase Switching

During the operating condition, $0\le t \le \varsigma _{\mathrm{p}_2 }$, expressions for the output voltages are same as for fast ramp input, i.e., (41) and (42). At $t=\varsigma _{p_2 }$, MP2 leaves the sub-saturation and enters into the sub-linear region. In the time limit $\varsigma _{p_2 } \le t \le \varsigma _{n_1 }$, the output voltages are given by

$$\begin{aligned} V_1&= V_{1_{{t}=\varsigma _{p_2 } } } - B_{n_1 } \left( {R_1 +\frac{( {C_2 +C_\mathrm{c} }) {\tau }_\mathrm{r} {\eta }_n U_{\mathrm{th}} }{( {C_1 C_2 + C_\mathrm{c} ( {C_1 + C_2 })})V_{\mathrm{DD}} }}\right) \left[ {\mathrm{e}^{\frac{\frac{V_{\mathrm{DD}} }{{\tau }_\mathrm{r} }( {t-\varsigma _{p_2 } })}{{\eta }_n U_{\mathrm{th}} }}- \mathrm{e}^{-\frac{V_{\mathrm{DD}} }{{\eta }_n U_{\mathrm{th}} }}} \right] \nonumber \\&\quad + \frac{C_\mathrm{c} }{C_1 C_2 +C_\mathrm{c} ( {C_1 + C_2 })}\gamma _{p_2 }\left[ {( {t-\varsigma _{p_2 } }) V_{\mathrm{DD}} -\int \limits _{\varsigma _{p_2 } }^{t} {V_2 } \mathrm{d}t} \right] \end{aligned}$$

(63)

$$\begin{aligned} V_2&= V_{\mathrm{DD}} + \mathrm{e}^{-\alpha _{p_2 } ( {t-\varsigma _{p_2 } })}( {V_{2_{\mathrm{t}=\varsigma _{p_2 } } } -V_{\mathrm{DD}} })\nonumber \\&-\frac{C_\mathrm{c} B_{n_1 } {\tau }_\mathrm{r} {\eta }_n U_{\mathrm{th}} \mathrm{e}^{-\frac{V_{\mathrm{DD}} }{{\eta }_n U_{\mathrm{th}} }}\left[ {\mathrm{e}^{\frac{\frac{V_{\mathrm{DD}} }{{\tau }_\mathrm{r} }( {t-\varsigma _{p_2 } })}{{\eta }_n U_{\mathrm{th}} }}- \mathrm{e}^{-\alpha _{p_2 } ( {t-\varsigma _{\mathrm{p}_2 } })}} \right] }{V_{\mathrm{DD}} \left[ {C_1 C_2 +C_\mathrm{c} ( {C_1 + C_2 })} \right] +( {C_1 +C_\mathrm{c} })\gamma _{p_2 } {\tau }_\mathrm{r} {\eta }_n U_{\mathrm{th}} }\end{aligned}$$

(64)

$$\begin{aligned}&\quad \mathrm{where}\,\,\alpha _{p_2 } =\frac{( {C_1 +C_\mathrm{c} })}{\left[ {C_1 C_2 +C_\mathrm{c} ( {C_1 +C_2 })} \right] (1+\gamma _{p_2 } R_2 )}\gamma _{p_2 }. \end{aligned}$$

(65)

Appendix 3

1.1 Estimation of Interconnect Impedance Parasitics

The interconnect impedance parasitics, i.e., resistance and capacitance are presented here and are computed using Ref. [15]. Figure 9 shows the cross-sectional dimensions of interconnect where interconnect is assumed to be placed between two co-planar interconnects and two orthogonal routing planes.

Fig. 9

Interconnect cross-sectional dimensions

As shown in Fig. 9, if w and h are the width and the height of the interconnect, respectively, s is the separation between two interconnects, $t$ is the thickness of the dielectric, the interconnect resistance per unit length is given as,

$$\begin{aligned} R = \frac{\rho }{{wt}}, \end{aligned}$$

(66)

where $\rho$ stands for the resistivity of the interconnect metal. The interconnect capacitance per unit length is calculated as

$$\begin{aligned} C = \varepsilon \left[ {\frac{{w}}{{h}}+2.22\left( {\frac{{s}}{{s}+0.70\mathrm{h}}}\right) ^{3.19}+1.17\left( {\frac{{s}}{{s}+1.51{h}}}\right) ^{0.76}\left( {\frac{t}{t+4.53{h}}}\right) ^{0.12}} \right] , \end{aligned}$$

(67)

where $\varepsilon$ is the relative permittivity. It consists of the sum of three contributions from left to right: the ideal parallel-plate capacitor, the parallel-plate corner effects, and the sidewall capacitor. The interconnect coupling capacitance per unit length is determined using

$$\begin{aligned} C_{\mathrm{c}}&= \varepsilon \left[ 1.14\frac{t}{{s}} \left( {\frac{{h}}{{h}+2.06{s}}}\right) ^{0.09}+0.74 \left( {\frac{{w}}{{w}+1.59 {s}}}\right) ^{1.14}\right. \nonumber \\&\quad \left. +1.16 \left( {\frac{{w}}{{w}+1.87 {s}}}\right) ^{0.16}\left( {\frac{{h}}{{h}+0.98{s}}}\right) ^{1.18} \right] . \end{aligned}$$

(68)