Keywords

4.1 Introduction

The conventional interconnect copper material is unable to meet the requirements of future technology needs, since it suffers from low reliability with downscaling of interconnect dimensions. Moreover, the resistivity of copper increases, due to electron-surface scattering and grain boundary scattering with smaller dimensions. Therefore, researchers are forced to find an alternative material for global VLSI interconnects. Carbon nanotubes have been proposed to be one of the potential candidates for VLSI interconnects due to their unique physical properties, such as extraordinary mobility, large mean free path, and high current carrying capability [1, 2].

Carbon nanotubes can be classified into single-walled carbon nanotube (SWCNT) and multiwalled carbon nanotube (MWCNT) [3–6]. The promising interconnect solution for global interconnect lengths are MWCNTs due to their high current carrying capabilities than SWCNT bundles. Naeemi et al. observed that for longer interconnects, MWCNTs can have conductivities several times greater than SWCNT bundles [6]. Hence, many researchers consider the MWCNTs as a potential solution for global interconnect material. The experimental and theoretical investigations of MWCNTs as interconnect material have been presented in [7] and [8], respectively.

The performance of an MWCNT interconnect line is generally evaluated by means of an equivalent transmission line model. Li et al. proposed a multiconductor transmission line (MTL) model to represent the MWCNT interconnect [9]. However, the analysis of MWCNT using the MTL model can be computationally expensive. For this reason, the equivalent single conductor (ESC) model was proposed in [8], using the assumption that voltage at an arbitrary cross section along MWCNT are the same, such that all nanotubes are connected in parallel at the both ends. The accuracy of the ESC model has been verified by several researchers [4, 8, 10]. They observed that the transient responses of ESC model and MTL model are in good agreement.

The FDTD technique has been used widely to analyze the transmission lines due to their better accuracy [11]. However, incorporation of different boundary conditions in the FDTD models is a challenging task. Previously, Paul [12, 13] incorporated the boundary conditions to analyze the transmission lines for resistive driver and resistive load boundaries. However, these studies were focused only on copper interconnects and hence, not suitable for next-generation graphene-based nanointerconnects. The quantum and contact resistances at the near-end and far-end terminals of a nanointerconnect line results in complex boundary conditions. For the first time, Liang et al. [14] proposed a crosstalk noise model for the analysis of MWCNT interconnects using FDTD technique. However, the authors represented the nonlinear CMOS driver by a resistive driver, thus limiting the accuracy of their model. Moreover, they did not validate their proposed model with respect to HSPICE. Therefore, a more accurate model is required that allows a better crosstalk-induced performance estimation of MWCNT interconnects.

The fabrication technique of MWCNT bundles was reported in [15], using thermal chemical vapor deposition technique. The authors have demonstrated the feasibility of growing perfectly aligned carbon nanotube bundles. Recently, Wang et al. [16] fabricated the MWCNTs arrays using microwave plasma chemical vapor deposition on Si substrate with interdigital electrodes. This method is able to control the thickness of MWCNT arrays based on the growth time. Although, the controlled growth of MWCNTs with high CNT density is realizable, the researchers are still facing some challenges in terms of large imperfect metal–nanotube contact resistance, poor control on number of shells, chirality and orientation, higher growth temperature during the fabrication process. However, efforts are underway to fabricate MWCNTs for interconnect applications.

This chapter presents an accurate numerical model for comprehensive crosstalk analysis of coupled MWCNT interconnects based on FDTD method. Using this method, the voltage and current can be accurately estimated at any particular point on the interconnect line. Since the proposed model requires less number of assumptions, the accuracy is very high. The nonlinear CMOS driver effects are incorporated using the modified alpha-power law model with suitable boundary conditions. Using the proposed FDTD method, the functional and dynamic crosstalk analysis is carried out. The results demonstrate that the proposed model has high accuracy that matches closely with the HSPICE results. In addition to this, the proposed model is highly time efficient than the HSPICE. Although, this chapter demonstrates the crosstalk effects on two coupled interconnect lines, the model can be extended to N lines.

The rest of the chapter is organized as follows: Sect. 4.2 describes the ESC model of an MWCNT. In Sect. 4.3, the FDTD method is developed for coupled MWCNT interconnect lines. Section 4.4 is devoted to the validation of proposed model for coupled-two lines. In Sect. 4.5, the sensitivity analysis is performed to evaluate the validity of the assumptions associated with the proposed model. Finally, Sect. 4.6 concludes this chapter.

4.2 Equivalent Single Conductor Model of the MWCNT Interconnect

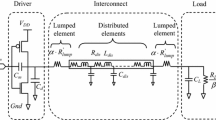
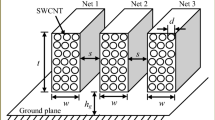
This section presents an equivalent RLC model of an MWCNT interconnect line. Consider a horizontal MWCNT bundle interconnect line positioned over a ground plane at a distance H and placed in a dielectric medium with dielectric constant ε. The geometry of an MWCNT interconnect is shown in Fig. 4.1. The coupling parasitics between the two MWCNT interconnects is shown in Fig. 4.2, where s is the spacing between the interconnect lines, and l 12 and c 12 represent the mutual inductance and coupling capacitance between the interconnect lines, respectively. The MWCNT interconnect consists of N number of tubes

Fig. 4.1
figure 1

Geometry of an MWCNT interconnect above the ground plane

Full size image
Fig. 4.2
figure 2

Cross-sectional view and coupling parasitics between the MWCNT interconnects

Full size image
$$ N = \text{1} + \text{int}\left[ {\frac{{(d_{N} - d_{1} )}}{2\delta }} \right] $$
(4.1)

where δ, d 1, and d N represent intershell distance, innermost shell diameter, and outermost shell diameter, respectively.

The MWCNT interconnect has been represented by an equivalent single conductor (ESC) model as shown in Fig. 4.3 [8]. The RLC parasitics of an MWCNT interconnect are primarily dependent on the number of conducting channels. The number of conducting channels in a CNT can be derived by adding all the subbands contributing to the current conduction. Using Fermi function, it can be expressed as

Fig. 4.3
figure 3

Electrical equivalent model of an MWCNT interconnect

Full size image
$$ N_{{{\text{ch}},i}} = \sum\limits_{{\text{subbands}}} {\frac{1}{{\exp \left( {\left| {E_{i} - E_{\text{F}} } \right|/k{}_{\text{B}}\,T} \right) + 1}}} \,\, $$
(4.2a)

where T is the temperature, k B is the Boltzmann constant, and E i is the lowest (or highest) energy for the subbands above (or below) the Fermi level E F.

A simplified form of expression (4.2a) is [6]:

$$ \begin{aligned} N_{{{\text{ch}},i}} & \approx k_{1} Td_{i} + k_{2} \,\,\,\,\,\,\,\,\, \,\,\,d_{i} > d_{\text{T}} /T \\ & \approx \text{2}\varvec{/}\text{3} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \,\,\,\,\,\,d_{i} < d_{\text{T}} / T \\ \end{aligned} $$
(4.2b)

where d i represents the diameter of CNT in an MWCNT, k 1 and k 2 are curve fitted constants. The value of d T (=1300 nm K) is determined by the gap between the subbands and the thermal energy of electrons. The RLC parasitics can be extracted a follows:

4.2.1 Resistance

Each shell in the MWCNT primarily demonstrates three different types of resistances: (1) quantum resistance (R Q) due to the finite conductance value of quantum wire if there is no scattering along the length; (2) imperfect metal–nanotube contact resistance (R MC) that exhibits a value ranging from zero to few kilo-ohms depending on the fabrication process [17–19]; and (3) scattering resistance (r s) due to acoustic phonon scattering and optical phonon scattering that occurs when the nanotube lengths exceed the mean free path of electrons. The scattering resistance appeared as per unit length distributed resistance along the line, whereas (1) and (2) are considered as lumped resistances placed at the contacts of near-end and far-end terminals. The overall effective lumped resistance at the near-end/far-end terminals of the MWCNT can be expressed as

$$ R_{{{\text{lump}},{\text{ESC}}}} = \frac{1}{2}\left[ {\sum\limits_{i = 1}^{N} {\left( {\frac{{R_{\text{Q}} }}{{2N_{{{\text{ch}},i}} \,}} + R_{{{\text{MC}},i}} } \right)}^{ - 1} } \right]^{ - 1} \quad \text{where}\quad R_{\text{Q}} = \frac{h}{{e^{2} }} \approx 25.8\,\,{\text{K}}\,\Omega $$
(4.3a)

The p.u.l. scattering resistance of an MWCNT can be expressed as

$$ r_{{{\text{s}},\text{ESC}}} = \frac{{{h \mathord{\left/ {\vphantom {h {e^{2} }}} \right. \kern-0pt} {e^{2} }}}}{{\sum\nolimits_{i = 1}^{N} {2N_{{{\text{ch}},i}} \,\lambda_{{\text{mfp}},i} } }}\quad \text{where}\quad \lambda_{{\text{mfp}},i} = \frac{{10^{3} d_{i} }}{{\left( {T/T_{0} } \right) - 2}},\;T_{0} = \text{1}00\,{\text{K}} $$
(4.3b)

where h and e represent the Planck’s constant and the charge of an electron, respectively.

4.2.2 Inductance

The MWCNT demonstrates two different types of inductances:

  1. (1)

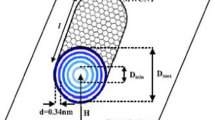
    Magnetic inductance: The magnetic inductance (l e ) is due to the magnetic field generation around a current-carrying conductor. In the presence of ground plane, the p.u.l. magnetic inductance of a CNT shell shown in Fig. 4.4 is given by [20]

    Fig. 4.4
    figure 4

    A single CNT shell above a ground plane

    Full size image
    $$ l_{e} = \frac{\mu }{2\pi }\cosh^{ - 1} \left( {\frac{d + 2H}{d}} \right) $$
    (4.4a)

    where d and H represent the shell diameter and height from the ground plane, respectively. Additionally, the intershell mutual inductance (l m) is mainly due to the magnetic field coupling between the adjacent shells in an MWCNT. The p.u.l. l m can be expressed as [9]

    $$ l_{{m}} = \frac{\mu }{2\pi }\ln \left( {\frac{{d_{i} }}{{d_{i - 1} }}} \right) $$
    (4.4b)
  2. (2)

    Kinetic inductance: The kinetic inductance (l k) is mainly due to the kinetic energy of electrons. By equating kinetic energy stored in each conducting channel of a CNT shell to the effective inductance, the kinetic inductance of each conducting channel (\( l_{\text{k}}^{\prime } \)) in a CNT can be expressed as [20]

    $$ l_{\text{k}}^{'} = \frac{h}{{2e^{2} v_{\text{F}} }} $$
    (4.4c)

    where v F is the Fermi velocity ≈ 8 × 105 m/s [21].

By adopting a recursive approach proposed in [8], the equivalent inductance (l k,ESC) of Fig. 4.3 can be expressed as

$$ l_{{{\text{equ}},\text{1}}} = l_{{{\text{k}},\text{1}}} $$
(4.4d)
$$ l_{{\text{equ},i}} = \left( {\frac{\text{1}}{{l_{{{\text{equ}},\,i - \text{1}}} \, + \,\,l_{\text{m}}^{{i - \text{1},i}} }}\, + \,\frac{\text{1}}{{l_{{\,{\text{k}},\,i}} }}} \right)^{{ - \text{1}}} ,\quad i = 2, 3,\, \ldots ,\,N $$
(4.4e)
$$ l_{{{\text{k}},\text{ESC}}} = l_{{\text{equ},N}} $$
(4.4f)

where

$$ l_{{m}}^{i - 1,i} = \frac{\mu }{2\pi }\ln \left( {d_{i} /d_{i - 1} } \right),\quad i = 2, 3, \ldots ,N $$
(4.4g)
$$ l_{{{\text{k}},i}} = \frac{1}{{2N_{{\text{ch},i}} }} \frac{h}{{2e^{2} v_{\text{F}} }}\quad 1 \le i \le N_{{}} $$
(4.4h)

4.2.3 Capacitance

The MWCNT interconnect consists of two types of capacitances:

  1. (1)

    Electrostatic capacitance: It represents the electrostatic field coupling between the CNT and the ground plane. The electrostatic capacitance (c e) of MWCNT appears between the external shell and the ground plane, as external shell shields the internal ones. The p.u.l. c e of a CNT shell shown in Fig. 4.4 can be expressed as [20]

    $$ c_{\text{e}} = \frac{2\pi \varepsilon }{{\cosh^{ - 1} \left( {\frac{d + 2H}{d}} \right)}} $$
    (4.5a)

    Additionally, the intershell coupling capacitance (c m ) is mainly due to the potential difference between adjacent shells in MWCNT. The p.u.l. c m can be expressed as [9]

    $$ c_{m} = \frac{2\pi \varepsilon }{{\ln \left( {\frac{{d_{i} }}{{d_{i - 1} }}} \right)}} $$
    (4.5b)
  2. (2)

    Quantum capacitance: It originates from the quantum electrostatic energy stored in a CNT shell when it carries current. According to the Pauli exclusion principle, it is only possible to add extra electrons into the CNT shell at an available state above the Fermi level. By equating this energy to the effective capacitance energy, the quantum capacitance of each conducting channel (\( c_{\text{q}}^{\prime } \)) in a CNT can be expressed as

$$ c_{\text{q}}^{\prime} = \,\,\frac{{2e^{2} }}{{hv_{\text{F}} }} $$
(4.5c)

The distributed line capacitance c q,ESC is expressed in terms of quantum capacitance (c q) and coupling capacitance (c m ) between shells

$$ c_{{{\text{equ}},\text{1}}} = c_{{{\text{q}},\text{1}}} $$
(4.5d)
$$ c_{{{\text{equ}},i}} = \left( {\frac{\text{1}}{{c_{{{\text{equ}},i - 1}} }} + \frac{1}{{c_{m}^{i - 1,i} }}} \right)^{ - 1} + c_{{{\text{q}},i}} ,\quad i = 2, 3, \ldots ,N $$
(4.5e)
$$ c_{{{\text{q}},{\text{ESC}}}} = c_{{{\text{equ}},N}} $$
(4.5f)

where

$$ c_{m}^{i - 1,i} = \frac{2\pi \varepsilon }{{\ln (d_{i} /d_{i - 1} )}},\quad i = 2, 3, \ldots ,N $$
(4.5g)
$$ c_{{{\text{q}},i}} = 2N_{{{\text{ch}},i}} \frac{{2e^{2} }}{{hv_{\text{F}} }}\quad 1 \le i \le N $$
(4.5h)

4.3 FDTD Model of MWCNT Interconnect

The FDTD method is used to model the coupled MWCNT interconnect lines. The coupled-two interconnect lines are analyzed in this section; however, the model can be extended to coupled-N lines with a low computational cost.

4.3.1 The MWCNT Interconnect Line

The coupled-two MWCNT interconnect line structure is shown in Fig. 4.5, where r s1, r s2 are the scattering resistances; l k1 , l k2 are the kinetic inductances; l e1 , l e2 are the magnetic inductances; c q1 , c q2 are the quantum capacitances; c e1 , c e2 are the electrostatic capacitances; and C L1, C L2 are the load capacitances of line 1 and line 2, respectively, where all these values are mentioned in p.u.l. The parameters c 12 and l 12 are the p.u.l. coupling capacitances and mutual inductances, respectively [22–32]. The position along the interconnect line, and time are denoted as z and t, respectively.

Fig. 4.5
figure 5

Coupled MWCNT interconnect lines

Full size image

For uniform coupled-two transmission lines the telegrapher’s equations in the transverse electromagnetic (TEM) mode [11] are represented as

$$ \frac{\text{d}}{{{\text{d}}z}}\varvec{V}(z,t) + \varvec{RI}(z,t) + \varvec{L}\frac{\text{d}}{{{\text{d}}t}}\varvec{I}(z,t) = 0 $$
(4.6a)
$$ \frac{\text{d}}{{{\text{d}}z}}\varvec{I}(z,t) + \varvec{C}\frac{\text{d}}{{{\text{d}}t}}\varvec{V}(z,t) = 0 $$
(4.6b)

where V and I are 2 × 1 column vectors of line voltages and currents, respectively. The line parasitic elements are obtained in 2 × 2 per unit length matrix form, i.e., \( \varvec{V} = \left[ {\begin{array}{*{20}c} {V_{1} } \\ {V_{2} } \\ \end{array} } \right],\;\varvec{I} = \left[ {\begin{array}{*{20}c} {I_{1} } \\ {I_{2} } \\ \end{array} } \right],\;\varvec{R} = \left[ {\begin{array}{*{20}c} {r_{{{\text{s}}1}} } & 0 \\ 0 & {r_{{{\text{s}}2}} } \\ \end{array} } \right],\;\varvec{L} = \left[ {\begin{array}{*{20}c} {l_{{{\text{k}}1}} + l_{e1} } & {l_{12} } \\ {l_{12} } & {l_{{{\text{k}}2}} + l_{e2} } \\ \end{array} } \right] \) and \( \varvec{C} = \left[ {\begin{array}{*{20}c} {\left( {1/c_{{{\text{q}}1}} + 1/c_{{{\text{e}}1}} } \right)^{ - 1} + c_{12} } & { - c_{12} } \\ { - c_{12} } & {\left( {1/c_{{{\text{q}}2}} + 1/c_{{{\text{e}}2}} } \right)^{ - 1} + c_{12} } \\ \end{array} } \right] \).

Central difference approximation is used to analyze the first-order differential Eqs. (4.6a) and (4.6b) by neglecting the higher order terms. This assumption results in a negligibly small loss of accuracy in the estimation of the transient response, since the value of time segment ∆t is limited by CFL condition [33]. Using the FDTD method, the analysis of telegrapher’s equations shows better accuracy, if the voltage and current points are chosen at the alternate space location and separated by one-half of the position discretization, i.e., ∆z/2 [12]. In the same manner, the solution time for V and I should also be separated by ∆t/2.

The interconnect line of length l is driven by a resistive driver at z = 0 and terminated by a capacitive load at z = l. The line is discretized into Nz uniform segments of length ∆z = l/Nz. The voltage and current solution points are discretized along the line as shown in Fig. 4.6.

Fig. 4.6
figure 6

Illustration of space discretization of line for FDTD implementation

Full size image

Applying finite difference approximations to (4.6a) results in

$$ \frac{{\varvec{V}_{{k+\text{1}}}^{{n+\varvec{1}}} - \,\varvec{V}_{k}^{{n+\varvec{1}}} }}{{\Delta z}} + \varvec{L}\frac{{\varvec{I}_{k}^{{n+{3/2}}} - \,\varvec{I}_{k}^{{n+{1/2}}} }}{{\Delta t}} + \varvec{R}\frac{{\varvec{I}_{k}^{{n+{3/2}}} + \varvec{I}_{k}^{{n+{1/2}}} }}{2} = 0 $$
(4.7a)
$$ \varvec{I}_{k}^{{n + \text{3/2}}} = \varvec{EFI}_{k}^{{n + 1/2}} + \varvec{E}\left[ {\varvec{V}_{k}^{{n + 1}} - \varvec{V}_{{k + 1}}^{{n + 1}} } \right]\quad \text{for}\,k \, = 1, 2, \ldots ,\,Nz $$
(4.7b)

where \( \varvec{E} = \left[ {\frac{{\Delta z}}{{\Delta t}}\varvec{L} + \frac{{\Delta z}}{2}\varvec{R}} \right]^{ - 1} \), \( \varvec{F} = \left[ {\frac{{\Delta z}}{{\Delta t}}\varvec{L} - \frac{{\Delta z}}{2}\varvec{R}} \right] \).

Applying finite difference approximations to (4.6b) results in

$$ \frac{{\varvec{I}_{k}^{{n + \text{1}\varvec{/}\text{2}}} - \,\,\varvec{I}_{{k - \text{1}}}^{{n + \text{1}\varvec{/}\text{2}}} }}{{\Delta z}} + \varvec{C}\frac{{\varvec{V}_{k}^{{n + \text{1}}} - \,\,\varvec{V}_{k}^{n} }}{{\Delta t}} = 0 $$
(4.8a)
$$ \varvec{V}_{k}^{{n + \text{1}}} = \varvec{V}_{k}^{n} + \varvec{D}\left[ {\varvec{I}_{{k - \text{1}}}^{{n + \text{1/2}}} - \varvec{I}_{k}^{{n + \text{1}\varvec{/}2}} } \right]\,\quad {\text{for}}\,k \, = 2, 3, \ldots ,\,Nz $$
(4.8b)

where \( \varvec{D} = \left[ {\frac{\Delta z}{\Delta t}\varvec{C}} \right]^{{ - {1}}} \).

4.3.2 Boundary Condition at Near-End Terminal

The voltage and current points at the near-end terminal are represented by V 1 and I 0, respectively. As indicated in Fig. 4.6, it is observed that to apply the boundary conditions in (4.8b), ∆z is replaced by ∆z/2. Therefore, at k = 1 Eq. (4.8b) becomes

$$ \varvec{V}_{\text{1}}^{{n+\text{1}}} = \varvec{V}_{\text{1}}^{n} + 2\varvec{D}\left[ {\varvec{I}_{\text{0}}^{{n+\text{1}\varvec{/}\text{2}}} - \varvec{I}_{\text{1}}^{{n+\text{1}\varvec{/}\text{2}}} } \right] $$
(4.9a)

The source current I 0 at (n + 1/2) time interval is obtained by averaging the source current at (n) and (n + 1) time intervals. Then Eq. (4.9a) becomes

$$ \varvec{V}_{1}^{{n+\text{1}}} = \varvec{V}_{1}^{n} + {2}\varvec{D}\left[ {\frac{{\varvec{I}_{0}^{{n+\text{1}}} + \varvec{I}_{0}^{n} }}{2} - \varvec{I}_{1}^{{n+\text{1}{/2}}} } \right] $$
(4.9b)

where I 0 is the driver current. Applying Kirchhoff’s current law (KCL) at near-end terminal, I 0 can be written as

$$ \varvec{V}_{0}^{{n+{1}}} = \varvec{V}_{{0}}^{n} + \varvec{A}\left[ {\frac{{\varvec{C}_{m} }}{\Delta t}(\varvec{V}_{s}^{{n+{1}}} - \varvec{V}_{s}^{n} ) + \varvec{I}_{{p}}^{n+1} - \varvec{I}_{{n}}^{n+1} - \varvec{I}_{0}^{n} } \right] $$
(4.9c)
$$ \varvec{V}_{1}^{{n+\text{1}}} \varvec{ = BV}_{1}^{n} + {2}\varvec{BD}\left[ {\frac{{\varvec{V}_{0}^{{n+\text{1}}} }}{{2\varvec{R}_{\text{lump}} }} + \frac{{\varvec{I}_{0}^{n} }}{2} - \varvec{I}_{1}^{{n+\text{1}{/2}}} } \right] $$
(4.9d)
$$ \varvec{I}_{0}^{n+1} = \frac{1}{{\varvec{R}_{\text{lump}} }}\left[ {\varvec{V}_{0}^{n+1} - \,\varvec{V}_{1}^{n+1} } \right] $$
(4.9e)

where \( \varvec{A} = \left[ {\frac{{\varvec{C}_{m} + \varvec{C}_{\text{d}} }}{{\Delta t}}} \right]^{{ - \text{1}}} ,\varvec{B} = \left[ {\varvec{U} + \frac{\varvec{D}}{{\varvec{R}_{\text{lump}} }}} \right]^{{ - \text{1}}} \) C m is the drain to gate coupling capacitance, C d is the drain diffusion capacitance of CMOS inverter, I p and I n are the PMOS and NMOS currents, respectively. The modified alpha-power law model that includes the drain conductance parameter is used to express the NMOS current as

$$ \varvec{I}_{{n}} = \left\{ {\begin{array}{*{20}l} 0 \hfill & {\varvec{V}_{S}\, \le\,V_{{{\text{tn}}}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{(off)}} } \hfill \\ {\varvec{K}_{ \ln } \left( {\varvec{V}_{s} - \varvec{V}_{\text{tn}} } \right)^{{\alpha_{n} /2}} \varvec{V}_{{0}} } \hfill & {\varvec{V}_{{0}}\,<\,\varvec{V}_{\text{DSATn}} \,\,\,\,\,{\text{(lin)}}} \hfill \\ {\varvec{K}_{\text{sn}} \left( {\varvec{V}_{s} - \varvec{V}_{\text{tn}} } \right)^{{\alpha_{n} }} (\text{1} + \sigma_{n} \varvec{V}_{{0}} )} \hfill & {\varvec{V}_{{0}}\,\ge \,\varvec{V}_{\text{DSATn}} \,\,\,\,\,{\text{(sat)}}} \hfill \\ \end{array} } \right.$$
(4.9f)

where K ln, K sn, V tn, α n , and σ n are the linear region transconductance parameter, saturation region transconductance parameter, threshold voltage, velocity saturation index, and drain conductance parameter of NMOS, respectively. In a similar manner, the PMOS current can be expressed as

$$\varvec{I}_{{p}} = \left\{ {\begin{array}{*{20}l} 0 & {\varvec{V}_{S}\, \ge \,\varvec{V}_{\text{DD}} - \left| {V_{\text{tp}} } \right|\,\,\,\,\,\,\,\,{\text{(off)}}} \hfill \\ {\varvec{K}_{\text{lp}} \left( {\varvec{V}_{\text{DD}} \, - \,\varvec{V}_{s} - \,\left| {\varvec{V}_{\text{tp}} } \right|} \right)^{{\alpha_{p} /2}} \left( {\varvec{V}_{\text{DD}} \, - \,\varvec{V}_{{0}}} \right)} \hfill & {\varvec{V}_{{0}}\, > \,\varvec{V}_{\text{DD}} - \varvec{V}_{\text{DSATp}} \,\,\,\;\,\,\,{\text{(lin)}}} \hfill \\ {\varvec{K}_{\text{sp}} \left( {\varvec{V}_{\text{DD}} \, - \,\varvec{V}_{s} - \left| {\varvec{V}_{\text{tp}} } \right|} \right)^{{\alpha_{p} }} \left( {\text{1} + \sigma_{p} \left( {\varvec{V}_{\text{DD}} { - }\,\varvec{V}_{{0}} } \right)\;\,} \right)} \hfill & {\varvec{V}_{{0}} \, \le\, \varvec{V}_{\text{DD}} - \;\varvec{V}_{\text{DSATp}} \,\,\,\,\,\,{\text{(sat)}}} \hfill \\ \end{array} } \right. $$
(4.9g)

4.3.3 Boundary Condition at Far-End Terminal

Here the objective is to derive the voltage expression at k = Nz + 1 and Nz + 2.

At k = Nz + 1, Eq. (4.8b) becomes

$$ \varvec{V}_{{Nz+\text{1}}}^{{n+\text{1}}} = \varvec{V}_{{Nz+\text{1}}}^{n} + {2}\varvec{D}\left( {\varvec{I}_{Nz}^{{n+\text{1}{/2}}} - \frac{{\varvec{I}_{{Nz+\text{1}}}^{{n+\text{1}}} + \varvec{I}_{{Nz+\text{1}}}^{n} }}{2}} \right) $$
(4.10a)

Applying KCL at far-end terminal, the output current (I Nz+1) can be expressed as

$$ \varvec{V}_{Nz+1} - \varvec{V}_{Nz+2} = \varvec{R}_{\text{lump}} \varvec{I}_{Nz+1} $$
(4.10b)

The discretized form of (4.10b) is

$$ \varvec{I}_{Nz+1}^{n+1} = \frac{1}{{\varvec{R}_{\text{lump}} }}\left[ {\varvec{V}_{Nz+1}^{n+1} - \varvec{V}_{Nz+2}^{n+1} } \right] $$
(4.10c)

Using (4.10a) and (4.10c) the far-end voltage V Nz+1 can be expressed as

$$ \varvec{V}_{{Nz+\text{1}}}^{{n+\text{1}}} = \varvec{BV}_{{Nz+\text{1}}}^{n}+2\varvec{BD}\left[ {\frac{{\varvec{V}_{Nz+2}^{{n+\text{1}}} }}{{2\varvec{R}_{\text{lump}} }} + \varvec{I}_{Nz}^{{n+\text{1}{/2}}} - \frac{{\varvec{I}_{{Nz+\text{1}}}^{n} }}{2}} \right] $$
(4.10d)

and the load voltage V Nz+2 is

$$ \varvec{V}_{{Nz+2}}^{{n+\text{1}}} = \varvec{V}_{{Nz+2}}^{n} + \frac{{\Delta t}}{{\varvec{C}_{L} }}\varvec{I}_{Nz+1}^{n} $$
(4.10e)

These equations are evaluated in a bootstrapping fashion. Initially, the voltages along the line are evaluated for a specific time from Eqs. (4.9c), (4.9d), (4.8b), (4.10e), and (4.10d) in terms of the previous values of voltage and current. Thereafter, the currents are evaluated from (4.9e), (4.7b), and (4.10c) in terms of these voltages and previous current values.

4.4 Validation of the Model

The coupled MWCNT interconnects are analyzed using the actual CMOS driver. The proposed model is implemented with the MATLAB. The industry standard HSPICE simulations are used for the validation of the results. The HSPICE simulations are carried out using the subcircuit model with 50 distributed segments for interconnect and using BSIM4 technology model for MOSFET. A symmetric CMOS driver is used to drive the interconnect load. The equivalent resistance of the driver is evaluated by averaging the resistance value over an interval when the input is between V DD and V DD/2 [34]. The signal integrity analysis is carried out at the global interconnect length of 1 mm for 32 nm technology and 0.9 V of V DD. The interconnect dimensions are based on the ITRS data [35]. The interconnect width and height from the ground plane are 48 and 110.4 nm, respectively. The spacing between the two interconnects is 48 nm. The relative permittivity of the inter layer dielectric medium is 2.25. The load capacitance and input transition time are 2 fF and 20 ps, respectively. The following RLC parasitics are used in the experiments [36–43]:

$$ \varvec{R = }\left[ {\begin{array}{*{20}c} {653.67} & 0 \\ 0 & {653.67} \\ \end{array} } \right]\frac{\text{k}\Omega }{\text{m}},\quad \varvec{L = }\left[ {\begin{array}{*{20}c} {14.83} & {0.61} \\ {0.61} & {14.83} \\ \end{array} } \right]\frac{{\upmu} {\text{H}}}{\text{m}}\quad {\text{and}}\quad \varvec{C = }\left[ {\begin{array}{*{20}c} {93.33} & { - 71.50} \\ { - 71.50} & {93.33} \\ \end{array} } \right]\frac{\text{pF}}{\text{m}} $$

In the interconnect system, lines 1 and 2 are considered as aggressor and victim lines, respectively. For the above-mentioned setup, the transient response is analyzed at the far-end terminal of the victim line using the proposed model, resistive driver-based model [14], and HSPICE simulations using CMOS driver. From Fig. 4.7, it can be observed that the model presented in [14] is unable to capture the timing waveform accurately. However, the proposed model is able to successfully capture the HSPICE waveform characteristics.

Fig. 4.7
figure 7

Transient response at the far-end terminal of the victim line when the aggressor and victim lines are switched out-of-phase

Full size image

The crosstalk-induced delay is analyzed under two different cases. First case considers out-phase delay where the input signals of aggressor and victim lines are switched out-of-phase. Second case considers in-phase delay where the input signals of aggressor and victim lines are switched in-phase. Figure 4.8a, b show out-phase and in-phase delay comparison, respectively, for different interconnect lengths. It can be clearly observed that the model proposed in [14], fails to estimate the crosstalk-induced delay for all interconnect lengths. The model proposed in [14] underestimates the delay for both out-phase and in-phase switching by average errors of 27.2 and 35.3 %, respectively.

Fig. 4.8
figure 8

Crosstalk-induced delay comparison a out-phase delay and b in-phase phase delay with the variation of interconnect length

Full size image

The functional crosstalk noise is analyzed when the aggressor line is switched and the victim line is kept in quiescent mode. Figure 4.9 depicts the noise peak voltage comparison on the victim line. It can be observed that the resistive driver model [14] overestimates the noise peak voltage, wherein the average error is observed to be 15 %.

Fig. 4.9
figure 9

Noise peak voltage comparison of victim line 2 with the variation of interconnect length

Full size image

To test the robustness, the proposed model is examined at different input transition times. The interconnect length is considered as 500 µm. Figure 4.10 depicts the computational error involved in predicting the crosstalk-induced propagation delay. It can be observed that the proposed model accurately predicts the delay for both out-phase and in-phase transitions. The average error involved is only 1.4 and 1.5 % during in-phase and out-phase switching, respectively. Contrastingly, with the resistive driver model [14], the average errors involved are 38.6 and 25.1 % for in-phase and out-phase switching, respectively.

Fig. 4.10
figure 10

Crosstalk-induced delay comparison on victim line 2 with the variation of input transition time

Full size image

Modified nodal analysis (MNA) is the core approach used in SPICE to formulate the system equations. Applying the Kirchhoff’s current law and following the energy conversion principle, the MNA generates the set of matrix equations. The order of the matrix is determined by the number of nodes and unknown variables in the circuit. The unknown variables are solved after the inversion of the matrix and therefore require more computational time. However, the FDTD operator is matrix free and therefore fast and memory efficient as compared to HSPICE simulations.

The efficiency of the proposed model is examined under different test cases. The analysis is carried out by varying the space segment while keeping the time segment constant for coupled interconnects. Using a PC with Intel Dual Core CPU (2.33 GHz, 4 GB RAM), the comparison results are provided in Table 4.1. Using the proposed model, it is observed that the CPU runtime reduces by an average of 91 % in comparison to HSPICE simulations. Additionally, the proposed model is compared with the HSPICE simulations using the same modified alpha-power law model. It is observed that the average CPU runtime reduces by 88 % in comparison to HSPICE simulations.

Table 4.1 CPU runtime comparison between proposed model and HSPICE with 1000 time segments
Full size table

4.5 Sensitivity Analysis

The primary assumptions made in the proposed work are for: (1) number of conducting channels and (2) contact resistance. This subsection presents the sensitivity analysis to evaluate the validity of these assumptions.

4.5.1 Sensitivity Analysis for Number of Conducting Channels

The number of conducting channels in a CNT can be obtained from expression (4.2b), which is an approximated form of (4.2a). Table 4.2 shows the variations in parasitics and crosstalk-induced performance parameters using Eqs. (4.2a) and (4.2b). The average percentage change in parasitics and performance parameters are just 2.3 and 2 %, respectively. It can be inferred that the parasitics and crosstalk-induced performance parameters are almost insensitive to the usage of approximated expression for obtaining N ch [44].

Table 4.2 Variation between (4.2a) and (4.2b) on parasitics and crosstalk-induced performance parameters
Full size table

4.5.2 Sensitivity Analysis for Contact Resistance

The value of imperfect metal contact resistance can range from the best case value of zero to the worst case value of few kilo-ohms depending on the fabrication process. As reported earlier [9], the R MC value is considered as 3.2 kΩ per shell. However, a sensitivity analysis on parasitic R lump,ESC and crosstalk-induced performance parameters for R MC varying from 0 to 8 kΩ is carried out and the results are presented in Table 4.3. A maximum variation of 5 % in R lump,ESC and almost no change in the crosstalk performance are noticed with the change in R MC. This is due to the fact that the crosstalk-induced performance parameters primarily depend on the scattering resistance and almost insensitive to the change in R MC.

Table 4.3 Variation of performance parameters due to change in R MC
Full size table

4.6 Summary

This chapter presented an accurate model to analyze the crosstalk effects in coupled MWCNT interconnect lines. The CMOS driver and the coupled MWCNT interconnect are modeled by modified alpha-power law model and FDTD method, respectively. It has been observed that the results of the proposed model exhibit a good agreement with HSPICE simulations. Over the random number of test cases, the average error in the propagation delay measurement is observed to be less than 2 %. Moreover, the sensitivity analysis is performed based on the assumptions used in the proposed model. It is observed that the percentage change in parasitic elements and performance parameters are almost negligible with respect to the assumptions associated with the model. This analysis suggests that with continuous advancements in FDTD technique the proposed model would play a significant role in performance analysis of MWCNT on-chip interconnects and would be potentially incorporated in TCAD simulators.