Delay-Dependent Stability for Discrete 2D Switched Systems with State Delays in the Roesser Model

Abstract

This paper is concerned with the problem of delay-dependent stability analysis for a class of two-dimensional (2D) discrete switched systems described by the Roesser model with state delays. First, the concept of average dwell time is extended to 2D switched systems with state delays. Then, based on the average dwell time approach, a delay-dependent sufficient condition for the exponential stability of the addressed systems is derived. All the results are formulated in terms of linear matrix inequalities (LMIs), which can be solved efficiently. A numerical example is given to illustrate the effectiveness of the proposed method.

1 Introduction

Two-dimensional (2D) systems are gaining momentum because of their broad applications in many areas such as multidimensional digital filtering, linear image processing, signal processing, and process control [8, 14, 18]. The stability analysis of 2D systems has attracted a great deal of interest, and some significant results have been obtained in [1, 10, 19, 36].

It is known that time delays frequently occur in practical systems and are often the source of instability, so it is of significance to study time-delay systems. Recently, many useful results on such systems have appeared. The resulting criteria can be classified into two categories: delay-independent and delay-dependent. Since delay-dependent criteria make use of information on the length of delays, they are less conservative than delay-independent ones. Recently, the free-weighting matrix approach [11] was employed to investigate the output feedback control of a linear discrete-time system with an interval time-varying delay. A new model transformation was analyzed and applied for the stability analysis of uncertain discrete-time systems with a time-varying delay in the state in [16]. In [24], a new delay-interval stability condition was established for systems with time delay varying in an interval. The stability problems of neural networks with time delays were investigated in [17, 38]. For 2D systems, some delay-independent stability results have appeared in [21, 32–34]. The issues of stability analysis, H _∞ control, and filtering for 2D discrete systems with constant delays have been investigated in [20, 22, 35]. Some results on the delay-dependent stability and stabilization of 2D discrete systems with time-varying delays have also been reported in the literature [6, 7, 9, 37].

On the other hand, switched systems have received considerable attention over the past several decades due to their extensive applications in, e.g., mechanical systems, the automotive industry, aircraft and air traffic control, and switched power converters. A switched system is a hybrid system consisting of a finite number of continuous-time or discrete-time subsystems and a switching signal specifying the switch between these subsystems. Several methods have been developed to study switched systems, such as the common Lyapunov function approach, the single Lyapunov function method, the average dwell time (ADT) scheme, and the multiple Lyapunov function method. In particular, the ADT method has been proven to be a more powerful and effective tool for stability analysis and stabilization of switched systems; see, for example, [5, 12, 13, 15, 25–29, 31, 39] and references cited therein.

Recently, there are a few reports on 2D discrete switched systems. Benzaouia et al. [2] first considered 2D switched systems with arbitrary switched sequences, and the stabilization problem of 2D discrete switched systems was investigated in [3]; a sufficient condition for the asymptotic stability of such systems was proposed and a stabilizing controller was developed in terms of linear matrix inequalities (LMIs). It should be noted that these papers focus on studying the asymptotic stability of the 2D switched systems, and the obtained results are based on common and multiple Lyapunov function approaches. In [30], the authors extended the concept of ADT in switched systems to 2D delay-free switched systems, and then designed a switching rule to guarantee the exponential stability of delay-free 2D switched systems. However, to the best of our knowledge, the problem of stability for 2D switched systems with state delays has not been investigated to date, especially for the exponential stability problem of 2D switched systems with state delays. Moreover, the method proposed in [30] cannot be directly applied to 2D switched systems with state delays. This motivates us to shorten this gap in the present investigation.

In this paper, we are interested in investigating the stability of 2D discrete switched systems represented by the Roesser model with state delays. The ADT approach is utilized for the stability analysis. The main contributions of this paper can be summarized as follows: (i) the concept of ADT is further extended to 2D switched systems with state delays, and a new Lyapunov–Krasovskii functional is constructed to investigate the stability of the system under consideration and a delay-dependent stability criterion is obtained; (ii) the exponential stability, which guarantees a decay rate where asymptotic stability does not, is first established for 2D switched systems with state delays, and the corresponding stability result is different from the asymptotical stability results presented in [7, 9]; (iii) all the results are formulated in terms of LMIs, which can be solved efficiently.

This paper is organized as follows. In Sect. 2, the problem formulation and some necessary lemmas are given. In Sect. 3, based on the ADT approach, the exponential stability problem of 2D discrete switched systems with state delays is addressed, and a delay-dependent sufficient condition for the existence of the exponential stability is derived in terms of a set of LMIs. A numerical example is provided to illustrate the effectiveness of the proposed approach in Sect. 4. The concluding remarks are given in Sect. 5.

Notation

Throughout this paper, the superscript “T” denotes the transpose, and the notation X≥Y (X>Y) means that matrix X−Y is positive semidefinite (positive definite, respectively). ∥⋅∥ denotes the Euclidean norm. I represents the identity matrix with an appropriate dimension. I _h is the identity matrix with n ₁ dimension and I _v is the identity matrix with n ₂ dimension. The asterisk ∗ in a matrix is used to denote the term that is induced by symmetry. The set of all nonnegative integers is represented by Z ₊.

2 Problem Formulation and Preliminaries

Consider the following 2D discrete linear switched systems with state delays:

$$ \left [ \begin{array}{c} x^{h} ( i + 1,j ) \\ x^{v} ( i,j + 1 ) \end{array} \right ] = A^{\sigma ( i,j )}\left [ \begin{array}{c} x^{h} ( i,j ) \\ x^{v} ( i,j ) \end{array} \right ] + A_{d}^{\sigma ( i,j )}\left [ \begin{array}{c} x^{h} ( i - d_{h} ( i ),j ) \\ x^{v} ( i,j - d_{v} ( j ) ) \end{array} \right ] $$

(1)

where x ^h(i,j) is the horizontal state in $R^{n_{1}}$, x ^v(i,j) is the vertical state in $R^{n_{2}}$, and x(i,j) is the whole state in R ⁿ with n=n ₁+n ₂. σ(i,j) is a switching rule which takes its values in the finite set $\underline{N}: = \{ 1, \ldots,N \}$, N is the number of subsystems, and i and j are integers in Z ₊. $\sigma ( i,j ) = k \in \underline{N}$ means that the kth subsystem is active. The matrices

$$ A^{k} = \left [ \begin{array}{c@{\quad }c} A_{11}^{k} & A_{12}^{k} \\ \noalign{\vspace*{4pt}} A_{21}^{k} & A_{22}^{k} \end{array} \right ], \qquad A_{d}^{k} = \left [ \begin{array}{c@{\quad }c} A_{d11}^{k} & A_{d12}^{k} \\ \noalign{\vspace*{4pt}} A_{d21}^{k} & A_{d22}^{k} \end{array} \right ],\quad k \in \underline{N} $$

(2)

where matrices $A_{11}^{k} \in R^{n_{1} \times n_{1}}$, $A_{12}^{k} \in R^{n_{1} \times n_{2}}$, $A_{21}^{k} \in R^{n_{2} \times n_{1}}$, $A_{22}^{k} \in R^{n_{2} \times n_{2}}$, $A_{d11}^{k} \in R^{n_{1} \times n_{1}}$, $A_{d12}^{k} \in R^{n_{1} \times n_{2}}$, $A_{d21}^{k} \in R^{n_{2} \times n_{1}}$, $A_{d22}^{k} \in R^{n_{2} \times n_{2}}$ are constant matrices. d _h (i) and d _v (j) are delays along the horizontal and vertical directions, respectively. We assume that d _h (i) and d _v (j) satisfy

$$ d_{hL} \le d_{h} ( i ) \le d_{hH},\qquad d_{vL} \le d_{v} ( j ) \le d_{vH} $$

(3)

where d _hL , d _hH , d _vL , and d _vH denote the lower and upper delay bounds along the horizontal and vertical directions, respectively. The boundary conditions are given by

(4)

where z ₁<∞ and z ₂<∞ are positive integers, and h _ij and v _ij are given vectors.

In the paper, it is assumed that the switch occurs only at each sampling point of i or j, and the switch sequence can be described as

$$ \bigl( ( i_{0},j_{0} ),\sigma ( i_{0},j_{0} ) \bigr),\quad \bigl( ( i_{1},j_{1} ),\sigma ( i_{1},j_{1} ) \bigr),\quad \ldots, \quad \bigl( ( i_{\kappa},j_{\kappa} ),\sigma ( i_{\kappa},j_{\kappa} ) \bigr), \ldots $$

(5)

where (i _κ ,j _κ ) denotes the κth switching instant. It should be noted that the value of σ(i,j) is only dependent on the value of i+j (see [3, 30]).

Remark 1

If there is only one subsystem in system (1), it will degenerate to the following 2D discrete systems with state delays:

$$\left [ \begin{array}{c} x^{h} ( i + 1,j ) \\ x^{v} ( i,j + 1 ) \end{array} \right ] = A\left [ \begin{array}{c} x^{h} ( i,j ) \\ x^{v} ( i,j ) \end{array} \right ] + A_{d} \left [ \begin{array}{c} x^{h} ( i - d_{h} ( i ),j ) \\ x^{v} ( i,j - d_{v} ( j ) ) \end{array} \right ]. $$

Definition 1

System (1) is said to be exponentially stable under σ(i,j) if for a given z≥0, there exist positive constants c and ξ, such that

$$ \sum_{i + j = D} \bigl \Vert x ( i,j ) \bigr \Vert ^{2} \le \xi e^{ - c ( D - z )}\sum_{i + j = z} \bigl \Vert x ( i,j ) \bigr \Vert _{C}^{2} $$

(6)

holds for all D≥z, where

Remark 2

From Definition 1, it is easy to see that when z is given, $\sum_{i + j = z} \Vert x ( i,j ) \Vert _{C}^{2}$ will be bounded and ∑ _i+j=D ∥x(i,j)∥² will tend to be zero exponentially as D goes to infinity, which also means ∥x(i,j)∥ tends to be zero.

Definition 2

[30]

For any i+j=D≥z=i _z +j _z , let N _σ(i,j)(z,D) denote the switching number of σ(i,j) on an interval [z,D). If

$$ N_{\sigma ( i,j )} ( z,D ) \le N_{0} + \frac{D - z}{\tau _{a}} $$

(7)

holds for given N ₀≥0 and τ _a ≥0, then the constant τ _a is called the average dwell time and N ₀ is the chatter bound.

Lemma 1

[4]

For a given matrix , where S ₁₁ and S ₂₂ are square matrices, the following conditions are equivalent:

• (i) S<0;

• (ii) S ₁₁<0, $S_{22} - S_{12}^{T}S_{11}^{ - 1}S_{12} < 0$;

• (iii) S ₂₂<0, $S_{11} - S_{12}S_{22}^{ - 1}S_{12}^{T} < 0$.

Lemma 2

[23]

For any vector ϕ(t)∈R ⁿ, two positive integers ω ₁ and ω ₂, and matrix 0<G∈R ^n×n, the following inequality holds:

$$- ( \omega _{2} - \omega _{1} + 1 )\sum _{t = \omega _{1}}^{\omega _{2}} \phi ^{T} ( t ) G\phi ( t ) \le - \Biggl[ \sum_{t = \omega _{1}}^{\omega _{2}} \phi ^{T} ( t ) \Biggr]G \Biggl[ \sum_{t = \omega _{1}}^{\omega _{2}} \phi ( t ) \Biggr]. $$

3 Main Results

In this subsection, we focus on the problem of stability analysis for 2D discrete switched system (1). The following theorem presents a delay-dependent sufficient condition for system (1) to be exponentially stable.

Theorem 1

Consider system (1), for given positive scalars d _hL , d _hH , d _vL , d _vH and α<1, if there exist positive definite symmetric matrices

with appropriate dimensions, $k \in \underline{N}$, such that

$$ \left [ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} \varPhi _{11} & \varLambda _{3}R_{2}^{k}A_{d}^{k} & \varLambda _{2}R_{3}^{k} & - \varLambda _{2}R_{2}^{k} & A^{kT} ( P^{k} + Q^{k} ) & ( A^{kT} - I_{n} )R_{3}^{k} \\ \noalign{\vspace*{4pt}} * & - \varLambda _{2}Q^{k} & 0 & 0 & A_{d}^{kT} ( P^{k} + Q^{k} ) & A_{d}^{kT}R_{3}^{k} \\ * & * & - \varLambda _{2} ( R_{3}^{k} + W^{k} ) & \varLambda _{2}R_{2}^{k} & 0 & 0 \\ \noalign{\vspace*{4pt}} * & * & * & - \varLambda _{2}R_{1}^{k} & 0 & 0 \\ * & * & * & * & - P^{k} - Q^{k} & 0 \\ * & * & * & * & * & - \varLambda _{3}^{ - 1}R_{3}^{k} \end{array} \right ] < 0, $$

(8)

where

$$\varLambda _{1} = \operatorname{diag} \bigl\{ ( d_{hH} - d_{hL} )I_{h}, ( d_{vH} - d_{vL} )I_{v} \bigr\}, $$

$$\varLambda _{2} = \operatorname{diag} \bigl\{ \alpha ^{1 + d_{hH}}I_{h},\alpha ^{1 + d_{vH}}I_{v} \bigr\}, \qquad \varLambda _{3} = \operatorname{diag} \bigl\{ \alpha d_{dH}^{2}I_{h},\alpha d_{vH}^{2}I_{v} \bigr\}, $$

$$R_{1}^{k} = \operatorname{diag} \bigl\{ R_{1h}^{k},R_{1v}^{k} \bigr\},\qquad R_{2}^{k} = \operatorname{diag} \bigl\{ R_{2h}^{k},R_{2v}^{k} \bigr\},\qquad R_{3}^{k} = \operatorname{diag} \bigl\{ R_{3h}^{k},R_{3v}^{k} \bigr\}, $$

holds. Then system (1) is exponentially stable for any switching signal with ADT satisfying

$$ \tau _{a} > \tau _{a}^{*} = \frac{\ln \chi}{ - \ln \alpha} $$

(9)

where χ≥1 satisfies

$$ P^{k} \le \chi P^{l},\qquad Q^{k} \le \chi Q^{l},\qquad W^{k} \le \chi W^{l},\qquad R^{k} \le \chi R^{l},\quad \forall k,l \in \underline{N}. $$

(10)

Proof

See the Appendix for the detailed proof. □

Remark 3

In Theorem 1, we propose a delay-dependent sufficient condition for the existence of the exponential stability for 2D discrete switched system (1). Note that this condition is obtained by using the ADT approach, and the parameter α plays a key role in obtaining $\tau _{a}^{ *}$.

Remark 4

It is easy to see that a larger α will be favorable for the feasibility of matrix inequality (8), while a smaller α is more expected to decrease $\tau _{a}^{ *}$. Thus we can first choose a smaller α; then by increasing the parameter α appropriately, we can find the feasible solution of P ^k, Q ^k, W ^k, and R ^ksuch that (8) holds, and $\tau _{a}^{ *}$ can be obtained from (9) and (10).

Remark 5

Note that when χ=1 in (9), the inequalities in (10) become P ^k=P ^l, Q ^k=Q ^l, W ^k=W ^l, and R ^k=R ^l, $\forall k,l \in \underline{N}$. In this case, we have $\tau _{a} > \tau _{a}^{ *} = 0$, which means that the switching signal can be arbitrary.

When d _hH =d _hL =d _h and d _vH =d _vL =d _v , system (1) generates to the following system:

$$ \left [ \begin{array}{c} x^{h} ( i + 1,j ) \\ x^{v} ( i,j + 1 ) \end{array} \right ] = A^{\sigma ( i,j )}\left [ \begin{array}{c} x^{h} ( i,j ) \\ x^{v} ( i,j ) \end{array} \right ] + A_{d}^{\sigma ( i,j )}\left [ \begin{array}{c} x^{h} ( i - d_{h},j ) \\ x^{v} ( i,j - d_{v} ) \end{array} \right ], $$

(11)

where d _h and d _v are constant delays along the horizontal and vertical directions, respectively. The boundary conditions are defined in (4). Then we have the following result.

Corollary 1

Consider system (11), for given positive constants d _h , d _v and α<1, if there exist positive definite symmetric matrices

with appropriate dimensions, $k \in \underline{N}$, such that

$$ \left [ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} \varTheta _{11} & \bar{\varLambda} _{3}R_{2}^{k}A_{d}^{k} + \bar{\varLambda} _{2}R_{3}^{k} & - \bar{\varLambda} _{2}R_{2}^{k} & A^{kT}P^{k} & ( A^{kT} - I_{n} )R_{3}^{k} \\ \noalign{\vspace*{4pt}} * & - \bar{\varLambda} _{2} ( R_{3}^{k} + W^{k} ) & \bar{\varLambda} _{2}R_{2}^{k} & A_{d}^{kT}P^{k} & A_{d}^{kT}R_{3}^{k} \\ \noalign{\vspace*{4pt}} * & * & - \bar{\varLambda} _{2}R_{1}^{k} & 0 & 0 \\ * & * & * & - P^{k} & 0 \\ * & * & * & * & - \bar{\varLambda} _{3}^{ - 1}R_{3}^{k} \end{array} \right ] < 0, $$

(12)

where

$$\varTheta _{11} = \bar{\varLambda} _{3}R_{1}^{k} - \bar{\varLambda} _{2}R_{3}^{k} + \alpha \bigl( - P^{k} + W^{k} \bigr) + \bar{\varLambda} _{3}R_{2}^{k} \bigl( A^{k} - I_{n} \bigr) + \bigl( A^{k} - I_{n} \bigr)^{T}R_{2}^{kT}\bar{\varLambda} _{3}, $$

$$\bar{\varLambda} _{2} = \operatorname{diag} \bigl\{ \alpha ^{1 + d_{h}}I_{h},\alpha ^{1 + d_{v}}I_{v} \bigr\}, \qquad \bar{\varLambda} _{3} = \operatorname{diag} \bigl\{ \alpha d_{h}^{2}I_{h},\alpha d_{v}^{2}I_{v} \bigr\} $$

holds. Then system (11) is exponentially stable for any switching signal with ADT satisfying (9), where χ≥1 satisfies

$$ P^{k} \le \chi P^{l},\qquad W^{k} \le \chi W^{l},\qquad R^{k} \le \chi R^{l},\quad \forall k,l \in \underline{N}. $$

(13)

Proof

Following the proof line of Theorem 1, the corollary can be obtained. □

Remark 6

It should be noted that when d _h (i)=0 and d _v (j)=0 in system (1), the stability result presented in Theorem 1 will reduce to the result of Theorem 1 proposed in [30].

4 Numerical Example

In this section, we present an example to illustrate the effectiveness of the proposed approach. Consider system (1) with parameters as follows:

$$A^{1} = \left [ \begin{array}{c@{\quad }c@{\quad }c} 0.8 & - 0.6 & 0.018 \\ 0.15 & 0.04 & 0 \\ 0.025 & 0 & 0.12 \end{array} \right ],\qquad A_{d}^{1} = \left [ \begin{array}{c@{\quad }c@{\quad }c} 0.12 & 0 & 0.06 \\ 0.12 & 0.03 & 0 \\ 0.035 & 0.15 & 0.04 \end{array} \right ], $$

$$A^{2} = \left [ \begin{array}{c@{\quad }c@{\quad }c} 0.9 & - 0.5 & 0.02 \\ 0.1 & 0.3 & 0 \\ 0.02 & 0 & 0.09 \end{array} \right ],\qquad A_{d}^{2} = \left [ \begin{array}{c@{\quad }c@{\quad }c} 0.1 & 0 & 0.05 \\ 0.1 & 0.02 & 0 \\ 0.03 & 0.12 & 0.03 \end{array} \right ], $$

$$d_{h} ( i ) = 3 + \sin \biggl( \frac{\pi i}{2} \biggr),\qquad d_{v} ( j ) = 4 + \sin \biggl( \frac{\pi j}{2} \biggr), $$

where the state dimensions are n ₁=2 and n ₂=1.

From the example, it is easy to get that the lower and upper delay bounds along the horizontal and the vertical directions are given by d _hL =2, d _hH =4, d _vL =3, and d _vH =5. By using the LMI Toolbox to solve Theorem 1, we find that the condition (8) holds when α is chosen in the interval [0.819,1). That is, the stability of the given system can be verified by applying the method proposed in the paper.

Taking α=0.85, the following solution is obtained:

$$P^{1} = \left [ \begin{array}{c@{\quad }c@{\quad }c} 0.1829 & - 0.1428 & 0 \\ - 0.1428 & 0.1985 & 0 \\ 0 & 0 & 0.0919 \end{array} \right ],\qquad Q^{1} = \left [ \begin{array}{c@{\quad }c@{\quad }c} 0.0124 & - 0.0019 & 0 \\ - 0.0019 & 0.0184 & 0 \\ 0 & 0 & 0.0245 \end{array} \right ], $$

$$P^{2} = \left [ \begin{array}{c@{\quad }c@{\quad }c} 0.209 & - 0.1859 & 0 \\ - 0.1859 & 0.221 & 0 \\ 0 & 0 & 0.0715 \end{array} \right ],\qquad Q^{2} = \left [ \begin{array}{c@{\quad }c@{\quad }c} 0.0067 & - 0.0025 & 0 \\ - 0.0025 & 0.0101 & 0 \\ 0 & 0 & 0.0224 \end{array} \right ], $$

$$W^{1} = \left [ \begin{array}{c@{\quad }c@{\quad }c} 0.0058 & - 0.0081 & 0 \\ - 0.0081 & 0.0214 & 0 \\ 0 & 0 & 0.0126 \end{array} \right ],\qquad W^{2} = \left [ \begin{array}{c@{\quad }c@{\quad }c} 0.0029 & - 0.0046 & 0 \\ - 0.0046 & 0.0101 & 0 \\ 0 & 0 & 0.0224 \end{array} \right ], $$

$$R_{h}^{1} = \left [ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 0.0038 & - 0.0053 & 0.0070 & - 0.0088 \\ - 0.0053 & 0.0096 & - 0.0054 & 0.0107 \\ 0.0070 & - 0.0054 & 0.0260 & - 0.0220 \\ - 0.0088 & 0.0107 & - 0.0220 & 0.0240 \end{array} \right ],\qquad R_{v}^{1} = \left [ \begin{array}{c@{\quad }c} 0.0016 & 0.0016 \\ 0.0016 & 0.0024 \end{array} \right ], $$

$$R_{h}^{2} = \left [ \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 0.0013 & - 0.0017 & 0.0046 & - 0.0056 \\ - 0.0017 & 0.0028 & - 0.0043 & 0.0065 \\ 0.0046 & - 0.0043 & 0.0297 & - 0.274 \\ - 0.0056 & 0.0065 & - 0.274 & 0.0301 \end{array} \right ],\qquad R_{v}^{2} = \left [ \begin{array}{c@{\quad }c} 0.0007 & 0.0007 \\ 0.0007 & 0.0012 \end{array} \right ]. $$

Furthermore, by (9) and (10), we get χ=8.4841 and $\tau _{a}^{*} = 13.16$. Therefore, according to Theorem 1, we obtain that under the ADT scheme τ _a >13.16, the given system is exponentially stable.

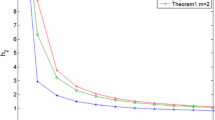
The simulation results are shown in Figs. 1, 2, 3 and 4 under arbitrary (randomly generated) boundary conditions. Figures 1, 2 and 3 plot the responses of three states, $x_{1}^{h} ( i,j )$, $x_{2}^{h} ( i,j )$, and x ^v(i,j), and Fig. 4 depicts the switching signal with ADT satisfying τ _a =14. From the simulation results, it can be observed that the proposed method is effective.

Fig. 1

The response of state $x_{1}^{h} ( i,j )$

Fig. 2

The response of state $x_{2}^{h} ( i,j )$

Fig. 3

The response of state x ^v(i,j)

Fig. 4

Switching signal

5 Conclusions

This paper has investigated the problem of stability analysis for a class of 2D discrete switched systems represented by the Roesser model with state delays. A delay-dependent sufficient condition for the exponential stability of the system under consideration has been derived in terms of LMIs via the average dwell-time approach. An example is also given to illustrate the applicability of the proposed approach.

Appendix: The proof of Theorem 1

Proof

Without loss of generality, we assume that the kth subsystem is active. We consider the following Lyapunov–Krasovskii functional candidate for the kth subsystem:

$$ V_{k} \bigl( x ( i,j ) \bigr) = V_{k}^{h} \bigl( x^{h} ( i,j ) \bigr) + V_{k}^{v} \bigl( x^{v} ( i,j ) \bigr), $$

(14)

where

$$V_{k}^{h} \bigl( x^{h} ( i,j ) \bigr) = \sum _{g = 1}^{5} V_{gk}^{h} \bigl( x^{h} ( i,j ) \bigr),\qquad V_{k}^{v} \bigl( x^{v} ( i,j ) \bigr) = \sum_{g = 1}^{5} V_{gk}^{v} \bigl( x^{v} ( i,j ) \bigr), $$

$$V_{1k}^{h} \bigl( x^{h} ( i,j ) \bigr) = x^{h} ( i,j )^{T}P_{h}^{k}x^{h} ( i,j ),$$

$$V_{2k}^{h} \bigl( x^{h} ( i,j ) \bigr) = \sum_{r = i - d_{h} ( i )}^{i} x^{h} ( r,j )^{T}Q_{h}^{k}x^{h} ( r,j ) \alpha ^{i - r}, $$

$$V_{3k}^{h} \bigl( x^{h} ( i,j ) \bigr) = \sum _{r = i - d_{hH}}^{i - 1} x^{h} ( r,j )^{T}W_{h}^{k}x^{h} ( r,j ) \alpha ^{i - r}, $$

$$V_{4k}^{h} \bigl( x^{h} ( i,j ) \bigr) = \sum _{s = - d_{hH} + 1}^{ - d_{hL}} \sum _{r = i + s}^{i - 1} x^{h} ( r,j )^{T}Q_{h}^{k}x^{h} ( r,j ) \alpha ^{i - r}, $$

$$V_{5k}^{h} \bigl( x^{h} ( i,j ) \bigr) = d_{hH}\sum_{s = - d_{hH}}^{ - 1} \sum _{r = i + s}^{i - 1} \eta ^{h} ( r,j )^{T}R_{h}^{k}\eta ^{h} ( r,j ) \alpha ^{i - r}, $$

$$V_{1k}^{v} \bigl( x^{v} ( i,j ) \bigr) = x^{v} ( i,j )^{T}P_{v}^{k}x^{v} ( i,j ),$$

$$V_{2k}^{v} \bigl( x^{v} ( i,j ) \bigr) = \sum_{t = j - d_{v} ( j )}^{j} x^{v} ( i,s )^{T}Q_{v}^{k}x^{v} ( i,s ) \alpha ^{j - t}, $$

$$V_{3k}^{v} \bigl( x^{v} ( i,j ) \bigr) = \sum _{t = j - d_{vH}}^{j - 1} x^{v} ( i,t )^{T}W_{v}^{k}x^{v} ( i,t ) \alpha ^{j - t}, $$

$$V_{4k}^{v} \bigl( x^{v} ( i,j ) \bigr) = \sum _{s = - d_{vH} + 1}^{ - d_{vL}} \sum _{t = j + s}^{j - 1} x^{v} ( i,t )^{T}Q_{v}^{k}x^{v} ( i,t ) \alpha ^{j - t}, $$

$$V_{5k}^{v} \bigl( x^{v} ( i,j ) \bigr) = d_{vH}\sum_{s = - d_{vH}}^{ - 1} \sum _{t = j + s}^{j - 1} \eta ^{v} ( i,t )^{T}R_{v}^{k}\eta ^{v} ( i,t ) \alpha ^{j - t}, $$

$$\eta ^{h} ( r,j ) = \left [ \begin{array}{c@{\quad }c} x^{h} ( r,j )^{T} & \delta ^{h} ( r,j )^{T} \end{array} \right ]^{T}, \qquad \eta ^{v} ( i,t ) = \left [ \begin{array}{c@{\quad }c} x^{v} ( i,t )^{T} & \delta ^{v} ( i,t )^{T} \end{array} \right ]^{T}, $$

$$\delta ^{h} ( r,j ) = x^{h} ( r + 1,j ) - x^{h} ( r,j ),\qquad \delta ^{v} ( i,t ) = x^{v} ( i,t + 1 ) - x^{v} ( i,t ), $$

where

are real matrices to be determined.

Then we have

(15)

(16)

(17)

(18)

(19)

(20)

(21)

(22)

(23)

(24)

By Lemma 2, it can be obtained from (19) and (24) that

(25)

(26)

Denote

$$\varLambda _{1} = \operatorname{diag} \bigl\{ ( d_{hH} - d_{hL} )I_{h}, ( d_{vH} - d_{vL} )I_{v} \bigr\}, $$

$$\varLambda _{2} = \operatorname{diag} \bigl\{ \alpha ^{1 + d_{hH}}I_{h},\alpha ^{1 + d_{vH}}I_{v} \bigr\}, \qquad \varLambda _{3} = \operatorname{diag} \bigl\{ \alpha d_{hH}^{2}I_{h},\alpha d_{vH}^{2}I_{v} \bigr\}. $$

From (25) and (26), we obtain the following relationship:

(27)

where

In addition, applying Lemma 1, inequality (8) is equivalent to the following inequality:

$$\left ( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c} \varPsi _{11} & \varPsi _{12} & \varLambda _{2}R_{3}^{k} & - \varLambda _{2}R_{2}^{k} \\ * & \varPsi _{22} & 0 & 0 \\ * & * & \varPsi _{33} & \varLambda _{2}R_{2}^{k} \\ \noalign{\vspace*{4pt}} * & * & * & - \varLambda _{2}R_{1}^{k} \end{array} \right ) < 0. $$

Thus, it is easy to obtain

$$ V_{k}^{h} ( i + 1,j ) + V_{k}^{v} ( i,j + 1 ) < \alpha \bigl( V_{k}^{h} ( i,j ) + V_{k}^{v} ( i,j ) \bigr). $$

(28)

Notice that for any nonnegative integer D>z=max(z ₁,z ₂), one has that V ^h(0,D)=V ^v(D,0)=0. Then summing up both sides of (28) from D−1 to 0 with respect to j and 0 to D−1 with respect to i, one gets

(29)

Assume that the switching number of σ(i,j) on an interval [z,D) is υ=N _σ(i,j)(z,D), and let (i _κ−υ+1,j _κ−υ+1),(i _κ−υ+2,j _κ−υ+2),…,(i _κ ,j _κ ) denote the switching points of σ(i,j) over the interval [z,D). Thus, denoting m _i =i _i +j _i , i=κ−υ+1,…,κ, it follows from (10) and (29) that

(30)

Notice from (14) that there exist two positive constants a and b(a<b) such that

(31)

Combining (30) and (31), we obtain

$$ \sum_{i + j = D} \bigl \Vert x ( i,j ) \bigr \Vert ^{2} < \frac{b}{a}e^{ - ( - \frac{\ln \chi}{\tau _{a}} - \ln \alpha ) ( D - z )}\sum _{i + j = z} \bigl \Vert x ( i,j ) \bigr \Vert _{C}^{2}. $$

(32)

By Definition 1, it follows from (9) that 2D discrete switched system (1) is exponentially stable. The proof is completed. □