Abstract
In this paper, we present a general method to derive the explicit constitutive relations for isotropic elastic 6-parameter shells made from a Cosserat material. The dimensional reduction procedure extends the methods of the classical shell theory to the case of Cosserat shells. Starting from the three-dimensional Cosserat parent model, we perform the integration over the thickness and obtain a consistent shell model of order \( O(h^5) \) with respect to the shell thickness h. We derive the explicit form of the strain energy density for 6-parameter (Cosserat) shells, in which the constitutive coefficients are expressed in terms of the three-dimensional elasticity constants and depend on the initial curvature of the shell. The obtained form of the shell strain energy density is compared with other previous variants from the literature, and the advantages of our constitutive model are discussed.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The theory of shells is an important branch of solid mechanics, since it investigates the behavior of thin (shell-like) bodies, which are widely used in civil and mechanical engineering, automotive and aircraft industry, etc.
One of the main issues of the shell theory (which is not yet completely solved) is the derivation of an appropriate two-dimensional continuum model for shells, using a dimensional reduction procedure starting from the parent three-dimensional continuum. Such a shell model should be simple enough to be amenable for engineering applications, but also it should be complex enough to capture the important features of shell deformation, such as stretching, bending, transverse shear deformation or drill. Therefore, one can find in the literature several proposed shell models, which have different degrees of complexity. For instance, in the classical theory of shells, the transverse shear deformation and drilling deformation are not taken into account. Thus, the elastically stored strain energy density \( W(\varvec{\varepsilon }, \varvec{\rho }) \) in the Koiter model can be decomposed additively in two parts: the membrane part \( W_{\mathrm {memb}}(\varvec{\varepsilon }) \), which is of order O(h) and depends on the change of metric tensor \( \varvec{\varepsilon } \), and the bending part \( W_{\mathrm {bend}}( \varvec{\rho }) \), which is of order \( O(h^3) \) and depends on the change of curvature tensor \( \varvec{\rho } \) (see, e.g., [14, 20, 36]).
One of the most general kinematical models for shells is given by the theory of 6-parameter shells, which was initially proposed by Reissner [30] and developed subsequently in many works, such as [12, 17, 21, 27]. This kinematical model coincides with the kinematical model of Cosserat shells, see also [4, 6, 9]. The deformation is described by means of the translation (3 parameters) and the orientation (or rotation: 3 additional parameters) of material points. In order to obtain an useful model for 6-parameter shells, which can be applied in practical problems, one needs to adjoin specific constitutive relations and to determine the expression of the shell strain energy density in terms of the three-dimensional elasticity constants of the material. In this respect, we mention that the strain energy density which is usually employed for 6-parameter shells has a relatively simple expression of order \( O(h^3) \), in which the constitutive coefficients are constant, i.e., they are independent of the initial curvature of the shell (see Sect. 2.3 and the references [12, 13]).
The goal of the present paper is to derive a refined form of the strain energy density of order \( O(h^5) \) for isotropic 6-parameter shells, starting from the three-dimensional Cosserat parent model. The dimensional reduction procedure is similar to that used in the classical shell theory, as presented systematically by Steigmann in [34,35,36]. In this way, we obtain the explicit form of the constitutive relations, including all the terms up to the order \( O(h^5) \), where the constitutive coefficients are expressed in terms of the elastic material constants and depend on the initial curvature of the shell. The present work generalizes the results obtained in [5], where the corresponding shell model of order \( O(h^3) \) has been presented. The constitutive model derived in our paper is very close to the model presented in [7], but we employ a simpler derivation method, which is also more general. Moreover, this new dimensional reduction procedure allows us to adjust the transverse shear coefficients (in accordance with those obtained by a \( \Gamma \)-convergence analysis) and to improve a higher-order term in the strain energy density. In Sect. 5.3, we discuss these improvements in detail and show that the model in [7] can be regarded as a special case of our present result.
Outline of the paper In Sect. 2, we review the kinematical model of 6-parameter shells and present the governing equations of the mechanical theory. Section 3 presents the dimensional reduction procedure: We start with the three-dimensional Cosserat model, which is described in Sect. 3.1. Then, we perform the integration over the thickness in Sect. 3.2 and use the method inspired by the classical shell theory [36]. In Sect. 4, we obtain the reduced (simplified) form of the strain energy density of order \( O(h^5) \) by adopting some simplifying assumptions for thin shells. The main result of the paper is the final form of the areal strain energy density given by (119). Finally, we write in Sect. 5 some alternative useful forms of the constitutive relations in terms of strain measures with clear mechanical significance. We also discuss the special case of the quadratic ansatz in Sect. 5.3 and present a detailed comparison with the previous models in [5, 7].
Summary of notations Let us present next some useful notations which will be used throughout this paper. The Latin indices \( i,j,k,\ldots \) range over the set \( \{1,2,3\} \), while the Greek indices \( \alpha ,\beta ,\gamma ,\ldots \) range over the set \( \{1,2\} \). The Einstein summation convention over repeated indices is used. A subscript comma preceding an index i (or \( \alpha \)) designates partial differentiation with respect to the variable \( x_i \) (or \( x_\alpha \, \), respectively), e.g. \( f,_i = \dfrac{\partial f}{\partial x_i}\, \). We denote by \( \,\delta _i^j\, \) the Kronecker symbol, i.e., \( \,\delta _i^j=1 \) for \( i=j \), while \(\,\delta _i^j=0 \) for \( i\ne j \).
We employ the direct tensor notation. Thus, \( \otimes \) designates the dyadic product, \( {\varvec{\mathbb {1}}}_3 = {\varvec{g}}_i\otimes \, \varvec{g}^i\, \) is the unit second-order tensor in the 3-space, and \( \mathrm {axl}({\varvec{W}}) \) stands for the axial vector of any skew-symmetric tensor \( {\varvec{W}} \).
Let \( \mathrm {tr}({\varvec{X}}) \) denote the trace of any second-order tensor \( {\varvec{X}} \). The symmetric part, skew-symmetric part and deviatoric part of \( {\varvec{X}} \) are defined by
The scalar product between any second-order tensors \( \,\varvec{A} = A^{ij}{\varvec{g}}_i\otimes {\varvec{g}}_j = A_{ij}\,{\varvec{g}}^i\otimes {\varvec{g}}^j\,\) and \(\, {\varvec{B}} = B^{kl}{\varvec{g}}_k\otimes {\varvec{g}}_l = B_{kl}\,{\varvec{g}}^k\otimes {\varvec{g}}^l\,\) is denoted by
If \( \, \underline{{\varvec{C}}} = C^{ijkl}{\varvec{g}}_i\otimes {\varvec{g}}_j\otimes {\varvec{g}}_k\otimes {\varvec{g}}_l \, \) is a fourth-order tensor, then we use the corresponding notations
For any vector \( {\varvec{v}} = v^i {\varvec{g}}_i = v_i\, {\varvec{g}}^i\), we write as usual
2 The governing equations of elastic six-parameter elastic shells
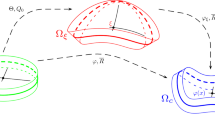
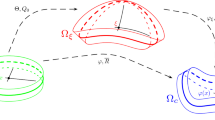
Let us denote with \( {\mathcal {S}}_c \) the deformed (current) configuration of a shell and with \( {\mathcal {S}}_\xi \) its reference configuration. We designate the midsurface of the reference configuration with \( \omega _\xi \subset \mathbb {R}^3\), which is determined by the parametric representation \( \varvec{y}_0(x_1,x_2) \), where \( {\varvec{y}}_0: \omega \subset \mathbb {R}^2 \rightarrow \omega _\xi \) is a vector mapping. The curvilinear coordinates \( (x_1,x_2) \) are assumed to be convected coordinates on the surface \( \omega _\xi \, \).
2.1 Geometry of the reference midsurface
In order to present the two-dimensional field equations of 6-parameter shells, we review first some basic relations pertaining to the geometry of the midsurface \( \omega _\xi \, \). We define as usual the covariant base vectors \( {\varvec{a}}_\alpha \) and the contravariant base vectors \( {\varvec{a}}^\alpha \) in the tangent plane of \( \omega _\xi \) by
and we also denote by
is the unit normal vector to the surface \(\omega _\xi \,\). The first fundamental tensor \( {\varvec{a}} \) and the second fundamental tensor \( {\varvec{b}} \) of the midsurface \( \omega _\xi \) are given by
where \( a_{\alpha \beta } = {\varvec{a}}_\alpha \cdot \varvec{a}_\beta \, \), \( \;b_{\alpha \beta } = - \varvec{a}_\alpha \cdot {\varvec{n}}_{0,\beta } \, \) and \( \text {Grad}_s\, \) is the surface gradient operator defined by
for any vector field \( {\varvec{f}}(x_1,x_2) \). Moreover, let \( \text {Div}_s\, \) designate the surface divergence operator given by
for any second-order tensor field \( {\varvec{T}}(x_1,x_2) \). The so-called alternator tensor \( {\varvec{c}} \) in the tangent plane is defined by
where \(\epsilon _{\alpha \beta }\,\) is the two-dimensional alternator (\(\epsilon _{12}=-\epsilon _{21}=1,\,\epsilon _{11}=\epsilon _{22}=0\)). We note that the fundamental tensors \( {\varvec{a}} \) and \( {\varvec{b}} \) are symmetric, while the alternator tensor \( {\varvec{c}} \) is skew-symmetric and fullfils \( {\varvec{c}}^2= -{\varvec{a}} \) and \( \mathrm {axl}({\varvec{c}}) = -\varvec{n}_0\,\), since we have
Moreover, the fundamental tensor \( {\varvec{a}} \) can be viewed as the projection tensor in the tangent plane, since \( \varvec{a}{\varvec{v}} = {\varvec{a}}(v_i{\varvec{a}}^i)= v_\alpha {\varvec{a}}^\alpha = {\varvec{v}} - (\varvec{v}\cdot {\varvec{n}}_0){\varvec{n}}_0\, \). The following relation of Cayley–Hamilton type holds
where \( H=\frac{1}{2}\mathrm {tr}\,{\varvec{b}}= \frac{1}{2} b^{\alpha }_{\alpha } \) is the mean curvature and \( K=\mathrm {det}\,{\varvec{b}}=\mathrm {det} \big ( b^{\alpha }_{\beta } \big )_{2\times 2} \) is the Gauß curvature of the midsurface \( \omega _\xi \, \).
2.2 Kinematical variables and strain measures
Let us refer the shell to the Cartesian coordinate frame \( Ox_1x_2x_3 \) with origin O and unit vectors \( \{\varvec{e}_1,{\varvec{e}}_2,{\varvec{e}}_3 \} \) along the coordinate axes \( Ox_i\, \). The kinematical structure of 6-parameter shells coincides with that of Cosserat shells. Thus, the reference configuration of the shell is described by the position vector \( {\varvec{y}}_0 \) and the initial microrotation tensor \( {\varvec{Q}}_0 \) given by
where the parameter domain \( \omega \) is assumed to be a bounded open domain with Lipschitz boundary \(\partial \omega \) in the \(Ox_1x_2\) plane. The vectors \(\{\varvec{d}^0_1 , \varvec{d}^0_2 , \varvec{d}^0_3\}\) represent the orthonormal triad of directors, which is attached to every point and describes the structure (orientation) of the reference configuration. The third director \( \varvec{d}^0_3 \) is chosen to coincide with the unit normal in the reference configuration, i.e.,
The deformation of the shell is characterized by the deformation function \( {\varvec{m}} \) and the microrotation tensor \( {\varvec{Q}}_e \) given by
where \(\{\varvec{d}_1 , \varvec{d}_2 , \varvec{d}_3\}\) is the orthonormal triad of directors which describes the orientation of points in the deformed configuration. Thus, the model has 6 degrees of freedom (3 for the translation \( {\varvec{m}} \) and 3 for the rotation \( {\varvec{Q}}_e \)) assigned to every point of the shell.
The strain measures of 6-parameter shells are usually defined in terms of \( {\varvec{m}} \) and \( {\varvec{Q}}_e \) as follows [12, 16, 21]: the shell strain tensor
and the shell bending-curvature tensor
Remark 2.1
In view of the decomposition \( {\varvec{\mathbb {1}}}_3= {\varvec{a}} + \varvec{n}_0\otimes {\varvec{n}}_0\, \), one can decompose the shell strain tensor \({\varvec{E}}^e\) into its ‘planar’ part \({\varvec{a}} {\varvec{E}}^e\) and its ‘transversal’ part \({\varvec{n}}_0 {\varvec{E}}^e\) according to
where the tensor \( \varvec{\varepsilon }^e \) characterizes the in-plane deformation of the shell, while the vector
describes the transverse shear deformation. Similarly, in view of \( {\varvec{a}}=-{\varvec{c}}^2 \), we can decompose the shell bending-curvature tensor as
where the planar tensor \( \varvec{\rho }^e \) ist the bending tensor given by (see f. (70) in [7])
Further, the transversal part \( \varvec{\nu }^e \) in (16) is also called the vector of drilling bendings [29] and is given by
Indeed, the last relation can be proved as follows
Remark 2.2
In the literature on nonlinear shells of Cosserat type, one can find also other variants of the shell strain measures. For instance, Altenbach and Zhilin [2, 3, 38] have employed the following strain tensor
i.e., in view of (12),
which accounts for the extensional and in-plane shear deformations in the theory of simple elastic shells.
As an alternative to the shell bending-curvature tensor \( {\varvec{K}}^e\) given in (13), one can use the so-called shell dislocation density tensor defined by
which was defined in [10] and employed in [11] to investigate the deformation of Cosserat elastic shells.
2.3 Balance equations and constitutive relations
Let \( {\varvec{N}} \) be the internal surface stress tensor and \( {\varvec{M}} \) the internal surface couple tensor (of the first Piola–Kirchhoff type). Also, we designate by
the surface gradient of the midsurface deformation \( \varvec{m} \), also called the shell deformation gradient. The equilibrium equations for 6-parameter shells are
where \( {\varvec{f}} \) and \( {\varvec{l}} \) stand for the external body forces and body couples, respectively. The balance equations (21) can be justified via the principle of virtual work (see, e.g., [16]) or from the condition that the equilibrium state is a stationary point of the energy functional (see Sect. 4.3 in [5]). To the equilibrium equations (21), we adjoin boundary conditions of mixed type prescribed on the boundary curve \(\partial \omega _\xi \,\) (see, e.g., [8, 15, 27])
where \(\partial \omega _f \cup \partial \omega _d = \partial \omega _\xi \,\) is a disjoint partition of the boundary curve. Here, \(\varvec{N}^*\) and \(\varvec{M}^*\) are the external boundary force and couple vectors, respectively, applied along the deformed boundary curve, but measured per unit length of \(\partial \omega _f\,\). On the portion of the boundary \(\partial \omega _d\), we have Dirichlet-type boundary conditions for the deformation vector \( \varvec{m} \) and the microrotation tensor \( \varvec{Q}_e\, \).
Under hyperelasticity assumptions, the stress and couple stress tensors \( \varvec{N} \) and \( \varvec{M} \) satisfy the following constitutive relations
where the elastically stored areal energy density \( \mathcal W_{\mathrm {shell}} \) for 6-parameter shells is given by
The question is: Which is the appropriate expression of the energy density \( {\mathcal {W}}_{\mathrm {shell}} \) in (24) for isotropic shells? The main goal of our paper is to give a good answer to this question, by proposing a new expression for the energy density \( {\mathcal {W}}_{\mathrm {shell}}( \varvec{E}^e,{\varvec{K}}^e) \), which generalizes and improves many previous results in the literature.
In [16], the general form of a quadratic energy density for isotropic shells is presented, but the constitutive coefficients are not determined in terms of the three-dimensional material constants. Thus, for instance, the following simplified expression of the energy density is proposed in [16]
or equivalently, in view of the relation \( \mathrm {tr}(\varvec{X}^2) = \Vert \mathrm {sym}({\varvec{X}})\Vert ^2 - \Vert \mathrm {skew}({\varvec{X}})\Vert ^2 \),
where \( \alpha _k \) and \( \beta _k \) are constant (general) constitutive coefficients. To use the energy density (25) in applications, the following values of the coefficients \( \alpha _k \) and \( \beta _k \) have been chosen in [12, 13] for an isotropic Cauchy material with Poisson ratio \( \nu \) and Young modulus E :
where \(C=\frac{E\,h}{1-\nu ^2}\,\) is the stretching (membrane) stiffness of the shell, \(D=\frac{E\,h^3}{12(1-\nu ^2)}\,\) is the bending stiffness, and \(\alpha _s=\frac{5}{6}\,\) and \(\alpha _t=\frac{7}{10}\) are two shear correction factors. By virtue of (25) and (26), we see that the concrete form of the strain energy density commonly used in the literature is
where \( \lambda \) and \( \mu \) are the Lamé constants of the isotropic and homogeneous elastic material. We observe in (27) that the constitutive coefficients do not depend on the initial curvature of the shell.
In [5], we have presented a more elaborate expression of the strain energy density \( \mathcal W_{\mathrm {shell}} \) of order \( O(h^3) \) for shells made of an isotropic Cosserat material with Cosserat couple modulus \( \mu _c\, \). This refined form can be written as (see f. (68) in [5])
where the bilinear form \( W_{\mathrm {Coss}} \) is defined for any second-order tensors \( {\varvec{X}}=X_{i\alpha }\varvec{a}^i\otimes {\varvec{a}}^\alpha \), \( \varvec{Y}=Y_{i\alpha }{\varvec{a}}^i\otimes {\varvec{a}}^\alpha \) by
The quadratic form \( W_{\mathrm {curv}} \) is defined in the sequel by (59). Compare the energy density (28)–(30) with (27). We remark in (28) the coupling between the in-plane deformation \( {\varvec{a}}{\varvec{E}}^e =\varvec{\varepsilon }^e\) and the bending tensor \( {\varvec{c}} {\varvec{K}}^e = -\varvec{\rho }^e \), as well as the occurrence of the mean curvature H, the Gauß curvature K and the tensor \( {\varvec{b}} \), which characterize the initial curvature of the shell.
In the present paper, we shall generalize the model (28) to include all the terms up to the order \( O(h^5) \) and obtain thus an improved shell model, see Eq. (119) for the final result.
3 Derivation of the constitutive model for shells
In order to obtain the areal strain energy density \(\mathcal W_{\mathrm {shell}}({\varvec{E}}^e,{\varvec{K}}^e) \) defined on the midsurface of the shell, we start from the energy density of the three-dimensional Cosserat shell-like body and perform the integration over the thickness. Let us present first the nonlinear three-dimensional model for Cosserat elastic continua.
3.1 The parent three-dimensional Cosserat model
Consider a Cosserat elastic continuum occupying the domain \(\Omega _\xi \subset \mathbb {R}^3\) in its reference configuration. The reference configuration \( \Omega _\xi \) is characterized by the parametric representation \(\varvec{\Theta }(x_1,x_2,x_3)\) with \( \varvec{\Theta }:\Omega _h \rightarrow \Omega _\xi \, \). For the curvilinear coordinates \((x_1,x_2,x_3)\) on \( \Omega _\xi \), we denote as usual the covariant base vectors by \({\varvec{g}}_i : = \varvec{\Theta },_i\) and the contravariant base vectors by \({\varvec{g}}^i\), with \( {\varvec{g}}^i\cdot \varvec{g}_j=\delta _j^i\, \). The parameter domain \( \Omega _h\subset \mathbb {R}^3 \) is referred to the Cartesian coordinate frame \( Ox_1x_2x_3 \) with othonormal vector basis \( \{{\varvec{e}}_1, {\varvec{e}}_2 , {\varvec{e}}_3 \} \) and position vector \( {\varvec{x}} = (x_1,x_2,x_3)= x_i\varvec{e}_i\, \). The gradient of the mapping \( \varvec{\Theta }\) is
Let \( \Omega _c\subset \mathbb {R}^3 \) be the deformed configuration of the Cosserat body and let \( \{ {\varvec{d}}_1, {\varvec{d}}_2, {\varvec{d}}_3 \} \) be the orthonormal triad of directors attached to every point of \( \Omega _c\, \). The deformation of the Cosserat continuum is characterized by the deformation function
and the elastic microrotation
where \( \{ {\varvec{d}}_1^0, {\varvec{d}}_2^0, {\varvec{d}}_3^0 \} \) is the orthonormal triad of directors in the reference configuration \( \Omega _\xi \, \). The initial directors \( \varvec{d}_i^0 \) and the initial microrotation tensor \( {\varvec{Q}}_0 \) are chosen such that (see [7])
i.e., \( {\varvec{Q}}_0\in \mathrm {SO}(3) \) is the orthogonal tensor from the polar decomposition of \( \nabla _x \varvec{\Theta }\). The deformation gradient \( {\varvec{F}}_\xi \) and the (non-symmetric) strain tensor \( \varvec{E} \) for nonlinear micropolar media are given by
while the strain measure for curvature (orientation change) is the so-called wryness tensor (see, e.g., [11, 28])
In the three-dimensional Cosserat model for isotropic materials presented in [25], the strain energy density \( W(\varvec{E},\varvec{\Gamma }) \) is expressed as the sum of two parts
Here, \(\mu >0\) is the shear modulus, \( \lambda \) is the Lamé constant, \(\kappa =\frac{1}{3}(3\lambda +2\mu )>0\) is the bulk modulus of classical isotropic elasticity, \(\,\mu _c\ge 0\) is the so-called Cosserat couple modulus, the coefficients \(b_1,\, b_2 ,\, b_3>0\) are dimensionless constitutive coefficients and the parameter \(\,L_c>0\,\) introduces an internal length (characteristic for the material). Under hyperelasticity assumptions, the stress tensor \( {\varvec{T}} \) and the couple stress tensor \( \overline{\varvec{M}} \) (of the first Piola–Kirchhoff type) satisfy the following constitutive equations
In view of Eqs. (38)–(40), we see that the tensors \( {\varvec{T}} \) and \( \overline{{\varvec{M}}} \) are linear functions of the strain measures \( \varvec{E} \) and \( \varvec{\Gamma }\). They are given explicitly by the constitutive relations
These explicit constitutive relations can be written in the compact form
where we define the fourth-order tensors of the elastic moduli \( \underline{{\varvec{C}}} \) and \( \underline{{\varvec{G}}} \) as follows
and \( g^{ij} = {\varvec{g}}^i\cdot {\varvec{g}}^j \). Note that the major symmetries \(\; C^{ijkl} = C^{klij} \), \(G^{ijkl} = G^{klij}\) are satisfied. Using these notations, the energy densities (38) and (39) can be expressed in the form
Thus, we see from the above relations that the model is physically linear, but it is geometrically nonlinear. The existence of minimizers for this three-dimensional Cosserat model has been proved under convexity assumptions in [23, 25].
3.2 Dimensional reduction procedure
Let us present the derivation method which allows us to obtain a Cosserat shell model of order \( O(h^5) \). This procedure is inspired by the classical theory of shells, see, e.g., [36].
For a shell-like body, we assume as usual the parametric representation \( \varvec{\Theta }\) of the following form
where \( {\varvec{y}}_0(x_1,x_2) \) is the parametrization of the midsurface and \( {\varvec{n}}_0(x_1,x_2) \) is the unit normal given by (2). Here, the parameter domain \( \Omega _h \) is a right cylinder of the form
where h is the thickness of the shell, assumed to be small, and \( x_3 \) is the coordinate in thickness direction.
For the three-dimensional shell-like body, the elastically stored energy is given by the volume integral
where \( W \big (\varvec{E} ,\varvec{\Gamma }\big ) \) is defined by (37). Now, we define the areal strain energy density for shells \( {\mathcal {W}}_{\mathrm {shell}} \) by the relation
where \( \omega _\xi = {\varvec{y}}_0( \omega ) \) is the midsurface. Thus, on the basis of relation (47), we determine \(\mathcal W_{\mathrm {shell}} \) by integrating the three-dimensional strain energy density \( W \big (\varvec{E} ,\varvec{\Gamma }\big ) \) over the thickness. For the elemental area \( \, \mathrm da \) and the elemental volume \( \, \mathrm dV \) in (47), we have the formulas (see, e.g., [7])
where we denote
Substituting (48) into (47), we obtain the relation
which holds also for any subset of \( \omega \). Thus, by virtue of (37) and (50), we have
We shall compute the two integrals in the right-hand side of (51) separately. To calculate the first integral, let us write the Taylor expansion of the integrand \( W_{\mathrm {mp}}(\varvec{E})\,b\, \) with respect to \( x_3\in \big ( -\frac{h}{2} , \frac{h}{2}\, \big ) \) about the point \( x_3=0 \) in the following form
where the argument \( \varvec{E} \) has been omitted for convenience. Also, we employ the notations \( \,f' := \dfrac{\partial f}{\partial x_3}\, \) for the derivative with respect to \( x_3 \,\), as well as \( f_0:= f(x_1,x_2,0) \), for any function \( f(x_1,x_2,x_3) \). By integration of the relation (52) with respect to \( x_3\), we find
In view of (49), we obtain \( b_0=1 \) , \( b_0'=-2H \) , \( b_0''= 2K \) , \( b_0'''= b_0^{(4)}= 0 \) and the derivatives appearing in (53) are given by
If we insert the expressions (54) into (53) and neglect the terms of order \( o(h^5) \), then we find the relation
To express the derivatives of \( W_{\mathrm {mp}} \) in a convenient form, let us introduce the bilinear form
such that
according to (38). With this notation, we get
and the relation (55) becomes
In the same way as in (52)–(58), we can calculate the last integral in (51). Indeed, if we introduce the bilinear form
with \( W_{\mathrm {curv}}({\varvec{X}})= W_{\mathrm {curv}}({\varvec{X}}, {\varvec{X}}) \) according to (39), then we obtain analogously
Further, in order to compute the derivatives of the strain measures \( \varvec{E}_0^{(k)} \) and \( \varvec{\Gamma }_0^{(k)} \) appearing in (58) and (60), we need to compute first the derivatives of the deformation gradient \( \varvec{F}_\xi \,\).
3.2.1 Derivatives of the deformation gradient with respect to \( x_3 \)
Consider the set \( \mathcal {T}_p \) of all tensors in the tangent plane, i.e., the set of all second-order tensors \( {\varvec{S}} \) of the form \( {\varvec{S}} = S_{\alpha \beta }{\varvec{a}}^\alpha \otimes {\varvec{a}}^\beta \). Note, for instance, that the tensors \( {\varvec{a}} \), \( {\varvec{b}} \) and \( {\varvec{c}} \) are elements of the linear space \( \mathcal {T}_p\, \). Moreover, the first fundamental tensor \( {\varvec{a}} \) plays the role of the identity tensor in the space \( \mathcal {T}_p\, \), since we have \( {\varvec{a}}{\varvec{S}}= {\varvec{S}}{\varvec{a}}= \varvec{S} \) for any \( {\varvec{S}}\in \mathcal {T}_p\, \). For the second fundamental tensor \( {\varvec{b}} \), we have by virtue of (8)
Thus, \( {\varvec{b}}^* \) is the cofactor of \( {\varvec{b}} \) in the space \( \mathcal {T}_p\, \). Further, let us introduce the tensors
which satisfy \( \varvec{\mu }\,\varvec{\mu }^{-1} = \varvec{\mu }^{-1} \varvec{\mu }= {\varvec{a}}\, \). With the help of the notation (62) we can express the base vectors \( \varvec{g}_i \) and \( {\varvec{g}}^j \) in terms of \( {\varvec{a}}_i \) and \( {\varvec{a}}^j \) in a simple way, namely (see, e.g., [29])
These relations show that \( \varvec{\mu }\, \) and \( \varvec{\mu }^{-1} \) admit the following representations
Let us compute next the derivatives of the tensors \( \varvec{\mu }\, \) and \( \varvec{\mu }^{-1} \) with respect to \( x_3 \,\): From (62)\( _1 \), we obtain directly
By differentiating repeatedly the relation \( \varvec{\mu }\,\varvec{\mu }^{-1} = {\varvec{a}}\, \) with respect to \( x_3 \,\), we obtain successively
If we write the relations (62), (65) and (66) on the midsurface (\( x_3=0 \)), then we get
Notice that, on the basis of the Cayley–Hamilton relation (8), we can write the powers of \( {\varvec{b}} \) in the form
Using the relations (63) and (64), we can now express the deformation gradient as follows
and hence,
Further, we differentiate the relation (70) to obtain the higher derivatives of the deformation gradient with respect to \( x_3 \,\):
and putting \( x_3=0 \) in (70) and (71), we find
These relations will be useful in the sequel.
3.2.2 Integration of the curvature energy density \( W_{\mathrm {curv}} \)
To obtain a simple form of the shell curvature energy in (60), we assume in this paper that the microrotation tensor \( {\varvec{Q}}_e \) is independent of \( x_3\, \), i.e.,
This condition means that the directors \( {\varvec{d}}_i^0 \) and \( {\varvec{d}}_i \) are functions of the surface coordinates \( (x_1,x_2) \) only, which is in line with the assumed thinness of the shell. As a consequence of (73) and (36), we obtain for the derivatives of the wryness tensor \( \varvec{\Gamma }\) the formula
In view of (63), the last relation reduces to
due to the symmetry of \( \varvec{\mu }^{-1} \) and the definition of the shell bending-curvature tensor (13). We put \( x_3=0 \) in (75), and using (67), we deduce
Taking into account (76), we compute the following expressions which appear in the energy density (60):
Thus, inserting (76) and (77) into (60), we obtain finally the form of the shell curvature energy density
If we substitute here \( {\varvec{b}}^2=2H \varvec{b}-K{\varvec{a}} \) in the last term, the relation (78) can be written in the alternative equivalent form
3.2.3 Integration of the strain energy density \( W_{\mathrm {mp}} \)
To proceed with the integration of the strain energy density in (58), we need to compute the derivatives \( \varvec{E}_0^{(k)}\, \). In view of the definition of the strain tensor (35) and the relation (73), we have
where \( ({\varvec{F}}_\xi )_0^{(k)} \) are given by (72). In order to express the derivatives \( \varvec{\varphi }_0^{(k)} \) appearing in (72), let us consider the Taylor expansion of the deformation function \( \varvec{\varphi }\) with respect to \( x_3\in ( -\frac{h}{2} , \frac{h}{2}\, ) \) about \( x_3=0 \), which reads
where the vectors \( {\varvec{m}} , \varvec{\alpha },\varvec{\beta }, \varvec{\gamma }, \varvec{\delta }\) and \( \varvec{\epsilon }\) are functions of \( (x_1, x_2) \) such that
Substituting (72) and (82) into (80), we obtain the derivatives of the strain tensor in the form
With the help of (83), we compute the following expressions appearing in relation (58):
Finally, we substitute (83) and (84) into the relation (58) and obtain the shell strain energy density corresponding to \( W_{\mathrm {mp}} \) in the form
where we have written here \( \nabla _s\, \) instead of \( \mathrm {Grad}_s\, \) for brevity.
In conclusion, we have obtained the areal strain energy density \( {\mathcal {W}}_{\mathrm {shell}} \) in the representation (51), where the two terms of the additive decomposition are given by (78) and (85).
In the next section, we show that the strain energy density (85) can be further reduced under appropriate assumptions for thin shells.
4 Simplifying assumptions for thin shells
Let us consider some assumptions and approximations valid for thin shells, which will lead us to a simplified expression of the energy density (85) and to the final form of the shell model.
The stress vector \( {\varvec{T}}{\varvec{n}}_0 \) acting on the surfaces \( x_3=\text{ constant } \) is assumed to be very small for thin shells, so we can approximate \( {\varvec{T}}{\varvec{n}}_0 \simeq {\varvec{0}} \,\). Hence, from the Taylor expansion of \( {\varvec{T}}{\varvec{n}}_0 \) with respect to \( x_3 \) we get
In the above relation, we consider that the coefficients of \( (x_3)^k \) (for \( k=0,1,2,3,4 \)) are vanishing, i.e., we assume
These relations represent five vectorial equations which will allow us to determine the five vectors \( \varvec{\alpha },\varvec{\beta }, \varvec{\gamma }, \varvec{\delta }\) and \( \varvec{\epsilon }\) of the expansion (81) in terms of \( \varvec{m} \) and \( {\varvec{Q}}_e \) (and finally in terms of \( \varvec{E}^e \) and \( {\varvec{K}}^e \)).
As a direct consequence of the conditions (87), let us prove first the following helpful results.
Lemma 4.1
For any vector field \( {\varvec{v}} \) and order of differentiation \( k\in \{0,1,2,3,4\} \), it holds
Proof
(i) In view of (87), we get
(ii) Using the definition of the scalar product and (87), we can write
(iii) Taking into account the definition (56) and the relation (41), we deduce
and the relation (88) is proved. \(\square \)
The determination of the five vectors \( \varvec{\alpha },\varvec{\beta }, \varvec{\gamma }, \varvec{\delta }\) and \( \varvec{\epsilon }\) will be pursued in five steps (a)–(e), respectively.
(a) Let us determine the vector \( \varvec{\alpha }\) from the first equation in (87), i.e., from the condition \( {\varvec{T}}_0{\varvec{n}}_0 = {\varvec{0}} \). This equation can be written successively in the following equivalent forms: In view of (41), we get
or, substituting here the relation (see (83)\( _1 \))
we obtain
which means
or, since \( {\varvec{u}} = {\varvec{a}}{\varvec{u}} + ({\varvec{u}}\cdot {\varvec{n}}_0){\varvec{n}}_0\, \),
or, since \( \mu +\mu _c>0 \) and \( \lambda +2\mu >0\, \),
and since \( {\varvec{Q}}_e{\varvec{n}}_0={\varvec{d}}_3\, \), we obtain the result
This expression of the vector \( \varvec{\alpha }\) will be inserted in the strain energy density (85), which is equivalent to (58). Indeed, if we substitute the solution (90) into (83)\( _1 \,\), we find
where we have introduced the linear operator \( L_{n_0} \) defined by
In our model, we do not take into account the surface gradients of the strain measures \( {\varvec{E}}^e \) and \( {\varvec{K}}^e \). Therefore, when computing the gradient of \( \varvec{\alpha }\) on the basis of relation (90), we make the approximation
So, by virtue of (93) and the relation (see [7, f.(70)])
we deduce
If we insert the last relation into (83)\( _2\) and use (12), then we get
(b) To determine the vector \( \varvec{\beta }\), we employ the second equation in (87), i.e., \( \varvec{T}'_0{\varvec{n}}_0 = {\varvec{0}} \). By virtue of (41), this equation can be written successively in the following equivalent forms:
or, inserting here (96),
which is an equation of the form (89) for the vector \( {\varvec{u}} = {\varvec{Q}}_e^T\varvec{\beta }\) and can be solved similarly to obtain the solution
since \( {\varvec{n}}_0({\varvec{c}}{\varvec{K}}^e) = \varvec{0}\). Then, substituting (98) into (96) and using the notation (92), we find
From (98), we can compute the gradient \( \mathrm {Grad}_s\varvec{\beta }\) in terms of the gradients of the strain measures \( {\varvec{E}}^e \) and \( {\varvec{K}}^e \). But, since we neglect the gradients of strain measures in our model, we shall approximate
on the basis of (98). Hence, using the relations (12), (95) and (100) into (83)\( _3\,\), we find
(c) In the next step, we determine the vector \( \varvec{\gamma }\) from the equation \( \varvec{T}''_0{\varvec{n}}_0 = {\varvec{0}} \), which is equivalent to \( \big ({\varvec{Q}}_e^T \varvec{T}\big )''_0{\varvec{n}}_0 = {\varvec{0}} \). Substituting here the relation (41) and using the result (101) we deduce the equation
This is an equation of the same form as (89) for the vector \( {\varvec{u}} = {\varvec{Q}}_e^T\varvec{\gamma } \) and we can solve it similarly to obtain the result
Inserting the vector \( \varvec{\gamma } \) given by (102) into (101) and using the notation (92), we derive
Moreover, the relation (102) shows that we can approximate \( \mathrm {Grad}_s\varvec{\gamma }\simeq {\varvec{0}} \) (since we neglect the gradients of strain measures), and hence, the derivative \( \varvec{E}'''_0 \) given by (83)\( _4 \) reduces to
(d) From the fourth equation \( \varvec{T}'''_0{\varvec{n}}_0 = {\varvec{0}} \) in (87), we can determine now the vector \( \varvec{\delta }\). We write this equation in the equivalent form \(\big ({\varvec{Q}}_e^T \varvec{T}\big )'''_0\,{\varvec{n}}_0 = {\varvec{0}} \), and using here (41) and (104), we find
We solve this equation in the same manner as equation (89), and we obtain
Inserting this in (104), we get
Further, on the basis of (105) we can approximate \( \mathrm {Grad}_s\varvec{\delta }\simeq {\varvec{0}} \) and the relation (83)\( _5 \) becomes
(e) To solve the equation \( \varvec{T}^{(4)}_0{\varvec{n}}_0 = {\varvec{0}} \), we repeat the procedure from step (d) and determine the vector
Hence, the relation (107) can be written in the condensed form
By doing this, we have finished to determine the vectors \( \varvec{\alpha },\varvec{\beta }, \varvec{\gamma }, \varvec{\delta }\) and \( \varvec{\epsilon }\) from the system of equations (87). Let us show next the following auxiliary results concerning the linear operator \( L_{n_0} \) defined in (92).
Lemma 4.2
-
(i)
For any two tensors \( \varvec{X}=X_{i\alpha }{\varvec{a}}^i\otimes {\varvec{a}}^\alpha \) and \( {\varvec{Y}}=Y_{i\alpha }{\varvec{a}}^i\otimes {\varvec{a}}^\alpha \), the following equality holds
$$\begin{aligned} W_{\mathrm {mp}}\big (L_{n_0}({\varvec{X}}),{\varvec{Y}}\big ) = W_{\mathrm {Coss}}({\varvec{X}},{\varvec{Y}}), \end{aligned}$$(110)where the bilinear form \( W_{\mathrm {Coss}} \) has been already defined in (29).
-
(ii)
If the conditions (87) are satisfied, then the following relation holds
$$\begin{aligned} W_{\mathrm {mp}}\big (L_{n_0}({\varvec{U}}),L_{n_0}(\varvec{V})\big ) = W_{\mathrm {Coss}}({\varvec{U}},\varvec{V})\qquad \text{ for } \text{ all }\quad {\varvec{U}},{\varvec{V}} \in \{ \varvec{E}^e,\,(\varvec{E}^e {\varvec{b}} + \varvec{c} {\varvec{K}}^e) {\varvec{b}}^k\;;\; k=0,1,2,3 \},\nonumber \\ \end{aligned}$$(111)where we have denoted for convenience \( {\varvec{b}}^0 =\varvec{a} \).
Proof
(i) Using the decomposition \( {\varvec{X}} = \varvec{a}{\varvec{X}} + {\varvec{n}}_0 \otimes ({\varvec{n}}_0\varvec{X}) \), we can rewrite the definition (56) in the form
for any tensors \( {\varvec{X}}=X_{i\alpha }{\varvec{a}}^i\otimes {\varvec{a}}^\alpha \), \( {\varvec{Y}}=Y_{i\alpha }\varvec{a}^i\otimes {\varvec{a}}^\alpha \), and comparing with (29), we deduce
Now, in view of (92) we get
and denoting for the moment the vector \( {\varvec{w}} := \, \dfrac{\mu -\mu _c}{\mu +\mu _c}\,\big ( {\varvec{n}}_0 \varvec{X}\big )+ \,\dfrac{\lambda }{\lambda +2\mu }\,\big (\text {tr}\varvec{X}\big )\,{\varvec{n}}_0 \,\), we find
Taking into account that \( {\varvec{Y}}{\varvec{n}}_0= \varvec{0} \) and substituting the vector \( {\varvec{w}} \), we deduce
in view of (113). Thus, the relation (110) is proved.
(ii) With the help of (110), we can prove now the relation (111). If we choose \( {\varvec{U}}={\varvec{V}}= {\varvec{E}}^e \) in (111), then using successively equations (91), (92), (88)\( _3 \) (Lemma 4.1) and (110), we get
Further, if we take \( {\varvec{U}}= {\varvec{E}}^e \) and \( {\varvec{V}}= ({\varvec{E}}^e{\varvec{b}} + \varvec{c}{\varvec{K}}^e){\varvec{b}}^k \), then we can write similarly
The last case \( {\varvec{U}}= ({\varvec{E}}^e{\varvec{b}} + {\varvec{c}}{\varvec{K}}^e){\varvec{b}}^k \) and \( {\varvec{V}}= ({\varvec{E}}^e{\varvec{b}} + {\varvec{c}}\varvec{K}^e){\varvec{b}}^l \) can be proved analogously (on the basis of (88)\( _3 \)). Then, the relation (111) is completely proved. \(\square \)
Finally, we are now able to write the simplified form of the strain energy density (85), which is equivalent to (58). If we employ the relation (111) (Lemma 4.2) in conjunction with (91), (99), (103), (106) and (109), we can calculate the terms appearing in the strain energy density (58) in the following way
since \( {\varvec{b}}^2-2H{\varvec{b}}+K{\varvec{a}}={\varvec{0}} \). Substituting (116) into (58), we find the reduced form of the strain energy density
The last relation can be written, in view of \( \varvec{b}\,{\varvec{b}}^*=K{\varvec{a}} \), in the alternative equivalent form
In conclusion, we have obtained the total strain energy density \({\mathcal {W}}_{\mathrm {shell}}( {\varvec{E}}^e, {\varvec{K}}^e) \) for the Cosserat shell model as the sum (51) of the strain energy density (118) and the curvature energy density (78), in the following form
where \( {\varvec{b}}^*= - {\varvec{b}}+2H{\varvec{a}} \), the bilinear form \( W_{\mathrm {Coss}} \) is defined in (29) and \( W_{\mathrm {curv}} \) in (59).
In the part \( {\mathcal {W}}_{\mathrm {memb,bend}} \) of the energy density, which accounts for combined stretching and bending deformations, we observe the coupling between the strain tensor \( {\varvec{E}}^e \) and the bending tensor \( {\varvec{c}} {\varvec{K}}^e \). Also, we see in the expression (119) the dependence of the constitutive coefficients on the initial curvature through the mean curvature H, the Gauß curvature K and the tensor \( {\varvec{b}} = -\text {Grad}_s\,\varvec{n}_0\,\).
Remark 4.3
Taking into account the relations (91), (99), (103), (106) and (109), we can write the Taylor expansion with respect to \( x_3 \) in the following form
The linear operator \( L_{n_0} \) defined by (92) satisfies the relation \( L_{n_0}({\varvec{X}}) {\varvec{a}} ={\varvec{X}}\) for any tensor \({\varvec{X}} = X_{i\alpha }{\varvec{a}}^i\otimes {\varvec{a}}^\alpha \). Hence, multiplying (120) with \( {\varvec{a}} \) we obtain for the projection \( \varvec{E}{\varvec{a}} \) of the three-dimensional strain tensor the following expression
Following the same line of thought as in [33], in view of relation (121) we can interpret the tensor \( \varvec{E}^e {\varvec{b}} + {\varvec{c}} {\varvec{K}}^e \) as a strain measure appropriate to bending for 6-parameter shells. Thus, we define the new mixed bending tensor by
Using the relations (12) and (95) into (122), we obtain \(\; \varvec{\varPhi }^e = ({\varvec{Q}}_e^T\mathrm {Grad}_s{\varvec{m}} - {\varvec{a}}) {\varvec{b}} + ({\varvec{Q}}_e^T \mathrm {Grad}_s{\varvec{d}}_3 + {\varvec{b}}) \), i.e.,
We notice that the mixed bending tensor (123) vanishes in the reference configuration indeed, since it reduces to \(\; {\varvec{Q}}_e^T\big [ ( \mathrm {Grad}_s{\varvec{y}}_0) \varvec{b} + \mathrm {Grad}_s{\varvec{d}}_3^0 \,\big ] = \varvec{Q}_e^T\big ( {\varvec{a}} {\varvec{b}} + \mathrm {Grad}_s\varvec{n}_0 \big ) = {\varvec{Q}}_e^T\big ( {\varvec{b}} - \varvec{b}\big ) = {\varvec{0}} \).
With this notation, we can express the strain energy density (117) in terms of the strain tensor \( \varvec{E}^e \) and the mixed bending tensor \( \varvec{\varPhi }^e \) as follows
5 Further remarks and special cases
In order to gain more insight in the mechanical meaning of the various terms in the energy density (119), we shall write the two parts \( {\mathcal {W}}_{\mathrm {memb,bend}}( {\varvec{E}}^e, {\varvec{K}}^e) \) and \( \mathcal {W}_{\mathrm {bend,curv}}( {\varvec{K}}^e) \) of the elastically stored energy in some other useful alternative forms.
5.1 Alternative expression of the shell strain energy density \( {\mathcal {W}}_{\mathrm {memb,bend}}( {\varvec{E}}^e, {\varvec{K}}^e) \)
We remark that the bending-curvature tensor \( {\varvec{K}}^e \) appears in the energy density \( {\mathcal {W}}_{\mathrm {memb,bend}}( {\varvec{E}}^e, {\varvec{K}}^e) \) in (118) only through the combination \( {\varvec{c}}{\varvec{K}}^e \). If we replace \( {\varvec{c}}{\varvec{K}}^e = - \varvec{\rho }^e\), where \( \varvec{\rho }^e \) is the bending tensor defined by (16), as well as \(\, {\varvec{b}}^*= - {\varvec{b}}+2H{\varvec{a}} \,\) and \( \,{\varvec{b}}^2=2H {\varvec{b}}-K{\varvec{a}}\, \) in (118), we can put the shell strain energy density in the form
which is expressed only in terms of the shell strain tensor \( {\varvec{E}}^e \), the bending tensor \( \varvec{\rho }^e \) and the combinations \( {\varvec{E}}^e{\varvec{b}} \) and \( \varvec{\rho }^e{\varvec{b}} \). One can see clearly in (125) the coupling terms for the strain measures \( {\varvec{E}}^e \) and \( \varvec{\rho }^e \).
Further, we would like to decompose the shell strain tensor \( {\varvec{E}}^e \) in the in-plane deformation tensor \( \varvec{\varepsilon }^e = {\varvec{a}}{\varvec{E}}^e \) and the transverse shear deformation vector \( \varvec{\gamma }^e = \varvec{n}_0{\varvec{E}}^e \), according to relations (14). Using the decomposition \( {\varvec{X}} = {\varvec{a}}{\varvec{X}} + {\varvec{n}}_0 \otimes ({\varvec{n}}_0{\varvec{X}}) \), we can write the bilinear form \( W_{\mathrm {Coss}}( {\varvec{X}}, {\varvec{Y}}) \) defined by (29) in the form
for any tensors \( {\varvec{X}}=X_{i\alpha }{\varvec{a}}^i\otimes {\varvec{a}}^\alpha \), \( {\varvec{Y}}=Y_{i\alpha }\varvec{a}^i\otimes {\varvec{a}}^\alpha \), where we introduce the bilinear form \( W_{\mathrm {mixt}}( {\varvec{X}}, {\varvec{Y}}) \) by
Then, in view of (14) and \( {\varvec{n}}_0\varvec{\rho }^e = {\varvec{0}} \), the relation (126) yields
Using relations of the type (128) in (125), we obtain the following alternative form of the strain energy density
which is written in terms of the strain measures \( \varvec{\varepsilon }^e\), \(\varvec{\gamma }^e\) and \( \varvec{\rho }^e \). Note that the last square bracket in (129) accounts for the transverse shear deformation and has the coefficient \(\; \dfrac{2\mu \,\mu _c}{\mu +\mu _c}\; \), i.e., the harmonic mean between the shear modulus \( \mu \) and the Cosserat couple modulus \( \mu _c\,\).
Remark 5.1
Let us point out the mechanical and geometrical significance of the strain measures \( \varvec{\gamma }^e \), \( \varvec{\varepsilon }^e\) and \( \varvec{\rho }^e \). For the transverse shear deformation vector \( \varvec{\gamma }^e \) given by (14), (15), we have clearly
i.e., we consider the scalar products between the tangent vectors to the deformed midsurface \( {\varvec{m}},_\alpha \) and the rotated normal \( {\varvec{Q}}_e{\varvec{n}}_0 = {\varvec{d}}_3\) (third director).
Next, the strain tensor of in-plane deformation \( \varvec{\varepsilon }^e\), which was introduced in (14), can be written in the form
This strain tensor has the same structure as the change of metric tensor
which is usually employed in the classical (Koiter) shell theory.
Further, the bending tensor \( \varvec{\rho }^e \) given by (16), (17) can be written as
This tensor is similar to the change of curvature tensor
which is commonly used in the Koiter shell model (\( {\varvec{n}} \) is the unit normal to the deformed midsurface), see, e.g., [14, 20, 36].
5.2 Alternative form of the shell curvature energy density \( \mathcal {W}_{\mathrm {bend,curv}}( {\varvec{K}}^e) \)
Let us express the bending-curvature tensor \( {\varvec{K}}^e \) in terms of the bending tensor \( \varvec{\rho }^e = -{\varvec{c}} {\varvec{K}}^e\) and the vector of drilling bendings \( \varvec{\nu }^e = {\varvec{n}}_0 {\varvec{K}}^e \), according to the decomposition (16), and insert this in the curvature energy density \( \mathcal {W}_{\mathrm {bend,curv}}( {\varvec{K}}^e) \) given by (78). To this aim, let us introduce the bilinear form \( W_{\mathrm {cps}} \) by
We employ the surface deviator operator \( \mathrm {dev}_s \,\), which was defined in [5, 11] by
With the help of \( \mathrm {dev}_s \,\) we can decompose any tensor \( {\varvec{X}}=X_{i\alpha }{\varvec{a}}^i\otimes {\varvec{a}}^\alpha \) as a direct sum (orthogonal decomposition)
Then, the definition (135) can be written alternatively
and
which shows that the quadratic form \( W_{\mathrm {cps}}( \varvec{U} ) \) is positive definite (since \( b_1,b_2,b_3>0 \)).
Let us prove next some useful relations.
Lemma 5.2
-
(i)
For any two tensors of the form \( {\varvec{U}}=U_{\alpha \beta }{\varvec{a}}^\alpha \otimes {\varvec{a}}^\beta , \; {\varvec{V}}=V_{\alpha \beta }{\varvec{a}}^\alpha \otimes {\varvec{a}}^\beta \) we have
$$\begin{aligned}&\mathrm {skew} ({\varvec{c}}\, {\varvec{U}}) \; = \; \dfrac{1}{2}\, \big ( \mathrm {tr}\, {\varvec{U}}\big )\, {\varvec{c}} \qquad \text{ and } \nonumber \\&\mathrm {skew} ({\varvec{c}}\, {\varvec{U}}) : \mathrm {skew} ({\varvec{c}}\, {\varvec{V}}) \;= \; \dfrac{1}{2}\, \big ( \mathrm {tr}\, {\varvec{U}}\big )\,\big ( \mathrm {tr}\, \varvec{V}\big ). \end{aligned}$$(140) -
(ii)
For any tensor of the form \( {\varvec{S}} = S_{\alpha \beta }{\varvec{a}}^\alpha \otimes {\varvec{a}}^\beta \) we have
$$\begin{aligned}&\Vert \mathrm {skew} ({\varvec{c}} {\varvec{S}}) \Vert ^2 \!=\! \dfrac{1}{2}\, \big ( \mathrm {tr}\, {\varvec{S}}\big )^2 ,\qquad \big [\mathrm {tr} ({\varvec{c}}\, {\varvec{S}})\big ]^2 = 2\, \Vert \mathrm {skew} \, {\varvec{S}} \Vert ^2 , \qquad \Vert \mathrm {dev_ssym}({\varvec{c}} {\varvec{S}}) \Vert ^2 \!=\! \Vert \mathrm {dev_ssym}\, {\varvec{S}} \Vert ^2 .\qquad \end{aligned}$$(141) -
(iii)
For any tensor \( {\varvec{X}}=X_{i\alpha }{\varvec{a}}^i\otimes {\varvec{a}}^\alpha \), we can represent the quadratic form \( W_{\mathrm {curv}}( {\varvec{X}}) \) in the following ways
$$\begin{aligned} W_{\mathrm {curv}}( {\varvec{X}})= & {} W_{\mathrm {curv}}({\varvec{a}} {\varvec{X}}) + \mu L_c^2\,\dfrac{b_1+b_2}{2}\, \Vert {\varvec{n}}_0{\varvec{X}} \Vert ^2 \nonumber \\= & {} W_{\mathrm {cps}}( {\varvec{c}}{\varvec{X}}) + \mu L_c^2\,\dfrac{b_1+b_2}{2}\, \Vert {\varvec{n}}_0{\varvec{X}} \Vert ^2. \end{aligned}$$(142)
Proof
(i) On the basis of the relation (see [10, f. (59)])
we deduce that
and the relation (140)\( _1 \) is proved. Further, using the last relation we can write
since \( {\varvec{c}} : {\varvec{c}} = \text {tr}({\varvec{c}}^T {\varvec{c}}) = \text {tr}(-{\varvec{c}}^2) = \text {tr}({\varvec{a}}) =2 \).
(ii) The relation (141)\( _1 \) follows directly from (140)\( _2 \) provided we choose \( {\varvec{U}} = \varvec{V} = {\varvec{S}} \). Also, we can obtain (141)\( _2 \) directly from (140)\( _2 \) if we put \( {\varvec{U}} = {\varvec{V}} = {\varvec{c}}{\varvec{S}} \) and take into account that \( {\varvec{c}}^2=-{\varvec{a}} \). To show the third relation in (141), let us prove the more general identity
which holds for any tensors \( \varvec{U}=U_{\alpha \beta }{\varvec{a}}^\alpha \otimes {\varvec{a}}^\beta , \; {\varvec{V}}=V_{\alpha \beta }{\varvec{a}}^\alpha \otimes {\varvec{a}}^\beta \). Indeed, using the orthogonal decomposition (137) we find
Then, in view of part (i) and the relation \( ({\varvec{c}}\, {\varvec{U}}) : ({\varvec{c}}\, {\varvec{V}}) = \text {tr}(\varvec{U}^T {\varvec{c}}^T {\varvec{c}}\, {\varvec{V}} ) = \text {tr}({\varvec{U}}^T {\varvec{V}} ) = {\varvec{U}} : {\varvec{V}} \) we deduce from (145) that
and the identity (144) is proved. If we put \( \varvec{U} = {\varvec{V}} = {\varvec{S}} \) in (144), we obtain the desired result (141)\( _3\, \).
(iii) The first equation in (142) follows directly from the definition (59) and the decomposition \( {\varvec{X}} = {\varvec{a}}{\varvec{X}} + {\varvec{n}}_0 \otimes (\varvec{n}_0{\varvec{X}}) \). Further, using the relations (138)–(141) and (144) we obtain
for any tensors \( {\varvec{X}}=X_{i\alpha }{\varvec{a}}^i\otimes {\varvec{a}}^\alpha ,\; {\varvec{Y}}=Y_{i\alpha }\varvec{a}^i\otimes {\varvec{a}}^\alpha \) . By virtue of (146), the second equation (142) is also proved and the proof is complete. \(\square \)
With the help of Lemma 5.2 (iii), we can rewrite the shell curvature energy density (78) in an alternative form, in terms of the bending tensor \( \varvec{\rho }^e = -{\varvec{c}} {\varvec{K}}^e\) and the vector of drilling bendings \( \varvec{\nu }^e = {\varvec{n}}_0 {\varvec{K}}^e \), as follows
Substituting \( \;{\varvec{b}}^2=2H {\varvec{b}}-K{\varvec{a}}\,\), the last relation can be written alternatively
One can see that the last square bracket in the energy density (148) (or (147)) accounts for the drilling bendings \( \varvec{\nu }^e\), whereas the first three terms account for the bending deformation characterized by the tensor \( \varvec{\rho }^e \).
5.3 Special case: the quadratic ansatz
In many papers on shell or plate modeling, the deformation function (or the displacement vector) is represented as a quadratic function in the thickness coordinate \( x_3 \), which coefficients depend on the surface coordinates \( (x_1,x_2) \). For instance, in [7] a quadratic ansatz for the deformation function \( \varvec{\varphi }\) is adopted. This is tantamount to assume that the vectors \( \varvec{\gamma } , \varvec{\delta }, \varvec{\epsilon }, \ldots \) vanish in the formula (81), i.e., we have
and the expansion (81) reduces to
By using the representation (150) together with the assumptions (approximations)
we can follow the same procedure as in Sect. 4 to obtain the following areal strain energy density corresponding to the quadratic ansatz
where \( \mathcal {W}_{\mathrm {bend,curv}}( {\varvec{K}}^e) \,\) is given by (78) (or (147)), while \(\, \mathcal W_{\mathrm {memb,bend}}^{(quad)}( {\varvec{E}}^e, {\varvec{K}}^e) \) has the following expression
Here, \(W_{\mathrm {mp}} \) is the quadratic form defined by (56). We notice that the only difference between the strain energy density (153) and the energy \( \mathcal W_{\mathrm {memb,bend}}( {\varvec{E}}^e, {\varvec{K}}^e) \) obtained for the general case in (118) is that the last term involves the quadratic form \( W_{\mathrm {mp}} \) in (153) instead of \( W_{\mathrm {Coss}} \) in (118). This difference is due to the truncated (quadratic) ansatz in (150). Nevertheless, we mention that the general correct result is given by (118), since it is necessary to consider the complete fifth-order representation (81) when deriving a shell model of order \( O(h^5) \).
Remark 5.3
The quadratic representation (150) has been adopted also in the work [5], where a model of order \( O(h^3) \) for Cosserat shells has been derived. Thus, using the same derivation method and the conditions (151), we have obtained in [5, f. (68)] the strain energy density \( \bar{\mathcal {W}}_{\mathrm {shell}}({\varvec{E}}^e,{\varvec{K}}^e) \) in the form (28), or equivalently
We observe that this expression is merely the truncation of the total strain energy density (119) which retains only the terms of order \( O(h^3) \). The relation between the model (154) and the classical Koiter shell model has been discussed in [5, Sect. 5.3].
Next, let us compare our results with the shell model obtained in [7], see also the work [18] which presents this model in matrix formulation. In [7, f. (65)], the following quadratic ansatz has been assumed
This is a special case of the representation (150), in which \( \varvec{\alpha }= \alpha {\varvec{d}}_3\, \), \( \varvec{\beta }= \beta {\varvec{d}}_3\, \) (i.e., the directions of the unknown vectors \( \varvec{\alpha }\) and \( \varvec{\beta }\) are prescribed to coincide with the third director \( {\varvec{d}}_3 \)), and the lengths of these vectors \( \alpha (x_1,x_2) \) and \( \beta (x_1,x_2) \) have to be determined. Then, the scalar fields \( \alpha \) and \( \beta \) have been determined in [7] on the basis of the assumptions
which is a weaker variant of the requirements (151), where only the normal components of the stress vectors \( \varvec{T}_0{\varvec{n}}_0 \) and \( {\varvec{T}}'_0{\varvec{n}}_0 \) are assumed to vanish. Using a different derivation procedure, the following areal strain energy density has been obtained (see [7, f. (104)])
where \( \mathcal {W}_{\mathrm {bend,curv}}( {\varvec{K}}^e) \) is given by (78) and the strain energy density \( \widehat{\mathcal {W}}_{\mathrm {memb,bend}}( {\varvec{E}}^e, {\varvec{K}}^e) \) has the form
To compare this result with the strain energy density \(\, \mathcal W_{\mathrm {memb,bend}}^{(quad)}( {\varvec{E}}^e, {\varvec{K}}^e) \) given by (153), we need to compare the two bilinear forms \( \,W_{\mathrm {mixt}} \,\) and \(\, W_{\mathrm {Coss}}\, \). To this aim, we employ the relation (126) as compared with
In this manner, we remark that the model (158) derived in [7] coincides with the strain energy density (153) obtained here in the case of quadratic ansatz, except for the transverse shear coefficients: The transverse shear coefficient in [7] is the arithmetic mean \( \dfrac{\mu +\mu _c}{2} \;\), whereas we obtain here as transverse shear coefficient the harmonic mean \(\; \dfrac{2\mu \,\mu _c}{\mu +\mu _c}\, \) (see (129)).
Further, in order to compare the strain energy density (158) from [7] with our result (129) obtained for the general case (extended ansatz), we employ the relations (159) and
together with the notations \( \varvec{\varepsilon }^e = {\varvec{a}}{\varvec{E}}^e \), \( \varvec{\gamma }^e = \varvec{n}_0{\varvec{E}}^e \), \( \varvec{\rho }^e = -\varvec{c}{\varvec{K}}^e \). By inserting these relations, we write the energy (158) in the following equivalent form
We are now able to compare directly the strain energy densities (129) and (160): Apart from the difference between the transverse shear coefficients (as mentioned above), we remark that the last term from (160) has been reduced in our refined analysis and does not appear in the general result (129).
In conclusion, the shell model obtained in [7] corresponds to the special case of quadratic ansatz (149)–(153), in the sense that the strain energy density \( \widehat{\mathcal {W}}_{\mathrm {memb,bend}}( {\varvec{E}}^e, {\varvec{K}}^e) \) from [7, f. (104)] coincides with \( \mathcal W_{\mathrm {memb,bend}}^{(quad)}( {\varvec{E}}^e, {\varvec{K}}^e) \) in (153), but with different transverse shear coefficients. Moreover, by comparing our general result (129) with the model (160) (obtained in [7]), we deduce that the last term in (160) has to be cancelled in the expression of the strain energy density, since this term is only a consequence of the rough (quadratic) truncation of the expansion of \( \varvec{\varphi }\) used in the special case of quadratic ansatz.
Thus, the developments of the present paper show that the model presented in [7] can be improved by discarding the last term in (160) and by adjusting the transverse shear coefficients to equal \(\dfrac{2\mu \,\mu _c}{\mu +\mu _c} \).
Remark 5.4
The difference between the transverse shear coefficients in the two models (129) versus (160) is due to the fact that in [7] the vectors \( \varvec{\alpha }\) and \( \varvec{\beta }\) are assumed to be collinear with \( \varvec{d}_3\, \) (cf. (155)), but in our present work the directions of \( \varvec{\alpha }\) and \( \varvec{\beta }\) are not prescribed a priori (see (81) or (150)).
The value of the transverse shear coefficient \(\; \dfrac{2\mu \,\mu _c}{\mu +\mu _c}\; \) derived in the present analysis is also confirmed by the \( \Gamma \)-convergence results obtained in the paper [26] in the case of Reissner–Mindlin plates.
We mention that the value of the transverse shear coefficient is adjusted in various shell or plate models by means of shear correction factors; see, e.g., the shear correction factors \(\alpha _s \,\), \(\alpha _t \) in Eqs. (26), (27) for 6-parameter shells. For the discussion on shear correction factors in the literature we refer to the papers [1, 13, 37], among others.
Remark 5.5
Under certain conditions, one can show that the obtained strain energy density (119) is coercive. This feature has been proved for related Cosserat shell models in [19], using the matrix formulation. Then, applying the general existence results for 6-parameter shells presented in [8], one can prove the existence of minimizers for the nonlinear shell model derived in the present work.
Remark 5.6
This Cosserat shell model of order \( O(h^5) \) can be employed in applications, e.g., to solve complex shell problems by numerical simulations. For a related planar Cosserat shell model of order \( O(h^3) \) derived in [22, 24], the numerical treatment has been presented in [32] using geodesic finite elements. Then, several concrete mechanical problems involving shells with large rotations have been solved numerically, see [31, 32].
6 Conclusions
In this paper, we have presented a simple general procedure to derive the explicit form of the areal strain energy density of order \( O(h^5) \) for isotropic 6-parameter elastic shells, starting from the three-dimensional Cosserat model. This derivation procedure is inspired by the corresponding method from the classical shell theory, see, e.g., [36]. The obtained closed-form strain energy density is written in Eq. (119), or in alternative forms in relations (129) and (148). Here, we can see the dependence of the constitutive coefficients on the initial curvature of the shell, as well as the coupling between stretching and bending deformations. The constitutive coefficients of the model are expressed explicitly in terms of the three-dimensional elasticity constants.
Finally, we have compared in Sect. 5.3 our results with the previous Cosserat shell model presented in [7] and have shown that the advantage of the new derivation procedure is twofold: Firstly, we obtain the transverse shear coefficient confirmed previously by a \( \Gamma \)-convergence analysis in [26] for the case of plates. Secondly, based on the extended ansatz (81), we are able to improve the expression of the strain energy density by discarding the last higher-order term in Eq. (160).
We mention that the obtained strain energy density (119) satisfies the invariance properties required by the local symmetry group of isotropic 6-parameter shells, which have been established in a general theoretical framework by Eremeyev and Pietraszkiewicz [16, Sect. 9].
References
Altenbach, H.: An alternative determination of transverse shear stiffnesses for sandwich and laminated plates. Int. J. Solids Struct. 37, 3503–3520 (2000)
Altenbach, H., Zhilin, P.A.: A general theory of elastic simple shells. Uspekhi Mekhaniki 11, 107–148 (1988) (in Russian)
Altenbach, H., Zhilin, P.A.: The theory of simple elastic shells. In: Kienzler, R., Altenbach, H., Ott, I. (eds.) Theories of Plates and Shells. Critical Review and New Applications, Euromech Colloquium 444, pp. 1–12. Springer, Heidelberg (2004)
Altenbach, J., Altenbach, H., Eremeyev, V.A.: On generalized Cosserat-type theories of plates and shells: a short review and bibliography. Arch. Appl. Mech. 80, 73–92 (2010)
Bîrsan, M.: Derivation of a refined six-parameter shell model: descent from the three-dimensional Cosserat elasticity using a method of classical shell theory. Math. Mech. Solids 25(6), 1318–1339 (2020)
Bîrsan, M., Altenbach, H.: A mathematical study of the linear theory for orthotropic elastic simple shells. Math. Methods Appl. Sci. 33, 1399–1413 (2010)
Bîrsan, M., Ghiba, I.D., Martin, R., Neff, P.: Refined dimensional reduction for isotropic elastic Cosserat shells with initial curvature. Math. Mech. Solids 24(12), 4000–4019 (2019)
Bîrsan, M., Neff, P.: Existence of minimizers in the geometrically non-linear 6-parameter resultant shell theory with drilling rotations. Math. Mech. Solids 19(4), 376–397 (2014)
Bîrsan, M., Neff, P.: Shells without drilling rotations: a representation theorem in the framework of the geometrically nonlinear 6-parameter resultant shell theory. Int. J. Eng. Sci. 80, 32–42 (2014)
Bîrsan, M., Neff, P.: On the dislocation density tensor in the Cosserat theory of elastic shells. In: Naumenko, K., Assmus, M. (eds.) Advanced Methods of Continuum Mechanics for Materials and Structures. Advanced Structured Materials, vol. 60, pp. 391–413. Springer, Singapore (2016)
Bîrsan, M., Neff, P.: Analysis of the deformation of Cosserat elastic shells using the dislocation density tensor. In: dell’Isola, F. (ed.) Advanced Methods of Continuum Mechanics for Materials and Structures. Advanced Structured Materials, vol. 69, pp. 13–30. Springer, Singapore (2017)
Chróścielewski, J., Makowski, J., Pietraszkiewicz, W.: Statics and Dynamics of Multifold Shells: Nonlinear Theory and Finite Element Method. Wydawnictwo IPPT PAN, Warsaw (2004) (in Polish)
Chróścielewski, J., Pietraszkiewicz, W., Witkowski, W.: On shear correction factors in the non-linear theory of elastic shells. Int. J. Solids Struct. 47, 3537–3545 (2010)
Ciarlet, P.G.: An Introduction to Differential Geometry with Applications to Elasticity. Springer, Dordrecht (2005)
Eremeyev, V.A., Pietraszkiewicz, W.: The nonlinear theory of elastic shells with phase transitions. J. Elast. 74, 67–86 (2004)
Eremeyev, V.A., Pietraszkiewicz, W.: Local symmetry group in the general theory of elastic shells. J. Elast. 85, 125–152 (2006)
Eremeyev, V.A., Pietraszkiewicz, W.: Thermomechanics of shells undergoing phase transition. J. Mech. Phys. Solids 59, 1395–1412 (2011)
Ghiba, I.D., Bîrsan, M., Lewintan, P., Neff, P.: The isotropic Cosserat shell model including terms up to O\( (h^5) \). Part I: derivation in matrix notation. J. Elast. 142, 201–262 (2020)
Ghiba, I.D., Bîrsan, M., Lewintan, P., Neff, P.: The isotropic Cosserat shell model including terms up to O\( (h^5) \). Part II: existence of minimizers. J. Elast. 142, 263–290 (2020)
Koiter, W.T.: A consistent first approximation in the general theory of thin elastic shells. In: Koiter, W.T. (ed.) The Theory of Thin Elastic Shells. IUTAM Symposium Delft 1960, pp. 12–33. North-Holland, Amsterdam (1960)
Libai, A., Simmonds, J.G.: The Nonlinear Theory of Elastic Shells, 2nd edn. Cambridge University Press, Cambridge (1998)
Neff, P.: A geometrically exact Cosserat-shell model including size effects, avoiding degeneracy in the thin shell limit. Part I: formal dimensional reduction for elastic plates and existence of minimizers for positive Cosserat couple modulus. Cont. Mech. Thermodyn. 16, 577–628 (2004)
Neff, P.: Existence of minimizers for a finite-strain micromorphic elastic solid. Proc. R. Soc. Edinb. 136A, 997–1012 (2006)
Neff, P.: A geometrically exact planar Cosserat shell-model with microstructure: Existence of minimizers for zero Cosserat couple modulus. Math. Models Methods Appl. Sci. 17, 363–392 (2007)
Neff, P., Bîrsan, M., Osterbrink, F.: Existence theorem for geometrically nonlinear Cosserat micropolar model under uniform convexity requirements. J. Elast. 121, 119–141 (2015)
Neff, P., Hong, K.-I., Jeong, J.: The Reissner–Mindlin plate is the \(\Gamma \)-limit of Cosserat elasticity. Math. Models Methods Appl. Sci. 20, 1553–1590 (2010)
Pietraszkiewicz, W.: Refined resultant thermomechanics of shells. Int. J. Eng. Sci. 49, 1112–1124 (2011)
Pietraszkiewicz, W., Eremeyev, V.A.: On natural strain measures of the non-linear micropolar continuum. Int. J. Solids Struct. 46, 774–787 (2009)
Pietraszkiewicz, W., Konopińska, V.: Drilling couples and refined constitutive equations in the resultant geometrically non-linear theory of elastic shells. Int. J. Solids Struct. 51, 2133–2143 (2014)
Reissner, E.: Linear and nonlinear theory of shells. In: Fung, Y.C., Sechler, E.E. (eds.) Thin Shell Structures, pp. 29–44. Prentice-Hall, Englewood Cliffs (1974)
Sander, O.: Interpolation und Simulation mit nichtlinearen Daten. Rundbrief GAMM 1(2015), 6–12 (2015)
Sander, O., Neff, P., Bîrsan, M.: Numerical treatment of a geometrically nonlinear planar Cosserat shell model. Comput. Mech. 57, 817–841 (2016)
Silhavý, M.: Curvature measures in linear shell theories. Preprint No. 22-2020, Institute of Mathematics, The Czech Academy of Sciences (2020)
Steigmann, D.J.: Two-dimensional models for the combined bending and stretching of plates and shells based on three-dimensional linear elasticity. Int. J. Eng. Sci. 46, 654–676 (2008)
Steigmann, D.J.: Extension of Koiter’s linear shell theory to materials exhibiting arbitrary symmetry. Int. J. Eng. Sci. 51, 216–232 (2012)
Steigmann, D.J.: Koiter’s shell theory from the perspective of three-dimensional nonlinear elasticity. J. Elast. 111, 91–107 (2013)
Vlachoutsis, S.: Shear correction factors for plates and shells. Int. J. Numer. Methods Eng. 33, 1537–1552 (1992)
Zhilin, P.A.: Applied Mechanics—Foundations of Shell Theory. State Polytechnical University Publisher, Sankt Petersburg (2006) (in Russian)
Acknowledgements
This research has been funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)—Project No. 415894848.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bîrsan, M. Alternative derivation of the higher-order constitutive model for six-parameter elastic shells. Z. Angew. Math. Phys. 72, 50 (2021). https://doi.org/10.1007/s00033-021-01475-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00033-021-01475-0