On the Dislocation Density Tensor in the Cosserat Theory of Elastic Shells

Abstract

We consider the Cosserat continuum in its finite strain setting and discuss the dislocation density tensor as a possible alternative curvature strain measure in three-dimensional Cosserat models and in Cosserat shell models. We establish a close relationship (one-to-one correspondence) between the new shell dislocation density tensor and the bending-curvature tensor of 6-parameter shells.

1 Indroduction

The Cosserat-type theories have recently seen a tremendous renewed interest for their prospective applicability to model physical effects beyond the classical ones. These comprise notably the so-called size-effects (“smaller is stiffer”).

In a finite strain Cosserat-type framework, the group of proper rotations $\mathrm {SO}(3)$ has a dominant place. The original idea of the Cosserat brothers (Cosserat and Cosserat 1909) to consider independent rotational degrees of freedom in addition to the macroscopic displacement was heavily motivated by their treatment of plate and shell theory. Indeed, in shell theory it is natural to attach a preferred orthogonal frame (triad) at any point of the surface, one vector of which is the normal to the midsurface, the other two vectors lying in the tangent plane. This is the notion of the “trièdre caché”. The idea to consider then an orthogonal frame which is not strictly linked to the surface, but constitutively coupled, leads to the notion of the “trièdre mobile”. And this then is already giving rise to a prototype Cosserat shell (6-parameter) theory. For an insightful review of various Cosserat-type shell models, we refer to Altenbach et al. (2010).

However, the Cosserat brothers have never proposed any more specific constitutive framework, apart from postulating euclidean invariance (frame-indifference) and hyperelasticity. For specific problems it is necessary to choose a constitutive framework and to determine certain strain and curvature measures. This task is still not conclusively done, see e.g. Pietraszkiewicz and Eremeyev (2009).

Among the existing models for Cosserat-type shells, we mention the theory of simple elastic shells (Altenbach and Zhilin 2004), which has been developed by Zhilin (1976, 2006) and Altenbach and Zhilin (1982, 1988). Later, this theory has been successfully applied to describe the mechanical behaviour of laminated, functionally graded, viscoelastic or porous plates in Altenbach (2000), Altenbach and Eremeyev (2008, 2009, 2010) and of multi-layered, orthotropic, thermoelastic shells in Bîrsan and Altenbach (2010, 2011), Bîrsan et al. (2013), Sadowski et al. (2015). Another remarkable approach is the general 6-parameter theory of elastic shells presented in Libai and Simmonds (1998), Chróścielewski et al. (2004), Eremeyev and Pietraszkiewicz (2004). Although the starting point is different, one can see that the kinematical structure of the nonlinear 6-parameter shell theory is identical to that of a Cosserat shell model, see also Bîrsan and Neff (2014a, b).

In this paper, we would like to draw attention to alternative curvature measures, motivated by dislocation theory, which can also profitably be used in the three-dimensional Cosserat model and the Cosserat shell model. The object of interest is Nye’s dislocation density tensor $\,\mathrm {Curl}\,{{\varvec{P}}}\,$. Within the restriction to proper rotations it turns out that Nye’s tensor provides a complete control of all spatial derivatives of rotations (Neff and Münch 2008) and we rederive this property for micropolar continua using general curvilinear coordinates. Then, we focus on shell-curvature measures and define a new shell dislocation density tensor using the surface Curl operator. Then, we prove that a relation analogous to Nye’s formula holds also for Cosserat (6-parameter) shells.

The paper is structured as follows. In Sect. 2 we present the kinematics of a three-dimensional Cosserat continuum, as well as the appropriate strain measures and curvature strain measures, written in curvilinear coordinates. Here, we show the close relationship between the wryness tensor and the dislocation density tensor, including the corresponding Nye’s formula. In Sect. 3, we define the $\,\mathrm {Curl}\,$ operator on surfaces and present several representations using surface curvilinear coordinates. These relations are then used in Sect. 4 to introduce the new shell dislocation density tensor and to investigate its relationship to the elastic shell bending-curvature tensor of 6-parameter shells.

2 Strain Measures of a Three-Dimensional Cosserat Model in Curvilinear Coordinates

Let be a Cosserat elastic body which occupies in its reference (initial) configuration the domain $\varOmega _\xi \subset \mathbb {R}^3$. A generic point of $\varOmega _\xi$ will be denoted by $(\xi _1,\xi _2,\xi _3)$. The deformation of the Cosserat body is described by a vectorial map ${{\varvec{\varphi }}}_\xi$ and a microrotation tensor ${{\varvec{R}}}_\xi \,$,

$$\begin{aligned} {{\varvec{\varphi }}}_\xi :\varOmega _\xi \rightarrow \varOmega _c\,, \quad {{\varvec{R}}}_\xi :\varOmega _\xi \rightarrow \mathrm {SO}(3) , \end{aligned}$$

where $\varOmega _c\,$ is the deformed (current) configuration. Let $(x_1,x_2,x_3)$ be some general curvilinear coordinates system on $\varOmega _\xi \,$. Thus, we have a parametric representation $\, {{\varvec{\varTheta }}}\,$ of the domain $\,\varOmega _\xi$

$$\begin{aligned} {{\varvec{\varTheta }}}:\varOmega \rightarrow \varOmega _\xi \,, \quad {{\varvec{\varTheta }}}(x_1,x_2,x_3)=(\xi _1,\xi _2,\xi _3), \end{aligned}$$

where $\,\varOmega \subset \mathbb {R}^3$ is a bounded domain with Lipschitz boundary $\partial \varOmega$. The covariant base vectors with respect to these curvilinear coordinates are denoted by ${{\varvec{g}}}_i$ and the contravariant base vectors by ${{\varvec{g}}}^j$ ($i,j=1,2,3$), i.e.

$$\begin{aligned} {{\varvec{g}}}_i=\dfrac{\partial {{\varvec{\varTheta }}}}{\partial x_i}\,={{\varvec{\varTheta }}}_{,i}\,,\quad {{\varvec{g}}}^j\cdot {{\varvec{g}}}_i=\delta ^j_i, \end{aligned}$$

where $\delta ^j_i$ is the Kronecker symbol. We employ the usual conventions for indices: the Latin indices $i,j,k,\ldots$ range over the set $\{1,2,3\}$, while the Greek indices $\alpha ,\beta ,\gamma ,\ldots$ are confined to the range $\{1,2\}\,$; the comma preceding an index i denotes partial derivatives with respect to $x_i\,$; the Einstein summation convention over repeated indices is also used.

Introducing the deformation function $\,{{\varvec{\varphi }}}\,$ by the composition

$$\begin{aligned} {{\varvec{\varphi }}}:={{\varvec{\varphi }}}_\xi \circ {{\varvec{\varTheta }}}:\varOmega \rightarrow \varOmega _c\,,\quad {{\varvec{\varphi }}}(x_1,x_2,x_3): = {{\varvec{\varphi }}}_\xi \big ( {{\varvec{\varTheta }}}(x_1,x_2,x_3)\big ), \end{aligned}$$

we can express the (elastic) deformation gradient ${{\varvec{F}}}$ as follows:

$$\begin{aligned} {{\varvec{F}}} := \nabla _\xi \,{{\varvec{\varphi }}}_\xi ( \xi _1,\xi _2,\xi _3)\, =\nabla _x\,{{\varvec{\varphi }}}(x_1,x_2,x_3)\cdot \big [\nabla _x {{\varvec{\varTheta }}}(x_1,x_2,x_3)\big ]^{-1}. \end{aligned}$$

Using the direct tensor notation, we can write

$$\begin{aligned} \nabla _x{{\varvec{\varphi }}}={{\varvec{\varphi }}}_{,i}\otimes {{\varvec{e}}}_{i}\,,\quad \nabla _x{{\varvec{\varTheta }}}={{\varvec{g}}}_{i}\otimes {{\varvec{e}}}_{i}\,,\quad \big [\nabla _x\,{{\varvec{\varTheta }}}\big ]^{-1}= {{\varvec{e}}}_{j}\otimes {{\varvec{g}}}^{j}, \end{aligned}$$

where $\,{{\varvec{e}}}_i\,$ are the unit vectors along the coordinate axes $Ox_i$ in the parameter domain $\,\varOmega \,$. Then, the deformation gradient can be expressed by

$$\begin{aligned} {{\varvec{F}}} = {{\varvec{\varphi }}}_{,i}\otimes {{\varvec{g}}}^{i}. \end{aligned}$$

Fig. 1

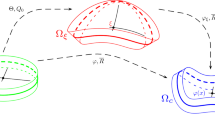
The reference (initial) configuration $\varOmega _\xi$ of the Cosserat continuum, the deformed (current) configuration $\varOmega _c$ and the parameter domain $\varOmega$ of the curvilinear coordinates $(x_1,x_2,x_3)$. The triads of directors $\{ {{\varvec{d}}}_i\}$ and $\{ {{\varvec{d}}}^0_i\}$ satisfy the relations ${{\varvec{d}}}_i={{\varvec{Q}}}_e{{\varvec{d}}}_i^0= \overline{{{\varvec{R}}}}{{\varvec{e}}}_i$ and ${{\varvec{d}}}_i^0= {{\varvec{Q}}}_0{{\varvec{e}}}_i\,$, where ${{\varvec{Q}}}_e$ is the elastic microrotation field, ${{\varvec{Q}}}_0$ the initial microrotation, and $\overline{{{\varvec{R}}}}$ the total microrotation field

The orientation and rotation of points in Cosserat (micropolar) media can also be described by means of triads of orthonormal vectors (called directors) attached to every point. We denote by $\{{{\varvec{d}}}_i^0 \}$ the triad of directors ($i=1,2,3$) in the reference configuration $\,\varOmega _\xi \,$ and by $\{{{\varvec{d}}}_i \}$ the directors in the deformed configuration $\,\varOmega _c\,$, see Fig. 1. We introduce the elastic microrotation ${{\varvec{Q}}}_e$ as the composition

$$\begin{aligned} {{\varvec{Q}}}_e:= {{\varvec{R}}}_\xi \circ {{\varvec{\varTheta }}}:\varOmega \rightarrow \mathrm {SO}(3 ),\quad {{\varvec{Q}}}_e (x_1,x_2,x_3):= {{\varvec{R}}}_\xi \big ({{\varvec{\varTheta }}}(x_1,x_2,x_3)\big ), \end{aligned}$$

which can be characterized with the help of the directors by the relations

$$\begin{aligned} {{\varvec{Q}}}_e{{\varvec{d}}}_i^0={{\varvec{d}}}_i\,, \quad \text {i.e.}, \quad {{\varvec{Q}}}_e={{\varvec{d}}}_i\otimes {{\varvec{d}}}_i^0. \end{aligned}$$

Let ${{\varvec{Q}}}_0$ be the initial microrotation (describing the position of the directors in the reference configuration $\,\varOmega _\xi$)

$$\begin{aligned}\,{{\varvec{Q}}}_0{{\varvec{e}}}_i ={{\varvec{d}}}_i^0\,, \quad \text {i.e.}, \quad {{\varvec{Q}}}_0={{\varvec{d}}}_i^0\otimes {{\varvec{e}}}_i. \end{aligned}$$

Then, the total microrotation $\overline{{{\varvec{R}}}}$ is given by

$$\begin{aligned} \overline{{{\varvec{R}}}}:\varOmega \rightarrow \mathrm {SO}(3 ),\quad \overline{{{\varvec{R}}}}(x_i):={{\varvec{Q}}}_e( x_i)\,{{\varvec{Q}}}_0( x_i) = {{\varvec{d}}}_j( x_i)\otimes {{\varvec{e}}}_j. \end{aligned}$$

The non-symmetric Biot-type stretch tensor (the elastic first Cosserat deformation tensor, see Cosserat and Cosserat (1909), p. 123, Eq. (43)) is now

$$\begin{aligned} \overline{{{\varvec{U}}}}_e:={{\varvec{Q}}}_e^T\, {{\varvec{F}}}= \big ({{\varvec{d}}}_i^0\otimes {{\varvec{d}}}_i\big )\,\big ({{\varvec{\varphi }}},_j\otimes {{\varvec{g}}}^j \big )= \big ({{\varvec{\varphi }}},_j\cdot \, {{\varvec{d}}}_i\big )\, {{\varvec{d}}}_i^0\otimes {{\varvec{g}}}^j. \end{aligned}$$

and the non-symmetric strain tensor for nonlinear micropolar materials is defined by

$$\begin{aligned} \overline{{{\varvec{E}}}}_e:=\overline{{{\varvec{U}}}}_e-{{\varvec{1}}}_3= \big ({{\varvec{\varphi }}},_j\cdot \, {{\varvec{d}}}_i- {{\varvec{g}}}_j\cdot {{\varvec{d}}}_i^0\big )\, {{\varvec{d}}}_i^0\otimes {{\varvec{g}}}^j , \end{aligned}$$

where ${{\varvec{1}}}_3= {{\varvec{g}}}_i\otimes {{\varvec{g}}}^i= {{\varvec{d}}}_i^0\otimes {{\varvec{d}}}_i^0\,$ is the unit three-dimensional tensor. As a strain measure for curvature (orientation change) one can employ the so-called wryness tensor ${{\varvec{\varGamma }}}$ given by:

$$\begin{aligned} {{\varvec{\varGamma }}}:= \mathrm {axl}\big ({{\varvec{Q}}}_e^T{{\varvec{Q}}}_{e,i}\big )\otimes {{\varvec{g}}}^i= {{\varvec{Q}}}_0\big [ \mathrm {axl}\big (\overline{{{\varvec{R}}}}^T\overline{{{\varvec{R}}}}_{,i}\big ) - \mathrm {axl}\big ({{\varvec{Q}}}_0^T{{\varvec{Q}}}_{0,i}\big ) \big ] \otimes {{\varvec{g}}}^i, \end{aligned}$$

(1)

where $\mathrm {axl}\big ({{\varvec{A}}}\big )$ denotes the axial vector of any skew-symmetric tensor ${{\varvec{A}}}$. For a detailed discussion on various strain measures of nonlinear micropolar continua we refer to the paper Pietraszkiewicz and Eremeyev (2009).

As an alternative to the wryness tensor $\,{{\varvec{\varGamma }}}\,$ one can make use of the $\,\mathrm {Curl}\,$ operator to define the so-called dislocation density tensor $\,\overline{{{\varvec{D}}}}_e\,$ by (Neff and Münch 2008)

$$\begin{aligned} \overline{{{\varvec{D}}}}_e:={{\varvec{Q}}}_e^T\,\mathrm {Curl}\,{{\varvec{Q}}}_e\,, \end{aligned}$$

(2)

which is another curvature measure for micropolar continua. Note that the $\,\mathrm {Curl}\,$ operator has various definitions in the literature, but we will make its significance clear in the next Sect. 2.1, where we present the $\,\mathrm {Curl}\,$ operator in curvilinear coordinates. The use of the dislocation density tensor $\,\overline{{{\varvec{D}}}}_e\,$ instead of the wryness tensor in conjuction with micropolar and micromorphic media has several advantages, as it was shown in Ghiba et al. (2015), Neff et al. (2014), Madeo et al. (2015). The relationship between the wryness tensor $\,{{\varvec{\varGamma }}}\,$ and the dislocation density tensor $\,\overline{{{\varvec{D}}}}_e\,$ is discussed in Sect. 2.2 in details.

Using the strain and curvature tensors $(\overline{{{\varvec{E}}}}_e\,,\,\overline{{{\varvec{D}}}}_e)$ the elastically stored energy density W for the isotropic nonlinear Cosserat model can be expressed as (Neff et al. 2015; Lankeit et al. 2016)

$$\begin{aligned} W(\overline{{{\varvec{E}}}}_e,\overline{{{\varvec{D}}}}_e)&= W_{\mathrm {mp}}(\overline{{{\varvec{E}}}}_e )+ W_{\mathrm {curv}}( \overline{{{\varvec{D}}}}_e),\qquad \mathrm {where} \nonumber \\ W_{\mathrm {mp}}(\overline{{{\varvec{E}}}}_e )&= \mu \,\Vert \,\mathrm {dev_3\,sym}\, \overline{{{\varvec{E}}}}_e\,\Vert ^2\, + \,\mu _c \, \Vert \,\mathrm {skew}\, \overline{{{\varvec{E}}}}_e\,\Vert ^2\, + \, \dfrac{\kappa }{2}\,\big (\mathrm {tr}\,\overline{{{\varvec{E}}}}_e\big )^2\,,\\ W_{\mathrm {curv}}( \overline{{{\varvec{D}}}}_e)&= \mu \,L_c^p\,\Big (a_1\Vert \,\mathrm {dev_3\,sym}\, \overline{{{\varvec{D}}}}_e\Vert ^2\, + \,a_2 \Vert \,\mathrm {skew}\, \overline{{{\varvec{D}}}}_e\Vert ^2\, + \, a_3\big (\mathrm {tr}\,\overline{{{\varvec{D}}}}_e\big )^2\Big )^{{p}/{2}}\,,\nonumber \quad \end{aligned}$$

(3)

where $\mu$ is the shear modulus, $\kappa$ is the bulk modulus of classical isotropic elasticity, and $\,\mu _c$ is called the Cosserat couple modulus, which are assumed to satisfy

$$\begin{aligned} \mu>0,\qquad \kappa>0,\qquad \text {and}\qquad \mu _c>0\,. \end{aligned}$$

The parameter $\,L_c$ introduces an internal length which is characteristic for the material, $a_i>0\,$ are dimensionless constitutive coefficients and $\,p\ge 2\,$ is a constant exponent. Here, $\,\, \mathrm {dev}_3\,{{\varvec{X}}}:={{\varvec{X}}}-\frac{1}{3}\,( \mathrm {tr}\,{{\varvec{X}}})\,{{\varvec{1}}}_3\,$ is the deviatoric part of any second order tensor ${{\varvec{X}}}$.

Under these assumptions on the constitutive coefficients, the existence of minimizers to the corresponding minimization problem of the total energy functional has been shown, e.g. in Neff et al. (2015), Lankeit et al. (2016).

2.1 The Curl Operator

For a vector field ${{\varvec{v}}}$, the (coordinate-free) definition of the vector $\mathrm {curl}\, {{\varvec{v}}}$ is

$$\begin{aligned} (\mathrm {curl}\, {{\varvec{v}}})\cdot {{\varvec{c}}}= \mathrm {div}({{\varvec{v}}}\times {{\varvec{c}}})&\quad \text {for all constant vectors}\,\,{{\varvec{c}}}, \end{aligned}$$

(4)

where $\cdot$ denotes the scalar product and $\times$ the vector product. The $\mathrm {Curl}$ of a tensor field $\,{{\varvec{T}}}$ is the tensor field defined by

$$\begin{aligned} \big (\mathrm {Curl}\, {{\varvec{T}}}\big )^T {{\varvec{c}}}= \mathrm {curl}\big ({{\varvec{T}}}^T {{\varvec{c}}}\big )&\quad \text {for all constant vectors}\,\,{{\varvec{c}}}. \end{aligned}$$

(5)

Remark 22.1

The operator $\mathrm {Curl}\,{{\varvec{T}}}$ given by (5) coincides with the $\mathrm {Curl}$ operator defined in Svendsen (2002), Mielke and Müller (2006). However, for other authors the $\mathrm {Curl}$ of $\,{{\varvec{T}}}$ is the transpose of $\mathrm {Curl}\,{{\varvec{T}}}$ defined by (5), see e.g. Gurtin (1981), Eremeyev et al. (2013).

Then, from (4) and (5) we obtain the following formulas

$$\begin{aligned} \mathrm {curl}\, {{\varvec{v}}} = -{{\varvec{v}}}_{,i}\times {{\varvec{g}}}^i,\qquad \qquad \mathrm {Curl}\, {{\varvec{T}}}= -{{\varvec{T}}}_{,i}\times {{\varvec{g}}}^i. \end{aligned}$$

(6)

Indeed, the Definition (4) yields

$$\begin{aligned} (\mathrm {curl}\, {{\varvec{v}}})\cdot {{\varvec{c}}} =\mathrm {div}({{\varvec{v}}}\times {{\varvec{c}}}) = ({{\varvec{v}}}\times {{\varvec{c}}})_{,i}\cdot {{\varvec{g}}}^i= ({{\varvec{v}}}_{,i}\times {{\varvec{c}}})\cdot {{\varvec{g}}}^i = ( {{\varvec{g}}}^i \times {{\varvec{v}}}_{,i})\cdot {{\varvec{c}}}, \end{aligned}$$

and the Eq. (6)$_1$ holds. Further, from (5) we get

$$\begin{aligned} \big (\mathrm {Curl}\, {{\varvec{T}}}\big )^T {{\varvec{c}}}= \mathrm {curl}\big ({{\varvec{T}}}^T {{\varvec{c}}}\big ) = {{\varvec{g}}}^i \times \big ({{\varvec{T}}}^T {{\varvec{c}}}\big )_{,i}= {{\varvec{g}}}^i \times \big ({{\varvec{T}}}_{,i}^T {{\varvec{c}}}\big )= \big ({{\varvec{g}}}^i \times {{\varvec{T}}}_{,i}^T \big ){{\varvec{c}}}, \end{aligned}$$

so it follows $\, \mathrm {Curl}\, {{\varvec{T}}}= \big ({{\varvec{g}}}^i \times {{\varvec{T}}}_{,i}^T \big )^T= - {{\varvec{T}}}_{,i}\times {{\varvec{g}}}^i$ and the relations (6) are proved.

In order to write the components of $\mathrm {curl}\, {{\varvec{v}}}$ and $\mathrm {Curl}\,{{\varvec{T}}}$ in curvilinear coordinates, we introduce the following notations

$$\begin{aligned} g_{ij}={{\varvec{g}}}_i . g_j\,,&\quad g=\det \big ( g_{ij}\big )_{3\times 3}\,>0. \end{aligned}$$

The alternating (Ricci) third-order tensor is

$$\begin{aligned} {{\varvec{\epsilon }}}=-{{\varvec{1}}}_3\times {{\varvec{1}}}_3= \epsilon _{ijk}\,{{\varvec{g}}}^i \otimes {{\varvec{g}}}^j\otimes {{\varvec{g}}}^k= \epsilon ^{ijk}{{\varvec{g}}}_i \otimes {{\varvec{g}}}_j\otimes {{\varvec{g}}}_k\,,\quad \mathrm {where}\\ \epsilon _{ijk}= \sqrt{g}\,e_{ijk}\,,\quad \epsilon ^{ijk}= \dfrac{1}{\sqrt{g}}\,e_{ijk}\,,\quad e_{ijk}=\left\{ \begin{array}{rl} 1, &{} \,\,(i,j,k) \text { is even permutation} \\ -1, &{} \,\,(i,j,k) \text { is odd permutation} \\ 0, &{} \,\,(i,j,k) \text { is no permutation} \end{array} \right. . \end{aligned}$$

The covariant, contravariant, and mixed components of any vector field ${{\varvec{v}}}$ and any tensor field $\,{{\varvec{T}}}$ are introduced by

$$\begin{aligned} {{\varvec{v}}}=v_k \,{{\varvec{g}}}^k=v^k {{\varvec{g}}}_k\,,\quad {{\varvec{T}}}= T_{jk}\,{{\varvec{g}}}^j\otimes {{\varvec{g}}}^k= T^{jk}{{\varvec{g}}}_j\otimes {{\varvec{g}}}_k= T^{j}_{\cdot \, k} \,{{\varvec{g}}}_j\otimes {{\varvec{g}}}^k. \end{aligned}$$

For the partial derivatives with respect to $x_i$ we have the well-known expressions

$$\begin{aligned} {{\varvec{v}}}_{,i} = v_{k|i} \,{{\varvec{g}}}^k\,,\qquad \qquad {{\varvec{T}}}_{,i}= T_{jk|i}\,{{\varvec{g}}}^j\otimes {{\varvec{g}}}^k= T^{j}_{\cdot \, k|i} \,{{\varvec{g}}}_j\otimes {{\varvec{g}}}^k, \end{aligned}$$

(7)

where a subscript bar preceding the index i denotes covariant derivative w.r.t. $x_i$.

Using the relations (7) in (6), we can write the components of $\mathrm {curl}\, {{\varvec{v}}}$ and $\mathrm {Curl}\,{{\varvec{T}}}$ as follows

$$\begin{aligned} \mathrm {curl}\, {{\varvec{v}}} =\epsilon ^{ijk}v_{j|i} \,{{\varvec{g}}}_k\,,&\mathrm {Curl}\, {{\varvec{T}}} = \epsilon ^{ijk}T_{sj|i} \,{{\varvec{g}}}^s\otimes {{\varvec{g}}}_k = \epsilon ^{ijk}T^{s}_{\cdot \,j|i} \,{{\varvec{g}}}_s\otimes {{\varvec{g}}}_k. \end{aligned}$$

(8)

Indeed, from (6)$_1$ and (7)$_1$ we find

$$\begin{aligned} \mathrm {curl}\, {{\varvec{v}}} = - \big ( v_{k|i} \,{{\varvec{g}}}^k \big ) \times {{\varvec{g}}}^i = - v_{k|i} \big ( {{\varvec{g}}}^k \times {{\varvec{g}}}^i \big ) = - v_{k|i} \big ( \epsilon ^{kij} {{\varvec{g}}}_j \big ) = \epsilon ^{ijk}v_{j|i}\,{{\varvec{g}}}_k. \end{aligned}$$

Analogously, from (6)$_2$ and (7)$_2$ we get

$$\begin{aligned} \mathrm {Curl}\, {{\varvec{T}}} = -\big ( T_{sk|i}\,{{\varvec{g}}}^s\otimes {{\varvec{g}}}^k \big ) \times {{\varvec{g}}}^i = -T_{sk|i}\,{{\varvec{g}}}^s\otimes \big ( {{\varvec{g}}}^k \times {{\varvec{g}}}^i\big ) = \epsilon ^{ijk}T_{sj|i} \,{{\varvec{g}}}^s\otimes {{\varvec{g}}}_k. \end{aligned}$$

Thus, Eq. (8) is proved.

Remark 22.2

In the special case of Cartesian coordinates, the relations (6) and (8) admit the simple form

$$\begin{aligned} \mathrm {curl}\, {{\varvec{v}}} = -{{\varvec{v}}}_{,i}\times {{\varvec{e}}}_i= e_{ijk}v_{j,i} \,{{\varvec{e}}}_k,\quad \mathrm {Curl}\, {{\varvec{T}}}= -{{\varvec{T}}}_{,i}\times {{\varvec{e}}}_i= e_{ijk}\,T_{sj,i} \,{{\varvec{e}}}_s\otimes {{\varvec{e}}}_k, \end{aligned}$$

where ${{\varvec{v}}}=v_i{{\varvec{e}}}_i$ and $\,{{\varvec{T}}}= T_{ij}{{\varvec{e}}}_i\otimes {{\varvec{e}}}_j$ are the corresponding coordinates. Moreover, in this case one can write

$$\begin{aligned} \mathrm {Curl}\,{{\varvec{T}}} \,=\, {{\varvec{e}}}_i \otimes \mathrm {curl}\big ({{\varvec{T}}}_i\big )\qquad \qquad \mathrm {for}\qquad \qquad {{\varvec{T}}}= {{\varvec{e}}}_i \otimes {{\varvec{T}}}_i, \end{aligned}$$

(9)

where $\, {{\varvec{T}}}_i=T_{ij}\,{{\varvec{e}}}_j$ are the three rows of the $3\times 3$ matrix $\,\big ( T_{ij}\big )_{3\times 3}\,$. The relation (9) shows that $\,\mathrm {Curl}\,$ is defined row-wise (Neff and Münch 2008): the rows of the $3\times 3$ matrix $\,\mathrm {Curl}\,{{\varvec{T}}}\,$ are, respectively, the three vectors $\,\mathrm {curl}\big ({{\varvec{T}}}_i\big )$, $i=1,2,3$.

Remark 22.3

In order to write the corresponding formula in curvilinear coordinates which is analogous to (9), we introduce the vectors $\, {{\varvec{T}}}_i:=T_{ij}\,{{\varvec{g}}}^j\,$ and $\, {{\varvec{T}}}^i:=T^{ij}\,{{\varvec{g}}}_j\,=T^i_{\cdot \, j}\,{{\varvec{g}}}^j \,$ such that it holds

$$\begin{aligned} {{\varvec{T}}}= {{\varvec{g}}}^i \otimes {{\varvec{T}}}_i \qquad \qquad \mathrm {and}\qquad \qquad {{\varvec{T}}}= {{\varvec{g}}}_i \otimes {{\varvec{T}}}^i. \end{aligned}$$

(10)

If we differentiate (10)$_1$ with respect to $x_j$ we get

$$\begin{aligned} {{\varvec{T}}}_{,j} = {{\varvec{g}}}^r_{\cdot \,,j} \otimes {{\varvec{T}}}_r + {{\varvec{g}}}^i \otimes {{\varvec{T}}}_{i,j} = -\varGamma ^r_{ji}{{\varvec{g}}}^i \otimes {{\varvec{T}}}_r + {{\varvec{g}}}^i \otimes {{\varvec{T}}}_{i,j} = {{\varvec{g}}}^i \otimes \big ( {{\varvec{T}}}_{i,j} -\varGamma ^r_{ji}\,{{\varvec{T}}}_r \big ) , \end{aligned}$$

where $\varGamma ^r_{ij}$ are the Christoffel symbols of the second kind. Hence, it follows

$$\begin{aligned} {{\varvec{T}}}_{,j} = {{\varvec{g}}}^i \otimes {{\varvec{T}}}_{i|j}\qquad \qquad \mathrm {with}\qquad \qquad {{\varvec{T}}}_{i|j}:= {{\varvec{T}}}_{i,j} -\varGamma ^r_{ji}\,{{\varvec{T}}}_r = {T}_{ik|j} \,{{\varvec{g}}}^k. \end{aligned}$$

(11)

Taking the vector product of (11)$_1$ with ${{\varvec{g}}}^j$ we obtain

$$\begin{aligned} \mathrm {Curl}\, {{\varvec{T}}} = - {{\varvec{T}}}_{,j} \times {{\varvec{g}}}^j = - \big ( {{\varvec{g}}}^i \otimes {{\varvec{T}}}_{i|j}\big ) \times {{\varvec{g}}}^j,\quad \text {i.e.} \end{aligned}$$

$$\begin{aligned} \mathrm {Curl}\, {{\varvec{T}}} = {{\varvec{g}}}^i \otimes \mathrm {curl}_{\mathrm {cov}}\big ({{\varvec{T}}}_i\big )\qquad \mathrm {where}\quad \mathrm {curl}_{\mathrm {cov}}\big ({{\varvec{T}}}_i\big ):= - {{\varvec{T}}}_{i|j} \times {{\varvec{g}}}^j. \end{aligned}$$

(12)

The relation (12) is the analogue of (9) for curvilinear coordinates. Similarly, by differentiating (10)$_2$ with respect to $x_j$ one can obtain the relation

$$\begin{aligned} \mathrm {Curl}\, {{\varvec{T}}} = {{\varvec{g}}}_i \otimes \mathrm {curl}_{\mathrm {cov}}\big ({{\varvec{T}}}^i\big )\qquad \text {where we denote} \end{aligned}$$

(13)

$$\begin{aligned} \mathrm {curl}_{\mathrm {cov}}\big ({{\varvec{T}}}^i\big ):= - {{\varvec{T}}}^{i}_{\cdot \,|j} \times {{\varvec{g}}}^j \qquad \mathrm {and}\quad {{\varvec{T}}}^{i}_{\cdot \,|j}:= {{\varvec{T}}}^{i}_{\cdot \,,j} + \varGamma ^i_{rj}\,{{\varvec{T}}}^r = {T}^{i}_{\cdot \,k|j} \,{{\varvec{g}}}^k. \end{aligned}$$

2.2 Relation Between the Wryness Tensor and the Dislocation Density Tensor

Let ${{\varvec{A}}}= A_{ij} {{\varvec{g}}}^i \otimes {{\varvec{g}}}^j$ be an arbitrary skew-symmetric tensor and $\mathrm {axl}({{\varvec{A}}})=a_k{{\varvec{g}}}^k$ its axial vector. Then, the following relations hold

$$\begin{aligned} \begin{array}{lcl} {{\varvec{A}}} &{} = &{} \mathrm {axl}({{\varvec{A}}})\times {{\varvec{1}}}_3 = {{\varvec{1}}}_3 \times \mathrm {axl}({{\varvec{A}}}), \\ \mathrm {axl}({{\varvec{A}}}) &{} = &{} -\frac{1}{2} \,{{\varvec{\epsilon }}}: {{\varvec{A}}} = -\frac{1}{2} \, \epsilon ^{ijk} A_{ij}\,{{\varvec{g}}}_k\,, \\ {{\varvec{A}}} &{} = &{} - {{\varvec{\epsilon }}}\, \mathrm {axl}({{\varvec{A}}}) = - \epsilon ^{ijk} a_k\, {{\varvec{g}}}_i\otimes {{\varvec{g}}}_j\,, \end{array} \end{aligned}$$

(14)

where the double dot product “:” of two tensors ${{\varvec{B}}}=B^{ijk}\,{{\varvec{g}}}_i\otimes {{\varvec{g}}}_j\otimes {{\varvec{g}}}_k$ and ${{\varvec{T}}}=T_{ij}\,{{\varvec{g}}}^i\otimes {{\varvec{g}}}^j$ is defined as $\,{{\varvec{B}}}:{{\varvec{T}}}\,=\, B^{ijk}T_{jk}\,{{\varvec{g}}}_i\,$.

Using these relations, we can derive the close relationship between the wryness tensor and the dislocation density tensor: it holds

$$\begin{aligned} \overline{{{\varvec{D}}}}_e = -{{\varvec{\varGamma }}}^T+(\mathrm {tr}\,{{\varvec{\varGamma }}})\,{{\varvec{1}}}_3,\quad \text {or equivalently}, \end{aligned}$$

(15)

$$\begin{aligned} {{\varvec{\varGamma }}}= - \overline{{{\varvec{D}}}}_e^T + \frac{1}{2} \, (\mathrm {tr}\,\overline{{{\varvec{D}}}}_e)\,{{\varvec{1}}}_3. \end{aligned}$$

(16)

Indeed, in view of the Eq. (14)$_3$ and the Definition (1) we have

$$\begin{aligned} {{\varvec{Q}}}_e^T{{\varvec{Q}}}_{e,k}\otimes {{\varvec{g}}}^k&= - {{\varvec{\epsilon }}}\, \mathrm {axl}(Q_e^T{{\varvec{Q}}}_{e,k})\otimes {{\varvec{g}}}^k = - {{\varvec{\epsilon }}}\,{{\varvec{\varGamma }}}\\&= - \big ( \epsilon _{ijr}\,{{\varvec{g}}}^i \otimes {{\varvec{g}}}^j\otimes {{\varvec{g}}}^r \big ) \big ( \varGamma ^s_{\cdot \,k} \,{{\varvec{g}}}_s \otimes {{\varvec{g}}}^k\big ) = -\epsilon _{ijs}\,\varGamma ^s_{\cdot \,k} \,{{\varvec{g}}}^i \otimes {{\varvec{g}}}^j\otimes {{\varvec{g}}}^k. \end{aligned}$$

Hence, we deduce

$$\begin{aligned} {{\varvec{Q}}}_e^T{{\varvec{Q}}}_{e,k}\, = -\epsilon _{ijs}\,\varGamma ^s_{\cdot \,k} \,{{\varvec{g}}}^i \otimes {{\varvec{g}}}^j. \end{aligned}$$

(17)

In view of (6)$_2$ , the Definition (2) can be written in the form

$$\begin{aligned} \overline{{{\varvec{D}}}}_e = {{\varvec{Q}}}_e^T\big (-{{\varvec{Q}}}_{e,k}\times {{\varvec{g}}}^k\big ) = -\big ({{\varvec{Q}}}_e^T{{\varvec{Q}}}_{e,k}\big )\times {{\varvec{g}}}^k . \end{aligned}$$

(18)

Inserting (17) in (18), we obtain

$$\begin{aligned} \overline{{{\varvec{D}}}}_e&= \epsilon _{ijs}\,\varGamma ^s_{\cdot \,k} \,\big ({{\varvec{g}}}^i \otimes {{\varvec{g}}}^j\big )\times {{\varvec{g}}}^k = \epsilon _{ijs}\,\varGamma ^s_{\cdot \,k} \,{{\varvec{g}}}^i \otimes \big ( \epsilon ^{jkr}{{\varvec{g}}}_r \big ) = \big (\epsilon _{jsi}\,\epsilon ^{jkr} \big )\varGamma ^s_{\cdot \,k} \,{{\varvec{g}}}^i \otimes {{\varvec{g}}}_r \\&= \big ( \delta ^k_s \,\delta ^r_i - \delta ^r_s \,\delta ^k_i \big )\varGamma ^s_{\cdot \,k} \,{{\varvec{g}}}^i \otimes {{\varvec{g}}}_r = \varGamma ^s_{\cdot \,s} \,{{\varvec{g}}}^i \otimes {{\varvec{g}}}_i - \varGamma ^s_{\cdot \,i} \,{{\varvec{g}}}^i \otimes {{\varvec{g}}}_s = (\mathrm {tr}\,{{\varvec{\varGamma }}})\,{{\varvec{1}}}_3 -{{\varvec{\varGamma }}}^T. \end{aligned}$$

Thus, the relation (15) is proved. If we apply the trace operator and the transpose in (15) we obtain also the relation (16). For infinitesimal strains this formula is well-known under the name Nye’s formula, and $(-\,{{\varvec{\varGamma }}})$ is also called Nye’s curvature tensor (Nye 1953). This relation has been first established in Neff and Münch (2008).

Let us find the components of the wryness tensor and the dislocation density tensor in curvilinear coordinates. To this aim, we write first the skew-symmetric tensor

$$\begin{aligned} {{\varvec{Q}}}_e^T{{\varvec{Q}}}_{e,i}&= \big ({{\varvec{d}}}^0_j \otimes {{\varvec{d}}}_j\big ) \big ({{\varvec{d}}}_{k,i} \otimes {{\varvec{d}}}_k^0 + {{\varvec{d}}}_{k} \otimes {{\varvec{d}}}_{k,i}^0\big )= \big ( {{\varvec{d}}}_j\cdot {{\varvec{d}}}_{k,i} \big )\, {{\varvec{d}}}^0_j \otimes {{\varvec{d}}}_k^0 + {{\varvec{d}}}^0_j \otimes {{\varvec{d}}}_{j,i}^0 \nonumber \\&= \big ( {{\varvec{d}}}_j\cdot {{\varvec{d}}}_{k,i} - {{\varvec{d}}}^0_j\cdot {{\varvec{d}}}^0_{k,i} \big )\, {{\varvec{d}}}^0_j \otimes {{\varvec{d}}}_k^0. \end{aligned}$$

(19)

Then, we obtain for the axial vector the equation

$$\begin{aligned} \mathrm {axl}\big ({{\varvec{Q}}}_e^T{{\varvec{Q}}}_{e,i}\big ) = -\frac{1}{2} \, e_{jks}\, \big ( {{\varvec{d}}}_j\cdot {{\varvec{d}}}_{k,i} - {{\varvec{d}}}^0_j\cdot {{\varvec{d}}}^0_{k,i} \big )\, {{\varvec{d}}}^0_s\,. \end{aligned}$$

(20)

Indeed, according to (14)$_2$ and (19) we can write

$$\begin{aligned} \mathrm {axl}\big ({{\varvec{Q}}}_e^T{{\varvec{Q}}}_{e,i}\big )&= -\frac{1}{2} \,{{\varvec{\epsilon }}}: \big ({{\varvec{Q}}}_e^T{{\varvec{Q}}}_{e,i}\big ) \\&= -\frac{1}{2} \,\big (e_{sjk}\,{{\varvec{d}}}_s^0 \otimes {{\varvec{d}}}_j^0 \otimes {{\varvec{d}}}_k^0 \big ) : \big [ \big ( {{\varvec{d}}}_l\cdot {{\varvec{d}}}_{r,i} - {{\varvec{d}}}^0_l\cdot {{\varvec{d}}}^0_{r,i} \big )\, {{\varvec{d}}}^0_l \otimes {{\varvec{d}}}_r^0 \,\big ] \\&= -\frac{1}{2} \, e_{jks}\, \big ( {{\varvec{d}}}_j\cdot {{\varvec{d}}}_{k,i} - {{\varvec{d}}}^0_j\cdot {{\varvec{d}}}^0_{k,i} \big )\, {{\varvec{d}}}^0_s \end{aligned}$$

and the relation (20) is proved. Using (20) in the Definition (1) we find the following formula for the wryness tensor

$$\begin{aligned} {{\varvec{\varGamma }}}\,=\, \frac{1}{2} \, e_{jks}\, \big ( {{\varvec{d}}}_{j,i}\cdot {{\varvec{d}}}_{k} - {{\varvec{d}}}^0_{j,i}\cdot {{\varvec{d}}}^0_{k} \big )\, {{\varvec{d}}}^0_s\otimes {{\varvec{g}}}^i. \end{aligned}$$

(21)

To obtain an expression for the components of $\overline{{{\varvec{D}}}}_e$ we insert (19) in (18) and we get

$$\begin{aligned} \overline{{{\varvec{D}}}}_e&= - \big ( {{\varvec{d}}}_j\cdot {{\varvec{d}}}_{k,i} - {{\varvec{d}}}^0_j\cdot {{\varvec{d}}}^0_{k,i} \big )\, \big ( {{\varvec{d}}}^0_j \otimes {{\varvec{d}}}_k^0\big )\times {{\varvec{g}}}^i \nonumber \\&= \big ( {{\varvec{d}}}_{j,i}\cdot {{\varvec{d}}}_{k} - {{\varvec{d}}}^0_{j,i}\cdot {{\varvec{d}}}^0_{k} \big )\, {{\varvec{d}}}^0_j \otimes \big ( {{\varvec{d}}}_k^0\times {{\varvec{g}}}^i \big ). \end{aligned}$$

(22)

We rewrite the last vector product as

$$\begin{aligned} {{\varvec{d}}}_k^0\times {{\varvec{g}}}^i = {{\varvec{d}}}_k^0\times \big [ \big ( {{\varvec{g}}}^i \cdot {{\varvec{d}}}_r^0 \big )\,{{\varvec{d}}}_r^0 \big ] = \big ( {{\varvec{g}}}^i \cdot {{\varvec{d}}}_r^0 \big )\,{{\varvec{d}}}_k^0\times {{\varvec{d}}}_r^0 = e_{krs} \big ( {{\varvec{g}}}^i \cdot {{\varvec{d}}}_r^0 \big )\,{{\varvec{d}}}_s^0 \end{aligned}$$

and we insert it in (22) to find the following expression for the dislocation density tensor

$$\begin{aligned} \overline{{{\varvec{D}}}}_e = e_{krs} \big ( {{\varvec{d}}}_{j,i}\cdot {{\varvec{d}}}_{k} - {{\varvec{d}}}^0_{j,i}\cdot {{\varvec{d}}}^0_{k} \big )\, \big ( {{\varvec{g}}}^i \cdot {{\varvec{d}}}_r^0 \big )\, {{\varvec{d}}}^0_j \otimes {{\varvec{d}}}_s^0\,. \end{aligned}$$

(23)

Remark 22.4

In the special case of Cartesian coordinates one can identify ${{\varvec{d}}}_i^0={{\varvec{e}}}_i,\,{{\varvec{g}}}^i={{\varvec{g}}}_i={{\varvec{e}}}_i$, and the relations (21) and (22) simplify to the forms

$$\begin{aligned} {{\varvec{\varGamma }}}&=\, \frac{1}{2} \, e_{iks}\, \big ( {{\varvec{d}}}_{k,j}\cdot {{\varvec{d}}}_{s} \big )\, {{\varvec{e}}}_i\otimes {{\varvec{e}}}_j, \\ \overline{{{\varvec{D}}}}_e&= e_{ijk} \, \big ( {{\varvec{d}}}_{j,i}\cdot {{\varvec{d}}}_{s} \big )\, {{\varvec{e}}}_s\otimes {{\varvec{e}}}_k. \end{aligned}$$

Remark 22.5

One can find various definitions of the wryness tensor in the literature, see e.g. Tambača and Velčić (2010), where ${{\varvec{\varGamma }}}$ is called the curvature strain tensor. Thus, one can alternatively define the wryness tensor by

$$\begin{aligned} {{\varvec{\varGamma }}}= {{\varvec{Q}}}_e^T\,{{\varvec{\omega }}}, \end{aligned}$$

(24)

where ${{\varvec{\omega }}}$ is the second order tensor given by

$$\begin{aligned} {{\varvec{\omega }}}= {{\varvec{\omega }}}_i\otimes {{\varvec{g}}}^i \qquad \text {with}\qquad {{\varvec{Q}}}_{e,i} = {{\varvec{\omega }}}_i\times {{\varvec{Q}}}_e. \end{aligned}$$

(25)

If we compare the Definition (1) with (24), (25), we see that indeed ${{\varvec{Q}}}_e^T\,{{\varvec{\omega }}}_i= \mathrm {axl}\big ({{\varvec{Q}}}_e^T{{\varvec{Q}}}_{e,i}\big )$, i.e.

$$\begin{aligned} {{\varvec{\omega }}}_i\, = \,{{\varvec{Q}}}_e\,\mathrm {axl}\big ({{\varvec{Q}}}_e^T{{\varvec{Q}}}_{e,i}\big ) = \mathrm {axl}\big ({{\varvec{Q}}}_{e,i}\,{{\varvec{Q}}}_e^T\big ). \end{aligned}$$

(26)

By a straightforward but lengthy calculation, one can prove that the vectors ${{\varvec{\omega }}}_i$ are expressed in terms of the directors by

$$\begin{aligned} {{\varvec{\omega }}}_i\, = \,\frac{1}{2} \big [ {{\varvec{d}}}_{j}\times {{\varvec{d}}}_{j,i} - {{\varvec{Q}}}_e \big ({{\varvec{d}}}^0_{j}\times {{\varvec{d}}}^0_{j,i} \big ) \big ]. \end{aligned}$$

(27)

Inserting (27) in (25)$_1$ and (24), we obtain the expression of the wryness tensor written with the help of the directors ${{\varvec{d}}}_i$

$$\begin{aligned} {{\varvec{\varGamma }}}\, = \, \,\frac{1}{2} \big [ {{\varvec{Q}}}_e^T \big ({{\varvec{d}}}_{j}\times {{\varvec{d}}}_{j,i}\big ) - {{\varvec{d}}}^0_{j}\times {{\varvec{d}}}^0_{j,i} \big ]\otimes {{\varvec{g}}}^i . \end{aligned}$$

(28)

3 The Curl Operator on Surfaces

Let $\mathcal {S}$ be a smooth surface embedded in the Euclidean space $\mathbb {R}^3$ and let ${{\varvec{y}}}_0(x_1,x_2)$, ${{\varvec{y}}}_0:\omega \rightarrow \mathbb {R}^3$, be a parametrization of this surface. We denote the covariant base vectors in the tangent plane by ${{\varvec{a}}}_1,{{\varvec{a}}}_2$ and the contravariant base vectors by ${{\varvec{a}}}^1,{{\varvec{a}}}^2$:

$$\begin{aligned} {{\varvec{a}}}_\alpha = \dfrac{\partial {{\varvec{y}}}_0}{\partial x_\alpha }\,={{\varvec{y}}}_{0,\alpha },\quad {{\varvec{a}}}_\alpha \cdot {{\varvec{a}}}^\beta =\delta _\alpha ^\beta \end{aligned}$$

and let

$$\begin{aligned} {{\varvec{a}}}_3= {{\varvec{a}}}^3= {{\varvec{n}}}_0= \dfrac{{{\varvec{a}}}_1\times {{\varvec{a}}}_2}{|{{\varvec{a}}}_1\times {{\varvec{a}}}_2| }, \end{aligned}$$

where ${{\varvec{n}}}_0$ is the unit normal to the surface. Further, we designate by

$$\begin{aligned} a_{\alpha \beta }={{\varvec{a}}}_\alpha \cdot {{\varvec{a}}}_\beta ,\qquad a^{\alpha \beta }={{\varvec{a}}}^\alpha \cdot {{\varvec{a}}}^\beta ,\qquad a =\sqrt{\mathrm {det}\, \big ( a_{\alpha \beta } \big ){}_{2\times 2}}\,= |{{\varvec{a}}}_1\times {{\varvec{a}}}_2|\,>0 \end{aligned}$$

and we have

$$\begin{aligned} {{\varvec{a}}}^\alpha \times {{\varvec{a}}}^\beta = \epsilon ^{\alpha \beta } {{\varvec{a}}}_3,\,\,\, {{\varvec{a}}}^3\times {{\varvec{a}}}^\alpha = \epsilon ^{\alpha \beta } {{\varvec{a}}}_\beta ,\,\,\, {{\varvec{a}}}_\alpha \times {{\varvec{a}}}_\beta = \epsilon _{\alpha \beta } {{\varvec{a}}}^3,\quad {{\varvec{a}}}_3\times {{\varvec{a}}}_\alpha = \epsilon _{\alpha \beta } {{\varvec{a}}}^\beta , \end{aligned}$$

(29)

where $\epsilon ^{\alpha \beta } =\,\dfrac{1}{a}\,e_{\alpha \beta },\,\, \epsilon _{\alpha \beta } ={a}\,e_{\alpha \beta }$ and $\,e_{\alpha \beta }$ is the two-dimensional alternator given by $e_{12}=-e_{21}=1, \,e_{11}=e_{22}=0$.

Then, ${{\varvec{a}}}= a_{\alpha \beta }{{\varvec{a}}}^\alpha \otimes {{\varvec{a}}}^\beta = a^{\alpha \beta }{{\varvec{a}}}_\alpha \otimes {{\varvec{a}}}_\beta ={{\varvec{a}}}_\alpha \otimes {{\varvec{a}}}^\alpha$ represents the first fundamental tensor of the surface $\mathcal {S}$, while the second fundamental tensor ${{\varvec{b}}}$ is defined by

$$\begin{aligned}&{{\varvec{b}}}= -\mathrm {Grad}_s\,{{\varvec{n}}}_0=- {{\varvec{n}}}_{0,\alpha }\otimes {{\varvec{a}}}^\alpha = b_{\alpha \beta }\,{{\varvec{a}}}^\alpha \otimes {{\varvec{a}}}^\beta =b^\alpha _\beta \,{{\varvec{a}}}_\alpha \otimes {{\varvec{a}}}^\beta , \quad \text {with}\\&b_{\alpha \beta }=- {{\varvec{n}}}_{0,\beta }\cdot {{\varvec{a}}}_\alpha = b_{\beta \alpha },\qquad b^{\alpha }_{\beta }=- {{\varvec{n}}}_{0,\beta }\cdot {{\varvec{a}}}^\alpha . \end{aligned}$$

The surface gradient $\mathrm {Grad}_s$ and surface divergence $\mathrm {Div}_s$ operators are defined for a vector field ${{\varvec{v}}}$ by

$$\begin{aligned} \mathrm {Grad}_s\,{{\varvec{v}}}\, =\, \dfrac{\partial {{\varvec{v}}}}{\partial x_\alpha }\,\otimes {{\varvec{a}}}^\alpha = {{\varvec{v}}}_{,\alpha }\otimes {{\varvec{a}}}^\alpha ,\qquad \mathrm {Div}_s\,{{\varvec{v}}}\, =\,\mathrm {tr}\big [ \mathrm {Grad}_s\,{{\varvec{v}}}\big ]= {{\varvec{v}}}_{,\alpha }\cdot {{\varvec{a}}}^\alpha . \end{aligned}$$

(30)

We also introduce the so-called alternator tensor ${{\varvec{c}}}$ of the surface (Zhilin 2006)

$$\begin{aligned} {{\varvec{c}}}=-{{\varvec{n}}}_0\times {{\varvec{a}}}=-{{\varvec{a}}}\times {{\varvec{n}}}_0= \epsilon ^{\alpha \beta }\,{{\varvec{a}}}_\alpha \otimes {{\varvec{a}}}_\beta = \epsilon _{\alpha \beta }\,{{\varvec{a}}}^\alpha \otimes {{\varvec{a}}}^\beta . \end{aligned}$$

(31)

The tensors ${{\varvec{a}}}$ and ${{\varvec{b}}}$ are symmetric, while ${{\varvec{c}}}$ is skew-symmetric and satisfies $\, {{\varvec{c}}}{{\varvec{c}}}=-{{\varvec{a}}}$. Note that the tensors ${{\varvec{a}}}\,$, ${{\varvec{b}}}\,$, and ${{\varvec{c}}}$ defined above are planar, i.e. they are tensors in the tangent plane of the surface. Moreover, ${{\varvec{a}}}$ is the identity tensor in the tangent plane.

We define the surface Curl operator $\mathrm {curl}_s$ for vector fields ${{\varvec{v}}}$ and, respectively, $\mathrm {Curl}_s$ for tensor fields ${{\varvec{T}}}$ by

$$\begin{aligned}&\big (\mathrm {curl}_s\,{{\varvec{v}}}\big )\cdot {{\varvec{k}}} \, = \, \mathrm {Div}_s\big ({{\varvec{v}}}\times {{\varvec{k}}}\big )\qquad \text {for all constant vectors }{{\varvec{k}}}, \end{aligned}$$

(32)

$$\begin{aligned}&\big (\mathrm {Curl}_s\,{{\varvec{T}}}\big )^T {{\varvec{k}}} \, = \, \mathrm {curl}_s\big ({{\varvec{T}}}^T {{\varvec{k}}}\big )\qquad \text {for all constant vectors }{{\varvec{k}}}. \end{aligned}$$

(33)

Thus, $\mathrm {curl}_s\,{{\varvec{v}}}$ is a vector field, while $\mathrm {Curl}_s\,{{\varvec{T}}}$ is a tensor field.

Remark 22.6

These definitions are analogous to the corresponding Definitions (4), (5) in the three-dimensional case. Notice that the curl operator on surfaces has a different significance for other authors, see e.g. Backus et al. (1996).

From the Definitions (32) and (33) it follows

$$\begin{aligned} \mathrm {curl}_s\,{{\varvec{v}}} = - {{\varvec{v}}}_{,\alpha }\times {{\varvec{a}}}^\alpha ,&\quad \mathrm {Curl}_s\,{{\varvec{T}}} = - {{\varvec{T}}}_{,\alpha }\times {{\varvec{a}}}^\alpha . \end{aligned}$$

(34)

Indeed, in view of (30) and (32) we have

$$\begin{aligned} \big (\mathrm {curl}_s\,{{\varvec{v}}}\big )\cdot {{\varvec{k}}}&= \mathrm {Div}_s\big ({{\varvec{v}}}\times {{\varvec{k}}}\big ) = \big ({{\varvec{v}}}\times {{\varvec{k}}}\big )_{,\alpha }\cdot {{\varvec{a}}}^\alpha = \big ({{\varvec{v}}}_{,\alpha }\times {{\varvec{k}}}\big )\cdot {{\varvec{a}}}^\alpha \\&= \big ({{\varvec{a}}}^\alpha \times {{\varvec{v}}}_{,\alpha }\big )\cdot {{\varvec{k}}} = \big (- {{\varvec{v}}}_{,\alpha }\times {{\varvec{a}}}^\alpha \big )\cdot {{\varvec{k}}}\quad \text {for all constant vectors }{{\varvec{k}}} \end{aligned}$$

and also

$$\begin{aligned} \big (\mathrm {Curl}_s\,{{\varvec{T}}}\big )^T {{\varvec{k}}} = \mathrm {curl}_s\big ({{\varvec{T}}}^T {{\varvec{k}}}\big ) = {{\varvec{a}}}^\alpha \times \big ({{\varvec{T}}}^T {{\varvec{k}}}\big )_{,\alpha } = {{\varvec{a}}}^\alpha \times \big ({{\varvec{T}}}^T_{,\alpha } {{\varvec{k}}}\big ) = \big ({{\varvec{a}}}^\alpha \times {{\varvec{T}}}^T_{,\alpha }\big ) {{\varvec{k}}}, \end{aligned}$$

which implies $\mathrm {Curl}_s\,{{\varvec{T}}} = \big ({{\varvec{a}}}^\alpha \times {{\varvec{T}}}^T_{,\alpha }\big )^T = - {{\varvec{T}}}_{,\alpha }\times {{\varvec{a}}}^\alpha$, so the relations (34) hold true.

To write the components of $\mathrm {curl}_s\,{{\varvec{v}}}$ and $\mathrm {Curl}_s\,{{\varvec{T}}}$ we employ the covariant derivatives on the surface. Let ${{\varvec{v}}}= v_i\,{{\varvec{a}}}^i$ be a vector field on $\mathcal {S}$. Then, we have

$$\begin{aligned}&{{\varvec{a}}}^\alpha _{\cdot ,\beta } = - \varGamma ^\alpha _{\beta \gamma }\, {{\varvec{a}}}^\gamma + b^\alpha _\beta \,{{\varvec{a}}}^3,\qquad {{\varvec{a}}}_{3,\beta } = - b^\alpha _\beta \,{{\varvec{a}}}_\alpha = -b_{\alpha \beta }\,{{\varvec{a}}}^\alpha ,\nonumber \\&{{\varvec{v}}}_{,\alpha } = ( v_{\beta |\alpha } - b_{\alpha \beta }\,v_3) {{\varvec{a}}}^\beta + (v_{3,\alpha }+ b_\alpha ^\beta \,v_\beta ){{\varvec{a}}}^3, \end{aligned}$$

(35)

where $v_{\beta |\alpha } = v_{\beta ,\alpha } - \varGamma ^\gamma _{\alpha \beta }\,v_\gamma \,$ is the covariant derivative with respect to $x_\alpha$. Inserting this relation in (34)$_1$ and using (29)$_{1,2}$ we obtain

$$\begin{aligned} \mathrm {curl}_s\,{{\varvec{v}}}\,=\, \epsilon ^{\alpha \beta }\big [ (v_{3,\beta }+ b^\gamma _\beta \,v_\gamma ){{\varvec{a}}}_\alpha + v_{\beta |\alpha }\, {{\varvec{a}}}_3 \big ]. \end{aligned}$$

(36)

For a tensor field ${{\varvec{T}}}=T_{ij}\,{{\varvec{a}}}^i\otimes {{\varvec{a}}}^j = T^{ij}\,{{\varvec{a}}}_i\otimes {{\varvec{a}}}_j = T^{i}_{\cdot \,j}\,{{\varvec{a}}}_i\otimes {{\varvec{a}}}^j$ on the surface, the derivative ${{\varvec{T}}}_{,\gamma }$ can be expressed as

$$\begin{aligned} {{\varvec{T}}}_{,\gamma } = \big ( T_{\alpha \beta |\gamma } - b_{\alpha \gamma }\,T_{3\beta } - b_{\beta \gamma }\,T_{\alpha 3} \big ) {{\varvec{a}}}^\alpha \otimes {{\varvec{a}}}^\beta + \big ( T_{\alpha 3|\gamma } + b^\beta _{\gamma }\,T_{\alpha \beta } - b_{\alpha \gamma }\,T_{3 3} \big ) {{\varvec{a}}}^\alpha \otimes {{\varvec{a}}}^3\nonumber \\ + \big ( T_{3\alpha |\gamma }+ b^\beta _{\gamma }\,T_{\beta \alpha } - b_{\alpha \gamma }\,T_{3 3} \big ) {{\varvec{a}}}^3\otimes {{\varvec{a}}}^\alpha + \big ( T_{3 3,\gamma } + b^\alpha _{\gamma }\,T_{\alpha 3} + b^\alpha _{\gamma }\,T_{3\alpha } \big ) {{\varvec{a}}}^3\otimes {{\varvec{a}}}^3, \end{aligned}$$

(37)

where the covariant derivatives are

$$\begin{aligned}&T_{\alpha \beta |\gamma } = T_{\alpha \beta ,\gamma } - \varGamma ^\delta _{\beta \gamma }\, T_{\alpha \delta } - \varGamma ^\delta _{\alpha \gamma }\, T_{\delta \beta },\\&T_{\alpha 3|\gamma } = T_{\alpha 3,\gamma } - \varGamma ^\beta _{\alpha \gamma }\, T_{\beta 3},\qquad T_{3\alpha |\gamma } = T_{3\alpha ,\gamma } - \varGamma ^\beta _{\alpha \gamma }\, T_{3\beta }. \end{aligned}$$

Using (37) in (34)$_2$ we obtain with the help of (29)$_{1,2}$ the decomposition

$$\begin{aligned} \mathrm {Curl}_s\,{{\varvec{T}}}&= \epsilon ^{\beta \gamma }\big (T_{\alpha 3|\gamma } \!+\! b^\sigma _{\gamma }\,T_{\alpha \sigma } \!-\! b_{\alpha \gamma }\,T_{3 3} \big ) {{\varvec{a}}}^\alpha \!\otimes \!{{\varvec{a}}}_\beta + \epsilon ^{\gamma \beta }\big (T_{\alpha \beta |\gamma }\! - \!b_{\alpha \gamma }\,T_{3\beta } \big ) {{\varvec{a}}}^\alpha \!\otimes \!{{\varvec{a}}}_3 \nonumber \\&\quad + \epsilon ^{\beta \gamma }\big (T_{3 3,\gamma } + b^\alpha _{\gamma }\,T_{\alpha 3} + b^\alpha _{\gamma }\,T_{3\alpha } \big ) {{\varvec{a}}}^3\!\otimes \!{{\varvec{a}}}_\beta + \epsilon ^{\gamma \beta }\big (T_{3\beta |\gamma }\! + \!b^\alpha _{\gamma }\,T_{\alpha \beta } \big ) {{\varvec{a}}}^3\!\otimes {{\varvec{a}}}_3. \end{aligned}$$

(38)

Alternatively, one can use the mixed components $T^{i}_{\cdot \,j}\,$ and write $\mathrm {Curl}_s\,{{\varvec{T}}}$ in the tensor basis $\{ \,{{\varvec{a}}}_i\otimes {{\varvec{a}}}_j \}$

$$\begin{aligned} \mathrm {Curl}_s\,{{\varvec{T}}}&= \epsilon ^{\beta \gamma }\big (T^{\alpha }_{\,\cdot \, 3|\gamma } \!+\! b^\sigma _{\gamma }\,T^{\alpha }_{\,\cdot \, \sigma } \!-\! b^\alpha _{\gamma }\,T^3_{\,\cdot \, 3} \big ) {{\varvec{a}}}_\alpha \!\otimes \!{{\varvec{a}}}_\beta + \epsilon ^{\gamma \beta }\big (T^{\alpha }_{\,\cdot \, \beta |\gamma }\! - \!b^\alpha _{\gamma }\,T^3_{\,\cdot \,\beta } \big ) {{\varvec{a}}}_\alpha \!\otimes \!{{\varvec{a}}}_3 \nonumber \\&\quad + \epsilon ^{\beta \gamma }\big (T^3_{\,\cdot \, 3,\gamma } + b_{\alpha \gamma }\,T^{\alpha }_{\,\cdot \, 3} + b^\alpha _{\gamma }\,T^3_{\,\cdot \,\alpha } \big ) {{\varvec{a}}}_3\!\otimes \!{{\varvec{a}}}_\beta + \epsilon ^{\gamma \beta }\big (T^3_{\,\cdot \,\beta |\gamma }\! + \!b_{\alpha \gamma }\,T^{\alpha }_{\,\cdot \, \beta } \big ) {{\varvec{a}}}_3\!\otimes {{\varvec{a}}}_3. \end{aligned}$$

(39)

where

$$\begin{aligned}&T^{\alpha }_{\,\cdot \, \beta |\gamma } = T^{\alpha }_{\,\cdot \, \beta ,\gamma } + \varGamma ^\alpha _{ \gamma \sigma }\, T^{\sigma }_{\,\cdot \, \beta } - \varGamma ^\sigma _{\beta \gamma }\, T^{\alpha }_{\,\cdot \, \sigma },\\&T^{\alpha }_{\,\cdot \, 3|\gamma } = T^{\alpha }_{\,\cdot \, 3,\gamma } + \varGamma ^\alpha _{\gamma \sigma }\, T^{\sigma }_{\,\cdot \, 3},\qquad T^{3}_{\,\cdot \, \beta |\gamma } = T^{3}_{\,\cdot \, \beta ,\gamma } - \varGamma ^\sigma _{\beta \gamma }\, T^{3}_{\,\cdot \, \sigma }. \end{aligned}$$

Remark 22.7

In order to obtain a formula analogous to (9) and (12), (13) for $\mathrm {Curl}_s\,$ we write ${{\varvec{T}}}$ in the form

$$\begin{aligned} {{\varvec{T}}} = {{\varvec{a}}}^i\otimes {{\varvec{T}}}_i = {{\varvec{a}}}_i\otimes {{\varvec{T}}}^i \qquad \text {with} \qquad {{\varvec{T}}}_i = T_{ij}\, {{\varvec{a}}}^j ,\quad {{\varvec{T}}}^i = T^{i}_{\,\cdot j}\,{{\varvec{a}}}^j. \end{aligned}$$

By differentiating the first equation with respect to $x_\gamma$ we get

$$\begin{aligned} {{\varvec{T}}}_{,\gamma }&= {{\varvec{a}}}^i_{\,\,, \gamma }\!\otimes \! {{\varvec{T}}}_i + {{\varvec{a}}}^i\!\otimes \! {{\varvec{T}}}_{i, \gamma } = \big (\! -\!\varGamma ^\alpha _{\beta \gamma }\,{{\varvec{a}}}^\beta + b^\alpha _{\gamma }\,{{\varvec{a}}}^3\big ) \!\otimes \! {{\varvec{T}}}_\alpha -b_{\alpha \gamma }\,{{\varvec{a}}}^\alpha \!\otimes \! {{\varvec{T}}}_3 + {{\varvec{a}}}^i\!\otimes \! {{\varvec{T}}}_{i, \gamma } \\&= {{\varvec{a}}}^\alpha \otimes \big ({{\varvec{T}}}_{\alpha , \gamma } -\varGamma ^\beta _{\alpha \gamma }\,{{\varvec{T}}}_\beta - b_{\alpha \gamma }\,{{\varvec{T}}}_3\big ) + {{\varvec{a}}}^3\otimes \big ({{\varvec{T}}}_{3, \gamma } + b^\alpha _{\gamma }\,{{\varvec{T}}}_\alpha \big ). \end{aligned}$$

Taking the vector product with ${{\varvec{a}}}^\gamma$ and using (34)$_2$ we find

$$\begin{aligned} \mathrm {Curl}_s\,{{\varvec{T}}} = - \big [ {{\varvec{a}}}^\alpha \otimes \big ({{\varvec{T}}}_{\alpha | \gamma } - b_{\alpha \gamma }\,{{\varvec{T}}}_3\big ) + {{\varvec{a}}}^3\otimes \big ({{\varvec{T}}}_{3, \gamma } + b^\alpha _{\gamma }\,{{\varvec{T}}}_\alpha \big ) \big ]\times {{\varvec{a}}}^\gamma , \end{aligned}$$

(40)

with $\,{{\varvec{T}}}_{\alpha | \gamma }\,:=\, {{\varvec{T}}}_{\alpha , \gamma } -\varGamma ^\beta _{\alpha \gamma }\,{{\varvec{T}}}_\beta \,$. Similarly, we obtain

$$\begin{aligned} \mathrm {Curl}_s\,{{\varvec{T}}} = - \big [ {{\varvec{a}}}_\alpha \otimes \big ({{\varvec{T}}}^{\alpha }_{\,\cdot \, | \gamma } - b^\alpha _{\gamma }\,{{\varvec{T}}}^3\big ) + {{\varvec{a}}}_3\otimes \big ({{\varvec{T}}}^{3}_{\,\cdot \, , \gamma } + b_{\alpha \gamma }\,{{\varvec{T}}}^\alpha \big ) \big ]\times {{\varvec{a}}}^\gamma , \end{aligned}$$

(41)

with $\,{{\varvec{T}}}^{\alpha }_{\,\cdot \, | \gamma }\,:=\, {{\varvec{T}}}^{\alpha }_{\,\cdot \, , \gamma } + \varGamma ^\alpha _{\beta \gamma }\,{{\varvec{T}}}^\beta \,$. The Eqs. (40) and (41) are the counterpart of the relations (12) and, respectively, (13) in the three-dimensional theory.

4 The Shell Dislocation Density Tensor

Let us present first the kinematics of Cosserat-type shells, which coincides with the kinematics of the 6-parameter shell model, see Chróścielewski et al. (2004), Eremeyev and Pietraszkiewicz (2006), Bîrsan and Neff (2014b).

We consider a deformable surface $\omega _\xi \subset \mathbb {R}^3$ which is identified with the midsurface of the shell in its reference configuration and denote with $(\xi _1,\xi _2,\xi _3)$ a generic point of the surface. Each material point is assumed to have 6 degrees of freedom (3 for translations and 3 for rotations). Thus, the deformation of the Cosserat-type shell is determined by a vectorial map ${{\varvec{m}}}_\xi$ and the microrotation tensor ${{\varvec{R}}}_\xi \,$

$$\begin{aligned} {{\varvec{m}}}_\xi :\omega _\xi \rightarrow \omega _c,&\quad {{\varvec{R}}}_\xi :\omega _\xi \rightarrow \mathrm {SO}(3), \end{aligned}$$

where $\omega _c$ denotes the deformed (current) configuration of the surface. We consider a parametric representation ${{\varvec{y}}}_0$ of the reference configuration $\omega _\xi$

$$\begin{aligned} {{\varvec{y}}}_0 :\omega \rightarrow \omega _\xi \,,&\quad {{\varvec{y}}}_0(x_1,x_2)=(\xi _1,\xi _2,\xi _3), \end{aligned}$$

where $\omega \subset \mathbb {R}^2$ is the bounded domain of variation (with Lipschitz boundary $\partial \omega$) of the parameters $(x_1,x_2)$. Using the same notations as in Sect. 3, we introduce the base vectors ${{\varvec{a}}}_i,\,{{\varvec{a}}}^j$ and the fundamental tensors ${{\varvec{a}}},\,{{\varvec{b}}}$ for the reference surface $\omega _\xi$.

The deformation function ${{\varvec{m}}}$ is then defined by the composition

$$\begin{aligned} {{\varvec{m}}}= {{\varvec{m}}}_\xi \circ {{\varvec{y}}}_0 :\omega \rightarrow \omega _c,&\quad {{\varvec{m}}}(x_1,x_2): = {{\varvec{m}}}_\xi \big ({{\varvec{y}}}_0(x_1,x_2)\big ). \end{aligned}$$

According to (30), the surface gradient of the deformation has the expression

$$\begin{aligned} \mathrm {Grad}_s\,{{\varvec{m}}}\, =\, {{\varvec{m}}}_{,\alpha }\otimes {{\varvec{a}}}^\alpha . \end{aligned}$$

(42)

As in the three-dimensional case (see Sect. 2) we define the elastic microrotation ${{\varvec{Q}}}_e$ by the composition

$$\begin{aligned} {{\varvec{Q}}}_e= {{\varvec{R}}}_\xi \circ {{\varvec{y}}}_0 :\omega \rightarrow \mathrm {SO}(3 ),&\quad {{\varvec{Q}}}_e ( x_1,x_2):= {{\varvec{R}}}_\xi \big ({{\varvec{y}}}_0( x_1,x_2)\big ), \end{aligned}$$

the total microrotation $\overline{{{\varvec{R}}}}$ by

$$\begin{aligned} \overline{{{\varvec{R}}}} :\omega \rightarrow \mathrm {SO}(3 ),&\quad \overline{{{\varvec{R}}}} (x_1,x_2)= {{\varvec{Q}}}_e ( x_1,x_2)\,{{\varvec{Q}}}_0 ( x_1,x_2), \end{aligned}$$

where ${{\varvec{Q}}}_0 :\omega \rightarrow \mathrm {SO}(3 )$ is the initial microrotation, which describes the orientation of points in the reference configuration.

To characterize the orientation and rotation of points in Cosserat-type shells, one employs (as in the three-dimensional case) a triad of orthonormal directors attached to each point. We denote by ${{\varvec{d}}}_i^0(x_1,x_2)$ the directors in the reference configuration $\omega _\xi$ and by ${{\varvec{d}}}_i(x_1,x_2)$ the directors in the deformed configuration $\omega _c\,$($i=1,2,3$). The domain $\omega$ is referred to an orthogonal Cartesian frame $Ox_1x_2x_3$ such that $\omega \subset Ox_1x_2\,$ and let ${{\varvec{e}}}_i\,$ be the unit vectors along the coordinate axes $Ox_i\,$. Then, the microrotation tensors can be expressed as follows

$$\begin{aligned} {{\varvec{Q}}}_e={{\varvec{d}}}_i\otimes {{\varvec{d}}}_i^0,\qquad \qquad \overline{{{\varvec{R}}}} = {{\varvec{Q}}}_e \,{{\varvec{Q}}}_0 = {{\varvec{d}}}_i\otimes {{\varvec{e}}}_i,\qquad \qquad {{\varvec{Q}}}_0 = {{\varvec{d}}}_i^0\otimes {{\varvec{e}}}_i. \end{aligned}$$

(43)

Remark 22.8

The initial directors ${{\varvec{d}}}_i^0$ are usually chosen such that

$$\begin{aligned} {{\varvec{d}}}_3^0 = {{\varvec{n}}}_0,&\quad {{\varvec{d}}}_\alpha ^0\cdot {{\varvec{n}}}_0 = 0, \end{aligned}$$

(44)

i.e. ${{\varvec{d}}}_3^0$ is orthogonal to $\omega _\xi$ and ${{\varvec{d}}}_\alpha ^0$ belong to the tangent plane. This assumption is not necessary in general, but it will be adopted here since it simplifies many of the subsequent expressions. In the deformed configuration, the director ${{\varvec{d}}}_3\,$ is no longer orthogonal to the surface $\omega _c\,$ (the Kirchhof–Love condition is not imposed). One convenient choice of the initial microrotation tensor ${{\varvec{Q}}}_0 = {{\varvec{d}}}_{i}^{0}\otimes {{\varvec{e}}}_i\,$ such that the conditions (44) be satisfied is ${{\varvec{Q}}}_0 = \mathrm {polar}\big ({{\varvec{a}}}_i\otimes {{\varvec{e}}}_i\big )$, as it was shown in Remark 10 of (Bîrsan and Neff 2014a).

Let us present next the shell strain and curvature measures. In the 6-parameter shell theory the elastic shell strain tensor ${{\varvec{E}}}_e$ is defined by (Chróścielewski et al. 2004, Eremeyev and Pietraszkiewicz 2006)

$$\begin{aligned} {{\varvec{E}}}_e\,=\, {{\varvec{Q}}}_e^T\, \mathrm {Grad}_s{{\varvec{m}}} - {{\varvec{a}}}. \end{aligned}$$

(45)

To write the components of ${{\varvec{E}}}_e$ we insert (42) and (43)$_1$ into (45)

$$\begin{aligned} {{\varvec{E}}}_e\,=\, \big ( {{\varvec{d}}}_i^0\otimes {{\varvec{d}}}_i \big )\big ( {{\varvec{m}}}_{,\alpha }\otimes {{\varvec{a}}}^\alpha \big ) - {{\varvec{a}}}_{\alpha }\otimes {{\varvec{a}}}^\alpha = \big ( {{\varvec{m}}}_{,\alpha }\cdot {{\varvec{d}}}_i- {{\varvec{a}}}_\alpha \cdot {{\varvec{d}}}_i^0 \big )\, {{\varvec{d}}}_i^0\otimes {{\varvec{a}}}^\alpha . \end{aligned}$$

As a measure of orientation (curvature) change, the elastic shell bending-curvature tensor ${{\varvec{K}}}_e$ is defined by (Chróścielewski et al. 2004, Eremeyev and Pietraszkiewicz 2006, Bîrsan and Neff 2014b)

$$\begin{aligned} {{\varvec{K}}}_e = \mathrm {axl}\big ( {{\varvec{Q}}}_e^T{{\varvec{Q}}}_{e,\alpha } \big ) \otimes {{\varvec{a}}}^\alpha = {{\varvec{Q}}}_0 \big [ \mathrm {axl}\big ( \overline{{{\varvec{R}}}}^T\overline{{{\varvec{R}}}}_{,\alpha } \big ) - \mathrm {axl}\big ( {{\varvec{Q}}}_0^T{{\varvec{Q}}}_{0,\alpha } \big ) \big ]. \end{aligned}$$

(46)

We remark the analogy to the Definition (1) of the wryness tensor ${{\varvec{\varGamma }}}$ in the three-dimensional theory. Following the analogy to (2), we employ next the surface curl operator $\mathrm {Curl}_s$ defined in Sect. 3 to introduce the new shell dislocation density tensor ${{\varvec{D}}}_e$ by

$$\begin{aligned} {{\varvec{D}}}_e = {{\varvec{Q}}}_e^T\,\mathrm {Curl}_s\,{{\varvec{Q}}}_e. \end{aligned}$$

(47)

In view of relation (34)$_2$, we can write this definition in the form

$$\begin{aligned} {{\varvec{D}}}_e = {{\varvec{Q}}}_e^T \big ({-}{{\varvec{Q}}}_{e,\alpha }\times {{\varvec{a}}}^\alpha \big )= -\big ({{\varvec{Q}}}_e^T{{\varvec{Q}}}_{e,\alpha }\big )\times {{\varvec{a}}}^\alpha . \end{aligned}$$

(48)

The tensor ${{\varvec{D}}}_e$ given by (47) represents an alternative strain measure for orientation (curvature) change in Cosserat-type shells.

In what follows, we want to establish the relationship between the shell bending-curvature tensor ${{\varvec{K}}}_e$ and the shell dislocation density tensor ${{\varvec{D}}}_e\,$. We observe that this relationship is analogous to the corresponding relations (19), (20) in the three-dimensional theory. More precisely, in the shell theory it holds

$$\begin{aligned} {{\varvec{D}}}_e = - {{\varvec{K}}}_e^T+ \big (\mathrm {tr}\,{{\varvec{K}}}_e\big ){{\varvec{1}}}_3\qquad \!\text {or equivalently,}\!\qquad {{\varvec{K}}}_e = - {{\varvec{D}}}_e^T+ \frac{1}{2}\big (\mathrm {tr}\,{{\varvec{D}}}_e\big ){{\varvec{1}}}_3. \end{aligned}$$

(49)

To prove (49), we designate the components of the shell bending-curvature tensor by ${{\varvec{K}}}_e = K_{i\alpha }\,{{\varvec{d}}}_i^0\otimes {{\varvec{a}}}^\alpha$ and use (16)$_3$ to write

$$\begin{aligned} \big ({{\varvec{Q}}}_e^T{{\varvec{Q}}}_{e,\alpha }\big )\otimes {{\varvec{a}}}^\alpha&= - {{\varvec{\epsilon }}}\, \mathrm {axl}\big ( {{\varvec{Q}}}_e^T{{\varvec{Q}}}_{e,\alpha } \big ) \otimes {{\varvec{a}}}^\alpha = - {{\varvec{\epsilon }}}\, {{\varvec{K}}}_e \\&= - \big ( e_{ijk}\, {{\varvec{d}}}_i^0 \otimes {{\varvec{d}}}_j^0 \otimes {{\varvec{d}}}_k^0 \big ) \big ( K_{s\alpha }\,{{\varvec{d}}}_s^0\otimes {{\varvec{a}}}^\alpha \big ) = - e_{ijs}\, K_{s\alpha }\,{{\varvec{d}}}_i^0 \otimes {{\varvec{d}}}_j^0 \otimes {{\varvec{a}}}^\alpha , \end{aligned}$$

which implies

$$\begin{aligned} {{\varvec{Q}}}_e^T{{\varvec{Q}}}_{e,\alpha }\,=\, - e_{ijs}\, K_{s\alpha }\,{{\varvec{d}}}_i^0 \otimes {{\varvec{d}}}_j^0 \end{aligned}$$

We substitute the last relation into (48) and derive

$$\begin{aligned} {{\varvec{D}}}_e&= \big ( e_{ijs}\, K_{s\alpha }\,{{\varvec{d}}}_i^0 \otimes {{\varvec{d}}}_j^0 \big )\times {{\varvec{a}}}^\alpha = \big ( e_{ijs}\, K_{s\alpha }\,{{\varvec{d}}}_i^0 \otimes {{\varvec{d}}}_j^0 \big )\times \big [\big ({{\varvec{a}}}^\alpha \!\cdot \!{{\varvec{d}}}^0_\beta \big )\, {{\varvec{d}}}^0_\beta \big ] \\&= \big ({{\varvec{a}}}^\alpha \!\cdot \!{{\varvec{d}}}^0_\beta \big ) \big [ e_{ijs}\, K_{s\alpha }\,{{\varvec{d}}}_i^0 \otimes \big ({{\varvec{d}}}_j^0 \times {{\varvec{d}}}^0_\beta \big )\big ] = \big ({{\varvec{a}}}^\alpha \!\cdot \!{{\varvec{d}}}^0_\beta \big ) \big [ e_{ijs}\, e_{j\beta m}\, K_{s\alpha }\,{{\varvec{d}}}_i^0 \otimes {{\varvec{d}}}_m^0 \big ] \\&= \big ({{\varvec{a}}}^\alpha \!\cdot \!{{\varvec{d}}}^0_\beta \big ) \big [ \big ( \delta _{im} \,\delta _{s\beta } - \delta _{i\beta } \,\delta _{sm}\big ) K_{s\alpha }\,{{\varvec{d}}}_i^0 \otimes {{\varvec{d}}}_m^0 \big ] \\&= \big ({{\varvec{a}}}^\alpha \!\cdot \!{{\varvec{d}}}^0_\beta \big ) \big [ - K_{s\alpha }\,{{\varvec{d}}}_\beta ^0 \otimes {{\varvec{d}}}_s^0 + K_{\beta \alpha }\,{{\varvec{d}}}_i^0 \otimes {{\varvec{d}}}_i^0 \big ] \\&= - K_{i\alpha } \big [ \big ({{\varvec{a}}}^\alpha \!\cdot \!{{\varvec{d}}}^0_\beta \big )\,{{\varvec{d}}}_\beta ^0 \big ]\otimes {{\varvec{d}}}_i^0 + K_{\beta \alpha }\big ({{\varvec{d}}}^0_\beta \!\cdot \!{{\varvec{a}}}^\alpha \big )\,{{\varvec{1}}}_3 \big ] \\&= - \big (K_{i\alpha } \, \varvec{d}_i^0\otimes {{\varvec{a}}}^\alpha \big )^T + \mathrm {tr}\big (K_{i\alpha } \, \varvec{d}_i^0\otimes {{\varvec{a}}}^\alpha \big )\,{{\varvec{1}}}_3 = - {{\varvec{K}}}_e^T+ \big (\mathrm {tr}\,{{\varvec{K}}}_e\big ){{\varvec{1}}}_3, \end{aligned}$$

which shows that (49)$_1$ holds true. Applying the trace operator to Eq. (49)$_1$ we get $\mathrm {tr}\,{{\varvec{K}}}_e = \frac{1}{2}\, \mathrm {tr}\,{{\varvec{D}}}_e\,$. Inserting this into (49)$_1$ we obtain (49)$_2\,$. The proof is complete.

Remark 22.9

As a consequence of relations (49) we deduce the relations between the norms, traces, symmetric and skew-symmetric parts of the two tensors in the forms

$$\begin{aligned}&\Vert {{\varvec{D}}}_e \Vert ^2 = \Vert {{\varvec{K}}}_e \Vert ^2 + \big (\mathrm {tr}\,{{\varvec{K}}}_e\big )^2,\qquad \Vert {{\varvec{K}}}_e \Vert ^2 = \Vert {{\varvec{D}}}_e \Vert ^2 - \dfrac{1}{4}\, \big (\mathrm {tr}\,{{\varvec{D}}}_e\big )^2,\\&\mathrm {tr}\,{{\varvec{D}}}_e = 2\, \mathrm {tr}\,{{\varvec{K}}}_e,\quad \mathrm {skew}\,{{\varvec{D}}}_e = \mathrm {skew}\,{{\varvec{K}}}_e,\quad \mathrm {dev_3sym}\,{{\varvec{D}}}_e = - \mathrm {dev_3sym}\,{{\varvec{K}}}_e.\nonumber \end{aligned}$$

(50)

Indeed the relations (50) can be easily proved if we apply the operators $\mathrm {tr}$, $\Vert \cdot \Vert$, $\mathrm {skew}$, $\mathrm {dev}_3$, and $\mathrm {sym}$ to the Eq. (49)$_1\,$. In view of (50)$_1\,$ and $\big ( \mathrm {tr}\,{{\varvec{K}}}_e\big )^2\le 3\,\Vert {{\varvec{K}}}_e \Vert ^2$, we obtain the estimate

$$\begin{aligned} \Vert {{\varvec{K}}}_e \Vert \le \Vert {{\varvec{D}}}_e \Vert \le 2\,\Vert {{\varvec{K}}}_e \Vert . \end{aligned}$$

(51)

In what follows, we write the components of the tensors ${{\varvec{K}}}_e$ and ${{\varvec{D}}}_e\,$. To this aim, we use the relations

$$\begin{aligned} {{\varvec{Q}}}_e^T{{\varvec{Q}}}_{e,\alpha }&= \big ( {{\varvec{d}}}_i^0\otimes {{\varvec{d}}}_i \big )\big ( {{\varvec{d}}}_{k,\alpha }\otimes {{\varvec{d}}}_k^0 + {{\varvec{d}}}_{k}\otimes {{\varvec{d}}}_{k,\alpha }^0 \big ) \nonumber \\&= \big ( {{\varvec{d}}}_i \cdot {{\varvec{d}}}_{k,\alpha }\big ) {{\varvec{d}}}_i^0\otimes {{\varvec{d}}}_k^0 + {{\varvec{d}}}_i^0\otimes {{\varvec{d}}}_{i,\alpha }^0 = \big ( {{\varvec{d}}}_i \cdot {{\varvec{d}}}_{k,\alpha } - {{\varvec{d}}}^0_i \cdot {{\varvec{d}}}^0_{k,\alpha }\big ) {{\varvec{d}}}_i^0\otimes {{\varvec{d}}}_k^0, \end{aligned}$$

(52)

which can be proved in the same way as Eq. (19). We compute the axial vector of the skew-symmetric tensor (52) and find (similar to (20))

$$\begin{aligned} \mathrm {axl}\big ( {{\varvec{Q}}}_e^T{{\varvec{Q}}}_{e,\alpha } \big ) = -\frac{1}{2} \, e_{ijk}\, \big ( {{\varvec{d}}}_j\cdot {{\varvec{d}}}_{k,\alpha } - {{\varvec{d}}}^0_j\cdot {{\varvec{d}}}^0_{k,\alpha } \big )\, {{\varvec{d}}}^0_i. \end{aligned}$$

(53)

By virtue of (53) the Definition (46) yields

$$\begin{aligned} {{\varvec{K}}}_e\, =&\, \frac{1}{2} \, e_{ijk}\, \big ( {{\varvec{d}}}_{j,\alpha }\cdot {{\varvec{d}}}_{k} - {{\varvec{d}}}^0_{j,\alpha }\cdot {{\varvec{d}}}^0_{k} \big )\, {{\varvec{d}}}^0_i\otimes {{\varvec{a}}}^\alpha \nonumber \\ =&\,\big ( {{\varvec{d}}}_{2,\alpha }\cdot {{\varvec{d}}}_{3} - {{\varvec{d}}}^0_{2,\alpha }\cdot {{\varvec{d}}}^0_{3} \big )\, {{\varvec{d}}}^0_1\otimes {{\varvec{a}}}^\alpha + \big ( {{\varvec{d}}}_{3,\alpha }\cdot {{\varvec{d}}}_{1} - {{\varvec{d}}}^0_{3,\alpha }\cdot {{\varvec{d}}}^0_{1} \big )\, {{\varvec{d}}}^0_2\otimes {{\varvec{a}}}^\alpha \nonumber \\&+ \big ( {{\varvec{d}}}_{1,\alpha }\cdot {{\varvec{d}}}_{2} - {{\varvec{d}}}^0_{1,\alpha }\cdot {{\varvec{d}}}^0_{2} \big )\, {{\varvec{d}}}^0_3\otimes {{\varvec{a}}}^\alpha , \end{aligned}$$

(54)

which gives the components $K_{i\alpha }$ of the shell bending-curvature tensor ${{\varvec{K}}}_e$ in the tensor basis $\{ {{\varvec{d}}}_i^0\otimes {{\varvec{a}}}^\alpha \}$.

For the components of ${{\varvec{D}}}_e$, we insert the relation (52) in the Eq. (48)

$$\begin{aligned} {{\varvec{D}}}_e = - \big ( {{\varvec{d}}}_i \cdot {{\varvec{d}}}_{k,\alpha } - {{\varvec{d}}}^0_i \cdot {{\varvec{d}}}^0_{k,\alpha }\big )\big ( {{\varvec{d}}}_i^0\otimes {{\varvec{d}}}_k^0\big )\times {{\varvec{a}}}^\alpha . \end{aligned}$$

Using that $\,{{\varvec{d}}}_k^0 \times {{\varvec{a}}}^\alpha = {{\varvec{d}}}_k^0\times \big [\big ({{\varvec{a}}}^\alpha \!\cdot \!{{\varvec{d}}}^0_\beta \big )\, {{\varvec{d}}}^0_\beta \big ]= \big ({{\varvec{a}}}^\alpha \!\cdot \!{{\varvec{d}}}^0_\beta \big )\,e_{k\beta j}\,{{\varvec{d}}}_j^0\,$, we obtain

$$\begin{aligned} {{\varvec{D}}}_e = e_{jk\beta }\big ( {{\varvec{d}}}_{i,\alpha } \cdot {{\varvec{d}}}_{k} - {{\varvec{d}}}^0_{i,\alpha } \cdot {{\varvec{d}}}^0_{k}\big )\big ({{\varvec{a}}}^\alpha \!\cdot \!{{\varvec{d}}}^0_\beta \big )\, {{\varvec{d}}}_i^0\otimes {{\varvec{d}}}_j^0\,, \end{aligned}$$

(55)

which shows the components of the shell dislocation density tensor in the tensor basis $\{ {{\varvec{d}}}_i^0\otimes {{\varvec{d}}}_j^0 \}$.

5 Remarks and Discussion

Herein we present some other ways to express the shell dislocation density tensor, the shell bending-curvature tensor and discuss their close relationship.

Remark 22.10

It is sometimes useful to express the components of the shell dislocation density tensor ${{\varvec{D}}}_e\,$ in the tensor basis $\{ {{\varvec{a}}}^i\otimes {{\varvec{a}}}_j \}$. If we multiply the relation (49)$_2$ with ${{\varvec{n}}}_0$ and take into account that ${{\varvec{K}}}_e {{\varvec{n}}}_0 = {{\varvec{0}}}$, then we find ${{\varvec{0}}} = - {{\varvec{D}}}^T_e {{\varvec{n}}}_0 + \frac{1}{2}\,\big ( \mathrm {tr}\,{{\varvec{D}}}_e\big ){{\varvec{n}}}_0 \,$, which means

$$\begin{aligned} {{\varvec{n}}}_0 \, {{\varvec{D}}}_e\, =\, \frac{1}{2}\,\big ( \mathrm {tr}\,{{\varvec{D}}}_e\big ){{\varvec{n}}}_0. \end{aligned}$$

It follows that the components of ${{\varvec{D}}}_e\,$ in the directions ${{\varvec{n}}}_0\otimes {{\varvec{a}}}_\alpha \,$ are zero, i.e. ${{\varvec{D}}}_e\,$ has the structure

$$\begin{aligned} {{\varvec{D}}}_e = {{\varvec{D}}}_\Vert + D_{\alpha 3}\, {{\varvec{a}}}^\alpha \otimes {{\varvec{n}}}_0 + \frac{1}{2}\,\big ( \mathrm {tr}\,{{\varvec{D}}}_e\big ){{\varvec{n}}}_0\otimes {{\varvec{n}}}_0, \end{aligned}$$

(56)

where $\,{{\varvec{D}}}_\Vert = {{\varvec{D}}}_e\, {{\varvec{a}}} = D^{\alpha \beta }{{\varvec{a}}}_\alpha \otimes {{\varvec{a}}}_\beta = D_{\alpha \,\cdot }^{\,\,\,\,\beta }\,{{\varvec{a}}}^\alpha \otimes {{\varvec{a}}}_\beta$ is the planar part of ${{\varvec{D}}}_e\,$ (the part in the tangent plane). If we insert (56) into (49)$_1$ and use $\,\frac{1}{2}\, \mathrm {tr}\,{{\varvec{D}}}_e = \mathrm {tr}\,{{\varvec{K}}}_e$, we get

$$\begin{aligned} {{\varvec{D}}}_\Vert + D_{\alpha 3}\, {{\varvec{a}}}^\alpha \otimes {{\varvec{n}}}_0 + \big ( \mathrm {tr}\,{{\varvec{K}}}_e\big ){{\varvec{n}}}_0\otimes {{\varvec{n}}}_0 = -K_{i\alpha }\,{{\varvec{a}}}^\alpha \otimes {{\varvec{d}}}_i^0 + \big ( \mathrm {tr}\,{{\varvec{K}}}_e\big ) \big ( {{\varvec{a}}} +{{\varvec{n}}}_0\otimes {{\varvec{n}}}_0 \big ), \end{aligned}$$

which implies (in view of (54)) that

$$\begin{aligned} D_{\alpha 3} = -K_{3\alpha } = {{\varvec{d}}}_{1}\cdot {{\varvec{d}}}_{2,\alpha } - {{\varvec{d}}}^0_{1}\cdot {{\varvec{d}}}^0_{2,\alpha }\qquad \!\text {and}\qquad \! {{\varvec{D}}}_\Vert = - \big ({{\varvec{K}}}_\Vert \big )^T+ \big (\mathrm {tr}\,{{\varvec{K}}}_e\big ){{\varvec{a}}}, \end{aligned}$$

(57)

where $\,{{\varvec{K}}}_\Vert \,= {{\varvec{a}}}\,{{\varvec{K}}}_e\, = K_{\beta \alpha }{{\varvec{d}}}^0_\beta \otimes {{\varvec{a}}}^\alpha$ is the planar part of ${{\varvec{K}}}_e$.

Remark 22.11

We observe that between the planar part $\,{{\varvec{D}}}_\Vert \,$ of $\,{{\varvec{D}}}_e\,$ and the planar part $\,{{\varvec{K}}}_\Vert \,$ of $\,{{\varvec{K}}}_e\,$ there exists a special relationship. The tensor $\,{{\varvec{D}}}_\Vert \,$ is the cofactor of the tensor $\,{{\varvec{K}}}_\Vert \,$. Let us explain this in more details: for any planar tensor ${{\varvec{S}}} = S^\alpha _{\,\cdot \,\beta }\,{{\varvec{a}}}_\alpha \otimes {{\varvec{a}}}^\beta$ we introduce the transformation

$$\begin{aligned} T( {{\varvec{S}}} ) = - {{\varvec{S}}}^T + \big ( \mathrm {tr}\,{{\varvec{S}}}\big )\,{{\varvec{a}}}. \end{aligned}$$

(58)

One can prove that this transformation has the properties

$$\begin{aligned} T\big (T( {{\varvec{S}}})\big ) = {{\varvec{S}}}\qquad \qquad \text {and}\qquad \qquad T( {{\varvec{S}}} ) = - {{\varvec{c}}} \,{{\varvec{S}}}\, {{\varvec{c}}}, \end{aligned}$$

(59)

where the alternator ${{\varvec{c}}}$ is defined in (31). Moreover, in view of (59)$_2$ and (31) we can write $T( {{\varvec{S}}} )$ in the tensor basis $\{ {{\varvec{a}}}^\alpha \otimes {{\varvec{a}}}_\beta \}$ as follows

$$\begin{aligned} T( {{\varvec{S}}} ) = S^2_{\,\cdot \, 2}\,{{\varvec{a}}}^1\otimes {{\varvec{a}}}_1 - S^2_{\,\cdot \, 1}\,{{\varvec{a}}}^1\otimes {{\varvec{a}}}_2 - S^1_{\,\cdot \, 2}\,{{\varvec{a}}}^2\otimes {{\varvec{a}}}_1 + S^1_{\,\cdot \, 1}\,{{\varvec{a}}}^2\otimes {{\varvec{a}}}_2, \end{aligned}$$

which shows that the $2\times 2$ matrix of the components of $T({{\varvec{S}}})$ in the basis $\{ {{\varvec{a}}}^\alpha \otimes {{\varvec{a}}}_\beta \}$ is the cofactor of the matrix of components of ${{\varvec{S}}}$ in the basis $\{ {{\varvec{a}}}_\alpha \otimes {{\varvec{a}}}^\beta \}$, since

$$\begin{aligned} \left( \begin{array}{cc} S^2_{\,\cdot \, 2} &{} \,\,- S^2_{\,\cdot \, 1} \\ - S^1_{\,\cdot \, 2} &{} \,\,S^1_{\,\cdot \, 1} \end{array} \right) = \mathrm {Cof} \left( \begin{array}{cc} S^1_{\,\cdot \, 1} &{} \,\,S^1_{\,\cdot \, 2} \\ S^2_{\,\cdot \, 1} &{} \,\, S^2_{\,\cdot \, 2} \end{array} \right) . \end{aligned}$$

If the tensor ${{\varvec{S}}}$ is invertible, then from the Cayley–Hamilton relation $\big ( {{\varvec{S}}}^T\big )^2 - \big ( \mathrm {tr}\,{{\varvec{S}}}\big ){{\varvec{S}}}^T + \mathrm {det} {{\varvec{S}}} = {{\varvec{0}}}$ and (58) we deduce

$$\begin{aligned} T( {{\varvec{S}}}) = - {{\varvec{S}}}^T + \big ( \mathrm {tr}\,{{\varvec{S}}}\big )\,{{\varvec{a}}} = \big ( \mathrm {det} {{\varvec{S}}}\big )\,{{\varvec{S}}}^{-T} =: \mathrm {Cof}\big ( {{\varvec{S}}}\big ). \end{aligned}$$

(60)

In our case, for the shell bending-curvature tensor ${{\varvec{K}}}_e$ we have $\mathrm {tr}\, {{\varvec{K}}}_e = \mathrm {tr}\big ({{\varvec{a}}} {{\varvec{K}}}_e\big ) = \mathrm {tr}\big ( {{\varvec{K}}}_\Vert \big )$, in view of (54). Then, the relation (57)$_2$ yields

$$\begin{aligned} {{\varvec{D}}}_\Vert = - \big ({{\varvec{K}}}_\Vert \big )^T+ \big (\mathrm {tr}\,{{\varvec{K}}}_\Vert \big )\,{{\varvec{a}}}. \end{aligned}$$

Using the relations (58)–(60) we see that $\,{{\varvec{D}}}_\Vert \,$ is the image of $\,{{\varvec{K}}}_\Vert \,$ under the transformation T, so that it holds

$$\begin{aligned} {{\varvec{D}}}_\Vert = T\big ({{\varvec{K}}}_\Vert \big ) = - {{\varvec{c}}} \,\big ({{\varvec{K}}}_\Vert \big )\, {{\varvec{c}}} = \mathrm {Cof}\big ( {{\varvec{K}}}_\Vert \big ),\\ {{\varvec{K}}}_\Vert = T\big ({{\varvec{D}}}_\Vert \big ) = - {{\varvec{c}}} \,\big ({{\varvec{D}}}_\Vert \big )\, {{\varvec{c}}} = \mathrm {Cof}\big ( {{\varvec{D}}}_\Vert \big ). \nonumber \end{aligned}$$

(61)

From (56), (57) we can write

$$\begin{aligned} {{\varvec{D}}}_e = \mathrm {Cof}\big ( {{\varvec{K}}}_\Vert \big ) - K_{ 3\alpha }\, {{\varvec{a}}}^\alpha \otimes {{\varvec{n}}}_0 + \big ( \mathrm {tr}\,{{\varvec{K}}}_\Vert \big ){{\varvec{n}}}_0\otimes {{\varvec{n}}}_0, \end{aligned}$$

(62)

which expresses once again the close relationship between the shell dislocation density tensor ${{\varvec{D}}}_e\,$ and the shell bending-curvature tensor ${{\varvec{K}}}_e$.

Remark 22.12

The shell bending-curvature tensor ${{\varvec{K}}}_e\,$ can also be expressed in terms of the directors ${{\varvec{d}}}_i\,$. In this respect, an analogous relation to the formula (28) for the wryness tensor (see Remark 22.5) holds

$$\begin{aligned} {{\varvec{K}}}_e \, = \, \,\frac{1}{2}\, \big [ {{\varvec{Q}}}_e^T \big ({{\varvec{d}}}_{i}\times {{\varvec{d}}}_{i,\alpha }\big ) - {{\varvec{d}}}^0_{i}\times {{\varvec{d}}}^0_{i,\alpha } \big ]\otimes {{\varvec{a}}}^\alpha . \end{aligned}$$

(63)

To prove (63), we write the two terms in the brackets in the following form

$$\begin{aligned} {{\varvec{Q}}}_e^T \big ({{\varvec{d}}}_{i}\times {{\varvec{d}}}_{i,\alpha }\big )&= \big ({{\varvec{d}}}_{k}^0\otimes {{\varvec{d}}}_{k}\big )\big ({{\varvec{d}}}_{i}\times {{\varvec{d}}}_{i,\alpha }\big ) = \big [{{\varvec{d}}}_{k}\cdot \big ({{\varvec{d}}}_{i}\times {{\varvec{d}}}_{i,\alpha }\big )\big ]\, {{\varvec{d}}}_{k}^0 \\&= \big [ {{\varvec{d}}}_{i,\alpha } \cdot \big ({{\varvec{d}}}_{k} \times {{\varvec{d}}}_{i} \big )\big ]\, {{\varvec{d}}}_{k}^0 = e_{kij}\,\big ({{\varvec{d}}}_{i,\alpha }\cdot {{\varvec{d}}}_{j}\big )\, {{\varvec{d}}}_{k}^0 \end{aligned}$$

and similarly

$$\begin{aligned} {{\varvec{d}}}^0_{i}\times {{\varvec{d}}}^0_{i,\alpha } = \big [{{\varvec{d}}}_{k}^0\cdot \big ({{\varvec{d}}}^0_{i}\times {{\varvec{d}}}^0_{i,\alpha }\big )\big ]\, {{\varvec{d}}}_{k}^0 = \big [ {{\varvec{d}}}^0_{i,\alpha } \cdot \big ({{\varvec{d}}}^0_{k} \times {{\varvec{d}}}^0_{i} \big )\big ]\, {{\varvec{d}}}_{k}^0 = e_{kij}\,\big ({{\varvec{d}}}^0_{i,\alpha }\cdot {{\varvec{d}}}^0_{j}\big )\, {{\varvec{d}}}_{k}^0. \end{aligned}$$

Inserting the last two relations into (63) we obtain

$$\begin{aligned} {{\varvec{K}}}_e \, = \, \,\frac{1}{2}\, e_{ijk}\, \big [\big ( {{\varvec{d}}}_{j,\alpha }\cdot {{\varvec{d}}}_{k} \big )\, {{\varvec{d}}}^0_i - \big ({{\varvec{d}}}^0_{j,\alpha }\cdot {{\varvec{d}}}^0_{k} \big )\, {{\varvec{d}}}^0_i \big ]\otimes {{\varvec{a}}}^\alpha , \end{aligned}$$

which holds true, by virtue of (54). Thus, (63) is proved.

We can put the relation (63) in the form

$$\begin{aligned}&{{\varvec{K}}}_e \, = \, {{\varvec{Q}}}_e^T \,{{\varvec{\omega }}}\qquad \text {where we define} \end{aligned}$$

(64)

$$\begin{aligned}&{{\varvec{\omega }}}= {{\varvec{\omega }}}_\alpha \otimes {{\varvec{a}}}^\alpha \qquad \text {with}\qquad {{\varvec{\omega }}}_\alpha = \,\frac{1}{2}\, \big [ {{\varvec{d}}}_{i}\times {{\varvec{d}}}_{i,\alpha } - {{\varvec{Q}}}_e \big ( {{\varvec{d}}}^0_{i}\times {{\varvec{d}}}^0_{i,\alpha }\big ) \big ]. \end{aligned}$$

(65)

If we compare the relations (64) and the Definition (46), we derive

$$\begin{aligned} {{\varvec{\omega }}}_\alpha = {{\varvec{Q}}}_e\,\mathrm {axl}\big ( {{\varvec{Q}}}_e^T{{\varvec{Q}}}_{e,\alpha } \big ) = \mathrm {axl}\big ( {{\varvec{Q}}}_{e,\alpha } \,{{\varvec{Q}}}_e^T \big ). \end{aligned}$$

Then, from (16) we deduce $\,\,\, {{\varvec{Q}}}_{e,\alpha } \,{{\varvec{Q}}}_e^T = {{\varvec{\omega }}}_\alpha \times {{\varvec{1}}}_3 \,\,\,$ and by multiplication with $\,{{\varvec{Q}}}_e\,$ we find

$$\begin{aligned} {{\varvec{Q}}}_{e,\alpha } \,= \, {{\varvec{\omega }}}_\alpha \times {{\varvec{Q}}}_e,\qquad \qquad&\alpha =1,2. \end{aligned}$$

(66)

Thus, the Eqs. (64), (65) can be employed for an alternative definition of the shell bending-curvature tensor, namely

$$\begin{aligned} {{\varvec{K}}}_e \, = \, {{\varvec{Q}}}_e^T \,{{\varvec{\omega }}}\,,\qquad \text {where}\qquad \! {{\varvec{\omega }}}= {{\varvec{\omega }}}_\alpha \otimes {{\varvec{a}}}^\alpha \!\!\qquad \text {and}\qquad \!\! {{\varvec{Q}}}_{e,\alpha } \,= \, {{\varvec{\omega }}}_\alpha \times {{\varvec{Q}}}_e. \end{aligned}$$

(67)

This is the counterpart of the relations (24), (25) for the wryness tensor in the three-dimensional theory of Cosserat continua. The relations (67) were used to define the corresponding shell bending-curvature tensor, e.g. in Altenbach and Zhilin (2004), Zhilin (2006).

Remark 22.13

As shown by relations (3) for the three-dimensional case, one can introduce the elastically stored shell energy density W as a function of the shell strain tensor and the shell dislocation density tensor

$$\begin{aligned} W=W\big ({{\varvec{E}}}_e \,,\, {{\varvec{D}}}_e \big ). \end{aligned}$$

(68)

If (68) is assumed to be a quadratic convex and coercive function, then the existence of solutions to the minimization problem of the total energy functional for Cosserat shells can be proved in a similar manner as in Theorem 6 of Bîrsan and Neff (2014a). In the proof, one should employ decisively the estimate (51) and the expressions of the shell dislocation density tensor $\, {{\varvec{D}}}_e\,$ established in the previous sections.