Abstract
We present a new way to discretize a geometrically nonlinear elastic planar Cosserat shell. The kinematical model is similar to the general six-parameter resultant shell model with drilling rotations. The discretization uses geodesic finite elements (GFEs), which leads to an objective discrete model which naturally allows arbitrarily large rotations. GFEs of any approximation order can be constructed. The resulting algebraic problem is a minimization problem posed on a nonlinear finite-dimensional Riemannian manifold. We solve this problem using a Riemannian trust-region method, which is a generalization of Newton’s method that converges globally without intermediate loading steps. We present the continuous model and the discretization, discuss the properties of the discrete model, and show several numerical examples, including wrinkling of thin elastic sheets in shear.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
We consider the numerical treatment of a geometrically nonlinear hyperelastic planar Cosserat shell model. This model has been obtained by dimensional reduction from a full three-dimensional Cosserat continuum model. Its degrees of freedom are the displacement m of the shell midsurface, together with the orientation of an orthonormal director triple \(\overline{R}\) at each point. Consequently, if \(\omega \) denotes the two-dimensional parameter domain, configurations of such a shell are pairs of functions
of suitable smoothness, where \(\text {SO}(3),\) the special orthogonal group, is the set of orthogonal \(3 \times 3\) matrices with determinant 1. We consider a hyperelastic material law of the form
where \(W_\mathrm{mp}\) is the membrane energy, \(W_\mathrm{bend}\) is the bending energy, and \(W_\mathrm{curv}\) is a curvature term depending only on the orientation field \(\overline{R}.\) This energy, originally proposed in [31, 34], is a second-order model, frame-invariant, and allows for large elastic strains and finite rotations. The membrane contribution \(W_\mathrm{mp}\) is polyconvex, and uniformly Legendre–Hadamard-elliptic. Existence of minimizers in the space \(H^1(\omega ,\,{\mathbb {R}}^3) \times W^{1,q}(\omega ,\,\text {SO}(3))\) has been shown in [31, 34] for any \(q\ge 2.\)
In this article we consider planar shells only, i.e., we assume that the undeformed configuration \((m_0,\,\overline{R}_0){\text {:}}\, (x,\,y) \mapsto ((x,\,y,\,0),\,\text {Id})\) is a stress-free state. However, our numerical treatment can also be generalized to a general nonplanar shell model. We arrive at the planar model in two steps: first, dimensional reduction of a parent three-dimensional Cosserat model yields a shell model with a quadratic membrane energy, suitable only for small membrane strains. We then generalize this shell model to obtain the finite-strain membrane term.
The shell formulation presented here is closely related to the theory of six-parameter shells with drilling rotations [12, 18, 27, 50]. A detailed comparison between the two approaches in the case of plates has been given in [6, 7], where we have shown existence results for isotropic, orthotropic, and composite plates. In [10] we have adapted the methods of [31] to prove the existence of minimizers for geometrically nonlinear six-parameter shells. In [9] we have considered shells insensitive to drilling rotations, and established a useful representation theorem for this case (corresponding to the Cosserat couple modulus \(\mu _c=0\)). Readers that are used to the notation used in the engineering literature may find [9, 10] a more accessible description of our shell model.
We also mention that the kinematic assumption underlying our Cosserat shell formulation is similar to the one used in describing a viscoelastic membrane, see [32, 49]. Indeed, the viscoelastic membrane is based on the same kinematics, but the independent rotations are evolving through a local evolution equation, whereas for the Cosserat planar shell model, they are determined by energy minimization.
Problems with directional or orientational degrees of freedom are notoriously difficult to discretize. This difficulty is caused by the nonlinearity of the orientation configuration space \(W^{1,q}(\omega ,\,\text {SO}(3))\) (or, in fact, any space of functions mapping into \(\text {SO}(3)\)). As a consequence, discretization methods based on piecewise linear or piecewise polynomial functions cannot be formulated directly for such spaces. Instead, previous discretizations have used ad hoc approaches, each with its particular shortcomings.
An obvious approach uses Euler angles to describe the rotations, and finite elements (FEs) to discretize the angles [54]. However, this leads to instabilities near certain configurations, and such models are suitable only for situations with moderately large rotations [22]. Also, the resulting discrete models are generally not objective.
Alternatively, rotations can be interpolated by means of the Lie algebra \({\mathfrak {so}}(3),\) i.e., the tangent space at the identity rotation. A rotation \(R \in \text {SO}(3)\) is represented as a rotation vector \(a \in {\mathfrak {so}}(3)\) with \(R = \exp a.\) Since \({\mathfrak {so}}(3)\) is a linear space, the rotation vectors a can be interpolated normally using FEs of first or higher order [28, 29]. This approach works only for orientation values bounded away from the cut locus of the identity rotation. To deal with larger rotations, [29] switches to a different tangent space when large rotations are detected.
Unfortunately, using a fixed tangent space for interpolation introduces a preferred direction into the discrete model. The discrete solution therefore depends on the orientation of the observer, and objectivity is not preserved.
For their model of a shell with a single director, Simo and Fox [43] propose to avoid nonlinear interpolation altogether. Instead, they introduce the director vector directions at the quadrature points as separate variables [45]. The discrete problem is solved using a Newton method. After each Newton step, the correction is interpolated from the vertices to the quadrature points. This is easily possible, since the corrections are elements of a tangent space (and hence a linear space). A similar approach is used in [15, 16] in the context of isogeometric analysis, where NURBS basis functions are employed for a geometrically exact representation of the director vector at the quadrature points. However, for a related model [44], Crisfield and Jelenić [14] showed that this approach leads to an artificial path dependence of the solution. An additional disadvantage is that discretization and solution algorithm are not clearly separated. This makes analyzing the method difficult.
One last approach regards the manifold \(\text {SO}(3)\) as a submanifold of a linear space. One can then interpolate in this space, and project the result back onto the manifold. To the knowledge of the authors this approach has never been used for shell models. For harmonic maps into the unit sphere it has been proposed and analyzed in [4]. The approach is attractive for its simplicity. However, the result of the discrete problem depends on the embedding. This is of particular importance in the case of rotations, which can be interpreted as a submanifold of \({\mathbb {R}}^{3 \times 3}\) (in which case the projection is the polar decomposition), but also (as quaternions) as a submanifold of \({\mathbb {R}}^4\) (see “Quaternion coordinates for SO(3)” in Appendix). Furthermore, the approach has only been investigated for discretizations of first order, and it is unclear whether higher approximation orders are possible as well.
In this article we propose a new discretization based on geodesic FEs (GFEs), which solves most of the shortcomings of the previous methods. GFE, originally introduced in [40, 41], are a natural generalization of standard Lagrangian FEs to spaces of functions mapping into a general Riemannian manifold M. The core idea is to write Lagrangian interpolation \(T_\mathrm{ref} \rightarrow {\mathbb {R}}\) of values \(v_1,\ldots ,v_m \in {\mathbb {R}}\) on a reference element \(T_\mathrm{ref}\) as a minimization problem
where the \(\lambda _1, \ldots , \lambda _m{\text {:}}\,T_\mathrm{ref} \rightarrow {\mathbb {R}}\) are the Lagrangian shape functions. For values \(v_1, \ldots , v_m\) in a Riemannian manifold M, this formulation can be generalized using the Riemannian distance
This construction is also known as the Karcher mean [24] or the Riemannian center of mass. It forms the basis of a general FE theory for functions mapping into a manifold M [40, 41]. FE spaces constructed this way are conforming in the sense that FE functions belong to the Sobolev space \(W^{1,q}(\omega ,\,M)\) for all \(q \ge 2.\) Since their formulation is based on metric properties of M, they are naturally equivariant under isometries of M. Optimal a priori discretization error bounds have been given in [20].
When using this technique for the case \(M = \text {SO}(3)\) considered here (but the same holds also when discretizing one-director models with \(M=S^2\) such as the one proposed in [43]), the resulting discrete model has many desirable properties. Since the FE spaces are conforming, there is no consistency error introduced when evaluating the continuous energy for FE functions. Since no angles and no “special orientations” appear in the discretization, the discrete model is not restricted to small or moderate rotations. Indeed, as we demonstrate in Sect. 6.3, arbitrary rotations in the deformation can be handled with ease. Finally, from the equivariance of the nonlinear interpolation follows that the frame invariance of the continuous model (1) is preserved by the discretization, and we obtain a completely frame-invariant discrete problem.
As an additional advantage, the fact that the FE space is contained in the continuous Ansatz space \(H^1(\omega ,\,{\mathbb {R}}^3) \times W^{1,q}(\omega ,\,\text {SO}(3))\) implies that properties of the tangent matrix can be inferred from corresponding properties of the continuous tangent operator. In particular, we directly obtain symmetry of the tangent matrix. The tangent matrix is positive definite if the continuous tangent operator is.
The algebraic formulation corresponding to the discrete problem is a minimization problem posed in the product space \({\mathcal {M}} :={\mathbb {R}}^{3N} \times \text {SO(3)}^N,\) where N is the number of Lagrange nodes of the grid. The space \({\mathcal {M}}\) is a 6N-dimensional Riemannian manifold. To solve this minimization problem we use a Riemannian trust-region algorithm [1], which is a globalized Newton method. As such, it is guaranteed to converge to at least a stationary point of the algebraic energy for any initial iterate, and without using intermediate loading steps. At each step of the method, a constrained quadratic minimization problem needs to be solved. We propose to use a monotone multigrid method [26, 40], which allows efficient and robust solutions of the constrained problems even on fine grids. As a variant of the Newton method, the trust-region algorithm requires tangent matrices of the energy. We obtain those matrices completely automatically by using automatic differentiation (AD) as implemented in the software ADOL-C [19, 48].
In this article we show four numerical examples. First, we simulate bending of a clamped beam using GFEs of different orders. The result shows that shear locking does not occur unless we are using first-order elements for the deformation. Then, we compute the post-critical behavior of an L-shaped beam. This was posed as a benchmark problem in [3, 44, 45, 54], and we compare our results with results given there. Thirdly, we demonstrate that our discretization does indeed allow unrestricted rotations. For this we simulate a long elastic strip, which we clamp on one short end, and subject it to several full rotations at the other end. Finally, to show that the Cosserat shell model can represent non-classical microstructure effects, we use it to produce wrinkles in a sheared rectangular membrane. Such shearing tests have been performed experimentally by [52], and we obtain excellent quantitative agreement with their results.
This article is structured as follows: In Sect. 2 we present the continuous model and discuss a few of its properties. Section 3 introduces the GFE method, specialized for the case \(M=\text {SO(3)}\) needed for the Cosserat shell model. Section 4 discusses the resulting discrete and algebraic models. Section 5 explains the Riemannian trust-region method used to find energy minimizers without loading steps. Section 6 gives the four numerical examples. Finally, an Appendix collects various important facts about \(\text {SO}(3)\) needed to implement the GFE method.
2 The continuous Cosserat shell model
In this chapter we present the planar Cosserat shell model and discuss its features. The detailed derivation of the shell model from a three-dimensional parent Cosserat model was presented in the papers [31, 34]. The intermediate shell model for infinitesimal strain is described in Sect. 2.1. The complete finite-strain model is then introduced in Sect. 2.2.
2.1 The small-strain planar Cosserat shell model
We consider a thin domain \(\Omega _h \subset {\mathbb {R}}^3\) of the form \(\Omega _h=\omega \times [{-}h/2,\,h/2],\) where \(\omega \) is a bounded domain in \({\mathbb {R}}^2\) with smooth boundary \(\partial \omega ,\) and \(h>0\) is the thickness of the planar shell. The domain \(\Omega _h\) is the region occupied by the reference configuration of the parent 3D Cosserat continuum. Let \(\{e_1,\,e_2,\,e_3\}\) be the unit vectors along the axes of the reference Cartesian coordinate system, denote by \(\varphi {\text {:}}\,\Omega _h \rightarrow {\mathbb {R}}^3\) the deformation, and by \(\overline{R}{\text {:}}\,\Omega _h\rightarrow \mathrm {SO}(3)\) the independent microrotation of this micropolar continuum.
For the planar shell model we want to find a reasonable approximation \((\varphi _s,\,\overline{R}_s)\) of \((\varphi ,\,\overline{R})\) involving only two-dimensional quantities, i.e., expressed with the help of functions of the in-plane coordinates \((x,\,y).\) Therefore, we assume a quadratic Ansatz in the thickness coordinate z for the finite deformation \(\varphi _s{\text {:}}\,\Omega _h\rightarrow {\mathbb {R}}^3\)
Here \(m{\text {:}}\,\omega \rightarrow {\mathbb {R}}^3\) describes the deformation of the midsurface of the shell, and \(\varvec{d}{\text {:}}\,\omega \rightarrow {\mathbb {R}}^3\) is an independent unit director. We assume the rotations \(\overline{R}_s{\text {:}}\,\Omega _h\rightarrow \mathrm {SO}(3)\) for thin and homogeneous shells to be independent of the thickness variable z, i.e.,
and we specialize the independent unit director \(\varvec{d}\) in the Ansatz (2) by choosing
Thus, the director \(\varvec{d}(x,\,y)\) is taken as the third column of the orthogonal matrix \(\overline{R}_s(x,\,y),\) and the model now also includes drilling rotations about the director \(\varvec{d}.\) The drilling rotations are determined by the first two columns of \(\overline{R}_s.\) For the sake of simplicity, we drop the index s and write \(\overline{R} \) instead of \(\overline{R}_s\) in what follows.
When the director \(\varvec{d}(x,\,y)\) is not normal to the midsurface \(m(x,\,y),\) then transverse shear deformation occurs. The scalar functions \(\rho _m,\,\rho _b{\text {:}}\,\omega \rightarrow {\mathbb {R}}\) in (2) describe the symmetric thickness stretch (for \(\rho _m\ne 1\)) and the asymmetric thickness stretch (for \(\rho _b\ne 0\)) about the midsurface. The scalar field \(\rho _m\) is mainly membrane related, while \(\rho _b\) is mainly bending related. Imposing that the stress vectors on the upper and lower surfaces of the shell have zero normal components (which is a common assumption in the theory of shells, see, e.g., [46], Sect. 5), we obtain the following expressions for \(\varrho _m\) and \(\varrho _b\) [31]
where the parameters \(\lambda ,\,\mu > 0\) are the Lamé constants of classical isotropic elasticity, and \(N_{\mathrm {res}},\,N_{\mathrm {diff}}{\text {:}}\,\omega \rightarrow {\mathbb {R}}^3\) are defined in terms of the prescribed tractions \(N^{\mathrm {trans}}\) on the transverse boundaries \(z={\pm } h/2\) by
The strain measures for the planar Cosserat shell model are the following: the micropolar non-symmetric stretch tensor \(\overline{U}\) is defined as
while the micropolar curvature tensor \({\mathfrak {K}}_s\) (of third order) and the micropolar bending tensor \({\mathfrak {K}}_b\) (of second order) are given by
We have used the superposed caret and bars for \(\hat{F},\, \overline{R},\,\overline{U}\) in order to distinguish these tensors from the classical notations in 3D elasticity for deformation gradient F, the continuum rotation \(R=\text {polar}(F),\) and the symmetric continuum stretch tensor \(U=R^TF=\sqrt{F^TF}.\)
We mention that the kinematical structure of this Cosserat shell model is in fact equivalent to the kinematical structure of nonlinear six-parameter resultant shell theory [12, 18, 27], as it was pointed out in [7–10].
As a result of the dimensional reduction procedure, the following two-dimensional minimization problem for the deformation of the midsurface \(m{\text {:}}\,\omega \rightarrow {\mathbb {R}}^3\) and the microrotation field \(\overline{R}{\text {:}}\,\omega \rightarrow \text {SO(3)}\) is obtained [31]:
Problem 1
Find a pair \((m,\,\overline{R})\) that minimizes the functional
subject to suitable boundary conditions for the deformation and rotation.
The three parts of the total elastically stored energy density of the shell correspond to membrane-strain \(W_{\mathrm{mp}},\) total curvature-strain \(W_{\mathrm{curv}}\) and specific bending-strain \(W_{\mathrm{bend}}.\) They have the expressions
where the additional parameter \(\mu _c\ge 0 \) is called the Cosserat couple modulus, and \(\kappa \) is a shear correction factor (\(0<\kappa \le 1\)). For \(\mu _c > 0\) the elastic strain energy density \(W_{\mathrm {mp}}(\overline{U})\) is uniformly convex in \(\overline{U},\) but for the important case \(\mu _c = 0\) this property is lost. Therefore, the case \(\mu _c = 0\) must be investigated separately. In the curvature energy density \(W_\mathrm{curv},\) the parameter \(L_c > 0\) is an internal length which is characteristic for the material, and is responsible for size effects. Note that \(W_{\mathrm {curv}}\) is a specific contribution which is strictly related to the new Cosserat effects and should not be confused with the bending terms. We mention that this is a first-order model, i.e., no second or higher derivatives of the independent variables m and \(\overline{R}\) appear. Also, the energy depends on the midsurface deformation m and microrotations \(\overline{R}\) only through the frame-indifferent measures \(\overline{U}\) and \({\mathfrak {K}}_s.\) Thus, in the absence of external forces, the planar shell model is fully frame-indifferent in the sense that
The reduced external loading functional \(\Pi (m,\,\overline{R}_3)\) appearing in (3) is a linear form in \((m,\,\overline{R}_3),\) defined in terms of the underlying three-dimensional loads by
where \(\gamma _s\times \left[ {-}\frac{h}{2},\,\frac{h}{2}\right] \subset \partial \omega \times \left[ {-}\frac{h}{2},\,\frac{h}{2}\right] \) is the part of the lateral boundary of \(\Omega _h\) where external surface forces and couples are prescribed. The vector fields \(\overline{f},\, \overline{M},\, \overline{N} \) and \(\overline{M}_c\) denote the resultant body force, resultant body couple, resultant surface traction and resultant surface couple, respectively [31].
For the Dirichlet boundary conditions we suppose that there exists a prescribed function \(g_d{\text {:}}\,\Omega _h \rightarrow {\mathbb {R}}^3,\) whose restriction to the Dirichlet part of the boundary gives the prescribed displacement. We further introduce the abbreviation
For the midsurface deformation m we then consider the boundary conditions
on the Dirichlet part \(\gamma _0\) of the boundary \(\partial \omega .\)
For the microrotations \(\overline{R}\) we can consider various possible alternative boundary conditions on \(\gamma _0,\) see [31, 34]. In what follows, we consider two types:
The existence of minimizers for this Cosserat planar shell model under various assumptions on the coefficients and boundary conditions has been proved in [31, 34]. For instance, in the case when the Cosserat couple modulus is positive (\(\mu _c>0\)) and for rigid director prescription boundary conditions (8) on \(\gamma _0,\) the following existence result has been shown in [31], using the direct method of the calculus of variations.
Theorem 1
Let \(\omega \subset {\mathbb {R}}^2\) be a bounded Lipschitz domain, and assume that the material parameters satisfy
Let the boundary data and external loads functions satisfy the regularity conditions
Then the minimization problem (3)–(5) with boundary conditions (6) and (8) admits at least one minimizing solution pair \((m,\,\overline{R})\in H^1(\omega ,\,{\mathbb {R}}^3) \times W^{1,q}(\omega ,\, \mathrm {SO}(3)).\)
In the case of zero Cosserat couple modulus (\(\mu _c=0\)) the mathematical treatment of the minimization problem is more difficult, due to the lack of unqualified coercivity of the energy function with respect to the midsurface deformation m. The corresponding existence result for this case has been proved in [34] using a new extended Korn’s first inequality for plates and elasto-plastic shells [30, 39]. In this case, we need q to be strictly larger than 2. However, the numerical evidence in Sect. 6 suggests that existence also holds for \(q=2.\) For the sake of simplicity, we present this result in the case of zero external loads, i.e., \(\overline{f}=0,\, \overline{M}=0,\,\overline{N} =0,\,\overline{M}_c=0.\)
Theorem 2
Let \(\omega \subset {\mathbb {R}}^2\) be a bounded Lipschitz domain and assume that the material parameters satisfy
Let the boundary data satisfy the regularity conditions
Then the minimization problem for the functional (3)–(5) with boundary conditions (6) and (8) admits at least one minimizing solution pair \((m,\,\overline{R})\in H^1(\omega ,\,{\mathbb {R}}^3) \times W^{1,q}(\omega ,\, \mathrm {SO}(3)).\)
The statement of Theorem 2 holds also in the case of non-vanishing external loads. In this respect, see the paper [34], where a modification of the external loading potential has been used.
Of particular interest is the choice of the new material parameters \(\mu _c\) (the Cosserat couple modulus) and \(L_c.\) Our model is derived from a 3D-Cosserat model in which the Cosserat couple modulus appears traditionally. It controls the skew-symmetric part of the stresses, and enforces \(\overline{R} = \text {polar}(\hat{F})\) for the limit case \(\mu _c \rightarrow \infty .\) From the literature, there does not exist a single material for which the value of the parameter \(\mu _c\) has been identified unambiguously. Considering this situation, in [33] it is argued that this parameter must be set to zero when modeling a continuous body. In [37, 38] the same question has been discussed in the larger framework of (infinitesimal) micromorphic continua with the same result: the absence of \(\mu _c\) leads to a more stringent physical description. Indeed, it implies that a linear Cosserat model collapses into classical linear elasticity.
However, in a geometrically nonlinear context, which is our case, a vanishing Cosserat couple modulus only implies that there is no first-order coupling between rotations and deformation gradients [35]. Compared with the classical Reissner–Mindlin kinematics without drill energy [36], setting \(\mu _c=0\) appears again as the most plausible choice. Since, therefore, there is no specific reason to have \(\mu _c>0,\) we omit this parameter.
The internal length \(L_c\) appears in Cosserat models as a measure of the length scale of the material microstructure. The numerical results of Sect. 6 show that values of \(L_c\) in the micrometer range lead to realistic results. However, we also note that the shell model with \(L_c\gg h\) can be useful for the description of graphene-sheets which have practically zero thickness but still show a bending stiffness. In a classical shell model, we would expect zero bending resistance.
2.2 A modified large strain Cosserat shell model
We observe that the planar shell model presented above is appropriate for finite rotations, but only small elastic membrane strains, since the membrane part \(W_{\mathrm {mp}}\) of the energy density I is quadratic. We now slightly generalize the model to allow for large elastic stretch as well. We consider again a minimization problem for the energy functional
formulated again in two-dimensional quantities m and \(\overline{R}.\) This time, we replace the membrane part of I by
In this expression, we have replaced the quadratic volumetric stretch part \(\text {tr}[\text {sym}(\overline{U}-\mathbbm {1})]^2\) of (4) by the non-quadratic expression
which is volumetrically exact. However, since
the quadratic membrane energy (4) of the previous section can be recovered by linearization at \(\mathbbm {1} \in {\mathbb {M}}^{3 \times 3}.\)
For the nonlinear modified model (10) we set the following expression for the modified thickness stretch
which can be used for the a posteriori reconstruction of the bulk deformation.
The modified membrane energy density (11) represents an improvement over the initial planar shell model (4) in various regards. Indeed, we note that
Moreover, for any fixed \(\overline{R}\) the energy \(W_{\mathrm {mp}}\) is polyconvex [17, 42] with respect to \(\nabla m,\) and it is uniformly Legendre–Hadamard elliptic, independently of \(\mu _c\ge 0.\)
The following existence result for the modified model, in the important case \(\mu _c = 0,\) was originally proved in [34]. Again, we assume vanishing external loads for simplicity.
Theorem 3
Let \(\omega \subset {\mathbb {R}}^2\) be a bounded Lipschitz domain and assume that the boundary data satisfies (9).
Then the minimization problem for the functional (10) with the parameters
with boundary conditions (6), (8) admits at least one minimizing solution pair \((m,\,\overline{R})\in H^1(\omega ,\,{\mathbb {R}}^3) \times W^{1,q}(\omega ,\, \text {SO(3)}),\) with
almost everywhere in \(\omega .\)
We note that the formulation (10) has the same linearized behavior as the initial model (3) and it reduces upon linearization to the classical infinitesimal-displacement Reissner–Mindlin model for the choice of parameters \(\mu _c=0\) and \(q>2.\)
Remark 1
The Cosserat model presented above can be extended to a general nonplanar shell model. Indeed, instead of the domain \(\Omega _h\) and the Ansatz for plates (2), one can begin with a shell-like (curved) thin domain and an appropriate Ansatz for shells. Then, the formal dimensional reduction to a two-dimensional shell model is derived analogously as in the case of plates, but involves additional tools from classical differential geometry of surfaces for the description of shell configurations. The resulting Cosserat shell model is quite general and has the advantage that it can be used to also describe elasto-plastic and visco–elasto-plastic material behavior. This work is currently in progress.
3 Geodesic finite elements
Discretization of the shell models presented in the previous section is difficult, because the orientation configuration space \(W^{1,q}(\omega ,\,\text {SO(3)})\) is not linear. As a consequence,linear, and more generally polynomial, interpolation is undefined in these spaces, and standard FE methods cannot be used.
GFEs are a generalization of standard FEs to problems for functions with values in a nonlinear Riemannian manifold M. We give a brief introduction and state the relevant features without proof. While GFEs can be constructed easily for very general M, we state all results here for the case \(M = \text {SO}(3)\) only. The interested reader is referred to the original publications [40, 41] for more details.
The definition of GFE spaces consists of two parts. First, nonlinear interpolation functions are constructed that interpolate values given on a reference element. Then, these interpolation functions are pieced together to form global FE spaces for a given grid.
3.1 Geodesic interpolation
We focus on the case of a two-dimensional domain \(\omega .\) All constructions and results work mutatis mutandis also for domains of other dimensions.
Let \(T_\mathrm{ref}\) be a triangle or quadrilateral in \({\mathbb {R}}^2.\) We call \(T_\mathrm{ref}\) the reference element. On \(T_\mathrm{ref}\) we assume the existence of a set of pth order Lagrangian interpolation polynomials, i.e., a set of Lagrange nodes \(a_i \in T_\mathrm{ref},\,i=1,\ldots ,m,\) and corresponding polynomial functions \(\lambda _i{\text {:}}\,T_\mathrm{ref} \rightarrow {\mathbb {R}}\) of order p such that
We want to generalize Lagrangian interpolation to the case of values \(R_1,\ldots ,R_m \in \text {SO(3)}\) associated to the Lagrange nodes \(a_i.\) In other words, we want to construct a function \(\Upsilon {\text {:}}\,T_\mathrm{ref} \rightarrow \text {SO(3)}\) such that \(\Upsilon (a_i) = R_i\) for all \(i = 1,\ldots ,m.\) This is a non-trivial task because \(\text {SO(3)}\) is not a vector space.
To motivate our construction we note that the usual Lagrangian interpolation of values \(v_1,\ldots ,v_m\) in \({\mathbb {R}}\) can be written as a minimization problem
for each \(\xi \in T_\mathrm{ref}.\) This formulation can be generalized to values in \(\text {SO(3)}.\) We use \(\text {dist}(\cdot ,\,\cdot )\) for the canonical (geodesic) distance on \(\text {SO(3)},\) which is
Definition 1
([41]) Let \(\{\lambda _i\}_{i=1}^m\) be a set of pth order scalar Lagrangian shape functions on the reference element \(T_\mathrm{ref},\) and let \(R_i \in \text {SO(3)},\,i=1,\ldots ,m\) be values at the corresponding Lagrange nodes. We call
pth order geodesic interpolation on \(\text {SO(3)}.\)
To make the construction easier to understand we work out a simple example.
Example
Let \(T_\mathrm{ref}\) be the reference triangle
and consider the first-order case \(p=1.\) In this case, the Lagrange nodes \(a_1,\,a_2,\,a_3\) are the triangle vertices, and the corresponding shape functions are
These are simply the barycentric coordinates of \(\xi \) with respect to \(T_\mathrm{ref}.\) Let \(R_1,\, R_2,\, R_3\) be given values on \(\text {SO(3)}.\) The image of \(T_\mathrm{ref}\) under \(\Upsilon \) is then a (possibly degenerate) geodesic triangle on \(\text {SO(3)}\) with corners \(R_1,\, R_2,\, R_3.\) In particular, the edges of \(T_\mathrm{ref}\) map onto geodesics on \(\text {SO(3)}\) ([40, Lemma 2.2 with Corollary 2.2]). Even more, the map \(\Upsilon \) is equivariant under permutations of the values \(R_1,\, R_2,\, R_3\) ([41, Lemma 4.3]), a property not shared by various other commonly used discretization techniques [28, 29, 45]. Figure 1 shows the corresponding second-order case.
While Definition 1 is an obvious generalization of Lagrangian interpolation in linear spaces, it is by no means clear that it leads to a well-defined interpolation function for all coefficient sets \(R_1,\ldots , R_m \in \text {SO(3)}\) and \(\xi \in T_\mathrm{ref}.\) Intuitively, for fixed \(\xi \in T_\mathrm{ref},\) one would expect the functional
to have a unique minimizer if the \(R_i \in \text {SO(3)}\) are close enough to each other in a certain sense. For the first-order case \(p=1,\) where all \(\lambda _i\) are non-negative on \(T_\mathrm{ref},\) this follows from a classic result of Karcher [24], which was later strengthened by Kendall [25] (see also [21]). Note that \(\text {SO}(3)\) is complete and has constant sectional curvature of 1 [51, Theorem 2.7.1].
Theorem 4
(Kendall [25]) Let \(B_\rho \) be an open geodesic ball of radius \(\rho < \pi / 2\) in \(\text {SO}(3),\) and \(R_1,\ldots ,R_m \in B_\rho .\) Let \(\{ \lambda _i\}_{i=1}^m\) be a set of first-order Lagrangian shape functions. Then the function
has a unique minimizer in \(B_\rho \) for all \(\xi \in T_\mathrm{ref}.\)
If the polynomial order p is larger than 1, the weights \(\lambda _i\) attain negative values on \(T_\mathrm{ref},\) and the results of Karcher and Kendall cannot be used anymore. Having all \(R_i\) in a convex ball still guarantees existence of a unique minimizer, but that minimizer may only be contained in a ball of larger size.
Theorem 5
(Sander [41]) Let \(B_D \subset B_\rho \) be two concentric geodesic balls in \(\text {SO(3)}\) of radii D and \(\rho ,\) respectively, and let \(R_1, \ldots ,R_m \in \text {SO(3)}.\) There are numbers D and \(\rho \) such that if \(R_1,\ldots ,R_m \in B_D,\) then the functional (12) has a unique minimizer in \(B_\rho .\)
A quantitative version of this result is given as Theorem 3.19 in [41]. Unfortunately is is quite technical and we have chosen to omit it here. When preparing the numerical examples of Sect. 6, we have not encountered any problems stemming from a possible ill-posedness of the interpolation for extreme configurations of the \(R_1,\ldots ,R_m.\)
To be able to use the interpolation functions as the basis of a FE theory, they need to have sufficient regularity. The following result follows directly from the implicit function theorem.
Theorem 6
Let \(R_1,\ldots ,R_m\) be coefficients on \(\text {SO(3)}\) with respect to a pth order Lagrange basis \(\{ \lambda _i \}\) on a domain \(T_\mathrm{ref}.\) Under the assumptions of Theorem 5, the function
is infinitely differentiable with respect to the \(R_i\) and \(\xi .\)
This result is proved in [40, 41] for interpolation in general manifolds.
3.2 Geodesic finite element functions
The interpolation functions of the previous section can be used to construct a generalization of Lagrangian FE spaces to functions with values in \(\text {SO(3)}.\)
For this, let \(\omega \) be the two-dimensional parameter domain of our planar Cosserat shell model, and suppose it has piecewise linear boundary. Let \({\mathcal {G}}\) be a conforming grid for \(\omega \) with triangle and/or quadrilateral elements. Let \(n_i \in \omega ,\, i=1,\ldots ,N\) be a set of Lagrange nodes such that for each element T of \({\mathcal {G}}\) there are m nodes \(a_{T,i}\) contained in T, and such that the pth order interpolation problem on T is well posed.
Definition 2
(GFEs [41]) Let \({\mathcal {G}}\) be a conforming grid on \(\omega .\) We call \(R_h {\text {:}}\,\omega \rightarrow \text {SO(3)}\) a GFE function if it is continuous, and for each element \(T \in {\mathcal {G}}\) the restriction \(R_h|_T\) is a geodesic interpolation in the sense that
where \({\mathcal {F}}_T{\text {:}}\,T \rightarrow T_\mathrm{ref}\) is affine or multilinear and the \(R_{T,i}\) are values in \(\text {SO(3)}\) corresponding to the Lagrange nodes \(a_{T,i}.\) The space of all such functions \(R_h\) will be denoted by \(V_{p,h}^{\text {SO(3)}}.\)
This construction has various desirable properties. As a first result we note that the functions constructed in this way are \(W^{1,q}\)-conforming for all \(q \ge 2.\) This follows from a slight generalization of the proof for Theorem 3.1 in [40].
Theorem 7
\(V_{p,h}^{\text {SO(3)}}(\omega ) \subset W^{1,q}(\omega ,\,\text {SO(3)})\) for all \(p \ge 1,\,q \ge 2.\)
Hence discrete approximation functions for the Cosserat microrotation field \(\overline{R}{\text {:}}\,\omega \rightarrow \text {SO(3)}\) are elements of the space \(W^{1,q}(\omega ,\,\text {SO(3)}),\) in which the Cosserat shell problem is well posed (Theorems 1 and 3). This means that the energies (3) and (10) can be directly evaluated for GFE functions, which simplifies the analysis considerably.
Since GFEs are defined using metric properties of \(\text {SO(3)}\) alone, we naturally get the following equivariance result.
Lemma 8
Let O(3) be the orthogonal group on \({\mathbb {R}}^3,\) which acts isometrically on \(\text {SO(3)}\) by left multiplication. Pick any element \(Q \in O(3).\) For any GFE function \(R_h \in V_{p,h}^{\text {SO(3)}}\) we define \(QR_h{\text {:}}\,\omega \rightarrow \text {SO(3)}\) by \((QR_h)(x) = Q(R_h(x))\) for all \(x \in \omega .\) Then \(QR_h \in V_{p,h}^{\text {SO(3)}}.\)
This lemma forms the basis of the frame-invariance of our discrete Cosserat shell model.
Optimal discretization error bounds for general GFE problems have been proved in [20]. The application of those abstract results to the energy functionals considered in this paper will be left for future work.
4 Discrete and algebraic Cosserat planar shell problem
We now discuss the minimization problem obtained by discretizing the continuous Cosserat shell model of Sect. 2 by GFEs. For that, assume that the two-dimensional domain \(\omega \) is discretized by a grid containing triangle and/or quadrilateral elements. For simplicity, we again assume that the domain boundary is resolved by the grid. We also assume that the grid resolves the Dirichlet boundary \(\gamma _0.\)
4.1 The discrete problem
The functional I given in (10) is defined on the Cartesian product of the spaces \(H^1(\omega ,\,{\mathbb {R}}^3)\) and \(W^{1,q}(\omega ,\,\text {SO}(3)).\) The first factor is a standard Sobolev space of vector-valued functions. For its discretization we introduce the space \(V_{p_1,h}^{{\mathbb {R}}^3}\) of conforming Lagrangian FEs of \(p_1\)th order with values in \({\mathbb {R}}^3.\) In the following we write \(m_h\) for discrete displacement functions from \(V_{p_1,h}^{{\mathbb {R}}^3}.\) For the rotation degree of freedom \(\overline{R}{\text {:}}\,\omega \rightarrow \text {SO}(3)\) we use the GFEs described in the previous chapter. Denote by \(V_{p_2,h}^\text {SO(3)}\) the \(p_2\)th order GFE space for functions on \(\omega \) with respect to the grid, and with values in \(\text {SO}(3).\) In the following we write \(\overline{R}_h\) for discrete microrotations from \(V_{p_2,h}^\text {SO(3)}.\)
It is well known that \(V_{p_1,h}^{{\mathbb {R}}^3} \subset H^1(\omega ,\,{\mathbb {R}}^3)\) (see, e.g., [11, Satz 5.2]). Additionally, we know from Theorem 7 that the FE space \(V_{p_2,h}^\text {SO(3)}\) is a subset of \(W^{1,q}(\omega ,\,\text {SO}(3))\) for all \(p_2 \in {\mathbb {N}}.\) Therefore, the energy functional I is well defined on the product space \(\mathbf {V}_h :=V_{p_1,h}^{{\mathbb {R}}^3} \times V_{p_2,h}^\text {SO(3)}\) for all \(p_1,\,p_2 \in {\mathbb {N}}.\) A suitable discrete approximation of the geometrically nonlinear planar Cosserat shell model therefore consists of the unmodified energy functional I restricted to the space \(\mathbf {V}_h.\)
In analogy to the continuous model, we consider the following boundary conditions for the discrete problem. Let \(g_{d,h} \in V_{h,p_1}^{{\mathbb {R}}^3}\) be a FE approximation of the Dirichlet boundary value function \(g_d{\text {:}}\,\omega \rightarrow {\mathbb {R}}^3,\) and let \(g_{d,h}^{\prime } \in V_{h,p_2}^{{\mathbb {R}}^3}\) be an approximation of the vector field \(g_d^{\prime }.\) Then we demand that the discrete displacement \(m_h\) fulfill the condition
For the microrotations \(\overline{R}\) we can define discrete approximations of the boundary conditions (7) and (8): we either leave them free, corresponding to homogeneous Neumann conditions for \(\overline{R},\) or, alternatively, corresponding to (8), we can specify the direction of the transversal director vector \(\overline{R}_3\) (rigid director prescription)
Summing up, the discrete Cosserat shell problem is:
Problem 2
(Discrete Cosserat shell problem) Find a pair of functions \((m_h,\,\overline{R}_h)\) with \(m_h \in V_{p_1,h}^{{\mathbb {R}}^3}\) and \(\overline{R}_h \in V_{p_2,h}^{\text {SO(3)}}\) that minimizes the functional I given in (10), subject to the constraints (13) and (14) on \(\gamma _0.\)
Note that frame indifference of the discrete model is retained naturally, because we simply restrict the frame-indifferent functional I to a subset \(V_{p_1,h}^{{\mathbb {R}}^3} \times V_{p_2,h}^{\text {SO(3)}}\) of its original domain of definition, and this subset is closed under rigid body motions (Lemma 8).
Remark 2
We have discretized the midsurface deformation m using standard FEs, and we have used the novel GFEs only for the rotation field \(\overline{R}.\) We can unify the two approaches when a more abstract viewpoint is taken. Indeed, revisiting the definitions of Sect. 3 it is obvious that GFEs may as well be defined for the target manifold \({\mathbb {R}}^3\) instead of \(\text {SO(3)};\) standard Lagrangian FEs are the result. In this sense, we have used GFEs for both the midsurface deformation and the microrotation field.
When the two orders \(p_1\) and \(p_2\) coincide \(p=p_1 = p_2,\) we can go one step further. Note that the space \(\text {SE}(3) :={\mathbb {R}}^3 \times \text {SO(3)}\) is well known as the special Euclidean group (the group of rigid body motions in \({\mathbb {R}}^3\)). We therefore introduce the GFE space \(V_{h,p}^\text {SE(3)},\) and observe that it is isomorphic to \(\mathbf {V}_h :=V_{p,h}^{{\mathbb {R}}^3} \times V_{p,h}^\text {SO(3)}.\) We can therefore also interpret the discrete Cosserat shell problem as a minimization problem in the single GFE space \(V_{h,p}^\text {SE(3)}.\)
4.2 The algebraic problem
For the numerical minimization of the Cosserat shell energy we need an algebraic formulation. For standard FEs there is a bijective correspondence between FE functions and coefficient vectors, via the representation of the functions with respect to a basis. For GFEs, the situation is more involved. Since GFE functions are continuous by definition, we can always associate a coefficient vector \(\overline{\overline{R}} \in \text {SO(3)}^{N_2}\) to a function \(\overline{R}_h \in V_{p_2,h}^{\text {SO(3)}}\) by pointwise evaluation at the \(N_2\) Lagrange nodes. To formalize this we introduce the evaluation operator
where \(n_i \in \omega ,\,i=1,\ldots ,N_2\) are the Lagrange nodes of the FE space of order \(p_{2}\) on the grid. However, for a given set of coefficients \(\overline{\overline{R}} \in \text {SO(3)}^{N_2}\) there may be more than one GFE function that interpolates \(\overline{\overline{R}}.\) This happens when the set of values violates the assumptions of Theorems 4 or 5 (depending on the FE approximation order \(p_2\)).
All GFE functions that do comply with the conditions of Theorems 4 or 5 element-wise can be identified with coefficient sets \(\overline{\overline{R}} \in \text {SO}(3)^{N_2}.\) In most cases this situation can be achieved by making the grid fine enough. This has been formalized in [41, Theorem 5.2], which we repeat here, adapted to the Cosserat shell problem.
Theorem 9
Let \(\overline{R}{\text {:}}\,\omega \rightarrow \text {SO(3)}\) be Lipschitz continuous in the sense that there exists a constant L such that
for all \(x,\,y \in \omega .\) Let \({\mathcal {G}}\) be a grid of \(\omega \) and h the length of the longest edge of \({\mathcal {G}}.\) Set \(\overline{\overline{R}} = {\mathcal {E}}_{p_2}(\overline{R}),\) tacitly extending the definition of \({\mathcal {E}}_{p_2}\) to all continuous functions \(\omega \rightarrow \text {SO(3)}.\) For h small enough, the inverse of \({\mathcal {E}}_{p_2}\) has only a single value in \(V_{p_2,h}^{\text {SO(3)}}\) for each \(\widetilde{\overline{R}} \in \text {SO(3)}^{N_2}\) in a neighborhood of \(\overline{\overline{R}}.\)
The restrictions posed by this theorem do not appear to pose any difficulties in practice. We therefore assume in the following that \({\mathcal {E}}_{p_2}\) is a (local) bijection.
Analogously to \({\mathcal {E}}_{p_2}\) we define the corresponding operator \({\mathcal {E}}_{p_1}\) doing point-wise evaluation of functions in \(V_{p_1,h}^{{\mathbb {R}}^3}.\) With these operators, it is straightforward to define the algebraic Cosserat shell energy
where I is the functional (10). The algebraic Cosserat shell problem then is:
Problem 3
(Algebraic Cosserat shell problem) Find a pair \(\bar{m} \in {\mathbb {R}}^{3N_1},\,\overline{\overline{R}} \in \text {SO(3)}^{N_2}\) that minimizes \(\bar{I},\) subject to suitable boundary conditions.
Implementation of Dirichlet boundary conditions for the deformation \(m_h\) is straightforward. For the rotation field we again have the choice between leaving the rotation free, or prescribing the transversal director vector \(\overline{R}_3\) (rigid director prescription)
for all Lagrange nodes \(n_i\) on the Dirichlet boundary \(\gamma _0.\)
Remark 3
If \(N_1 = N_2 = N\) we can also interpret the functional (15) as being defined on the manifold \(({\mathbb {R}}^3 \times \text {SO(3)})^N.\)
It was mentioned in Sect. 2 that the shell energy is frame-invariant in the sense that
where Q is any element of \(\text {SO(3)},\) acting on functions in \(H^1(\omega ,\,{\mathbb {R}}^3)\) and \(W^{1,q}(\omega ,\,\text {SO(3)})\) by pointwise multiplication. By the equivariance property (Lemma 8) of GFEs this frame invariance does not get lost by discretization.
Theorem 10
The algebraic energy functional \(\bar{I}\) is frame-invariant in the sense that
for all \(Q \in \text {SO(3)},\) which, by an abuse of notation, now acts on the components of \(\bar{m}\) and \(\overline{\overline{R}}.\)
This sets the GFE discretization apart from alternative approaches like [28, 29], which do not have this property.
5 Numerical minimization of the algebraic energy
All previous work on nonlinear shell elements has used the Newton method to solve the resulting nonlinear systems of equations. However, it is well known that this method converges only locally. Therefore, a sequence of loading steps is traditionally used to obtain a solution. These loading steps have to be selected carefully to make sure that the Newton solver converges at each loading step. This selection of loading steps can be tedious in practice.
For energy minimization problems there exist globalized versions of the Newton method, i.e., methods that converge for any initial iterate, without using intermediate loading steps. One such method is the so-called trust-region method [13], which replaces each Newton step with a quadratic minimization problem on a convex set. Under reasonable conditions, it degenerates to a standard Newton method when close enough to a solution, and hence local quadratic convergence is recovered.
While the standard trust-region method works for energies defined on Euclidean spaces, a generalization to energies on Riemannian manifolds has been introduced and investigated by Absil et al. [1]. This Riemannian trust-region method can be applied to the algebraic Cosserat energy (15), which is defined on the product manifold \({\mathbb {R}}^{3N_1} \times \text {SO(3)}^{N_2}.\) As an extension of Newton’s method, it shows locally quadratic behavior. On the other hand, it can be shown to converge globally without intermediate loading steps.
5.1 Trust-region methods
We briefly review the trust-region method for Euclidean spaces [13], and then show how it can be generalized to functionals on a Riemannian manifold. Consider a twice continuously differentiable functional
supposed to be coercive and bounded from below. Given any initial iterate \(x^0 \in {\mathbb {R}}^N,\) we want to find a local minimizer of J.
The Newton method does this in the following way. Let \(x^k \in {\mathbb {R}}^N\) be any iterate. Approximate J around \(x^k\) by the quadratic Taylor expansion
which in this context is called a quadratic model of J around \(x^k.\) The variable s is to be interpreted as a correction \(s = x - x^k.\) Then, compute a stationary point \(s^k\) of \(m_k,\) and use it as the correction to the next iterate
Computing the stationary point \(s^k\) is done by the well-known Newton update formula
Observe that if the Hessian \(\partial ^2 J(x^k)\) is positive definite at all iterates, then the algorithm produces a sequence of iterates with decreasing energy, i.e., \(J(x^{k+1}) \le J(x^k)\) for all \(k \in {\mathbb {N}}.\) However, iterates with indefinite \(\partial ^2 J(x^k)\) may lead to energy increase.
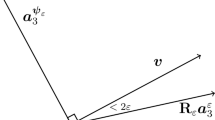
To enforce global convergence of this, the trust-region method first replaces the search for a stationary point of \(m_k\) by a minimization problem for a minimizer \(s^k\) of \(m_k.\) As a consequence, iterates of the trust-region method are energy decreasing in all cases. Secondly, it notes that the quadratic model \(m_k\) is a good approximation of J only in a neighborhood of \(x^k.\) This observation is made explicit by restricting the minimization problem for \(m_k\) to a ball of radius \(\rho _k\) around \(x^k,\) the name-giving trust region (Fig. 2). In other words, the Newton step (17) is replaced by
Since we now look for a minimizer on a compact set only, Problem (18) is well-defined even if \(\partial ^2 J\) is not positive definite.
Unlike the original Newton method, the trust-region method is monotone in the sense that \(J(x^{k+1}) \le J(x^k)\) for all \(k \in {\mathbb {N}}.\) A more quantitative monitoring of the energy decrease allows to control the trust-region radius, i.e., the trust in the quality of the quadratic approximation. The quality of the correction step \(s^k\) is estimated by comparing the functional decrease to the model decrease. If the quotient
is smaller than a fixed value \(\eta _1,\) then the step is rejected, and \(s^k\) is recomputed for a smaller trust-region radius. Otherwise the step is accepted. If \(\kappa _k\) is larger than a second value \(\eta _2,\) the trust-region radius is enlarged for the next step. Common values are \(\eta _1 = 0.01\) and \(\eta _2 = 0.9\) [13].
For the trust-region algorithm, the following convergence properties can be shown.
Theorem 11
([13, Theorems 6.4.6 and 6.5.5]) Suppose that J is twice continuously differentiable, bounded from below, and such that its Hessian remains bounded for all \(x \in {\mathbb {R}}^N.\)
-
(1)
For all initial iterates we get
$$\begin{aligned} \lim _{k \rightarrow \infty } \left\| {\partial J\left( x^k\right) }\right\| = 0. \end{aligned}$$ -
(2)
Suppose that \(\{x^{k_i}\}\) is a subsequence of the iterates converging to the first-order critical point \(x_{*}.\) Suppose furthermore that \(s^k \ne 0\) for all k sufficiently large. Finally suppose that \(\partial ^2 J(x_*)\) is positive definite. Then the complete sequence of iterates \(\{x^k\}\) converges to \(x_*,\) eventually the step quality \(\kappa _k\) remains above \(\eta _2,\) and the trust-region radius \(\rho _k\) is bounded away from zero.
In particular, since \(\kappa _k > \eta _2\) for all k large enough, the trust-region radius grows near local minimizers, the method eventually degenerates to a pure Newton method, and we get locally quadratic convergence.
Various algorithms for solving the constrained quadratic minimization problems (18) been proposed in the literature. The monograph [13] gives a good overview.
Trust-region methods are much more convenient than standard Newton methods, because they relieve the user of the tedious load-stepping. They typically do not need more iterations than a Newton method. If the tangent problems are very badly conditioned (which, for our shell model, is unfortunately the case if \(L_c\) is small), then Newton methods can be faster because they can use direct solvers to solve the inner problems. Trust-region methods, on the other hand, need to employ iterative solvers, whose convergence speed depends on the matrix condition number. This argument becomes void if large problems are considered, because for such problems the memory consumption of direct solvers makes their use impossible. Also, constructing iterative solver that are Taylor-made for the tangent problems of nonlinear Cosserat shell models may lead to a large speed increase. This is a subject of future research.
5.2 Riemannian trust-region methods
The algebraic energy functional \(\bar{I}\) defined in (15) is not a functional of the type (16). Rather, its domain of definition is the nonlinear manifold \({\mathbb {R}}^{3N_1} \times \text {SO(3)}^{N_2}.\) The trust-region method has been generalized to such energies by Absil et al. [1]. Let M be a Riemannian manifold with metric g, and \(J{\text {:}}\, M \rightarrow {\mathbb {R}}\) twice differentiable and bounded from below (in our case: \(M ={\mathbb {R}}^{3N_1} \times \text {SO(3)}^{N_2}\)). The basic idea of such a Riemannian trust-region algorithm is that in a neighborhood of a point \(x \in M\) the functional J can be lifted onto the tangent space \(T_xM.\) There, a vector space trust-region subproblem can be solved and the result transported back onto M (Fig. 3).
More formally, let again \(k \in {\mathbb {N}}\) be an iteration number and \(x^k \in M\) the current iterate. We obtain the lifted functional by setting
Let \(\rho _k > 0\) be the current trust-region radius. The Riemannian metric g turns \(T_{x^k} M\) into a Banach space with the norm \(||\cdot ||_{x^k} = \sqrt{g_{x^k}(\cdot ,\, \cdot )}.\) There, the trust-region subproblem reads
with the quadratic, but not necessarily convex model
Here \(\nabla \hat{J}_k\) is the Riemannian gradient and \(\text {Hess}\hat{J}_k\) the Riemannian Hessian of \(\hat{J}_k\) (see [1] for definitions), and both are evaluated at \(0 \in T_{x^k}M.\) Note that (21) is independent of a specific coordinate system on \(T_{x^k}M.\) As a minimization problem of a continuous function on a compact set, (20) has at least one solution \(s^k,\) which generates the new iterate by
As in trust-region methods in linear spaces, the quality of a correction step \(s^k\) is estimated by comparing the functional decrease and the model decrease. The quotient (19) now takes the form
For this method, Absil et al. proved global convergence to first-order stationary points, and, depending on the exactness of the inner solver, locally superlinear or even locally quadratic convergence [1]. For our numerical results we use the monotone multigrid method [26] together with a \(\infty \)-norm trust-region. Details can be found in [40].
5.3 Computing the algebraic tangent problem numerically
Solving the constrained quadratic problems (20) numerically involves the algebraic Riemannian gradient \(\nabla \bar{I}\) and Hessian \(\text {Hess}\bar{I}\) of the functional \(\bar{I}.\) While those could in principle be evaluated analytically, such an approach is involved and error prone (Consider the derivative formulas for the gradient in [40, Chap. 5]). It is much more convenient to use automatic differentiation (AD) to compute the derivatives. AD is a technique to algorithmically compute first and higher derivatives of functions given in form of computer programs [19]. This includes computer programs involving iterative solvers like the Newton method used to evaluate GFE functions (see “Quaternion coordinates for SO(3)” in Appendix). Many good implementations of AD are available as external libraries, and the choice can have a considerable impact on the computational cost of assembling the tangent problem. For this article we have used the open-source ADOL-C software [48], which is one of the few that provides all the features needed to compute first and second derivatives of the energy functionals considered here.
For simplicity we assume that the deformation m and the microrotation \(\overline{R}\) have been discretized with finite elements of equal approximation order. Then there is an equal number of Lagrange nodes \(N = N_1 = N_2\) for both of them, and we can consider the algebraic energy \(\bar{I}\) as being defined on the manifold \(M = ({\mathbb {R}}^3 \times \text {SO(3)})^N.\)
Unfortunately, current AD tools do not directly support derivatives of energies defined on manifolds. We therefore use the following trick. Interpret elements R of \(\text {SO(3)}\) as unit vectors q in \({\mathbb {R}}^4\) using quaternion coordinates (see “Quaternion coordinates for SO(3)” in Appendix). The algebraic energy functional \(\bar{I}\) can then be interpreted as being defined on \(({\mathbb {R}}^3 \times S^3)^N \subset {\mathbb {R}}^{7N}.\) To extend \(\bar{I}\) to a neighborhood of \(({\mathbb {R}}^3 \times S^3)^N\) in \({\mathbb {R}}^{7N}\) we first introduce \(\bar{q} \in {\mathbb {R}}^{4N},\) a vector of quaternions. Componentwise normalization leads to a vector of unit quaternions, which we denote by \(\bar{q}/{|\bar{q}|} \in (S^3)^N\) in an abuse of notation. Using the map F defined in (28) we can construct \(F(\bar{q}/{|\bar{q}|}) \in \text {SO(3)}^N\) (the application of F again component-wise). Then we set
which is a smooth functional on an open subset of the Euclidean space \({\mathbb {R}}^{7N}.\) Given a computer implementation of \(\tilde{I},\) an AD system like ADOL-C can then compute the Euclidean gradient \(\partial \tilde{I} \in {\mathbb {R}}^{7N}\) and Hessian \(\partial ^2 \tilde{I} \in {\mathbb {R}}^{7N \times 7N}\) automatically.
To obtain the Riemannian gradient \(\nabla \bar{I}\) and Hessian \(\text {Hess}\bar{I}\) we need additional manipulations. For the gradient we use the following well-known result (see, e.g., [1], Sect. 3.6.1).
Lemma 12
Let M be a smooth Riemannian manifold isometrically embedded in a Euclidean space \({\mathbb {R}}^l.\) For each \(x \in M\) let \(P_x{\text {:}}\, T_x{\mathbb {R}}^l \rightarrow T_xM\) be the orthogonal projection onto the tangent space at x. Let \(f{\text {:}}\,M \rightarrow {\mathbb {R}}\) be continuously differentiable and \(\tilde{f}\) a smooth extension of f to a neighborhood of M in \({\mathbb {R}}^l.\) Then
where \(\nabla \) is the gradient operator on M, and \(\partial \) is the gradient in \({\mathbb {R}}^l.\)
Since \(\bar{I}\) is defined on the N-fold product of \({\mathbb {R}}^3 \times \text {SO(3)}\) we obtain the Riemannian gradient \(\nabla \bar{I}\) by applying Lemma 12 to each factor. Hence, the Riemannian gradient is given by componentwise projection
where \(P_x\) is the orthogonal projector from \(v \in {\mathbb {R}}^7\) to \({\mathbb {R}}^3 \times T_x S^3.\) This projector can be constructed from the corresponding projector for \({\mathbb {R}}^3\) (which is the identity), and the corresponding projector for \(S^3\)
A similar formula for the Riemannian Hessian is given in the following lemma. As we now consider second derivatives, the curvature of \(\text {SO(3)}\) comes into play.
Lemma 13
(Absil et al. [2]) With the same notation as in Lemma 12, we have
where \({\mathfrak {A}}_x(z,\,v)\) is the Weingarten map of M, and \(P_x^\perp \) is the orthogonal projector onto the normal space of M at x.
The Weingarten map for the unit sphere in \({\mathbb {R}}^4\) is [2]
and the orthogonal projector onto the normal space at \(x \in S^3\) is
Written in canonical coordinates of \({\mathbb {R}}^{7N},\) the matrix \(\text {Hess}\tilde{I}\) is a sparse symmetric \(7N \times 7N\)-matrix, consisting of dense \(7 \times 7\) blocks. Using this representation for numerical computations is undesirable for two reasons. First of all, it is rank deficient, because the extended functional \(\tilde{I}\) is constant along each normal vector of \(S^3.\) Secondly, it is bigger than necessary: since \(\text {SO(3)}\) (or the set of unit quaternions for that matter) is only three-dimensional, the entire Riemannian Hessian should fit into a \(6N \times 6N\) matrix. To construct such a representation for the Riemannian Hessian at a point \((\bar{m},\, \bar{q}) \in {\mathbb {R}}^{7N}\) we pick a basis for the tangent space of \(({\mathbb {R}}^3 \times S^3)^N\) at \((\bar{m},\, \bar{q}),\) and write \(\text {Hess}\tilde{I}\) in that basis. Luckily, such a basis is easily available. For the components in \({\mathbb {R}}^3,\) the canonical basis can be used. For any point \(q \in S^3,\) an orthonormal basis of \(T_q S^3\) is given by
and this basis depends smoothly on q. We combine the vectors to a \(7 \times 6\)-matrix
whose columns form an orthonormal basis of \({\mathbb {R}}^3 \times S^3.\)
We denote by D the block-diagonal \(7N \times 6N\)-matrix where the ith block is \(D_{q_i}\) as given by (23). Then, in these new coordinates, the Riemannian Hessian has the algebraic form
This matrix has no degenerate directions caused by the embedding of the configuration space into \({\mathbb {R}}^{7N}.\) Indeed, it is again completely intrinsic. In each iteration of the trust-region solver, this is the matrix used to define the quadratic model.
Finally, we point out one lucky coincidence that helps to increase efficiency. AD systems such as ADOL-C are able to compute the product \((\partial ^2 \tilde{I}) D\) directly. This is noticeably cheaper than using AD to compute \(\partial ^2 \tilde{I}\) and later multiplying by D, because \((\partial ^2 \tilde{I}) D\) has fewer entries than \(\partial ^2 \tilde{I}\) (\(7N \times 6N\) compared to \(7N \times 7N\)). We noted a decrease of about 10 % of the time needed to assemble the Riemannian Hessian (24).
Deformation test of a clamped cantilever. Left reference grid and deformed grid, right vertical deflection as a function of the grid refinement for five different discretization order combinations. In the legend, the first number is the discretization order for the midsurface deformation, and the second number is the order of the microrotation discretization. Only the discretization using first-order elements for both deformation and microrotations shows locking behavior
Left L-shape structure with boundary conditions, right the grid, which is the one also used in [54]
6 Numerical tests
We now present several numerical tests. These demonstrate the capabilities of both our Cosserat shell model and of our discretization. First, we demonstrate that the elements do not suffer from shear locking, as long as the midsurface deformations are discretized with finite elements of at least second order. Then, we reproduce quantitative results from the literature (Sect. 6.2), and show how the model and discretization can handle large rotations with ease (Sect. 6.3). In Sect. 6.4 we simulate the wrinkling of a polyimide sheet, and find very good quantitative correspondence with experimental data. All examples in this chapter were programmed using the Dune libraries ([5], http://www.dune-project.org).
We deliberately do not give detailed measurements of the time spent in the various steps of the energy minimization algorithm. Automatic differentiation of the energy functional to get the algebraic tangent matrices and numerical solution of the constraint tangent problems together consume virtually all run-time, and neither of the two consistently dominates the other. Time spent assembling the tangent problems may possibly be reduced by switching to a different AD library. The run-time behavior of the iterative multigrid solver for the constraint quadratic problems is more difficult to judge. Due to the smallness of some of the parameters appearing in the Cosserat energy I, the tangent problems are very badly conditioned. Therefore, in many cases the multigrid solver will simply iterate until a prescribed maximum number of iterations has been reached, and the wall-time taken by the solver is simply a multiple of this number. On the other hand, even in such cases the multigrid solver produces enough energy decrease for the outer trust-region method to converge. The precise interplay between the maximum number of allowed iterations of the multigrid solver and the convergence behavior of the trust-region method is delicate, and we have not investigated it here. There is hope that further insight into the problem structure will allow to construct preconditioners that will greatly speed up the multigrid convergence. Alternatively, one may consider replacing the trust-region constraint by a line search globalization, which would allow to use a direct solver for the tangent problems.
6.1 Deflection of a cantilever
To investigate the shear locking behavior of the proposed discretization, we use the classic benchmark of a clamped cantilever loaded transversally at one end. We see that there is no locking provided that the deformation m is discretized using at least second-order finite element functions.
Let the reference domain \(\omega \) be the rectangle \((0,\,100)\,\mathrm {mm} \times (0,\,10)\,\mathrm {mm}.\) We clamp the cantilever at one short end by requiring \(m(x) = (x_1,\, x_2,\, 0)\) and \(\overline{R}_3(x) = (0,\,0,\,1)\) for all \(x \in \{0\}\,\mathrm {mm} \times (0,\,10)\,\mathrm {mm}.\) For the shell material parameters we use the values given in Table 1. We load the cantilever by applying a transversal surface load at the far edge of magnitude 18 N.
We discretize the domain by ten quadrilateral elements (Fig. 4). From this grid, we create a sequence of finer grids by repeated uniform refinement. On this sequence of grids we discretize the solution space by five different GFE spaces: first, we use the same approximation order for deformation and microrotations, testing orders one, two, and three. Then, as the microrotations are related to the first derivative of the deformation m, we also investigate two combinations where the microrotation field is discretized with one order lower than the deformation field.
For these different discretizations we measure the cantilever deflection as a function of the mesh size. The results are shown in Fig. 4. One can see that all but one discretizations give the same value for the deflection, and that that value is independent from the grid resolution. The exception is the discretization using first-order elements for the deformation. There, the discrete model is much stiffer for coarse elements, and the deflection only approaches the correct value asymptotically for high grid resolutions. We conclude that shear locking is not an issue with GFEs, if at least second-order elements are used for the deformation m. This agrees with the results given in [23].
For all further examples in the chapter we have used second-order elements both for the deformation and for the microrotations.
6.2 Deformation of an L-shape
We begin by comparing our approach to a benchmark problem taken from the literature. The following setup is used by Wriggers and Gruttmann [54], who compare their discrete model with the ones from [3, 44, 45] for the same problem. Our aim here is twofold: we want to show that our discrete model can reproduce quantitative results from the literature. Also, we want to highlight the speed and stability of our solver.
Let \(\omega \) be the L-shaped domain depicted in Fig. 5. Sizes of the shape are given in the figure, and we set the plate thickness to 0.6 mm. We model the material with the finite-strain hyperelastic material of Sect. 2.2. The material parameters are given in Table 1. The Lamé constants \(\mu ,\,\lambda \) correspond to the values \(E = 71\,240\,\text {N}/\mathrm{mm}^2,\,\nu =0.31\) given in [54]. As argued in Sect. 2.1, the coupling modulus \(\mu _c\) is set to \(\mu _c = 0\) N/mm. We set the curvature exponent q appearing in the curvature energy term \(W_\mathrm{curv}\) to \(q=2,\) and the internal length \(L_c\) to \(0.6\,\upmu \)m, following the suggestions of Sect. 2.1.
Out-of-plane deflection as a function of the load. Left own simulation. Right corresponding plot taken from [54]
The boundary conditions are depicted on the left of Fig. 5. The structure is clamped on the left vertical end \(\gamma _0.\) By this we mean that on \(\gamma _0\) we set \(m(x,\,y) = (x,\,y,\,0),\) and the rigid director description \(\overline{R}_3 = (0,\,0,\,1)^T\) for the microrotations \(\overline{R}.\) On the lower horizontal end \(\gamma _s\) we prescribe a uniform surface loadFootnote 1 P in the direction of the first unit basis vector. Zero Neumann boundary conditions are set everywhere else for displacements and rotations. We discretize the domain using 99 quadrilateral elements as depicted on the right of Fig. 5. The equations are discretized using second-order (i.e., nine-node) GFEs.
The first aim of this experiment is to study the buckling behavior of the structure for different values of P. When the structure is loaded, it deforms in-plane as long as the load P stays below a critical value \(P_s.\) For loads beyond this value, the structure starts to buckle laterally. An example deformation using \(P = 1.62\) N is shown in Fig. 6.
Since the in-plane deformation remains a stationary point of the energy even for loads larger than \(P_s,\) a perturbation needs to be applied to trigger the buckling. We do this by starting the trust-region method at the asymmetric initial iterate
This adds a little kink in the corner of the domain, which is enough to trigger the buckling.
A plot showing the lateral average displacement of \(\gamma _s\) is shown in Fig. 7. For comparison we have also given the corresponding plot from [54]. It can be seen that the critical value we obtain is between 1.188 and 1.224 N. This is in good agreement to the other values from the literature [3, 44, 45, 54], which we print in Table 2.
Behavior of the Riemannian trust-region solver for the configuration shown in Fig. 6. Left hyperelastic energy per iteration step. Center maximum norm of the correction per iteration. Right radius of the trust-region per iteration. The vertical axis has logarithmic scale in all three images. Note how the solver enters quadratic convergence after iteration 310, and how the trust-region opens up simultaneously
In a second step we want to highlight a few properties of the solver. For this we use the configuration described above with the surface load \(P= 1.62\) N at \(\gamma _s\) shown in Fig. 6. We solve the problem in a single loading step, using the trust-region method described in Sect. 5.2. For the quadratic minimization problems we use a monotone multigrid method as described in [40]. The \(\infty \)-norm is used to define the trust region. We scale the rotation part of the norm by a factor of \(10^{-3},\) so that corrections to the deformation (with numerical values in the two-digit range) are treated equally to corrections to the rotations (which cannot get larger than \(\pi \)).
We start the trust-region solver at the initial iterate given in (25) with an initial trust-region radius of 0.1.Footnote 2 We terminate the iteration as soon as the maximum norm of the correction drops below \(3\times 10^{-6}.\) This criterion was achieved after 334 iterations. Figure 8, left, shows the energy I per iteration (in a semi-logarithmic plot), and we observe that the trust-region method really is monotonically energy-decreasing. The sharp drop in the first few steps corresponds to a decrease of the membrane energy, which dominates the initial configuration (25).
Figure 8 also shows the correction step length and the trust-region radius per iteration step. We note that both remain bounded in the one-digit range until the solver reaches the vicinity of the minimizer at about iteration 310. At this point the behavior is as predicted by Theorem 11: the quadratic models start to match the energy functional very well. Correspondingly, the trust-region radius starts to increase, and the method turns into a pure Newton method. The expected fast local convergence can be observed in the plot of the correction step length. We stress that this solution is computed in a single loading step, i.e., without any path-following mechanism.
6.3 Torsion of a long elastic strip
The purpose of the next numerical example is to show that, unlike, e.g., the approach in [22], our discretization can easily handle large rotations. For this we simulate torsion of a long elastic strip, which we clamp at one short end. Using prescribed displacements, the other short edge is then rotated around the center line of the strip, to a final position of three full revolutions.
Let \(\omega = (0,\,100)\,\text {mm} \times (-5,\,5)\,\text {mm}\) be the parameter domain, and \(\gamma _0\) and \(\gamma _1\) be the two short ends. We clamp the shell on \(\gamma _0\) by requiring
and we prescribe a parameter dependent displacement
For each increase of t by 1 this models one full revolution of \(\gamma _1\) around the shell central axis. Homogeneous Neumann boundary conditions are applied to the remaining boundary degrees of freedom. The material parameters are given in Table 3. We discretize the domain with \(10 \times 1\) quadrilateral elements, and use second-order (nine-node) GFEs to discretize the problem.
The result is pictured in Fig. 9 for several values of t. Having little bending stiffness, the configuration stays symmetric throughout the parameter range. Indeed, by increasing the length scale parameter \(L_c\) one can produce materials that are stiffer in bending. Strips of such material buckle sideways even at only two revolutions.
In order to arrive at configurations with more than one full twist, several intermediate loading steps have to be taken. This is not because the Riemannian trust-region solver would not converge for \(t\ge 1.\) Rather, it would converge, but to a minimizer in the wrong homotopy group (i.e., the minimizing configuration would never show more than a single twist). We note also that the finite-strain membrane energy (11) is essential for this example. Indeed, there appears to be no stable local minimizer of the small-strain energy (3) that corresponds to a twofold rotated strip. When the energy-minimizing Riemannian trust-region algorithm is used to minimize the small-strain energy starting from the two-revolutions configuration, the algorithm converges to the completely planar configuration.
6.4 Wrinkling of a sheared rectangular plastic sheet
In our last numerical example we demonstrate that our shell model does indeed display microstructure. We do this by simulating the wrinkling of a thin rectangular plastic sheet under shearing. Such wrinkling has been studied experimentally by Wong and Pellegrino [52]. Numerical simulations of their experiments can be found in [53] using the commercial FE software Abaqus, and in [47] using a Koiter model with a finite difference discretization. We obtain a good match between their experimental and our numerical results.
Simulation results of the shearing tests. The color visualizes the elevation of the wrinkles, and the color scale has been chosen to match the one used in [47]. (Color figure online)
Experimental results of the shearing tests. Images taken from Wong and Pellegrino [52]
Wrinkle amplitudes at the plane \(y= 64\) mm. Black lines experimental results from Wong and Pellegrino [52]. Red lines our simulation results. Observe that the number of wrinkles is almost identical, but the amplitudes predicted by our simulation are generally too large. (Color figure online)
The experiment consists of a rectangular plastic sheet of dimension \(380\,\text {mm} \times 128\,\text {mm}.\) The sheet is clamped on the long horizontal edges, and free on the short vertical ones. More mathematically, we prescribe Dirichlet boundary conditions \(m(x,\,y) = (x,\,y,\,0),\,\overline{R}_3(x) = (0,\,0,\,1)^T\) on the lower horizontal edge. On the vertical sides of the domain we prescribe zero forces and moments. On the top horizontal side we apply a small horizontal shearing \(\delta _h\) and a vertical prestress \(\delta _v\) by prescribing the Dirichlet boundary condition \(m(x,\,y) = (x + \delta _h,\, y+\delta _v,\, 0),\,\overline{R}_3(x,\,y) = (0,\,0,\,1)^T.\)
Following Wong and Pellegrino, we set the Lamé constants to \(\mu = 5.6452 \times 10^9\,\mathrm {N}/\mathrm {m}^2\) and \(\lambda = 2.1796 \times 10^9\,\mathrm {N}/\mathrm {m}^2,\) which corresponds to the values \(E = 3.5\,\text {GPa},\nu = 0.31\) given in [52]. The shell thickness is \(h = 25\,\upmu \)m. Additionally, we set the Cosserat couple modulus \(\mu _c = 0,\) the curvature exponent \(q = 2,\) and the internal length scale \(L_c = 0.025\,\upmu \mathrm {m}.\) In [52], Wong and Pellegrino state that they vertically prestress their sheets slightly, but no numbers are given. For their own numerical simulations described in [53], they use a value of \(\delta _v = 0.5\) mm. In our own numerical experiments we found that \(\delta _v = 0.5\) mm leads to wrinkles that are too vertical, in particular if there is not much shearing. Low values of \(\delta _v\) on the other hand do not produce enough wrinkles. Best results were obtained using values between 0.2 and 0.4 mm.
We numerically reproduce two of the four shearing experiments described in [52]. The first has a shearing value of \(\delta _h = 0.5\) mm. For this we discretize the domain by a structured grid with \(120 \times 40 = 4800\) quadrilateral elements, and second-order GFEs. We set the vertical prestress to \(\delta _v = 0.2\) mm, and start the trust-region solver from the node-wise interpolant of the function
together with the Dirichlet boundary values on the top horizontal side. The cosine waves were added to break the initial symmetry. No attempt was made to influence the simulation results by deliberate adjustments of the initial value.
Plots of the wrinkle elevation are shown on the left of Fig. 10. The results of the corresponding experiment of Wong and Pellegrino can be seen in Fig. 11, also on the left. We obtain a very good quantitative match with our simulation. In particular, we obtain almost the same number of wrinkles (Fig. 12). Moreover, observe how the simulation faithfully reproduces a lot of the fine structure, such as the secondary wrinkles near the horizontal sides, and the wrinkles near the vertical sides.
On the other hand, the amplitudes predicted by our simulation are slightly larger than the ones observed in the experiments. Also, the wrinkles are inclined at a slightly steeper angle than the experimental ones. This suggests that the prestress values \(\delta _v\) is still too large. However, as mentioned above, a lower value of \(\delta _v\) leads to a lower number of wrinkles.
The second experiment uses a larger shear value of \(\delta _h = 3\) mm. With the other parameters as above we obtain a result that is qualitatively correct, but the number of wrinkles is less than what Wong and Pellegrino observed in their experiments. A better match is obtained by increasing the vertical prestress to \(\delta _v = 0.4\) mm and using a fine grid with \(240 \times 80 = 19,200\) elements. This simulation is what is plotted on the right of Figs. 10, 11, and 12. Now we observe a very good quantitative agreement also for this more extreme case, with the same restrictions as for the low-shear case. Since we have not observed artificial stiffness introduced by our discretization, we suspect that using the finer grid makes the trust-region algorithm end up in a different local minimizers of the energy.
Notes
Here we deliberately differ from [54], where a point load is used.
Note that this radius bounds both corrections to m and to \(\overline{R},\) so it cannot be assigned a unit.
In [40] it was proposed to use a Riemannian trust-region method instead of the simpler Newton method. Such a choice guarantees convergence of the solver. However, in practice we never observed convergence issues even for the simpler Newton method.
References
Absil P-A, Mahony R, Sepulchre R (2008) Optimization algorithms on matrix manifolds. Princeton University Press, Princeton
Absil P-A, Mahony R, Trumpf J (2013) An extrinsic look at the Riemannian Hessian. In: Geometric science of information, lecture notes in computer science, vol 8085. Springer, Berlin, pp 361–368
Argyris JH, Balmer H, Doltsinis JH, Dunne PC, Haase M, Kleiber M, Malejannakis GA, Mlejnek JP, Müller M, Scharpf DW (1979) Finite element method—the natural approach. Comput Methods Appl Mech Eng 17(18):1–106
Bartels S, Prohl A (2007) Constraint preserving implicit finite element discretization of harmonic map flow into spheres. Math Comput 76(260):1847–1859
Bastian P, Blatt M, Dedner A, Engwer C, Klöfkorn R, Kornhuber R, Ohlberger M, Sander O (2008) A generic grid interface for adaptive and parallel scientific computing. Part II: implementation and tests in DUNE. Computing 82(2–3):121–138
Bîrsan M, Neff P (2012) On the equations of geometrically nonlinear elastic plates with rotational degrees of freedom. Ann Acad Rom Sci Ser Math Appl 4:97–103
Bîrsan M, Neff P (2013) Existence theorems in the geometrically non-linear 6-parameter theory of elastic plates. J Elast 112:185–198
Bîrsan M, Neff P (2014a) On the characterization of drilling rotation in the 6-parameter resultant shell theory. In: Pietraszkiewiecz W, Górski J (eds) Shell structures: theory and applications, vol 3. CRC Press/Balkema, Taylor and Francis Group, London, pp 61–64
Bîrsan M, Neff P (2014) Shells without drilling rotations: a representation theorem in the framework of the geometrically nonlinear 6-parameter resultant shell theory. Int J Eng Sci 80:32–42
Bîrsan M, Neff P (2014) Existence of minimizers in the geometrically non-linear 6-parameter resultant shell theory with drilling rotations. Math Mech Solids 19(4):376–397
Braess D (2013) Finite Elemente, 5th edn. Springer, Berlin
Chróścielewski J, Makowski J, Pietraszkiewicz W (2004) Statics and dynamics of multifold shells: nonlinear theory and finite element method. Wydawnictwo IPPT PAN, Warsaw (in Polish)
Conn A, Gould N, Toint P (2000) Trust-region methods. SIAM, Philadelphia
Crisfield M, Jelenić G (1999) Objectivity of strain measures in the geometrically exact three-dimensional beam theory and its finite-element implementation. Proc R Soc Lond A 455:1125–1147
Dornisch W, Klinkel S (2014) Treatment of Reissner–Mindlin shells with kinks without the need for drilling rotation stabilization in an isogeometric framework. Comput Methods Appl Mech Eng 276:35–66
Dornisch W, Klinkel S, Simeon B (2013) Isogeometric Reissner–Mindlin shell analysis with exactly calculated director vectors. Comput Methods Appl Mech Eng 253:491–504
Ebbing V, Balzani D, Schröder J, Neff P, Gruttmann F (2009) Construction of anisotropic polyconvex energies and applications to thin shells. Comput Mater Sci 46:639–641
Eremeyev V, Pietraszkiewicz W (2006) Local symmetry group in the general theory of elastic shells. J Elast 85:125–152
Griewank A, Walther A (2008) Evaluating derivatives: principles and techniques of algorithmic differentiation, 2nd edn. SIAM, Philadelphia
Grohs P, Hardering H, Sander O (2014) Optimal a priori discretization error bounds for geodesic finite elements. Found Comput Math. doi:10.1007/s10208-014-9230-z
Groisser D (2004) Newton’s method, zeroes of vector fields, and the Riemannian center of mass. Adv Appl Math 33(1):95–135
Gruttmann F, Wagner W, Meyer L, Wriggers P (1993) A nonlinear composite shell element with continuous interlaminar shear stresses. Comput Mech 13:175–188
Hakula H, Leino Y, Pitkäranta J (1996) Scale resolution, locking, and high-order finite element modelling of shells. Comput Methods Appl Mech Eng 133(3–4):157–182
Karcher H (1977) Mollifier smoothing and Riemannian center of mass. Commun Pure Appl Math 30:509–541
Kendall WS (1990) Probability, convexity, and harmonic maps with small image. I: uniqueness and fine existence. Proc Lond Math Soc s3–61(2):371–406
Kornhuber R (1997) Adaptive monotone multigrid methods for nonlinear variational problems. B.G. Teubner, Stuttgart
Libai A, Simmonds J (1998) The nonlinear theory of elastic shells, 2nd edn. Cambridge University Press, Cambridge
Müller W (2009) Numerische Analyse und Parallele Simulation von nichtlinearen Cosserat-Modellen. PhD Thesis, Karlsruher Institut für Technologie
Münch I (2007) Ein geometrisch und materiell nichtlineares Cosserat-Model — Theorie, Numerik und Anwendungsmöglichkeiten. PhD Thesis, Universität Karlsruhe
Neff P (2002) On Korn’s first inequality with nonconstant coefficients. Proc R Soc Edinb 132A:221–243
Neff P (2004) A geometrically exact Cosserat-shell model including size effects, avoiding degeneracy in the thin shell limit. Part I: formal dimensional reduction for elastic plates and existence of minimizers for positive Cosserat couple modulus. Contin Mech Thermodyn 16:577–628
Neff P (2005) A geometrically exact viscoplastic membrane-shell with viscoelastic transverse shear resistance avoiding degeneracy in the thin-shell limit. Part I: the viscoelastic membrane-plate. ZAMP 56(1):148–182
Neff P (2006) The Cosserat couple modulus for continuous solids is zero viz the linearized Cauchy-stress tensor is symmetric. Z Angew Math Mech 86:892–912
Neff P (2007) A geometrically exact planar Cosserat shell-model with microstructure: existence of minimizers for zero Cosserat couple modulus. Math Models Methods Appl Sci 17:363–392
Neff P, Fischle A, Münch I (2008) Symmetric Cauchy-stresses do not imply symmetric Biot-strains in weak formulations of isotropic hyperelasticity with rotational degrees of freedom. Acta Mech 197:19–30
Neff P, Hong K-I, Jeong J (2010) The Reissner–Mindlin plate is the \(\Gamma \)-limit of Cosserat elasticity. Math Models Methods Appl Sci 20:1553–1590
Neff P, Ghiba I, Madeo A, Placidi L, Rosi G (2014a) The relaxed micromorphic continuum: existence, uniqueness and continuous dependence in dynamics. Math Mech Solids. doi:10.1177/1081286513516972
Neff P, Ghiba I, Madeo A, Placidi L, Rosi G (2014b) A unifying perspective: the relaxed linear micromorphic continuum. Contin Mech Thermodyn 26:639–681
Pompe W (2003) Korn’s first inequality with variable coefficients and its generalizations. Comment Math Univ Carol 44:57–70
Sander O (2012) Geodesic finite elements on simplicial grids. Int J Numer Methods Eng 92(12):999–1025
Sander O (2015) Geodesic finite elements of higher order. IMA J Numer Anal. doi:10.1093/imanum/drv016
Schröder J, Neff P, Ebbing V (2008) Anisotropic polyconvex energies on the basis of crystallographic motivated structural tensors. J Mech Phys Solids 56(12):3486–3506
Simo J, Fox D (1989) On a stress resultant geometrically exact shell model. Part I: formulation and optimal parametrization. Comput Methods Appl Mech Eng 72:267–304
Simo J, Vu-Quoc L (1986) A three-dimensional finite-strain rod model. Part II: computational aspects. Comput Methods Appl Mech Eng 58(1):79–116
Simo J, Fox D, Rifai M (1990) On a stress resultant geometrically exact shell model. Part III: computational aspects of the nonlinear theory. Comput Methods Appl Mech Eng 79(1):21–70
Steigmann DJ (2013) Koiter’s shell theory from the perspective of three-dimensional nonlinear elasticity. J Elast 111(1):91–107
Taylor M, Bertoldi K, Steigmann DJ (2014) Spatial resolution of wrinkle patterns in thin elastic sheets at finite strain. J Mech Phys Solids 62:163–180
Walther A, Griewank A (2012) Getting started with ADOL-C. In: Naumann U, Schenk O (eds) Combinatorial scientific computing. Chapman-Hall CRC Computational Science, Boca Raton. pp 181–202
Weinberg K, Neff P (2008) A geometrically exact thin membrane model—investigation of large deformations and wrinkling. Int J Numer Methods Eng 74(6):871–893
Wiśniewski K (2010) Finite rotation shells. Basic equations and finite elements for Reissner kinematics. Springer, Dordrecht
(1974) Spaces of constant curvature, 3rd edn. Publish or Perish, Inc., Boston
Wong YW, Pellegrino S (2006a) Wrinkled membranes part I: experiments. J Mech Mater Struct 1(1):1–23
Wong YW, Pellegrino S (2006b) Wrinkled membranes part III: numerical simulations. J Mech Mater Struct 1(1):63–95
Wriggers P, Gruttmann F (1993) Thin shells with finite rotations formulated in Biot stresses: theory and finite element formulation. Int J Numer Methods Eng 36:2049–2071
Acknowledgments
The authors would like to thank Kshitij Kulshreshtha for his help with the ADOL-C automatic differentiation system, and Ingo Münch for the interesting discussions on the discretization of finite strain Cosserat problems.
Author information
Authors and Affiliations
Corresponding author
Additional information
This article was written while Oliver Sander was employed at the Institut für Geometrie und Praktische Mathematik, RWTH Aachen, Germany.
Appendix: Implementation of geodesic finite elements for \(\text {SO}(3)\)
Appendix: Implementation of geodesic finite elements for \(\text {SO}(3)\)
In this Appendix we explain how the geodesic interpolation (Definition 1) that forms the basis of the GFE method can be implemented in practice. Since the definition of the interpolation function
uses a minimization formulation, its use in practice warrants a few explanations.
The Cosserat shell energies of Sect. 2 are both first-order energies. Hence, to evaluate them for a given GFE function \(\overline{R}_h\) we need to compute function values \(\overline{R}_h(x) \in \text {SO(3)}\) and first derivatives \(\nabla \overline{R}_h(x){\text {:}}\,{\mathbb {R}}^2 \rightarrow T_{\overline{R}_h(x)}\text {SO(3)}\) at given (quadrature) points \(x \in \omega .\) Using the integral transformation formula this can be reduced to computing values and first derivatives of the interpolation function \(\Upsilon \) on the reference element \(T_\mathrm{ref}.\)
Finding minimizers of the energy by a Riemannian trust-region method additionally requires the gradient \(\nabla \bar{I}\) and the Hessian \(\text {Hess}\bar{I}\) of the algebraic Cosserat shell energy (15). By the chain rule, expressions for these include derivatives of \(\Upsilon \) and \(\nabla \Upsilon \) with respect to the coefficients \(R_1,\ldots ,R_m.\) These can in principle be computed semi-analytically [40]. However, we have found using an AD system much more convenient (see Sect. 5.3).
1.1 Quaternion coordinates for \(\text {SO}(3)\)
While the construction and theory of GFEs is completely coordinate-free, an implementation necessarily needs some sort of coordinates for \(\text {SO(3)}.\) The naive approach uses the canonical embedding of \(\text {SO(3)}\) into \({\mathbb {R}}^{3 \times 3}.\) However, quaternion coordinates allow a more efficient implementation.
Let
be the set of unit quaternions, i.e., the unit sphere \(S^3 \subset {\mathbb {R}}^4\) equipped with quaternion multiplication
The unit quaternions \({\mathbb {H}}_{{|1|}}\) form a smooth compact manifold embedded in \({\mathbb {R}}^4,\) and global coordinates on \({\mathbb {H}}_{{|1|}}\) are naturally given by this embedding. The tangent space at a point \(p \in {\mathbb {H}}_{{|1|}}\) is
hence tangent vectors \(v \in T_p {\mathbb {H}}_{{|1|}}\) can be treated as vectors in \({\mathbb {R}}^4.\) For any \(q\in {\mathbb {H}}_{|1|},\) the projection \(P_q{\text {:}}\,T_q{\mathbb {R}}^4 \rightarrow T_q {\mathbb {H}}_{|1|}\) is given by
A Riemannian structure for \({\mathbb {H}}_{{|1|}}\) is obtained by inheriting the metric of the surrounding space
For a point \(p \in {\mathbb {H}}_{{|1|}}\) and a tangent vector \(v \in T_p {\mathbb {H}}_{{|1|}},\) the exponential map \(\exp _p{\text {:}}\,T_p {\mathbb {H}}_{{|1|}} \rightarrow {\mathbb {H}}_{{|1|}}\) is then given by [1, Example 5.4.1]
The unit quaternions can be used to represent rotations, because there is a natural relationship between \({\mathbb {H}}_{{|1|}}\) and \(\text {SO(3)}.\) More precisely, the map \(F{\text {:}}\, {\mathbb {H}}_{{|1|}} \rightarrow {\mathbb {R}}^{3 \times 3}\)
is a Lie group homomorphism from \({\mathbb {H}}_{{|1|}}\) onto \(\text {SO(3)}.\) It is two-to-one, meaning that for each point \(p \in {\mathbb {H}}_{{|1|}}\) there is exactly one other point, namely \({-}p,\) representing the same rotation \(F(p) = F(-p) \in \text {SO(3)}.\) Using quaternion coordinates for rotations reduces the memory footprint and computing times considerably. For the rest of this chapter we use upper case letters \(Q,\,R\) for elements of \(\text {SO(3)},\) and lower case letters \(p,\,q\) for quaternions.
1.2 The canonical distance of \(\text {SO}(3)\) in quaternion coordinates
The metric structure of the set of unit quaternions is identical to the metric structure of the unit sphere in \({\mathbb {R}}^4.\) The geodesics of \({\mathbb {H}}_{{|1|}}\) are the segments of great circles. Any two points \(p,\,q \in {\mathbb {H}}_{{|1|}}\) can be connected by such segments; hence \({\mathbb {H}}_{{|1|}}\) is geodesically complete. If \(p \ne -q\) there is a unique shortest geodesic that connects p and q. For all pairs of points \(p = {-}q\) there are infinitely many minimizing geodesics, each of length \(\pi .\) Hence the injectivity radius of \({\mathbb {H}}_{{|1|}}\) is \(\text {inj}({\mathbb {H}}_{{|1|}}) = \pi .\)
The Riemannian distance between two points p and q is the length of the shortest arc of a great circle connecting p to q. Let \(\gamma {\text {:}}\,[0,\,1] \rightarrow S^3\) be such an arc. Its length is given by
We now use this to express the canonical distance on \(\text {SO}(3)\) in terms of quaternion coordinates. To avoid confusion we now always write \(\text {dist}_{{\mathbb {H}}_{{|1|}}}\) or \(\text {dist}_{\text {SO(3)}}.\) First note that F defined in (28) is a scaling in the sense that
for any \(v \in T_q {\mathbb {H}}_{{|1|}}.\) Let \(R_1,\, R_2 \in \text {SO(3)}\) be two rotations and let \(p,\,q \in {\mathbb {H}}_{{|1|}}\) be such that \(F(p) = R_1\) and \(F(q) = R_2.\) We first consider the simpler case that \(\text {dist}_{{\mathbb {H}}_{{|1|}}}(p,\,q) < \pi /2.\) Suppose that \(\gamma \) is the shortest path from p to q. Then, by (30), \(F(\gamma )\) is a shortest path from F(p) to F(q) in \(\text {SO(3)},\) and
For the general case, we also have to take into account that \({\mathbb {H}}_{{|1|}}\) is a double cover of \(\text {SO}(3).\) Let \(p,\,q \in {\mathbb {H}}_{{|1|}}\) be such that \(\text {dist}_{{\mathbb {H}}_{{|1|}}}(p,\,q) > \pi /2.\) Then q represents the same element of \(\text {SO}(3)\) as \({-}q,\) but \(\text {dist}_{{\mathbb {H}}_{{|1|}}}(p,\,{-}q) = \pi - \text {dist}_{{\mathbb {H}}_{{|1|}}}(p,\,q) < \pi /2.\) The distance on \(\text {SO}(3)\) for arbitrary \(p,\,q\) given in terms of the distance on \({\mathbb {H}}_{{|1|}}\) is therefore
Note that this metric is continuous, but not differentiable at points \(p,\,q\) with \(\text {dist}_{{\mathbb {H}}_{{|1|}}}(p,\,q) = \pi /2.\) This comes as no surprise as this is precisely the case when F(q) is in the cut locus of F(p).
For an algorithmic evaluation of the interpolation formula (26) we will need first and second derivatives of \(\text {dist}_{\text {SO(3)}}(R,\,\cdot )^2\) with respect to its second argument, for fixed arbitrary \(R \in \text {SO(3)}.\) We use (31), and Lemmas 12 and 13 on the derivatives of scalar-valued functions on embedded manifolds. For these, we need an extension of \(\text {dist}_{{\mathbb {H}}_{{|1|}}}\) to a neighborhood of \({\mathbb {H}}_{{|1|}}\) in \({\mathbb {R}}^4.\) We choose
This is well-defined and smooth on a neighborhood of \({\mathbb {H}}_{|1|}\) in \({\mathbb {R}}^4.\) For ease of notation we define \(\alpha {\text {:}}\,[{-}1,\,1] \rightarrow {\mathbb {R}},\,\alpha (x) :=\arccos ^2(x).\)
We now compute the first derivative of \(\text {dist}_{\text {SO(3)}}(R,\,\cdot )^2\)
for arbitrary but fixed \(R \in \text {SO(3)}.\) Note that
With (22), (29), and \({|q|} = 1\) we get for the coefficients \(i=1,\ldots ,4\) of (32)
where p is any one of the two points on \({\mathbb {H}}_{{|1|}}\) with \(F(p) = R.\) Note that since \(\text {dist}_{{\mathbb {H}}_{{|1|}}}(p,\,q) \le \pi /2\) if and only if \(\langle p,\,q\rangle \ge 0\) this is equivalent to
The derivative of \(\alpha (x) = \arccos ^2(x)\) can be given in closed form
However, this expression gets numerically unstable around \(x=1.\) There, the series expansion
has to be used instead.
For the second derivative of \(\text {dist}_{\text {SO(3)}}(R,\,\cdot )^2\) we note that
for any \(p \in {\mathbb {R}}^4.\) Using Lemma 13 we obtain
where again \(p \in {\mathbb {H}}_{{|1|}}\) is such that \(F(p) = R.\)
The second derivative of \(\alpha (x)\) is
Again, near \(x=1\) this gets unstable and has to be replaced by its series expansion
1.3 Evaluation of geodesic interpolation functions
We now discuss how values and first derivatives of the interpolation function \(\Upsilon \) can be computed in practice. Unfortunately, there are no closed-form expressions for the solution of the minimization problem (26), and it therefore needs to be solved numerically. As its objective functional (written in quaternion coordinates)
is defined on the Riemannian manifold \({\mathbb {H}}_{{|1|}} \subset {\mathbb {R}}^4\) we use a Riemannian Newton method as presented in [1].Footnote 3 Under the assumptions of Theorems 4 (for \(p=1\)) and 5 (for \(p>1\)), \(f_\xi \) is \(C^\infty \) ([40, Lemma 2.4]), and strictly convex on an open geodesic ball containing the \(R_i\) ([24, Theorem 1.2] and [41, Lemma 3.11], respectively).
One step of the Riemannian Newton method on \({\mathbb {H}}_{{|1|}}\) takes the following form. With k the iteration number let \(q_k \in {\mathbb {H}}_{{|1|}}\) be the current iterate. We use the exponential map \(\exp _{q_k}{\text {:}}\,T_{q_k} {\mathbb {H}}_{{|1|}} \rightarrow {\mathbb {H}}_{{|1|}}\) (see (27)) to define lifted functionals
The Newton update at step k is then
Using \(\nabla \exp 0 = \text {Id}\) we see that the gradient of \(\hat{f}_k\) at \(0 \in T_{q_k} {\mathbb {H}}_{{|1|}}\) is
and that the Hessian is
The two derivatives of the distance function have been given in (33) and (34). The matrix \(\text {Hess}\hat{f}_k(0)\) is \(4 \times 4,\) and has a one-dimensional kernel, which is the normal space of \(S^3\) in \({\mathbb {R}}^4\) at \(q_k.\) We use a rank-aware direct solver for the Newton update systems (35). The Newton solver typically needs only a handful of iterations to converge up to machine precision.
In the proof of Lemma 6 the implicit function theorem was used to show under what circumstances the derivative \(\partial \Upsilon / \partial \xi \) exists. Here we use it again for the actual computation. For ease of notation we introduce \(\widetilde{\Upsilon } :=F^{-1}(\Upsilon ),\) which gives interpolation points expressed as quaternions. By [40, Lemma 2.4] the functional \(f_\xi \) is smooth. Hence, its minimizer can be characterized by
where
Taking the total derivative of (36) with respect to \(\xi \) we get
By [41, Lemma 3.11] the matrix
is invertible on the three-dimensional subspace \(T_{\widetilde{\Upsilon }(R_1,\ldots ,R_m;\,\xi )} {\mathbb {H}}_{{|1|}} \subset {\mathbb {R}}^4,\) and hence \(\partial \widetilde{\Upsilon }(R_1,\ldots ,R_m;\,\xi ) / \partial \xi \) can be computed as the solution of the linear system of equations
Using the definition (37) we see that in coordinates \(\partial \Phi / \partial \xi \) is a \(4 \times 2\)-matrix, where the ith column is
Hence evaluating the derivative of a GFE function amounts to an evaluation of its value (to know where to evaluate the derivatives of \(\Phi \)) and the solution of the symmetric linear system (38).
Rights and permissions
About this article
Cite this article
Sander, O., Neff, P. & Bîrsan, M. Numerical treatment of a geometrically nonlinear planar Cosserat shell model. Comput Mech 57, 817–841 (2016). https://doi.org/10.1007/s00466-016-1263-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00466-016-1263-5