1 Introduction

Self-potential survey is performed mainly for mineral exploration, geothermal exploration, cavity detection, hydrogeophysics and environmental and engineering investigations. Our target is to determine the model parameters of a buried structure of economic interest such as ore mineralization from self-potential anomalies which reveal themselves as anomalies on the maps or the profiles. Many authors solved such problem (Anderson, 1984; Corwin, 1984; Corwin & Hover, 1979; Fitterman & Corwin, 1982; Jouniaux et al., 2009; Markiewicz et al., 1984; Oliveti & Cardarelli, 2019; De Witte, 1948; Yungul, 1950). Mehanee (2014) and Biswas (2017) give interesting reviews. The measured anomalies are mainly used in qualitative means that is to help geological conclusions. Nevertheless, a single residual anomaly might be clear and so simple in appearance so it can be identified from the regional background and the nearby geologic interferences. In this case, it can be considered as a result of a single structure. Consequently, it would be very helpful to use quantitative techniques to determine the depth and shape of the buried object by simulating a model with simple geometry.

Simultaneous determination of the depth and shape of a buried structure from self-potential data has drawn considerable attention. Abdelrahman and Sharafeldin (1997) developed a least-squares minimization technique to obtain the parameters of the buried bodies from residual self-potential anomaly profiles. On the other hand, Abdelrahman et al. (l998) and Essa (2019) showed that numerical horizontal derivative anomalies and moving residual anomalies obtained from SP data using filters of successive window lengths could be utilized to resolve the shape and depth of a buried object. Gobashy (2000) showed that the ill-posed SP inverse problem is also an ill conditioned and non-linear problem, such complex ill-posed conditions were greatly damped by simultaneous minimization of an objective function of depth and shape factor using nonlinear simplex polytope algorithm. Abdelazeem and Gobashy (2006) used the Genetic algorithm for a fast and stable inversion for the true parameters through the optimization of objective function even when adding high level of noise to synthetic data. Fedi and Abbas (2013) have calculated the depth using Extreme Points method (DEXP) on self-potential data.

Moreover, several other excellent numerical methods were reported in the geophysical literatures for interpreting SP anomalies. Patella (1997) and Revil et al. (2001) presented the tomography technique for the identification of an underground causative SP source system assuming that the monopole charge accumulates and extends the distribution of dipoles, respectively. Minsley et al. (2007) utilized a model regulation approach that selects a class of solutions which fit the data with 3D sources that are spatially compact. Moreover, an algorithm to locate self-potential sources was developed by Gibert and Pessel (2001) using the wavelet analysis. Eventually, Biswas and Sharma (2015) presented a simulated annealing global optimization scheme for the sake of interpreting self-potential anomaly of idealized bodies. However, they indicated that the optimization method is able to determine all model parameters accurately when the shape factor is fixed in the process. Obviously, the limitations of most of the above algorithms are that they may not interpret a self-potential anomaly profile of a short length. Also, in these methods a very good match between the model and observations may have taken place but this does not necessarily guarantee that the correct solution has been found, particularly, when dealing with field problems.

More recently, Abdelrahman et al. (2019) developed a minimization approach to depth and shape determination from self-potential anomalies due to sources of simple geometry (e.g., spheres, cylinders, dikes, contacts) that resemble mineralized bodies. In their method, the Nelder–Mead simplex algorithm is applied to solve a nonlinear equation in depth for each fixed shape factor using the anomaly values at few points on the anomaly profile. The algorithm is achieved through two steps. First, it computes the standard deviation of the depths determined using different characteristic distances for each value of the shape factor. Second, it chooses the optimum shape and depth with minimum standard deviation. However, most of the minimization approaches solve nonlinear equations to determine the model parameters of the buried mineralized zone from self-potential anomalies using usually lengthy and tedious procedures. Also, the least-squares minimization methods have no capability of avoiding highly noisy data points. Finally, Abdelazeem et al. (2019) introduced a meta- heuristic algorithm to provide a solution to self-potential anomalies. The method is based on utilizing Whale optimization algorithm which gives good approximation solution.

In the present paper, we introduce a simple and fast method to determine automatically the depth, shape, polarization angle, and electric dipole moment from residual self-potential (SP) anomalies due ore bodies of simple geometry. The calculation needs only four characteristic points defining the anomaly and their corresponding distances on the anomaly profile. The inverse problem of depth determination from residual SP anomaly is solved by a linear equation for each shape factor. Using all successful combinations of the four characteristic points and their corresponding distances, a procedure is developed and practiced for automated determination of the best model parameters. Because the present method uses all successful combinations of data points, it has the capability of enhancing the interpretation results. The benefits of the proposed method over both the linear and non-linear least squares methods is that it is capable of minimizing the effect of errors in the data points which results in an enhanced interpretation outcome. The technique is practiced on noisy synthetic data. The validity, the technique is applied to two field examples from Indonesia and Turkey. Within all the examined cases, the resulting depths and shapes are in a very good agreement with actual ones.

2 Theory

The general self-potential anomaly expressions generated by a sphere, an infinitely long horizontal cylinder and a semi-infinite vertical cylinder can be presented as (Abdelrahman & Sharafeldin, 1997)

$$V\left({x}_{i},z,q\right)=K\frac{{x}_{i}\mathrm{cos}\theta +z\mathrm{sin}\theta }{({x}_{i}^{2}+{z}^{2}{)}^{q}},$$
$$q = \left\{ {\begin{array}{*{20}l} {0.5\quad {\text{for}}\quad {\text{a}}\;{\text{~semi-infinite~}}\;{\text{vertical~}}\;{\text{cylinder~~}}} \\ {1.0\quad {\text{for}}\quad {\text{~a~}}\;{\text{horizontal~}}\;{\text{cylinder~~}}} \\ {1.5\quad {\text{for~}}\quad {\text{a~}}\;{\text{sphere}}} \\ \end{array} .} \right.$$
$$i = 0, + 1,2,3, \ldots ,N,$$
(1)

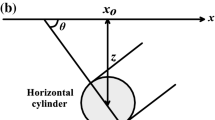
z is the depth of the body, xi the horizontal position coordinate, K the electric dipole moment, Ψ the polarization angle, and q is the shape factor. The geometries are shown in Fig. 1.

Fig. 1
figure 1

Parameters for a sphere and a horizontal cylinder (a) and a vertical cylinder (b) used in this study

Full size image

For all shapes (q), Eq. (1) gives the following four SP anomaly values: V(N), V–N). V(M) and V(− M) at their corresponding distances xi =  ± N, and xi =  ± M, respectively

$$V\left(N\right)=K\frac{N\mathrm{cos}\psi +z\mathrm{sin}\psi }{({N}^{2}+{z}^{2}{)}^{q}},$$
(2)
$$V\left(-N\right)=K\frac{-N\mathrm{cos}\psi +z\mathrm{sin}\psi }{({N}_{}^{2}+{z}^{2}{)}^{q}},$$
(3)
$$V\left(M\right)=K\frac{M\mathrm{cos}\psi +z\mathrm{sin}\psi }{({M}^{2}+{z}^{2}{)}^{q}},$$
(4)

and

$$V\left(-M\right)=K\frac{-M\mathrm{cos}\psi +z\mathrm{sin}\psi }{({M}^{2}+{z}^{2}{)}^{q}}.$$
(5)

Let F = V(N) − V(− N) and L = V(M) − V(− M), then using Eqs. (2), (3), (4) and (5), we obtain

$$F=2K\frac{N\mathrm{cos}\psi }{({N}_{}^{2}+{z}^{2}{)}^{q}},$$
(6)

and

$$L=2K\frac{M\mathrm{cos}\psi }{({M}_{}^{2}+{z}^{2}{)}^{q}}.$$
(7)

Using Eqs. (6) and (7), we obtain.

$$z=\sqrt{\frac{(\text{PM/N}{)}^{\text{1/q}}{N}^{2}-{M}^{2}}{(1-(\text{PM/N}{)}^{\text{1/q}})}},$$
(8)

where

$${\text{P }} = {\text{F}}/{\text{L}}$$

In this way, we are able to eliminate K and \(\psi\) from Eq. (1) by introducing four pieces of information, namely, V(N), V(− N), V(M), and V(− M).

For all shapes, Eq. (8) will converge to a depth solution when N ≠ M, N + M ≠ 0, \((\text{PM/N}{)}^{\text{1/q}}{N}^{2}>{M}^{2}\), and \(1>(\text{PM/N}{)}^{\text{1/q}}\). These conditions should be implemented in any computer program in order to determine a reliable depth estimate from all successful combinations of N and M. Theoretically, one successful value of N and M is sufficient to determine the depth to the buried structure from Eq. (8), but in practice, more successful combinations of N and M is desirable because of the presence of noise in the data. However, Eq. (8) can be also used not only to determine the depth but also to estimate simultaneously the shape of the buried structure.

For each N and M value, apply Eq. (8) to the residual anomaly profile, yielding depth solutions (z) for all possible q values. We then compute the standard deviation of depths for each value of the shape factor. A search algorithm is used to find the value of the shape factor at which the standard deviation of the depths is a minimum. The minimum standard deviation is used as a criterion for determining the optimum depth and the shape of the buried body. When the best value of the shape is used, the resulting standard deviation of the depths is always less than the standard deviations computed when using wrong values of the shape factor. The average depth of all depths computed from all successful combinations at the best shape factor is taken as the best depth of the buried structure.

Moreover, let S = V(N) + V(− N), then using Eqs. (2) and (3), we obtain

$$S=2K\frac{z\mathit{sin}\psi }{({N}^{2}+{z}^{2}{)}^{q}}.$$
(9)

Knowing the computed depth (zc) and the shape factor qc, and using Eqs. (6) and (9), the polarization angle and the eclectic dipole moment can be computed from the following relationships, respectively

$$\psi _{{\text{c}}} = {\text{tan}}^{{ - {\text{1}}}} \left( {{\text{SN }}/{\text{ F z}}_{{\text{c}}} } \right),$$
(10)

and

$${\text{k}}_{{\text{c}}} ~ = ~{\text{S}}({\text{N}}^{{\text{2}}} + {\text{z}}^{{\text{2}}} _{{\text{c}}} )^{{\text{q}}} /{\text{ 2 z}}_{{\text{c}}} {\text{sin}}\Psi _{{\text{c}}}$$
(11)

which are valid for any N value. For each N value, knowing the four model parameters, Eq. (1) is used to generate the inverted field. We then measure the goodness of fit between the observed values and the values computed from the estimated parameters. The simplest way to compare two self-potential profiles is to compute the root-mean-square (rms) of the differences between the observed and the fitted anomalies. A search algorithm is then used to find the N value at which the model parameters give the minimum rms between the observed data and inverted data. The model parameters which give the least root-mean-square error are the best and the used N is the best one.

A pseudo code for the proposed search algorithm which is used to determine the best depth, shape factor, polarization angle, and the electric dipole moment using STD and rms criteria is as follows:

figure a

To summarize, the automatic interpretation scheme based on the above procedures for analyzing real data is illustrated in Fig. 2a,b.

Fig. 2
figure 2

a Search algorithm for best q and z using minimum standard deviation. b Search algorithm for best psi and k using minimum rms.

Full size image

3 Theoretical Examples

We have computed three different residual self-potential anomalies due to a semi−infinite vertical cylinder (q = 0.5, z = 3 units, ψ = 50°, and k = − 50 mV) a horizontal cylinder(q = 1, z = 5 units, ψ = 40°, and k = − 300 mV), and a sphere(q = 1.5, z = 8 unit, ψ = 50°, and k = − 800 mV) each with a profile length = 30 units with 1 unit interval. The model equations are:

$$V_{1} \left( {x_{i} ,z,q} \right) = - 50\frac{{x_{i} \cos 50{^\circ } + 3\sin 50{^\circ }}}{{(x_{i}^{2} + 3^{2} )^{{0.5}} }},\;{\text{for}}\;{\text{ semi-infinite}}\;{\text{ vertical }}\;{\text{cylinder,}}$$
(12)
$$V_{2} \left( {x_{i} ,z,q} \right) = - 300\frac{{x_{i} \cos 40{^\circ } + 5\sin 40{^\circ }}}{{(x_{i}^{2} + 5^{2} )^{{1.0}} }},\;{\text{ for }}\;{\text{horizontal }}\;{\text{cylinder,}}$$
(13)

and

$$V_{3} \left( {x_{i} ,z,q} \right) = - 800\frac{{x_{i} \cos 50{^\circ } + 8\sin 50{^\circ }}}{{(x_{i}^{2} + 8^{2} )^{{1.5}} }},~\;{\text{for}}\;{\text{ sphere}}.$$
(14)

To test the stability of our method in the presence of noise. we have added 10% as a suitable percentage of Gaussian random errors to each residual self-potential anomaly to produce noisy data using the following equation

$${V}_{rnd1}({x}_{i})={V}_{1}({x}_{i})\left[1+(RND(i)-0.5)\times 0.1\right],$$
(15)

where Vrnd1(xi) is the contaminated anomaly value at xi and RND (i) is a pseudo-random number whose range is (0, 1). The interval of the pseudo random number is an open interval, i.e. it does not include the extremes values 0 and 1.

Equation (8) has been applied to each noisy residual anomaly profile, yielding depth solutions for all possible q values (0.1, 0.2, 0.3, …, and 1.5) for all successful combinations of N and M. The standard deviation search algorithm is used to determine the best depth and shape factor. For each N value, we computed the best polarization angle and the dipole moment from Eqs. (10) and (11), respectively. The numerical results are given in Table 1. In this Table, it is numerically verified that when the data contain 10% random errors, the minimum STD and minimum rms occur at z = 3.16 units, q = 0.5, Ψ = 48.57, and k = − 48.32 mV for the semi-infinite vertical cylinder model; z = 5.26 units and q = 1.0, Ψ = 37.35°, for the horizontal cylinder model; and z = 8.34 units and q = 1.5, Ψ = 46.07°, and k = − 789.5 mV, for the sphere model. In all cases, the estimated model parameters are in good agreement with true ones (Figs. 3, 4, and 5). In all cases examined, the range of the percentage of error varies from 0.0 to 6.6. This percentages are practically accepted when interpreting noisy data. This demonstrates that the present method will give reliable model parameters (z, q, Ψ, and K) even when the residual self-potential anomaly is contaminated with random errors.

Fig. 3
figure 3

Noisy synthetic anomaly (V1) of a buried semi-infinite vertical cylinder as obtained from Eq. (11) after adding 10% random error

Full size image
Fig. 4
figure 4

Noisy synthetic anomaly (V2) of a buried horizontal cylinder as obtained from Eq. (12) after adding 10% random error

Full size image
Fig. 5
figure 5

Noisy synthetic anomaly (V3) of a buried sphere as obtained from Eq. (13) after adding 10% random error

Full size image

4 Field Examples

To examine the applicability of the present method, the following mineral field examples are presented.

4.1 Buried Drum Self-Potential Anomaly, Bandung, Indonesia

Figure 6a shows the self-potential anomaly measured over a metallic drum containing powder and metal junk, with 0.6 m diameter and length equals 1.2 m buried at depth of 2.5 m (Srigutomo et al., 2006).The length of the anomaly profile is 6.56 m and digitized at interval of 0.82 m. The obtained results using the present approach are given in Fig. 6, where 1396 successful combinations are used. Figure 6b shows the Subsurface structure (modified after SUNGKONO, 2020). The model parameters are very close to the true model parameters given by Srigutomo et al., (2006), and Abdelazeem et al., (2019). The model misfits some measurable values because the field data are influenced by the surrounding medium transverse anisotropy.

Fig. 6
figure 6

a Observed SP profile over a buried drum model, Bandung, Indonesia. b Subsurface structure (modified after SUNGKONO, 2020)

Full size image

4.2 Suleymnkoy Anomaly, Turkey

Figure 7 shows the Suleymnkoy SP anomaly map, Ergani Copper district, Turkey. The sp measurements were performed and described in Yungul (1950). A self-potential anomaly profile of 165 m length along the line AA′ of this map is shown in Fig. 8. The anomaly profile is digitized at an interval of 1.0313 m. The total number of data points is 161. We applied our interpretation method to the observed anomaly thus obtained. 119,256 successful combinations of N and M were used from a total of 285,131 when the range of q values is from 0.5 to 1.5 step 0.1. The results are summarized in Fig. 8. The minimum STD and rms values occurs at q = 1.3, z = 43.1 m, \(\psi\) =12.9°, and k = − 157,805 mV. This suggests that the shape of the ore body can be approximated by a sphere or, practically, two superimposed structures of different shapes buried at a depth of about 43 m. The computed anomaly profile using the parameters obtained by our method, agrees with the observed profile (Fig. 8). The results agree well with those obtained in Yungul (1950), Bhattachacharya and Roy (1981), Abdelrahman and Sharafeldin (1997), who assumed or determined a sphere model.

Fig. 7
figure 7

Suleymnkoy SP anomaly map, Ergani Copper district, Turkey (modified after Yungul, 1950)

Full size image
Fig. 8
figure 8

Observed SP profile on line AA′, of the Suleymnkoy Copper ore body, Turkey

Full size image

However, this anomaly was interpreted by Abdelrahman et al. (2015) as due to two superimposed structures. They suggest that the shape of the buried deeper structure resembles a sphere buried at depth of 43.6 m and the shape of the buried shallow structure resembles a semi-infinite vertical cylinder buried at a depth of 23.9 m. In all cases, the depth of the buried source estimated by our method is in excellent agreement with depth obtained by Abdelrahman et al. (2015).

5 Discussion and Conclusions

Determination of the model parameters of buried simple geometrical bodies using self-potential data can be established using the proposed method. A highly effective and fast numerical approach is developed to use the anomaly values at four characteristic points and their corresponding distances on the residual anomaly profile for addressing simultaneously the model parameters of the buried object. The repetition of the procedure using the successful combinations of such two pairs of measured points will result in the best outcome. The benefits of the proposed method over both the linear and non-linear least squares methods is that it is capable of minimizing the effect of errors in the data points which results in an enhanced interpretation outcome. Our approach is more advantageous than many least-squares inversion method in determining the model parameters of the buried structure from residual self-potential anomaly. Based on our experience with minimization techniques, they work well when precise residual anomalies are available and when the sources are truly idealized. However, when precise residual anomalies are not available and when the sources are not truly idealized as in cases dealing with field problems, a very good match between the model and observations may have occurred but this not necessarily guarantee that the correct solution has been found. Also, the minimization technique for two or more unknowns always produces good results from synthetic data with and without random noise. In case of the field data, good results may only be obtained when using very good initial guesses on the model parameters (q, z, \(\psi\), and k) On the other hand, because the present method uses all successful combinations of data points, it has the capability of enhancing the interpretation results, a good match between the model and observations may have not occurred but our approach guarantees that the correct solution has been found.

Finally, another advantage of this method over the other methods of interpreting self-potential residual anomalies is that the effect of the reference or base line is removed completely. This is because of the fact that the subtraction of the numerical value of V(− N) from V(N) and the subtraction of the numerical value of V(− M) from V(M) will eliminate the constant base line and a zero-order regional polynomial. Also, the technique dose not depend on the value of the anomaly at origin of the profile (V(0)) nor on the zero-anomaly distance (xo).

On the other hand, it is evident from the field examples that our method gives good insight from self-potential data of short or long profile length concerning the nature of the buried structure. This because of the fact that the geologic situation is not complicated. The present method may not be applied to real data in complex geologic situation to obtain reliable or detailed information about the different buried structures. This is true because each SP measurement determines at the station location, the sum of all effects from the surface downward.

Table 1 Numerical results of noisy self-potential anomalies due to a semi-infinite vertical cylinder (q = 0.5, z = 3 units, ψ = 50°, k = − 50 mV) a horizontal cylinder (q = 1, z = 5 units, ψ = 40 o, k = − 300 mV) and a sphere (q = 1.5, z = 8 unit, ψ = 50°, k = − 800 mV)
Full size table