Keywords

5.1 Introduction

Self-potential method can be considered as one of the most effective geophysical techniques in solving different geophysical problems (Sundararajan et al. 1998; Drahor 2004; Mehanee 2014; Essa 2020; Elhussein 2020). Self-potential anomalies produced by natural potential difference which resulted due to the oxidation-reduction process of mineralized rocks which in contact with the ground water (Essa et al. 2008; Essa 2020).

To apply the self-potential technique in solving the different geophysical problems, the different subsurface geological bodies was approximated to simple geometrical bodies (like, sphere, cylinder and thin sheet) (Essa 2011; Mehanee 2014, 2015; Biswas 2017; Essa and Elhussein 2017; Sungkono and Warnana 2018; Essa 2020). To estimate the different parameters (like, amplitude coefficient, depth, polarization angle and body origin), different techniques were created and developed to overcome the ill-posedness and non-uniqueness problems (Tarantola 2005; Sharma and Biswas 2013; Essa 2019). From these techniques, gradient techniques (Abdelrahman et al. 2004, 2009b; Essa and Elhussein 2017), moving average techniques (Abdelrahman et al. 2006a; Mehanee et al. 2011; Essa 2019), characteristic curves and nomograms (Yungul 1950; Fitterman 1979; Essa 2007; Abdelrahman et al. 2009a), nonlinear and liner least squares techniques (Abdelrahman et al. 2006b; Essa et al. 2008), Euler deconvolution method (Agarwal and Srivastava 2009); most of the previous methods require a priori information, other methods estimate the different parameters with high uncertainty as the accuracy of the estimated parameters mainly depends upon the accuracy of the regional-residual separation. Nowadays new recent techniques have been developed, like particle swarm optimization (Essa 2019, 2020), genetic-price technique (Di Maio et al. 2019), black-hole technique (Sungkono and Warnana 2018).

This chapter review different techniques applied to the different synthetic and real field self-potential data to estimate the different bodies parameters.

5.2 Methodology

5.2.1 Forward Modeling

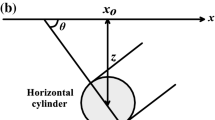
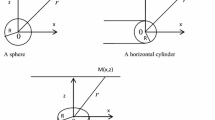
The SP anomaly (V) caused by simple geometrical structures at any given point (p) (Bhattacharya and Roy 1981; Essa 2019) (Fig. 5.1) is given by:

Fig. 5.1
figure 1

A sketch showing the different geometrical shapes and their parameters: a sphere, b horizontal cylinder and c vertical cylinder

Full size image
$$V\left( {x_{j} } \right) = K\frac{{\left( {x_{j} - d} \right)cos\theta - z sin\theta }}{{\left( {\left( {x_{j} - d} \right)^{2} + z^{2} } \right)^{q} }},\,\,\, i = 0, 1, 2, 3, \ldots , N$$
(5.1)

where K is the amplitude factor (mV x m2q−1), z is the depth to the structure (m), d is the source origin (m), \(\theta\) is the angle of polarization (degrees), q is the shape factor (dimensionless) which takes the following values: 1.5 for sphere, 1 for horizontal cylinder and 0.5 for vertical cylinder (Essa et al. 2008; Di Maio et al. 2016; Essa 2019).

5.2.2 Least Squares Inversion Technique

Essa et al. (2008) developed a least square inversion approach to estimate the different bodies parameters, by determining the depth applying the nonlinear equation:

$$\delta \left( z \right) = 0,$$
(5.2)

After estimating the depth, the angle of polarization is then calculated by the least square, also, the amplitude factor is then determined from the estimate depth and the polarization angle.

5.2.3 Particle Swarm Optimization

Essa (2019) developed a method based upon the PSO algorithm and the second moving average for estimating the different structures parameters. PSO is stochastic in its nature, the idea of PSO is based upon a group of birds or fishes looking for food, the group of birds represent the models, and the paths of particles represent the solutions (Essa 2019). The algorithm starts with random models, then the location and the velocity of the particles are updated using the following formulas, respectively.

$$x_{i}^{k + 1} = x_{j}^{k} + V_{j}^{k + 1}$$
(5.3)
$$V_{j}^{k + 1} = c_{3} V_{j}^{k} + c_{1} rand\left( {T_{best} - x_{j}^{k + 1} } \right) + c_{2} rand\left( {J_{best} - x_{j}^{k + 1} } \right),$$
(5.4)

where \(x _{j}^{k}\) is the location of jth particle at the iteration kth; \(V_{j}^{k}\) is the velocity of the jth model at the iteration kth; rand is any random number between [0, 1]; \(c_{1} \,{\text{and}}\,\, c_{2}\) are cognitive and social factors and equal 2 (Parsopoulos and Vrahatis 2002; Singh and Biswas 2016; Essa 2019); \(c_{3}\) is the inertial coefficient which governs the velocity of the model and usually takes a value less than one; \(T_{best}\) is the best location for individual model, and \(J_{best}\) is the global best location for any model in the group.

5.2.4 Neural Network Algorithm

Al-Garni (2009) proposed an approach based mainly on neural network (modular algorithm) to estimate the different structures parameters.

5.3 Synthetic Examples

5.3.1 Sphere Model

A noise free SP anomaly was generated using sphere model with the following parameters: K = 1200 mV x m2, z = 6, \(\theta\) = 45°, d = 55 m, q = 1.5 and the profile length = 100 m (Fig. 5.2).

Fig. 5.2
figure 2

Self-potential anomaly profile of sphere model (\(K\) = 1200 mV × m2, z = 6 m, \(\theta\) = 45°, \(q\) = 1.5, and d = 55 m) and profile length 100 m

Full size image

The different previous techniques were applied to estimate the different parameters. First the least square inversion technique was applied to the SP profile and the parameters were estimated accurately with no error (Table 5.1), then the PSO technique produce the parameters with 0% error (Table 5.1), Finally, the data were subjected to neural network and the parameters were estimated efficiently (Table 5.1).

Table 5.1 A correlation between results obtained from different methods applied to the self-potential anomaly of sphere model (\(K\) = 1200 mV × m2, z = 6 m, \(\theta\) = 45°, \(q\) = 1.5, and d = 55 m)
Full size table

To test the effect of noisy data on the different techniques, a 10% random noise was added to the previous SP model. For least square inversion technique, the estimated parameters are: K = 1020 mV x m2, z = 6.5, \(\theta\) = 47°; while for PSO technique, the estimated parameters are: K = 1140 mV x m2, z = 5.8, \(\theta\) = 44.5°, d = 54.9 m, q = 1.45; and in case of neural network, the estimated parameters are: K = 1350 mV x m2, z = 6.3, \(\theta\) = 45.7°, q = 1.57 (Table 5.2). The error of the estimated parameters is shown in (Table 5.2).

Table 5.2 A correlation between results obtained from different methods applied to the self-potential anomaly of H.C. model (\(K\) = 900 mV × m, z = 6.5 m, \(\theta\) = 40o, \(q\) = 1, and d = 60 m)
Full size table

5.3.2 Horizontal Cylinder Model

A noise free SP anomaly was generated using horizontal cylinder model with the following parameters: K = 900 mV x m, z = 6.5, \(\theta\) = 40°, d = 60 m, q = 1 and the profile length = 100 m (Fig. 5.3).

Fig. 5.3
figure 3

Self-potential anomaly profile of H.C. model (\(K\) = 900 mV × m, z = 6.5 m, \(\theta\) = 40°, \(q\) = 1, and d = 60 m) and profile length 100 m

Full size image

The different previous techniques were applied to estimate the different parameters. First the least square inversion technique was applied to the SP profile and the parameters were estimated accurately with no error (Table 5.1), then the PSO technique produce the parameters with 0% error (Table 5.2), Finally, the data were subjected to neural network and the parameters were estimated efficiently (Table 5.2).

To test the effect of noisy data on the different techniques, a 10% random noise was added to the previous SP model. For least square inversion technique, the estimated parameters are: K = 1000 mV x m, z = 7.1, \(\theta\) = 41.5°; while for PSO technique, the estimated parameters are: K = 960 mV x m, z = 6.6, \(\theta\) = 40.2°, d = 60.11 m, q = 1.04; and in case of neural network, the estimated parameters are: K = 1010 mV x m, z = 6.3, \(\theta\) = 39.7°, q = 0.9 (Table 5.2). The error of the estimated parameters is shown in (Table 5.2).

5.4 Field Example

5.4.1 Malachite Mine, USA Real Data

Malachite mine is composed of amphibolite belt which surrounded by gneiss and schist (Essa 2019). Self-potential profile was designed and measured by Heiland et al. (1945), the profile was taken above massive sulfide ore body which located in the Malachite mine. The profile length was 164 m, digitized at 1.25 m (Fig. 5.4). The SP profile was then subjected to the three different techniques to determine and compare between the parameters estimated from these different methods (Table 5.3). From Table 5.3 the parameters estimated using least square inversion method (Essa et al. 2008) are: K = 275.39 mV, z = 12.87, \(\theta\) = 103.58o; while the parameters estimated by using PSO technique (Essa 2019) are: K = 236.53 mV, z = 13.74, \(\theta\) = 99.31o d = 0.20 m, q = 0.45; finally, the parameters estimated using neural network (Al-Garni 2009) are: K = 268.41 mV, z = 13.2, \(\theta\) = 105o, q = 0.63.

Fig. 5.4
figure 4

Self-potential anomaly profile of Malachite mine, USA field example

Full size image
Table 5.3 A correlation between results obtained from different methods applied to the self-potential anomaly of Malachite mine, USA field example
Full size table

5.5 Conclusions

A comparative study was made in this chapter to see the differences between different methods in application to the self-potential data from different geological structures (Sphere, horizontal cylinder and vertical cylinder). the different methods are least-square (Essa 2008), neural network (Al-Garni 2009) and PSO (Essa 2019). These different methods were applied to two different synthetic data without and with 10% random noise and one real data from USA. The methods estimate the different structures parameters (K, z, d, \(\theta\) and q) efficiently and accurately.