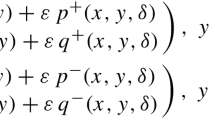On the Number of Limit Cycles Bifurcating from a Quartic Reversible Center

Abstract

This paper deals with the bifurcation of limit cycles from a quartic reversible and non-Hamiltonian system. By using the averaging theory and some mathematical technique on estimating the zeros of the function, we show that under small polynomial perturbation of degree $3n+1$, at most $3n-3$ limit cycles bifurcate from the period annulus of the unperturbed system for $n>3$, while at most 2n limit cycles appear from the period annulus of the unperturbed system for $n=1, 2, 3$. And the upper bound for the latter case is sharp.

1 Introduction

The second part of the famous Hilbert’s 16th problem asks for the maximum number of limit cycles of planar real polynomial differential equations of degree n [19]. To attack this problem, many interesting and profound results have been established under various conditions. For example, the bifurcation of limit cycles from the periodic orbits around a center has been extensively studied in the literatures [9, 14, 20,21,22, 24,25,26, 31, 33, 37] and the references therein. Simultaneously, quite a few innovative methods have been proposed based on the Poincaré map [5, 10, 23], the Poincaré-Pontryagin-Melnikov integrals or the Abelian integrals [2, 3, 11, 36], the inverse integrating factor [15,16,17, 35], and the averaging function [4, 6, 12, 18, 22, 25, 26, 32] which is actually equivalent to the Abelian integrals in the plane.

As for the averaging theory, it gives a quantitative relation between the solutions of a non-autonomous periodic differential system and its averaged differential equation which is autonomous. For some differential equations, the problem about the number of limit cycles bifurcating from the unperturbed systems can be reduced to the exploration of hyperbolic equilibrium points of the corresponding averaged equations by using the averaging method. Hence, the averaging method has played a crucial role in the study of limit cycles of the differential systems. Now some elegant results on the number of limit cycles of the differential systems have been obtained, such as [1, 7, 13, 18, 20, 22, 24, 31,32,33, 37] and so on.

Generally, it is challenging to estimate the number of limit cycles in perturbations of a polynomial differential system of high degree. In the present paper, we choose a quartic differential system as follow

$$\begin{aligned} \begin{aligned} \dot{x}&=-y+x^{3}y+xy^{3},\\ \dot{y}&=x+x^{2}y^{2}+y^{4}, \end{aligned} \end{aligned}$$

(1.1)

and study the bifurcation of limit cycles from it under any small polynomial perturbation of degree $3n+1$ by the averaging method and some mathematical technique on estimating the zeros of the function.

Clearly, system (1.1) has

$$\begin{aligned} H(x,y)=\frac{1}{3(x^{2}+y^{2})^{\frac{3}{2}}}-\frac{x}{\sqrt{x^{2}+y^{2}}}=c \end{aligned}$$

as its first integral with the integrating factor $\frac{1}{(x^{2}+y^{2})^{5/2}}$, and the unique finite singularity (0, 0) as its isochronous center. The period annulus, denoted by $\{(x, y)|H(x,y)=c, c\in (1, +\infty )\}$, starts at the center (0, 0) and terminates at the separatrix passing the infinite degenerate singularity on the equator.

We summarize our main results as follows.

Theorem 1.1

Consider the following system

$$\begin{aligned} \begin{aligned} \dot{x}&=-y+x^{3}y+xy^{3}+\varepsilon f(x,y),\\ \dot{y}&=x+x^{2}y^{2}+y^{4}+\varepsilon g(x,y), \end{aligned} \end{aligned}$$

(1.2)

with any sufficiently small parameter $|\varepsilon |\ne 0$, and the real polynomials f(x, y) and g(x, y) of degree $3n+1$ in x and y, given by

$$\begin{aligned} \begin{aligned} f(x,y)=\sum _{k=1}^{n}\sum _{l+m=1+3k}a_{lm}x^{l}y^{m}, \quad g(x,y)=\sum _{k=1}^{n}\sum _{l+m=1+3k}b_{lm}x^{l}y^{m}. \end{aligned} \end{aligned}$$

Then using the first order averaging method, we have

• 1. For $n=1, 2, 3$, at most 2n limit cycles arise from the period annulus around the center of the unperturbed system (1.2)$|_{\varepsilon =0}$, respectively. Moreover, in every case, this upper bound is sharp.

• 2. For any $n>3$, at most $3n-3$ limit cycles arise from the period annulus around the center of the unperturbed system (1.2)$|_{\varepsilon =0}$.

Remark 1.2

The result for $n=1$ has been proved in [29]. We list it here for the completeness.

Remark 1.3

We remark that the perturbations in (1.2) exclude all terms of degrees 3n and $3n+2$, because the computations of the averaged function will become too much complicated with them. Ideally, these terms should be included in the analysis, and more limit cycles may appear with general perturbations of degree n.

The rest of this paper is organized as follows. In Sect. 2, we give an introduction on the averaging theory and present some important results about the integrals. Section 3 is devoted to the proof of Theorem 1.1 by computing the first order averaged function and exploring the number of its simple zeros for two cases. Some discussions are stated in Sect. 4.

2 Preliminary Results

In this section, we briefly introduce the averaging theory and prove some results about the integrals which will be used in the proof of the main theorem. More details for the averaging method, including applications, can be found in [27, 34].

2.1 Averaging Theory

Consider the system

$$\begin{aligned} x'(t)=F_{0}(t,x), \end{aligned}$$

(2.1)

with $F_{0}: {\mathbb {R}}\times \Omega \rightarrow \mathbb {R}^{n}$ a $\mathcal {C}^{2}$ function, T-periodic in the first variable, and $\Omega$ is an open subset of $\mathbb {R}^{n}$. Assume that there exists an open and bounded V with its closure $Cl(V)\subset \Omega$, and system (2.1) has Cl(V) as its submanifold of periodic solutions such that for each $z\in Cl(V), x(t,z)$ is T-periodic, where x(t, z) denotes the solution of system (2.1) with $x(0,z)=z$. The set Cl(V) is isochronous for system (2.1), i.e. it is a set formed only by periodic orbits having the same period.

Then the linearization of system (2.1) along the periodic solution x(t, z) takes the form

$$\begin{aligned} y'=D_{x}F_{0}(t,x(t,z))y, \end{aligned}$$

(2.2)

and denote by $M_{z}(t,z)$ a fundamental matrix of this linear system satisfying that $M_{z}(0,z)$ is the identity matrix.

Let $\varepsilon$ be sufficiently small and we consider a perturbation of system (2.1) of the form

$$\begin{aligned} x'(t)=F_{0}(t,x)+\varepsilon F_{1}(t,x)+\varepsilon ^{2} F_{2}(t,x,\varepsilon ), \end{aligned}$$

(2.3)

with $F_{1}: \mathbb {R}\times \Omega \rightarrow \mathbb {R}^{n}$ and $F_{2}: \mathbb {R}\times \Omega \times (-\varepsilon _{0},\varepsilon _{0})\rightarrow \mathbb {R}^{n}$ are $\mathcal {C}^{2}$ functions, T-periodic in the first variable. Then, an answer to the problem of the bifurcation of T-periodic solutions from the x(t, z) contained in Cl(V) is given in the following result.

Lemma 2.1

(Perturbations of an isochronous set) Assume that there exists an open and bounded set V with $Cl(V)\subset \Omega$ such that for each $z\in Cl(V)$, the solution x(t, z) is T-periodic, then we consider the function $\mathcal {F}: Cl(V)\rightarrow \mathbb {R}^{n}$

$$\begin{aligned} \mathcal {F}(z)=\int _{0}^{T}M_{z}^{-1}(t,z)F_{1}(t,x(t,z))\mathrm{d}t. \end{aligned}$$

(2.4)

If there exists $a\in V$ with $\mathcal {F}(a)=0$ and det$((d\mathcal {F}/dz)(a))\ne 0$, then there exists a T-periodic solution $\varphi (t,\varepsilon )$ of system (2.3) such that $\varphi (0,\varepsilon )\rightarrow a$ as $\varepsilon \rightarrow 0$.

Lemma 2.1 goes back to [28, 30], see Buicǎ et al. [8] for a shorter proof.

2.2 Some Results About Integrals

For $\rho \in (1,+\infty )$ and $j\in \mathbb {Z}$, we define

$$\begin{aligned} I_{j}(\rho )=\int _{0}^{2\pi }\frac{1}{(\cos \theta +\rho )^{j}}\mathrm{d}\theta . \end{aligned}$$

(2.5)

By a straightforward computation, we obtain the following result.

Lemma 2.2

For $\rho \in (1, +\infty ), m, j\in \mathbb {N}$ and $m,j\ge 1$, we have

$$\begin{aligned} \int _{0}^{2\pi }\frac{\cos ^{m}\theta }{(\cos \theta +\rho )^{j}}\mathrm{d}\theta =\sum _{k=0}^{m}\left( {\begin{array}{c}m\\ k\end{array}}\right) (-\rho )^{k}I_{j+k-m}(\rho ). \end{aligned}$$

Moreover, we have

Lemma 2.3

For $\rho \in (1, +\infty ), j \in \mathbb {Z}\setminus \{1\}$, the integrals $I_{j}, I_{j-1}$ and $I_{j-2}$ defined above satisfy

$$\begin{aligned} \rho ^{2}I_{j}(\rho )=I_{j}(\rho )+\frac{2j-3}{j-1}\rho I_{j-1}(\rho )+\frac{2-j}{j-1}I_{j-2}(\rho ). \end{aligned}$$

Proof

Note that

$$\begin{aligned} \begin{aligned} I_{j-1}(\rho )&=\int _{0}^{2\pi }\frac{\cos \theta +\rho }{(\cos \theta +\rho )^{j}}\mathrm{d}\theta =\rho I_{j}(\rho )+\int _{0}^{2\pi } \frac{d(\sin \theta )}{(\cos \theta +\rho )^{j}}\\&=\rho I_{j}(\rho )-j\int _{0}^{2\pi }\frac{\sin ^{2}\theta }{(\cos \theta +\rho )^{j+1}}\mathrm{d}\theta \\&=\rho I_{j}(\rho )-j\int _{0}^{2\pi }\frac{1-\cos ^{2}\theta }{(\cos \theta +\rho )^{j+1}}\mathrm{d}\theta \\&=\rho I_{j}(\rho )-jI_{j+1}(\rho )+j\rho ^{2}I_{j+1}(\rho )+jI_{j-1}(\rho )-2j\rho I_{j}(\rho ). \end{aligned} \end{aligned}$$

Then

$$\begin{aligned} j\rho ^{2}I_{j+1}(\rho )=jI_{j+1}(\rho )+(2j-1)\rho I_{j}(\rho )+(1-j)I_{j-1}(\rho ). \end{aligned}$$

Replacing j by $j-1$, we can obtain Lemma 2.3. $\square$

Lemma 2.4

For $\rho \in (1, +\infty )$ and $j\in \mathbb {Z}$, we have

$$\begin{aligned} I_{j}(\rho )=\frac{1}{(\rho ^{2}-1)^{j-\frac{1}{2}}}I_{1-j}(\rho ). \end{aligned}$$

(2.6)

Moreover,

$$\begin{aligned} I_{j}(\rho )=Q_{-j}(\rho )~~~~ j\le 0;~~~~~~~ I_{j}(\rho )=\frac{Q_{j-1}(\rho )}{(\rho ^{2}-1)^{j-\frac{1}{2}}},~~~~ j\ge 1, \end{aligned}$$

(2.7)

where $Q_{j}$ stands for a polynomial of degree j.

Proof

Obviously, equality (2.6) is true for $j=0, 1$. Now we prove the result for case $j\ge 2$ by induction.

Suppose that (2.6) holds for j and $j+1$, that is

$$\begin{aligned} (\rho ^{2}-1)^{j-\frac{1}{2}}I_{j}(\rho )=I_{1-j}(\rho ),~~(\rho ^{2}-1)^{j+\frac{1}{2}}I_{j+1}(\rho )=I_{-j}(\rho ). \end{aligned}$$

(2.8)

We need to show that

$$\begin{aligned} (\rho ^{2}-1)^{j+\frac{3}{2}}I_{j+2}(\rho )=I_{-(j+1)}(\rho ). \end{aligned}$$

(2.9)

Using Lemma 2.3, we have

$$\begin{aligned} (\rho ^{2}-1)I_{j+2}(\rho )=\frac{2j+1}{j+1}\rho I_{j+1}(\rho )-\frac{j}{j+1}I_{j}(\rho ). \end{aligned}$$

Multiplying the above equality by $(\rho ^{2}-1)^{j+\frac{1}{2}}$, we get

$$\begin{aligned} (\rho ^{2}-1)^{j+\frac{3}{2}}I_{j+2}(\rho )=\frac{2j+1}{j+1}\rho (\rho ^{2}-1)^{j+\frac{1}{2}}I_{j+1}(\rho )-\frac{j}{j+1}(\rho ^{2}-1)^{j+\frac{1}{2}}I_{j}(\rho ). \end{aligned}$$

Then it follows from (2.8) that

$$\begin{aligned} (\rho ^{2}-1)^{j+\frac{3}{2}}I_{j+2}(\rho )=\frac{2j+1}{j+1}\rho I_{-j}(\rho )-\frac{j}{j+1}(\rho ^{2}-1)I_{1-j}(\rho ). \end{aligned}$$

(2.10)

Using Lemma 2.3 again, we have

$$\begin{aligned} (\rho ^{2}-1)I_{1-j}(\rho )=\frac{2j+1}{j}\rho I_{-j}(\rho )-\frac{j+1}{j}I_{-(j+1)}(\rho ). \end{aligned}$$

(2.11)

Substituting (2.11) into (2.10), we obtain (2.9), then (2.6) holds for $j\in \mathbb {Z}^{+}\cup \{0\}$.

When $j>1$, we have

$$\begin{aligned} I_{1-j}(\rho )=(\rho ^{2}-1)^{j-\frac{1}{2}}I_{j}(\rho ). \end{aligned}$$

Let $m=1-j<0$, then we have

$$\begin{aligned} I_{m}(\rho )=(\rho ^{2}-1)^{\frac{1}{2}-m}I_{1-m}(\rho )=\frac{1}{(\rho ^{2}-1)^{m-\frac{1}{2}}}I_{1-m}(\rho ), \end{aligned}$$

which implies that (2.6) holds for $j\in \mathbb {Z}^{-}$. Hence (2.6) is true for all $j\in \mathbb {Z}$.

By the definition and (2.6), we obtain (2.7). This completes the proof of Lemma 2.4. $\square$

From the above results, we get Corollary 2.5.

Corollary 2.5

• 1. For $k\in \mathbb {N}$, we have

  $$\begin{aligned} I_{-(2k+1)}(\rho )=\rho Q_{k}(\rho ^{2}),~~I_{-2k}(\rho )=Q_{k}(\rho ^{2}),~~I_{2k+1}(\rho )=\frac{Q_{k}(\rho ^{2})}{(\rho ^{2}-1)^{2k+\frac{1}{2}}}. \end{aligned}$$

• 2. For $k\in \mathbb {N}\setminus \{0\}$, we have

  $$\begin{aligned} I_{2k}(\rho )=\frac{\rho Q_{k-1}(\rho ^{2})}{(\rho ^{2}-1)^{2k-\frac{1}{2}}}, \end{aligned}$$

  where $Q_{j}$ stands only for a polynomial of degree j. The difference in several equalities is ignored.

A straightforward computation leads to Lemma 2.6 immediately.

Lemma 2.6

The following explicit expressions hold.

$$\begin{aligned} \begin{aligned}&I_{0}(\rho )=2\pi ,~~I_{1}(\rho )=\frac{2\pi }{(\rho ^{2}-1)^{\frac{1}{2}}},~~I_{2}(\rho )=\frac{2\pi \rho }{(\rho ^{2}-1)^{\frac{3}{2}}},\\&I_{-1}(\rho )=2\pi \rho ,~I_{-2}(\rho )=\pi (2\rho ^{2}+1),~I_{-3}(\rho )=\pi (2\rho ^{3}+3\rho ). \end{aligned} \end{aligned}$$

3 Proof of Theorem 1.1

We split the proof into three steps: first derive the explicit expression of the averaged function, then prove Theorem 1.1 for the odd and even cases, respectively.

In the polar coordinates, system (1.2) becomes the form

$$\begin{aligned} \begin{aligned} \dot{r}&=r^{4}\sin \theta +\varepsilon F(r,\theta ),\\ \dot{\theta }&=1+\varepsilon G(r,\theta ), \end{aligned} \end{aligned}$$

(3.1)

where

$$\begin{aligned} \begin{aligned} F(r,\theta )&=\sum _{k=1}^{n}\sum _{l+m=1+3k}r^{l+m} \left( a_{lm}\cos ^{l+1}\theta \sin ^{m}\theta +b_{lm}\cos ^{l}\theta \sin ^{m+1}\theta \right) ,\\ G(r,\theta )&=\sum _{k=1}^{n}\sum _{l+m=1+3k}r^{l+m-1} \left( b_{lm}\cos ^{l+1}\theta \sin ^{m}\theta -a_{lm}\cos ^{l}\theta \sin ^{m+1}\theta \right) . \end{aligned} \end{aligned}$$

Obviously, system (3.1) is equivalent to

$$\begin{aligned} \frac{dr}{\mathrm{d}\theta }=r^{4}\sin \theta +\varepsilon F_{1}(r,\theta )+O(\varepsilon ^{2}) \end{aligned}$$

(3.2)

where

$$\begin{aligned} \begin{aligned} F_{1}(r,\theta )&=\sum _{k=1}^{n}\sum _{l+m=1+3k}r^{l+m+3}\big (a_{lm}\cos ^{l}\theta \sin ^{m+2}\theta -b_{lm}\cos ^{l+1}\theta \sin ^{m+1}\theta \big )\\&\quad +\sum _{k=1}^{n}\sum _{l+m=1+3k}r^{l+m}\big (a_{lm}\cos ^{l+1}\theta \sin ^{m}\theta +b_{lm}\cos ^{l}\theta \sin ^{m+1}\theta \big ). \end{aligned} \end{aligned}$$

3.1 First Order Averaged Function

In this subsection, we first derive the formula for the first averaged function $\mathcal {F}(z)$ of system (3.2), then obtain the associated function whose zeros coincide with those of $\mathcal {F}(z)$.

It is not difficult to know that the closed orbits of system (3.2)$|_{\varepsilon =0}$ takes the form

$$\begin{aligned} r_{0}(\theta , z)=\frac{1}{\left( 3\cos \theta -3+\frac{1}{z^{3}}\right) ^{\frac{1}{3}}},\quad z\in (0,\root 3 \of {1/6}) \end{aligned}$$

with period $2\pi$ and the initial condition $r_{0}(0, z)=z$. The linearization of system (3.2)$|_{\varepsilon =0}$ along $r_{0}(\theta ,z)$ takes the form

$$\begin{aligned} \dot{y}=\frac{4\sin \theta }{3(\cos \theta -1)+\frac{1}{z^{3}}}y. \end{aligned}$$

Take the fundamental matrix of the above system

$$\begin{aligned} M_{z}(\theta ,z)=\frac{1}{z^{4}\left( 3\cos \theta -3+\frac{1}{z^{3}}\right) ^{4/3}}, \end{aligned}$$

and its inverse

$$\begin{aligned} M_{z}^{-1}(\theta ,z)=z^{4}\left( 3\cos \theta -3+\frac{1}{z^{3}}\right) ^{4/3}, \end{aligned}$$

then from Lemma 2.1, the averaged function of system (3.2) can be expressed as

$$\begin{aligned} \begin{aligned} \mathcal {F}(z)&=\int _{0}^{2 \pi }M_{z}^{-1}(\theta ,z)\cdot F_{1}(r, \theta )|_{r=r_{0}(\theta , z)}\mathrm{d}\theta \\&=\int _{0}^{2 \pi }z^{4}(3\cos \theta +3\rho )^{4/3}\Bigg \{\sum _{k=1}^{n}\sum _{l+m=1+3k}r^{l+m+3}\big (a_{lm}\cos ^{l}\theta \sin ^{m+2}\theta \\ {}&\quad -b_{lm}\cos ^{l+1}\theta \sin ^{m+1}\theta \big )\\&\quad +\sum _{k=1}^{n}\sum _{l+m=1+3k}r^{l+m}\big (a_{lm}\cos ^{l+1}\theta \sin ^{m}\theta +b_{lm}\cos ^{l}\theta \sin ^{m+1}\theta \big )\Bigg \}\\&\qquad \Bigg |_{r=\frac{1}{(3\cos \theta +3\rho )^{1/3}}}\mathrm{d}\theta \\&=z^{4}\Bigg \{\sum _{k=1}^{n}\int _{0}^{2 \pi }\sum _{l+m=1+3k}\frac{a_{lm}\cos ^{l}\theta \sin ^{m+2}\theta -b_{lm}\cos ^{l+1}\theta \sin ^{m+1}\theta }{3^{k}(\cos \theta +\rho )^{k}}\mathrm{d}\theta \\&\quad +\sum _{k=1}^{n}\int _{0}^{2 \pi }\sum _{l+m=1+3k}\frac{a_{lm}\cos ^{l+1}\theta \sin ^{m}\theta +b_{lm}\cos ^{l}\theta \sin ^{m+1}\theta }{3^{k-1}(\cos \theta +\rho )^{k-1}}\mathrm{d}\theta \Bigg \}\\&=z^{4}\Bigg \{\sum _{k=1}^{n}\int _{0}^{2 \pi }\frac{R_{3k+3}(\cos \theta ,\sin \theta )}{3^{k}(\cos \theta +\rho )^{k}}\mathrm{d}\theta +\sum _{k=1}^{n}\int _{0}^{2 \pi }\frac{R_{3k+2}(\cos \theta ,\sin \theta )}{3^{k-1}(\cos \theta +\rho )^{k-1}}\mathrm{d}\theta \Bigg \}, \end{aligned} \end{aligned}$$

(3.3)

where $\rho =-1+1/(3z^{3})\in (1,+\infty )$, $R_{l}(x,y)$ stands for a homogeneous polynomial of degree l in x and y.

Noting that

$$\begin{aligned} \begin{aligned} \int _{0}^{2\pi }\frac{\cos ^{p}\theta \sin ^{2q+1}\theta }{(\cos \theta +\rho )^{k}}\mathrm{d}\theta&=\int _{0}^{2\pi }\frac{\cos ^{p}\theta \sin ^{2q+1}\theta }{(\cos \theta +\rho )^{k-1}}\mathrm{d}\theta =0,\\ \int _{0}^{2\pi }\frac{\cos ^{p}\theta \sin ^{2q}\theta }{(\cos \theta +\rho )^{k}}\mathrm{d}\theta&=\int _{0}^{2\pi } \frac{\cos ^{p}\theta (1-\cos ^{2}\theta )^{q}}{(\cos \theta +\rho )^{k}}\mathrm{d}\theta ,\\ \int _{0}^{2\pi }\frac{\cos ^{p}\theta \sin ^{2q}\theta }{(\cos \theta +\rho )^{k-1}}\mathrm{d}\theta&=\int _{0}^{2\pi }\frac{\cos ^{p}\theta (1-\cos ^{2}\theta )^{q}}{(\cos \theta +\rho )^{k-1}}\mathrm{d}\theta \end{aligned} \end{aligned}$$

for any nonnegative integer numbers p and q, we get

$$\begin{aligned} \mathcal {F}(z)=z^{4}\Bigg \{\sum _{k=1}^{n}\int _{0}^{2 \pi }\frac{S_{3k+3}(\cos \theta )}{(\cos \theta +\rho )^{k}}\mathrm{d}\theta +\sum _{k=2}^{n}\int _{0}^{2 \pi }\frac{T_{3k+2}(\cos \theta )}{(\cos \theta +\rho )^{k-1}}\mathrm{d}\theta \Bigg \}, \end{aligned}$$

where $S_{l}(x, y)$ and $T_{l}(x, y)$ denote the polynomials of degree l in x and y, respectively. Then define the function

$$\begin{aligned} \begin{aligned} G(\rho )=\sum _{k=1}^{n}\int _{0}^{2 \pi }\frac{S_{3k+3}(\cos \theta )}{(\cos \theta +\rho )^{k}}\mathrm{d}\theta +\sum _{k=2}^{n}\int _{0}^{2 \pi }\frac{T_{3k+2}(\cos \theta )}{(\cos \theta +\rho )^{k-1}}\mathrm{d}\theta , \end{aligned} \end{aligned}$$

we obtain Remark 3.1.

Remark 3.1

The non-zero zeros of $\mathcal {F}(z)$ coincide with those of the function $G(\rho )$. In the following, we study the zeros of the function $G(\rho )$ for $\rho \in (1, +\infty )$ instead of $\mathcal {F}(z)$ for $z\in (0, \root 3 \of {1/6})$.

From the definitions, we know that the degree of $S_{3k+3}$ is odd when k is even, and even when k is odd, while it is opposite for $T_{3k+2}$. This fact yields

$$\begin{aligned} \begin{aligned}&\sum _{k=1}^{n}\frac{S_{3k+3}(\cos \theta )}{(\cos \theta +\rho )^{k}}\\&\quad =\frac{S_{6,0}+S_{6,2}\cos ^{2}\theta +S_{6,4}\cos ^{4}\theta +S_{6,6}\cos ^{6}\theta }{\cos \theta +\rho }\\&\qquad +\frac{S_{9,1}\cos \theta +S_{9,3}\cos ^{3}\theta +S_{9,5}\cos ^{5}\theta +S_{9,7}\cos ^{7}\theta +S_{9,9}\cos ^{9}\theta }{(\cos \theta +\rho )^{2}}\\ {}&\qquad +\cdots +\frac{S_{3n+3}(\cos \theta )}{(\cos \theta +\rho )^{n}},\\&\sum _{k=2}^{n}\frac{T_{3k+2}(\cos \theta )}{(\cos \theta +\rho )^{k-1}}\\ {}&\quad =\frac{T_{8,0}+T_{8,2}\cos ^{2}\theta +T_{8,4}\cos ^{4}\theta +T_{8,6}\cos ^{6}\theta +T_{8,8}\cos ^{8}\theta }{\cos \theta +\rho }\\&\qquad +\cdots +\frac{T_{3n+2}(\cos \theta )}{(\cos \theta +\rho )^{n-1}}, \end{aligned} \end{aligned}$$

(3.4)

where $S_{i,j}$ and $T_{i,j}$ are dependent on the perturbation coefficients $a_{lm}$ and $b_{lm}$. After some simplification, we have

$$\begin{aligned} G(\rho )&=\sum _{k=1}^{n}\int _{0}^{2 \pi }\frac{S_{3k+3}(\cos \theta )}{(\cos \theta +\rho )^{k}}\mathrm{d}\theta +\sum _{k=2}^{n}\int _{0}^{2 \pi }\frac{T_{3k+2}(\cos \theta )}{(\cos \theta +\rho )^{k-1}}\mathrm{d}\theta \nonumber \\&=\int _{0}^{2\pi }\Bigg [B_{0,0}\cdot (\cos \theta +\rho )^{2n+3}+B_{1,1}\rho \cdot (\cos \theta +\rho )^{2n+2}\nonumber \\&\quad +(B_{2,0}+B_{2,2}\rho ^{2})\cdot (\cos \theta +\rho )^{2n+1}\nonumber \\&\quad +\cdots +(B_{2n+2,0}+B_{2n+2,2}\rho ^{2}+\cdots +B_{2n+2,2n+2}\rho ^{2n+2})\cdot (\cos \theta +\rho )\nonumber \\&\quad +(B_{2n+3,1}\rho +B_{2n+3,3}\rho ^{3}+\cdots +B_{2n+3,2n+3}\rho ^{2n+3})\nonumber \\&\quad +\frac{B_{2n+4,0}+B_{2n+4,2}\rho ^{2} +\cdots +B_{2n+4,2n+4}\rho ^{2n+4}}{\cos \theta +\rho }\nonumber \\&\quad +\frac{B_{2n+5,1}\rho +B_{2n+5,3}\rho ^{3}+\cdots +B_{2n+5,2n+5}\rho ^{2n+5}}{(\cos \theta +\rho )^{2}}\nonumber \\&\quad +\cdots +\frac{B_{3n+3}\rho ^{m(i)}}{(\cos \theta +\rho )^{n}}\Bigg ]\mathrm{d}\theta \nonumber \\&=B_{0,0}\cdot I_{-(2n+3)}(\rho )+B_{1,1}\rho \cdot I_{-(2n+2)}(\rho )+(B_{2,0}+B_{2,2}\rho ^{2})\cdot I_{-(2n+1)}(\rho )\nonumber \\&\quad +\cdots +(B_{2n+2,0}+B_{2n+2,2}\rho ^{2}+\cdots +B_{2n+2,2n+2}\rho ^{2n+2})\cdot I_{-1}(\rho )\nonumber \\&\quad +(B_{2n+3,1}\rho +B_{2n+3,3}\rho ^{3}+\cdots +B_{2n+3,2n+3}\rho ^{2n+3})\cdot I_{0}(\rho )\nonumber \\&\quad +(B_{2n+4,0}+B_{2n+4,2}\rho ^{2}+\cdots +B_{2n+4,2n+4}\rho ^{2n+4})I_{1}(\rho )\nonumber \\&\quad +(B_{2n+5,1}\rho +B_{2n+5,3}\rho ^{3}+\cdots +B_{2n+5,2n+5}\rho ^{2n+5})I_{2}(\rho )\nonumber \\&\quad +\cdots +B_{3n+3}\rho ^{m(n)}I_{n}(\rho ), \end{aligned}$$

(3.5)

where $I_{n}(\rho )$ is defined as before, the coefficient $B_{i,j}$ depends on the coefficients of $S_{i,j}$ and $T_{i,j}$, that is, they are the functions of any real perturbation coefficients $a_{lm}$ and $b_{lm}$. Moreover, we obtain

$$\begin{aligned} B_{3n+3}\rho ^{m(n)}=\sum _{i=0}^{\frac{3n+3}{2}}B_{3n+3,2i}\rho ^{2i} \end{aligned}$$

(3.6)

for the odd number n, and

$$\begin{aligned} B_{3n+3}\rho ^{m(n)}=\sum _{i=0}^{\frac{3n+2}{2}}B_{3n+3,2i+1}\rho ^{2i+1} \end{aligned}$$

for the even number n.

Lemma 3.2

For the coefficients $B_{3n+3,2i}$ and $B_{3n+3,2i+1}$ defined above, the following statements are true.

• 1. When n is odd, we have

  $$\begin{aligned} \sum _{i=0}^{\frac{3n+3}{2}}B_{3n+3,2i}=0; \end{aligned}$$

• 2. When n is even, we have

  $$\begin{aligned} \sum _{i=0}^{\frac{3n+2}{2}}B_{3n+3,2i+1}=0. \end{aligned}$$

Proof

For the odd number n, it follows from (3.3) and (3.4) that

$$\begin{aligned} \frac{S_{3n+3}(\cos \theta )}{(\cos \theta +\rho )^{n}}= & {} \frac{S_{3n+3,0}+S_{3n+3,2}\cos ^{2}\theta +\cdots +S_{3n+3,3n+3}\cos ^{3n+3}\theta }{(\cos \theta +\rho )^{n}}\nonumber \\= & {} \sum _{2p+2q=1+3n}\frac{a_{2p,2q}\cos ^{2p}\theta \sin ^{2q+2}\theta }{3^{n}(\cos \theta +\rho )^{n}}\nonumber \\&-\sum _{2p+2q=3n-1}\frac{b_{2p+1,2q+1}\cos ^{2p+2}\theta \sin ^{2q+2}\theta }{3^{n}(\cos \theta +\rho )^{n}}. s\end{aligned}$$

(3.7)

Comparing (3.6) with (3.7), we have

$$\begin{aligned} \begin{aligned} B_{3n+3,2i}=S_{3n+3,2i}\left( {\begin{array}{c}2i\\ 0\end{array}}\right) =S_{3n+3,2i}. \end{aligned} \end{aligned}$$

Substituting the above equality and $\cos \theta =1$ into (3.7), we can obtain the first result.

Similarly, the second result follows from

$$\begin{aligned} \begin{aligned} \frac{S_{3n+3}(\cos \theta )}{(\cos \theta +\rho )^{n}}&=\frac{S_{3n+3,1}\cos \theta +S_{3n+3,3}\cos ^{3}\theta +\cdots +S_{3n+3,3n+3}\cos ^{3n+3}\theta }{(\cos \theta +\rho )^{n}}\\&=\sum _{2p+2q=3n}\frac{a_{2p+1,2q}\cos ^{2p+1}\theta \sin ^{2q+2}-b_{2p,2q+1}\cos ^{2p+1}\theta \sin ^{2q+2}\theta }{3^{n}(\cos \theta +\rho )^{n}}. \end{aligned} \end{aligned}$$

This completes the proof of Lemma 3.2. $\square$

3.2 Proof of Theorem 1.1 for the Odd Case

This subsection aims at proving Theorem 1.1 for the odd number n by studying the zeros of the function $G(\rho )$. In addition, an example is given to illustrate that the upper bound of the number of limit cycles for $n=3$ can be reached.

When n is odd, we have

$$\begin{aligned} G(\rho )= & {} B_{0,0}\cdot I_{-(2n+3)}(\rho )+B_{1,1}\rho \cdot I_{-(2n+2)}(\rho )+(B_{2,0}+B_{2,2}\rho ^{2})\cdot I_{-(2n+1)}(\rho )\nonumber \\&+\cdots +(B_{2n+2,0}+B_{2n+2,2}\rho ^{2}+\cdots +B_{2n+2,2n+2}\rho ^{2n+2})\cdot I_{-1}(\rho )\nonumber \\&+(B_{2n+3,1}\rho +B_{2n+3,3}\rho ^{3}+\cdots +B_{2n+3,2n+3}\rho ^{2n+3})\cdot I_{0}(\rho )\nonumber \\&+(B_{2n+4,0}+B_{2n+4,2}\rho ^{2}+\cdots +B_{2n+4,2n+4}\rho ^{2n+4})I_{1}(\rho )\nonumber \\&+(B_{2n+5,1}\rho +B_{2n+5,3}\rho ^{3}+\cdots +B_{2n+5,2n+5}\rho ^{2n+5})I_{2}(\rho )\nonumber \\&+\cdots +\sum _{i=0}^{\frac{3n+3}{2}}B_{3n+3,2i}\rho ^{2i} I_{n}(\rho )\nonumber \\= & {} \sum _{t=0}^{n+1}I_{-(2t+1)}(\rho )\sum _{i=0}^{n-t+1}B_{2n-2t+2,2i}\rho ^{2i}\nonumber \\&+\sum _{t=0}^{n+1}I_{-(2t)}(\rho )\sum _{i=0}^{n-t+1} B_{2n-2t+3,2i+1}\rho ^{2i+1}\nonumber \\&+\sum _{t=0}^{\frac{n-1}{2}}I_{2t+1}(\rho )\sum _{i=0}^{n+t+2}B_{2n+2t+4,2i}\rho ^{2i}\nonumber \\&+\sum _{t=1}^{\frac{n-1}{2}}I_{2t}(\rho ) \sum _{i=0}^{n+t+1}B_{2n+2t+3,2i+1}\rho ^{2i+1}. \end{aligned}$$

(3.8)

To simplify (3.8), we list Lemmas 3.3-3.4 which can be derived from Corollary 2.5.

Lemma 3.3

For any integer $k\ge 0$, we get

$$\begin{aligned} \begin{aligned}&I_{-(2k+1)}(\rho )\sum _{i=0}^{n-k+1}B_{2n-2k+2,2i}\rho ^{2i}\\ {}&=M_{2n+3,1}^{(k)}\rho +M_{2n+3,3}^{(k)}\rho ^{3}+\cdots +M_{2n+3,2n+3}^{(k)}\rho ^{2n+3},\\&I_{-(2k)}(\rho )\sum _{i=0}^{n-k+1}B_{2n-2k+3,2i+1}\rho ^{2i+1}\\ {}&=N_{2n+3,1}^{(k)}\rho +N_{2n+3,3}^{(k)}\rho ^{3}+\cdots +N_{2n+3,2n+3}^{(k)}\rho ^{2n+3}, \end{aligned} \end{aligned}$$

where all coefficients $M_{2n+3,2i+1}^{(k)}$ and $N_{2n+3,2i+1}^{(k)}$ are the linear combination of $B_{2n-2k+2,2i}$ and $B_{2n-2k+3,2i+1}$ given above.

Lemma 3.4

The following statements are true.

• 1. For any integer $k\ge 1$, we have

  $$\begin{aligned} \begin{aligned} I_{2k}(\rho )\sum _{i=0}^{n+k+1}B_{2n+2k+3,2i+1}\rho ^{2i+1}=\frac{\rho }{(\rho ^{2}-1)^{2k-\frac{1}{2}}} \cdot \sum _{i=0}^{n+2k}B_{2n+4k+1,2i+1}^{(k)}\rho ^{2i+1}. \end{aligned} \end{aligned}$$

• 2. For any integer $k\ge 0$, we have

  $$\begin{aligned} \begin{aligned} I_{2k+1}(\rho )\sum _{i=0}^{n+k+2}B_{2n+2k+4,2i}\rho ^{2i}=\frac{1}{(\rho ^{2}-1)^{2k+\frac{1}{2}}} \cdot \sum _{i=0}^{n+2k+2}B_{2n+4k+4,2i}^{(k)}\rho ^{2i}. \end{aligned} \end{aligned}$$

where the coefficients $B_{2n+4k+1,2i+1}^{(k)}$ and $B_{2n+4k+4,2i}^{(k)}$ are the linear combinations of $B_{2n+2k+3,2i+1}$ and $B_{2n+4k+4,2i}$, respectively.

Moreover, we have

Lemma 3.5

• 1. For the odd number n, define

  $$\begin{aligned} \begin{aligned} h_{1}(\omega ^{2}):=\sum _{i=0}^{2n+1}B_{4n+2,2i}^{(\frac{n-1}{2})}(1+\omega ^{2})^{2i}(1-\omega ^{2})^{4n-2i+2}, \end{aligned} \end{aligned}$$

  then we have $h_{1}(\omega ^{2})=\omega ^{2}\cdot R^{*}_{4n}(\omega ^{2})$, where $R^{*}_{4n}(x)$ denotes a symmetrical polynomials of degree 4n in x.

• 2. For the even number n, define

  $$\begin{aligned} \begin{aligned} h_{2}(\omega ^{2}):=\sum _{i=0}^{2n}B_{4n+1,2i+1}^{(\frac{n}{2})}(1+\omega ^{2})^{2i+2}(1-\omega ^{2})^{4n-2i}, \end{aligned} \end{aligned}$$

  then we have $h_{2}(\omega ^{2})=\omega ^{2}\cdot R^{**}_{4n}(\omega ^{2})$, where $R^{**}_{4n}(x)$ denotes a symmetrical polynomials of degree 4n in x.

Proof

Here we only prove the first result, the second one is similar.

In fact, using Corollary 2.5, we have

$$\begin{aligned} \begin{aligned} I_{n}(\rho )\sum _{i=0}^{\frac{3n+3}{2}}B_{3n+3,2i}\rho ^{2i}&=\frac{Q_{\frac{n-1}{2}}(\rho ^{2})}{(\rho ^{2}-1)^{n-\frac{1}{2}}} \sum _{i=0}^{\frac{3n+3}{2}}B_{3n+3,2i}\rho ^{2i}\\&=\frac{1}{(\rho ^{2}-1)^{n-\frac{1}{2}}}\bigg [\sum _{j=0}^{\frac{n-1}{2}}q_{\frac{n-1}{2},2j}\rho ^{2j}\bigg ] \sum _{i=0}^{\frac{3n+3}{2}}B_{3n+3,2i}\rho ^{2i}. \end{aligned} \end{aligned}$$

On the other hand, when $k=\frac{n-1}{2}$ in the second equality of Lemma 3.4, we also get

$$\begin{aligned} \begin{aligned} I_{n}(\rho )\sum _{i=0}^{\frac{3n+3}{2}}B_{3n+3,2i}\rho ^{2i}=\frac{1}{(\rho ^{2}-1)^{n-\frac{1}{2}}} \sum _{i=0}^{2n+1}B_{4n+2,2i}^{(\frac{n-1}{2})}\rho ^{2i}. \end{aligned} \end{aligned}$$

Hence we have

$$\begin{aligned} \Bigg [\sum _{j=0}^{\frac{n-1}{2}}q_{\frac{n-1}{2},2j}\rho ^{2j}\Bigg ]\sum _{i=0}^{\frac{3n+3}{2}}B_{3n+3,2i}\rho ^{2i} =\sum _{i=0}^{2n+1}B_{4n+2,2i}^{(\frac{n-1}{2})}\rho ^{2i}. \end{aligned}$$

(3.9)

Let $\rho =\frac{1+\omega ^{2}}{1-\omega ^{2}}$ in (3.9) and define

$$\begin{aligned} \begin{aligned} h_{1}(\omega ^{2})&:=\sum _{i=0}^{2n+1}B_{4n+2,2i}^{(\frac{n-1}{2})}(1+\omega ^{2})^{2i}(1-\omega ^{2})^{4n-2i+2}\\&=\Bigg [\sum _{j=0}^{\frac{n-1}{2}}q_{\frac{n-1}{2},2j}(1+\omega ^{2})^{2j}(1-\omega ^{2})^{n-2j-1}\Bigg ] \cdot \\ {}&\quad \Bigg [\sum _{i=0}^{\frac{3n+3}{2}}B_{3n+3,2i}(1+\omega ^{2})^{2i}(1-\omega ^{2})^{3n-2i+3}\Bigg ]. \end{aligned} \end{aligned}$$

From Lemma 3.2, it is not difficult to know that $h_{1}(x)$ is a symmetrical polynomial of degree $4n+1$ with zero constant term. Then we obtain

$$\begin{aligned} h_{1}(\omega ^{2})=\omega ^{2}\cdot R^{*}_{4n}(\omega ^{2}), \end{aligned}$$

where $R^{*}(x)$ is a symmetrical polynomial of degree 4n in x. This is just the first result of Lemma 3.5. $\square$

Using Lemmas 3.3–3.5, (3.8) can be simplified as

$$\begin{aligned} G(\rho )&=\sum _{t=0}^{n+1}I_{-(2t+1)}(\rho )\sum _{i=0}^{n-t+1}B_{2n-2t+2,2i}\rho ^{2i}\nonumber \\&\quad +\sum _{t=0}^{n+1}I_{-2t}(\rho ) \sum _{i=0}^{n-t+1}B_{2n-2t+3,2i+1}\rho ^{2i+1}\nonumber \\&\quad +\sum _{t=0}^{\frac{n-1}{2}}I_{2t+1}(\rho )\sum _{i=0}^{n+t+2}B_{2n+2t+4,2i}\rho ^{2i}\nonumber \\&\quad +\sum _{t=1}^{\frac{n-1}{2}}I_{2t}(\rho ) \sum _{i=0}^{n+t+1}B_{2n+2t+3,2i+1}\rho ^{2i+1}\nonumber \\&=\sum _{t=0}^{\frac{n-1}{2}}\frac{1}{(\rho ^{2}-1)^{2t+\frac{1}{2}}}\cdot \sum _{i=0}^{n+2t+2}B_{2n+4t+4,2i}^{(t)}\rho ^{2i}\nonumber \\&\quad +\sum _{t=1}^{\frac{n-1}{2}}\frac{\rho }{(\rho ^{2}-1)^{2t-\frac{1}{2}}}\cdot \sum _{i=0}^{n+2t}B_{2n+4t+1,2i+1}^{(t)}\rho ^{2i+1}\nonumber \\&\quad +\big (D_{2n+3,1}\rho +D_{2n+3,3}\rho ^{3}+\cdots +D_{2n+3,2n+3}\rho ^{2n+3}\big ), \end{aligned}$$

(3.10)

where

$$\begin{aligned} D_{2n+3,2i+1}=\sum _{k=0}^{n+1}\bigg (M_{2n+3,2i+1}^{(k)}+N_{2n+3,2i+1}^{(k)}\bigg ) \end{aligned}$$

for $i=1, 2, \ldots , n$. Making the transformation $\rho =(1+\omega ^{2})/(1-\omega ^{2})$ for $\omega \in (0,1)$ in (3.10), we have

$$\begin{aligned}&\tilde{G}(\omega ):=G(\rho )\big |_{\rho =\frac{1+\omega ^{2}}{1-\omega ^{2}}}\\&=\Bigg [D_{2n+3,1}\bigg (\frac{1+\omega ^{2}}{1-\omega ^{2}}\bigg )+D_{2n+3,3}\bigg (\frac{1+\omega ^{2}}{1-\omega ^{2}}\bigg )^{3}\\&\quad +\cdots +D_{2n+3,2n+3}\bigg (\frac{1+\omega ^{2}}{1-\omega ^{2}}\bigg )^{2n+3}\Bigg ]\\&\quad +\sum _{t=0}^{\frac{n-1}{2}}\Bigg [\frac{(1-\omega ^{2})^{4t+1}}{(2\omega )^{4t+1}}\cdot \sum _{i=0}^{n+2t+2}B_{2n+4t+4,2i}^{(t)} \bigg (\frac{1+\omega ^{2}}{1-\omega ^{2}}\bigg )^{2i}\Bigg ]\\&\quad +\sum _{t=1}^{\frac{n-1}{2}}\Bigg [\frac{(1+\omega ^{2})\cdot (1-\omega ^{2})^{4t-2}}{(2\omega )^{4t-1}} \cdot \sum _{i=0}^{n+2t}B_{2n+4t+1,2i+1}^{(t)}\bigg (\frac{1+\omega ^{2}}{1-\omega ^{2}}\bigg )^{2i+1}\Bigg ]\\&=\frac{1}{(2\omega )^{2n-1}\cdot (1-\omega ^{2})^{2n+3}}\Bigg \{\sum _{t=0}^{\frac{n-3}{2}}\big (2\omega \big )^{2n-4t-2}\cdot \\&\quad \Bigg [ \sum _{m=0}^{n+2t+2}B_{2n+4t+4,2m}^{(t)}\big (1-\omega ^{2}\big )^{2n+4t-2m+4}\cdot \big (1+\omega ^{2}\big )^{2m}\Bigg ]\\&\quad +h_{1}(\omega ^{2})+\sum _{t=1}^{\frac{n-1}{2}}\big (2\omega \big )^{2n-4t}\cdot \\&\quad \Bigg [ \sum _{m=0}^{n+2t}B_{2n+4t+1,2m+1}^{(t)} \big (1-\omega ^{2}\big )^{2n+4t-2m}\cdot \big (1+\omega ^{2}\big )^{2m+2}\Bigg ]\\&\quad +\big (2\omega \big )^{2n-1}\cdot \Bigg [\sum _{m=0}^{n+1}D_{2n+3,2m+1}\big (1-\omega ^{2}\big )^{2n-2m+2}\cdot \big (1+\omega ^{2}\big )^{2m+1}\Bigg ]\Bigg \}\\&=\frac{1}{(2\omega )^{2n-3}\cdot (1-\omega ^{2})^{2n+3}}\Bigg \{\sum _{t=0}^{\frac{n-3}{2}}\big (2\omega \big )^{2n-4t-4}\cdot \\&\quad \Bigg [ \sum _{m=0}^{n+2t+2}B_{2n+4t+4,2m}^{(t)}\big (1-\omega ^{2}\big )^{2n+4t-2m+4}\cdot \big (1+\omega ^{2}\big )^{2m}\Bigg ]\\&\quad +\frac{1}{4}R_{4n}^{*}(\omega ^{2})+\sum _{t=1}^{\frac{n-1}{2}}\big (2\omega \big )^{2n-4t-2} \cdot \\&\quad \Bigg [ \sum _{m=0}^{n+2t}B_{2n+4t+1,2m+1}^{(t)}\big (1-\omega ^{2}\big )^{2n+4t-2m}\cdot \big (1+\omega ^{2}\big )^{2m+2}\Bigg ]\\&\quad +\big (2\omega \big )^{2n-3}\cdot \Bigg [\sum _{m=0}^{n+1}D_{2n+3,2m+1}\big (1-\omega ^{2}\big )^{2n-2m+2}\cdot \big (1+\omega ^{2}\big )^{2m+1}\Bigg ]\Bigg \}\\&=\frac{1}{(2\omega )^{2n-3}\cdot (1-\omega ^{2})^{2n+3}}\Big [W_{4n}(\omega ^{2})+\big (2\omega \big )^{2n-3}\cdot W_{2n+3}(\omega ^{2})\Big ], \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} W_{4n}(\omega ^{2})&=\sum _{t=0}^{\frac{n-3}{2}}\big (2\omega \big )^{2n-4t-4}\\&\quad \cdot \Bigg [ \sum _{m=0}^{n+2t+2}B_{2n+4t+4,2m}^{(t)}\big (1-\omega ^{2}\big )^{2n+4t-2m+4}\cdot \big (1+\omega ^{2}\big )^{2m}\Bigg ]\\&\quad +\frac{1}{4}R_{4n}^{*}(\omega ^{2})+\sum _{t=1}^{\frac{n-1}{2}}\big (2\omega \big )^{2n-4t-2} \\&\quad \cdot \Bigg [ \sum _{m=0}^{n+2t}B_{2n+4t+1,2m+1}^{(t)}\big (1-\omega ^{2}\big )^{2n+4t-2m}\cdot \big (1+\omega ^{2}\big )^{2m+2}\Bigg ],\\ W_{2n+3}(\omega ^{2})&=\sum _{m=0}^{n+1}D_{2n+3,2m+1}\big (1-\omega ^{2}\big )^{2n-2m+2}\cdot \big (1+\omega ^{2}\big )^{2m+1}. \end{aligned} \end{aligned}$$

A straightforward calculation yields that the coefficients in the function $W_{4n}(\omega ^{2})+\big (2\omega \big )^{2n-3}\cdot W_{2n+3}(\omega ^{2})$ are symmetrical with respect to $\omega$, then when $\omega _{0}\ne 0$ is one root of $\tilde{G}(\omega )=0$, so is $1/\omega _{0}$.

Moreover, we have Lemma 3.6.

Lemma 3.6

For the odd number $n\ge 3$, the function $\tilde{G}(\omega )$ can be expressed as

$$\begin{aligned} \tilde{G}(\omega )=\frac{1-\omega }{(2\omega )^{2n-3}\cdot (1+\omega )^{2n+3}}\cdot g(\omega ), \end{aligned}$$

(3.11)

where $g(\omega )$ is a symmetrical polynomial of degree $6n-4$, and the ordered list of coefficients of $g(\omega )$ changes its sign at most $6n-6$ times. Consequently, the function $\tilde{G}(\omega )$ has at most $3n-3$ simple zeros in $\omega \in (0,1)$.

Proof

Note the fact

$$\begin{aligned} \lim _{z\rightarrow 0}\int _{0}^{2 \pi }\Bigg [\sum _{k=1}^{n}\frac{S_{3k+3}(\cos \theta )}{(\cos \theta -1+\frac{1}{3z^{3}})^{k}} +\sum _{k=1}^{n}\frac{T_{3k+2}(\cos \theta )}{(\cos \theta -1+\frac{1}{3z^{3}})^{k-1}}\Bigg ]\mathrm{d}\theta \\ =0, \end{aligned}$$

which implies $\tilde{G}(1)=0$. Hence we have

$$\begin{aligned} \begin{aligned} \tilde{G}(\omega )&=\frac{1}{(2\omega )^{2n-3}\cdot (1-\omega ^{2})^{2n+3}}\Big [W_{4n}(\omega ^{2})+\big (2\omega \big )^{2n-3}\cdot W_{2n+3}(\omega ^{2})\Big ]\\&=\frac{1-\omega }{(2\omega )^{2n-3}\cdot (1+\omega )^{2n+3}}\cdot g(\omega ), \end{aligned} \end{aligned}$$

where g(w) is such a polynomial of degree $6n-4$ that satisfies the property

$$\begin{aligned} \begin{aligned} W_{4n}(\omega ^{2})+\big (2\omega \big )^{2n-3}\cdot W_{2n+3}(\omega ^{2})=(1-\omega )^{2n+4}\cdot g(\omega ). \end{aligned} \end{aligned}$$

(3.12)

Without loss of generality, suppose $g(\omega )=\sum _{i=0}^{6n-4}a_{i}\omega ^{i}$. Since the coefficients of $\omega$ and $\omega ^{8n-1}$ in (3.12) are identically equal to zero, we get

$$\begin{aligned} \begin{aligned} a_{1}-(2n+4)a_{0}=0, \quad a_{6n-5}-(2n+4)a_{6n-4}=0, \end{aligned} \end{aligned}$$

(3.13)

that is $a_{1}=(2n+4)a_{0}$, $a_{6n-5}=(2n+4)a_{6n-4}$.

Thus the ordered list of coefficients of $g(\omega )$ changes its sign at most $6n-6$ times. Recall that $g(\omega )$ are symmetrical with respect to $\omega$, then its roots appear in such the pairs as $w_{0}\ne 0$ and $1/w_{0}$. Hence $g(\omega )$ has at most $3n-3$ zeros in $\omega \in (0,1)$. The proof of Lemma 3.6 is completed. $\square$

Based on Lemma 3.6, we have the following result.

Corollary 3.7

System (3.2) for the odd number n has at most $3n-3$ periodic solutions arising from the periodic annulus around the center (0, 0) of system (3.2)$|_{\varepsilon =0}$, and for the case $n=3$, this upper bound can be reached.

Proof

The first result follows directly from Lemma 3.6. Now we prove the second one.

Consider the following perturbed system

$$\begin{aligned} \begin{aligned} \dot{x}&=-y+x^{3}y+xy^{3}+\varepsilon \sum _{k=1}^{3}\sum _{l+m=1+3k}c_{lm}x^{l}y^{m},\\ \dot{y}&=x+x^{2}y^{2}+y^{4}+\varepsilon \sum _{k=1}^{3}\sum _{l+m=1+3k}d_{lm}x^{l}y^{m}, \end{aligned} \end{aligned}$$

(3.14)

From (3.3), (3.11) and (3.14), we get the averaged function

$$\begin{aligned} \mathcal {F}(z)=z^{4}\cdot \tilde{G}(\omega )= & {} \frac{(1-\omega ^{2})^{4/3}}{6^{4/3}}\cdot \frac{1-\omega }{\omega ^{3}\cdot (1+\omega )^{9}}\cdot g(\omega )\nonumber \\= & {} \frac{(1-\omega )^{7/3}}{6^{4/3}\cdot \omega ^{3}\cdot (1+\omega )^{23/3}}\cdot g(\omega ) \end{aligned}$$

(3.15)

where

$$\begin{aligned} \begin{aligned} g(\omega )&=-\frac{\pi }{1728}\cdot \Big (\frac{f_{1}}{10}\omega ^{14}+f_{1}\omega ^{13}+f_{2}\omega ^{12}+f_{3}\omega ^{11}+f_{4}\omega ^{10} +f_{5}\omega ^{9}+f_{6}\omega ^{8} \\&\quad +f_{7}\omega ^{7}+f_{6}\omega ^{6}+f_{5}\omega ^{5}+f_{4}\omega ^{4}+f_{3}\omega ^{3}+f_{2}\omega ^{2}+f_{1}\omega +\frac{f_{1}}{10}\Big ) \end{aligned} \end{aligned}$$

with

$$\begin{aligned} \begin{aligned} f_{1}&=80\,d_{{91}}+400\,c_{{100}},\\ f_{2}&=96\,d_{{73}}+1240\,c_{{100}}+96\,c_{{82}}+56\,d_{{91}}-192\,d_{{61}}- 384\,c_{{70}},\\ f_{3}&=41\,d_{{37}}+175\,d_{{55}}-55\,d_{{73}}-120\,d_{{25}}+7\,c_{{46}}+65\, c_{{64}}+295\,c_{{82}}+47\,d_{{19}}\\&\quad -24\,c_{{16}} -120\,c_{{52}}-408\,d_{{7}}-432\,c_{{4}}-25\,c_{{10}}+144\,d_{{13}}-24\,c_{{34}}-312\,d_{{43 }}\\&\quad -144\,c_{{22}}-432\,c_{{40}}+432\,d_{{31}} -600\,d_{{61}}+1825\,c_{{100}}\\&\quad +335\,d_{{91}}-3000\,c_{{70}}+c_{{28}},\\ f_{4}&=266\,c_{{64}}+70\,c_{{46}}-170\,d_{{55}}-1584\,d_{{61}}-9648\,c_{{70}} +410\,d_{{37}}+314\,d_{{73}}\\&\quad +10\,c_{{28}}-250\,c_{{10}}+1810\,c_{{100}}+470\,d_{{19}}-4320\,c_{{4}}-240\,c_{{16}}-1440\,c_{{22}}\\&\quad -240\,c_{{34}}-2016\,c_{{40}}-1200\,c_{{52}}-26\,c_{{82}}-4080\,d_{{7}}-816\,d_{{43}}+2016\,d_{{31}}\\&\quad -1200\,d_{{25}}+1440\,d_{{13}}-130\,d_{{91}},\\ f_{5}&=-400\,d_{{73}}+320\,d_{{91}}-2880\,d_{{61}}-800\,c_{{100}}+1424\,d_{{ 19}}-4608\,c_{{22}}\\&\quad +400\,d_{{55}}-400\,d_{{37}}-17088\,d_{{7}}+4608\,d_{{13}}-4608\,c_{{40}}+400\,c_{{82}}\\&\quad -1728\,c_{{34}}-2880\,c_{{52}}-880 \,c_{{10}}-18432\,c_{{4}}-1344\,c_{{16}}+112\,c_{{28}}\\&\quad +400\,c_{{46}}-400\,c_{{64}}-20160\,c_{{70}}-2880\,d_{{25}}+4608\,d_{{31}}-1728\,d_{{ 43}},\\ f_{6}&=-5520\,c_{{16}}+534\,c_{{64}}-870\,c_{{46}}-870\,c_{{82}}-7776\,c_{{22 }}-30288\,c_{{70}}+790\,c_{{28}}\\&\quad -41760\,c_{{4}}-4560\,d_{{25}}-2290\,c_{{100}}-3216\,c_{{34}}-36240\,d_{{7}}-4560\,c_{{52}}\\&\quad -7200\,c_{{40}}- 1270\,d_{{19}}+7776\,d_{{13}}-630\,d_{{55}}+390\,d_{{37}}+7200\,d_{{31}}\\&\quad -2640\,d_{{43}}+390\,d_{{73}}-734\,d_{{91}}-3984\,d_{{61}}-550\,c_{{ 10}},\\ f_{7}&=-8928\,c_{{22}}-8784\,c_{{16}}-5520\,d_{{25}}-882\,d_{{37}}-54432\,c_{ {4}}-690\,d_{{73}}\\&\quad -4450\,c_{{100}}+8352\,d_{{31}} -3408\,c_{{34}}-45648\,d_{{7}}-1826\,c_{{28}}+8928\,d_{{13}}\\&\quad +3410\,c_{{10}}+450\,d_{{55}}- 4560\,d_{{61}}-1342\,d_{{19}}-34320\,c_{{70}}-2832\,d_{{43}}\\&\quad +210\,c_{{82}}+130\,d_{{91}}+786\,c_{{46}}-930\,c_{{64}}-5520\,c_{{52}}-8352\,c_ {{40}}. \end{aligned} \end{aligned}$$

Evidently, the function $g(\omega )$ is the symmetrical polynomial of degree 14, and the ordered list of coefficients of $g(\omega )$ changes its sign at most 12 times, so $g(\omega )$ has at most 6 simple zeros in $\omega \in (0,1)$, which means that the averaged function $\mathcal {F}(z)$ in (3.15) also has at most six zeros locating at $(0, \root 3 \of {1/6})$. In the following, we construct a family of systems whose first averaged functions have exactly six simple zeros in this interval.

For example, consider a family of systems

$$\begin{aligned} \dot{x}&=-y+x^{3}y+xy^{3}+\varepsilon \Bigg [c_{40}x^{4}+c_{31}x^{3}y+c_{22}x^{2}y^{2}+c_{13}xy^{3}\nonumber \\&\quad +\bigg (-\frac{2}{5}\,c_{{100}}-\frac{1}{5}\,c_{{82}}-\frac{1982312879}{70778880}\bigg )x^{7} +c_{61}x^{6}y+c_{52}x^{5}y^{2}+c_{43}x^{4}y^{3}\nonumber \\&\quad +\frac{14377520035}{382205952}x^{3}y^{4} +c_{25}x^{2}y^{5}+c_{07}y^{7}+c_{100}x^{10}+c_{91}x^{9}y+c_{82}x^{8}y^{2}\nonumber \\&\quad +c_{73}x^{7}y^{3} +c_{55}x^{5}y^{5}+c_{37}x^{3}y^{7} -\frac{311748125}{21233664}x^{2}y^{8}+c_{19}xy^{9}\Bigg ],\nonumber \\ \dot{y}&=x+x^{2}y^{2}+y^{4}+\varepsilon \Bigg [d_{40}x^{4}+c_{40}x^{3}y+d_{22}x^{2}y^{2}\nonumber \\&\quad +\bigg (\frac{14}{5}\,c_{{100}}+\frac{7}{5}\,c_{{82}}-\frac{5736812501}{212336640}\bigg )x^{6}y\nonumber \\&\quad +c_{22}xy^{3}+d_{04}y^{4}+d_{70}x^{7}+d_{52}x^{5}y^{2}\nonumber \\&\quad +\frac{127718550845}{382205952}x^{4}y^{3} +d_{34}x^{3}y^{4}-c_{52}x^{2}y^{5}+d_{16}xy^{6}\nonumber \\&\quad +d_{100}x^{10}+\left( -5\,c_{{100}}+\frac{1}{8}\right) x^{9}y+d_{82}x^{8}y^{2}\nonumber \\&\quad +\left( -\frac{3627079267}{21233664}-6\,c_{{100}}+c_{{82}}\right) x^{7}y^{3} +d_{64}x^{6}y^{4}\nonumber \\&\quad +d_{46}x^{4}y^{6}+d_{28}x^{2}y^{8}+d_{010}y^{10}\Bigg ], \end{aligned}$$

(3.16)

where the coefficients $c_{ij}$ and $d_{ij}$ are any real constants.

In the polar coordinates, system (3.16) takes the form

$$\begin{aligned} \dot{r}= & {} r^{4}\sin \theta +\varepsilon \bigg \{\bigg [c_{40}\cos ^{5}\theta +(c_{31}+d_{40})\cos ^{4}\theta \sin \theta +(c_{22}+c_{40})\cos ^{3}\theta \sin ^{2}\theta \nonumber \\&+(c_{13}+d_{22})\cos ^{2}\theta \sin ^{3}\theta +c_{22}\cos \theta \sin ^{4}\theta \bigg ]r^{3}\nonumber \\&+\bigg [\bigg (-\frac{2}{5}c_{100}-\frac{c_{82}}{5}-\frac{1982312879}{7077880}\bigg )\cos ^{8}\theta \nonumber \\&+(c_{61}+d_{70})\cos ^{7}\theta \sin \theta +c_{52}\cos ^{6}\theta \sin ^{2}\theta +(c_{43}+d_{52})\cos ^{5}\theta \sin ^{3}\theta \nonumber \\&+\frac{142096070880}{382205952}\cos ^{4}\theta \sin ^{4}\theta +(c_{25}+d_{34})\cos ^{3}\theta \sin ^{5}\theta -c_{52}\cos ^{2}\theta \sin ^{6} \theta \nonumber \\&+(c_{07}+d_{16})\cos \theta \sin ^{7}\theta \bigg ]r^{7}+\bigg [(c_{100}+d_{100})\cos ^{11}\theta +c_{91}\cos ^{10}\theta \sin \theta \nonumber \\&+\bigg (c_{82}-5c_{100}+\frac{1}{8}\bigg )\cos ^{9}\theta \sin ^{2}\theta +(c_{73}+d_{82})\cos ^{8}\theta \sin ^{3}\theta \nonumber \\&+\bigg (-\frac{3627079267}{21233664}-6c_{100}+c_{82}\bigg )\cos ^{7}\theta \sin ^{4}\theta +(c_{55}+d_{64})\cos ^{6}\theta \sin ^{5}\theta \nonumber \\&+(c_{37}+d_{46})\cos ^{4}\theta \sin ^{7}\theta -\frac{311748125}{21233664}\cos ^{3}\theta \sin ^{8}\theta \nonumber \\&+(c_{19}+d_{28})\cos ^{2}\theta \sin ^{9}\theta +d_{010}\sin ^{11}\theta \bigg ]r^{10}\bigg \},\nonumber \\ \dot{\theta }= & {} 1+\varepsilon \bigg \{\bigg [d_{40}\cos ^{5}\theta +(d_{22}-c_{31})\cos ^{3}\theta \sin ^{2}\theta +(d_{04}-c_{13})\cos \theta \sin ^{4}\theta \bigg ]r^{3}\nonumber \\&+\bigg [\bigg (\frac{16}{5}c_{100}+\frac{8}{5}c_{82}+\frac{26265767}{26542080}\bigg )\cos ^{7}\theta \sin \theta +d_{70}\cos ^{8}\theta \nonumber \\&\qquad +(d_{52}-c_{61})\cos ^{8}\theta \sin ^{2}\theta \nonumber \\&+\bigg (\frac{127718550845}{382205952}-c_{52}\bigg )\cos ^{5}\theta \sin ^{3}\theta +(d_{34}-c_{43})\cos ^{4}\theta \sin ^{4}\theta \nonumber \\&-\bigg (c_{52}+\frac{14377520035}{382205952}\bigg )\cos ^{3}\theta \sin ^{5}\theta \nonumber \\&+(d_{16}-c_{25})\cos ^{2}\theta \sin ^{6}\theta -c_{07}\sin ^{8}\theta \bigg ]r^{6}\nonumber \\&+\bigg [d_{100}\cos ^{11}\theta +\bigg (-6c_{100}+\frac{1}{8}\bigg )\cos ^{10}\theta \sin \theta +(d_{82}-c_{91})\cos ^{9}\theta \sin ^{2}\theta \nonumber \\&+\bigg (-\frac{3627079267}{21233664}-6c_{100}\bigg )\cos ^{8}\theta \sin ^{3}\theta +(d_{64}-c_{73})\cos ^{8}\theta \sin ^{4}\theta \nonumber \\&+(d_{46}-c_{55})\cos ^{5}\theta \sin ^{6}\theta +(d_{28}-c_{37})\cos ^{3}\theta \sin ^{8}\theta \nonumber \\&+\frac{311748125}{21233664}\cos ^{2}\theta \sin ^{9}\theta +(d_{010}-c_{19})\cos \theta \sin ^{10}\theta \bigg ]r^{9}\bigg \}. \end{aligned}$$

(3.17)

Using the first order averaging theory, we obtain the averaged function of system (3.17)

$$\begin{aligned} \begin{aligned}&\mathcal {F}(z)=\frac{(1-\omega ^{2})^{4/3}}{6^{4/3}}\cdot \tilde{G}(\omega )\\&\qquad =-\frac{(1-\omega )^{7/3}\pi }{1728\cdot 6^{4/3}\omega ^{3}\cdot (1+\omega )^{23/3}}\cdot \bigg ({\omega }^{14}+10\,{\omega }^{13}-{\frac{64709}{144}}\,{\omega }^{12}+{\frac{71885}{16}}\,{\omega }^{11}\\&\qquad -{\frac{14576899}{648}}\,{\omega }^{10} +{\frac{345891785}{5184}}\,{\omega }^{9}-{\frac{2603509747}{20736} }\,{\omega }^{8}+{\frac{1602359665}{10368}}\,{\omega }^{7}\\ {}&\qquad -{\frac{ 2603509747}{20736}}\,{\omega }^{6}+{\frac{345891785}{5184}}\,{\omega }^{5} -{\frac{14576899}{648}}\,{\omega }^{4}\\ {}&\qquad +{\frac{71885}{16}}\,{\omega }^{3}-{\frac{64709}{144}}\,{\omega }^{2}+10\,\omega +1\bigg )\\&\qquad =-\frac{(1-\omega )^{7/3}\pi }{1728\cdot 6^{4/3}\omega ^{3}\cdot (1+\omega )^{23/3}}\cdot \Bigg (\omega +{\frac{61}{4}}+\frac{1}{4}\,\sqrt{3705}\Bigg )\\ {}&\qquad \quad \Bigg ( \omega +{\frac{61}{4}}-\frac{1}{4}\,\sqrt{3705}\Bigg )\Bigg (\omega -\frac{4}{3}\Bigg )\Bigg (\omega -\frac{3}{4}\Bigg ) \\&\qquad \quad \cdot \Bigg (\omega -\frac{3}{2}\Bigg )\Bigg (\omega -\frac{2}{3}\Bigg ) \Bigg (\omega -\frac{1}{2}\Bigg )\Bigg (\omega -\frac{1}{3}\Bigg )\Bigg (\omega -\frac{1}{4}\Bigg )\\ {}&\quad \qquad \Bigg (\omega -\frac{1}{6}\Bigg )(\omega -6)(\omega -4 )(\omega -3)(\omega -2), \end{aligned} \end{aligned}$$

which has just six simple zeros $\omega _{1}=3/4,\omega _{2}=2/3,\omega _{3}=1/2,\omega _{4}=1/3,\omega _{5}=1/4$ and $\omega _{6}=1/6$ in (0, 1). Then we can get six corresponding closed orbits, that is

$$\begin{aligned} \begin{aligned} r_{1}\bigg (\theta ,\frac{7^{1/3}}{96^{1/3}}\bigg )&=\frac{1}{(3\cos \theta +\frac{75}{7})^{1/3}},~~ r_{2}\bigg (\theta ,\frac{5^{1/3}}{54^{1/3}}\bigg )=\frac{1}{(3\cos \theta +\frac{39}{5})^{1/3}},\\ r_{3}\bigg (\theta ,\frac{1}{2}\bigg )&=\frac{1}{(3\cos \theta +5)^{1/3}},~~ r_{4}\bigg (\theta ,\frac{4^{1/3}}{3}\bigg )=\frac{1}{(3\cos \theta +\frac{15}{4})^{1/3}},\\ r_{5}\bigg (\theta ,\frac{5^{1/3}}{32^{1/3}}\bigg )&=\frac{1}{(3\cos \theta +\frac{17}{5})^{1/3}}, ~~r_{6}\bigg (\theta ,\frac{35^{1/3}}{6}\bigg )=\frac{1}{(3\cos \theta +\frac{111}{35})^{1/3}}. \end{aligned} \end{aligned}$$

Using Lemma 2.1, system (3.17) has exactly six periodic solutions bifurcating from the above six closed orbits, respectively. This completes the proof of Corollary 3.7. $\square$

By virtue of Corollary 3.7 and the averaging theory, we obtain

Lemma 3.8

For the odd number $n\ge 3$ and any sufficiently small $|\varepsilon |\ne 0$, system (1.2) has at most $3n-3$ limit cycles bifurcating from the periodic annulus around the center (0, 0) of the unperturbed system (1.2)$|_{\varepsilon =0}$, and this upper bound for the case $n=3$ is sharp.

3.3 Proof of Theorem 1.1 for the Even Case

We first simplify the function $G(\rho )$ defined by (3.5), then give the estimate on the number of limit cycles bifurcating from the period annulus around the center of the unperturbed system (1.2)$|_{\varepsilon =0}$ for the even number n.

Similar to (3.10), we have

$$\begin{aligned} G(\rho )&=B_{0,0}\cdot I_{-(2n+3)}(\rho )+B_{1,1}\rho \cdot I_{-(2n+2)}(\rho )+(B_{2,0}+B_{2,2}\rho ^{2})\cdot I_{-(2n+1)}(\rho )\\&\quad +\cdots +(B_{2n+2,0}+B_{2n+2,2}\rho ^{2}+\cdots +B_{2n+2,2n+2}\rho ^{2n+2})\cdot I_{-1}(\rho )\\&\quad +(B_{2n+3,1}\rho +B_{2n+3,3}\rho ^{3}+\cdots +B_{2n+3,2n+3}\rho ^{2n+3})\cdot I_{0}(\rho )\\&\quad +(B_{2n+4,0}+B_{2n+4,2}\rho ^{2}+\cdots +B_{2n+4,2n+4}\rho ^{2n+4})I_{1}(\rho )\\&\quad +(B_{2n+5,1}\rho +B_{2n+5,3}\rho ^{3}+\cdots +B_{2n+5,2n+5}\rho ^{2n+5})I_{2}(\rho )\\&\quad +\cdots +\sum _{i=0}^{\frac{3n+2}{2}}B_{3n+3,2i+1}\rho ^{2i+1}I_{n}(\rho )\\&=\sum _{t=0}^{n+1}I_{-(2t+1)}(\rho )\sum _{i=0}^{n-t+1}B_{2n-2t+2,2i}\rho ^{2i}\\&\quad +\sum _{t=0}^{n+1}I_{-(2t)}(\rho )\sum _{i=0}^{n-t+1}B_{2n-2t+3,2i+1}\rho ^{2i+1}\\&\quad +\sum _{t=0}^{\frac{n-2}{2}}I_{2t+1}(\rho )\sum _{i=0}^{n+t+2}B_{2n+2t+4,2i}\rho ^{2i}\\&\quad +\sum _{t=1}^{\frac{n}{2}}I_{2t}(\rho )\sum _{i=0}^{n+t+1}B_{2n+2t+3,2i+1}\rho ^{2i+1}\\&=\sum _{t=0}^{\frac{n-2}{2}}\frac{1}{(\rho ^{2}-1)^{2t+\frac{1}{2}}}\cdot \sum _{i=0}^{n+2t+2}B_{2n+4t+4,2i}^{(t)}\rho ^{2i}\\&\quad +\sum _{t=1}^{\frac{n}{2}}\frac{\rho }{(\rho ^{2}-1)^{2t-\frac{1}{2}}}\cdot \sum _{i=0}^{n+2t}B_{2n+4t+1,2i+1}^{(t)}\rho ^{2i+1}\\&\quad +\big (D_{2n+3,1}\rho +D_{2n+3,3}\rho ^{3}+\cdots +D_{2n+3,2n+3}\rho ^{2n+3}\big ), \end{aligned}$$

where $D_{2n+3,2i+1}, i=1,2,\cdots , n$ are defined as before. Making the same transformation $\rho =(1+\omega ^{2})/(1-\omega ^{2})$ for $\omega \in (0, 1)$, the above formula becomes

$$\begin{aligned}&\bar{G}(\omega ):=G(\rho )\big |_{\rho =\frac{1+\omega ^{2}}{1-\omega ^{2}}}\nonumber \\&\quad =\Bigg [D_{2n+3,1}\bigg (\frac{1+\omega ^{2}}{1-\omega ^{2}}\bigg )+D_{2n+3,3} \bigg (\frac{1+\omega ^{2}}{1-\omega ^{2}}\bigg )^{3}\nonumber \\&\qquad \quad +\cdots +D_{2n+3,2n+3}\bigg (\frac{1+\omega ^{2}}{1-\omega ^{2}}\bigg )^{2n+3}\Bigg ]\nonumber \\&\qquad +\sum _{t=0}^{\frac{n-2}{2}}\Bigg [\frac{(1-\omega ^{2})^{4t+1}}{(2\omega )^{4t+1}}\cdot \sum _{i=0}^{n+2t+2}B_{2n+4t+4,2i}^{(t)} \big (\frac{1+\omega ^{2}}{1-\omega ^{2}}\big )^{2i}\Bigg ]\nonumber \\&\qquad +\sum _{t=1}^{\frac{n}{2}}\Bigg [\frac{(1+\omega ^{2})\cdot (1-\omega ^{2})^{4t-2}}{(2\omega )^{4t-1}} \cdot \sum _{i=0}^{n+2t}B_{2n+4t+1,2i+1}^{(t)}\big (\frac{1+\omega ^{2}}{1-\omega ^{2}}\big )^{2i+1}\Bigg ]\nonumber \\&\quad =\frac{1}{(2\omega )^{2n-1}\cdot (1-\omega ^{2})^{2n+3}}\Bigg \{\sum _{t=0}^{\frac{n-2}{2}} \big (2\omega \big )^{2n-4t-2} \cdot \nonumber \\&\qquad \Bigg [\sum _{m=0}^{n+2t+2}B_{2n+4t+4,2m}^{(t)}\big (1-\omega ^{2}\big )^{2n+4t-2m+4}\cdot \big (1+\omega ^{2}\big )^{2m}\Bigg ]\nonumber \\&\qquad +\sum _{t=1}^{\frac{n-2}{2}}\big (2\omega \big )^{2n-4t}\cdot \Bigg [\sum _{m=0}^{n+2t}B_{2n+4t+1,2m+1}^{(t)} \big (1-\omega ^{2}\big )^{2n+4t-2m}\nonumber \\&\qquad \cdot \big (1+\omega ^{2}\big )^{2m+2}\Bigg ]+h_{2}(\omega ^{2})\nonumber \\&\qquad +\big (2\omega \big )^{2n-1}\cdot \Bigg [\sum _{m=0}^{n+1}D_{2n+3,2m+1}\big (1-\omega ^{2}\big )^{2n-2m+2}\cdot \big (1+\omega ^{2}\big )^{2m+1}\Bigg ]\Bigg \}\nonumber \\&\quad =\frac{1}{(2\omega )^{2n-3}\cdot (1-\omega ^{2})^{2n+3}}\Bigg \{\sum _{t=0}^{\frac{n-2}{2}} \big (2\omega \big )^{2n-4t-4} \nonumber \\&\qquad \cdot \Bigg [\sum _{m=0}^{n+2t+2}B_{2n+4t+4,2m}^{(t)}\big (1-\omega ^{2}\big )^{2n+4t-2m+4}\cdot \big (1+\omega ^{2}\big )^{2m}\Bigg ]\nonumber \\&\qquad +\sum _{t=1}^{\frac{n-2}{2}}\big (2\omega \big )^{2n-4t-2}\cdot \Bigg [\sum _{m=0}^{n+2t}B_{2n+4t+1,2m+1}^{(t)}\big (1-\omega ^{2}\big )^{2n+4t-2m} \nonumber \\&\qquad \cdot \big (1+\omega ^{2}\big )^{2m+2}\Bigg ]+\frac{1}{4}R_{4n}^{**}(\omega ^{2})\nonumber \\&\qquad +\big (2\omega \big )^{2n-3}\cdot \Bigg [\sum _{m=0}^{n+1}D_{2n+3,2m+1}\big (1-\omega ^{2}\big )^{2n-2m+2}\cdot \big (1+\omega ^{2}\big )^{2m+1}\Bigg ]\Bigg \}\nonumber \\&\quad =\frac{1}{(2\omega )^{2n-3}\cdot (1-\omega ^{2})^{2n+3}}\Bigg [U_{4n}(\omega ^{2})+\big (2\omega \big )^{2n-3}\cdot U_{2n+3}(\omega ^{2})\Bigg ], \end{aligned}$$

(3.18)

where

$$\begin{aligned} \begin{aligned}&U_{4n}(\omega ^{2})\\&\quad =\sum _{t=0}^{\frac{n-2}{2}} \big (2\omega \big )^{2n-4t-4} \cdot \Bigg [\sum _{m=0}^{n+2t+2}B_{2n+4t+4,2m}^{(t)}\big (1-\omega ^{2}\big )^{2n+4t-2m+4}\cdot \big (1+\omega ^{2}\big )^{2m}\Bigg ]\\&\qquad +\sum _{t=1}^{\frac{n-2}{2}}\big (2\omega \big )^{2n-4t-2}\cdot \Bigg [\sum _{m=0}^{n+2t}B_{2n+4t+1,2m+1}^{(t)}\big (1-\omega ^{2}\big )^{2n+4t-2m} \\&\qquad \cdot \big (1+\omega ^{2}\big )^{2m+2}\Bigg ]+\frac{1}{4}R_{4n}^{**}(\omega ^{2}),\\&U_{2n+3}(\omega ^{2})\\&\quad =\sum _{m=0}^{n+1}D_{2n+3,2m+1}\big (1-\omega ^{2}\big )^{2n-2m+2}\cdot \big (1+\omega ^{2}\big )^{2m+1}. \end{aligned} \end{aligned}$$

(3.19)

Hence, for the even number n, we have the following results.

Lemma 3.9

• 1. For $n=2$, the function $\bar{G}(\omega )$ can be expressed as

  $$\begin{aligned} \bar{G}(\omega )=\frac{1-\omega }{\omega \cdot (1+\omega )^{7}}\cdot \bar{g}(\omega ), \end{aligned}$$

  where $\bar{g}(\omega )$ is a symmetrical polynomial of degree 8, having at most 4 simple zeros in $\omega \in (0,1)$. Consequently, the function $\bar{G}(\omega )$ has at most 4 simple zeros in $\omega \in (0,1)$. Moreover, this upper bound is sharp.

• 2. For the even number $n\ge 4$, the function $\bar{G}(\omega )$ can be expressed as

  $$\begin{aligned} \bar{G}(\omega )=\frac{1-\omega }{(2\omega )^{2n-3}\cdot (1+\omega )^{2n+3}}\cdot \bar{g}(\omega ), \end{aligned}$$

  where $\bar{g}(\omega )$ is a symmetrical polynomial of degree $6n-4$, and the ordered list of coefficients of $\bar{g}(\omega )$ changes its sign at most $6n-6$ times. Consequently, the function $\bar{G}(\omega )$ has at most $3n-3$ simple zeros in $\omega \in (0,1)$.

Proof

The proof of the second result is similar to Lemma 3.6. Now we begin to prove the first one.

Consider the following quartic system

$$\begin{aligned} \begin{aligned} \dot{x}&=-y+x^{3}y+xy^{3}+\varepsilon \sum _{k=1}^{2}\sum _{l+m=1+3k}c_{lm}x^{l}y^{m},\\ \dot{y}&=x+x^{2}y^{2}+y^{4}+\varepsilon \sum _{k=1}^{2}\sum _{l+m=1+3k}d_{lm}x^{l}y^{m}. \end{aligned} \end{aligned}$$

The formula (3.18) associated to the above system takes the form

$$\begin{aligned} \bar{G}(\omega )=\frac{1-\omega }{\omega \cdot (1+\omega )^{7}}\cdot \bar{g}(\omega ), \end{aligned}$$

where

$$\begin{aligned} \bar{g}(\omega )=\frac{\pi }{72}\cdot \big (f_{0}\omega ^{8}+f_{1}\omega ^{7}+f_{2}\omega ^{6}+f_{3}\omega ^{5}+f_{4}\omega ^{4} +f_{3}\omega ^{3}+f_{2}\omega ^{2}+f_{1}\omega +f_{0}\big ) \end{aligned}$$

with

$$\begin{aligned} \begin{aligned} f_{0}&=16\,c_{{70}}+8\,d_{{61}},\\ f_{1}&=18\,c_{{04}}+c_{{16}}+6\,c_{{22}}+c_{{34}}+18\,c_{{40}}+5\,c_{{52}}+93 \,c_{{70}}+17\,d_{{07}}-6\,d_{{13}}\\&\quad +5\,d_{{25}}-18\,d_{{31}}+13\,d_{{43}}+9\,d_{{61}},\\ f_{2}&=144\,c_{{04}}+8\,c_{{16}}+48\,c_{{22}}+8\,c_{{34}}+48\,c_{{40}}+40\,c_{ {52}}+200\,c_{{70}}+136\,d_{{07}}\\&\quad -48\,d_{{13}}+40\,d_{{25}}-48\,d_{{31}}+8\,d_{{43}}+40\,d_{{61}},\\ f_{3}&=462\,c_{{04}}+39\,c_{{16}}+90\,c_{{22}}+55\,c_{{34}}+78\,c_{{40}}+35\,c _{{52}}+347\,c_{{70}}+423\,d_{{07}}\\&\quad -90\,d_{{13}}+35\,d_{{25}}-78\,d_{{ 31}}+43\,d_{{43}}+31\,d_{{61}},\\ f_{4}&=672\,c_{{04}}+144\,c_{{16}}+96\,c_{{22}}+16\,c_{{34}}+96\,c_{{40}}+80\, c_{{52}}+368\,c_{{70}}+528\,d_{{07}}\\&\quad -96\,d_{{13}}+80\,d_{{25}}-96\,d_{{ 31}}+16\,d_{{43}}+64\,d_{{61}}. \end{aligned} \end{aligned}$$

Since $\bar{g}(\omega )$ is a symmetrical polynomial of degree 8, it has at most 4 simple zeros in $\omega \in (0,1)$. Hence $\bar{G}(\omega )$ also has four as the upper bound of the number of its zeros in $\omega \in (0,1)$. To show this upper bound can be reached, we consider the following quartic system

$$\begin{aligned} \dot{x}&=-y+x^{3}y+xy^{3}+\varepsilon \Bigg [c_{40}x^{4}+c_{31}x^{3}y+c_{22}x^{2}y^{2}+c_{13}xy^{3}\\&\quad +\left( \frac{13483}{7680}-c_{70}-d_{07}\right) y^{4} +c_{70}x^{7}\\&\quad +c_{61}x^{6}y+c_{52}x^{5}y^{2}+c_{43}x^{4}y^{3}+\left( -\frac{114853}{7680}+5c_{70}\right) x^{3}y^{4}+c_{25}x^{2}y^{5}\\&\quad +\left( -\frac{29399}{7680}+3c_{70}+d_{07}\right) xy^{6}+c_{07}y^{7}\Bigg ],\\ \dot{y}&=x+x^{2}y^{2}+y^{4}+\varepsilon \Bigg [d_{40}x^{4}+c_{40}x^{3}y+d_{22}x^{2}y^{2}+c_{22}xy^{3}+d_{04}y^{4}+d_{70}x^{7}\\&\quad +(\frac{1}{8}-2c_{70})x^{6}y+d_{52}x^{5}y^{2}-\left( 5c_{70}+\frac{8633}{3840}\right) x^{4}y^{3}+d_{34}x^{3}y^{4}\\&\quad -c_{52}x^{2}y^{5} +d_{16}xy^{6}+d_{07}y^{7}\Bigg ], \end{aligned}$$

where the coefficients $c_{ij}$ and $d_{ij}$ are any real constants. The corresponding function $\bar{G}(\omega )$ can be expressed as

$$\begin{aligned} \begin{aligned} \bar{G}(\omega )&=\frac{\pi (1-\omega )}{72\omega (1+\omega )^{7}}\cdot \bigg ({\omega }^{8}-{\frac{917}{60}}\,{\omega }^{7}+{\frac{10747}{120}}\,{ \omega }^{6}-{\frac{15211}{60}}\,{\omega }^{5} +{\frac{21677}{60}}\,{ \omega }^{4}\\&\quad -{\frac{15211}{60}}\,{\omega }^{3}+{\frac{10747}{120}}\,{\omega }^{2}-{\frac{917}{60}}\,\omega +1 \bigg )\\ {}&c\frac{\pi (1-\omega )}{72\omega (1+\omega )^{7}}\cdot \left( \omega -\frac{1}{2}\right) (\omega -2) \left( \omega -\frac{1}{3}\right) (\omega -3)\left( \omega -\frac{1}{4}\right) \\&\quad (\omega -4) (\omega -5)\left( \omega -\frac{1}{5}\right) , \end{aligned} \end{aligned}$$

which has exactly four simple zeros $\omega _{1}=1/2,\omega _{2}=1/3,\omega _{3}=1/4,\omega _{4}=1/5$. So we complete the proof of the first result. $\square$

Based on Lemma 3.9, we have Corollary 3.10.

Corollary 3.10

For any sufficiently small $|\varepsilon |\ne 0$, the following properties hold.

• 1. For $n=2$, system (3.2) has at most 4 periodic solutions bifurcating from the periodic annulus around the center (0, 0) of system (3.2)$|_{\varepsilon =0}$, and this upper bound is sharp.

• 2. For the even number $n\ge 4$, system (3.2) has at most $3n-3$ periodic solutions bifurcating from the periodic annulus around the center (0, 0) of system (3.2)$|_{\varepsilon =0}$.

Equivalently, we have Lemma 3.11.

Lemma 3.11

For any sufficiently small $|\varepsilon |\ne 0$, the following statements are true.

• 1. For $n=2$, system (1.2) has at most 4 limit cycles bifurcating from the periodic annulus around the center (0, 0) of system (1.2)$|_{\varepsilon =0}$, and this upper bound is sharp.

• 2. For the even number $n\ge 4$, system (1.2) has at most $3n-3$ limit cycles bifurcating from the periodic annulus around the center (0, 0) of system (1.2)$|_{\varepsilon =0}$.

Proof of Theorem 1.1

Theorem 1.1 follows directly from Lemmas 3.8 and 3.11. $\square$

4 Discussions

In this paper, we obtained a bound for the maximum number of limit cycles that bifurcate from a non-Hamiltonian quartic reversible center by adding perturbed terms which are the sum of homogeneous polynomials of degree $3k+1$ for $1\le k\le n$. Our initial idea is to consider general degree n perturbations of the center, but the main difficulty exists in the technical and cumbersome computations of the averaged function. We leave this as a future research problem.

By observing the proofs of Lemma 3.6, Corollary 3.7, and Lemma 3.9, we have an intuition that the difference between the obtained number of limit cycles in cases $n=2$ and $n\ge 3$ lies in the relation of coefficients of the resulting polynomial $g(\omega )$, see equation (3.13). In addition, in the proof of Corollary 3.7 for $n=3$, we noticed a fact that the variables in the coefficients of the function $g(\omega )$ (see (3.15)) are quite enough. So we have a conjecture that for any $n\ge 4$, the bound $3n-3$ is also sharp. However, we cannot prove this conjecture. Maybe the problem can be solved with the aid of some beautiful mathematical techniques or most advanced computing technologies. How to explain the upper bound is sharp remains a question for further investigation.