Introduction

One of the old problems in the theory of dynamical systems is to find an upper bound for the number of limit cycles in polynomial vector fields defined in the plane, and investigate their relative positions. This problem is as know Hilbert’s 16th problem. More precisely, consider a near-Hamiltonian system

$$\begin{aligned} {\dot{x}} = H_y + \varepsilon p(x, y,\delta ),~~~~{\dot{y}} = -H_x + \varepsilon q(x, y,\delta ), \end{aligned}$$
(1)

where p, q and H are real analytic functions, \(\varepsilon \) is a small positive parameter and \(\delta \in D\) is a vector parameter that D is a compact subset of \({\mathbb {R}}^N\). Assume that the unperturbed system

$$\begin{aligned} {\dot{x}}=H_{y},\;\;\;\;\;{\dot{y}}=-H_{x}, \end{aligned}$$
(2)

has a continuous family of ovals \(L_h\) defined by \(H(x,y)=h\) for \(h\in (h_1,h_2)\). Then, associated to perturbed system (1), we define an Abelian integral of the form

$$\begin{aligned} M(h,\delta )=\oint _{L_h}q dx-p dy. \end{aligned}$$

By Poincaré–Pontryagin Theorem [11], the number of isolated zeros of \(M(h,\delta )\), counted with multiplicity, gives an upper bound for the number of limit cycles of (1). Hence, Abelian integral plays an important role in the study of bifurcation of limit cycles from system (1). The study of the asymptotic expansion of \(M(h,\delta )\) near critical values of H, in order to study the isolated zeros of Abelian integrals, is a valuable problem. There have been many studies on the limit cycle bifurcations studying the asymptotic expansion of \(M(h,\delta )\) when H being a polynomial e.g. [4, 8,9,10] and the references contained in those papers. But when the Hamiltonian function H is not a polynomial, there are very few results on this area. For instance, the authors of [3] studied the number of limit cycles for perturbed pendulum-like equations on the cylinder, in which the associated Hamiltonian is given by \(H(x, y) =\frac{y^2}{2}+ 1-\cos (x)\). An excellent work is done by Villadelprat et al. in [2] based on a “computer assisted proof” using interval arithmetic. Also, the authors of [7] considered a non-polynomial potential system that the associated Hamiltonian is given by \(H(x, y) =\frac{1}{2}y^2+\frac{1}{2}(e^{-2x}+1)-e^{-x}\). By Chebyshev criterion, they showed that the cyclicity of the period annulus of this system under the small perturbation is at most two.

Han et al. [6] proposed a novel nonlinear oscillator with strong irrational nonlinearities having smooth and discontinuous characteristics depending on the values of a smooth parameter. In fact, they considered

$$\begin{aligned} \ddot{x}+(x+\alpha )\left( 1-\frac{1}{\sqrt{(x+\alpha )^2 +\beta ^2}}\right) +(x-\alpha )\left( 1-\frac{1}{\sqrt{(x-\alpha )^2+\beta ^2}}\right) =0, \end{aligned}$$
(3)

where \(\alpha ,\beta >0\) are real numbers. By letting \({\dot{x}}=y\), Eq. (3) can be written in the following form:

$$\begin{aligned} {\dot{x}}=y,\quad {\dot{y}}=-F(x,\alpha ,\beta ), \end{aligned}$$
(4)

where

$$\begin{aligned} F(x,\alpha ,\beta )=(x+\alpha )\left( 1-\frac{1}{\sqrt{(x+\alpha )^2+\beta ^2}}\right) +(x-\alpha )\left( 1-\frac{1}{\sqrt{(x-\alpha )^2+\beta ^2}}\right) . \end{aligned}$$

System (4) is a Hamiltonian system with the Hamiltonian function

$$\begin{aligned} H(x,y)=\frac{1}{2}\,{y}^{2}+{x}^{2}-\,\sqrt{(x+\alpha )^2+\beta ^2}-\,\sqrt{(x-\alpha )^2+\beta ^2}+2\,\sqrt{\alpha ^2+\beta ^2}=\frac{1}{2}\,y^2+H_0(x). \end{aligned}$$
(5)

We see that although the above Hamiltonian is not a polynomial, its level curves are anyway branches of an algebraic curve of degree 8. More explicitly, it is

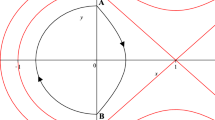
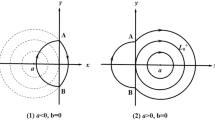
$$\begin{aligned} \left( \frac{1}{2}y^2+x^2-h\right) ^4-4(x^2+\alpha ^2+\beta ^2) \left( \frac{1}{2}y^2+x^2-h\right) ^2+16\alpha ^2\,x^2=0,\quad \alpha ,\beta >0. \end{aligned}$$

The phase portraits of system (4) are shown in Fig. 1, where \(C:=(\frac{4\sqrt{5}}{25},\frac{8\sqrt{5}}{25})\) and

$$\begin{aligned} \lambda _1&=\left\{ (\alpha ,\beta )\;|\; \exists (x,\alpha ),\;\beta >\frac{8\sqrt{5}}{25},\; s.t.\; F=F_x=0\right\} , \\ \lambda _2&=\left\{ (\alpha ,\beta )\;|\; \exists (x,\alpha ),\;\beta <\frac{8\sqrt{5}}{25},\; s.t.\; F=F_x=0\right\} , \\ \lambda _3&=\left\{ (\alpha ,\beta )\;|\; \exists (x_i,\alpha ),\; s.t.\; F=F_x=0,\; i=1,2\right\} . \end{aligned}$$

Since \(H_0(x)\) in (5) is an even function and \(H_0(x) \sim A\,x^2 + B\,x^4 + \cdots \) near zero, where \(A=1-\frac{\beta ^2}{(\alpha ^2+\beta ^2)^\frac{3}{2}}\) and \(B=\frac{\beta ^2(\beta ^2-4\alpha ^2)}{4(\alpha ^2+\beta ^2)^\frac{7}{2}}\), then a double homoclinic loop through a triple critical point exists if and only if \(A=0,\;B<0\). An easy calculation yields the conditions \(\alpha ^2+\beta ^2-\beta ^{\frac{4}{3}}=0\), \(\alpha ^2<\alpha ^2+\beta ^2<5\alpha ^2\). Therefore, \(\lambda _2\) is the simple curve

$$\begin{aligned} \alpha =\beta ^{\frac{2}{3}}\sqrt{1-\beta ^{\frac{2}{3}}},\;\;\;\;\; \beta \in \left( 0,\frac{8}{5\sqrt{5}}\right) . \end{aligned}$$

Along the curve \(\lambda _2\), the phase portrait of system (4) is shown in Fig. 2.

Fig. 1
figure 1

Bifurcation diagram and phase portraits of system (4)

Full size image

The explicit expressions for the algebraic curves \(\lambda _1\) and \(\lambda _3\) are the following:

$$\begin{aligned}&\lambda _1: \alpha ^6+3\alpha ^4\beta ^2+3\alpha ^2\beta ^4+\beta ^6-\beta ^4=0, \\&\lambda _3: 256\alpha ^8+768\alpha ^6\beta ^2+768\alpha ^4\beta ^4\\&\quad +256\alpha ^2\beta ^6-768\alpha ^6+2784\alpha ^4\beta ^2 +96\alpha ^2\beta ^4+768\alpha ^4-96\alpha ^2\beta ^2\\&~~~ -27\beta ^4-256\alpha ^2=0. \end{aligned}$$

In this paper, we take a codimension one case from the bifurcation diagram of the model, which corresponds to double cuspidal loop in the phase portrait. In fact, we will focus on the case \((\alpha ,\beta )\in \lambda _2\). Our aim is to study the limit cycles generated by small perturbations of the non-polynomial planar Hamiltonian system (4) when \((\alpha ,\beta )\in \lambda _2\). The limit cycles under consideration correspond to critical levels of the Hamiltonian, that is they are located in a small vicinity of a separatrix contour or a critical point.

The core of the present paper consists of extensive asymptotic calculations of the related line integrals which appear in the first-order approximation of the displacement map near the critical levels of the Hamiltonian. Most of the formulas are generated by computer manipulation programs such as Maple. We follow the ideas and use formulas from the paper [5] by Han Maoan et al. published in 2012, too. In Sect. 2, we perturb system (4) with \((\alpha ,\beta ) \in \lambda _2\), and then, we study the generated limit cycles by using the asymptotic expansions of the associated Melnikov functions. The formulation of the main result of the paper is given in Theorem 2.6 (see Sect. 2.4).

We illustrate our results on the example when \(\alpha =\beta \); see Sect. 3.

Study of System (4) Under Small Perturbations

In this section, we consider the following perturbed system

$$\begin{aligned} {\dot{x}}&=y+\varepsilon \,p(x,y,\delta ),\nonumber \\ {\dot{y}}&=-F(x,\alpha ,\beta )+\varepsilon \,q(x,y,\delta ), \end{aligned}$$
(6)

where p, q are \(C^\omega \) functions, \(\varepsilon \) is a small parameter and \(\delta \in D\subset {\mathbb {R}}^m\) with D a compact set. Our system is a perturbation of the Hamiltonian system (4) with the Hamiltonian function (5).

System (4) with \(\alpha =\beta ^{\frac{2}{3}}\sqrt{1-\beta ^{\frac{2}{3}}}\), \(\beta \in (0,\frac{8}{5\sqrt{5}})\), has a nilpotent saddle at A(0, 0), two centers at \(C_1(x^*, 0)\) and \(C_2(-x^*,0)\) in which the value of \(x^*\) is implicitly obtained from the equation \(F(x,\alpha ,\beta )=0\) and a double homoclinic loop \(L_0\) passing through the nilpotent saddle A. Also, system (4) has three families \(L_1\), \(L_2\) and \(L_3\) of periodic orbits near \(L_0 : H(x,y)=0\), which yield three Melnikov functions as follows :

$$\begin{aligned} M(h,\delta )&=\oint _{L_1}q\,dx-p\,dy,\quad for\;\; 0<-h\ll 1\\ {\widetilde{M}}(h,\delta )&=\oint _{L_2}q\,dx-p\,dy,\quad for\;\; 0<-h\ll 1\\ M^*(h,\delta )&=\oint _{L_3}q\,dx-p\,dy\quad for\;\; 0<h\ll 1. \end{aligned}$$

Our main goal in this section is to study the expansions of these Melnikov functions and use the first nonvanishing coefficients of the expansions to give a lower bound of the number of limit cycles produced near the double homoclinic loop \(L_0\).

Fig. 2
figure 2

Phase portrait of system (4) when \((\alpha ,\beta ) \in \lambda _2\)

Full size image

Before continuing the discussion, let’s remind that we can write

$$\begin{aligned} M(h,\delta )=\oint _{H=h}q\,dx-p\,dy=\iint _{H\le h}(p_x+q_y)\,dx\,dy=\oint _{H=h}{\tilde{q}}(x,y,\delta )\,dx, \end{aligned}$$

where

$$\begin{aligned} {\tilde{q}}(x, y, \delta ) = q(x,y,\delta )-q(x,0,\delta )+\int _{0}^{y}p_x(x,u,\delta )\,du \end{aligned}$$

satisfies \({\tilde{q}}_y = p_x+q_y\) and \({\tilde{q}}(x, 0, \delta ) = 0\). Then \({\tilde{q}}(x, y, \delta ) = \sum _{j\ge 1}\,{q}_j(x)\,y^j\), where

$$\begin{aligned} {q}_{j+1}(x) =\frac{1}{(j+1)!}\frac{\partial ^j}{\partial \,y^j} ({p}_x+{q}_y)\Big |_{\varepsilon =y=0}. \end{aligned}$$
(7)

Asymptotic Expansions of the Melnikov Functions M and \({\widetilde{M}}\)

In this section, we calculate the expansions of \(M(h,\delta )\) and \({\widetilde{M}}(h,\delta )\). First, we start by writting

$$\begin{aligned} M(h,\delta )&=\oint _{L_1}{\tilde{q}}(x,y,\delta )\, dx=\int _{L_1^{(1)}}{\tilde{q}}\,dx+\int _{L_1-L_1^{(1)}}{\tilde{q}}\, dx=I_1(h,\delta )+\int _{L_1-L_1^{(1)}}{\tilde{q}}\,dx,\nonumber \\ {\widetilde{M}}(h,\delta )&=\oint _{L_2}{\tilde{q}}(x,y,\delta )\, dx=\int _{L_2^{(1)}}{\tilde{q}}\,dx+\int _{L_2-L_2^{(1)}}{\tilde{q}}\, dx=I_2(h,\delta )+\int _{L_2-L_2^{(1)}}{\tilde{q}}\,dx, \end{aligned}$$
(8)

Where \(L_1:=\{(x,y)~|~H(x,y)=\frac{1}{2}y^2+H_0(x)=h,~x>0,~0<-h\ll 1\}\), \(L_2:=\{(x,y)~|~H(x,y)=\frac{1}{2}y^2+H_0(x)=h,~x<0,~0<-h\ll 1\}\) and \(L_1^{(1)}=\{(x,y)~|~H(x,y)=h, \eta (h)\le x \le x_0\}\), \(L_2^{(1)}=\{(x,y)~|~H(x,y)=h, x'_0\le x \le \eta '(h)\}\) (for the definitions of \(x_0\), \(x'_0\), \(\eta (h)\) and \(\eta '(h)\) see Fig. 3), and the second terms in \(M(h,\delta )\) and \({\widetilde{M}}(h,\delta )\) are analytic functions in h for \(0<-h\ll 1\).

Fig. 3
figure 3

Position of \(\eta (h)\), \(\zeta (h)\) and \(x_1\)

Full size image

To study the analytical properties of \(I_1(h,\delta )\) and \(I_2(h,\delta )\) at \(h = 0\), we note that for |h| small enough the equation \(H(x,y)=h\) has two \(C^\omega \) solutions \(y^{\pm }=\pm \sqrt{2}w(1+O(|x,w|))\), where \(w=\sqrt{h-H_0(x)}\). Denote \(u=\psi (x)=\root 4 \of {-H_0(x)}\) and \(u_0=\psi ({x_0})>0\). Then, we have the following result on the expansion of the functions \(I_1(h,\delta )\) and \(I_2(h,\delta )\) near \(h = 0\).

Lemma 2.1

The functions \(I_1(h,\delta )\) and \(I_2(h,\delta )\) introduced in (8), for \(0<-h\ll 1\), can be written as

$$\begin{aligned} I_1(h,\delta )= & {} \chi _1(h,u_0)+\sum _{r=0}^{3}\,I^*_{1,r}(h)\,I_{r,0}(h,u_0),\\ I_2(h,\delta )= & {} \chi _2(h,u_0)+\sum _{r=0}^{3}(-1)^r\,I^*_{1,r}(h)\,I_{r,0}(h,u_0), \end{aligned}$$

where \(\chi _1(h,u_0), \chi _2(h,u_0)\) are analytic functions in h, \(I_{r,0}(h,u_0)=\int _{|h|^{\frac{1}{4}}}^{u_0}u^{r}\sqrt{h+u^4}\,du\), and \(I^*_{1,r}(h)=\sum _{m,j\ge 0}r_{4m+r,j}\alpha ^*_{4m+r,j}\beta ^*_{4m+r}h^{j+m}\) for \(r=0,1,2,3\), with

$$\begin{aligned} \alpha ^*_{k,j}= & {} \left\{ \begin{array}{ll} 2^j\frac{(2j+1)!!}{(4j+k+3)(4j+k-1)\ldots (k+7)}&{}\quad k\ge 0,\;\; j\ge 1\;;\\ 1&{}\quad k\ge 0,\;\; j=0, \end{array}\right. \\ \beta ^*_{4m+r}= & {} \left\{ \begin{array}{ll} \frac{(-1)^m(r+1)(r+5)\ldots (r+4m-3)}{(r+7)(r+11)\ldots (r+4m+3)}&{}\quad m\ge 1,\;\; 0\le r \le 3\;;\\ 1&{}\quad m=0,\;\; 0\le r \le 3. \end{array}\right. \end{aligned}$$

Here, the coefficients \(r_{k,j}\) are given by the Taylor expansion coefficients of the functions

$$\begin{aligned} {\tilde{q}}_j(u)=\frac{{\bar{q}}_j(x)}{\psi '(x)}\bigg |_{x=\psi ^{-1}(u)}=\sum _{k=0}^{\infty } r_{k,j}u^{k}, \end{aligned}$$

in u, which appear along the proof.

Proof

We have that

$$\begin{aligned} I_1(h,\delta )&=\int _{L_1^{(1)}}{\tilde{q}}\,dx=\int _{\eta (h)}^{x_0} ({\tilde{q}}(x,y^+,\delta )-{\tilde{q}}(x,y^-,\delta ))\,dx\nonumber \\&=\sum _{j\ge 0}\int _{\eta (h)}^{x_0}{\bar{q}}_j(x)\,w^{2j+1}\,dx, \;\;\;\; where \;\;\; {\bar{q}}_j(x)=2^{j+\frac{3}{2}}q_{2j+1}(x). \end{aligned}$$
(9)

Therefore,

$$\begin{aligned} I_1(h,\delta )= \sum _{j\ge 0}\int _{|h|^{\frac{1}{4}}}^{u_0}{\tilde{q}}_j(u)w^{2j+1}\,du=\sum _{k\ge 0}{r}_{k,j}I_{k,j}, \end{aligned}$$

where \(w=\sqrt{h+u^4}\) and

$$\begin{aligned} {\tilde{q}}_j(u)=\frac{{\bar{q}}_j(x)}{\psi '(x)}\bigg |_{x=\psi ^{-1}(u)}=\sum _{k\ge 0}{{r}_{k,j}u^{k}},\quad I_{k,j}=\int _{|h|^{\frac{1}{4}}}^{u_0}u^{k}w^{2j+1}\,du. \end{aligned}$$
(10)

Similarly, we have that

$$\begin{aligned} I_2(h,\delta )&= \int _{L_2^{(1)}}{\tilde{q}}\,dx=\int _{x'_0}^{\eta '(h)}({\tilde{q}}(x,y^+,\delta )-{\tilde{q}}(x,y^-,\delta ))\,dx\\&= \sum _{j\ge 0}\int _{-u_0}^{-|h|^{\frac{1}{4}}}{\tilde{q}}_j(u)w^{2j+1}\,du=\sum _{k\ge 0}(-1)^k{r}_{k,j}I_{k,j}. \end{aligned}$$

To calculate \(I_{k,j}\), by using the formula (27) given in [5], namely,

$$\begin{aligned} \int u^{k}(h+u^4)^{j+\frac{1}{2}}\,du=\frac{u^{k+1} (h+u^4)^{j+\frac{1}{2}}}{4j+k+3}+\frac{4\left( j+\frac{1}{2}\right) h}{4j+k+3}\int u^{k}(h+u^4)^{j-\frac{1}{2}}\,du, \end{aligned}$$

we have that

$$\begin{aligned} I_{k,j}(h,u_0)=\varphi _{k,j}(u_0,h)+\frac{4 \left( j+\frac{1}{2}\right) h}{4j+k+3}\,I_{k,j-1}(h,u_0), \end{aligned}$$

where

$$\begin{aligned} \varphi _{k,j}(u_0,h)=\frac{u_0^{k+1}(h+u_0^4)^{j+\frac{1}{2}}}{4j+k+3}\in C^{\omega }. \end{aligned}$$

It follows that

$$\begin{aligned} I_{k,j}=\bar{\varphi }_{k,j}+\alpha ^*_{k,j}h^j\,I_{k,0},\quad k\ge 0,\;\; j\ge 1, \end{aligned}$$
(11)

where \(\bar{\varphi }_{k,j}\in C^{\omega }\), and

$$\begin{aligned} \alpha ^*_{k,j}=\left\{ \begin{array}{ll} 2^j\frac{(2j+1)!!}{(4j+k+3)(4j+k-1)\ldots (k+7)}&{}\quad k\ge 0,\;\; j\ge 1;\\ 1&{}\quad k\ge 0,\;\; j=0. \end{array}\right. \end{aligned}$$

Further, using the formula (29) given in [5], namely,

$$\begin{aligned} \int u^{k}(h+u^4)^{\frac{1}{2}}\,du=\frac{u^{k-3}(h+u^4)^{\frac{3}{2}}}{k+3}-\frac{(k-3)h}{k+3}\int u^{k-4}(h+u^4)^{\frac{1}{2}}\,du, \end{aligned}$$

we have that

$$\begin{aligned} I_{k,0}=\psi _{k}-\frac{k-3}{k+3}\,h\,I_{k-4,0},\quad k\ge 4, \quad \psi _k\in C^{\omega }. \end{aligned}$$

It follows that

$$\begin{aligned} I_{4m+r,0}={\tilde{\psi }}_{4m+r}+\beta ^*_{4m+r}h^m\,I_{r,0},\quad k\ge 0,\;\; j\ge 1, \end{aligned}$$
(12)

where \({\tilde{\psi }}_{4m+r}\in C^{\omega }\) and

$$\begin{aligned} \beta ^*_{4m+r}=\left\{ \begin{array}{ll} \frac{(-1)^m(r+1)(r+5)\ldots (r+4m-3)}{(r+7)(r+11)\ldots (r+4m+3)}&{}\quad m\ge 1,\;\; 0\le r \le 3\;;\\ 1&{}\quad m=0,\;\; 0\le r \le 3. \end{array}\right. \end{aligned}$$

By (11) and (12), we get that

$$\begin{aligned} I_{k,j}=\bar{\varphi }_{k,j}+\alpha ^*_{k,j}{\tilde{\psi }}_k h^j+\alpha ^*_{k,j}\beta ^*_k\,h^{j+m}\,I_{r,0},\;\;\;\;\;for\;\;k=4m+r,\;\;m\ge 0,\;\;0\le r \le 3. \end{aligned}$$
(13)

Hence, by (9), (11) and (13) we get

$$\begin{aligned} I_1(h,\delta ) =&\sum _{k\ge 0}r_{k,0}\,I_{k,0}+\sum _{\begin{array}{c} 0\le k\le 3 \\ \;j\ge 1 \end{array}}r_{k,j}\,I_{k,j}+\sum _{\begin{array}{c} k=4m+r\\ 0\le r\le 3 \\ m,j\ge 1 \end{array}}r_{k,j}\,I_{k,j}\\ =&\sum _{\begin{array}{c} m\ge 1\\ 0\le r \le 3 \end{array}}r_{4m+r,0}{\tilde{\psi }}_{4m+r}+\sum _{r=0}^{3}\left( \sum _{m\ge 0}r_{4m+r,0}\beta ^*_{4m+r}\,h^m\right) I_{r,0}+\sum _{k=0}^{3}\sum _{j\ge 1}r_{k,j}\bar{\varphi }_{k,j}\\&+\sum _{k=0}^{3}\left( \sum _{j\ge 1}r_{k,j}\alpha ^*_{k,j}\,h^j\right) I_{k,0}+\sum _{r=0}^{3}\sum _{m,j\ge 1}r_{4m+r,j}\left( \bar{\varphi }_{4m+r,j}+\alpha ^*_{4m+r,j}{\tilde{\psi }}_{4m+r}h^j\right) \\&+\sum _{r=0}^{3}\left( \sum _{m,j\ge 1}r_{4m+r,j}\alpha ^*_{4m+r,j}\beta ^*_{4m+r}h^{j+m}\right) I_{r,0}. \end{aligned}$$

Thus,

$$\begin{aligned} I_1(h,\delta )=\chi _1(h,u_0)+\sum _{r=0}^{3}\,I^*_{1,r}(h)\,I_{r,0}(h,u_0), \end{aligned}$$
(14)

and in a similar way,

$$\begin{aligned} I_2(h,\delta )=\chi _2(h,u_0)+\sum _{r=0}^{3}(-1)^r\,I^*_{1,r}(h)\,I_{r,0}(h,u_0), \end{aligned}$$
(15)

with \(\chi _1(h,u_0), \chi _2(h,u_0)\in C^{\omega }\) and \(I^*_{1,r}(h)=\sum _{m,j\ge 0}r_{4m+r,j}\alpha ^*_{4m+r,j}\beta ^*_{4m+r}h^{j+m}\) for \(r=0,1,2,3\). \(\square \)

To gain the analytical properties of the functions \(I_{r,0}(h)\), we let \(v=|h|^{\frac{1}{4}}/u\) in (10) for \((k,j)=(r,0)\), and obtain

$$\begin{aligned} I_{r,0}(h)=|h|^{\frac{r}{4}+\frac{3}{4}}\int _{|h|^{\frac{1}{4}}/u_0}^{1}v^{-r-4}\sqrt{1-v^4}\,dv. \end{aligned}$$

Note that for \(0 \le v \le 1\) we have the following convergent series

$$\begin{aligned} \sqrt{1-v^4}=\sum _{j\ge 0}{c}_jv^{4j}=1-\frac{v^4}{2}-\frac{v^8}{8}-\frac{v^{12}}{16}+O\left( v^{16}\right) . \end{aligned}$$

Then, for \(r=1\), we have

$$\begin{aligned} I_{1,0}(h,u_0)=|h|\,c_1\left( -\ln |h|^{\frac{1}{4}}+\ln |u_0|\right) +\hat{\varphi }_1(h,u_0)=-\frac{1}{8}h\ln |h|+{\tilde{\varphi }}_1(h,u_0), \end{aligned}$$
(16)

where

$$\begin{aligned}{\tilde{\varphi }}_1(h,u_0)=-\frac{1}{2}|h|\ln |u_0|+\displaystyle \sum _{\begin{array}{c} j\ge 0\\ j\ne 1 \end{array}}\frac{c_j\left( |h|-u_0^{4(1-j)}|h|^j\right) }{4(j-1)}.\end{aligned}$$

For \(r\ne 1\), we have

$$\begin{aligned} I_{r,0}(h,u_0)=|h|^{\frac{r}{4}+\frac{3}{4}}\sum _{j\ge 0}c_j\int _{|h|^{\frac{1}{4}}/u_0}^{1}v^{-r+4j-4}\,dv={\tilde{A}}_r|h|^{\frac{r}{4}+\frac{3}{4}}+{\tilde{\varphi }}_r(h,u_0), \end{aligned}$$
(17)

where \({\tilde{A}}_r=\sum _{j\ge 0}\frac{c_j}{4j-r-3}\) and \({\tilde{\varphi }}_r(h,u_0)=-\sum _{j\ge 0}\frac{c_j\,u_0^{r-4j+3}}{4j-r-3}|h|^j\).

Furthermore, for the constants \({\tilde{A}}_r\) in (17), since \({\tilde{A}}_r\) is independent of \(u_0\), we can take \(u_0 = 1\). Then

$$\begin{aligned} {\tilde{\varphi }}_r(h,1)=-\displaystyle \sum _{j\ge 0}\frac{c_j}{4j-r-3}|h|^j=\frac{1}{r+3}+\frac{|h|}{2r-2}+O(|h|^2). \end{aligned}$$

Thus, by (10), for \(0<-h\ll 1\) we have

$$\begin{aligned} \frac{\partial I_{r,0}(h,u_0)}{\partial h}=-\left( {\frac{r}{4}+\frac{3}{4}}\right) {\tilde{A}}_r|h|^{\frac{r}{4}-\frac{1}{4}}+\frac{1}{2r-2}+O(|h|). \end{aligned}$$
(18)

On the other hand, by (10), we have that

$$\begin{aligned} \frac{\partial I_{r,0}(h,u_0)}{\partial h}=\frac{1}{2}\int _{|h|^{\frac{1}{4}}}^{1}\frac{u^{r}\,du}{\sqrt{h+u^4}}=\frac{1}{2}|h|^{\frac{r}{4}-\frac{1}{4}}\int _{|h|^{\frac{1}{4}}}^{1}\frac{v^{-r}\,du}{\sqrt{1-v^4}}. \end{aligned}$$
(19)

  • For \(r=0\), comparing (18) and (19) gives

    $$\begin{aligned} {\bar{A}}_0=-\frac{2}{3}\lim _{h\rightarrow 0}\frac{\frac{\partial I_{r,0}(h,u_0)}{\partial h}}{|h|^{-\frac{1}{4}}}=-\frac{2}{3}\int _{0}^{1}\frac{\,dv}{\sqrt{1-v^4}}= -0.8740191850. \end{aligned}$$

  • For \(r=2\), note that

    $$\begin{aligned} \int _{|h|^{\frac{1}{4}}}^{1}\frac{v^{-2}}{\sqrt{1-v^4}}\,dv&=\int _{|h|^{\frac{1}{4}}}^{1}{v^{-2}}\left[ 1+\left( \frac{1}{\sqrt{1-v^4}}-1\right) \right] \,dv\\&=-(1-|h|^{-\frac{1}{4}})+\int _{|h|^{\frac{1}{4}}}^{1}\frac{v^2\,dv}{\sqrt{1-v^4}(1+\sqrt{1-v^4})}. \end{aligned}$$

    Therefore, by substituting the above into (19), we get

    $$\begin{aligned} \frac{\partial I_{r,0}(h,u_0)}{\partial h}=-\frac{1}{2}|h|^{\frac{1}{4}}+\frac{1}{2}+\frac{1}{2}|h|^{\frac{1}{4}}\int _{|h|^{\frac{1}{4}}}^{1}\frac{v^2\,dv}{\sqrt{1-v^4}(1+\sqrt{1-v^4})}. \end{aligned}$$

    Consequently,

    $$\begin{aligned} {\bar{A}}_2=-\frac{4}{5}\lim _{h\rightarrow 0}\frac{\frac{\partial I_{r,0}(h,u_0)}{\partial h}}{|h|^{\frac{1}{4}}}=-\frac{4}{5}\left[ -\frac{1}{2}+\frac{1}{2}\int _{0}^{1}\frac{v^2\,dv}{\sqrt{1-v^4}(1+\sqrt{1-v^4})}\right] =0.2396280472. \end{aligned}$$

Proposition 2.2

Let \(L_0= {\bar{L}}_0 \cup {\tilde{L}}_0\) be a double homoclinic loop defined by \(H(x, y) = 0\), where \({\bar{L}}_0 = L_0{|}_{x\ge 0}\) and \({\tilde{L}}_0 = L_0{|}_{x\le 0}\). Then for the functions \(M(h, \delta )\) and \({\widetilde{M}}(h,\delta )\) given in (8), we have

$$\begin{aligned} M(h,\delta )&= c_0+c_1|h|^{\frac{3}{4}}+c_2\,h\ln |h|+c_3\,h +c_4|h|^{\frac{5}{4}}+c_5|h|^{\frac{7}{4}} +c_6\,h^2\ln |h|+O(|h|^2),\nonumber \\ {\widetilde{M}}(h,\delta )&={\tilde{c}}_0+c_1|h|^{\frac{3}{4}} -c_2\,h\ln |h|+{\tilde{c}}_3\,h+c_4|h|^{\frac{5}{4}} +c_5|h|^{\frac{7}{4}}-c_6\,h^2\ln |h|+O(|h|^2), \end{aligned}$$
(20)

in which

$$\begin{aligned} c_0&= M(0, \delta ) =\oint _{{\bar{L}}_0}\,q\,dx - \,p\,dy{|}_{\varepsilon =0}, \quad {\tilde{c}}_0 = {\widetilde{M}}(0, \delta ) =\oint _{{\tilde{L}}_0}\,q\,dx - \,p\,dy{|}_{\varepsilon =0},\nonumber \\ c_1&= {\bar{A}}_0\,r_{00}, \quad c_2=-\frac{1}{8}\,r_{10},\nonumber \\ c_3&=\oint _{{\bar{L}}_0}\left[ (\,p_x+\,q_y){|}_{\varepsilon =0}-a_0-a_1\,x\right] \,dt+O_1(c_1)+O_1(c_2),\nonumber \\ {\tilde{c}}_3&=\oint _{{\tilde{L}}_0}\left[ (\,p_x+\,q_y){|}_{\varepsilon =0}-a_0-a_1\,x\right] \,dt+O_1(c_1)+O_1(c_2),\nonumber \\ c_4&={\bar{A}}_2\,r_{20},\quad c_5=-{\bar{A}}_0 \left( \frac{6}{7}\,r_{01}-\frac{1}{7}\,r_{40}\right) ,\quad c_6=-\frac{1}{32}(3\,r_{11}-\,r_{50}), \end{aligned}$$
(21)

with \(a_0 = (p_x + q_y)|_{\varepsilon =x=y=0}\), \(a_1 = (p_{xx} + q_{yx})|_{\varepsilon =x=y=0}\), \(O_1(c)\) denotes c times a constant, and \(r_{ij}\) will be introduced in the proof.

Proof

By (8), (14), (15), (16) and (17), for \(0<-h\ll 1\) we have

$$\begin{aligned} M(h,\delta )=\varphi _1(h,\delta )+{\bar{A}}_0\,I_{10}^*(h)|h|^{\frac{3}{4}}-\frac{1}{8}\,h\ln |h|\,I_{11}^*(h)+{\bar{A}}_2\,I_{12}^*(h)|h|^{\frac{5}{4}},\nonumber \\ {\widetilde{M}}(h,\delta )=\varphi _2(h,\delta )+{\bar{A}}_0\,I_{10}^*(h)|h|^{\frac{3}{4}}+\frac{1}{8}\,h\ln |h|\,I_{11}^*(h)+{\bar{A}}_2\,I_{12}^*(h)|h|^{\frac{5}{4}}, \end{aligned}$$
(22)

where

$$\begin{aligned} I_{10}^*&=r_{00}\alpha _{00}^*\beta _0^*+\left( r_{40}\alpha _{40}^*\beta _4^*+r_{01}\alpha _{01}^*\beta _0^*\right) \,h+O(h^2),\\ I_{11}^*&=r_{10}\alpha _{10}^*\beta _1^*+\left( r_{50}\alpha _{50}^*\beta _5^*+r_{11}\alpha _{11}^*\beta _1^*\right) \,h+O(h^2),\\ I_{12}^*&=r_{20}\alpha _{20}^*\beta _2^*+O(h), \end{aligned}$$

and

$$\begin{aligned} \alpha _{00}^*&= \alpha _{10}^*=\alpha _{20}^*=\alpha _{40}^*=\alpha _{50}^*=1,\;\;\; \alpha _{01}^*=\frac{6}{7},\;\;\; \alpha _{11}^*=\frac{3}{4},\\ \beta _0^*&= \beta _1^*=\beta _2^*=1,\quad \beta _4^*=-\frac{1}{7},\quad \beta _5^*=-\frac{1}{4}. \end{aligned}$$

Therefore, we can obtain the expansion of \(M(h,\delta )\) by inserting the above into (22) with \(c_0=\varphi _1(0,\delta )=M(0,\delta )\) and \({\tilde{c}}_0=\varphi _2(0,\delta )={\widetilde{M}}(0,\delta )\) given by (21), and

$$\begin{aligned} c_1&= {\bar{A}}_0\,r_{00}, \quad c_2=-\frac{1}{8}\,r_{10}, \quad c_4={\bar{A}}_2\,r_{20},\\ c_5&= -{\bar{A}}_0\left( \frac{6}{7}\,r_{01}-\frac{1}{7}\,r_{40}\right) ,\quad c_6=-\frac{1}{32}(3\,r_{11}-\,r_{50}). \end{aligned}$$

Note that, by Taylor expansion, we obtain \(x=\psi ^{-1}(u)={\tau _0}u+{\tau _1}\,{u}^{3}+{\tau _2}\,{u}^{5}+O(u^7)\), where

$$\begin{aligned} \tau _0&=\frac{\sqrt{2}\root 3 \of {\beta }}{\root 4 \of {-5\,{\beta }^{2/3}+4}},\quad \tau _1=-\frac{ 21\,{\beta }^{11/3}+8\,{\beta }^{7/3}-28\,{\beta }^{3}}{ \left( -2\,\sqrt{-{\beta }^{2/3} \left( 5\,{\beta }^{2/3}-4 \right) }\beta \right) ^{3/2}{\beta }^{2/3} \left( 5\,{\beta }^{2/3}-4 \right) },\\ \tau _2&=-\frac{1}{32}\,{\sqrt{-2\,\sqrt{-{\beta }^{2/3} \left( 5\,{\beta }^{2/3}-4 \right) }\beta }\sqrt{-{\beta }^{2/3} \left( 5\,{\beta }^{2/3}-4 \right) } \left( 40125\,{\beta }^{{\frac{37}{3}}}-192300\,{\beta }^{{ \frac{35}{3}}}+379440\,{\beta }^{11}\right. }\\&\quad \left. -385664\,{\beta }^{\frac{31}{3}} +198592\,{\beta }^{\frac{29}{3}}-33024\,{\beta }^{9}-11264\,{\beta }^{ \frac{25}{3}}+4096\,{\beta }^{\frac{23}{3}} \right) \left( 78125 \,{\beta }^{{\frac{43}{3}}}-437500\,{\beta }^{\frac{41}{3}}\right. \\&\quad \left. -1400000 \,{\beta }^{\frac{37}{3}}+1120000\,{\beta }^{\frac{35}{3}}+143360 \,{\beta }^{\frac{31}{3}}-16384\,{\beta }^{\frac{29}{3}}+1050000\, {\beta }^{13}-537600\,{\beta }^{11} \right) ^{-1}, \end{aligned}$$

and \(\frac{1}{\psi '(x)}=\lambda _0+\lambda _1\,x^2+\lambda _2\,x^4+O(x^6)\), where

$$\begin{aligned} \lambda _0&=-{\frac{\sqrt{2}{\beta }^{-{\frac{20}{3}}}}{5\,{\beta }^{2/3}-4} \left( -{\beta }^{{\frac{28}{3}}} \left( 5\,{\beta }^{2/3}-4 \right) \right) ^{3/4}},\\ \lambda _1&=\frac{3}{8}\,{\frac{\sqrt{2}{\beta }^{2/3} \left( 105\,{\beta }^{8/3}-224\,{\beta }^{2}+152\,{\beta }^{4/3}-32\,{\beta }^{2/3} \right) }{ \left( 5\,{ \beta }^{2/3}-4 \right) ^{2}\root 4 \of {-{\beta }^{{\frac{28}{3}}} \left( 5\,{\beta }^{2/3}-4 \right) }}},\\ \lambda _2&=-\frac{\sqrt{2}}{128} \left( 862125\,{\beta }^{16/3}-4313100\,{\beta }^{14/3}+ 9080880\,{\beta }^{4}\right. \\&\quad \left. -10357888\,{\beta }^{10/3}+6830528\,{\beta }^{8/3}- 2545920\,{\beta }^{2}\right. \\&\quad \left. +472064\,{\beta }^{4/3}-28672\,{\beta }^{2/3}\right) \left( {\, \left( -5\,\beta +4\,\root 3 \of {\beta } \right) ^{2}\left( 5\,{\beta }^{2/3}-4 \right) ^{3}\root 4 \of {-{\beta }^{{\frac{28}{3}}} \left( 5\,{\beta }^{2/3}-4 \right) }}\right) ^{-1}. \end{aligned}$$

Suppose that \(p(x,y)=\sum _{i+j\ge 0}\,a_{ij}\,x^i\,y^j\) and \(q(x,y)=\sum _{i+j\ge 0}\,b_{ij}\,x^i\,y^j\). Now, we calculate \(r_{ij}\) in (10). Note that, by (7), we have

$$\begin{aligned} {\bar{q}}_0&=2\sqrt{2}\,q_1=2\sqrt{2}\left( p_x+q_y\right) \Big |_{\varepsilon =y=0}=2\sqrt{2}\,\displaystyle \sum _{i=0}^{\infty }\left[ (i+1)\,a_{i+1,0}+\,b_{i1}\right] \,x^i, \\ {\bar{q}}_1&=4\sqrt{2}\,q_3=\frac{2}{3}\sqrt{2}\left( p_{xyy}+q_{yyy}\right) \Big |_{\varepsilon =y=0}=\frac{4}{3}\sqrt{2}\,\displaystyle \sum _{i=0}^{\infty }\left[ (i+1)\,a_{i+1,2}+\,3\,b_{i3}\right] \,x^i. \end{aligned}$$

Then

$$\begin{aligned} r_{00}&= {\tilde{q}}_0(0)=2\sqrt{2}\,\lambda _0\,\left( a_{10}+b_{01}\right) ,\;\;\;\;\;\;\;\;\;r_{10}=2\sqrt{2}\,\lambda _0\,\tau _0\,\left( 2\,a_{20}+b_{11}\right) ,\nonumber \\ r_{20}&= 2\sqrt{2}\,\tau _0^2\left( \,\lambda _0\,\left( 3\,a_{30}+b_{21}\right) +\,\lambda _1\,\left( \,a_{10}+b_{01}\right) \right) ,\nonumber \\ r_{40}&= 2\sqrt{2}\left( \lambda _{{0}} \left( 2\, \left( 3\,a_{{30}}+b_{{21}} \right) \tau _{{0}}\tau _{{1}}+ \left( 5\,a_{{50}}+b_{{41}} \right) {\tau _{{0}}}^{4}\right) +\lambda _{{1}}{\tau _{{0}}}^{4} \left( 3\,a_{{30}}+b_{{21}} \right) \right. \nonumber \\&\quad +\left. \left( \lambda _{{2}}{\tau _{{0}}}^{4}+2\,\lambda _{{1}}\tau _{{0}}\tau _{{1}} \right) \left( a_{{10}}+b_{{01}} \right) \right) ,\nonumber \\ r_{50}&=\,2\sqrt{2}\left( \lambda _{{0}} \left( \left( 2\,a_{{2}}+b_{{11}} \right) \tau _{{2}}+3\, \left( 4\,a_{{40}}+b_{{31}} \right) {\tau _{{0}}}^{2}\tau _{{1}}+ \left( 6\,a_{{60}}+b_{{51}} \right) {\tau _{{0}}}^{5} \right) +\lambda _{{1}}{\tau _{{0}}}^{2} \left( \left( 2\,a_{{20}}+b_{{11}} \right) \tau _{{1}}\right. \right. \nonumber \\&\quad \left. \left. + \left( 4\,a_{{40}}+b_{{31}} \right) {\tau _{{0}}}^{3} \right) + \left( \lambda _{{2}}{\tau _{{0}}}^{4}+2\,\lambda _{{1}}\tau _{ {0}}\tau _{{1}} \right) \left( 2\,a_{{20}}+b_{{11}} \right) \tau _{{0}}\right) ,\nonumber \\ r_{01}&=\frac{4}{3}\sqrt{2}\,\lambda _0\,\left( a_{12}+\,3\,b_{03}\right) ,\;\;\;\;\;\;\;\;\;r_{11}=\frac{4}{3}\sqrt{2}\,\lambda _0\,\tau _0\,\left( 2\,a_{22}+\,3\,b_{13}\right) . \end{aligned}$$
(23)

To prove the formulas of \(c_3\) and \({\tilde{c}}_3\) in (21) see [5]. \(\square \)

Asymptotic Expansion of the Melnikov Function \(M^*\)

In this section, we calculate the expansion of \(M^*(h,\delta )\). We start by writting

$$\begin{aligned} M^*(h,\delta )&=\oint _{L_3}{\tilde{q}}(x,y,\delta )\, dx=\int _{L_3^{(1)}}{\tilde{q}}\,dx+\int _{L_3^{(2)}}{\tilde{q}}\, dx+\int _{L_3-L_3^{(1)}-L_3^{(2)}}{\tilde{q}}\,dx\nonumber \\&=I_3^{(1)}(h,\delta )+I_3^{(2)}(h,\delta )+\int _{L_3-L_3^{(1)} -L_3^{(2)}}{\tilde{q}}\,dx, \end{aligned}$$
(24)

where \(L_3:=\{(x,y)~|~H(x,y)=\frac{1}{2}y^2+H_0(x)=h,~0< h\ll 1\}\), \(L_3^{(1)}=\{(x,y)~|~H(x,y)=h, x'_0\le x \le x_0, y>0\}\) and \(L_3^{(2)}=\{(x,y)~|~H(x,y)=h, x'_0\le x \le x_0, y<0\}\) (for the definitions of \(x_0\) and \(x'_0\) see Fig. 4) and the third term in \(M^*(h,\delta )\) is an analytic function in h for \(0<h\ll 1\).

To study the analytical properties of the functions \(I_3^{(1)}(h,\delta )\) and \(I_3^{(2)}(h,\delta )\) at \(h = 0\), we have the following result.

Lemma 2.3

Suppose that \(u=\psi (x)=\root 4 \of {-H_0(x)}\), \(u_0=\psi ({x_0})>0\) and \(w=\sqrt{h+u^4}\). Then,

$$\begin{aligned} I_3^{(1)}(h,u_0)&=\chi _3(h,u_0)+\sum _{r=0}^{1}\,{\tilde{I}}^*_{1,r}(h)\,{\tilde{I}}_{r,1}(h,u_0),\\ I_3^{(2)}(h,u_0)&=\chi _4(h,u_0)+\sum _{r=0}^{1}\,{\tilde{I}}^*_{1,r}(h)\,{\tilde{I}}_{r,1}(h,u_0), \end{aligned}$$

where \(\chi _3(h,u_0), \chi _4(h,u_0)\) are some analytic functions in h, \({\tilde{I}}_{r,1}(h,u_0)= \int _{0}^{u_0}u^{2r}\sqrt{h+u^4}du\), and \({\tilde{I}}^*_{1,r}(h)=\sum _{\begin{array}{c} k=2m+r\\ m\ge 0,\;j\ge 1\;odd \end{array}}{\tilde{r}}_{k,j}{\tilde{\alpha }}_{k,j}{\tilde{\beta }}_{k}\,h^{m+[\frac{j}{2}]}\) for \(r=0,1\), with

$$\begin{aligned} {\tilde{\alpha }}_{k,j}= & {} \left\{ \begin{array}{ll} \frac{6.10.\cdots .2j}{(2k+7)(2k+11)\ldots (2k+2j+1)}&{}\quad k\ge 0,\;\; j\ge 3\;odd\;;\\ 1&{}\quad k\ge 0,\;\; j=1, \end{array}\right. \\ {\tilde{\beta }}_{k}= & {} \left\{ \begin{array}{ll} \frac{(-1)^m(2k-3)(2k-7)\ldots (2k+1-4m)}{(2k+3)(2k-1)\ldots (2k-4m+7)}&{}\quad k=2m+r,\;\;\;m\ge 1,\;\; r=0,1\;;\\ 1&{}\quad k=0,1. \end{array}\right. \end{aligned}$$

Here, the coefficients \({\tilde{r}}_{k,j}\) are given by the Taylor expansion coefficients of the functions

$$\begin{aligned} {\tilde{q}}_j(u)+{\tilde{q}}_j(-u)=\sum _{k=0}^{\infty } {\tilde{r}}_{k,j} u^{2k}, \end{aligned}$$

in u, which appear along the proof.

Proof

In view of (24), we can write

$$\begin{aligned} I_3^{(1)}(h,\delta )&=\int _{L_3^{(1)}}{\tilde{q}}\, dx=\int _{x'_0}^{x_0}{\tilde{q}}\left( x,y^+,\delta \right) \, dx=\sum _{j\ge 1}\int _{x'_0}^{x_0}\,{\bar{q}}_j\,w^{j}\, dx=\sum _{j\ge 1}\int _{u'_0}^{u_0}{\tilde{q}}_j(u)\,w^{j}\,du\nonumber \\&=\sum _{j\ge 1}\int _{0}^{u_0}\left[ {\tilde{q}}_j(u)+{\tilde{q}}_j(-u)\right] \,w^{j}\,du =\sum _{j\ge 1, k\ge 0}{\tilde{r}}_{k,j}{\tilde{I}}_{k,j}, \end{aligned}$$
(25)
Fig. 4
figure 4

The line segment \(\{x=x_0\}\) and \(\{x=x'_0\}\)

Full size image

where

$$\begin{aligned} {\tilde{q}}_i(u)=\frac{{\bar{q}}_i(x)}{\psi '(x)}\bigg |_{x=\psi ^{-1}(u)},\;\;\; {\tilde{q}}_i(u)+{\tilde{q}}_i(-u)=\sum _{k=0}^{\infty } {{\tilde{r}}_{k,i}u^{2k}},~~{\tilde{I}}_{k,j}=\int _{0}^{u_0}u^{2k}w^{j}\,du. \end{aligned}$$
(26)

In the same way, we get,

$$\begin{aligned} I_3^{(2)}(h,\delta )&=\int _{L_3^{(2)}}{\tilde{q}}\, dx=\int _{x_0}^{x'_0}{\tilde{q}}(x,y^-,\delta )\, dx=\sum _{j\ge 1}\int _{x_0}^{x'_0}\,(-1)^j{\bar{q}}_j\,w^{j}\, dx\\&=-\sum _{j\ge 1}\int _{u'_0}^{u_0}(-1)^j{\tilde{q}}_j(u)\,w^{j}\,du\\&=-\sum _{j\ge 1}\int _{0}^{u_0}(-1)^j\left[ {\tilde{q}}_j(u)+{\tilde{q}}_j(-u)\right] \,w^{j}\,du=-\sum _{j\ge 1, k\ge 0}(-1)^j{\tilde{r}}_{k,j}{\tilde{I}}_{k,j}. \end{aligned}$$

To calculate \({\tilde{I}}_{k,j}\), we see that by (26) \({\tilde{I}}_{k,j}\in C^{\omega }\) for \(j>0\) and even. For \(j\ge 3\) and odd, similar to (11), we obtain that

$$\begin{aligned} {\tilde{I}}_{k,j}={\tilde{\varphi }}_{k,j}+{\tilde{\alpha }}_{k,j}h^{[\frac{j}{2}]}\,{\tilde{I}}_{k,1},\quad k\ge 0, \end{aligned}$$
(27)

where \({\tilde{\varphi }}_{k,j}\in C^{\omega }\) and

$$\begin{aligned} {\tilde{\alpha }}_{k,j}=\left\{ \begin{array}{ll} \frac{6.10.\cdots .2j}{(2k+7)(2k+11)\ldots (2k+2j+1)}&{}\quad k\ge 0,\;\; j\ge 3\;odd\;;\\ 1&{}\quad k\ge 0,\;\; j=1. \end{array}\right. \end{aligned}$$

Also, similar to (12), we get that

$$\begin{aligned} {\tilde{I}}_{k,1}=\bar{\psi }_{k}+{\tilde{\beta }}_{k}h^m\,{\tilde{I}}_{r,1}, \end{aligned}$$
(28)

for \(2k=4m+2r\) with \( r=0,1\), \(m\ge 1\) and

$$\begin{aligned} {\tilde{\beta }}_{k}=\left\{ \begin{array}{ll} \frac{(-1)^m(2k-3)(2k-7)\ldots (2k+1-4m)}{(2k+3)(2k-1)\ldots (2k-4m+7)}&{}\quad k=2m+r,\;\;\;m\ge 1,\;\; r=0,1\;;\\ 1&{}\quad k=0,1. \end{array}\right. \end{aligned}$$

Therefore, by (25), (27) and (28), we have that

$$\begin{aligned} I_3^{(1)}(h,u_0) =&\sum _{\begin{array}{c} k\ge 0\\ j\ge 1 \;odd \end{array}}{\tilde{r}}_{k,j}\,{\tilde{I}}_{k,j}+\cdots =\sum _{k\ge 0}{\tilde{r}}_{k,1}\,{\tilde{I}}_{k,1}+\sum _{\begin{array}{c} k\ge 0\\ j\ge 3\;odd \end{array}}{\tilde{r}}_{k,j}\,{\tilde{I}}_{k,j}+\cdots \\ =&\sum _{k\ge 0}{\tilde{r}}_{k,1}{\tilde{I}}_{k,1}+\sum _{\begin{array}{c} k\ge 0\\ j\ge 3\;odd \end{array}}{\tilde{r}}_{i,j}{\tilde{\alpha }}_{i,j}h^{[\frac{j}{2}]}{\tilde{I}}_{k,1}+\cdots =\sum _{\begin{array}{c} k\ge 0\\ j\ge 1\;odd \end{array}}{\tilde{r}}_{i,j}{\tilde{\alpha }}_{i,j}h^{[\frac{j}{2}]}{\tilde{I}}_{k,1}+\cdots \\ =&\sum _{\begin{array}{c} 0\le k\le 1\\ j\ge 1\;odd \end{array}}{\tilde{r}}_{i,j}{\tilde{\alpha }}_{i,j}h^{[\frac{j}{2}]}{\tilde{I}}_{k,1}+\sum _{\begin{array}{c} k=2m+r \\ m\ge 1,\;0 \le r\le 1 \\ j\ge 1\;odd \end{array}}{\tilde{r}}_{i,j}{\tilde{\alpha }}_{i,j}{\tilde{\beta }}_i h^{m+[\frac{j}{2}]}{\tilde{I}}_{k,1}+\cdots \\ =&\sum _{\begin{array}{c} k=2m+r \\ m\ge 0,\;0\le r\le 1 \\ j\ge 1\;odd \end{array}}{\tilde{r}}_{i,j}{\tilde{\alpha }}_{i,j}{\tilde{\beta }}_i h^{m+[\frac{j}{2}]}{\tilde{I}}_{k,1}+\cdots \\ =&\sum _{r=0}^{1}{\tilde{I}}^*_{1,r}{\tilde{I}}_{r,1}(h,u_0)+\cdots , \end{aligned}$$

where “\(\cdots \)” in each equation denotes a \(C^\omega \) function and \({\tilde{I}}^*_{1,r}(h)=\sum _{\begin{array}{c} k=2m+r\\ m\ge 0,\;j\ge 1\;odd \end{array}}{\tilde{r}}_{k,j}{\tilde{\alpha }}_{k,j}{\tilde{\beta }}_{k}h^{m+[\frac{j}{2}]}\). Hence,

$$\begin{aligned} I_3^{(1)}(h,u_0)=\chi _3(h,u_0)+\sum _{r=0}^{1}\,{\tilde{I}}^*_{1,r}(h)\,{\tilde{I}}_{r,1}(h,u_0), \end{aligned}$$
(29)

where \(\chi _3(h,u_0)\in C^\omega \). Similarly, we have that

$$\begin{aligned} I_3^{(2)}(h,u_0)=\chi _4(h,u_0)+\sum _{r=0}^{1}\,{\tilde{I}}^*_{1,r}(h)\,{\tilde{I}}_{r,1}(h,u_0), \end{aligned}$$
(30)

where \(\chi _4(h,u_0)\in C^\omega \). \(\square \)

To obtain the analytical properties of the functions \({\tilde{I}}_{r,1}(h,u_0)\), we let \(v=u/h^{\frac{1}{4}}\) in (26) for \(k=r\) and \(j=1\), and we get

$$\begin{aligned} {\tilde{I}}_{r,1}(h,u_0)=h^{\frac{r}{2}+\frac{3}{4}}\int _{0}^{u_0h^{-\frac{1}{4}}}v^{2r}(1+v^4)^\frac{1}{2}\,dv=h^{\frac{r}{2}+\frac{3}{4}}\left[ B_{N_r}+\psi _{N_r}(h,u_0)\right] , \end{aligned}$$

where

$$\begin{aligned} B_{N_r}=&\int _{0}^{N}v^{2r} ({1+v^4})^{\frac{1}{2}}\,dv, \;\;\;\;\;\;\;\;\;\;\; N>1,\\ \psi _{N_r}(h,u_0)=&\int _{N}^{u_0/h^{1/4}}v^{2r} ({1+v^4})^{\frac{1}{2}}\,dv=\int _{h^{1/4}/u_0}^{1/N} v^{-2r-4}\sqrt{1+v^4}\,dv. \end{aligned}$$

Note that for \(0 \le v \le 1\) we have the following convergent series

$$\begin{aligned} \sqrt{1+v^4}=\sum _{j\ge 0}{\tilde{c}}_jv^{4j}=1+\frac{v^4}{2}-\frac{v^8}{8}+\frac{v^{12}}{16}+O\left( v^{16}\right) . \end{aligned}$$

So,

$$\begin{aligned} \psi _{N_r}(h,u_0)=\sum _{j\ge 0}{\tilde{c}}_j\int _{h^{1/4}/u_0}^{1/N}v^{4j-2r-4}\,dv. \end{aligned}$$

Let \(j_r = \frac{r}{2}+\frac{3}{4}\). Then \(4j-2r-4=4(j-j_r)-1\) and

$$\begin{aligned} {\tilde{I}}_{r,1}(h,u_0)=h^{j_r}\left[ B_{N_r}+\sum _{j\ge 0}{\tilde{c}}_j\frac{N^{4(j_r-j)}}{4(j_r-j)}\right] -\sum _{j\ge 0}{\tilde{c}}_j\frac{u_0^{4(j_r-j)}}{4(j_r-j)}\,h^j=h^{j_r}{\bar{A}}_r+{\tilde{\varphi }}_r(h,u_0), \end{aligned}$$
(31)

where \({\tilde{\varphi }}_r\) is analytic for \(0\le h\ll 1\).

To determine the constants \({\bar{A}}_r\) in (31), as \({\bar{A}}_r\) is independent of \(u_0\), we can take \(u_0 = 1\). Thus, by (31), we get

$$\begin{aligned} \bar{\varphi }_r(h,1)=-\sum _{j\ge 0}{\tilde{c}}_j\frac{h^j}{4(j-j_r)}=\frac{1}{2r+3}+\frac{h}{4r-2}+O(h^2). \end{aligned}$$

Then, by (26), for \(0<h\ll 1\) we have

$$\begin{aligned} \frac{\partial {\tilde{I}}_{r,1}(h,u_0)}{\partial h}=j_r{\bar{A}}_r\,h^{j_r-1}+\frac{1}{4r-2}+O(h). \end{aligned}$$
(32)

On the other hand, by (26), we have

$$\begin{aligned} \frac{\partial {\tilde{I}}_{r,1}(h,u_0)}{\partial h}=\frac{1}{2}\int _{0}^{1}\frac{u^{2r}\,du}{\sqrt{h+u^4}}=\frac{1}{2}h^{j_r-1}\int _{0}^{h^{-\frac{1}{4}}}\frac{v^{2r}\,du}{\sqrt{1+v^4}}. \end{aligned}$$
(33)

  • For \(r=0\), comparing (32) and (33) gives

    $$\begin{aligned} {\bar{A}}_0=\frac{1}{2\,j_r}\lim _{h\rightarrow 0}\frac{\frac{\partial {\tilde{I}}_{r1}}{\partial h}}{h^{j_r-1}}=\frac{2}{3}\int _{0}^{\infty }\frac{\,dv}{\sqrt{1+v^4}}= 1.236049785 \end{aligned}$$

  • For \(r=1\), by using \(\frac{v^2}{\sqrt{1+v^4}}=1-\frac{1}{\sqrt{1+v^4}(v^2+\sqrt{1+v^4})}\), it follows from (33) that

    $$\begin{aligned} \frac{\partial {\tilde{I}}_{r,1}(h,u_0)}{\partial h}=\frac{1}{2}-\frac{1}{2}h^{\frac{1}{4}}\int _{0}^{h^{-\frac{1}{4}}}\frac{\,dv}{\sqrt{1+v^4}(v^2+\sqrt{1+v^4})}. \end{aligned}$$

    Comparing the above with (32) we obtain

    $$\begin{aligned} {\bar{A}}_1=-\frac{2}{5}\int _{0}^{\infty }\frac{\,dv}{\sqrt{1+v^4}(v^2+\sqrt{1+v^4})}=-0.3388852337. \end{aligned}$$

Proposition 2.4

For the functions \(M^*(h, \delta )\) given in (24), we have the following expansion:

$$\begin{aligned} M^*(h,\delta )=c^*_0+c^*_1\,h^{\frac{3}{4}}+c^*_2\,h+c^*_3\,h^{\frac{5}{4}}+c^*_4\,h^{\frac{7}{4}}+O(h^2), \end{aligned}$$
(34)

where

$$\begin{aligned} c_0^*&= M^*(0, \delta ) =\oint _{{L}_0}\,q\,dx - \,p\,dy{|}_{\varepsilon =0}=c_0+{\tilde{c}}_0,\nonumber \\ c_1^*&= 2 {\tilde{A}}_0\,{\tilde{r}}_{01}, \quad c_3^*=2{\tilde{A}}_1{\tilde{r}}_{11}, \quad c_4^*=2{\tilde{A}}_0 \left( -\frac{1}{7}\,{\tilde{r}}_{21}+\frac{6}{7}\,{\tilde{r}}_{03}\right) ,\nonumber \\ c_2^*&= \oint _{{L}_0}\left[ (\,p_x+\,q_y){|}_{\varepsilon =0}-a_0\right] \,dt+O_1(c_1^*). \end{aligned}$$
(35)

Proof

By (24), (29), (30), and (31) for \(0<h\ll 1\) we have

$$\begin{aligned} M^*(h,\delta )=\varphi ^*(h,\delta )+2\,h^{\frac{3}{4}}\left[ {\tilde{A}}_0\,{\tilde{I}}_{10}^*(h)+{\tilde{A}}_1\,h^{\frac{1}{2}}\,{\tilde{I}}_{11}^*(h)\right] , \end{aligned}$$
(36)

where

$$\begin{aligned} {\tilde{I}}_{10}^*(h)&=\sum _{\begin{array}{c} k=2m\\ m\ge 0,\;j\ge 1\;odd \end{array}}{\tilde{r}}_{k,j}{\tilde{\alpha }}_{k,j}{\tilde{\beta }}_{k}h^{m+[\frac{j}{2}]}={\tilde{r}}_{01}{\tilde{\alpha }}_{01}{\tilde{\beta }}_0+({\tilde{r}}_{21}{\tilde{\alpha }}_{21}{\tilde{\beta }}_2+{\tilde{r}}_{03}{\tilde{\alpha }}_{03}{\tilde{\beta }}_0)\,h+O(h^2),\\ {\tilde{I}}_{11}^*(h)&=\sum _{\begin{array}{c} k=2m+1\\ m\ge 0,\;j\ge 1\;odd \end{array}}{\tilde{r}}_{k,j}{\tilde{\alpha }}_{k,j}{\tilde{\beta }}_{k}h^{m+[\frac{j}{2}]}={\tilde{r}}_{11}\tilde{\alpha }_{11}\tilde{\beta }_1+O(h), \end{aligned}$$

with

$$\begin{aligned} \tilde{\alpha }_{01}=\tilde{\beta }_0=\tilde{\beta }_1=1,\quad \tilde{\alpha }_{11}=\tilde{\alpha }_{21}=1,\quad \tilde{\beta }_2=-\frac{1}{7},\quad \tilde{\alpha }_{03}=\frac{6}{7}. \end{aligned}$$

Therefore, we can obtain the given expansion for \(M^*(h,\delta )\) by inserting the above into (34) with \(c_0^*=M^*(0,\delta )=c_0+{\tilde{c}}_0\), and

$$\begin{aligned} c_1^*=2 {\tilde{A}}_0\,{\tilde{r}}_{01}, \quad c_3^*=2{\tilde{A}}_1{\tilde{r}}_{11}, \quad c_4^*=2{\tilde{A}}_0\left( -\frac{1}{7}\,{\tilde{r}}_{21} +\frac{6}{7}\,{\tilde{r}}_{03}\right) , \end{aligned}$$

To calculate \({\tilde{r}}_{ij}\), as before assume that \(x=\psi ^{-1}(u)={\tau _0}u+{\tau _1}\,{u}^{3}+{\tau _2}\,{u}^{5}+O(u^7)\) and \(\frac{1}{\psi '(x)}=\lambda _0+\lambda _1\,x^2+\lambda _2\,x^4+O(x^6)\). Then we observe that

$$\begin{aligned} {\tilde{r}}_{01}&=\,2\sqrt{2}\,\lambda _0\,\left( a_{10}+b_{01}\right) ,\nonumber \\ {\tilde{r}}_{11}&=\,2\sqrt{2}\,\tau _0^2\left( \,\lambda _0\,\left( 3\,a_{30}+b_{21}\right) +\,\lambda _1\,\left( \,a_{10}+b_{01}\right) \right) ,\nonumber \\ {\tilde{r}}_{21}&=\,2\sqrt{2}\left( \lambda _{{0}} \left( 2\, \left( 3\,a_{{30}}+b_{{21}} \right) \tau _{{0}}\tau _{{1}}+ \left( 5\,a_{{50}}+b_{{41}} \right) {\tau _{{0}}}^{4}\right) +\lambda _{{1}}{\tau _{{0}}}^{4} \left( 3\,a_{{30}}+b_{{21}} \right) \right. \nonumber \\&\quad +\left. \left( \lambda _{{2}}{\tau _{{0}}}^{4}+2\,\lambda _{{1}}\tau _{{0}}\tau _{{1}} \right) \left( a_{{10}}+b_{{01}} \right) \right) ,\nonumber \\ {\tilde{r}}_{03}&= \frac{4}{3}\sqrt{2}\,\lambda _0\,\left( a_{12}+\,3\,b_{03}\right) . \end{aligned}$$
(37)

To prove the formula of \(c_3^*\) in (35) see [5]. \(\square \)

Remark 2.5

Under the conditions of Propositions 2.2 and 2.4, it is easy to see that

$$\begin{aligned} c_1^*=\frac{2\,{\tilde{A}}_0}{{\bar{A}}_0}\,c_1,\quad c_3^*=\frac{2\,{\tilde{A}}_1}{{\bar{A}}_2}\,c_4,\quad c_4^*=-\frac{2\,{\tilde{A}}_0}{{\bar{A}}_0}\,c_5. \end{aligned}$$

Asymptotic Expansion of the Melnikov Function Near the Centers

In this section, we calculate the expansions of \({M}_1(h,\delta )\) and \({M}_2(h,\delta )\) near the centers \(C_1\) and \(C_2\), respectively. First, we calculate the expansion of \({M}_1(h,\delta )\). By introducing the transformation \((x,y) = (X-x^*,Y)\), we shift \(C_1(x^*,0)\) to the origin. Then (rewriting again X as x and Y as y) we get

$$\begin{aligned} {\dot{x}}&=y+\varepsilon {\bar{p}}(x,y,\delta ),\nonumber \\ {\dot{y}}&=-2\,(x+x^*)+\frac{\,(x+x^*+\alpha )}{\sqrt{\,(x+x^*+\alpha )^2+\beta ^2}}+\frac{\,(x+x^*-\alpha )}{\sqrt{\,(x+x^*-\alpha )^2+\beta ^2}}+\varepsilon {\bar{q}}(x,y,\delta ), \end{aligned}$$
(38)

where

$$\begin{aligned} {\bar{p}}(x,y,\delta )= p(x+x^*,y,\delta )=\sum _{i+j\ge 0}{\bar{a}}_{ij}\,x^i\,y^j,\quad {\bar{q}}(x,y,\delta )= q(x+x^*,y,\delta )=\sum _{i+j\ge 0}{\bar{b}}_{ij}\,x^i\,y^j. \end{aligned}$$

For \(\varepsilon =0\) the Hamiltonian function of system (38) is

$$\begin{aligned} {\bar{H}}(x,y)=\frac{\,{y}^{2}}{2}+{(x+x^*)}^{2}-\sqrt{(x+x^*+\alpha )^2+\beta ^2}-\sqrt{(x+x^*-\alpha )^2+\beta ^2}+c=\frac{y^2}{2}+{\bar{H}}_0(x), \end{aligned}$$

where \(c=-{x^*}^2+\sqrt{(x^*+\alpha )^2+\beta ^2}+\sqrt{(x^*-\alpha )^2+\beta ^2}\) is a constant. Recall that \(\alpha =\beta ^{\frac{2}{3}}\sqrt{1-\beta ^{\frac{2}{3}}}\) and \(\beta \in (0,\frac{8}{5\sqrt{5}})\).

The Hamiltonian system (38)\(|_{\varepsilon =0}\) has a family of periodic orbits \(\Gamma _h\;:\;{\bar{H}}(x, y) = h\) for \(h > 0\) small, surrounding the origin. So, we have

$$\begin{aligned} M_1(h,\delta )=\oint _{\Gamma _h}{\bar{q}}\,dx-{\bar{p}}\,dy=\iint _{{\bar{H}}\le h}({\bar{p}}_x+{\bar{q}}_y)\,dx\,dy=\oint _{\Gamma _h}{\hat{q}}(x,y,\delta )\,dx, \end{aligned}$$

where

$$\begin{aligned} {\hat{q}}(x, y, \delta ) = {\bar{q}}(x,y,\delta )-{\bar{q}}(x,0,\delta )+\int _{0}^{y}{\bar{p}}_x(x,u,\delta )\,du \end{aligned}$$

verifies \({\hat{q}}_y = {\bar{p}}_x+{\bar{q}}_y\) and \({\hat{q}}(x, 0, \delta ) = 0\). If \({\bar{p}}_x(x, y, \delta ) + {\bar{q}}_y(x, y, \delta ) =\sum _{i+j\ge 0} c_{ij}\,x^i\,y^j\), then \({\hat{q}}(x, y, \delta ) = \,y\sum _{i+j\ge 0} {\hat{b}}_{ij}\,x^i\,y^j = \sum _{j\ge 1}{\hat{q}}_j(x)\,y^j\), where

$$\begin{aligned} {\hat{q}}_{j+1}(x) =\frac{1}{(j+1)!}\frac{\partial ^j}{\partial \,y^j}\left( {\bar{p}}_x+{\bar{q}}_y\right) \Big |_{\varepsilon =y=0}=\sum _{i\ge 1}{\hat{b}}_{ij}\,x^i,\quad j\ge 0. \end{aligned}$$

Note that the equation \({\bar{H}}(x,y)=h\) has two \(C^\omega \) solutions \(y^{\pm }=\pm \sqrt{2}w(1+O(|x,w|))\), where \(w=\sqrt{h-{\bar{H}}_0(x)}\). Let \(\zeta _1(h) < 0\) and \(\zeta _2(h) > 0\) be the solutions of the equation \({\bar{H}}_0 (x) = h\). Then

$$\begin{aligned} M_1(h,\delta )=\oint _{\Gamma _h}{\hat{q}}\,dx=\int _{\zeta _1}^{\zeta _2}({\hat{q}}(x,y^+,\delta )-{\hat{q}}(x,y^-,\delta ))\,dx=\sum _{j\ge 0}\int _{\zeta _1}^{\zeta _2}\,q_j^*(x)\,w^{2j+1}\,dx, \end{aligned}$$

where \(q_j^*=2^{3j+\frac{3}{2}}{\hat{q}}_{2j+1}\). Let \(u^2={\bar{H}}_0(x)\). Then, by introducing the variable \(u = \psi (x)=sgn(x)({{\bar{H}}_0(x)})^{\frac{1}{2}}\), we obtain

$$\begin{aligned} M_1(h,\delta )=\sum _{j\ge 0}\int _{-\sqrt{h}}^{\sqrt{h}}\,{\check{q}}_j(u)\,w^{2j+1}\,du=\sum _{j\ge 0}\int _{0}^{\sqrt{h}}\,\left( \check{q}_j(u)+\check{q}_j(-u)\right) \,w^{2j+1}\,du=\sum _{i+j\ge 0}{\bar{r}}_{ij}{\bar{I}}_{ij}, \end{aligned}$$

where \(w=\sqrt{h-u^2}\), \(\check{q}_j(u)=\frac{q_j^*(x)}{\psi '(x)}\Big |_{x=\psi ^{-1}(u)}\), \(\check{q}_j(u)+\check{q}_j(-u)=\sum _{j\ge 0}{\bar{r}}_{ij}\,u^{2i}\) and \({\bar{I}}_{ij}=\int _{0}^{\sqrt{h}}u^{2i}\,w^{2j+1}\,du\). By introducing \(v = \frac{u}{\sqrt{h}}\), we get

$$\begin{aligned} {\bar{I}}_{ij}=h^{i+j+1}\int _{0}^{1}v^{2i}\,\left( 1-v^2\right) ^{j}\sqrt{1-v^2}\,dv=h^{i+j+1}\,J_{ij}. \end{aligned}$$

Therefore,

$$\begin{aligned} M_1(h,\delta )=\,h\sum _{i+j\ge 0}{\bar{r}}_{ij}\,{J}_{ij}\,h^{i+j}=\,h\sum _{k\ge 0}b_k(\delta )\,h^{k},\;\;\;\;\; where\;\;\; b_k(\delta )=\sum _{i+j=k}{\bar{r}}_{ij}\,{J}_{ij}. \end{aligned}$$
(39)

For computing \(\{b_k\}\), note that, by Taylor expansion, we obtain \(x=\psi ^{-1}(u)=\nu _1\,u+\nu _2\,u^2+\nu _3\,u^3+O(u^4)\), \(\frac{1}{\psi '(x)}=\gamma _0+\gamma _1\,x+\gamma _2\,x^2+O(x^3)\), where

$$\begin{aligned} \nu _1&= \left( 6\,{x^*}^{2}\sqrt{{\alpha }^{2}+2\,\alpha \,x^*+{\beta }^{2}+{x^*}^{2}}\sqrt{{\alpha }^{2}-2\,\alpha \,x^*+{\beta }^{2}+{x^*}^{2 }}+4\,{\alpha }^{2}{x^*}^{2}+4\,{\beta }^{2}{x^*}^{2}+4\,{x^*}^{4}\right. \\&\quad +\sqrt{{\alpha }^{2}-2\,\alpha \,x^*+{\beta }^{2}+{x^*}^{2}}{\alpha }^{2}+2\,\sqrt{{ \alpha }^{2}-2\,\alpha \,x^*+{\beta }^{2}+{x^*}^{2}}x^*\alpha +\sqrt{{\alpha }^{2}-2\,\alpha \,x^*+{\beta }^{2}+{x^*}^{2}}{\beta }^{2}\\&\quad -3\,{x^*}^{2}\sqrt{{\alpha }^{2}-2\,\alpha \,x^*+{\beta }^{2}+{x^*}^{2}} +\sqrt{{\alpha }^{2}+2\,\alpha \,x^*+{\beta }^{2}+{x^*}^{2}}{\alpha }^{2}-2\,\sqrt{{\alpha }^{2}+2\, \alpha \,x^*+{\beta }^{2}+{x^*}^{2}}x^*\alpha \\&\quad +\sqrt{{\alpha }^{2}+2\,\alpha \,x^*+{\beta }^{2}+{x^*}^{2}}{\beta }^{2}-3\,{x^*}^{2}\sqrt{{\alpha }^{2}+2\, \alpha \,x^*+{\beta }^{2}+{x^*}^{2}}\\&\quad \left. -\sqrt{{\alpha }^{2}+2\,\alpha \,x^*+{\beta }^{2}+{x^*}^{2}}\sqrt{{\alpha }^{2}-2\,\alpha \,x^*+{\beta }^{2}+{x^*}^{2}}+{ \alpha }^{2}-{\beta }^{2}-{x^*}^{2} \right) ^{-\frac{1}{2}}\,\\&\quad \times \left( \sqrt{{\alpha }^{2}-2\,\alpha \,x^*+{\beta }^{2}+{x^*}^{2}}{\alpha }^{2}+2\,\sqrt{{\alpha }^{2}-2 \,\alpha \,x^*+{\beta }^{2}+{x^*}^{2}}x^*\alpha +\sqrt{{\alpha }^{2}-2\,\alpha \,x^*+{\beta }^{2}+{x^*}^{2}}{\beta }^{2}\right. \\&\quad +{x^*}^{2}\sqrt{{\alpha }^{2}-2\, \alpha \,x^*+{\beta }^{2}+{x^*}^{2}}+\sqrt{{\alpha }^{2}+2\,\alpha \,x^*+{\beta }^{2}+{x^*}^{2}}{\alpha }^{2}-2\,\sqrt{{\alpha }^{2}+2\,\alpha \,x^*+{\beta } ^{2}+{x^*}^{2}}x^*\alpha \\&\quad \left. +\sqrt{{\alpha }^{2}+2\,\alpha \,x^*+{\beta }^{2}+{x^*}^{2}}{\beta }^{2}+{x^*}^{2}\sqrt{{\alpha }^{2}+2\,\alpha \,x^*+{\beta }^{2}+{x^* }^{2}} \right) ^{\frac{1}{2}}\,\\ \gamma _0&= \left( \phantom {\left. \left. +2 \,\sqrt{{\alpha }^{2}+2\,x^*\alpha +{\beta }^{2}+{x^*}^{2}}\sqrt{{\alpha }^{2}-2\,x^*\alpha +{\beta }^{2}+{x^*}^{2}}{\alpha }^{4}\right) ^{\frac{1}{2}}\right) }\sqrt{2}\sqrt{{\alpha }^{4}+2\,{\alpha }^{2}{\beta }^{2}-2\,{\alpha }^{2}{x^*}^{2}+{\beta }^{4}+2\,{\beta }^{2}{x^*}^{2}+{x^*}^{4}}\right. \left( -8\,\sqrt{{\alpha }^{2}-2\,x^*\alpha +{\beta }^{2}+{x^*}^{2}}{x^*}^{4}\right. \\&\quad +4\,\sqrt{{\alpha }^{2}+ 2\,x^*\alpha +{\beta }^{2}+{x^*}^{2}}\sqrt{{\alpha }^{2}-2\,x^*\alpha +{\beta }^{2}+{x^*}^{2}}{\alpha }^{2}{\beta }^{2}-9\,\sqrt{{\alpha }^{2}+2\,x^*\alpha +{\beta }^{2}+{x^*}^{2}}{\beta }^{2}{x^*}^{2}\\&\quad +2\,\sqrt{{\alpha }^{2}+2\,x^*\alpha +{\beta }^{2}+{x^* }^{2}}\sqrt{{\alpha }^{2}-2\,x^*\alpha +{\beta }^{2}+{x^*}^{2}}{\beta }^{4}+6\,\sqrt{{\alpha }^{2}+ 2\,x^*\alpha +{\beta }^{2}+{x^*}^{2}}\alpha \,{\beta }^{2}x^*\\&\quad +18\,\sqrt{{\alpha }^{2}+2\,x^*\alpha +{\beta }^{2}+{x^*}^{2}}\sqrt{{\alpha }^{2}-2\,x^* \alpha +{\beta }^{2}+{x^*}^{2}}{x^*}^{4}-8\,\sqrt{{\alpha }^{2}+2\,x^*\alpha +{\beta }^{2}+{x^*}^{2}}{\alpha }^{3}x^*\\&\quad -\sqrt{{\alpha }^{2}+2\,x^*\alpha +{\beta }^{2}+{x^*}^{2}}{\alpha }^{2}{\beta }^{2}+8\,\sqrt{{\alpha }^{2}+2\,x^*\alpha +{\beta }^{2}+{x^*}^{2}}{\alpha }^{2}{x^*}^{2}-\sqrt{{\alpha }^{2 }+2\,x^*\alpha +{\beta }^{2}+{x^*}^{2}}{\beta }^{4}\\&\quad +8\,\sqrt{{\alpha }^{2}+2\,x^*\alpha +{\beta }^{2}+{x^*}^{2}}\alpha \,{x^*}^{3}-20\,\sqrt{{\alpha }^{2}+2\,x^*\alpha +{\beta }^{2}+{x^*}^{2}}\sqrt{{\alpha }^{2}-2\,x^*\alpha +{\beta }^{2}+{x^*}^{2}}{\alpha }^{2}{x^*}^{2}\\&\quad +20\,\sqrt{{\alpha }^{2}+2\,x^*\alpha +{\beta }^{2}+{x^*}^{2}}\sqrt{{\alpha } ^{2}-2\,x^*\alpha +{\beta }^{2}+{x^*}^{2}}{\beta }^{2}{x^*}^{2}+8\,\sqrt{{\alpha }^{2}-2\,x^*\alpha +{\beta }^{2}+{x^*}^{2}}{\alpha }^{3}x^*\\&\quad -\sqrt{{\alpha }^{2}-2\,x^*\alpha +{\beta }^{2}+{x^*}^{2}}{\alpha }^{2}{\beta }^{2} +8\,\sqrt{{\alpha }^{2}-2\,x^*\alpha +{\beta }^{2}+{x^*}^{2}}{\alpha }^{2}{x^*}^{2}-{\beta }^{4}\sqrt{{\alpha }^{2}-2\,x^*\alpha +{\beta }^{2}+{x^*}^{2}}\\&\quad -6\,\sqrt{{\alpha }^{2}-2\,x^*\alpha +{\beta }^{2}+{x^*}^{2}}\alpha \,{\beta }^{2}x^*-8\,\sqrt{{\alpha }^{2}-2\,x^*\alpha +{\beta }^{2}+{x^*}^{2}}\alpha \,{x^*}^{3}-9\,\sqrt{{\alpha }^{2}-2\,x^*\alpha +{\beta }^{2}+{x^*}^{2}}{\beta }^{2}{x^*}^{2}\\&\quad \left. \left. +2 \,\sqrt{{\alpha }^{2}+2\,x^*\alpha +{\beta }^{2}+{x^*}^{2}}\sqrt{{\alpha }^{2}-2\,x^*\alpha +{\beta }^{2}+{x^*}^{2}}{\alpha }^{4}\right) ^{\frac{1}{2}}\right) \\&\quad \times \left( \root 4 \of {{\alpha }^{2}+2\,x^*\alpha +{\beta }^{2}+{x^*}^{2}}\root 4 \of {{\alpha }^{2} -2\,x^*\alpha +{\beta }^{2}+{x^*}^{2}} \left( 2\,{\alpha }^{4}+4\,{\alpha }^{2}{\beta }^{2}-8\,{\alpha }^{2}{x^*}^{2}+2\,{\beta }^{4}+8\,{\beta }^{2}{x^*}^{ 2}+6\,{x^*}^{4}\right. \right. \\&\quad +2\,\alpha \,\sqrt{{\alpha }^{2}+2\,x^*\alpha +{\beta }^{2}+{x^*}^{2}}x^*-\sqrt{{\alpha }^{2}+2\,x^*\alpha +{\beta }^{2}+{x^*}^{2}}{\beta }^{2} -2\,{x^*}^{2}\sqrt{{\alpha }^{2}+2\,x^*\alpha +{\beta }^{2}+{x^*}^{2}}\\&\quad \left. \left. -2\,\alpha \,\sqrt{{\alpha }^{2}-2\,x^*\alpha +{\beta }^{2}+{x^*}^{2}}x^*-\sqrt{{ \alpha }^{2}-2\,x^*\alpha +{\beta }^{2}+{x^*}^{2}}{\beta }^{2}-2\,{x^*}^{2}\sqrt{{\alpha }^{2}-2\,x^*\alpha +{\beta }^{2}+{x^*}^{2}} \right. \right) ^{-1}, \end{aligned}$$

where \(\alpha =\beta ^{\frac{2}{3}}\sqrt{1-\beta ^{\frac{2}{3}}}\) and the other coefficients have long terms that can be easily calculated by using the Taylor expansion. Also,

$$\begin{aligned} q_0^*(x)&=\,2\sqrt{2}{\hat{q}}_1=\,2\sqrt{2}({\bar{p}}_x+{\bar{q}}_y)|_{\varepsilon =y=0}=\,2\sqrt{2}\sum _{i=1}^{\infty } \left( {\bar{b}}_{i1}+(i+1){\bar{a}}_{i+1,0}\right) \,x^i,\\ q_1^*(x)&=\,16\sqrt{2}{\hat{q}}_3=\,\frac{8}{3}\sqrt{2}({\bar{p}}_{xyy}+{\bar{q}}_{yyy})|_{\varepsilon =y=0}=\,\frac{16}{3}\sqrt{2}\sum _{i=1}^{\infty } \left( 3{\bar{b}}_{i3}+(i+1){\bar{a}}_{i+1,2}\right) \,x^i. \end{aligned}$$

Thus,

$$\begin{aligned} {\bar{r}}_{00}=&\,4\sqrt{2}\,\gamma _{{0}} \left( {\bar{a}}_{{10}}+{\bar{b}}_{{01}} \right) ,\quad {\bar{r}}_{01}={\frac{32}{3}\sqrt{2}\,\gamma _{{0}} \left( {\bar{a}}_{{12}}+3\,{\bar{b}}_{{03}} \right) },\\ {\bar{r}}_{10}=&\, 4\,\sqrt{2} \left[ \gamma _{{0}} \left( \nu _{{2}} \left( 2\,{\bar{a}}_{{20}}+{\bar{b}}_{{11}}\right) +{\nu _{{1}}}^{2 } \left( 3\,{\bar{a}}_{{30}}+{\bar{b}}_{{21}} \right) \right) +\gamma _{{1}}{\nu _{{1}}}^{2} \left( 2\,{\bar{a}}_{{20}}+{\bar{b}}_{{11}} \right) \right. \\&\quad \left. + \left( \gamma _{{2}}{\nu _{{1}}}^{2}+\gamma _{{1}}\nu _{{2}} \right) \left( {\bar{a}}_{{10}}+{\bar{b}}_{{01}} \right) \right] . \end{aligned}$$

Therefore,

$$\begin{aligned} b_0(\delta )={\bar{r}}_{00}\,J_{00},\quad b_1(\delta )={\bar{r}}_{10}\,J_{10}+{\bar{r}}_{01}\,J_{01}, \end{aligned}$$
(40)

where

$$\begin{aligned} J_{00}=\displaystyle \int _{0}^{1}\sqrt{1-v^2}\,dv=\frac{\pi }{4},\;\;\;\;J_{10}=\displaystyle \int _{0}^{1}\,v^2\sqrt{1-v^2}\,dv=\frac{\pi }{16},\;\;\;\;J_{01}=\displaystyle \int _{0}^{1}\,(1-v^2)\sqrt{1-v^2}\,dv=\frac{\,3\,\pi }{16}. \end{aligned}$$

Now, we calculate the expansion of \({M}_2(h,\delta )\). First, by introducing the transformation \((x,y) = (X+x^*,Y)\), we shift \(C_2(-x^*,0)\) to the origin. Then (rewriting again X as x and Y as y) we get

$$\begin{aligned} {\dot{x}}&=y+\varepsilon {\hat{p}}(x,y,\delta ),\\ {\dot{y}}&=-2\,(x-x^*)+\frac{\,(x-x^*+\alpha )}{\sqrt{\,(x-x^*+\alpha )^2+\beta ^2}}+\frac{\,(x-x^*-\alpha )}{\sqrt{\,(x-x^*-\alpha )^2+\beta ^2}}+\varepsilon {\hat{q}}(x,y,\delta ),\nonumber \end{aligned}$$
(41)

where

$$\begin{aligned} {\hat{p}}(x,y,\delta )= p(x-x^*,y,\delta )=\sum _{i+j\ge 0}{\hat{a}}_{ij}\,x^i\,y^j,\;\;\;\;\;\;\;\;\;\;\;\;{\hat{q}}(x,y,\delta )= q(x-x^*,y,\delta )=\sum _{i+j\ge 0}{\hat{b}}_{ij}\,x^i\,y^j. \end{aligned}$$

For \(\varepsilon =0\) the Hamiltonian function of system (41) is

$$\begin{aligned} {\hat{H}}(x,y)=\frac{\,{y}^{2}}{2}+{(x-x^*)}^{2}-\sqrt{(x-x^*+\alpha )^2+\beta ^2}-\sqrt{(x-x^*-\alpha )^2+\beta ^2}+c=\frac{y^2}{2}+{\bar{H}}_0(x), \end{aligned}$$

where \(c=-{x^*}^2+\sqrt{(-x^*+\alpha )^2+\beta ^2}+\sqrt{(-x^*-\alpha )^2+\beta ^2}\) is a constant.

The Hamiltonian system (41)\(|_{\varepsilon =0}\) has a continuous family of periodic orbits \(\gamma _h\;:\;{\hat{H}}(x, y) = h\) for \(h > 0\) small, surrounding the origin. So, similar to \(M_1\), we have

$$\begin{aligned} M_2(h,\delta )=\oint _{\gamma _h}{\hat{q}}\,dx-{\hat{p}}\,dy=\iint _{{\hat{H}}\le h}({\hat{p}}_x+{\hat{q}}_y)\,dx\,dy=\oint _{\gamma _h}\breve{q}(x,y,\delta )\,dx, \end{aligned}$$

where

$$\begin{aligned} \breve{q}(x, y, \delta ) = {\hat{q}}(x,y,\delta )-{\hat{q}}(x,0,\delta )+\int _{0}^{y}{\hat{p}}_x(x,u,\delta )\,du \end{aligned}$$

verifies \(\breve{q}_y = {\hat{p}}_x+{\hat{q}}_y\) and \(\breve{q}(x, 0, \delta ) = 0\). If \({\hat{p}}_x(x, y, \delta ) + {\hat{q}}_y(x, y, \delta ) =\sum _{i+j\ge 0} {\hat{c}}_{ij}\,x^i\,y^j\), then \(\breve{q}(x, y, \delta ) = \,y\sum _{i+j\ge 0} \breve{b}_{ij}\,x^i\,y^j = \sum _{j\ge 1}\breve{q}_j(x)\,y^j\), where

$$\begin{aligned} \breve{q}_{j+1}(x) =\frac{1}{(j+1)!}\frac{\partial ^j}{\partial \,y^j}({\hat{p}}_x+{\hat{q}}_y)\Big |_{\varepsilon =y=0}=\sum _{i\ge 1}\breve{b}_{ij}\,x^i,\quad j\ge 0. \end{aligned}$$

Note that the equation \({\hat{H}}(x,y)=h\) has two \(C^\omega \) solutions \(y^{\pm }=\pm \sqrt{2}w(1+O(|x,w|))\), where \(w=\sqrt{h-{\hat{H}}_0(x)}\). Let \(\bar{\zeta }_1(h) < 0\) and \(\bar{\zeta }_2(h) > 0\) be the solutions of the equation \({\hat{H}}_0 (x) = h\). Then

$$\begin{aligned} M_2(h,\delta )=\oint _{\gamma _h}\breve{q}\,dx=\int _{\bar{\zeta }_1}^{\bar{\zeta }_2}(\breve{q}(x,y^+,\delta )-\breve{q}(x,y^-,\delta ))\,dx=\sum _{j\ge 0}\int _{\bar{\zeta }_1}^{\bar{\zeta }_2}\,\check{q}_j(x)\,w^{2j+1}\,dx, \end{aligned}$$

where \(\check{q}_j=2^{3j+\frac{3}{2}}\breve{q}_{2j+1}\). Let \(u^2={\hat{H}}_0(x)\). Then, by introducing the variable \(u = \rho (x)=sgn(x)({{\hat{H}}_0(x)})^{\frac{1}{2}}\), we obtain

$$\begin{aligned} M_2(h,\delta )=\sum _{j\ge 0}\int _{-\sqrt{h}}^{\sqrt{h}}\,q^*_j(u)\,w^{2j+1}\,du=\sum _{j\ge 0}\int _{0}^{\sqrt{h}}\,(q^*_j(u)+q^*_j(-u))\,w^{2j+1}\,du=\sum _{i+j\ge 0}{\hat{r}}_{ij}{\hat{I}}_{ij}, \end{aligned}$$

where \(w=\sqrt{h-u^2}\), \(q^*_j(u)=\frac{\check{q}_j(x)}{\rho '(x)}\Big |_{x=\rho ^{-1}(u)}\), \(q^*_j(u)+q^*_j(-u)=\sum _{j\ge 0}{\hat{r}}_{ij}\,u^{2i}\) and \({\hat{I}}_{ij}=\int _{0}^{\sqrt{h}}u^{2i}\,w^{2j+1}\,du\). By introducing \(v = \frac{u}{\sqrt{h}}\), we get,

$$\begin{aligned} {\hat{I}}_{ij}={\bar{I}}_{ij}=h^{i+j+1}\int _{0}^{1}v^{2i}\,(1-v^2)^{j}\sqrt{1-v^2}\,dv=h^{i+j+1}\,J_{ij}. \end{aligned}$$

Thus,

$$\begin{aligned} M_2(h,\delta )=\,h\sum _{i+j\ge 0}{\hat{r}}_{ij}\,{J}_{ij}\,h^{i+j}=\,h\sum _{k\ge 0}{\bar{b}}_k(\delta )\,h^{k},\quad where\; {\bar{b}}_k(\delta )=\sum _{i+j=k}{\hat{r}}_{ij}\,{J}_{ij}. \end{aligned}$$
(42)

For computing \(\{{\bar{b}}_k\}\), we see that \(x=\rho ^{-1}(u)=\nu _1\,u-\nu _2\,u^2+\nu _3\,u^3-\nu _4\,u^4+O(u^5)\) and \(\frac{1}{\rho '(x)}=\gamma _0-\gamma _1\,x+\gamma _2\,x^2+O(x^3)\), because of symmetry. Then

$$\begin{aligned} {\hat{r}}_{00}&= \,4\sqrt{2}\,\gamma _{{0}} \left( {\hat{a}}_{{10}}+{\hat{b}}_{{01}} \right) ,\quad {\hat{r}}_{01}={\frac{32}{3}\sqrt{2}\,\gamma _{{0}} \left( {\hat{a}}_{{12}}+3\,{\hat{b}}_{{03}} \right) },\\ {\hat{r}}_{10}&=\, 4\,\sqrt{2} \left[ \gamma _{{0}} \left( -\nu _{{2}} \left( 2\,{\hat{a}}_{{20}}+{\hat{b}}_{{11}}\right) +{\nu _{{1}}}^{2 } \left( 3\,{\hat{a}}_{{30}}+{\hat{b}}_{{21}} \right) \right) \right. \\&\quad \left. -\gamma _{{1}}{\nu _{{1}}}^{2} \left( 2\,{\hat{a}}_{{20}}+{\hat{b}}_{{11}} \right) + \left( \gamma _{{2}}{\nu _{{1}}}^{2}+\gamma _{{1}}\nu _{{2}} \right) \left( {\hat{a}}_{{10}}+{\hat{b}}_{{01}} \right) \right] . \end{aligned}$$

Therefore,

$$\begin{aligned} {\bar{b}}_0(\delta )={\hat{r}}_{00}\,J_{00},\quad {\bar{b}}_1(\delta )={\hat{r}}_{10}\,J_{10}+{\hat{r}}_{01}\,J_{01}. \end{aligned}$$
(43)

Limit Cycle Bifurcation

In this section, by using the first nonvanishing coefficients of the expansions obtained in the previous sections, we discuss about the number of limit cycles which can be generated from system (6).

Let \(L_0= {\bar{L}}_0 \cup {\tilde{L}}_0\) be a double homoclinic loop defined by \(H(x, y) = 0\). Assume that \(H(x^*,0)=h_{c_1}\) and \(H(-x^*,0)=h_{c_2}\). Consider the expantions of M, \({\widetilde{M}}\), \(M^*\), \(M_1\) and \(M_2\), then we have the following theorems.

Theorem 2.6

Under the above conditions, If there exists some \(\delta _0 \in {\mathbb {R}}^m\) such that

$$\begin{aligned} c_0(\delta _0)&= {\tilde{c}}_0(\delta _0) = c_{1}(\delta _0) = c_{2}(\delta _0) = c_{3}(\delta _0) = {\tilde{c}}_3(\delta _0) =0,\;\; c_{4}(\delta _0) \ne 0,\\ b_0(\delta _0)&= b_1(\delta _0) = \cdots = b_{k_1-1}(\delta _0) = 0,\;\; b_{k_1}(\delta _0) \ne 0,\\ {\bar{b}}_0(\delta _0)&= {\bar{b}}_1(\delta _0) = \cdots = {\bar{b}}_{k_2-1}(\delta _0) = 0,\;\; {\bar{b}}_{k_2}(\delta _0) \ne 0, \end{aligned}$$

and

$$\begin{aligned} rank\frac{\partial (c_0, {\tilde{c}}_0, c_1, c_{2} , c_{3}, {\tilde{c}}_3 ,b_0,b_1,\ldots , b_{k_1-1},{\bar{b}}_0,{\bar{b}}_1,\ldots , {\bar{b}}_{k_2-1})}{\partial (\delta _1, \ldots , \delta _k)}= 6+k_1+k_2, \end{aligned}$$
(44)

then (6) can have \(8+k_1 + k_2 + \frac{1-sgn(M(h_2,\delta _0)M_1(h_1,\delta _0))}{2}+\frac{1-sgn({\widetilde{M}}(h_4,\delta _0)M_2(h_3,\delta _0))}{2}\) limit cycles for some \((\varepsilon , \delta )\) near \((0, \delta _0)\) from which 8 limit cycles are near the double homoclinic loop, \(k_1\) limit cycles are near the center \(C_1\), \(k_2\) limit cycles are near the center \(C_2\), \(\frac{1-sgn(M_1(h_1,\delta _0)M(h_2,\delta _0))}{2}\) limit cycle is located between \(C_1\) and \({\bar{L}}_0\) and \(\frac{1-sgn({\widetilde{M}}(h_4,\delta _0)M_2(h_3,\delta _0))}{2}\) limit cycle is located between \(C_2\) and \({\tilde{L}}_0\), where \(h_1 = h_{c_1}+\varepsilon _1\), \(h_2 = 0-\varepsilon _2\), \(h_3 = h_{c_2}+\varepsilon _3\), \(h_4 = 0-\varepsilon _4\) with \(\varepsilon _1\), \(\varepsilon _2\), \(\varepsilon _3\) and \(\varepsilon _4\) are positive and very small.

Proof

Since \(c_{4}(\delta _0) \ne 0\), in the same way as in Theorem 3.1 in [5], we can conclude that 8 limit cycles occur near the double homoclinic loop \(L_0\). By (44), we know that \(b_0,b_1,\ldots ,b_{k_1-1},{\bar{b}}_0,{\bar{b}}_1,\ldots ,{\bar{b}}_{k_2-1}\) can be taken as free parameters. Now, we change the sign of these parameter to obtain the zeros of \(M_j(h,\delta )\) for \(j = 1, 2\). If

$$\begin{aligned} b_{j-1}b_{j}<0,\quad j=1,\ldots ,k_1,\quad 0<|b_0| \ll |b_1| \ll \ldots \ll |b_{k_1}|, \end{aligned}$$

then we can find \(k_1\) limit cycles are near the center \(C_1\). If

$$\begin{aligned} {\bar{b}}_{j-1}{\bar{b}}_{j}<0,\quad j=1,\ldots ,k_2,\quad 0<|{\bar{b}}_0| \ll |{\bar{b}}_1| \ll \ldots \ll |{\bar{b}}_{k_2}|, \end{aligned}$$

then we can find \(k_2\) limit cycles are near the center \(C_2\).

It is clear that if there exists \(h_1 = h_{c_1}+\varepsilon _1\) and \(h_2 = 0-\varepsilon _2\) with \(\varepsilon _1\) and \(\varepsilon _2\) positive and very small such that \(M_1(h_1,\delta _0).M(h_2,\delta _0))<0\), then we have \(\frac{1-sgn(M_1(h_1,\delta _0)M(h_2,\delta _0))}{2}=1\) limit cycle is located between \(C_1\) and \({\bar{L}}_0\). Similarly, for \(h_3 = h_{c_2}+\varepsilon _3\) and \(h_4 = 0-\varepsilon _4\) with \(\varepsilon _3\) and \(\varepsilon _4\) positive and very small, we have \(\frac{1-sgn({\widetilde{M}}(h_4,\delta _0)M_2(h_3,\delta _0))}{2}\) limit cycle is located between \(C_2\) and \({\tilde{L}}_0\). \(\square \)

The next two theorems can be proved similarly.

Theorem 2.7

Under the conditions of Theorem 2.6, if there exists some \(\delta _0 \in {\mathbb {R}}^m\) such that

$$\begin{aligned} c_0(\delta _0)&= {\tilde{c}}_0(\delta _0) = c_{1}(\delta _0) = c_{2}(\delta _0) = c_{3}(\delta _0) = {\tilde{c}}_3(\delta _0) = c_{4}(\delta _0) =0,\;\; c_{5}(\delta _0) \ne 0,\\ b_0(\delta _0)&= b_1(\delta _0) = \cdots = b_{k_1-1}(\delta _0) = 0,\;\; b_{k_1}(\delta _0) \ne 0,\\ {\bar{b}}_0(\delta _0)&= {\bar{b}}_1(\delta _0) = \cdots = {\bar{b}}_{k_2-1}(\delta _0) = 0,\;\; {\bar{b}}_{k_2}(\delta _0) \ne 0, \end{aligned}$$

and

$$\begin{aligned} rank\frac{\partial (c_0, {\tilde{c}}_0, c_1, c_{2} , c_{3}, {\tilde{c}}_3, c_4 ,b_0,b_1,\ldots , b_{k_1-1},{\bar{b}}_0,{\bar{b}}_1,\ldots , {\bar{b}}_{k_2-1})}{\partial (\delta _1, \ldots , \delta _k)}= 7+k_1+k_2, \end{aligned}$$

then (6) can have \(10+k_1 + k_2 + \frac{1-sgn(M(h_2,\delta _0)M_1(h_1,\delta _0))}{2}+\frac{1-sgn({\widetilde{M}}(h_4,\delta _0)M_2(h_3,\delta _0))}{2}\) limit cycles for some \((\varepsilon , \delta )\) near \((0, \delta _0)\) from which 10 limit cycles are near the double homoclinic loop, \(k_1\) limit cycles are near the center \(C_1\), \(k_2\) limit cycles are near the center \(C_2\), \(\frac{1-sgn(M(h_2,\delta _0)M_1(h_1,\delta _0))}{2}\) limit cycle is located between \(C_1\) and \({\bar{L}}_0\) and \(\frac{1-sgn({\widetilde{M}}(h_4,\delta _0)M_2(h_3,\delta _0))}{2}\) limit cycle is located between \(C_2\) and \({\tilde{L}}_0\), where \(h_1 = h_{c_1}+ \varepsilon _1\), \(h_2 = 0-\varepsilon _2\), \(h_3 = h_{c_2}+ \varepsilon _3\), \(h_4 = 0-\varepsilon _4\) with \(\varepsilon _1\), \(\varepsilon _2\), \(\varepsilon _3\) and \(\varepsilon _4\) are positive and very small.

Theorem 2.8

Under the conditions of Theorem 2.6, if there exists some \(\delta _0 \in {\mathbb {R}}^m\) such that \(M^*(h_0,\delta )\ne 0\) for some \(h_0\) and,

$$\begin{aligned} c_0(\delta _0)&= {\tilde{c}}_0(\delta _0) = c_{1}(\delta _0) = c_{2}(\delta _0) = c_{3}(\delta _0) = {\tilde{c}}_3(\delta _0) = c_{4}(\delta _0) = c_{5}(\delta _0) =0,\;\; c_{6}(\delta _0) \ne 0,\\ b_0(\delta _0)&= b_1(\delta _0) = \cdots = b_{k_1-1}(\delta _0) = 0,\;\; b_{k_1}(\delta _0) \ne 0,\\ {\bar{b}}_0(\delta _0)&= {\bar{b}}_1(\delta _0) = \cdots = {\bar{b}}_{k_2-1}(\delta _0) = 0,\;\; {\bar{b}}_{k_2}(\delta _0) \ne 0, \end{aligned}$$

and,

$$\begin{aligned} rank\frac{\partial (c_0, {\tilde{c}}_0, c_1, c_{2} , c_{3}, {\tilde{c}}_3, c_4 ,b_0,b_1,\ldots , b_{k_1-1},{\bar{b}}_0,{\bar{b}}_1,\ldots , {\bar{b}}_{k_2-1})}{\partial (\delta _1, \ldots , \delta _k)}= 8+k_1+k_2, \end{aligned}$$

then (6) can have \(12+k_1 + k_2 + \frac{1-sgn(M(h_2,\delta _0)M_1(h_1,\delta _0))}{2}+\frac{1-sgn({\widetilde{M}}(h_4,\delta _0)M_2(h_3,\delta _0))}{2}\) limit cycles for some \((\varepsilon , \delta )\) near \((0, \delta _0)\) from which 12 limit cycles are near the double homoclinic loop, \(k_1\) limit cycles are near the center \(C_1\), \(k_2\) limit cycles are near the center \(C_2\), \(\frac{1-sgn(M(h_2,\delta _0)M_1(h_1,\delta _0))}{2}\) limit cycle is located between \(C_1\) and \({\bar{L}}_0\) and \(\frac{1-sgn({\widetilde{M}}(h_4,\delta _0)M_2(h_3,\delta _0))}{2}\) limit cycle is located between \(C_2\) and \({\tilde{L}}_0\), where \(h_1 = h_{c_1}+\varepsilon _1\), \(h_2 = 0-\varepsilon _2\), \(h_3 = h_{c_2}+ \varepsilon _3\), \(h_4 = 0-\varepsilon _4\) with \(\varepsilon _1\), \(\varepsilon _2\), \(\varepsilon _3\) and \(\varepsilon _4\) are positive and very small.

Application

In this section, we provide an example as an application of our main results. Let \(\beta =\frac{1}{\sqrt{8}}\), then \(\alpha =\beta ^{\frac{2}{3}}\sqrt{1-\beta ^{\frac{2}{3}}}=\frac{1}{\sqrt{8}}\) and system (4) becomes,

$$\begin{aligned} {\dot{x}}&=y,\nonumber \\ {\dot{y}}&=-2\,x+\frac{1}{4}\,{\frac{2\,\sqrt{2}+8\,x}{\sqrt{2\,x\sqrt{2}+4\,{x}^{2}+1}}}+\frac{1}{4}\,{\frac{-2\,\sqrt{2}+8\,x}{\sqrt{-2\,x\sqrt{2}+4\,{x}^{2}+1}}}, \end{aligned}$$
(45)

with the Hamiltonian function,

$$\begin{aligned} H(x,y)=\frac{1}{2}\,{y}^{2}+{x}^{2}-\frac{1}{2}\,\sqrt{2\,x\sqrt{2}+4\,{x}^{2}+1}-\frac{1}{2}\,\sqrt{-2\,x\sqrt{2}+4\,{x}^{2}+1}+1. \end{aligned}$$
(46)

We Consider the following perturbation,

$$\begin{aligned} {\dot{x}}&=y,\nonumber \\ {\dot{y}}&=-2\,x+\frac{1}{2}\,{\frac{\,\sqrt{2}+4\,x}{\sqrt{2\,x\sqrt{2}+4\,{x}^{2}+1}}}+\frac{1}{2}\,{\frac{-\,\sqrt{2}+4\,x}{\sqrt{-2\,x\sqrt{2}+4\,{x}^{2}+1}}}+\varepsilon f(x,\delta )y, \end{aligned}$$
(47)

where \(f(x,\delta )=a_0+a_1\,x+\cdots +a_7\,x^7+a_8\,x^{8}\) and \(\delta =(a_0,a_1,\ldots ,a_8)\in {\mathbb {R}}^9\).

We have the following theorem.

Theorem 3.1

System (47) can have 13 limit cycles.

Proof

System (45) has a nilpotent saddle at A(0, 0), two centers at \(C_1(x^*, 0)\) and \(C_2(-x^*,0)\) with \(x^*=0.9013700925\), and a double homoclinic loop \(L_0= {\bar{L}}_0 \cup {\tilde{L}}_0\) passing through the nilpotent saddle A, defined by \(H(x, y) = 0\), where \({\bar{L}}_0 = L_0{|}_{x\ge 0}\) and \({\tilde{L}}_0 = L_0{|}_{x\le 0}\). Note that, by (46), we have that

$$\begin{aligned}&{\bar{L}}_0 : y^2=-\,2{\,x}^{2}+\,\sqrt{2\,x\sqrt{2}+4\,{x}^{2}+1}+\,\sqrt{-2\,x\sqrt{2}+4\,{x}^{2}+1}-2,\quad 0\le x \le \root 4 \of {3},\\&{\tilde{L}}_0 : y^2=-\,2{\,x}^{2}+\,\sqrt{2\,x\sqrt{2}+4\,{x}^{2}+1}+\,\sqrt{-2\,x\sqrt{2}+4\,{x}^{2}+1}-2,\quad -\root 4 \of {3}\le x \le 0. \end{aligned}$$

From Proposition 2.2, we know that

$$\begin{aligned} c_0(\delta )&= M(0,\delta )=\oint _{{\bar{L}}_0}f(x)y\,dx=\sum _{i=0}^{8}\,a_i\,I_i,\quad {\tilde{c}}_0(\delta ) = {\tilde{M}}(0,\delta )=\oint _{{\tilde{L}}_0}f(x)y\,dx=\sum _{i=0}^{8}\,a_i\,{\tilde{I}}_i,\\ c_{3}(\delta )&=\oint _{{\bar{L}}_0}\sum _{i=2}^na_ix^i\,dt=\sum _{i=2}^{8}\,a_i\,J_i,\quad {\tilde{c}}_{3}(\delta ) =\oint _{{\tilde{L}}_0}\sum _{i=2}^na_ix^i\,dt=\sum _{i=2}^{8}\,a_i\,{\tilde{J}}_i, \end{aligned}$$

where

$$\begin{aligned} I_i&=\oint _{{\bar{L}}_0}x^iy\,dx=2\int _{0}^{\root 4 \of {3}}\,x^i\,\sqrt{-\,2{\,x}^{2}+\,\sqrt{2\,x\sqrt{2}+4\,{x}^{2}+1}+\,\sqrt{-2\,x\sqrt{2}+4\,{x}^{2}+1}-2}\,dx,\\ {\tilde{I}}_i&=\oint _{{\tilde{L}}_0}x^iy\,dx=2\int _{-\root 4 \of {3}}^{0}\,x^i\,\sqrt{-\,2{\,x}^{2}+\,\sqrt{2\,x\sqrt{2}+4\,{x}^{2}+1}+\,\sqrt{-2\,x\sqrt{2}+4\,{x}^{2}+1}-2}\,dx,\\ J_i&=\oint _{{\bar{L}}_0}x^i\,dt=2\int _{0}^{\root 4 \of {3}}\frac{\,x^i}{\sqrt{-\,2{\,x}^{2}+\,\sqrt{2\,x\sqrt{2}+4\,{x}^{2}+1}+\,\sqrt{-2\,x\sqrt{2}+4\,{x}^{2}+1}-2}}\,dx,\\ {\tilde{J}}_i&=\oint _{{\tilde{L}}_0}x^i\,dt=2\int _{-\root 4 \of {3}}^{0}\frac{\,x^i}{\sqrt{-\,2{\,x}^{2}+\,\sqrt{2\,x\sqrt{2}+4\,{x}^{2}+1}+\,\sqrt{-2\,x\sqrt{2}+4\,{x}^{2}+1}-2}}\,dx. \end{aligned}$$

Using Maple we find that

$$\begin{aligned} I_0&={\tilde{I}}_0=0.8520193230, \quad I_1=-{\tilde{I}}_1=0.6927396352, \quad I_2={\tilde{I}}_2=0.6267093568, \;\;\\ I_3&=-{\tilde{I}}_3=0.6080411464,\quad I_4={\tilde{I}}_4=0.6195116802, \quad I_5=-{\tilde{I}}_5=0.6542775182,\\ I_6&={\tilde{I}}_6=0.7101531116, \quad I_7=-{\tilde{I}}_7=0.7875161356, \quad I_8={\tilde{I}}_8=0.8884959544, \end{aligned}$$

and

$$\begin{aligned} J_2&={\tilde{J}}_2=4.774680819, \quad J_3=-{\tilde{J}}_3=4.715807320, \quad J_4={\tilde{J}}_4=5.253456626,\\ J_5&=-{\tilde{J}}_5=6.124821684\quad J_6={\tilde{J}}_6=7.321105054, \quad J_7=-{\tilde{J}}_7=8.892929226,\\ J_8&={\tilde{J}}_8=10.92543392. \end{aligned}$$

Consequently, we obtain that

$$\begin{aligned} c_0&=\,0.8520193230\,a_{{0}}+ 0.6927396352\,a_{{1}}+ 0.6267093568\,a_{{2}}+ 0.6080411464\,a_{{3}}+ 0.6195116802\,a_{{4}}\\&\quad + 0.6542775182\,a_{{5}}+ 0.7101531116\,a_{{6}}+ 0.7875161356\,a_{{7}}+ 0.8884959544\,a_{{8}},\\ {\tilde{c}}_0&=\,0.8520193230\,a_{{0}}- 0.6927396352\,a_{{1}}+ 0.6267093568\,a_{{2}}- 0.6080411464\,a_{{3}}+ 0.6195116802\,a_{{4}}\\&\quad - 0.6542775182\,a_{{5}}+0.7101531116\,a_{{6}}- 0.7875161356\,a_{{7}}+ 0.8884959544\,a_{{8}},\\ c_3&=\,4.774680819\,a_{{2}}+ 4.715807320\,a_{{3}}+ 5.253456626\,a_{{4}}+ 6.124821684\,a_{{5}}+ 7.321105054\,a_{{6}}\\&\quad + 8.892929226\,a_{{7}}+10.92543392\,a_{{8}},\\ {\tilde{c}}_3&=\,4.774680819\,a_{{2}} - 4.715807320\,a_{{3}}+ 5.253456626\,a_{{4}}- 6.124821684\,a_{{5}}+ 7.321105054\,a_{{6}}\\&\quad - 8.892929226\,a_{{7}}+10.92543392\,a_{{8}}. \end{aligned}$$

Furthermore, from Proposition 2.2, we get that,

$$\begin{aligned} c_1&=-2.233794126\, a_0,\quad c_2=-\frac{1}{6}\sqrt{3}\, a_1,\quad c_4=0.3750381616\, a_0+0.5000508821\, a_2,\\ c_5&=1.650968872\, a_0+0.2659278720\, a_2+0.2127422976\, a_4,\\ c_6&=0.4570689630\, a_1+0.7216878361\, a_3+0.4811252243\, a_5. \end{aligned}$$

Finally, we calculate the coefficients \(b_j\), \(j = 0,1,\cdots \), in (39). First, by introducing the transformation \((x,y) = (X-x^*,Y)\), we shift \(C_1(x^*,0)\) to the origin. Then (rewriting again X as x and Y as y) we get,

$$\begin{aligned} {\dot{x}}&=y,\nonumber \\ {\dot{y}}&=-2\,(x+x^*)+\frac{1}{4}\,{\frac{2\,\sqrt{2}+8\,(x+x^*)}{\sqrt{2\,(x+x^*)\sqrt{2}+4\,{(x+x^*)}^{2}+1}}}\nonumber \\&\quad +\frac{1}{4}\,{\frac{-2\,\sqrt{2}+8\,(x+x^*)}{\sqrt{-2\,(x+x^*)\sqrt{2}+4\,{(x+x^*)}^{2}+1}}}+\varepsilon {\hat{f}}(x)y, \end{aligned}$$
(48)

where

$$\begin{aligned} {\hat{f}}(x)=f(x+x^*,\delta )={\hat{a}}_0+{\hat{a}}_1\,x+\cdots +{\hat{a}}_8\,x^8. \end{aligned}$$

For \(\varepsilon =0\) the Hamiltonian function of system (48) is,

$$\begin{aligned} {\bar{H}}(x,y)&=\frac{1}{2}\,{y}^{2}+{(x+x^*)}^{2}-\frac{1}{2}\,\sqrt{2\,(x+x^*)\sqrt{2}+4\,{(x+x^*)}^{2}+1}\\&\quad -\frac{1}{2}\,\sqrt{-2\,(x+x^*)\sqrt{2}+4\,{(x+x^*)}^{2}+1}+1.1433077145. \end{aligned}$$

By the formulas of \(b_j\), in (40) for \(j=0,1\), we obtain

$$\begin{aligned} b_0&=\,1.157557250\,\sqrt{2}\,\pi \left( a_{{0}}+ 0.9013700925\,a_{{1}}+0.8124680437\,a_{{2}}+ 0.7323343957\,a_{{3}}+ 0.6601043220\,a_{{4}}\right. \\&\quad \left. +0.5949982938\,a_{{5}}+ 0.5363136671\,a_{{6}}+ 0.4834170997\,a_{{7}}+0.4357377159\,a_{{8}}\right) ,\\ b_1&=\,\pi \left( 1.783836705\,a_{{0}}- 0.4279155516\,a_{{1}}+ 1.031864517\,a_{{2}}+ 5.139643557\,a_{{3}}+ 11.06971485\,a_{{4}}\right. \\&\quad + 18.16201114\,a_{{5}}+25.89465002\,a_{{6}}+ 33.86056122\,a_{{7}}+ 41.74763006\,a_{{8}}\left. \right) . \end{aligned}$$

By introducing the transformation \((x,y) = (X+x^*,Y)\), we shift \(C_2(-x^*,0)\) to the origin. Then (rewriting again X as x and Y as y) we get,

$$\begin{aligned} {\dot{x}}&=y,\nonumber \\ {\dot{y}}&=-2\,(x-x^*)+\frac{1}{4}\,{\frac{2\,\sqrt{2}+8\,(x-x^*)}{\sqrt{2\,(x-x^*)\sqrt{2}+4\,{(x-x^*)}^{2}+1}}}\nonumber \\&\quad +\frac{1}{4}\,{\frac{-2\,\sqrt{2}+8\,(x-x^*)}{\sqrt{-2\,(x-x^*)\sqrt{2}+4\,{(x-x^*)}^{2}+1}}}+\varepsilon {\bar{f}}(x)y, \end{aligned}$$
(49)

where,

$$\begin{aligned} {\bar{f}}(x)=f(x-x^*,\delta )={\bar{a}}_0+{\bar{a}}_1\,x+\cdots +{\bar{a}}_8\,x^8. \end{aligned}$$

For \(\varepsilon =0\) the Hamiltonian function of system (49) is,

$$\begin{aligned} {\bar{H}}(x,y)=&\frac{1}{2}\,{y}^{2}+{(x-x^*)}^{2}-\frac{1}{2}\,\sqrt{2\,(x-x^*)\sqrt{2}+4\,{(x-x^*)}^{2}+1}\\&-\frac{1}{2}\,\sqrt{-2\,(x-x^*)\sqrt{2}+4\,{(x-x^*)}^{2}+1}+1.1433077145. \end{aligned}$$

By the formulas of \(b_j\), in (40) for \(j=0,1\), we obtain

$$\begin{aligned} {\bar{b}}_0&=1.157557248\,\sqrt{2} \,\pi \left( a_{{0}}- 0.9013700925\,a_{{1}}+ 0.8124680437\,a_{{2}}-0.7323343957\,a_{{3}}+ 0.6601043220\,a_{{4}}\right. \\&\quad \left. -0.5949982938\,a_{{5}}+ 0.5363136671\,a_{{6}}- 0.4834170997\,a_{{7}}+0.4357377159\,a_{{8}}\right) ,\\ {\bar{b}}_1&=\,\pi \left( - 0.1663960129\,a_{{1}}+ 0.3889846550\,a_{{2}}- 1.060341107\,a_{{3}}+ 2.041024002\,a_{{4}}- 3.219541028\,a_{{5}}\right. \\&\quad \left. + 4.507717919\,a_{{6}}- 5.836755818\,a_{{7}}+ 7.153881753\,a_{{8}}+ 0.5653947622\,a_{{0}}\right) .\\ \end{aligned}$$
  1. (i)

    We can find \(\delta _0=(0, 0, \,a_2^*, \,a_3^*, \,a_4^*, \,a_5^*, \,a_6^*, \,a_7^*, \,a_8)\) with

    $$\begin{aligned} a_2^*&= -1.462202842\,a_8,\quad a_3^*= -0.4461010105\,a_8,\quad a_4^*= 3.733915692\,a_8,\\ a_5^*&=0.7592286090\,a_8,\quad a_6^*= -3.218072410\,a_8,\quad a_7^*=-0.2863413586\,a_8, \end{aligned}$$

    such that \((c_0, {\tilde{c}}_0, c_1, c_2, c_3, {\tilde{c}}_3, b_0, {\bar{b}}_0)(\delta _0)=(0, 0, 0, 0, 0, 0, 0, 0)\), and

    $$\begin{aligned} c_4(\delta _0)=-0.7311758210\,a_8,\quad b_1(\delta _0)= 0.041997177\,\pi \,a_8,\quad {\bar{b}}_1(\delta _0)=-0.600087669\,\pi \,a_8. \end{aligned}$$

    Hence, for \(h_1 =-1.143307714+\varepsilon _1\), \(h_2 =0+\varepsilon _2\), \(h_3 =-1.143307714+\varepsilon _3\), \(h_4 =0+\varepsilon _4\) with \(\varepsilon _1\), \(\varepsilon _2\), \(\varepsilon _3\) and \(\varepsilon _4\) positive and sufficiently small, we have

    $$\begin{aligned} M_1(h_1,\delta _0)&=b_1(\delta _0)h_1^2+O\left( h_1^3\right) >0,\quad M(h_2,\delta _0)=c_4(\delta _0)|h_2|^{\frac{5}{4}}+O\left( |h_2|^{\frac{7}{4}}\right)<0,\\ M_2(h_3,\delta _0)&={\bar{b}}_1(\delta _0)\,h_3^2+O\left( h_3^2\right)<0,\quad {\widetilde{M}}(h_4,\delta _0)=c_4(\delta _0)|h_4|^{\frac{5}{4}}+O\left( |h_4|^{\frac{7}{4}}\right) <0. \end{aligned}$$

    Therefore, \(\frac{1-sgn(M_1(h_1,\delta _0)M(h_2,\delta _0))}{2}=1\) and \(\frac{1-sgn(M_2(h_3,\delta _0){\widetilde{M}}(h_4,\delta _0))}{2}=0\). Also, an easy computation shows that

    $$\begin{aligned} rank\frac{\partial (c_0(\delta ),{\tilde{c}}_0(\delta ),c_1(\delta ),c_2(\delta ),c_3(\delta ),{\tilde{c}}_3(\delta ),b_0(\delta ),{\bar{b}}_0(\delta ))}{\partial (a_0,a_1,a_2,a_3,a_4,a_5,a_6,a_7)}\Big |_{\delta =\delta _0}=8. \end{aligned}$$

    Thus, by Theorem 2.6 there exists some \((a_0, a_1, a_2, a_3, a_4, a_5, a_6, a_7, a_8)\) near \(\delta _0\) such that system (47) has 11 limit cycles, from which eight limit cycles are near the double homoclinic loop \(L_0\), one limit cycle is near the center \(C_1\), one limit cycle is near the center \(C_2\) and one limit cycle lies between \(C_1\) and \({\bar{L}}_0\).

  2. (ii)

    We can find \(\delta _0=(0, 0, 0, \,a_3^*, \,a_4^*, \,a_5^*, \,a_6^*, \,a_7^*, \,a_8)\) with

    $$\begin{aligned} a_3^*&= -2.130496054\,a_8,\quad a_4^*= 1.55819359\,a_8,\quad a_5^*= 3.625935646\,a_8,\\ a_6^*&=-2.610444224\,a_8,\quad a_7^*= -1.367513456\,a_8, \end{aligned}$$

    such that \((c_0, {\tilde{c}}_0, c_1, c_2, c_3, {\tilde{c}}_3, c_4, b_0)(\delta _0)=(0, 0, 0, 0, 0, 0, 0, 0)\), and

    $$\begin{aligned} c_5(\delta _0)=0.3314936861\,a_8,\quad b_1(\delta _0) = -0.00063048\,\pi \,a_8,\quad {\bar{b}}_0(\delta _0) = 0.1483763082\,\sqrt{2}\,\pi \,a_8. \end{aligned}$$

    Thus, for \(h_1 =-1.143307714+\varepsilon _1\), \(h_2 =0+\varepsilon _2\), \(h_3 =-1.143307714+\varepsilon _3\), \(h_4 =0+\varepsilon _4\) with \(\varepsilon _1\), \(\varepsilon _2\), \(\varepsilon _3\) and \(\varepsilon _4\) positive and sufficiently small, we have

    $$\begin{aligned} M_1(h_1,\delta _0)&=b_1(\delta _0)h_1^2+O\left( h_1^3\right)<0,\quad M(h_2,\delta _0)=c_5(\delta _0)|h_2|^{\frac{7}{4}}+O\left( |h_2|^2\ln |h_2|\right)>0,\\ M_2(h_3,\delta _0)&={\bar{b}}_0(\delta _0)\,h_3+O\left( h_3^2\right) <0,\quad {\widetilde{M}}(h_4,\delta _0)=c_5(\delta _0)|h_4|^{\frac{7}{4}}+O\left( |h_4|^2\ln |h_4|\right) >0. \end{aligned}$$

    Hence, \(\frac{1-sgn(M_1(h_1,\delta _0)M(h_2,\delta _0))}{2}=1\) and \(\frac{1-sgn(M_2(h_3,\delta _0){\widetilde{M}}(h_4,\delta _0))}{2}=1\). Also, an easy computation shows that

    $$\begin{aligned} rank\frac{\partial (c_0(\delta ),{\tilde{c}}_0(\delta ),c_1(\delta ),c_2(\delta ),c_3(\delta ),{\tilde{c}}_3(\delta ),c_4(\delta ),{b}_0(\delta ))}{\partial (a_0,a_1,a_2,a_3,a_4,a_5,a_6,a_7)}\Big |_{\delta =\delta _0}=8. \end{aligned}$$

    Therefore, by Theorem 2.7, there exists some \((a_0, a_1, a_2, a_3, a_4, a_5, a_6, a_7, a_8)\) near \(\delta _0\) such that system (47) has 13 limit cycles, from which ten limit cycles are near the double homoclinic loop \(L_0\), one limit cycle is near the center \(C_1\), one limit cycle lies between \(C_1\) and \({\bar{L}}_0\) and one limit cycle lies between \(C_2\) and \({\tilde{L}}_0\).

  3. (iii)

    We can find \(\delta _0=(0, 0, 0, \,a_3^*, \,a_4^*, \,a_5^*, \,a_6^*, \,a_7^*, \,a_8)\) with

    $$\begin{aligned} a_3^*&= 2.14389217\,a_8,\quad a_4^*= 1.558193598\,a_8,\quad a_5^*=-3.648734787\,a_8,\\ a_6^*&=-2.610444224\,a_8,\quad a_7^*= 1.376112101\,a_8, \end{aligned}$$

    such that \((c_0, {\tilde{c}}_0, c_1, c_2, c_3, {\tilde{c}}_3, c_4, {\tilde{b}}_0)(\delta _0)=(0, 0, 0, 0, 0, 0, 0, 0)\), and

    $$\begin{aligned} c_5(\delta _0)=0.3314936861\,a_8,\quad b_0(\delta _0)=-10.45484998\,\sqrt{2}\,\pi \,a_8,\quad {\bar{b}}_1(\delta _0)=0.009010108\,\pi \,a_8. \end{aligned}$$

    In consequently, for \(h_1 =-1.143307714+\varepsilon _1\), \(h_2 =0+\varepsilon _2\), \(h_3 =-1.143307714+\varepsilon _3\), \(h_4 =0+\varepsilon _4\) with \(\varepsilon _1\), \(\varepsilon _2\), \(\varepsilon _3\) and \(\varepsilon _4\) positive and sufficiently small, we have

    $$\begin{aligned} M_1(h_1,\delta _0)&=b_0(\delta _0)h_1+O\left( h_1^2\right)>0,\quad M(h_2,\delta _0)=c_5(\delta _0)|h_2|^{\frac{7}{4}}+O\left( |h_2|^2\ln |h_2|\right)>0,\\ M_2(h_3,\delta _0)&={\bar{b}}_1(\delta _0)\,h_3^2+O\left( h_3^3\right)>0,\quad {\widetilde{M}}(h_4,\delta _0)=c_5(\delta _0)|h_4|^{\frac{7}{4}}+O\left( |h_4|^2\ln |h_4|\right) >0. \end{aligned}$$

    Then \(\frac{1-sgn(M_1(h_1,\delta _0)M(h_2,\delta _0))}{2}=0\) and \(\frac{1-sgn(M_2(h_3,\delta _0){\widetilde{M}}(h_4,\delta _0))}{2}=0\). Also, an easy computation shows that,

    $$\begin{aligned} rank\frac{\partial (c_0(\delta ),{\tilde{c}}_0(\delta ),c_1(\delta ),c_2(\delta ),c_3(\delta ),{\tilde{c}}_3(\delta ),c_4(\delta ),{\tilde{b}}_0(\delta ))}{\partial (a_0,a_1,a_2,a_3,a_4,a_5,a_6,a_7)}\Big |_{\delta =\delta _0}=8. \end{aligned}$$

    Therefore, by Theorem 2.7, there exists some \((a_0, a_1, a_2, a_3, a_4, a_5, a_6, a_7, a_8)\) near \(\delta _0\) such that system (47) has 11 limit cycles, from which ten limit cycles are near the double homoclinic loop \(L_0\) and one limit cycle is near the center \(C_2\). \(\square \)