The Limit Cycles of the Higgins–Selkov Systems

Abstract

In this paper, we investigate the problem of limit cycles for general Higgins–Selkov systems with degree $n+1$. In particular, we first prove the uniqueness of limit cycles for a general Liénard system, which allows for discontinuity. Then, by changing the Higgins–Selkov systems into Liénard systems, theorems and some techniques for Liénard systems can be applied. After, we prove the nonexistence of limit cycles if the bifurcation parameter is outside an open interval. Finally, we complete the analysis of limit cycles for the Higgins–Selkov systems showing its uniqueness.

1 Introduction and Main Results

In the qualitative theory of planar polynomial differential systems, it is well known how difficult is to study the famous Hilbert’s 16th problem, see Ilyashenko (2002), Li (2003) and Zhang et al. (1992). Up to now there are seldom works having solved the problem of exact number of limit cycles for polynomial differential systems.

The most important physiological function of carbohydrates is to provide energy for organisms’ life activities. Glucose catabolism is the main way for organisms to obtain energy. There are three main pathways for the oxidative decomposition of glucose in organisms. Among them, the anaerobic oxidation of glucose is called glycolysis. We consider the following polynomial differential system of arbitrary degree

$$\begin{aligned} \begin{array}{l} \dot{x}=1-xy^n, \\ \dot{y}=ay(-1+xy^{n-1}) \end{array} \end{aligned}$$

(1)

which was proposed first by Higgins (1964) and modified further by Selkov (1968) for studying the biological nonlinear glycolytic oscillations, and was called the Higgins–Selkov system. Here n is a positive integer and a is a real parameter. Artés et al. (2018) characterized the global dynamics described in the Poincaré disc for system (1) as $n=2$ and $a\in {\mathbb {R}} \backslash (1,3)$. Moreover, there are two conjectures stated in Artés et al. (2018) on the the number of limit cycles of systems (1) when $a\in (1,3)$. After, Chen and Tang (2019) proved these conjectures, which complete the global phase portraits of system (1) when $n=2$.

Recently, Brechmann and Rendall (2018) researched the uniqueness of limit cycles for system (1) and additionally proved that no limit cycles exist when $a\in (0,1/(n-1))$. Llibre and Mousavi (2021) classified the phase portraits of system (1) for $n= 3, 4, 5, 6$ in the Poincaré disc for all the values of the parameter a and determined in function of the parameter a the regions of the phase space with biological meaning.

The aim of this paper is to give a clearer study and answer for the existence and the exact number of limit cycles of system (1). We have the following main results.

Theorem 1

For every positive integer $n\ge 3$, there exists a unique constant $a^*\in (1/(n-1), (2^n-1)/(2^n-2))$ such that system (1) has no periodic orbits when $a\in (-\infty , 1/(n-1)]\cup [a^*, +\infty )$ and has a unique limit cycle when $a\in (1/(n-1), a^*)$, which is stable and hyperbolic. Moreover, when the limit cycle exists, its amplitude increases with a.

Remark that the bifurcation diagrams of the limit cycles for system (1) are similar to those in Fig. 1 for $n=3,5$ and in Fig. 2 for $n=4,6$ of Llibre and Mousavi (2021), respectively.

An outline of this paper is as follows: A theorem on the uniqueness of limit cycles for general Liénard systems is presented in Sect. 2, which we need in our study of the limit cycles of the Higgins–Selkov system. In Sect. 3, we obtain the existence and the exact number of limit cycles of the Higgins–Selkov system and then prove our main theorem.

2 Preliminaries

In order to study the number of limit cycles for system (1), we need the following preliminary results. We first recall the uniqueness theorem of Zhang (1958) or in Zhang (1986) on the number of limit cycles of the following generalized Liénard systems

$$\begin{aligned} \begin{array}{l} \dot{x}= -\phi (y)-{\hat{F}}(x), \\ \dot{y}= {\hat{g}}(x). \end{array} \end{aligned}$$

(2)

Let

$$\begin{aligned} {\hat{G}}(x):=\int _0^x{\hat{g}}(s)\mathrm{d}s. \end{aligned}$$

Theorem 2

Consider the generalized Liénard system (2) for $x\in (-\infty , +\infty )$, when $\phi (y)$, ${\hat{F}}(x)$ and ${\hat{g}}(x)$ satisfy the following conditions:

• (i) ${\hat{g}}(x)$ is Lipschitz in any finite interval, $x\hat{g}(x)>0$ for all $x\ne 0$, and ${\hat{G}}(-\infty )={\hat{G}}(+\infty )=+\infty$.

• (ii) ${\hat{f}}(x)=\hat{F}'(x)$ is ${\mathcal {C}}^0$, ${\hat{F}}(0)=0$, ${\hat{f}}(x)/{\hat{g}}(x)$ is nondecreasing in $(-\infty ,0)\cup (0,+\infty )$ and ${\hat{f}}(x)/{\hat{g}}(x)$ is not a constant when |x| is small.

• (iii) $\phi (y)$ is Lipschitz in any finite interval, $y\phi (y)>0$ for all $y\ne 0$, $\phi (y)$ is nondecreasing, $\phi (-\infty )=-\infty$, $\phi (+\infty )=+\infty$, $\phi (y)$ has right-derivative $\phi _+'(0)$ and left-derivative $\phi _-'(0)$ at $y=0$, $\phi _-'(0)\phi _+'(0)\ne 0$ when ${\hat{f}}(0)=0$.

Then system (2) has at most one limit cycle. Moreover the limit cycle is stable when it exists.

In fact, we can find many differential systems of the form (2), but many of them do not satisfy the conditions of Theorem 2. Thus we propose the following three questions:

• (a) When ${\hat{G}}(-\infty )={\hat{G}}(+\infty )\ne +\infty$ and the other conditions of Theorem 2 hold, does the conclusion of Theorem 2 still hold?

• (b) When either ${\hat{f}}(x)$ or ${\hat{g}}(x)$ has a discontinuity point $x_0$ of the second kind (i.e., $\lim _{x\rightarrow x_0+}{\hat{g}}(x)$ or $\lim _{x\rightarrow x_0-}{\hat{g}}(x)$ does not exist) and the other conditions of Theorem 2 hold, does the conclusion of Theorem 2 still hold?

• (c) When ${\hat{g}}(x)$ has a discontinuity point at $x=0$ of the first kind (i.e., $\lim _{x\rightarrow 0+}{\hat{g}}(x) \ne \lim _{x\rightarrow 0-}{\hat{g}}(x)$) and the other conditions of Theorem 2 hold, does the conclusion of Theorem 2 still hold?

For example, we have that $G(-\infty )=G(+\infty )\ne +\infty$ when ${\hat{g}}(x)=x/(1+x^2)^2$. Either ${\hat{f}}(x)$ or ${\hat{g}}(x)$ has a discontinuity point at $x=-1$ of the second kind when ${\hat{f}}(x)=1/a-(n-1)/(x+1)^n$ or ${\hat{g}}(x)=x/(x+1)^n$.

Here we will show why the condition $G(-\infty )=G(+\infty )=+\infty$ is necessary in the proof of Theorem 2 of Zhang (1986). Zhang (1986) only need to research the following special Liénard system

$$\begin{aligned} \begin{array}{l} \dot{u}= -\phi (y)-{\hat{F}}(x(u)), \\ \dot{y}= u, \end{array} \end{aligned}$$

(3)

because system (2) can be changed into system (3) through the transformation $u=\sqrt{2G(x)}\mathrm{Sgn}(x)$ and $\mathrm{d}t\rightarrow \big (\sqrt{2G(x)}\mathrm{sgn} (x)/{\hat{g}}(x)\big )\mathrm{d}t$. However, the transformation is not an 1–1 transformation in $(-\infty , +\infty )$ when $G(-\infty )=G(+\infty )\ne +\infty$.

For these reasons, we give the following theorem without the aforementioned conditions.

Theorem 3

Consider system (2) in the interval $(\alpha ,\beta )$, where $\alpha$ and $\beta$ eventually can be $-\infty$ and $+\infty$, respectively. Assume that $\phi (y)$, ${\hat{F}}(x)$ and ${\hat{g}}(x)$ satisfy the following conditions:

• (i) ${\hat{g}}(x):=g_0(x)+c ~\mathrm{sgn}(x)$, $x\hat{g}(x)>0$ for all $x\ne 0$, where $c\ge 0$ and $g_0(x)$ is Lipschitz in any finite interval and $g_0(0)=0$.

• (ii) ${\hat{f}}(x)=\hat{F}'(x)$ is ${\mathcal {C}}^0(\alpha ,\beta )$, ${\hat{F}}(0)=0$, ${\hat{f}}(0)\ne 0$, ${\hat{f}}(x)/{\hat{g}}(x)$ is nondecreasing in $(\alpha ,0)\cup (0,\beta )$ and ${\hat{f}}(x)/{\hat{g}}(x)$ is not a constant when |x| is small.

• (iii) $\phi (y)$ is Lipschitz in any finite interval, $y\phi (y)>0$ for all $y\ne 0$, $\phi (y)$ is increasing, $\phi (-\infty )=-\infty$, $\phi (+\infty )=+\infty$, $\phi (y)$ has right-derivative $\phi _+'(0)$ and left-derivative $\phi _-'(0)$ at $y=0$, $\phi _-'(0)\phi _+'(0)\ne 0$ when ${\hat{f}}(0)=0$.

Then system (2) has at most one limit cycle in $(\alpha ,\beta )$. Moreover the limit cycle is stable when it exists.

Proof

Since the vector field of system (2) is Lipschitz for $c=0$, its solutions exist and are unique except at $x=0$. Since the vector field of system (2) is discontinuous at the line $\Sigma :=\{(x,y): x=0\}$ for $c>0$, we need to study the dynamics on $\Sigma$ and we will adapt the Filippov method, see di Bernardo et al. (2008) and Kuznetsov et al. (2003). Let

$$\begin{aligned} \delta := \langle (1,0), (-\phi (y), -c) \rangle \langle (1,0), (-\phi (y), c) \rangle =\phi ^2(y), \end{aligned}$$

where $\langle \cdot , \cdot \rangle$ denotes the inner product. As defined in di Bernardo et al. (2008) and Kuznetsov et al. (2003), the crossing set is

$$\begin{aligned} \Sigma _c=\{(x,y)\in \Sigma : \delta >0 \}=\{(x,y)\in \Sigma : y\ne 0 \}. \end{aligned}$$

The sliding set $\Sigma _s$ is the complement to $\Sigma _c$, which is given by

$$\begin{aligned} \Sigma _s=\{(x,y)\in \Sigma : \delta \le 0 \}=\{(x,y)\in \Sigma : y=0 \}. \end{aligned}$$

Therefore except at the origin, all orbits crossing any point are unique. In other words, all periodic orbits are crossing.

Assume that $\gamma$ is a periodic orbit of system (2). Then we have that $\gamma$ is hyperbolic if $\oint _{\gamma }\mathrm{div}( -\phi (y)- {\hat{F}}(x),{\hat{g}}(x))\mathrm{d}t\ne 0$, see, for instance, Theorem 1.23 of Dumortier et al. (2006). Moreover, $\gamma$ is stable (resp. unstable) if

$$\begin{aligned} \oint _{\gamma }\mathrm{div}(-\phi (y)-{\hat{F}}(x),{\hat{g}}(x))\mathrm{d}t<0 ~(\mathrm{resp.}~ >0). \end{aligned}$$

In order to prove the uniqueness of limit cycles of system (2), assume that system (2) has at least two limit cycles, where $\gamma _1$, $\gamma _2$ are the innermost limit cycles and $\gamma _1$ lies in the bounded region surrounded by $\gamma _2$.

Actually we must have ${\hat{f}}(0)<0$. Otherwise, if ${\hat{f}}(0)>0$ we can obtain ${\hat{f}}(x)>0$ since ${\hat{f}}(x)/{\hat{g}}(x)$ is nondecreasing and $x{\hat{g}}(x)>0$. For $x>0$ near the origin, we can get ${\hat{f}}(x)>0$ by the continuity of ${\hat{f}}(x)$ at $x=0$ and then ${\hat{f}}(x)/{\hat{g}}(x)>0$, implying ${\hat{f}}(x)/{\hat{g}}(x)>0$ for all $x>0$ by the monotonicity of this function. Thus, we have ${\hat{f}}(x)>0$ for all $x>0$. Similarly for all $x<0$ we can also get ${\hat{f}}(x)>0$. Then, by Green formula we have

$$\begin{aligned} 0=\oint _{\gamma _i}(-\phi (y)-{\hat{F}}(x))\mathrm{d}y+{\hat{g}}(x)\mathrm{d}x=-\oint _{{\mathcal D}_i}{\hat{f}}(x)\mathrm{d}x\mathrm{d}y, \end{aligned}$$

which contradicts the fact that ${\hat{f}}(x)>0$, where ${\mathcal D}_i$ is the bounded region surrounded by $\gamma _i$ for $i=1,2$. Here, note that the Dulac criterion cannot be applied because the vector field of system (2) is not ${\mathcal {C}}^1$. Thus, we get ${\hat{f}}(0)< 0$ if a periodic orbit exists.

Moreover, we claim that the equation ${\hat{f}}(x)=0$ has at most one positive root and one negative root, where a connect set of roots is viewed as one root. Otherwise, assume that ${\hat{f}}(x)$ has two positive zeros $x_1$ and $x_2$ such that $0<x_1<x_2$. Then, there exists a real $x_0\in (x_1,x_2)$ satisfying ${\hat{f}}(x_0)/{\hat{g}}(x_0)>0={\hat{f}}(x_2)/{\hat{g}}(x_2)$, which contradicts the nondecreasing of ${\hat{f}}(x)/{\hat{g}}(x)$. Thus, the claim is proved.

Applying Green formula again, we have that system (2) has no periodic orbits when ${\hat{f}}(x)\le 0$ for all $x\in (\alpha ,\beta )$. Therefore, if system (2) exhibits periodic orbits, there is an $x_3\in (\alpha ,\beta )$ such that ${\hat{f}}(x_3)>0$. In the following, we divide the proof of the uniqueness of limit cycles of system (2) in three cases.

Case (I) First, we consider the case $x_3>0$ if ${\hat{f}}(x_3)>0$. Then, there is a unique value $x_4\in (0,\beta )$ such that ${\hat{F}}(x_4)=0$. Moreover, if there exist two different points $x_{41}, x_{42} \in (0,\beta )$ such that ${\hat{F}}(x_{41})=0$ and ${\hat{F}}(x_{42})=0$, we can get an ${\tilde{x}}_4\in (x_{41}, x_{42})$ satisfying ${\hat{f}}({\tilde{x}}_4)=0$, which contradicts the nondecreasing of ${\hat{f}}(x)/{\hat{g}}(x)$ for $x>0$.

We claim that any periodic orbit must surround the point $(x_4, 0)$. So no periodic orbits exist if $x_4$ does not exist. Let

$$\begin{aligned} E(x,y)=\int _0^y \phi (s)ds+\int _0^x \hat{g}(s)ds \end{aligned}$$

(4)

which implies that

$$\begin{aligned} \dfrac{\mathrm{d}E(x,y)}{\mathrm{d}t}=-{\hat{g}}(x){\hat{F}}(x). \end{aligned}$$

It is to note that ${\hat{g}}(x){\hat{F}}(x)<0$ for all $x\in (\alpha ,x_4)$. Assume that system (2) exhibits a periodic orbit $\gamma$, which lies in the strip $x\in (\alpha ,x_4)$. Then, we can find that

$$\begin{aligned} 0=\oint _{\gamma }\mathrm{d}E=\oint _{\gamma }-{\hat{g}}(x){\hat{F}}(x)\mathrm{d}t>0. \end{aligned}$$

Thus, the claim is proved.

Now we will prove that

$$\begin{aligned} \oint _{\gamma _1}{\hat{f}}(x)\mathrm{d}t<\oint _{\gamma _2}{\hat{f}}(x)\mathrm{d}t. \end{aligned}$$

(5)

Fig. 1

Limit cycles of system (2) in the Case (I)

Consider the two limit cycles $\gamma _1=\widehat{A_1B_1C_1D_1H_1I_1A_1}$ and $\gamma _2=\widehat{A_2B_2C_2D_2H_2I_2A_2}$ of Fig. 1. Notice that the limit cycle $\gamma _i$ intersects the graphic of the function $y=\phi ^{-1}(-{\hat{F}}(x))$ at the points $C_i$ and $I_i$ for $i=1,2$, respectively. Since

$$\begin{aligned} \oint _{\gamma _1}{\hat{g}}(x)\mathrm{d}t=\oint _{\gamma _1}\mathrm{d}y=0=\oint _{\gamma _2} \mathrm{d}y=\oint _{\gamma _2}{\hat{g}}(x)\mathrm{d}t, \end{aligned}$$

we only need to prove

$$\begin{aligned} \oint _{\gamma _1} f_1(x)\mathrm{d}t<\oint _{\gamma _2} f_1(x)\mathrm{d}t, \end{aligned}$$

(6)

which is equivalent to (5), where

$$\begin{aligned} f_1(x):={\hat{f}}(x)+b{\hat{g}}(x) \end{aligned}$$

(7)

for any constant $b\in {\mathbb {R}}$. It is clear that $f_1(x)/{\hat{g}}(x)$ is still nondecreasing if $f(x)/{\hat{g}}(x)$ is nondecreasing. Fixing

$$\begin{aligned} b=-{\hat{f}}(x_{I_1})/{\hat{g}}(x_{I_1})<0, \end{aligned}$$

we have $f_1(x_{I_1})=0$. Moreover, we have $f_1(x)/{\hat{g}}(x)\ge 0$ for $x_{I_1}<x<0$ and $f_1(x)/{\hat{g}}(x)\le 0$ for $x<x_{I_1}$, because $f_1(x_{I_1})/{\hat{g}}(x_{I_1})=0$ and $f_1(x)/{\hat{g}}(x)$ is nondecreasing. Thus, $f_1(x)\le 0$ if $x_{I_1}<x<0$, and $f_1(x)\ge 0$ if $x<x_{I_1}$, because ${\hat{g}}(x)<0$ for $x<0$.

Denote by $P=(x_P, y_P)$ for an arbitrary point P. We can find a point $J_1(x_{J_1},y_{J_1})$ in the curve $y=\phi ^{-1}(-{\hat{F}}(x))$ such that $f_1(x_{J_1})=0$ and $x_{J_1}\in (0, x_{C_1})$. Otherwise, $f_1(x)<0$ for all $x\in (0, x_{C_1})$, and if the point $J_1$ does not exist, then $f_1(x)\le 0$ for all $x\in (x_{I_1}, x_{C_1})$. Thus, we obtain

$$\begin{aligned} \oint _{\gamma _1} f_1(x)\mathrm{d}t<0. \end{aligned}$$

(8)

However, the origin is a source and the periodic orbit $\gamma _1$ is internally stable because $f_1(x)<0$ for small x, implying $\oint _{\gamma _1} f_1(x)\mathrm{d}t\ge 0$. It induces a contradiction with inequality (8). Thus, the point $J_1$ exists. Moreover, we have $f_1(x)\ge 0$ for $x>x_{J_1}$, and $f_1(x)\le 0$ for all $0<x<x_{J_1}$, because ${\hat{g}}(x)>0$ for $x>0$ and $f_1(x)/{\hat{g}}(x)$ is nondecreasing.

Assume that the line $x=x_{J_1}$ intersects with the graphic of the function $y=\phi ^{-1}(-{\hat{F}}(x))$ at the points $B_i$ and $D_i$ for $i=1,2$, respectively. Notice that

$$\begin{aligned} x_{B_1}=x_{B_2}=x_{D_1}=x_{D_2}=x_{J_1}. \end{aligned}$$

Let $y=y_1(x)$ and $y=y_2(x)$ be the orbit segments $\widehat{A_1B_1}$ and $\widehat{A_2B_2}$, respectively. Since $y_1<y_2$ and the function $\phi (x)$ is increasing, we have $\phi (y_1)<\phi (y_2)$. Then, we have

$$\begin{aligned} \begin{array}{rl} \displaystyle \int _{\widehat{B_1A_1}} f_1(x)\mathrm{d}t-\int _{\widehat{B_2A_2}} f_1(x)\mathrm{d}t =&{}\displaystyle \int _0^{x_{B_1}}\dfrac{f_1(x)}{\phi (y_1)+ {\hat{F}}(x)}\mathrm{d}x-\int _0^{x_{B_2}}\dfrac{ f_1(x)}{\phi (y_2)+{\hat{F}}(x)}\mathrm{d}x\\ =&{}\displaystyle \int _0^{x_{B_1}}\dfrac{ f_1(x)(\phi (y_2)-\phi (y_1))}{(\phi (y_1)+{\hat{F}}(x))(\phi (y_2)+{\hat{F}}(x))}<0. \end{array} \end{aligned}$$

(9)

It is similar to prove that

$$\begin{aligned} \begin{array}{l} \displaystyle \int _{\widehat{H_1D_1}}f_1(x)\mathrm{d}t-\int _{\widehat{H_2D_2}} f_1(x)\mathrm{d}t<0, \\ \displaystyle \int _{\widehat{A_1I_1}} f_1(x)\mathrm{d}t-\int _{\widehat{A_2P_2}} f_1(x)\mathrm{d}t<0, \\ \displaystyle \int _{\widehat{I_1H_1}}f_1(x)\mathrm{d}t-\int _{\widehat{Q_2H_2}}f_1(x)\mathrm{d}t<0, \end{array} \end{aligned}$$

(10)

where $P_2, Q_2\in \gamma _2$ and $x_{P_2}=x_{Q_2}=x_{I_1}$.

Let $x=x_1(y)$ and $x=x_2(y)$ be the orbit segments $\widehat{D_1C_1B_1}$ and $\widehat{D_2C_2B_2}$, respectively. Then, we have

$$\begin{aligned} \begin{array}{rl} \displaystyle \int _{\widehat{D_1C_1B_1}} f_1(x)\mathrm{d}t- \displaystyle \int _{\widehat{D_2C_2B_2}} f_1(x)\mathrm{d}t<&{} \displaystyle \int _{\widehat{D_1C_1B_1}}{\hat{f}}(x)\mathrm{d}t- \displaystyle \int _{\widehat{M_2N_2}}{\hat{f}}(x)\mathrm{d}t \\ =&{} \displaystyle \int _{y_{M_2}}^{y_{N_2}}\left( \dfrac{{\hat{f}}(x_1)}{{\hat{g}}(x_1)}-\dfrac{{\hat{f}}(x_2)}{{\hat{g}}(x_2)}\right) \mathrm{d}y<0, \end{array} \end{aligned}$$

(11)

where $M_2, N_2\in \gamma _2$, $y_{M_2}=y_{D_1}$ and $y_{N_2}=y_{B_1}$. Since $f_1(x)\ge 0$ for all $x<x_{I_1}$, we have

$$\begin{aligned} \int _{\widehat{P_2I_2Q_2}} f_1(x)\mathrm{d}t>0. \end{aligned}$$

(12)

Therefore, (6) holds from (9)–(12). Notice that the origin is a source and the periodic orbit $\gamma _1$ is internally stable. Thus, $\oint _{\gamma _1}{\hat{f}}(x)\mathrm{d}t\ge 0$. It follows from (5) that $\oint _{\gamma _2}{\hat{f}}(x)\mathrm{d}t>0$. Consequently, $\gamma _2$ is stable and hyperbolic. By the Poincaré–Bendixson theorem [see for instance Corollary 1.30 of Dumortier et al. (2006)], it is impossible for the existence of two consecutive stable limit cycles. Therefore, system (2) has at most two limit cycles. Moreover, $\gamma _1$ is semi-stable and $\gamma _2$ is stable if they exist.

In order to induce a contradiction for the case that $\gamma _1$ is semi-stable, we construct an auxiliary vector field $(-\phi (y)-{{\tilde{F}}}(x),{\hat{g}}(x))$, where ${{\tilde{F}}}(x)={\hat{F}}(x)+\epsilon R(x)$ and

$$\begin{aligned} R(x):=\left\{ \begin{array}{ll} 0, &{} \mathrm{if} ~x\le x_4, \\ {\hat{F}}(x), &{}\mathrm{if} ~x> x_4, \end{array} \right. \end{aligned}$$

for small $|\epsilon |$. We can check that the vector field $(-\phi (y)-{{\tilde{F}}}(x),{\hat{g}}(x))$ is rotated with respect to the parameter $\epsilon$; see Zhang et al. (1992, Chapter 4.3) or Perko (1975). Consider the following system

$$\begin{aligned} \begin{array}{l} \dot{x}= -\phi (y)-{{\tilde{F}}}(x), \\ \dot{y}= {\hat{g}}(x). \end{array} \end{aligned}$$

(13)

System (13) is exactly system (2) if $\epsilon =0$. Moreover, we can check that system (13) still satisfies all assumptions of Theorem 3. In other words, system (13) has at most two limit cycles. Further, we can find that $\gamma _1$ will split into at least two limit cycles for $\epsilon <0$ by Zhang et al. (1992, Theorem 3.4 of Chapter 4). Then, system (13) can have three limit cycles, a contradiction with the previous result. Therefore, we have proven that system (2) has at most one periodic orbit in the case $x_3>0$ if ${\hat{f}}(x_3)>0$.

Fig. 2

Limit cycles of system (2) in the Case (III)

Case (II) Second, we consider the case that there must be $x_3<0$ if ${\hat{f}}(x_3)>0$. Since the proof is similar to the Case (I), we omit it.

Case (III) We consider the case that $x_3$ can be negative or positive if ${\hat{f}}(x_3)>0$. We claim that the equation ${\hat{F}}(x)=0$ has either one nonzero root or two nonzero roots. Notice that the equation ${\hat{F}}(x)=0$ cannot have two positive roots or two negative roots. Otherwise if there exist two different points $x_{41}, x_{42} \in (0,\beta )$ or $\in (\alpha , 0)$ such that ${\hat{F}}(x_{41})=0$ and ${\hat{F}}(x_{42})=0$, we can get a point ${\tilde{x}}_4\in (x_{41}, x_{42})$ satisfying ${\hat{f}}({\tilde{x}}_4)=0$, which contradicts the nondecreasing of the function ${\hat{f}}(x)/{\hat{g}}(x)$. On the other hand, if the equation ${\hat{F}}(x)=0$ has not nonzero roots, we get $\mathrm{d}E/\mathrm{d}t\ge 0$ for $x\in (\alpha , \beta )$ from (4), implying that no periodic orbits exist. If the equation ${\hat{F}}(x)=0$ has a unique nonzero root, we consider that the nonzero root is $x_+\in (0,\beta )$ for simplicity. If system (2) has a periodic orbit, it must surround $(x_+, 0)$. Otherwise, this is a contradiction with the fact that $\mathrm{d}E/\mathrm{d}t\ge 0$. When equation ${\hat{F}}(x)=0$ has one positive root $x_+\in (0,\beta )$ and a negative root $x_-\in (\alpha , 0)$, if system (2) has a periodic orbit, it must surround at least one of the points $(x_+, 0)$ and $(x_-,0)$. Otherwise again we have a contradiction with the fact that $\mathrm{d}E/\mathrm{d}t\ge 0$. Without loss of generality, we can assume that any limit cycle surrounds $(x_+,0)$.

Assume that system (2) has three limit cycles $\gamma _1,\gamma _2,\gamma _3$ as the ones shown in Fig. 2, where $\gamma _1$ is the innermost one, $\gamma _3$ surrounds $\gamma _1$ and $\gamma _2$, the points $A_i,B_i,C_i, D_i, H_i$, $I_i J_i,K_i\in \gamma _i$, the periodic orbit $\gamma _i$ intersects the graphic of the function $y=\phi ^{-1}(-{\hat{F}}(x))$ at the points $C_i$ and $J_i$ for $i=1,2, 3$, respectively. Notice that

$$\begin{aligned}&x_{B_i}=x_{D_i}, \quad x_{A_i}=x_{H_i}=0, \quad x_{K_2}=x_{K_3}=x_{I_2}=x_{I_3}=x_{J_4}, \\&f(x_{B_i})=0, \quad f(x_{J_4})=0, \quad \alpha<x_{J_3}<x_{J_2}<x_{J_4}<x_{J_1}<0, \end{aligned}$$

for $i=1, 2, 3$.

In a similar way to the proof of Case (I), we shall obtain that system (2) has at most one periodic orbit in the strip $x\in (x_{J_4},\beta )$. Moreover, the periodic orbit is stable if it exists. Now we shall prove that

$$\begin{aligned} \oint _{\gamma _1}{\hat{f}}(x)\mathrm{d}t<\oint _{\gamma _2}{\hat{f}}(x)\mathrm{d}t<\oint _{\gamma _3}{\hat{f}}(x)\mathrm{d}t. \end{aligned}$$

(14)

Notice that the function $y=\phi (x)$ has the same properties as in Case (I) when $x>0$, as it is shown in Figs. 1 and 2. Thus, we can obtain that

$$\begin{aligned} \begin{array}{l} \int _{\widehat{H_1C_1A_1}}{\hat{f}}(x)\mathrm{d}t< \int _{\widehat{H_2C_2A_2}}{\hat{f}}(x)\mathrm{d}t, \\ \int _{\widehat{H_2C_2A_2}}{\hat{f}}(x)\mathrm{d}t < \int _{\widehat{H_3C_3A_3}}{\hat{f}}(x)\mathrm{d}t. \end{array} \end{aligned}$$

(15)

To prove the first inequality of (14), it suffices to prove inequality (6). Using the auxiliary function $f_1(x)$ in (7) for the Case (I) again, we can prove that

$$\begin{aligned} \int _{\widehat{A_1J_1H_1}} f_1(x)\mathrm{d}t<\int _{\widehat{A_2J_2H_2}} f_1(x)\mathrm{d}t. \end{aligned}$$

(16)

From (15) and (16), we get

$$\begin{aligned} \oint _{\gamma _1}{\hat{f}}(x)\mathrm{d}t<\oint _{\gamma _2}{\hat{f}}(x)\mathrm{d}t. \end{aligned}$$

(17)

Moreover, we can calculate that

$$\begin{aligned}&\int _{\widehat{A_2K_2}} {\hat{f}}(x)\mathrm{d}t-\int _{\widehat{A_3K_3}} {\hat{f}}(x)\mathrm{d}t<0, \nonumber \\&\int _{\widehat{K_2J_2I_2}} {\hat{f}}(x)\mathrm{d}t-\int _{\widehat{K_3J_3I_3}} {\hat{f}}(x)\mathrm{d}t<0, \\&\int _{\widehat{I_2H_2}} {\hat{f}}(x)\mathrm{d}t-\int _{\widehat{I_3H_3}} {\hat{f}}(x)\mathrm{d}t<0 \nonumber \end{aligned}$$

(18)

doing a similar calculation as in Case (I) for $x>0$. Thus, from (15) and (18), we get the second inequality of (14), i.e.,

$$\begin{aligned} \oint _{\gamma _2}{\hat{f}}(x)\mathrm{d}t<\oint _{\gamma _3}{\hat{f}}(x)\mathrm{d}t. \end{aligned}$$

(19)

It follows from (17) and (19) that (14) holds. Since the origin is a source, we have

$$\begin{aligned} \oint _{\gamma _1}{\hat{f}}(x)\mathrm{d}t\ge 0,\quad \text{ implying } \quad \oint _{\gamma _2}{\hat{f}}(x)\mathrm{d}t>0 \quad \text{ and }\quad \oint _{\gamma _3}{\hat{f}}(x)\mathrm{d}t>0, \end{aligned}$$

from inequality (14). However, it is impossible to have two consecutive stable limit cycles. Therefore, system (2) cannot have three periodic limit cycles and there are at most two limit cycles.

We divide the rest of the proof in two subcases. First, we consider the subcase that $\gamma _1$ only surrounds one of the points $(x_+, 0)$ and $(x_-, 0)$. In Case (I), we have proved that for this kind of periodic orbits, as $\gamma _1$, at most one can exist, and it is stable. Thus, its consecutive periodic orbit $\gamma _2$ is internally unstable and then $\oint _{\gamma _2}{\hat{f}}(x)\mathrm{d}t\le 0$. Moreover inequality (17) holds and $\gamma _2$ is stable, indicating a contradiction. Therefore, the periodic orbit $\gamma _2$ does not exist and system (2) has exact one periodic orbit $\gamma _1$ if such periodic orbit exists.

Now we consider the subcase that system (2) has no such kind of periodic orbits like $\gamma _1$. We assume that system (2) has two periodic orbits $\gamma _2$ and $\gamma _3$, which surround both points $(x_+, 0)$ and $(x_-, 0)$. Since the origin is a source, we have

$$\begin{aligned} \oint _{\gamma _2}{\hat{f}}(x)\mathrm{d}t\ge 0, \quad \text{ implying } \quad \oint _{\gamma _3}{\hat{f}}(x)\mathrm{d}t>0, \end{aligned}$$

by inequality (19). Therefore, $\gamma _2$ is semi-stable and $\gamma _3$ is stable. Using the auxiliary vector field (13) again, we can get that system (13) still satisfies all conditions of this theorem and has at most two limit cycles. However, by the rotated properties of system (13), the semi-stable $\gamma _2$ will split into at least two limit cycles for $\epsilon \ne 0$ by Zhang et al. (1992, Theorem 3.4 of Chapter 4). Then, system (13) can have three limit cycles, a contradiction. Thus, we have proven that system (2) has at most one periodic orbit in the case (III) and the proof is completed. $\square$

Remark 4

The conditions $\phi (-\infty )=-\infty$, $\phi (+\infty )=+\infty$ are needed only if $(\alpha , \beta )$ is unbounded. If $(\alpha , \beta )$ is a bounded interval, these conditions can be deleted in Theorem 3.

Notice that the vector field is Lipschitz if $c=0$ in Theorem 3. Thus, the results of Theorem 3 also hold when system (2) is Lipschitz or further smooth.

The modified Liénard system (21) of the Higgins–Selkov (1) is Lipschitz except at the line $x=1$, which is a discontinuity point of the second kind for the functions in the system. So we need to apply Theorem 3 for showing the uniqueness of the limit cycles.

3 Proof of Theorem 1

Notice that system (1) cannot have periodic orbits when $a\le 0$, because the unique equilibrium (1, 1) is a saddle as $a<0$ or ${\dot{y}}\equiv 0$ as $a=0$. Thus, in the following we only consider the case $a> 0$. Moreover, the periodic orbits of system (1) must lie in the region

$$\begin{aligned} \{(x,y)\in {\mathbb {R}}^2 ~|~ x>0, y>0\}, \end{aligned}$$

since the x-axis is invariant and ${\dot{x}}|_{x=0}=1$.

In order to simplify the computations and the analysis we do the following change of coordinates

$$\begin{aligned} (x,y,t)\rightarrow \left( \dfrac{y_1-x_1}{a}, x_1, \dfrac{t_1}{a}\right) , \end{aligned}$$

changing system (1) into

$$\begin{aligned} \begin{array}{l} \dot{x}_1=-x_1+\dfrac{x_1^n y_1}{a} -\dfrac{x_1^{n+1}}{a}, \\ \dot{y}_1= 1-x_1. \end{array} \end{aligned}$$

(20)

Obviously the periodic orbit of system (20) only exists in the region $x_1>0$, because $\dot{y}_1= 1>0$ and $\dot{x}_1=0$ on the line $x_1=0$. Moreover, system (20) can be changed into the following Liénard system

$$\begin{aligned} \begin{array}{l} \dot{x}=y-F(x), \\ \dot{y}=-g(x), \end{array} \end{aligned}$$

(21)

where

$$\begin{aligned} F(x):=\dfrac{1}{(x+1)^{n-1}} +\dfrac{x}{a} -1 \quad \text{ and } \quad g(x):= \dfrac{x}{a (x+1)^n}, \end{aligned}$$

doing the transformation $(x_1,y_1, t_1)\rightarrow \left( x+1, ay+(a+1),t/(x+1)^n \right)$. Here we only need to consider $x>-1$ for the problem of limit cycles of system (21), because system (21) is equivalent to system (1) as $a>0$ and $x>-1$. Note that $x=-1$ is a discontinuous line for system (21).

From Brechmann and Rendall (2018) system (21) has no periodic orbits when $a\in (0, 1/(n-1))$. In the following, we prove that system (21) may have periodic orbits only if $a> 1/(n-1)$. Here we cannot use the methods of Chen and Tang (2019), because it is difficult to decide when the equations

$$\begin{aligned} \dfrac{g(z_1)}{ f(z_1)}=\dfrac{g(z_2)}{f(z_2)} ~\mathrm{and}~ F(z_1)= F(z_2), \end{aligned}$$

have solutions or not for an arbitrary integer n. We need to use a new method and technique.

Proposition 5

For $a>0$, the amplitude of the stable or unstable limit cycle of system (21) surrounding the origin varies monotonically with respect to the parameter a.

Proof

Notice that we can change system (21) into the following equivalent form

$$\begin{aligned} \begin{array}{l} \dot{x}=y-{\check{F}}(x), \\ \dot{y}=-a g(x) \end{array} \end{aligned}$$

(22)

by the transformation of coordinates $(x,y,t)\rightarrow \Big (x, y/\sqrt{a}, \sqrt{a}t \Big )$, where

$$\begin{aligned} F(x):=\sqrt{a}\Big (\dfrac{1}{(x+1)^{n-1}}-1\Big ) +\dfrac{x}{\sqrt{a}}. \end{aligned}$$

From the calculation in Llibre and Mousavi (2021), we have the value of the following determinant

$$\begin{aligned}&\left| \begin{array}{ll} y- \left( \sqrt{a_1}\Big (\dfrac{1}{(x+1)^{n-1}}-1\Big ) +\dfrac{x}{\sqrt{a_1}} \right) &{} -\dfrac{x}{(x+1)^n} \\ y- \left( \sqrt{a_2}\Big (\dfrac{1}{(x+1)^{n-1}}-1\Big ) +\dfrac{x}{\sqrt{a_2}} \right) &{} -\dfrac{x}{(x+1)^n} \end{array} \right| \\&\quad = (\sqrt{a_1}-\sqrt{a_2})\left( \frac{x\Big (1-(x+1)^{n-1}\Big )}{(x+1)^{2 n-1}}-\frac{1}{\sqrt{a_1 a_2}} \frac{x^{2}}{(x+1)^n}\right) \le 0 \end{aligned}$$

for $a_2<a_1$, $a_2, a_1\in (0, +\infty )$ and $x>-1$.

Thus, the vector field of system (22) is a generalized rotated vector field [see Zhang et al. (1992, Chapter 4.3) or Perko (1975)] with respect to the parameter a if $x>-1$. Moreover, from Zhang et al. (1992, Theorem 3.5, Chapter 4), the amplitude of the stable or unstable limit cycle of system (22) surrounding the origin varies monotonically with respect to the positive parameter a. $\square$

Proposition 6

System (21) has no periodic orbits when $a\in (-\infty , 1/(n-1)]$.

Proof

By Artés et al. (2018) and Chen and Tang (2019), system (21) has no periodic orbits for $a\le 1$ when $n=2$. In the rest of this proof, we only consider $n\ge 3$. We only need to consider system (21) and its limit cycles in the region $x>-1$. Assume that

$$\begin{aligned} F(x_1)=F(x_2),~G(x_1)=G(x_2) \end{aligned}$$

(23)

for $n\ge 3$ and $-1<x_1<0<x_2$, where

$$\begin{aligned} G(x) :=\int _0^x g(s)\mathrm{d}s=\dfrac{1}{a(n-1)(n-2)} -\dfrac{n x-x+1}{a(x+1)^{n-1}(n-1)(n-2)} . \end{aligned}$$

It follows from (23) that

$$\begin{aligned} \dfrac{1}{(x_1+1)^{n-1}}+\dfrac{x_1}{a}-1= & {} \dfrac{1}{(x_2+1)^{n-1}}+\dfrac{x_2}{a}-1,\dfrac{1}{(2-n)} \dfrac{1}{(x_1+1)^{n-2}}+\dfrac{1}{(n-1)} \nonumber \\ \end{aligned}$$

(24)

$$\begin{aligned} \dfrac{1}{(x_1+1)^{n-1}}= & {} \dfrac{1}{(2-n)} \dfrac{1}{(x_2+1)^{n-2}}+\dfrac{1}{(n-1)} \dfrac{1}{(x_2+1)^{n-1}}. \end{aligned}$$

(25)

From (24), we have

$$\begin{aligned}&\dfrac{1}{(x_1+1)^{n-1}}-\dfrac{1}{(x_2+1)^{n-1}}=-\dfrac{x_1-x_2}{a} \end{aligned}$$

(26)

$$\begin{aligned} \Leftrightarrow&\dfrac{1}{(x_1+1)^{n-2}} =-\dfrac{(x_1+1)(x_1-x_2)}{a}+\dfrac{x_1+1}{(x_2+1)^{n-1}}. \end{aligned}$$

(27)

Furthermore, it follows from (25) and (26) that

$$\begin{aligned} \dfrac{1}{(2-n)} \left( \dfrac{1}{(x_1+1)^{n-2}}-\dfrac{1}{(x_2+1)^{n-2}} \right)= & {} \dfrac{1}{(n-1)} \left( \dfrac{1}{(x_2+1)^{n-1}}-\dfrac{1}{(x_1+1)^{n-1}}\right) \nonumber \\= & {} \dfrac{x_1-x_2}{a(n-1)}. \end{aligned}$$

(28)

Moreover, we calculate from (27) and (28) that

$$\begin{aligned} \begin{array}{l} \dfrac{1}{(2-n)} \left( - \dfrac{(x_1+1)(x_1-x_2)}{a}+\dfrac{x_1+1}{(x_2+1)^{n-1}}-\dfrac{1}{(x_2+1)^{n-2}} \right) =\dfrac{x_1-x_2}{a(n-1)}, \\ \dfrac{1}{(2-n)} \left( -\dfrac{(x_1+1)(x_1-x_2)}{a}+\dfrac{1}{(x_2+1)^{n-1}}(x_1-x_2) \right) =\dfrac{x_1-x_2}{a(n-1)},\\ \dfrac{1}{(2-n)} \left( -\dfrac{(x_1+1)}{a}+\dfrac{1}{(x_2+1)^{n-1}} \right) =\dfrac{1}{a(n-1)}, \\ x_1=\dfrac{a}{(x_2+1)^{n-1}}-\dfrac{1}{n-1}. \end{array} \end{aligned}$$

(29)

Substituting (29) into (24), we have

$$\begin{aligned} \dfrac{1}{\Big (\dfrac{a}{(x_2+1)^{n-1}}+\dfrac{n-2}{n-1}\Big )^{n-1}}- \dfrac{1}{a(n-1)}-\dfrac{x_2}{a}=0. \end{aligned}$$

(30)

Let

$$\begin{aligned} H(x,a):=\dfrac{1}{\Big (\dfrac{a}{(x+1)^{n-1}}+\dfrac{n-2}{n-1}\Big )^{n-1}}- \dfrac{x}{a}-\dfrac{1}{a(n-1)}. \end{aligned}$$

(31)

Then, we have that

$$\begin{aligned} \dfrac{\mathrm{d}H}{\mathrm{d}x}(x,a)= \dfrac{a(n-1)^2}{ H_1^n(x,a)} -\dfrac{1}{a}, \end{aligned}$$

(32)

where

$$\begin{aligned} H_1(x,a)=\Big (\dfrac{a}{(x+1)^{n-1}}+ \dfrac{n-2}{n-1}\Big ) (x+1). \end{aligned}$$

Now we consider the case $a=1/(n-1)$. From (31) and (32), we get

$$\begin{aligned} H(x, 1/(n-1))=\dfrac{1}{\Big (\dfrac{1}{(n-1)(x+1)^{n-1}}+\dfrac{n-2}{n-1}\Big )^{n-1}}-(n-1)x-1 \end{aligned}$$

and

$$\begin{aligned} \dfrac{\mathrm{d}H}{\mathrm{d}x}(x, 1/(n-1))= \dfrac{n-1}{H_1^n(x, 1/(n-1))} -(n-1), \end{aligned}$$

where

$$\begin{aligned} H_1(x, 1/(n-1))=\Big (\dfrac{1}{(n-1)(x+1)^{n-1}}+\dfrac{n-2}{n-1}\Big ) (x+1). \end{aligned}$$

Then, we claim that

$$\begin{aligned} \dfrac{\mathrm{d}H}{\mathrm{d}x}(x, 1/(n-1)) <0. \end{aligned}$$

Actually, we have

$$\begin{aligned} \dfrac{\mathrm{d}H_1}{\mathrm{d}x}(x, 1/(n-1))= & {} \Big (\dfrac{1}{(n-1)(x+1)^{n-2}}+\dfrac{n-2}{n-1}(x+1) \Big )' \\= & {} \dfrac{n-2}{n-1} \Big (\dfrac{-1}{(x+1)^{n-1}}+1 \Big )>0, \end{aligned}$$

for $n\ge 3$ and $x\ge 0$, implying $\min \{ H_1(x, 1/(n-1))\}_{x\ge 0} =H_1(0, 1/(n-1))=1$. Thus, we get $H'(x, 1/(n-1))\le 0$ and then

$$\begin{aligned} \max \{H(x, 1/(n-1))\}_{x\ge 0}=H(0, 1/(n-1))=0. \end{aligned}$$

In other words, Eq. (30) has no solutions for $x_2>0$, and then, Eq. (23) have no solutions $\{x_1, x_2\}$ such that $-1<x_1<0<x_2$ if $n\ge 3$ and $a=1/(n-1)$. Thus, from continuity we have $F(x_1)> F(x_2)$, or $F(x_1)< F(x_2)$ if $G(x_1)=G(x_2)$. Moreover, we have that $F(0)=0$ and $x g(x)>0$. Therefore, by Proposition 2.1 of Chen and Chen (2015), system (21) has no periodic orbits for $a=1/(n-1)$.

Now consider the case $a<1/(n-1)$. When $a\le 0$, either the unique equilibrium (1, 1) of system (1) is a saddle or the system has an invariant line through equilibrium (1, 1), which implies nonexistence of periodic orbits. The vector field of equivalent system (22) of system (21) is a generalized rotated vector field with respect to a for $x>-1$ and $a>0$ by the proof of Proposition 5. Moreover, the amplitude of the stable or unstable limit cycle surrounding the origin of (21) varies monotonically with respect to a. Assume that system (21) exhibits limit cycles for $a=a_0\in (0,1/(n-1))$, where $\gamma$ is the innermost limit cycle. Since the origin of (21) is stable, then $\gamma$ is internally unstable. Note that the amplitude of an unstable limit cycle decreases as a increases by Zhang et al. (1992, Theorem 3.5, Chapter 4). When a increases from $a=a_0$ to $a=1/(n-1)$, the origin keeps stability. Therefore, $\gamma$ does not disappear for $a=1/(n-1)$. This is a contradiction to our above analysis as $a=1/(n-1)$, and the proof is completed. $\square$

When

$$\begin{aligned} a=a_n:=\dfrac{2^n-1}{2^n-2}, \end{aligned}$$

we give the following lemma for the region where periodic orbits exist. Obviously, $a_n>1$ for $n\ge 3$.

Proposition 7

When $a=a_n$ for $n\ge 3$, periodic orbits of system (21) only exist in the strip $x\in (-1, 1.6)$.

Proof

Note that any periodic orbit of system (1) must lie in the first quadrant and the y-axis of system (1) is changed into the line $y=x-1$ of system (21). Therefore, the periodic orbits of system (21) cannot intersect the line $y=x-1$.

Assume that $\Gamma$ is a periodic orbit of system (21) and $\Gamma$ intersects with the curve $y=F(x)$ at the point $(x^*, F(x^*))$ in the right half-plane. Then, $x\le x^*$ as $(x,y)\in \Gamma$. If $x^*\le 1$, we have that $\Gamma$ lies in the strip $x\in (-1, 1]$ and this lemma is proven. In the following, we consider the case $x^*> 1$.

Let $y={{\tilde{y}}}(x)<F(x)$ denote the orbit segment of $\Gamma$ as $0\le x\le x^*$. For $x\ge 1$ and $a=a_n$, we have that ${{\tilde{y}}}(x)>x-1$ and

$$\begin{aligned} \frac{\mathrm{d}{{\tilde{y}}}(x)}{\mathrm{d}x}=\frac{g(x)}{F(x)-{{\tilde{y}}}(x)}>\frac{g(x)}{F(x)-x+1} \ge x, \end{aligned}$$

(33)

which implies

$$\begin{aligned} {{\tilde{y}}}(x)<\frac{1}{2}(x^2-(x^*)^2)+{{\tilde{y}}}(x^*) \end{aligned}$$

(34)

for $1\le x<x^*$. Actually, the inequality $g(x)/(F(x)-x+1)\ge x$ in (33) is equivalent to the inequality

$$\begin{aligned} a\ge \frac{\varphi _1(x)}{\varphi _2(x)}, \end{aligned}$$

(35)

where $\varphi _1(x)=x-\frac{1}{(x+1)^n}$ and $\varphi _2(x)=x-\frac{1}{(x+1)^{n-1}}$. Notice that for $x\ge 1$ we get the maximum value of the positive function $\varphi _1(x)-\varphi _2(x)$ at $x=1$, implying that the function $\varphi _1(x)/\varphi _2(x)$ has its maximum value $a_n$ also at $x=1$ and the inequality (33) is obtained.

We can find that the curve

$$\begin{aligned} \Upsilon : y=\frac{1}{2}x^2-\frac{1}{2} \end{aligned}$$

is tangent to the line $y=x-1$ at the point (1, 0). Moreover, the curves $\Upsilon$ and $y=F(x)$ have a unique intersection point at $({\tilde{x}}^*, {\tilde{y}}^*)$ for $x\ge 1$. Actually, from $F(x)=y=\frac{1}{2}x^2-\frac{1}{2}$ and $a=a_n$ we get that

$$\begin{aligned} P(x):= \frac{1}{(x+1)^{n-1}}+\frac{(2^n-2)x}{2^n-1}-\frac{x^2}{2}-\frac{1}{2}=0. \end{aligned}$$

Applying

$$\begin{aligned} P'(x)=(1-n)\frac{1}{(x+1)^n}+\frac{2^n-2}{2^n-1}-x<0 \end{aligned}$$

for $x\ge 1$, $P(1)=(2^{n-1}-1)/(2^{2n-1}-2^{n-1})>0$ and $P(1.6)=2.6^{1-n}-0.18-1.6/(2^n-1)<0$, we get a unique value ${\tilde{x}}^*$ such that $P({\tilde{x}}^*)=0$ and $1<{\tilde{x}}^*<1.6$.

In the following, we prove that $x^*< {\tilde{x}}^*$. Otherwise, if $x^*\ge {\tilde{x}}^*$, we have $-(x^*)^2/2+{{\tilde{y}}}(x^*)\le -1/2$, inducing

$$\begin{aligned} {{\tilde{y}}}(x)<\frac{1}{2}(x^2-(x^*)^2)+{{\tilde{y}}}(x^*)\le \frac{1}{2} x^2 -\frac{1}{2} \end{aligned}$$

for $x=1$ by (34). Hence, we can obtain that the curve $y={{\tilde{y}}}(x)$ has intersection points with the line $y=x-1$, indicating a contradiction. Therefore, $x^*<{\tilde{x}}^*$. In other words, the periodic orbits of system (21) must lie in the region $x\in (-1, 1.6)$. The lemma is proven. $\square$

Proposition 8

System (21) has no periodic orbits when $a\ge a_n$ for $n\ge 3$.

Proof

By Artés et al. (2018) and Chen and Tang (2019), there is a $a^*\in (1,3)$ such that system (21) has no periodic orbits for $a>a^*$ when $n=2$. When $n=3$ and $a=a_n$, we can calculate numerically that the function H(x, a) in (31) has not zeros as x lies between ${\tilde{x}}^*$ and the positive zero of F(x), where the curves $\Upsilon$ and $y=F(x)$ intersect at $({\tilde{x}}^*, {\tilde{y}}^*)$ for $x\ge 1$, as shown in the proof of Proposition 7. By Proposition 2.1 of Chen and Chen (2015) system (21) has no periodic orbits when $n=3$ and $a=a_n$. In the rest of this proof, we only need consider the case $n\ge 4$.

From (32), we have that

$$\begin{aligned} \dfrac{\mathrm{d}H}{\mathrm{d}x}(x,a)= \dfrac{a(n-1)^2}{ H_1^n(x,a)} -\dfrac{1}{a} \end{aligned}$$

and

$$\begin{aligned} \frac{\mathrm{d} H_1(x,a)}{\mathrm{d}x}=-\frac{a(n-2)}{(x+1)^{n-1}}+ \dfrac{n-2}{n-1} \left\{ \begin{array}{l}<0,~0<x<x_0, \\ =0,~x=x_0, \\>0,~x>x_0, \end{array}\right. \end{aligned}$$

where

$$\begin{aligned} x_0=\root n-1 \of {a(n-1)}-1>0 \end{aligned}$$

as $a\ge a_n>1$. Further, we obtain

$$\begin{aligned} \min _{x>-1} \{H_1(x,a)\}=H_1(x_0,a), \end{aligned}$$

implying

$$\begin{aligned} \max _{x>-1} \left\{ \dfrac{\mathrm{d}H}{\mathrm{d}x}(x,a)\right\} =\dfrac{\mathrm{d}H}{\mathrm{d}x}(x_0,a)=\frac{n-1}{\root n-1 \of {a(n-1)}}-\frac{1}{a}>0. \end{aligned}$$

Moreover, we have

$$\begin{aligned} \lim _{x\rightarrow +\infty }\dfrac{\mathrm{d}H}{\mathrm{d}x}(x,a)<0 \end{aligned}$$

and

$$\begin{aligned} \dfrac{\mathrm{d}H}{\mathrm{d}x}(0,a)=\dfrac{a(n-1)^2}{ \Big (a+ \dfrac{n-2}{n-1}\Big )^n} -\dfrac{1}{a}=\frac{H_2(a)}{a \Big (a+ \dfrac{n-2}{n-1}\Big )^n}<0, \end{aligned}$$

where

$$\begin{aligned} H_2(a)=a^2(n-1)^2- \Big (a+ \dfrac{n-2}{n-1}\Big )^n, \end{aligned}$$

because

$$\begin{aligned} \frac{\mathrm{d} H_2(a)}{\mathrm{d} a}= & {} 2a(n-1)^2-n\Big (a+ \dfrac{n-2}{n-1}\Big )^{n-1}<\frac{\mathrm{d} H_2(a)}{\mathrm{d} a}|_{a=1}<0, \\ \frac{\mathrm{d}^2 H_2(a)}{\mathrm{d} a^2}= & {} 2(n-1)^2-n(n-1)\Big (a+ \dfrac{n-2}{n-1}\Big )^{n-2}<\frac{\mathrm{d}^2 H_2(a)}{\mathrm{d} a^2}|_{a=1}<0, \\ \frac{\mathrm{d}^3 H_2(a)}{\mathrm{d} a^3}= & {} -n(n-1)(n-2)\Big (a+ \dfrac{n-2}{n-1}\Big )^{n-3}<0. \end{aligned}$$

Notice that

$$\begin{aligned} H(0,a)=\dfrac{1}{\big (a+\dfrac{n-2}{n-1}\big )^{n-1}} -\dfrac{1}{a(n-1)}<0 \end{aligned}$$

from (31) and a similar discussion as $\mathrm{d}H(0,a)/\mathrm{d}x<0$.

If the inequality $H(x,a)<0$ always holds as $a\ge 1$, we can get that system (21) has no periodic orbits by Proposition 2.1 of Chen and Chen (2015) and a similar discussion as the proof of Proposition 6. So, in the following, we consider the case that there exists a value $x_*>x_0$ such that

$$\begin{aligned} \max _{x>-1} \{ H(x,a)\}= H(x_*,a)>0. \end{aligned}$$

Without loss of generality, we assume that

$$\begin{aligned} H(x_0,a)=1-\dfrac{x_0}{a}-\dfrac{1}{a(n-1)} >0. \end{aligned}$$

When $H(x_0,a)\le 0$, we can research by a similar way. Thus, there are values $x_1$ and $x_2$ such that $x_1>x_2>0$ and $H(x,a)>0$ (resp. $<0$) for $x\in (x_2,x_1)$ (resp. $x\in (0,x_2)\cup (x_1,+\infty )$) when $n\ge 4$, as shown in Fig. 3.

Fig. 3

$y=H(x,a)$

The function $F'(x)$ has a unique zero at $x=\root n \of {a(n-1)}-1>0$, and there exists a unique positive $x_3$ such that $F(x_3)=0$ and $F(x)>0$ (resp. $<0$) for $x\in (-1, 0)\cup (x_3,+\infty )$ (resp. $x\in (0,x_3)$). Letting $z_0=\root n-1 \of {a(n-1)}$, we can find that $z_0>1$ and

$$\begin{aligned} F(x_0)= & {} \frac{1}{a(n-1)}+\frac{\root n-1 \of {a(n-1)}-1}{a}-1 \\= & {} \frac{1}{z_0^{n-1}}-1+\frac{z_0-1}{a} \\= & {} (1-z_0)\left( \frac{1+z_0+\cdots +z_0^{n-2}}{z_0^{n-1}}-\frac{1}{a}\right) \\= & {} (1-z_0)\left( \frac{1+z_0+\cdots +z_0^{n-2}}{z_0^{n-1}}-\frac{n-1}{z_0^{n-1}}\right) <0, \end{aligned}$$

indicating $x_0<x_3$.

Consider the case $a=a_n>1$. Calculating the equation $F(x_3)=0$ from (21), we can let

$$\begin{aligned} x_3=\frac{(n-k(n))a_n}{n-1}, \end{aligned}$$

(36)

where $k\in (1, 1.5)$ and $k=k(n)$ is decreasing in n. Specially, $x_3=1$ as $n\rightarrow +\infty$ and $x_3 \approx 0.92$ as $n=4$. Further, by (36) we have that

$$\begin{aligned} H(x_3,a_n)= & {} \frac{1}{(1+\frac{(k-1)a_n-1}{n-1})^{n-1}}+\frac{k-n-1/a_n}{n-1} \\= & {} \dfrac{1-H_3(n)}{(1+\frac{(k-1)a_n-1}{n-1})^{n-1}}>0, \end{aligned}$$

where

$$\begin{aligned} H_3(n)= & {} \Big (1-\frac{k-1-1/a_n}{n-1}\Big )\Big (1+\frac{(k-1)a_n-1}{n-1}\Big )^{n-1} \\= & {} \Big ( 1+(1-\frac{1}{a_n})\frac{((k-1)a_n-1)}{n-1} - \frac{((k-1)a_n-1)^2}{a_n(n-1)^2} \Big )\Big (1+\frac{(k-1)a_n-1}{n-1}\Big )^{n-2} \\< & {} 1, \end{aligned}$$

because $a_n>1$ and $(k-1)a_n-1<0$. Thus, we can get $x_0<x_3<x_1$. From Proposition 7, any limit cycle of system (21) must lie in the region $\{(x,y)\in {\mathbb {R}}^2 |x<1.6\}$. Hence, we consider the solution of (23) satisfying $x_3<x<2$ for $x>0$. In order to prove $H(x,a_n)>0$ for $x_3<x<2$, we only need to show $H(2,a_n)>0$ by Fig. 3. We can compute that

$$\begin{aligned} \frac{\partial (a H(2,a))}{\partial a}=\dfrac{1-\dfrac{1}{1/(n-1)+3^{n-1}(n-2)/(a(n-1)^2)} }{\Big (a 3^{1-n}+(n-2)/(n-1)\Big )^{n-1}}>0 \end{aligned}$$

as $n> 3$ and $a\in [1, a_n+\varepsilon ]$ for small enough $\varepsilon >0$. It implies that the function aH(2, a) is increasing in a for $a\in [1, a_n+\varepsilon ]$. Thus, from $H(2,1)>0$ we can get $H(2,a_n)>0$. Moreover, we have

$$\begin{aligned} H(2,1)=\frac{1}{\left( 3^{1-n}+ \dfrac{n-2}{n-1}\right) ^{n-1}}-2-\frac{1}{n-1}=\frac{1-{\hat{H}}(n)}{\left( 3^{1-n}+ \dfrac{n-2}{n-1}\right) ^{n-1}}, \end{aligned}$$

where

$$\begin{aligned} {\hat{H}}(n) = \left( 2+\frac{1}{n-1}\right) \left( 3^{1-n}+ \dfrac{n-2}{n-1}\right) ^{n-1}. \end{aligned}$$

In the following, we prove that ${\hat{H}}(n)<1$ and then $H(2,1)>0$. First, we get

$$\begin{aligned} H_4(n)= & {} \ln \root n-1 \of { {\hat{H}}(n)} \\= & {} \frac{1}{n-1}\ln \left( 2+\frac{1}{n-1}\right) +\ln \left( 3^{1-n}+ 1-\frac{1}{n-1}\right) \\= & {} u\ln (2+u)+\ln (3^{-\frac{1}{u}}+ 1-u), \end{aligned}$$

where $u=\frac{1}{n-1}\in (0, \frac{1}{3}]$. Noticing that

$$\begin{aligned}&~{\hat{H}}(4)\le 0.814<1, ~{\hat{H}}(5)\le 0.76<1, ~{\hat{H}}(6)\le 0.74<1, \\&~{\hat{H}}(7)\le 0.738<1 , ~{\hat{H}}(8)\le 0.736<1 \end{aligned}$$

and ${\hat{H}}(n)\rightarrow \frac{2}{e}$ as $n\rightarrow +\infty$. We can only consider the case $n\ge 9$ and $u\in (0, \frac{1}{8}]$ for proving the inequality ${\hat{H}}(n)<1$. Moreover,

$$\begin{aligned} H'_4 (n)= & {} \ln (2+u)+\frac{u}{2+u}+ \frac{\frac{3^{-\frac{1}{u}}\ln 3}{u^2}-1}{3^{-\frac{1}{u}}+ 1-u} \\= & {} \xi _1(u)+\xi _2(u), \end{aligned}$$

where

$$\begin{aligned} \xi _1(u)= & {} \ln (2+u)+\frac{u}{2+u}-1, \\ \xi _2(u)= & {} \frac{3^{-\frac{1}{u}}-u +\frac{3^{-\frac{1}{u}}\ln 3}{u^2}}{3^{-\frac{1}{u}}+ 1-u} =:\frac{\xi _3(u)}{3^{-\frac{1}{u}}+ 1-u}. \end{aligned}$$

In addition, for $u\in (0, \frac{1}{8}]$ we get

$$\begin{aligned} \xi '_1(u)= & {} \frac{1}{2+u}+\frac{2}{(2+u)^2}>0, \\ \xi '_3(u)= & {} -1+ \frac{3^{-\frac{1}{u}} \ln 3}{u^2} +\frac{3^{-\frac{1}{u}}\ln ^23}{u^4}-2\frac{3^{-\frac{1}{u}}\ln 3}{u^3} \\= & {} \left( -1 +\frac{3^{-\frac{1}{u}}\ln ^23}{u^4}\right) + \frac{3^{-\frac{1}{u}} \ln 3}{u^2}\left( 1 -\frac{2}{u}\right) <0. \end{aligned}$$

It follows that

$$\begin{aligned}&\xi _1(u)\le \xi _1\left( \frac{1}{8}\right) =\ln (17/8)-16/17<0, \\&\xi _3(u)\le \lim _{u\rightarrow 0+}\xi _3(u)= 0, \end{aligned}$$

indicating $H'_4 (n)<0$ and then ${\hat{H}}(n)<1$. Therefore, we get $H(2,1)>0$ and then $H(2,a_n)>0$, implying that $H(x,a_n)>0$ for $x\in [x_3,2]$. In other words, the equations (23) have no roots for $a=a_n$. By Proposition 2.1 of Chen and Chen (2015), system (21) has no periodic orbits when $n\ge 3$ and $a=a_n$. Since the amplitude of the stable or unstable limit cycle of system (21) varies monotonically in a by Proposition 5, system (21) has no periodic orbits when $n\ge 3$ and $a\ge a_n$. $\square$

When $a\in (1/(n-1), a_n)$, we will study the existence and uniqueness of limit cycle in the following proposition.

Proposition 9

For $n\ge 3$, there exists a constant $a^*\in (1/(n-1), a_n)$ such that system (21) has a unique limit cycle when $a\in (1/(n-1), a^*)$ and no periodic orbits when $a\in (a^*, +\infty )$. Moreover, the limit cycle is stable and hyperbolic, and its amplitude increases with a.

Proof

By Zhang et al. (1992, Theorem 3.5, Chapter 4) and Proposition 5, the amplitude of the stable limit cycle surrounding the origin of (21) is monotonous with respect to a as $x>-1$ and $a>0$. From Llibre and Mousavi (2021), the Hopf bifurcation occurs and a stable limit cycle appears when a varies from $1/(n-1)$ to $1/(n-1)+\epsilon$, where $\epsilon >0$ is small. The amplitude of the stable limit cycle is sufficiently small for small enough $\epsilon >0$. Thus, the amplitude of the stable limit cycle increases as a increases.

On the other hand, system (21) has no periodic orbits when $a\in (-\infty , 1/(n-1)] \cup [a_n,+\infty )$ by Propositions 6 and 8, and has a unique finite equilibrium at the origin. Therefore, there exists $a^*\in (1/(n-1), a_n)$ such that the amplitude of the stable limit cycle approaches infinity when $a=a^*-\epsilon$ for sufficiently small $\epsilon >0$ by the continuity of the vector field and the monotonous properties of amplitude of the stable limit cycle in parameter a.

Fig. 4

Numerical phase portraits of system (1)

In the following, we will prove the uniqueness of periodic orbits when $a\in (1/(n-1), a^*)$. From system (21), we calculate

$$\begin{aligned} \dfrac{\mathrm{d}\big (f(x)/g(x)\big )}{\mathrm{d}x} = a \dfrac{n-1}{x^2}+\dfrac{((n-1) x-1) (x+1)^{n-1}}{ x^2} = \dfrac{Q(x)}{ x^2}, \end{aligned}$$

(37)

where $Q(x):=a(n-1) + ((n-1) x-1) (x+1)^{n-1}$, and

$$\begin{aligned} Q'(x):= n(n-1) x (x+1)^{n-2}. \end{aligned}$$

(38)

Notice that $Q(0)=a(n-1)-1>0$ since $a>1/(n-1)$. Moreover, it is easy to see that $Q(x)>0$ when $x\in [1/(n-1), +\infty )$. When $x\in [0, 1/(n-1))$, we get $Q'(x)\ge 0$ from (38). Thus

$$\begin{aligned} \min \{Q(x)\}_{x\in [0, 1/(n-1))}=Q(0)>0, \end{aligned}$$

inducing $Q(x)>0$ in this case. When $x\in (-1,0]$ we get $Q'(x)\le 0$ from (38). Thus,

$$\begin{aligned} \min \{Q(x)\}_{x\in (-1, 0]}=Q(0)>0, \end{aligned}$$

also inducing $Q(x)>0$ in this case. Therefore, we obtain $Q(x)>0$ when $x\in (-1, +\infty )$, and then, the function f(x)/g(x) is increasing from (37) when $x\in (-1, 0) \cup (0, +\infty )$.

Moreover, we can verify that $x g(x)>0$ for all $x\ne 0$, $F(0)=0$, $F'(0)\ne 0$ and f(x)/g(x) is not a constant when |x| is small. Hence, all conditions in Theorem 3 hold and we can get that system (21) has at most one limit cycle in $(-1, +\infty )$. Moreover, the limit cycle is stable if it exists. Notice that for our system (21), the function $\phi (y)=y$ in the general system (2). The proposition is proven. $\square$

From Propositions 5–9, we can obtain Theorem 1.

At last, some numerical examples are provided as follows to verify our theoretical results for $n=3$.

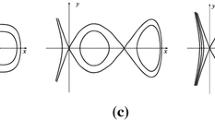
Consider parameters in the supercritical Hopf bifurcation curve of system (1) for $n=3$, i.e., $a=1/(n-1)=0.5$. Then, the unique equilibrium (1, 1) is a stable weak focus, as shown in Fig. 4a. When $a=0.55$, equilibrium (1, 1) is an unstable hyperbolic focus and the Hopf bifurcation generates a stable hyperbolic limit cycle, as shown in Fig. 4b. When $a=0.6$, equilibrium (1, 1) is still an unstable hyperbolic focus and the stable hyperbolic limit cycle disappears at infinity, as shown in Fig. 4c.