Keywords

1 Introduction

In a graph with n vertices, a k-cycle/path packing is a set of \(\frac{n}{k}\) vertex-disjoint k-cycles/paths (i.e., a simple cycle/path on k different vertices) covering all vertices. For an edge-weighted complete graph, every edge has a non-negative weight. Moreover, it is called a metric graph if the weight satisfies the triangle inequality; Otherwise, it is called a general graph. Given a (metric/general) graph, the maximum weight (metric/general) k-cycle/path packing problem (kCP/kPP) is to find a k-cycle/path packing such that the total weight of the k-cycles/paths in the packing is maximized.

When \(k=n\), kCP becomes the well-known maximum weight traveling salesman problem (MAX TSP). One may obtain approximation algorithms of kCP and kPP by using approximation algorithms of MAX TSP. In the following, we let \(\alpha \) (resp., \(\beta \)) denote the current-best approximation ratio of MAX TSP on metric (resp., general) graphs. We have \(\alpha =7/8\) [19] and \(\beta =4/5\) [9].

1.1 Related Work

For \(k=2\), kCP and kPP are equivalent with the maximum weight perfect matching problem, which can be solved in \(O(n^3)\) time [10, 20]. For \(k\ge 3\), metric kCP and kPP become NP-hard [17], and general kCP and kPP become APX-hard even on \(\{0,1\}\)-weighted graphs (i.e., a complete graph with edge weights 0 and 1) [22]. There is a large number of contributions on approximation algorithms.

General kCP. For \(k=3\), Hassin and Rubinstein [13, 14] proposed a randomized \((0.518-\varepsilon )\)-approximation algorithm, Chen et al. [7, 8] proposed an improved randomized \((0.523-\varepsilon )\)-approximation algorithm, and Van Zuylen [32] proposed a deterministic algorithm with the same approximation ratio. For lager k, Li and Yu [21] proposed a 2/3-approximation algorithm for \(k=4\) and a \(\beta \cdot (1-1/k)^2\)-approximation algorithm for \(k\ge 5\). On \(\{0,1\}\)-weighted graphs, Bar-Noy et al. [2] gave a 3/5-approximation algorithm for \(k=3\). Note that Berman and Karpinski [4] gave a 6/7-approximation algorithm for the Maximum Path Cover Problem, which seeks a set of node disjoint paths such that the number of edges in all the paths is maximal. Their algorithm could be used to obtain a \((6/7-\varepsilon )\)-approximation algorithm for general kCP and kPP with \(k=n\) on \(\{0,1\}\)-weighted graphs.

Metric kCP. For \(k=3\), Hassin et al. [15] firstly gave a deterministic 2/3-approximation algorithm and Chen et al. [5] proposed a randomized \((0.66768-\varepsilon )\)-approximation algorithm. For lager k, Li and Yu [21] proposed a 3/4-approximation algorithm for \(k=4\), a 3/5-approximation algorithm for \(k=5\), and an \(\alpha \cdot (1-1/k)^2\)-approximation algorithm for \(k\ge 6\).

General kPP. For \(k=3\), Hassin and Rubinstein [13] proposed a randomized \((0.5223-\varepsilon )\)-approximation algorithm, Chen et al. [27] proposed a deterministic \((0.5265-\varepsilon )\)-approximation algorithm, and Bar-Noy et al. [2] proposed an improved 7/12-approximation algorithm. For lager k, Hassin and Rubinstein [11] proposed a 3/4-approximation algorithm for \(k=4\), and a \(\beta \cdot (1-1/k)\)-approximation algorithm for \(k\ge 5\). On \(\{0,1\}\)-weighted graphs, Hassin and Schneider [16] gave a 0.55-approximation algorithm for \(k=3\) and the ratio was improved to 3/4 [2].

Metric kPP. Li and Yu [21] proposed a 3/4-approximation algorithm for \(k=3\), a 3/4-approximation algorithm for \(k=5\), and an \(\alpha \cdot (1-1/k)\)-approximation algorithm for \(k\ge 6\). The best-known result for \(k=4\) is still 3/4 due to the general 4PP, by Hassin and Rubinstein [11]. On \(\{1,2\}\)-weighted graphs, there is a 9/10-approximation algorithm for \(k=4\) [23].

General/metric kCP and kPP can be seen as a special case of the weighted k-set packing problem, which admits an approximation ratio of \(\frac{1}{k-1}-\varepsilon \) [1], \(\frac{2}{k+1}-\varepsilon \) [3], and \(\frac{2}{k+1-1/31850496}-\varepsilon \) [24]. Recently, these results have been further improved (see [25, 26, 28]). They can be used to obtain a \(1/1.786\approx 0.559\)-approximation ratio for general 3CP [28].

1.2 Our Results

We study approximation algorithms for metric/general kCP and kPP.

Firstly, we consider metric kCP. We propose a \((7/8-0.125/k)(1-1/k)\)-approximation algorithm for constant odd k and a \(7/8\cdot (1-1/k+\frac{1}{k(k-1)})\)-approximation algorithm for even k, which improve the best-known approximation ratio of 3/5 for \(k=5\) [21] and \(7/8\cdot (1-1/k)^2\) for \(k\ge 6\) [21]. Moreover, we propose an algorithm based on the maximum weight matching, which can further improve the approximation ratio from 17/25 to 7/10 for \(k=5\). An illustration of the improved results for metric kCP with \(k\ge 5\) can be seen in Table 1.

Table 1. Improved approximation ratios for metric kCP with \(k\ge 5\)
Full size table

Secondly, we consider metric kPP. We propose a \(\frac{27k^2-48k+16}{32k^2-36k-24}\)-approximation algorithm for even \(10\ge k\ge 6\), which improves the best-known approximation ratio of \(7/8\cdot (1-1/k)\) [11]. An illustration of the improved results for metric kPP with even \(10\ge k\ge 6\) can be seen in Table 2.

Table 2. Improved approximation ratios for metric kPP with even \(10\ge k\ge 6\)
Full size table

At last, we focus on the case of \(k=4\) for metric/general kCP and kPP. For metric 4CP, we propose a 5/6-approximation algorithm, improving the best-known ratio 3/4 [21], and as a corollary, we also give a 7/8-approximation algorithm on (1, 2)-weighted graphs. For general 4CP, we propose a 3/4-approximation algorithm, improving the best-known ratio 2/3 [21]. For metric 4PP, we propose a 14/17-approximation algorithm, improving the best-known ratio 3/4 [11]. An illustration of the improved results for the case of \(k=4\) can be seen in Table 3.

Table 3. Improved results for the case of \(k=4\)
Full size table

Due to limited space, the proofs of lemmas and theorems marked with “*” were omitted and they can be found in the full version of this paper [31].

1.3 Paper Organization

The remaining parts of the paper are organized as follows. In Sect. 2, we introduce basic notations. In Sect. 3, we consider metric kCP. In Sect. 3.1, we present a better reduction from metric kCP to metric TSP, which has already led to an improved ratio for \(k\ge 5\). In Sect. 3.2, by using some properties of the current-best approximation algorithm for metric TSP, we obtain a further improved ratio. In Sect. 3.2, we consider a simple algorithm based on matching with a better ratio for \(k=5\). In Sect. 4, we consider metric kPP and propose an improved algorithm for even \(10\ge k\ge 6\). Note that metric kPP is harder to improve, unlike metric kCP. In Sect. 5, we propose non-trivial algorithms for metric/general kCP and kPP with \(k=4\). In Sect. 5.1, we obtain a better algorithm for general 4CP. In Sect. 5.2, we obtain a better algorithm for metric 4CP. In Sect. 5.3, we obtain a better approximation algorithm for metric 4PP. Finally, we make the concluding remarks in Sect. 6.

2 Preliminaries

We use \(G=(V, E)\) to denote an undirected complete graph with n vertices such that \(n\bmod k=0\). There is a non-negative weight function \(w: E\rightarrow \mathbb {R}_{\ge 0}\) on the edges in E. For an edge \(uv\in E\), we use w(u, v) to denote its weight. A graph is called a metric graph if the weight function satisfies the triangle inequality; Otherwise, it is called a general graph. For any weight function \(w:X\rightarrow \mathbb {R}_{\ge 0}\), we define \(w(Y)=\sum _{x\in Y}w(x)\) for any \(Y\subseteq X\).

Two subgraphs or subsets of edges of a graph are vertex-disjoint if they do not appear a common vertex. We only consider simple paths and simple cycles with more than two vertices. The length of a path/cycle is the number of vertices it contains. A cycle packing is a set of vertex-disjoint cycles such that the length of each cycle is at least three and all vertices in the graph are covered. Given a cycle packing \(\mathcal {C}\), we use \(l(\mathcal {C})\) to denote the minimum length of cycles in \(\mathcal {C}\). We also use \(\mathcal {C}^*\) to denote the maximum weight cycle packing. A path (resp., cycle) on k different vertices \(\{v_1,v_2,\dots ,v_k\}\) is called a k-path (resp., k-cycle), denoted by \(v_1v_2\cdots v_k\) (resp., \(v_1v_2\cdots v_kv_1\)). A k-path packing (resp., k-cycle packing) in graph G is a set of vertex-disjoint n/k k-paths (resp., k-cycles) such that all vertices in the graph are covered. Note that we can obtain a k-cycle packing by completing every k-path of a k-path packing. Let \(\mathcal {P}^*_k\) (resp., \(\mathcal {C}^*_k\)) denote the maximum weight k-path packing (resp., k-cycle packing). We can get \(w(\mathcal {C}^*)\ge w(\mathcal {C}^*_k)\) for \(k\ge 3\).

A 2-path packing is called a matching of size n/2. The maximum weight matching of size n/2 is denoted by \(\mathcal {M}^*\). An n-cycle is called a Hamiltonian cycle. MAX TSP is to find a maximum weight Hamiltonian cycle. We simply use general/metric TSP to denote MAX TSP in general/metric graphs. We use \(H^*\) to denote the maximum weight Hamiltonian cycle. For a k-path \(P=v_{1}v_{2}\cdots v_{k}\) where k is even, we define \(\widetilde{w}(P)=\sum _{i=1}^{k/2}w(v_{2j-1},v_{2j})\).

3 Approximation Algorithms for Metric kCP

In this section, we improve the approximation ratio for metric kCP with \(k\ge 5\). We will first present a better black-box reduction from metric kCP to metric TSP, which is sufficient to improve the previous ratio for \(k\ge 5\). Then, based on the approximation algorithm for metric TSP, we prove an improved approximation ratio. Finally, we consider a matching-based algorithm that can further improve the ratio of metric 5CP.

3.1 A Better Black-Box

Given an \(\alpha \)-approximation algorithm for metric TSP, Li and Yu [21] proposed an \(\alpha \cdot (1-1/k)^2\)-approximation algorithm for metric kCP. We will show that the ratio can be improved to \(\alpha \cdot (1-0.5/k)(1-1/k)\). Moreover, for even k, the ratio can be further improved to \(\alpha \cdot (1-0.5/k)(1-1/k+\frac{1}{k(k-1)})\). We first consider a simple algorithm, denoted by Algorithm 1, which mainly contains three following steps.

  • Step 1. Obtain a Hamiltonian cycle H using an \(\alpha \)-approximation algorithm for metric TSP;

  • Step 2. Get a k-path packing \(\mathcal {P}_k\) with \(w(\mathcal {P}_k)\ge (1-1/k)w(H)\) from H: we can obtain a k-path packing by deleting one edge per k edges from H; since there are \((1-1/k)n\) edges in \(\mathcal {P}_k\) and n edges in H, if we carefully choose the initial edge, we can make sure that the weight of \(\mathcal {P}_k\) is at least \((1-1/k)n\cdot (1/n)\cdot w(H)\), i.e., on average each edge has a weight of at least \((1/n)\cdot w(H)\).

  • Step 3. Obtain a k-cycle packing \(\mathcal {C}_k\) by completing the k-path packing \(\mathcal {P}_k\).

To analyze the approximation quality, we use the path patching technique, which has been used in some papers [12, 18, 19].

Lemma 1

([12, 18]). Let G be a metric graph. Given a cycle packing \(\mathcal {C}\), there is a polynomial-time algorithm to generate a Hamiltonian cycle H such that \(w(H)\ge (1-0.5/l(\mathcal {C}))w(\mathcal {C})\).

Since the length of every k-cycle in the maximum weight k-cycle packing \(\mathcal {C}^*_k\) equals to k, we have \(l(\mathcal {C}^*_k)=k\). By Lemma 1, we have the following lemma.

Lemma 2

\(w(H^*)\ge (1-0.5/k)w(\mathcal {C}^*_k)\).

Theorem 1

Given an \(\alpha \)-approximation algorithm for metric TSP, Algorithm 1 is a polynomial-time \(\alpha \cdot (1-0.5/k)(1-1/k)\)-approximation algorithm for metric kCP.

Proof

By the algorithm, we can easily get that \(w(\mathcal {C}_k)\ge w(\mathcal {P}_k)\ge (1-1/k)w(H)\ge \alpha \cdot (1-1/k)w(H^*)\). By Lemma 2, we have \(w(\mathcal {C}_k)\ge \alpha \cdot (1-0.5/k)(1-1/k)w(\mathcal {C}^*_k)\). Therefore, the algorithm achieves an approximation ratio of \(\alpha \cdot (1-0.5/k)(1-1/k)\) for metric kCP.\(\square \)

Next, we propose an improved \(\alpha \cdot (1-0.5/k)(1-1/k+\frac{1}{k(k-1)})\)-approximation algorithm for even k, denoted by Algorithm 2. The previous two steps of Algorithm 2 are the same as Algorithm 1. However, Algorithm 2 will obtain a better k-cycle packing in Step 3:

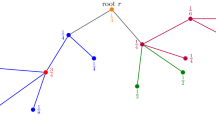
New Step 3. For each k-path \(P_i=v_{i1}v_{i2}\cdots v_{ik}\in \mathcal {P}_k\), we obtain \(k-1\) k-cycles \(\{C_{i1},\dots ,C_{i(k-1)}\}\) where \(C_{ij}=v_{i1}v_{i2}\cdots v_{ij}v_{ik}v_{i(k-1)}\cdots v_{i(j+1)}v_{i1}\) (See Fig. 1 for an illustration); let \(C_{ij_i}\) denote the maximum weight cycle from these cycles; return a k-cycle packing \(\mathcal {C}_k=\{C_{ij_i}\}_{i=1}^{n/k}\).

Fig. 1.
figure 1

An illustration of the k-cycle \(C_{ij}\) obtained from \(P_i\), where \(j\in \{1,2,\dots ,k-1\}\)

Full size image

Lemma 3

It holds that \(w(\mathcal {C}_k)\ge \frac{k-2}{k-1}w(\mathcal {P}_k)+\frac{2}{k-1}\widetilde{w}(\mathcal {P}_k)\).

Proof

Since \(C_{ij_i}\) is the maximum weight cycle from these cycles, we have

$$\begin{aligned} w(C_{ij_i})&\ge \frac{1}{k-1}\sum _{j=1}^{k-1}w(C_{ij})\\ &= \frac{1}{k-1}\sum _{j=1}^{k-1}(w(P_i)+w(v_{i1},v_{i(j+1)})+w(v_{ij},v_{ik})-w(v_{ij},v_{i(j+1)}))\\ &= \frac{1}{k-1}\left( (k-1)w(P_i)+\sum _{j=1}^{k-1}(w(v_{i1},v_{i(j+1)})+w(v_{ij},v_{ik}))-w(P_i)\right) \\ &= \frac{1}{k-1}\left( (k-2)w(P_i)+\sum _{j=1}^{k-1}(w(v_{i1},v_{i(j+1)})+w(v_{ij},v_{ik}))\right) .\\ \end{aligned}$$

By the triangle inequality, we can get that

$$\begin{aligned} \sum _{j=1}^{k-1}w(v_{i1},v_{i(j+1)})=&\ w(v_{i1},v_{i2})+\sum _{j=2}^{k/2}(w(v_{i1},v_{i(2j-1)})+w(v_{i1},v_{i(2j)}))\\ \ge &\ w(v_{i1},v_{i2})+\sum _{j=2}^{k/2}w(v_{i(2j-1)},v_{i(2j)})\\ =&\ \sum _{j=1}^{k/2}w(v_{i(2j-1)},v_{i(2j)})\\ =&\ \widetilde{w}(P_i). \end{aligned}$$

Similarly, we can get \(\sum _{j=1}^{k-1}w(v_{ij},v_{ik})\ge \widetilde{w}(P_i)\). Hence,

$$\begin{aligned} w(C_{ij_i})\ge &\ \frac{1}{k-1}\left( (k-2)w(P_i)+\sum _{j=1}^{k-1}(w(v_{i1},v_{i(j+1)})+w(v_{ij},v_{ik}))\right) \\ \ge &\ \frac{(k-2)w(P_i)+2\widetilde{w}(P_i)}{k-1}. \end{aligned}$$

By doing this for all k-paths in \(\mathcal {P}_k\), we can get a k-cycle packing \(\mathcal {C}_k\) such that \(w(\mathcal {C}_k)\ge \frac{(k-2)w(\mathcal {P}_k)+2\widetilde{w}(\mathcal {P}_k)}{k-1}\).\(\square \)

Theorem 2

Given an \(\alpha \)-approximation algorithm for metric TSP, for metric kCP with even k, Algorithm 2 is a polynomial-time \(\alpha \cdot (1-0.5/k)(1-1/k+\frac{1}{k(k-1)})\)-approximation algorithm.

Proof

Recall that all k-paths in \(\mathcal {P}_k\) are obtained from the \(\alpha \)-approximate Hamiltonian cycle H. By deleting one edge per k edges from a Hamiltonian cycle H and choosing the initial edge carefully, we can get a k-path packing \(\mathcal {P}_k\) such that

$$ (k-2)w(\mathcal {P}_k)+2\widetilde{w}(\mathcal {P}_k)\ge \frac{(k-2)(k-1)+k}{k}w(H)=\frac{(k-1)^2+1}{k}w(H) $$

since \((k-2)w(\mathcal {P}_k)+2\widetilde{w}(\mathcal {P}_k)\) contains the weight of \(\frac{n(k-2)(k-1)+nk}{k}\) (multi-)edges in H. By Lemma 3, we can obtain a k-cycle packing \(\mathcal {C}_k\) such that

$$\begin{aligned} w(\mathcal {C}_k)\ge &\ \frac{(k-2)w(\mathcal {P}_k)+2\widetilde{w}(\mathcal {P}_k)}{k-1}\\ \ge &\ \frac{(k-1)^2+1}{k(k-1)}w(H)\\ =&\ \left( 1-1/k+\frac{1}{k(k-1)}\right) w(H). \end{aligned}$$

Since \(w(H)\ge \alpha \cdot w(H^*)\ge \alpha \cdot (1-0.5/k)w(\mathcal {C}^*_k)\) by Lemma 2, we have \(w(\mathcal {C}_k)\ge \alpha \cdot (1-0.5/k)(1-1/k+\frac{1}{k(k-1)})w(\mathcal {C}^*_k)\).\(\square \)

Note that for metric TSP there is a randomized \((7/8-O(1/\sqrt{n}))\)-approximation algorithm [12], a deterministic \((7/8-O(1/\root 3 \of {n}))\)-approximation algorithm [6], and a deterministic 7/8-approximation algorithm [19]. By Theorem 2, we obtain an approximation ratio of \(7/8\cdot (1-0.5/k)(1-1/k)\) for metric kCP with odd k, and \(7/8\cdot (1-0.5/k)(1-1/k+\frac{1}{k(k-1)})\) for metric kCP with even k.

3.2 A Further Improvement

In this subsection, we show that the approximation ratio of Algorithm 2 can be further improved based on the properties of the 7/8-approximation algorithm for metric TSP [19]. We recall the following result.

Lemma 4

([19]). Let G be a metric graph with even n. There is a polynomial-time algorithm to get a Hamiltonian cycle H with \( w(H)\ge \frac{5}{8}w(\mathcal {C}^*)+\frac{1}{2}w(\mathcal {M}^*). \)

For any k-cycle packing with k being even or Hamiltonian cycle with an even number of vertices, the edges can be decomposed into two edge-disjoint matchings of size n/2. We can get the following bounds.

Lemma 5

It holds that \(w(\mathcal {M}^*)\ge \frac{1}{2}w(\mathcal {C}^*_k)\) for even k and \(w(\mathcal {M}^*)\ge \frac{1}{2}w(H^*)\) for even n.

Note that for metric kCP with even k, the number of vertices is always even since it satisfies \(n\bmod k=0\). But for odd k, the number may be odd, and then there may not exist a matching of size n/2. Since we mainly consider the improvements for constant k, for the case of odd k and n, we can first use \(n^{O(k)}=n^{O(1)}\) time to enumerate a k-cycle in \(\mathcal {C}^*_k\), and then consider an approximate k-cycle packing in the rest graph. The approximation ratio preserves. Hence, we may assume that n is even for the case of constant k.

Theorem 3 (*)

For metric kCP, there is a \((7/8-0.125/k)(1-1/k)\)-approximation algorithm for constant odd k and a \(7/8\cdot (1-1/k+\frac{1}{k(k-1)})\)-approximation algorithm for even k.

3.3 An Improved Algorithm Based on Matching

Consider metric kCP with odd k. By deleting the least weighted edge from every k-cycle in \(\mathcal {C}^*_k\), we can get a k-path packing \(\mathcal {P}_k\) with \(w(\mathcal {P}_k)\ge (1-1/k)w(\mathcal {C}^*_k)\). Note that \(\mathcal {P}_k\) can be decomposed into two edge-disjoint matchings of size \(p{:}{=}(n/k)\cdot (k-1)/2\). Let \(\mathcal {M}^*_p\) be the maximum weight matching of size p, which can be computed in polynomial time [10, 20]. Then, we can get \(2w(\mathcal {M}^*_p)\ge w(\mathcal {P}_k)\ge (1-1/k)w(\mathcal {C}^*_k)\). Note that there are also n/k isolated vertices not covered by \(\mathcal {M}^*_p\). Next, we construct a k-cycle packing using \(\mathcal {M}^*_p\) with the isolated vertices. The algorithm, denoted by Algorithm 3, is shown as follows.

  • Step 1. Arbitrarily partition the p edges of \(\mathcal {M}^*_p\) into n/k sets with the same size, denoted by \(\mathcal {S}_1,\mathcal {S}_2,\dots ,\mathcal {S}_{n/k}\). Note that each edge set contains \(m{:}{=}(k-1)/2\) edges. For each of the n/k edge sets, arbitrarily assign an isolated vertex.

  • Step 2. Consider an arbitrary edge set \(\mathcal {S}_i=\{e_1,e_2,\dots ,e_{m}\}\) with the isolated vertex v. Assume w.o.l.g. that \(w(e_1)\ge w(e_m)\ge w(e_i)\) for \(2\le i<m\), i.e., \(w(e_1)+w(e_m)\ge (2/m)w(\mathcal {S}_i)\). Orient each edge \(e_i\) uniformly at random from the two choices. Let \(t_i\) (resp., \(h_i\)) denote the tail (resp., head) vertex of \(e_i\). Construct a k-cycle \(C_i\) such that \(C_i=vt_1h_1t_2h_2\cdots t_mh_mv\).

  • Step 3. Get a k-cycle packing \(\mathcal {C}_k\) by packing the k-cycles from the edge sets and the isolated vertices.

Algorithm 3 can be derandomized efficiently by conditional expectations [29].

Next, we analyze the expected weight of \(C_i=vt_1h_1t_2h_2\cdots t_mh_mv\), obtained from the edge set \(\mathcal {S}_i\) and the isolated vertex v.

Lemma 6

It holds that \(\mathbb {E}[w(v,t_1)]\ge \frac{1}{2}w(e_1)\), \(\mathbb {E}[w(v,h_m)]\ge \frac{1}{2}w(e_m)\), and \(\mathbb {E}[w(h_i,t_{i+1})]\ge \frac{1}{4}(w(e_i)+w(e_{i+1}))\) for \(1\le i<m\).

Proof

Consider \(\mathbb {E}[w(v,t_1)]\). Since we orient the edge \(e_1\) uniformly at random, each vertex of \(e_1\) has a probability of 1/2 being \(t_1\). Hence, we can get \(\mathbb {E}[w(v,t_1)]=\frac{1}{2}\sum _{u\in e_1}w(v,u)\ge \frac{1}{2}w(e_1)\) by the triangle inequality. Similarly, we can get \(\mathbb {E}[w(v,h_m)]\ge \frac{1}{2}w(e_m)\).

Consider \(\mathbb {E}[w(h_i,t_{i+1})]\). We can get \(\mathbb {E}[w(h_i,t_{i+1})]=\frac{1}{4}\sum _{u\in e_i}\sum _{w\in e_{i+1}}w(u,w)\). Let \(e_i=u'u''\) and \(e_{i+1}=o'o''\). By the triangle inequality, we can get that

$$\begin{aligned} \sum _{u\in e_i}\sum _{w\in e_{i+1}}w(u,w)=&\ w(u',o')+w(u',o'')+w(u'',o')+w(u'',o'')\\ \ge &\ w(o',o'')+w(u',u'')\\ =&\ w(e_i)+w(e_{i+1}). \end{aligned}$$

Therefore, \(\mathbb {E}[w(h_i,t_{i+1})]\ge \frac{1}{4}(w(e_i)+w(e_{i+1}))\) for \(1\le i<m\).\(\square \)

Lemma 7

It holds that \(\mathbb {E}[w(C_i)]\ge \frac{3m+1}{2m}w(\mathcal {S}_i)\).

Proof

Note that

$$\begin{aligned} w(C_i)=&\ w(v,t_1)+w(v,h_m)+\sum _{i=1}^{m-1}(w(t_i,h_i)+w(h_i,t_{i+1}))\\ =&\ w(\mathcal {S}_i)+w(v,t_1)+w(v,h_m)+\sum _{i=1}^{m-1}w(h_i,t_{i+1}). \end{aligned}$$

We can get that

$$\begin{aligned} \mathbb {E}[w(C_i)]\ge &\ w(\mathcal {S}_i)+\frac{1}{2}(w(e_1)+w(e_m))+\frac{1}{4}\sum _{i=1}^{m-1}(w(e_i)+w(e_{i+1}))\\ =&\ w(\mathcal {S}_i)+\frac{1}{2}(w(e_1)+w(e_m))+\frac{1}{2}w(\mathcal {S}_i)-\frac{1}{4}(w(e_1)+w(e_m))\\ =&\ \frac{3}{2}w(\mathcal {S}_i)+\frac{1}{4}(w(e_1)+w(e_m))\\ \ge &\ \left( \frac{3}{2}+\frac{1}{2m}\right) w(\mathcal {S}_i)\\ =&\ \frac{3m+1}{2m}w(\mathcal {S}_i), \end{aligned}$$

where the first inequality follows from Lemma 6, and the second from \(w(e_1)+w(e_m)\ge (2/m)w(\mathcal {S}_i)\) by the algorithm.\(\square \)

Theorem 4

For metric kCP with odd k, Algorithm 3 is a polynomial-time \((3/4-0.25/k)\)-approximation algorithm.

Proof

Recall that \(2w(\mathcal {M}^*_p)\ge (1-1/k)w(\mathcal {C}^*_k)\) and \(\mathcal {M}^*_p=\bigcup _{i=1}^{n/k}\mathcal {S}_i\). Using a derandomization based on conditional expectations [29], by Lemma 7, we can get that

$$ w(\mathcal {C}_k)\ge \sum _{i=1}^{n/k}\frac{3m+1}{2m}w(\mathcal {S}_i)=\frac{3m+1}{2m}w(\mathcal {M}^*_p)\ge \frac{3m+1}{4m}\left( 1-\frac{1}{k}\right) w(\mathcal {C}^*_k). $$

Since \(m=(k-1)/2\), we can get an approximation ratio of \(\frac{3m+1}{4m}(1-\frac{1}{k})=3/4-0.25/k\).\(\square \)

By Theorem 4, we obtain a 7/10-approximation algorithm for metric 5CP, which improves the previous ratio 17/25 in Theorem 3, and the ratio 3/5 in [21].

Corollary 1

For metric 5CP, Algorithm 3 is a 7/10-approximation algorithm.

4 Approximation Algorithms for Metric kPP

In this section, we consider metric kPP. Using a reduction from metric kPP to metric TSP, metric kPP admits a \(7/8\cdot (1-1/k)\)-approximation algorithm [11]. Note that, unlike metric kCP, it is not easy to construct a better black box to improve the ratio. However, we will combine the properties of the 7/8-approximation algorithm for metric TSP with an algorithm based on matching to obtain a better approximation ratio for even \(6\le k\le 10\). Next, we assume that k is even.

The first algorithm, denoted by Algorithm 4, is to use the reduction from metric kPP to metric TSP [11].

  • Step 1. Obtain a Hamiltonian cycle H using the 7/8-approximation algorithm for metric TSP [19];

  • Step 2. Get a k-path packing \(\mathcal {P}_k\) with \(w(\mathcal {P}_k)\ge (1-1/k)w(H)\) from H using the same method in Step 2 of Algorithm 1.

For every \(P_i=v_{i1}v_{i2}\cdots v_{ik}\in \mathcal {P}^*_k\), let \(\mathcal {E}_{i}^{'}=\{v_{i(2j-1)}v_{i(2j)}\}_{j=1}^{k/2}\) and \(\mathcal {E}_{i}^{''}=\{v_{i(2j)}v_{i(2j+1)}\}_{j=1}^{(k-2)/2}\). Then, we can obtain a matching \(\mathcal {M}_{n/2}=\bigcup _{i}\mathcal {E}_{i}^{'}\) of size n/2 and a matching \(\mathcal {M}_p=\bigcup _{i}\mathcal {E}_{i}^{''}\) of size \(p{:}{=}(n/k)\cdot (k-2)/2\). Note that \(w(\mathcal {M}_{n/2})+w(\mathcal {M}_p)=w(\mathcal {P}^*_k)\). We have the following bounds.

Lemma 8

(\(^{\boldsymbol{*}}\)). \(w(\mathcal {C}^*_k)\ge \frac{k-2}{k-1}w(\mathcal {P}^*_k)+\frac{2}{k-1}w(\mathcal {M}_{n/2})\).

Lemma 9

(\(^{\boldsymbol{*}}\)). \(w(\mathcal {P}_k)\ge \frac{5k-10}{8k}w(\mathcal {P}^*_k)+\frac{2k+3}{4k}w(\mathcal {M}_{n/2})\).

Next, we propose an algorithm, denoted by Algorithm 5, to obtain another k-path packing \(\mathcal {P}'_k\), which can be used to make a trade-off with \(\mathcal {P}_k\). The framework of Algorithm 5 is similar to Algorithm 3 in Sect. 3.3. Let \(\mathcal {M}^*_p\) denote the maximum weight matching of size \(p=(n/k)\cdot (k-2)/2\), which can be computed in polynomial time [10, 20]. Note that \(w(\mathcal {M}^*_p)\ge w(\mathcal {M}_p)\). There are 2n/k isolated vertices not covered by \(\mathcal {M}^*_p\). Next, we construct a k-path packing using \(\mathcal {M}^*_p\) with isolated vertices. Algorithm 5 mainly contains three steps.

  • Step 1. Arbitrarily partition the p edges of \(\mathcal {M}^*_p\) into n/k sets with the same size, denoted by \(\mathcal {S}_1,\mathcal {S}_2,\dots ,\mathcal {S}_{n/k}\). Note that each edge set contains \(m{:}{=}(k-2)/2\) edges. For each of the n/k edge sets, arbitrarily assign two isolated vertices.

  • Step 2. Consider an arbitrary edge set \(\mathcal {S}_i=\{e_1,e_2,\dots ,e_{m}\}\) with the two isolated vertices u and v. Assume w.o.l.g. that \(w(e_1)\ge w(e_m)\ge w(e_i)\) for \(2\le i<m\), i.e., \(w(e_1)+w(e_m)\ge (2/m)w(\mathcal {S}_i)\). Orient each edge \(e_i\) uniformly at random from the two choices. Let \(t_i\) (resp., \(h_i\)) denote the tail (resp., head) vertex of \(e_i\). Construct a k-path \(P'_i\) such that \(P'_i=ut_1h_1t_2h_2\cdots t_mh_mv\).

  • Step 3. Get a k-path packing \(\mathcal {P}'_k\) by packing the k-paths from the edge sets and the isolated vertices.

Algorithm 5 can also be derandomized by conditional expectations.

Next, we analyze the expected weight of \(P'_i=ut_1h_1t_2h_2\cdots t_mh_mv\), obtained from the edge set \(\mathcal {S}_i\) and the two isolated vertices u and v.

Lemma 10

(\(^{\boldsymbol{*}}\)). It holds that \(\mathbb {E}[w(u,t_1)]\ge \frac{1}{2}w(e_1)\), \(\mathbb {E}[w(v,h_m)]\ge \frac{1}{2}w(e_m)\), and \(\mathbb {E}[w(h_i,t_{i+1})]\ge \frac{1}{4}(w(e_i)+w(e_{i+1}))\) for \(1\le i<m\).

Lemma 11

(\(^{\boldsymbol{*}}\)). It holds that \(\mathbb {E}[w(\mathcal {P}'_k)]\ge \frac{3k-4}{2k-4}w(\mathcal {M}^*_p)\).

Lemma 12

(\(^{\boldsymbol{*}}\)). \(w(\mathcal {P}'_k)\ge \frac{3k-4}{2k-4}w(\mathcal {M}_p)\).

Theorem 5 (*)

There is a \(\frac{27k^2-48k+16}{32k^2-36k-24}\)-approximation algorithm for metric kPP with even k.

The approximation ratio in Theorem 5 is better than \(7/8\cdot (1-1/k)\) for even \(10\ge k\ge 6\). For \(k=4\), the ratio is even worse than the ratio 3/4 in [11]. But, in the next section, we show an improved \(14/17\approx 0.823\)-approximation algorithm.

5 Approximation Algorithms for the Case of \(k=4\)

In this section, we study the case of \(k=4\) for metric/general kCP and kPP. For metric 4CP, we improve the best-known ratio from 3/4 [21] to 5/6. For general 4CP, we improve the best-known ratio from 2/3 [21] to 3/4. For metric 4PP, we improve the best-known ratio from 3/4 [11] to 14/17.

5.1 General 4CP

Zhao and Xiao [30] observed some structural properties of the minimum weight 4-cycle packing and the minimum weight matching of size n/2. In fact, these properties even hold for the maximum weight 4-cycle packing \(\mathcal {C}^*_4\) and the maximum weight matching \(\mathcal {M}^*\) of size n/2.

Lemma 13

([30]). Given \(\mathcal {C}^*_4\) and \(\mathcal {M}^*\), there is a way to color edges in \(\mathcal {C}^*_4\) with red and blue such that

  1. (1)

    the blue (resp., red) edges form a matching of size n/2 \(\mathcal {M}_b\) (resp., \(\mathcal {M}_r\));

  2. (2)

    \(\mathcal {C}^*_4=\mathcal {M}_b\cup \mathcal {M}_r\);

  3. (3)

    \(\mathcal {M}_b\cup \mathcal {M}^*\) is a cycle packing and the length of every cycle is divisible by 4.

An alternative proof of Lemma 13 could be found in [23]. Next, we describe the approximation algorithm for general 4CP, denoted by Algorithm 6.

  • Step 1. Find a maximum weight matching \(\mathcal {M}^*\) of size n/2.

  • Step 2. Construct a multi-graph \(G/\mathcal {M}^*\) such that there are n/2 super-vertices one-to-one corresponding to the n/2 edges in \(\mathcal {M}^*\), i.e., there is a function f, and for two super-vertices \(f(e_i),f(e_j)\) such that \(e_i,e_j\in \mathcal {M}^*\), there are four super-edges \(f(e_i)f(e_j)\) between them, corresponding to the four edges uv with a weight of w(u, v) (\(u\in e_i, v\in e_j\)).

  • Step 3. Find a maximum weight matching \(\mathcal {M}^{**}_{n/4}\) of size n/4 in graph \(G/\mathcal {M}^*\). Note that \(\mathcal {M}^*\cup \mathcal {M}^{**}_{n/4}\) corresponds to a 4-path packing \(\mathcal {P}_4\) in graph G.

  • Step 4. Obtain a 4-cycle packing \(\mathcal {C}_4\) by completing the 4-path packing \(\mathcal {P}_4\).

Note that \(w(\mathcal {C}_4)\ge w(\mathcal {P}_4)=w(\mathcal {M}^*)+w(\mathcal {M}^{**}_{n/4})\).

Lemma 14

(\(^{\boldsymbol{*}}\)). \(w(\mathcal {M}^{**}_{n/4})\ge \frac{1}{2}w(\mathcal {M}_b)\).

Lemma 15

(\(^{\boldsymbol{*}}\)). \(w(\mathcal {P}_4)\ge \frac{1}{2}w(\mathcal {M}^*)+\frac{1}{2}w(\mathcal {C}^*_4)\).

Theorem 6 (*)

Algorithm 6 is a 3/4-approximation algorithm for general 4CP.

5.2 Metric 4CP

Li and Yu [21] proved an almost trivial approximation ratio of 3/4. We show that their algorithm, denoted by Algorithm 7, actually achieves an approximation ratio of 5/6.

  • Step 1. Find a maximum weight matching \(\mathcal {M}^*\) of size n/2.

  • Step 2. Construct a multi-graph \(G/\mathcal {M}^*\) such that there are n/2 super-vertices one-to-one corresponding to the n/2 edges in \(\mathcal {M}^*\), i.e., there is a function f, and for two super-vertices \(f(e_i),f(e_j)\) such that \(e_i,e_j\in \mathcal {M}^*\), there are two super-edges \(f(e_i)f(e_j)\) between them, corresponding to the edge sets \(\{uz,xy\}\) and \(\{uy,xz\}\) with a weight of \(w(u,z)+w(x,y)\) and \(w(u,y)+w(x,z)\) (\(ux\in e_i, yz\in e_j\)).

  • Step 3. Find a maximum weight matching \(\mathcal {M}^{**}_{n/4}\) of size n/4 in graph \(G/\mathcal {M}^*\). Note that \(\mathcal {M}^*\cup \mathcal {M}^{**}_{n/4}\) corresponds to a 4-cycle packing \(\mathcal {C}_4\) in graph G if we decompose each super-edge of \(\mathcal {M}^{**}_{n/4}\) into two normal edges.

  • Step 4. Return \(\mathcal {C}_4\).

Note that \(\mathcal {C}_4\) is the maximum weight 4-cycle packing containing the edges of \(\mathcal {M}^*\) by the optimality of \(\mathcal {M}^{**}_{n/4}\). Recall that we can get a 4-path packing \(\mathcal {P}_4\) such that \(w(\mathcal {P}_4)\ge \frac{1}{2}w(\mathcal {M}^*)+\frac{1}{2}w(\mathcal {C}^*_4)\) by Lemma 15. Moreover, if \(\mathcal {P}_4=\{u_ix_iy_iz_i\}_{i=1}^{n/4}\), \(\mathcal {M}^*\) represents the edge set \(\{u_ix_i,y_iz_i\}_{i=1}^{n/4}\). Let \(\overline{\mathcal {P}_4}\) denote the edge set \(\{u_iz_i\}_{i=1}^{n/4}\).

Lemma 16

(\(^{\boldsymbol{*}}\)). \(w(\mathcal {C}_4)\ge \frac{3}{4}w(\mathcal {C}^*_4)+w(\overline{\mathcal {P}_4})\).

Lemma 17

(\(^{\boldsymbol{*}}\)). \(w(\mathcal {C}_4)\ge w(\mathcal {C}^*_4)-2w(\overline{\mathcal {P}_4})\).

Theorem 7 (*)

Algorithm 7 is a 5/6-approximation algorithm for metric 4CP.

On \(\{1,2\}\)-weighted graphs we may obtain a better approximation ratio.

Theorem 8 (*)

On \(\{1,2\}\)-weighted graphs, Algorithm 7 is a 7/8-approximation algorithm for metric 4CP.

5.3 Metric 4PP

At last, we will consider metric 4PP. Recall that we can get a 4-path packing \(\mathcal {P}_4\) such that \(w(\mathcal {P}_4)\ge \frac{1}{2}w(\mathcal {M}^*)+\frac{1}{2}w(\mathcal {C}^*_4)\) by Lemma 15. For metric 4PP, we will construct another 4-path packing \(\mathcal {P}'_4\). The algorithm, denoted by Algorithm 8, is shown as follows.

  • Step 1. Obtain a 4-path packing \(\mathcal {P}_4\) such that \(w(\mathcal {P}_4)\ge \frac{1}{2}w(\mathcal {M}^*)+\frac{1}{2}w(\mathcal {C}^*_4)\) using Algorithm 6.

  • Step 2. Obtain a maximum weight matching \(\mathcal {M}^{**}_{n/4}\) of size n/4 in graph G. Note that there are also n/2 isolated vertices not covered by \(\mathcal {M}^{**}_{n/4}\).

  • Step 3. Arbitrarily assign two isolated vertices \(u_i,z_i\) for each edge \(x_iy_i\in \mathcal {M}^{**}_{n/4}\). Assume w.l.o.g. that \(w(u_i,x_i)+w(y_i,z_i)\ge w(z_i,x_i)+w(y_i,u_i)\).

  • Step 4. Obtain another 4-path packing \(\mathcal {P}'_4\) by taking a 4-path \(u_ix_iy_iz_i\) for every edge \(x_iy_i\in \mathcal {M}^{**}_{n/4}\) with the two isolated vertices \(u_i,z_i\).

Let \(\mathcal {C}_4\) be the 4-cycle packing obtained by completing the maximum weight 4-path packing \(\mathcal {P}^*_4\), i.e., for every 4-path \(P_i=u_ix_iy_iz_i\in \mathcal {P}_4\), we obtain a 4-cycle \(C_i=u_ix_iy_iz_iu_i\). Then, let \(\mathcal {C}_4=\mathcal {P}^*_4\cup \overline{\mathcal {P}^*_4}\). Moreover, let \(\mathcal {C}_4=\mathcal {M}_1\cup \mathcal {M}_2\) such that \(\mathcal {M}_1\) and \(\mathcal {M}_2\) are two matchings of size n/2, and \(\mathcal {M}_1\cap \overline{\mathcal {P}^*_4}=\emptyset \). Obtain another 4-cycle packing \(\mathcal {C}'_4\) such that for every 4-path \(P_i=u_ix_iy_iz_i\in \mathcal {P}_4\) there is a 4-cycle \(C'_i=u_ix_iz_iy_iu_i\) in \(\mathcal {C}'_4\).

Lemma 18

(\(^{\boldsymbol{*}}\)). \(w(\mathcal {P}_4)\ge \max \{\frac{1}{2}w(\mathcal {M}_1)+\frac{1}{2}w(\mathcal {P}^*_4)+\frac{1}{2}w(\overline{\mathcal {P}^*_4}),\frac{3}{2}w(\mathcal {M}_1)-w(\overline{\mathcal {P}^*_4})\}\).

Lemma 19

(\(^{\boldsymbol{*}}\)). \(w(\mathcal {P}'_4)\ge 2w(\mathcal {P}^*_4)-2w(\mathcal {M}_1)\).

Theorem 9 (*)

There is a 14/17-approximation algorithm for metric 4PP.

6 Conclusion

In this paper, we consider approximation algorithms for metric/general kCP and kPP. Most of our results are based on simple algorithms but with deep analysis. In the future, it would be interesting to improve these approximation ratios, even on \(\{0,1\}\)-weighted or \(\{1,2\}\)-weighted graphs. In particular, one challenging direction is to design better algorithms for metric/general 3CP and 3PP.