A Fast $(2 + 2/7)$-Approximation Algorithm for Capacitated Cycle Covering

Abstract

We consider the capacitated cycle covering problem: given an undirected, complete graph G with metric edge lengths and demands on the vertices, we want to cover the vertices with vertex-disjoint cycles, each serving a demand of at most one. The objective is to minimize a linear combination of the total length and the number of cycles. This problem is closely related to the capacitated vehicle routing problem (CVRP) and other cycle cover problems such as min-max cycle cover and bounded cycle cover. We show that a greedy algorithm followed by a post-processing step yields a $(2 + 2/7)$-approximation for this problem by comparing the solution to a polymatroid relaxation. We also show that the analysis of our algorithm is tight and provide a $2 + \epsilon$ lower bound for the relaxation.

1 Introduction

Our work is motivated by the classical and well-studied capacitated vehicle routing problem (CVRP) which was introduced by Dantzig and Ramser [7]. In this problem we are given an undirected, complete graph $G = (V, E)$ with metric edge lengths $\ell : E \rightarrow \mathbb {R}_{\ge 0}$ and a distinguished vertex $s \in V$ which is called the depot. Moreover, every vertex is assigned a demand b(v). The goal is to cover V with cycles $C_1, \ldots , C_k$ such that each cycle visits s, satisfies $b(C_i) \le 1$ and the total length $\sum _{i = 1}^{k}{\ell (C_i)}$ is minimum. Here $b(C_i) := \sum _{v\in V(C_i)} b(v)$ is the total demand of the vertices of $C_i$ and $\ell (C_i) := \sum _{e\in E(C_i)} \ell (e)$ is the total length of the edges of $C_i$.

The CVRP has received a large amount of attention in the last 60 years. While there has been much progress regarding computational results (see e.g. [16, 17, 19]), from the viewpoint of approximation algorithms little progress has been made. The simple optimal tour partitioning algorithm by Altinkemer and Gavish [1], which achieves an approximation ratio of 3.5, has not been improved in the past 30 years. (In fact, the approximation ratio is $2+\alpha$ where $\alpha$ is the best known approximation ratio for TSP.) For the case where all vertices have demand 1/Q for some $Q\in \mathbb {N}$, the tour partitioning algorithm by Haimovich and Kan [12] from 1985 has approximation ratio $1+\alpha$, which is currently 2.5, and this result is also still the best known.

Significant improvements have only been achieved in special cases, such as when the metric is Euclidean [8, 13] or arises from graphs with special structure [2,3,4, 14]. The only result for the general case is by Bompadre et al. [5] who improved the approximation guarantee by $\varTheta (1/Q^3)$ where Q is the least common denominator of the (rational) demands b.

In this paper we study a variant of the CVRP, where we do not have a depot vertex that must be visited by every tour, but instead have a fixed opening cost $\gamma > 0$ per tour. Formally, this problem, which we call the capacitated cycle covering problem (CCCP), is defined as follows. We are given an undirected, complete graph $G = (V, E)$ with metric edge lengths $\ell : E \rightarrow \mathbb {R}_{\ge 0}$, vertex demands $b : V \rightarrow [0, 1]$, and an opening cost $\gamma \in \mathbb {R}_{\ge 0}$. The goal is to compute a capacitated cycle cover, i.e. cycles $C_1, \ldots , C_k$ in G, such that every $v \in V$ is contained in exactly one cycle and $b(C_i) \le 1$ for all i, minimizing the total cost $\sum _{i = 1}^{k}{\ell (C_k)} + \gamma k$. Here it is allowed that a cycle contains only one or two vertices.

To the best of our knowledge, this precise problem formulation has not appeared in the literature. However, besides the capacitated vehicle routing problem, the CCCP is also closely related to other cycle covering problems. This includes min-max cycle cover and bounded cycle cover which were first studied by Even et al. [10]. In the former problem we are asked to compute a cycle cover $C_1, \ldots , C_k$ which minimizes $\max _{i = 1}^{k}{\ell (C_i)}$ where k is part of the input. In the latter we wish to find a cycle cover $C_1, \ldots , C_k$ with $\ell (C_i) \le 1$ for all i with minimum k. Recently, Yu et al. [20, 21] provided new approximation algorithms for the these problems with approximation ratios of 5 and $4 + 4/7$ respectively. Their algorithms need $O(n^5)$ time, where here and in the following $n:= |V|$.

Even more recently, Das et al. [9] studied the min-max variant of the capacitated cycle covering problem. In this problem we wish to find a capacitated cycle cover $C_1, \ldots , C_k$ where k is part of the input such that $\max _{i = 1}^{k}{\ell (C_i)}$ is minimized. They provide a 196-approximation algorithm for min-max capacitated tree cover which implies a 392-approximation algorithm for the cycle cover variant.

1.1 Our Results and Techniques

Note that the capacitated cycle covering problem includes both the TSP (for $b \equiv 0$ and suitably large $\gamma$) and bin packing (for $\ell \equiv 0$) and is thus $\mathrm {NP}$-hard to approximate within a factor of $3/2 - \epsilon$. Hence, we are primarily interested in approximation algorithms and relaxations for the problem. Our main result is the following theorem.

Theorem 1

Given an instance of the capacitated cycle covering problem, we can compute a $(2 + 2/7)$-approximate solution in $O(n^2)$ time.

We remark that if the pairwise distances between all vertices are given explicitly, the input has size $n^2$ and hence the runtime is linear.

The first step of our algorithm is to compute a carefully chosen spanning forest in our input graph. Having such a forest, we turn it into a capacitated cycle cover as follows. We first ensure that every connected component of the forest contains vertices of total demand at most 1. This is done by splitting large components into smaller ones if necessary. Then from every connected component of the forest we can compute a cycle of at most twice the length of the forest component. See Sect. 2.

The most important part of our algorithm is to choose the initial spanning forest. We do not solve a tree covering problem as a black box but anticipate that we will have to double edges and split up large components. To compute our spanning forest we use a linear programming relaxation, which we call the tree cover LP. This LP is closely related to a natural LP relaxation for the capacitated vehicle routing problem. Moreover, the tree cover LP has the important property that the set of feasible solutions is a polymatroid. This allows us to solve the LP very efficiently using the polymatroid greedy algorithm. See Sect. 3.

We then analyze a simple randomized rounding algorithm that rounds a fractional LP solution to a spanning forest. For this we exploit that the extreme point solutions of our LP relaxation are highly structured. As a result, we obtain a randomized $(2 + 2/7)$-approximation algorithm for the CCCP and also show that the ratio between our solution for CCCP and the value of the tree cover LP is at most $2 + 2/7$. See Sect. 4.

Then we show that we can derandomize our algorithm and obtain a simple and deterministic greedy algorithm for computing our spanning forest (Sect. 5). This will complete the proof of Theorem 1.

Finally, we provide two forms of lower bounds for our analysis: we prove that the analysis of our deterministic algorithm is tight and we show a $2 + \epsilon$ lower bound on the gap between the tree cover LP and the capacitated cycle covering problem (Sect. 6).

2 Tree Splitting

In the following we will call a set U of vertices large if $b(U) :=\sum _{u\in U} b(u) > 1$ and small otherwise. A common and useful technique for dealing with capacities in facility location and vehicle routing problems is to cluster vertices into clusters with demands between 1/2 and 1 (see e.g. [10, 14, 15, 20]). By making sure that the demand in each cluster is at least 1/2, we can guarantee that we have at most twice as many clusters as necessary. This idea can be used to prove the following lemma.

Lemma 1 (Tree Splitting)

Let $T=(V,E)$ be a tree and $b : V \rightarrow [0, 1]$ some vertex demands with $b(V) > 1$, i.e. V is large. Then we can partition V into $k \le 2 b(V)$ many small sets $R_1, \ldots , R_k$ and find edge-disjoint connected subgraphs $T_1, \ldots , T_k$ of T such that $R_i \subseteq V(T_i)$, i.e. $T_i$ is a Steiner tree with terminal set $R_i$, for all i. Moreover, this can be done in linear time.

We defer the proof to Appendix A. As a corollary, we get a simple construction which turns any forest F in G into a solution to the capacitated cycle covering problem. For an edge set F, we denote by $\mathcal {C}(F)$ the collection of vertex sets of the connected components of (V, F).

Lemma 2

Let (V, F) be a forest. Then we can compute in linear time a feasible solution $C_1, \ldots , C_k$ to the CCCP with cost bounded by

$$\begin{aligned} 2 \ell (F) + \gamma \cdot \sum _{A \in \mathcal {C}(F)}{u(A)} \end{aligned}$$

(1)

where $\ell (F):= \sum _{e\in F} \ell (e)$ and $u : 2^V \rightarrow \mathbb {R}_{\ge 0}$ is given by

$$\begin{aligned} u(A) := {\left\{ \begin{array}{ll} 1 &{} \mathrm {if\,\, } A \mathrm {\,\, is\,\, small}, \\ 2 b(A) &{} \mathrm {if\,\, } A \mathrm {\,\, is\,\, large}. \end{array}\right. } \end{aligned}$$

(2)

Proof

We first apply Lemma 1 to all large connected components of F. Together with the remaining small connected components, this yields a partition of V into k small sets $R_1,\ldots , R_k$ and Steiner trees $T_1,\ldots , T_k$ with terminal sets $R_1,\ldots , R_k$ respectively, where $k \le \sum _{A \in \mathcal {C}(F)}{u(A)}$. Then we turn each Steiner tree $T_i$ with terminal set $R_i$ into a cycle $C_i$ with vertex set $R_i$ and $\ell (C_i) \le 2 \ell (T_i)$. This is accomplished by the standard technique of ordering the elements of $R_i$ as they appear in a depth-first search of $T_i$. Equivalently, one can double all edges of $T_i$, find an Eulerian walk, and shortcut this walk to a cycle on $R_i$. Shortcutting does not increase the length since $\ell$ is metric.   $\square$

Thus in the following sections we will discuss how to find a forest F such that (1) is at most $(2 + 2/7)$ times the cost of an optimum capacitated cycle cover.

3 The Tree Cover LP

To obtain a lower bound on the cost of an optimum solution to the CCCP, we use the following linear program.

(3)

where $\ell (x) := \sum _{e\in E} x_e\ell (e)$, $x(E):= \sum _{e\in E} x_e$, and E[A] denotes the set of edges in E that have both endpoints in A.

Note that LP (3) is rather a relaxation of a tree covering problem than of capacitated cycle covering: integral solutions are edge sets of forests in which every connected component contains vertices of total demand at most 1. Nonetheless, it provides a lower bound for the cost of an optimum CCCP solution because every feasible solution to the CCCP contains such a forest. Hence we get the following.

Lemma 3

Let $(G,\ell ,b,\gamma )$ be an instance of the CCCP. Then the optimum value of the LP (3) is a lower bound on the cost of an optimum solution of the CCCP.

We would like to remark that the tree cover LP (3) is related to the following natural LP relaxation for the CVRP:

(4)

where $\delta (A)$ denotes the set of edges with exactly one endpoint in A and $\delta (v) :=\delta (\{v\})$. (To see that (4) is a relaxation of the CVRP, note that we need at least b(A) cycles for covering the vertices in A and each cycle contains the depot s.)

The optimal tour partitioning algorithm for the CVRP [1] computes a solution of cost at most 3.5 times the value of (4) (see e.g. [18]). In particular, the integrality gap of (4) is at most 3.5. The following LP is equivalent to (4) in the sense that every feasible solution to one of the LPs is also a feasible solution for the other.

Therefore, for every feasible solution x to (4), the restriction of x to $G-s$ is a feasible solution to the tree cover LP (3).

In the remaining part of this section we explain how one can solve the tree cover LP (3) by a greedy algorithm. The key insight for proving this is that (3) is equivalent to optimizing over a polymatroid.

Lemma 4

Let P be the set of feasible solutions to the LP (3). Then

$$ P = \left\{ x \in \mathbb {R}^E \;\left| \; \begin{array}{llr} x(F) &{}\le r(F) &{} \quad \forall F \subseteq E, \\ x &{}\ge 0 &{} \end{array}\right. \right\} $$

where $r(F) := \sum _{A \in \mathcal {C}(F)}{(|A| - \max \{1, b(A)\})}.$ Moreover, r is monotone, submodular, and satisfies $r(\emptyset ) = 0$. Thus P is a polymatroid.

We sketch the proof of Lemma 4 in Appendix B. Algorithm 1 formally describes the polymatroid greedy algorithm for solving (3).

Note that $\mathcal {C}$ remains a partition of the vertex set. At the end of iteration i it contains the vertex sets of the connected components of $(V,\{e_1,\ldots ,e_i\})$. Moreover, the support $\{e\in E : x_e > 0\}$ of the returned LP solution x is the edge set of a forest (by the condition in line 5). This structure will be useful in the next section, where we analyze an algorithm for rounding x to an integral vector.

Lemma 5

Algorithm 1 computes an optimum solution of the LP (3).

Proof (Sketch)

By Lemma 4 we know that LP (3) optimizes over a polymatroid. Thus the polymatroid greedy algorithm which sets $x_{e_i} := r(\{e_1, \ldots , e_i\}) - r(\{e_1, \ldots , e_{i - 1}\})$ for every $i \le m$ produces an optimal solution. One can verify that Algorithm 1 sets x to exactly those values.   $\square$

4 Randomized Rounding

We will now show how we can round the fractional solution x generated by Algorithm 1 to a forest F while bounding the cost (1) of the resulting CCCP solution. More precisely, we will prove the following theorem.

Theorem 2 (Randomized rounding)

Let x be a solution of the tree-covering LP (3) computed by Algorithm 1. Define a random edge set $F \subseteq E$ by independently picking each edge e with probability $\min \{1, (1 + 1/7) x_e\}$. Then

$$ \mathbb {E}\left[ \sum _{A \in \mathcal {C}(F)}{u(A)}\right] \le \left( 2 + \frac{2}{7}\right) (|V| - x(E)), $$

where u is defined by (2), and $\mathbb {E}[2 \ell (F)] \le \left( 2 + 2/7\right) \ell (x)$.

Note that this implies that the total cost (1) is at most $2+ 2/7$ times the objective value $\ell (x) + \gamma (|V| - x(E))$ of our optimum LP solution x. The scaling factor $1 + 1/7$ on the probabilities $x_e$ is chosen to decrease the expected number of components of (V, F) (while increasing the expected length) such that we lose the same factor in both cost terms wrt. the LP. By Lemmas 2 and 3, Theorem 2 yields a randomized $(2+ 2/7)$-approximation algorithm for the CCCP.

In the rest of this section we prove Theorem 2. We may assume wlog. that $(V,\{e_1,\ldots , e_m\})$ is connected; otherwise we prove the statement for each connected component. Let $E'$ be the set of edges $e_i$ for which the condition in line 5 of Algorithm 1 was fulfilled. Every such edge $e_i =\{v,w\} \in E'$ connected two sets $C,C' \in \mathcal {C}$ in iteration i of Algorithm 1. Let $C^{v}_{e_i} \in \{C,C'\}$ be the set containing v and let $C^{w}_{e_i} \in \{C,C'\}$ be the other set (containing w). By construction of $\mathcal {C}$ in Algorithm 1, $(V,E')$ is a spanning tree. Thus, F is always a forest. Moreover, the subgraphs of $(V, \{e_1, \ldots , e_{i-1}\} \cap E')$ induced by $C^{v}_{e_i}$ and $C^{w}_{e_i}$ are connected.

Lemma 6

For every set $F\subseteq E'$, we have

$$ \sum _{A \in \mathcal {C}(F)}{u(A)}\le 2\cdot (|V| - x(E)) + \sum _{e\in E'\setminus F} \sum _{u\in e} \max \{1 - 2 b(C^{u}_e), 0\}. $$

Proof

We first consider the case $\mathcal {C}(F) = \{ V\}$ and hence $F=E'$. Then we have $x(E) \le |V| - \max \{1, b(V)\}$ since x is a feasible solution to (3) and hence $u(V) \le \max \{1, 2b(V)\} \le 2 (|V| -x(E))$. Now assume $\mathcal {C}(F) \ne \{ V\}$ and compute

(5)

where we used in the last inequality that x is a feasible solution to (3).

Recall that $\mathcal {C}(F) \ne \{V\}$ and $(V,E')$ is a spanning tree. Consider some $A\in \mathcal {C}(F)$ and let i minimum such that $e_i =\{v,w\} \in \delta (A) \cap E'$, where wlog. $v\in A$. So $v \in A \cap C^{v}_{e_i} \ne \emptyset$. Since the subgraphs of $(V, \{e_1, \ldots , e_{i-1}\}\cap E')$ induced by $C^{v}_{e_i}$ and $C^{w}_{e_i}$ are connected and i was chosen minimal, we have $C^{v}_{e_i} \subseteq A$. Hence, $\max \{1 - 2 b(C^{v}_{e_i}), 0\} \ge \max \{1 - 2b(A), 0\}$. Note that $e_i\in E'\setminus F$ because $e_i\in \delta (A)$ and $A\in \mathcal {C}(F)$. Hence,

because $\mathcal {C}(F)$ is a partition of V. Together with (5) this completes the proof.   $\square$

Lemma 7

Let x be a solution of the tree-covering LP (3) computed by Algorithm 1. Define a random edge set $F \subseteq E$ by independently picking each edge e with probability $\min \{1, (1 + 1/7) x_e\}$. Then

Proof

We consider an edge $e\in E'$ and a vertex $u\in e$. If $x_e < 1$, by the definition of $x_e$ in Algorithm 1 we have $x_e \ge 1-b(C^{u}_e)$ and therefore

Hence,

(6)

Let $1 \le i < j \le m$ with $e_i=\{u,v\},e_j=\{u',v'\}\in E'$ with $x_{e_i}, x_{e_j} <1$. We claim that if the vertex sets $C^u_{e_i}$ and $C^{u'}_{e_j}$ are both small, then they are disjoint. In iteration i of Algorithm 1, we merge $C^u_e$ and $C^{v}_e$ into a single component $C^u_e \cup C^{v}_e$. This new component must be large because $x_{e_i} < 1$. During the course of the algorithm we only merge components of the partition $\mathcal {C}$ of V. Therefore either $C^u_{e_i}$ and $C^{u'}_{e_j}$ are disjoint, or $C^u_e \cup C^{v}_e \subseteq C^{u'}_{e_j}$ which implies that $C^{u'}_{e_j}$ is large. Hence,

$$ \sum _{e\in E': x_e <1} \sum _{u\in e : C^u_e\text { small}} b(C^u_e) \le b(V) \le |V| - x(E), $$

where $b(V) \le |V| - x(E)$ holds because x is a feasible solution to (3). Together with (6) this completes the proof.   $\square$

The bound $\mathbb {E}[2 \ell (F)] \le \left( 2 + 2/7\right) \ell (x)$ follows directly from the linearity of expectation. Hence, Lemmas 6 and 7 imply Theorem 2.

5 A Fast and Deterministic Algorithm

In this section we show how one can derandomize our $(2 + 2/7)$-approximation algorithm. Algorithm 2 formally describes the computation of the forest (V, F). The partition $\mathcal {C}$ is updated exactly as in Algorithm 1. However, now we do not compute the value $x_{e_i}$ but instead directly round it in a deterministic way (lines 7–10).

Lemma 8

Algorithm 2 computes a forest (V, F) with

$$\begin{aligned} 2 \ell (F) + \gamma \cdot \sum _{A \in \mathcal {C}(F)}{u(A)} \le \left( 2+\frac{2}{7}\right) \cdot \mathrm {LP}, \end{aligned}$$

(7)

where $\mathrm {LP}$ denotes the value of (3).

We defer the proof to Appendix C. Note that the runtime of Algorithm 2 is dominated by sorting the edges E in line 2. In a preprocessing step, one can compute a minimum spanning tree wrt. to $\ell$ and remove all edges not contained in this tree. This yields a total runtime of $O(\theta + n \log {n})$ where $\theta = O(n^2)$ is the time needed to compute an MST. Lemmas 8, 3, and 2 thus directly imply our main result Theorem 1.

6 Lower Bounds

In this section we show that the approximation ratio of Algorithm 2 followed by the Algorithm from Lemma 2 is at least $(2 + 2/7)$, i.e. we show that the analysis in the preceding sections is tight. Moreover, we show that the cost of an optimum solution to the CCCP might be more than twice the value of the tree cover LP (3).

Theorem 3

For any $\epsilon > 0$ there is a CCCP instance where Algorithm 2 computes an edge set $F \subseteq E$, such that there is no capacitated cycle cover $C_1, \ldots , C_k$ with cost at most $(2 + 2/7 - \epsilon ) \mathrm {LP}$ and where $V(C_i)$ is connected in (V, F) for all $i \in \{1,\ldots ,k\}$.

We defer the proof of Theorem 3 to Appendix D. We remark that although Theorem 3 shows that our analysis of Algorithm 2 followed by the Algorithm from Lemma 2 is tight, it might be that the analysis of our randomized rounding algorithm is not.

We now show that the cost of an optimum solution to the CCCP might be more than twice the value of the tree cover LP (3). We define

$$\textstyle \rho := \sup \left\{ \frac{\mathrm {OPT}(\mathcal {I})}{\mathrm {LP}(\mathcal {I})} \;\left| \; \mathcal {I}\text { is a CCCP instance}\right. \right\} . $$

Here we use $\mathrm {OPT}(\mathcal {I})$ to refer to the minimum cost of a CCCP solution on the instance $\mathcal {I}=(G, \ell , b, \gamma )$. Similarly, $\mathrm {LP}(\mathcal {I})$ refers to the solution value of the tree cover LP (3) for the instance $\mathcal {I}$.

Theorem 4

$\rho \ge 2 + \frac{62}{11745} > 2.005$.

To prove Theorem 4 we use the following lemma that can be proven by an argument similar to Goemans [11], and Carr and Vempala [6].

Lemma 9

Let $G=(V,E)$ a complete graph and $b : V \rightarrow [0, 1]$ some vertex demands. Moreover, let $(x_e)_{e \in E}$ be a feasible solution to the tree cover LP (3) such that the support of x is the edge set of a tree T. Then there are weights $\lambda _1, \ldots , \lambda _k > 0$, small sets $R_1, \ldots , R_k \subseteq V$ and trees $T_1, \ldots , T_k$ in T such that $R_i \subseteq V(T_i)$ for all i and

• $\sum _{i=1}^k \lambda _i \le \rho (|V| -x(E))$,

• $\sum _{i : e\in T_i} \lambda _i \le \frac{\rho }{2} x_e$ for every $e\in E$, and

• $\sum _{i : v \in R_i} \lambda _i \ge 1$ for every $v \in V$.

Fig. 1.

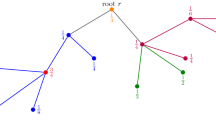
A family of LP solutions x that together with Lemma 9 proves Theorem 4. Here, the demands for the vertex r and the vertices $v_1, \ldots , v_k$ are 0 and the demand of the vertices $w_{i,j}$ for $i=1,\ldots ,k$ and $j=1,\ldots ,16$ are 1/23. The constants are chosen to maximize the lower bound obtained from this family of instances. In the figure edges e with $x_e > 0$ are shown. One can verify that this is indeed a feasible solution to the tree cover LP (3).

We consider the family of LP solutions depicted in Fig. 1. One can show that if $\rho < 2 + \frac{62}{11745}$ and k is sufficiently large, it is not possible to find weights $\lambda _i$, vertex sets $R_i$, and trees $T_i$ as in Lemma 9. This implies Theorem 4.

Appendices

A Sketch of the Proof of Lemma 1

Pick an arbitrary root r for T. Then we perform the following splitting-off procedure (similar to Algorithm A in [15]).

As long as the vertex set V(T) of the tree T remains large, we iterate the following. Let v be maximally far away from r with the property that $V(T_v)$ is large, where $T_v$ is the subtree rooted at v. Let $w_1, \ldots , w_l$ be the children of v. Since $b(V(T_v)) = b(v) + \sum _{i = 1}^{l}{b(V(T_{w_l}))}$, we must have that $b(v) \ge 1/2$ or there exists a set $N \subseteq \{1,\ldots ,l\}$ with $\sum _{i \in N}{b(V(T_{w_i}))} \in [1/2, 1]$. In the first case we split off a singleton tree $(\{v\},\emptyset )$ covering the vertex v and replace v in T by a Steiner vertex, i.e. we set its demand to zero. In the second case we split off a tree covering all vertices contained in the subtrees $T_{w_i}$ for $i \in N$; the Steiner tree for this set of terminals contains v as a Steiner vertex and for $i \in N$ contains the edge $\{v,w_i\}$ and the subtree $T_{w_i}$. Thus we then remove these subtrees from T.

Let $T_1, \ldots , T_{k - 1}$ be the Steiner trees split off during this algorithm and let $T_k$ be the remaining tree. Moreover, let $R_1, \ldots , R_k$ be the respective terminal sets of these Steiner trees. Then we know that $b(R_i) \ge 1/2$ for all $i \le k - 2$ and $b(R_{k - 1}) + b(R_k) \ge 1$. Thus $2 b(V) = 2 \sum _{i = 1}^{k}{b(R_i)} \ge k.$

B Sketch of the Proof of Lemma 4

The key part is showing that r is indeed submodular. For this let $F' \subseteq F \subseteq E$ be arbitrary and $e \in E \setminus F$. We need to show that

$$ r(F' \cup \{e\}) - r(F') \ge r(F \cup \{e\}) - r(F). $$

Let $A_1, A_2 \in \mathcal {C}(F)$ be the two components of F joined by e. Moreover, let $A'_1, A'_2 \in \mathcal {C}(F')$ be the same for $F'$. We can assume that $A'_1 \subseteq A_1$ and $A'_2 \subseteq A_2$ since $F' \subseteq F$. Then one can show that

$$\begin{aligned} r(F \cup \{e\}) - r(F)&= \max \{1, b(A_1)\} + \max \{1, b(A_2)\} - \max \{1, b(A_1 \cup A_2)\} \end{aligned}$$

and

$$\begin{aligned} r(F' \cup \{e\}) - r(F')&= \max \{1, b(A'_1)\} + \max \{1, b(A'_2)\} - \max \{1, b(A'_1 \cup A'_2)\}. \end{aligned}$$

So the submodularity of r reduces to observation that the expression

$$ \max \{1, x\} + \max \{1, y\} - \max \{1, x + y\} $$

is non-increasing in x and y for $x,y\ge 0$.

C Sketch of the Proof of Lemma 8

Note that the partition $\mathcal {C}$ in iteration i of Algorithm 2 is the same as in iteration i of Algorithm 1; here we assume wlog. that the edges are sorted in the same order in both algorithms. Hence, we apply lines 7–10 of Algorithm 2 precisely for those edges $e_i$ for which we set $x_{e_i}$ in line 7 of Algorithm 1. We define $E'$ as in Sect. 4 and also define $C^u_e\subseteq V$ for an edge $e\in E'$ and a vertex $u\in e$ as before.

Let x be the output of Algorithm 1. It is easy to verify that the choice of which edges we include in the forest F in lines 7–10 of Algorithm 2 is such that we minimize

$$\begin{aligned} \sum _{e\in F} 2\cdot \ell (e) + \sum _{e\in E\setminus F} \sum _{u\in e} \gamma \cdot \max \{1 - 2 b(C^{u}_e), 0\} \end{aligned}$$

(8)

among all set F with $\{ e\in E : x_e =1\} \subseteq F \subseteq \{e\in E : x_e > 0\}$. By Lemma 7 there exists such an edge set F where (8) is at most $(2+2/7)\cdot \ell (x) + 2/7 \cdot \gamma \cdot (|V| - x(E))$. Hence, also the edge set F computed by Algorithm 2 fulfills this bound. By Lemma 6 this implies the claimed bound (7).

D Proof of Theorem 3

For $n \in \mathbb {N}$ with $n\ge 4$, let $G = (V,E)$ be the complete graph on the vertices $v_1, \ldots , v_n$ with the metric $\ell$ on V given by $\ell (v_i, v_j) := \frac{1}{4} |i - j|,$ i.e. $(G, \ell )$ is the metric closure of a path. Assign uniform demands of $b(v) := 1/4$ to every vertex v and let $\gamma := 1$. Then we observe that $\mathrm {LP}(G, \ell , b, \gamma ) = \frac{7}{16} n$. See Fig. 2.

But now consider what Algorithm 2 does on this instance. Assume that the edges are sorted such that $e_i = \{v_i, v_{i + 1}\}$ for all $i \in \{1, \ldots , n - 1\}$. The algorithm will then buy the edges $e_1$ to $e_3$. But it will not buy any other edge as

$$\textstyle \gamma \max \{1 - 2 b(v_{i + 1}), 0\} = \frac{1}{2} = 2 \ell (\{v_i, v_{i + 1}\}) $$

for all $i \in \{1, \ldots , n - 1\}$. So the condition in line 9 is never satisfied except for the first three iterations of the loop. Hence, any CCCP solution which is “contained” in the connected components of F (i.e. it does not contain a cycle $C_i$ where $V(C_i)$ is not connected in (V, F)), must contain at least $n - 4$ singleton cycles.

Fig. 2.

An optimum solution to the tree cover LP (3) for instance from the proof of Theorem 3 for $n=12$. For every solid edge e we have $x_e = 1$ and for every dotted edge e we have $x_e = 3 / 4$.

Finally, we conclude that any such CCCP solution has a cost of at least

$$\begin{aligned} n - 4\ =\ \frac{n - 4}{\frac{7}{16} n} \mathrm {LP}\ \ge \ \Bigl (\frac{16}{7} - \epsilon \Bigr ) \mathrm {LP}\ =\ \Bigl (2 + \frac{2}{7} - \epsilon \Bigr ) \mathrm {LP}\end{aligned}$$

for n large enough.