Numerical Study of the Impacts of Forced Vibration on Thermocapillary Bubble Migration in a Rotating Cylinder

Abstract

In a non-uniform temperature gradient fluid medium, the surface tension varies according to the local temperature conditions. The surface tension in the cold fluid region is greater than that in the hot region. Therefore, in a zero-gravity stagnant fluid of a non-uniform temperature field, this difference in surface tension creates a net force acting on the fluid particles, which leads to a general fluid motion from the hot region to the cold region.

1 Introduction

In a non-uniform temperature gradient fluid medium, the surface tension varies according to the local temperature conditions. The surface tension in the cold fluid region is greater than that in the hot region. Therefore, in a zero-gravity stagnant fluid of a non-uniform temperature field, this difference in surface tension creates a net force acting on the fluid particles, which leads to a general fluid motion from the hot region to the cold region. This phenomenon is known as Marangoni or thermocapillary migration phenomenon. It is necessary to carry out an appropriate numerical simulation on the behavior of bubbles under the influence of forced vibration and rotation in a microgravity fluid medium in order to achieve a better understanding of this complicated phenomenon. Clearly, an in-depth understanding of the flow patterns, including the shape and the area of the varying complex interfaces, is of vital importance to the understanding and prediction of the physics behind these flow systems and as the flow patterns of some regimes remain largely undiscovered; consequently, accurate predictions of flow patterns are highly desirable. This is the goal of the present study, wherein this microgravity phenomenon is numerically investigated in a three-dimensional domain (3D).

2 Methodology

The thermocapillary motion of a bubble was first examined experimentally by Young, Block, and Goldstein [1], when Reynolds number (Re) and Marangoni number (Ma) are small, which means that both convective momentum and energy transport are negligible, who also found an analytical expression for its terminal velocity in the creeping flow:

$$V_{YGB} = \frac{{2\left| {{{{\text{d}}\sigma } \mathord{\left/ {\vphantom {{{\text{d}}\sigma } {{\text{d}}T}}} \right. \kern-\nulldelimiterspace} {{\text{d}}T}}} \right|r_{b} \lambda {{{\text{d}}T} \mathord{\left/ {\vphantom {{{\text{d}}T} {{\text{d}}x}}} \right. \kern-\nulldelimiterspace} {{\text{d}}x}}}}{{(2\mu + 3\mu^{\prime})(2\lambda + \lambda^{\prime} )}}$$

(1)

commonly called the YGB model, which is suitable for small Reynolds and Marangoni numbers:

$$\text{Re}_{\text{T}} = {{r_{b} V_{T} } \mathord{\left/ {\vphantom {{r_{b} V_{T} } v}} \right. \kern-\nulldelimiterspace} v}$$

(2)

$$Ma_{T} = {{r_{b} V_{T} } \mathord{\left/ {\vphantom {{r_{b} V_{T} } \alpha }} \right. \kern-\nulldelimiterspace} \alpha } = {\text{Re}}_{T} \cdot \Pr$$

(3)

where Prandtl number is the ratio of kinematic viscosity to thermal diffusivity:

$$\Pr = {\nu \mathord{\left/ {\vphantom {\nu \alpha }} \right. \kern-\nulldelimiterspace} \alpha }$$

(4)

and ν is the kinematic viscosity in m²/s: $\nu = {\mu \mathord{\left/ {\vphantom {\mu \rho }} \right. \kern-\nulldelimiterspace} \rho }$.

The velocity $V_{T}$ derived from the tangential stress balance at the free surface is used for scaling the migration velocity (m/s) in Eqs. (2) and (3):

$$V_{T} = \frac{{\left( {{{{\text{d}}\sigma } \mathord{\left/ {\vphantom {{{\text{d}}\sigma } {{\text{d}}T}}} \right. \kern-\nulldelimiterspace} {{\text{d}}T}}} \right) \cdot \left( {{{{\text{d}}T} \mathord{\left/ {\vphantom {{{\text{d}}T} {{\text{d}}x}}} \right. \kern-\nulldelimiterspace} {{\text{d}}x}}} \right) \cdot r_{b} }}{\mu }$$

(5)

where $\mu$ and $\mu^{\prime}$, $\lambda$ and $\lambda^{^{\prime}}$ are the dynamic viscosity and thermal conductivity of continuous phase and bubble, respectively. ρ is the density and $r_{d}$ is the radius of the bubble. The constant ${{{\text{d}}\sigma } \mathord{\left/ {\vphantom {{{\text{d}}\sigma } {{\text{d}}T}}} \right. \kern-\nulldelimiterspace} {{\text{d}}T}}{ }$ or $\sigma_{T}$ is the rate of change of interfacial tension, and ${{{\text{d}}T} \mathord{\left/ {\vphantom {{{\text{d}}T} {{\text{d}}x}}} \right. \kern-\nulldelimiterspace} {{\text{d}}x}}$ is the temperature gradient imposed in the continuous phase fluid.

3 VOF Model and Computational Procedure

The governing continuum conservation equations for two-phase flow were solved using the Ansys Fluent commercial software package [2], and the volume of fluid (VOF) method was used to track the liquid/gas interface. This method deals with completely separated phases with no diffusion. The geometric reconstruction scheme, based on the piece-wise linear interface calculation (PLIC) method of Young’s [3] in Ansys Fluent, was chosen for the current investigation. Geo-reconstruction is an added module to the already existing VOF scheme that allows for a more accurate definition of the free surface [4].The movement of the gas–liquid interface is tracked based on the distribution of the volume fraction of the gas, i.e.,$\alpha_{G}$, in a computational cell, where the value of $\alpha_{G}$ is 0 for the liquid phase and 1 for the gas phase. Therefore, the gas–liquid interface exists in the cell where $\alpha_{G}$ lies between 0 and 1. A single momentum equation, which is solved throughout the domain and shared by all the phases, is given by:

$$\frac{\partial }{\partial t}(\rho \vec{\nu }) + \nabla \cdot (\rho \vec{\nu }\vec{\nu }) = - \nabla p + \nabla \cdot [\mu (\nabla \vec{\nu } + \nabla \vec{\nu }^{T} )] + \vec{F}$$

(6)

In Eq. 6, $\vec{F}$ represents volumetric forces at the interface, resulting from the surface tension force per unit volume. The continuum surface force (CSF) model proposed by Brackbill et al. [5] is used to compute the surface tension force for the cells containing the gas–liquid interface:

$$\vec{F} = \sigma \left( {{{\rho k\vec{n}} \mathord{\left/ {\vphantom {{\rho k\vec{n}} {\frac{1}{2}(\rho_{L} + \rho_{G} )}}} \right. \kern-\nulldelimiterspace} {\frac{1}{2}(\rho_{L} + \rho_{G} )}}} \right)$$

(7)

where σ is the coefficient of surface tension,

$$\sigma = \sigma_{0} + \sigma_{T} (T_{0} - T{) }$$

(8)

and $\sigma_{0}$ is the surface tension at a reference temperature T₀, and T is the liquid temperature.

4 Results

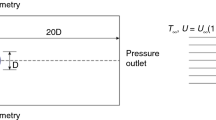
A constant temperature gradient of 0.208 K/mm was prescribed for each simulation, and the corresponding thermal Reynolds (Re_T) and Marangoni (Ma_T) numbers for all cases were set to 257 and 4188, respectively. The thermocapillary flow pattern and trajectory of a single gas bubble in a stationary, vibrated and rotating cylinder are illustrated in the figures below. These two cylinders have the same vibration amplitude and frequency, A_P = 0.02 m/s², f = 0.2 Hz. Thus, the bubble path in the non-rotary container adhered to the wall and then went up toward the higher temperature. In a vibrating rotating cylinder, which vibrates with the same vibration capacity, the bubble migrates toward the hotter side and rotates around the axis of rotation due to the angular speed of the container. By comparing the two forms, we can found that there are three major forces that affect the flow of the bubble, namely vibration, rotation and thermocapillary forces. More detailed on the effect of these three forces on the bubble movement in the lack of gravity will be addressed in the next part.

As amplitude gets larger, bubble goes from small to longer oscillations around the axis of rotation and toward the hotter side demonstrating the effect of the three forces on the bubble shape and behavior. Figures 1 and 2 illustrate that at the vibration amplitude selected and beyond, can cause a major reduction in the bubble velocity toward the hotter side and becomes considerable at higher vibration amplitude, and affects the forces acting on and consequently the translational motion of the bubbles. Figures 3 and 4 show the results of the numerical simulations of stationary and vibrating/rotating cylinder. In other words, increasing the speed of rotation attracts the bubble in the direction of the axis of rotation, while increasing the vibration amplitude, it distancing it from the axis of rotation and vice versa. In the case of vibration with rotation, the bubble remains rotating around the axis of rotation and does not center the cylinder.

Fig. 1

Bubble oscillations around the X-coordinate, d_b = 9 mm

Fig. 2

Bubble migration toward the hotter side, d_b = 9 mm

Fig. 3

Bubble dynamics in stationary, vibrating and rotating cylinder d_b = 9 mm, ∇T = 0.208 K/mm

Fig. 4

Bubble dynamics in a vibrating/rotating cylinder, d = 9 mm, ω = 1 rads⁻¹

5 Conclusions

The thermocapillary flow of isolated bubble in a vibrating/rotating container was studied for single bubble migrating with different amplitudes. Small vibrations/rotations aboard space platforms can have significant effects on bubble movement. Conducting future experiments on this topic aboard the space station will be of interest to us since better understanding of the vibration effects will help us better understand the onset of oscillation mechanisms and ways to design g-jitter resistant thermocapillary bubble migration in the future. Since zero gravity is difficult to achieve in a laboratory setting, one can demonstrate the relevant phenomena using numerical simulations. Simulating these phenomena also allowed one to study the effects of altering the sensitivities of different parameters. It therefore may be concluded that computer simulations proving their worth as a valuable tool to study the complex problems in zero-gravity conditions and one can observe the credentials of numerical modeling to simulate realistic 3D Marangoni cases. This has important implications on the Marangoni flow characteristics in space.