Introduction

The vortex shedding phenomenon from a bluff body leads to oscillating forces which induce structural vibration. This phenomenon is known as vortex-induced vibration (VIV) and can be found in a wide range of applications including nuclear reactors, heat exchangers, marine industry, bridges, buildings and chimneys. The VIV of a cylinder in cross-flow has been studied by researches in the past few decades due to its practical applications and importance in the design of structures [1]. Vortex shedding modes, oscillation amplitude branches (namely ‘initial,’ ‘upper’ and ‘lower’) and lock-in (the natural frequency of the cylinder is close to the vortex shedding frequency) are some subjects in the VIV which have been investigated [2]. The large amplitude of oscillations, significant increases in the drag and lift fluctuations and acoustic noise are the effects of VIV which can cause fatigue in the structures of offshore and wind turbines. Hence, various techniques have been presented to control and suppress VIV responses, which are classified as passive and active methods [3].

Most researches have been focused on the hydrodynamic characteristics of VIV [4], although the effects of cylinder vibration can be significant on the heat transfer characteristics, especially in lock-in or synchronization range [5,6,7]. The VIV of the cylinder can consider as a passive method in the heat transfer enhancement technology, unlike the pulsating flow is an active method. The effects of velocity oscillation frequency and amplitude, porosity and magnetic field in pulsating flow on heat transfer have been studied [5].

Adding nanoparticles (e.g., \({\text{Al}}_{2} {\text{O}}_{3}\) or \({\text{CuO}}\)) to the base fluid (e.g., water, ethylene glycol and oil) is a passive method in the heat transfer enhancement technology [8,9,10,11]. This fluid suspension which is called nanofluid [12] is widely used in the thermal process to increase heat transfer due to their improved thermophysical properties [13,14,15,16,17,18]. The heat transfer and the viscous effect cause energy loss in any thermofluidic systems, so it is essential to calculate entropy generation to determine the irreversibilities. The entropy generation minimization (EGM) approach is used to optimizing thermofluidic systems and decreasing the irreversibilities [13,14,15,16, 19].

Although there are many studies concerning the effect of using nanofluid [20,21,22,23,24,25], pulsating flow [26, 27] or both on heat transfer of stationary circular cylinder [28, 29], a few types of research have been performed for the oscillating cylinder. In the present work, for the first time, the effects of the combination of passive (nanofluid and VIV) and active (pulsating flow) methods on convective heat transfer and entropy generation of the circular cylinder have been investigated which can be important in heat exchangers.

Problem description

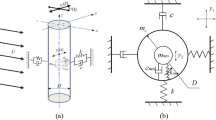
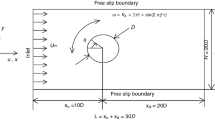
In this work, the forced convection of pulsating nanofluid flow over an elastically mounted cylinder which is free to oscillate in cross-flow (y-axis) is studied numerically. The configuration sketch of flow over the cylinder with a rectangular computational domain is shown in Fig. 1. The overall size of the domain in the inline and the transverse directions is 30D and 20D, respectively. The center of the cylinder is placed at 10D upstream from the inlet boundary, 20D downstream from the outlet boundary and 10D from the lateral boundaries. The grid which is used to solve the problem is illustrated in Fig. 2.

Fig. 1
figure 1

Sketch of the circular cylinder: a computational domain and the boundary conditions b close-up view of a flexibly mounted cylinder

Full size image
Fig. 2
figure 2

Grid used to solve the problem

Full size image

Governing equations and numerical method

The nanofluid used in the present study is \({\text{Al}}_{2} {\text{O}}_{3}\)–water which consists of nanoparticles with an average size of 29 nm. The thermophysical properties (dynamic viscosity, thermal conductivity, specific heat capacity, density) of the base fluid and the nanoparticles which are used for the calculations are presented in Table 1.

Table 1 Thermo-physical properties of \({\text{Al}}_{2} {\text{O}}_{3}\) nanoparticles and pure water
Full size table

The following assumptions for nanofluid are considered: The nanofluid is homogenous, thermal equilibrium (locally) exists between the two phases and dynamic viscosity, and thermal conductivity of the nanofluid is dependent on temperature [32]. The governing equations for unsteady, incompressible nanofluid consist of the continuity, the momentum and the energy equations. Thus, in vector form, the conservation equations in an arbitrary Lagrangian–Eulerian (ALE) frame [33] are expressed as:

$${\mathbf{\nabla }} \cdot {\mathbf{V}}_{{{\mathbf{nf}}}} = 0$$
(1)
$$\rho \left[ {\frac{{\partial {\mathbf{V}}_{{{\mathbf{nf}}}} }}{\partial t} + \left( {\left( {{\mathbf{V}}_{{{\mathbf{nf}}}} - \widehat{\varvec{V}}} \right) \cdot \nabla } \right){\mathbf{V}}_{{{\mathbf{nf}}}} } \right] = - {\mathbf{\nabla }}P + \mu_{\text{nf}} \nabla^{2} {\mathbf{V}}_{{{\mathbf{nf}}}}$$
(2)
$$\rho_{\text{nf}} c_{\text{nf}} \left[ {\frac{{\partial T_{\text{nf}} }}{\partial t} + \left( {{\mathbf{V}}_{{{\mathbf{nf}}}} - \widehat{\varvec{V}}} \right) \cdot \nabla T_{\text{nf}} } \right] = {\mathbf{\nabla }} \cdot \left( {k_{\text{nf}} {\mathbf{\nabla }}T_{\text{nf}} } \right)$$
(3)

where \(\rho\),\({\mathbf{V}}\), P and µ are the density, velocity, pressure and dynamic viscosity of the fluid, respectively. Furthermore, T and k are the temperature and fluid conductivity, respectively. Subscript nf stands for the nanofluid. Also \(\widehat{\varvec{V}}\) is the velocity of the mesh movement in y direction. The local Nusselt number on the cylinder which depends on the angular position (θ) and time (t) is determined as follows:

$${\text{Nu}}_{\text{loc}} \left( {\theta ,t} \right) = \frac{{h\left( {\theta ,t} \right)D}}{{k_{\text{bf}} }}$$
(4)

where \(k_{\text{bf}}\) is the base fluid thermal conductivity. \(h\left( {\theta ,t} \right)\) is the convective heat transfer coefficient on the cylinder surface and calculated as follows:

$$h = \frac{{q^{\prime \prime } \left( {\theta ,t} \right)}}{{T_{\text{w}} - T_{\infty } }}$$
(5)

where \(q^{\prime \prime } \left( {\theta ,t} \right)\) is the heat flux from the cylinder surface. By integrating the local Nusselt number on the cylinder surface, the surface-average Nusselt number is obtained:

$${\text{Nu}}\left( t \right) = \frac{1}{2\pi }\mathop \int \limits_{0}^{2\pi } {\text{Nu}}_{\text{loc}} \left( {\theta ,t} \right){\text{d}}S$$
(6)

The time-average of Nusselt number can be calculated by integrating the surface-average Nusselt number in a period of cylinder’s displacement (\(\tau\)):

$$\overline{\text{Nu}} = \frac{1}{\tau }\mathop \int \limits_{0}^{\tau } {\text{Nu}}\left( t \right){\text{d}}t$$
(7)

Total entropy generation in a two-dimensional problem is evaluated as follows:

$$S_{\text{gen}}^{\prime \prime \prime } = \frac{k}{{T^{2} }}\left[ {\left( {\frac{\partial T}{\partial X}} \right)^{2} + \left( {\frac{\partial T}{\partial Y}} \right)^{2} } \right] + \frac{\mu }{T}\left\{ {2\left[ {\left( {\frac{\partial u}{\partial X}} \right)^{2} + \left( {\frac{\partial v}{\partial Y}} \right)^{2} } \right] + \left( {\frac{\partial u}{\partial Y} + \frac{\partial v}{\partial X}} \right)^{2} } \right\}$$
(8)

The first term in the right-hand side of Eq. 9 is the entropy generation due to the heat transfer (\(S_{{{\text{g}},{\text{ht}}}}^{\prime \prime \prime }\)), and the second term is the entropy generation due to the fluid friction (\(S_{{{\text{g}},{\text{ff}}}}^{\prime \prime \prime }\)). Furthermore, to assess the contribution of the heat transfer and the fluid friction in total irreversibility, a non-dimensional parameter, the Bejan number (Be), is defined as follows [14]:

$$S_{\text{n}} = S_{\text{gen}}^{\prime \prime \prime } \frac{{kT_{\text{in}}^{2} }}{{q_{\text{cyl}}^{{{\prime \prime 2}}} }}$$
(9)
$$S_{{{\text{n}},{\text{ff}}}} = S_{{{\text{g}},{\text{ff}}}}^{\prime \prime \prime } \frac{{kT_{\text{in}}^{2} }}{{q_{\text{cyl}}^{{{\prime \prime 2}}} }}$$
(10)
$$S_{{{\text{n}},{\text{ht}}}} = S_{{{\text{g}},{\text{ht}}}}^{\prime \prime \prime } \frac{{kT_{\text{in}}^{2} }}{{q_{\text{cyl}}^{{{\prime \prime }2}} }}$$
(11)
$${\text{Be}} = \frac{{S_{{{\text{g}},{\text{ht}}}}^{\prime \prime \prime } }}{{S_{\text{gen}}^{\prime \prime \prime } }}$$
(12)

By using the mixture model [34], the density of nanofluid is obtained as follows:

$$\rho_{\text{nf}} = \left( {1 - \alpha } \right)\rho_{\text{bf}} + \alpha \rho_{\text{np}}$$
(13)

where \(\alpha\) is the volume fraction of nanoparticles. Subscripts nf, bf and np denote the nanofluid, the base fluid and the nanoparticle, respectively. The thermal conductivity of nanofluid is assumed as the combination of two parts [35]:

$$k_{\text{nf}} = k_{\text{static}} + k_{\text{brownian}}$$
(14)

Hamilton–Crosser model [36] is used to estimate \(k_{\text{static}}\) and \(k_{\text{brownian}}\):

$$k_{\text{static}} = k_{\text{bf}} \left[ {\frac{{(k_{{{\text{np}},{\text{eff}}}} + 2k_{\text{bf}} ) - 2\alpha \left( {k_{\text{bf}} - k_{{{\text{np}},{\text{eff}}}} } \right)}}{{(k_{{{\text{np}},{\text{eff}}}} + 2k_{\text{bf}} ) - \alpha \left( {k_{\text{bf}} - k_{{{\text{np}},{\text{eff}}}} } \right)}}} \right]$$
(15)
$$k_{\text{brownian}} = 5 \times 10^{4} \alpha C_{{{\text{p}}.{\text{bf}}}} \rho_{\text{bf}} \sqrt {\frac{{k_{\text{b}} T}}{{d_{\text{np}} \rho_{\text{np}} }}} g\left( {T,\alpha ,d_{\text{np}} } \right)$$
(16)

where \(k_{\text{b}}\) is the Boltzmann constant and equals to \(1.3806503 \times 10^{ - 23} \frac{J}{k}\). The term \(k_{{{\text{np}}.{\text{eff}}}}\) accounts for the effects of interfacial thermal resistance and is calculated as follows:

$$k_{{{\text{np}},{\text{eff}}}} = \frac{{d_{\text{np}} }}{{R_{\text{b}} + \left( {\frac{{d_{\text{np}} }}{{k_{\text{np}} }}} \right)}}$$
(17)

where \(R_{\text{b}}\) is the Kapitza resistance (\(4 \times 10^{ - 8} \frac{{{\text{km}}^{2} }}{\text{W}}\)). Similar to Eq. 15, the effective viscosity is obtained as follows:

$$\mu_{\text{nf}} = \mu_{\text{static}} + \mu_{\text{brownian}}$$
(18)
$$\mu_{\text{static}} = \frac{{\mu_{\text{bf}} }}{{\left( {1 - \alpha } \right)^{{\frac{5}{2}}} }}$$
(19)
$$\mu_{\text{brownian}} = 5 \times 10^{4} \alpha \rho_{\text{bf}} \sqrt {\frac{{k_{\text{b}} T}}{{d_{\text{np}} \rho_{\text{np}} }}} g\left( {T,\alpha ,d_{\text{np}} } \right)$$
(20)

The function g is a semi-empirical relation for water-\({\text{Al}}_{2} {\text{O}}_{3}\) nanofluid and determined as follows [37]:

$$\begin{aligned} g & = \left[ {\left( {a + b\;\ln \left( {d_{\text{np}} } \right) + c\;\ln \left( \alpha \right) + d\;\ln \left( \alpha \right)\ln \left( {d_{\text{np}} } \right) + e\;\ln \left( {d_{\text{np}} } \right)^{2} } \right)} \right]\ln \left( T \right) \\ & \quad + \;\left[ {m + h\;\ln \left( {d_{\text{np}} } \right) + i\;\ln \left( \alpha \right) + j\;\ln \left( \alpha \right)\ln \left( {d_{\text{np}} } \right) + k\;\ln \left( {d_{\text{np}} } \right)^{2} } \right] \\ \end{aligned}$$
(21)

where the coefficients a–k are listed in Table 2.

Table 2 Constant parameters of Eq. 22
Full size table

The cylinder displacement in the cross-flow is calculated by using a mass–spring–damping system as follows:

$$m_{\text{eq}} \ddot{y} + C_{\text{eq}} \dot{y} + k_{\text{eq}} y = f_{\text{l}} \left( t \right)$$
(22)

where y, \(\dot{y}\) and \(\ddot{y}\) are the displacement, velocity and acceleration of the cylinder in the cross-flow direction, respectively.\({\text{f}}_{\text{l}} \left( {\text{t}} \right)\) is the time-dependent lift force on the cylinder. The non-dimensional form of governing equation for the oscillating cylinder is expressed as:

$$\frac{{{\text{d}}^{2} y^{*} }}{{{\text{d}}t^{*2} }} + \left( {\frac{4\pi \zeta }{{V_{\text{r}} }}} \right)\frac{{{\text{d}}y^{*} }}{{{\text{d}}t^{*} }} + \left( {\frac{{4\pi^{2} }}{{V_{\text{r}}^{2} }}} \right)y^{*} = \frac{{C_{\text{L}} }}{{2m_{\text{r}} }}$$
(23)

where \(V_{\text{r}} = U_{\infty } /\left( {f_{\text{n}} D} \right)\) is the reduced velocity, \(f_{\text{n}} = \left( {2\pi } \right)^{ - 1} \sqrt {k_{\text{eq}} /m_{\text{eq}} }\) is the structural natural frequency of the cylinder, \(m_{\text{r}} = m_{\text{eq}} /\left( {\rho D^{2} } \right)\) is the mass ratio, \(\zeta = C_{\text{eq}} /\left( {2\sqrt {m_{\text{eq}} k_{\text{eq}} } } \right)\) is the damping ratio and \(C_{\text{L}} = {{f_{\text{L}} \left( t \right)} \mathord{\left/ {\vphantom {{f_{\text{L}} \left( t \right)} {\frac{1}{2}\rho U_{\infty }^{2} D}}} \right. \kern-0pt} {\frac{1}{2}\rho U_{\infty }^{2} D}}\) is the lift coefficient.

In this work, the governing equations with the arbitrary Lagrangian–Eulerian frame are solved by using the finite volume method (commercial software FLUENT). An improved fourth-order Runge–Kutta algorithm is employed to solve the cylinder displacement equation (Eq. 22). So, in order to determine the velocity and the displacement of the cylinder and the thermophysical properties of nanofluid, two user-defined functions (UDFs, programmed in C language) are embedded into the code. The PISO (pressure implicit with splitting of operator) algorithm for velocity–pressure coupling is used to calculate the coupling between the pressure and velocity fields. The second-order upwind scheme is implemented to discretize the momentum and energy convective terms. Convergence criteria are chosen to be \(10^{ - 6}\) for velocity components, continuity and energy equations to achieve reliable results. The first-order implicit scheme is applied for time discretization. The non-dimensional time step is set to \(U_{\infty } \Delta t/D = 0.002\), to ensure that the results are independent of the time step size and the requirement of Courant–Friedrichs–Lewy (CFL) number being smaller than one [38].

Grid independence study and validation

The grid independence study is conducted on four grids with different densities for the stationary cylinder at Reynolds number of 150 and air (with constant properties) as the fluid. The properties of air are evaluated at 350 k. Table 3 compares the calculated averaged Nusselt numbers and lift and drag coefficients for different grid sizes. The difference between the results of meshes with the size of 34,000 and 87,000 is less than 0.03%. Therefore, the mesh with 34,000 cells is selected because of less calculation time needed compared to the more refined grid.

Table 3 Grid size independence study
Full size table

To establish the validity of the numerical method and accuracy of VIV computations, different cases were studied. In the first validation test case, numerical simulation of flow over a stationary cylinder at Re = 100 and 200 was performed (air as the fluid) and the lift and the drag coefficients (\(C_{\text{d}} , C_{\text{l}}\)), the Strouhal (St) number and the Nusselt number are compared with the numerical and experimental results obtained from other researchers. Also, the calculated Nusselt numbers are compared with the Churchill and Bernstein correlation [39] (Eq. 24). Good agreement between the numerical and the experimental results with current modeling is observed (Tables 4 and 5).

$${\text{Nu}} = 0.3 + \frac{{0.62\;\text{Re}^{{\frac{1}{2}}} \Pr^{{\frac{1}{3}}} }}{{\left[ {1 + \left( {\frac{0.4}{\Pr }} \right)^{{\frac{2}{3}}} } \right]^{{\frac{1}{4}}} }}\left[ {1 + \left( {\frac{\text{Re}}{282000}} \right)^{{\frac{5}{8}}} } \right]^{{\frac{4}{5}}}$$
(24)
Table 4 Comparison of the calculated results with those reported in the literature. Re = 100
Full size table
Table 5 Comparison of the calculated results with those reported in the literature. Re = 200
Full size table

In the second validation test case, the simulation is performed for the VIV of a cylinder with the convective heat transfer at Re = 150, \(m_{\text{r}} = 2\) and \(\zeta = 0\). Water at 300 k with constant properties is used as the fluid. The maximum amplitude of vibrations is compared with those reported by researchers in Fig. 3 and achieved good agreement. The average Nusselt number for different reduced velocities is compared with those by Izadpanah et al. [40] in Fig. 4. The agreement between the present results and other numerical results is excellent.

Fig. 3
figure 3

Comparison of the cylinder displacement amplitude with the literature (ζ = 0)

Full size image
Fig. 4
figure 4

Comparison of the Nusselt number with the literature (ζ = 0)

Full size image

Results and discussion

In this section, a complete numerical result for the forced convection heat transfer and entropy generation of pulsating nanofluid flow past a vibrating circular cylinder is presented for \(m_{\text{r}} = 2\) and \(\zeta = 0.01\). The thermo-hydrodynamic characteristics are investigated in the range of \(0 \le \alpha \le 5\)%, \(3 \le V_{\text{r}} \le 8\) and \(0 \le \beta \le 1\). This result section is divided into two subsections. The role of VIV (of nanofluid flow) on the heat transfer enhancement and entropy generation under the influence of constant inlet velocity is analyzed in ‘Vortex-induced vibrations of a cylinder: constant inlet velocity’ section and under pulsating inlet velocity in ‘Vortex-induced vibrations of a cylinder with oscillating inlet velocity’ section.

Vortex-induced vibrations of a cylinder: constant inlet velocity

Figure 5 shows time histories of lift coefficient, averaged Nusselt number and entropy generation on the cylinder for \(\alpha = 5\%\) and \(V_{\text{r}} = 4\). Furthermore, the vorticity contours of four different positions of the cylinder (namely a, b, c and d) are shown in this figure. As can be seen, the vortex shedding pattern is 2S (two single vortices shed per cycle) mode with two vortex streets. The vortices are shed in near maximum or minimum amplitude of cylinder displacement. The lift coefficient is in the same phase as the cylinder displacement. Since in one period of cylinder displacement two periods of Nusselt number (or entropy generation) occurred, the frequency of Nusselt number is two times of cylinder displacement. The time history of Nusselt number is similar to that of the entropy generation with the same frequency.

Fig. 5
figure 5

Lift coefficient, Nusselt number and total entropy generation for different positions of the cylinder in a period of vibrations

Full size image

Figure 6 illustrates time histories of Nusselt number, entropy generation, their fast Fourier transform (FFT) analysis and corresponding vorticity contours for \(V_{\text{r}} = 3 - 8\) and \(\alpha = 5\%\). The vorticity contours are captured when the cylinder is located in its maximum position. The vortex shedding pattern for all reduced velocities is 2S mode with one or two vortex streets. The amplitude of cylinder displacement, Nusselt number and entropy generation is considerable for reduced velocities of 4–7, and the dominant frequency ratio of displacement (\(f/f_{0}\)) is close to one in these reduced velocities, so these reduced velocities are in the lock-in region. In the FFT analysis of Nusselt number and entropy generation at \(V_{\text{r}} = 4\), two dominant frequencies are observed. Each of them is related to one of the two pikes which are existed in a period of Nusselt number or entropy generation.

Fig. 6
figure 6

Displacement, Nusselt number and total entropy generation for different reduced velocities of the cylinder

Full size image

The local entropy generation and the Nusselt number on the maximum position of the cylinder are illustrated in Fig. 7. These plots show that the maximum entropy generation and Nusselt number are related to the stagnation point of the cylinder. The local entropy generation and the Nusselt number decrease continuously from the stagnation point to the boundary layer separation point. Moreover, because of flow mixing due to vortex forming and shedding, these two values increase in the rear of the cylinder. Figure 8 depicts the effects of the nanoparticle concentration on the local entropy generation and Nusselt number. As can be seen, by increasing the nanoparticle concentration, the local Nusselt number increases. The maximum local Nusselt number increases by 19% in comparison with the pure water.

Fig. 7
figure 7

Local entropy generation and Nusselt number plots when the cylinder is located at its maximum position, the results are plotted for different reduced velocities

Full size image
Fig. 8
figure 8

Local entropy generation and Nusselt number plots when the cylinder is located at its maximum position, the results are plotted for different nanofluid concentrations

Full size image

The variation in averaged Nusselt number (\(\overline{\text{Nu}}\)), the total non-dimensional entropy generation (\({\text{S}}_{{{\text{n}},{\text{total}}}}\)) and Bejan number (\({\text{Be}}\)) versus the reduced velocity for different values of the nanoparticle volume fraction (\(\alpha\)) are shown in Fig. 9. By increasing the nanoparticle concentration, the fluid thermal conductivity increases, and consequently, the heat transfer rate from the cylinder enhances. It is worth noting that when the induced lift force frequency is synchronized with the natural frequency of the system (a definition that was introduced by Sarpkaya [46]), the heat transfer rate from the cylinder surface increases compared to the stationary cylinder. Thus, at \(\alpha = 5\%\) and \(V_{\text{r}} = 4\;{\text{and}}\;5\) the Nusselt number reaches to its maximum because of higher nanoparticle volume fraction and maximum displacement amplitude. According to this figure, the maximum heat transfer enhancement with respect to the stationary cylinder is 26.1%. Moreover, for \(V_{\text{r}} = 3,7\;{\text{and}}\;8\), the average Nusselt number is smaller than the fixed cylinder Nusselt number. These results clearly show that the lock-in phenomenon can highly affect the heat transfer from a vibrating cylinder by means of different vortex shedding patterns and frequencies. By increasing the volume fraction of nanoparticles (\(\alpha\)), the total non-dimensional entropy generation (\(S_{{{\text{n}},{\text{total}}}}\)) decreases. For \(V_{\text{r}} = 4\;{\text{and}}\;5\), \({\text{S}}_{{{\text{n}},{\text{total}}}}\) is minimum because of better heat transfer performance from the cylinder surface. Based on the results of these figures, synchronization can profoundly affect the entropy generation in the domain. Furthermore, using nanofluid with \(\alpha = 5\%\) can decrease \(S_{{{\text{n}},{\text{total}}}}\) by 21% which leads to a significant reduction in the irreversibility produced by the heat transfer and the fluid friction. In analyzing the entropy generation, the Bejan number indicates the fraction of thermal entropy generation compared to the total entropy generation. As can be seen in Fig. 9c, by increasing \(\alpha\), the Bejan number decreases due to the heat transfer enhancement. Thus, the minimum and the maximum of Bejan number are related to \(V_{\text{r}} = 4\), \(\alpha = 5\) (with the maximum heat transfer rate from the cylinder) and \(V_{\text{r}} = 8\), \(\alpha = 0\) (with the minimum heat transfer rate from the cylinder), respectively.

Fig. 9
figure 9

Average Nusselt number, total non-dimensional entropy generation and Bejan number for different reduced velocities and nanofluid concentrations

Full size image

There are two sources of entropy generation, e.g., due to fluid friction and heat transfer. Because the Bejan number is greater than 0.5 (≈ 1), the entropy generation due to the fluid friction can be neglected compared to the latter. Hence, Fig. 10 illustrates the contours of the entropy generation due to heat transfer in the domain. As can be seen from these figures, the entropy generation distribution in the domain is very similar to the vortex pattern of the cylinder. And this is because the temperature gradients are higher in the vortexes due to mixing the fluid in these regions.

Fig. 10
figure 10

Entropy generation contours in the domain due to heat transfer

Full size image

Vortex-induced vibrations of a cylinder with oscillating inlet velocity

In this part of the study, the effects of harmonic inlet velocity with different frequencies and amplitudes on displacement, heat transfer and entropy generation of the cylinder are studied. Implemented harmonic inlet velocity is described as follows [47]:

$$U_{{\left( {\text{t}} \right)}} = U_{\infty } \left( {1 + \beta \sin 2\pi ft} \right)$$
(25)

The inlet velocity consists of two parts: a constant part (\(U_{\infty }\)) and a harmonic part. The constant part is used for calculating Reynolds number and reduced velocity. The harmonic part causes inlet velocity oscillations, and its average is equal to zero in a period of inlet velocity oscillations. Constant \(\beta\) controls the inlet velocity oscillation amplitude, and the inlet velocity is constant for \(\beta = 0\). Furthermore, \(f\) and \(t\) are the frequency of oscillations and time (s). Simulation is performed for reduced velocities of 4 and 6. The natural frequency of the system for these reduced velocities is 31 and 21 Hz, respectively. The inlet velocity frequency is set equal to these two natural frequencies.

Figure 11 depicts the vorticity contours of the cylinder for different inlet velocity oscillation amplitudes at \(V_{\text{r}} = 4\;{\text{and}}\;6\). As can be observed, the vortex shedding pattern for \(\beta = 0, 0.01, 0.10,\;{\text{and}}\;0.25\) at both reduced velocities is 2S mode with one or two vortex streets, whereas for \(\beta = 1\), two pairs of vortices are shed from the cylinder (at two vortex streets) in one cycle of vibration (2P mode). Each pair of vortices contains the strong (first one) and weak (second one) vortices. The second vertex disappears due to the friction in downstream.

Fig. 11
figure 11

Vortex shedding pattern of the cylinder for different values of the parameter \(\beta\)

Full size image

Figure 12 shows time histories of the averaged Nusselt number, entropy generation, the cylinder displacement and their FFT analyses for different \(\beta\) at \({\text{V}}_{\text{r}} = 4\). The maximum variation in Nusselt number and entropy generation occurs at \(\beta = 1\), although in this inlet velocity oscillation amplitude the cylinder displacement amplitude is lower than other \(\beta\). In other words, at \(\beta = 1\) the variation in heat transfer increases and the vibration of cylinder suppresses. There are two dominant frequencies in FFT analysis of \(\beta = 1\), which are related to two extremum points in a period of cylinder displacement and are due to the vortex shedding pattern (2P mode). The FFT analyses indicate that the dominant frequency of each of the three parameters can be significantly affected by the values of \(\beta\).

Fig. 12
figure 12

Nusselt number, total entropy generation and non-dimensional displacement of the cylinder and their FFT for \(V_{\text{r}} = 4\)

Full size image

Figure 13 illustrates time histories of the averaged Nusselt number, the entropy generation, the cylinder displacement and their FFT analyses for different \(\beta\) at \({\text{V}}_{\text{r}} = 6\). Unlike \({\text{V}}_{\text{r}} = 4\), in this reduced velocity the variations in inlet velocity oscillation amplitude have not considerable effects on the cylinder displacement; also the dominant frequency of displacement at all \(\beta\) is close to one. But, like \({\text{V}}_{\text{r}} = 4\), the maximum variation in the Nusselt number and the entropy generation are related to \(\beta = 1\).

Fig. 13
figure 13

Nusselt number, total entropy generation and non-dimensional displacement of the cylinder and their FFT for \({V}_{\text{r}} = 6\)

Full size image

Conclusions

Forced convection heat transfer and entropy generation of Al2O3–H2O nanofluid flow past a vibrating circular cylinder using a mass–spring–damping system were investigated. To evaluate the irreversibilities produced by the heat transfer and the friction, the entropy generation in the domain was evaluated. It was found that by increasing nanoparticle concentrations up to 5%, heat transfer from the cylinder can be enhanced by 26.1% compared to heat transfer from a fixed cylinder (pure water as fluid). In the lock-in region, both the average Nusselt number and the maximum amplitude of the cylinder displacement increased considerably. The entropy generation due to heat transfer was dominant, and it can be investigated by inspecting Fig. 7c (where \(Be \approx 1\)). Furthermore, it was shown that by using nanofluid with \(\alpha = 5\%\), the non-dimensional entropy generation can be reduced by 21% in the domain. To investigate the effects of free stream velocity oscillations on the cylinder displacement, the heat transfer, and the entropy generation, a harmonic part was added to it. By increasing the inlet velocity oscillation amplitude, the vortex shedding pattern changes from 2S to 2P. The inlet velocity oscillation amplitude had considerable effects on the variations in heat transfer, entropy generation and cylinder displacement (especially at \(= 1\)).