1 Introduction

Researchers have always been interested in the movement of drops or bubbles in a fluid under a temperature gradient [1,2,3]. The uneven surface tension, caused by the temperature gradient, creates shear stresses at the interface between two immiscible fluids. Viscosity forces caused by temperature gradients cause bubbles or drops to move from colder to hotter regions. This phenomenon is known as thermocapillary migration. Zhang et al. [4] state that thermocapillary force can regulate bubble/droplet dynamics, heat and mass transfer, as well as fluid dynamics in microgravity or space.

Young et al. [5] conducted the first experiment in 1959 wherein a small bubble was displaced in a direction opposite to vertical by applying a negative temperature gradient while accounting for gravity. Subsequently, in a zero gravity environment, Thompson et al. [6] observed experimentally Marangoni flow in three fluids: silicone oil, ethylene glycol, and ethanol. The migration of droplets and bubbles in space shuttles has been the subject of numerous on-board studies. Temperature field disturbance caused by bubble/drop movement, was identified interferometrically by Wozniak et al. [7]. The obtained results and the numerical results showed a strong qualitative agreement. For high Marangoni numbers, it is challenging to determine experimentally whether the steady velocities of the bubble migration have been reached. This is why Xie et al. [8] observed some discrepancies between their experimental results and predictions based on numerical data. Consequently, intricate behaviors that require additional research were observed. Cui et al. [9] studied the migration of a single bubble and the interaction between two migrating bubbles for large Ma in an onboard experiment. The results of the experiment showed that the smaller bubble migrates more slowly when it is passed by a larger one, and they also found that the data were consistent with theoretical predictions and computational findings. In general, especially in space, it is difficult to perform experiments to observe bubble or drop behavior and collect detailed data on it. Fortunately, in order to better understand thermocapillary migration phenomena and overcome experimental challenges, scientists have been able to test a number of hypotheses that were previously impossible to verify, through the use of CFD studies. Herrmann et al. [10] made numerical predictions, regarding thermocapillary drop motion and deformation. Comparable results were obtained when comparing the Volume of Fluid (VOF) and Refined Level Set Grid (RLSG) methods for tracking the phase interface. Using Ansys-Fluent software, Alhendal et al. [11,12,13] developed a CFD model to compute the migration of single and multiple bubbles/droplets in a zero-gravity environment for both low and high Marangoni numbers. Further studies on the migration of two or more bubbles were conducted after the motion of a single bubble was modeled [14, 15]. Additional factors that may affect the bubble/drop migration include rotation [16, 17] and vibration [18, 19]. Changes in the shape or boundary conditions of the container can cause a range of bubble/drop motion behaviors, as illustrated by the works of [20,21,22,23,24]. In this paper, the cylindrical container is filled by silicone oil containing a Fluorinert FC-75 droplet. It is heated from the top, cooled from the bottom, and a heat flux is applied to both sidewalls. This container is vibrating horizontally in X axis. The influence of vibration on droplet migration for different heat fluxes is discussed. The flow pattern describing the droplet motion as well as the droplet’s arrival time will be presented for various vibration amplitudes from 0.005 to 0.02 m/s2 and sidewalls heat fluxes from 5 to 30 W.

YGB linear model, developed by Young et al. [5], is adopted to calculate the migration velocity of bubbles and droplets:

$${V}_{YGB}=\frac{2\left|\frac{d\sigma }{dT}\right|{r}_{d}\lambda \frac{dT}{dx}}{(2\mu +3{\mu }^{\prime})(2\lambda +\lambda ^{\prime})}$$
(1)

that works well with low Reynolds and Marangoni numbers:

$$R{e}_{T}=\frac{{r}_{d}{V}_{T}}{\nu }$$
(2)
$$Ma_{T}=\frac{{r}_{d}{V}_{T}}{\alpha }={\mathit{Re}}_{T}.Pr$$
(3)

where the ratio of thermal diffusivity to kinematic viscosity is known as the Prandtl number:

$$\mathit{Pr}=\frac{\nu }{\alpha }$$
(4)

v: the kinematic viscosity, is measured in m2/s:

$$\nu =\frac{\mu }{\rho }$$
(5)

Equations (2) and (3) use the velocity \({V}_{T}\), which is obtained from the tangential stress balance at the free surface, to scale the migration velocity (m/s).

$${V}_{T}=\frac{\frac{d\sigma }{dT}\!.\frac{dT}{dx}\!.{r}_{d}}{\mu }$$
(6)

where \(\mu\) and \({\mu }{\prime},\lambda and {\lambda }{\prime}\) are the droplet's and the host fluid's respective dynamic viscosity and thermal conductivity. Where \({r}_{d}\) is the droplet radius and \(\rho\) is the host fluid density. The interfacial tension rate change is expressed by the constant \(d\sigma /dT\), also known as \({\sigma }_{T}\). The temperature gradient applied to the host fluid is expressed as dT/dX.

2 Problem statement:

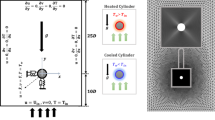
A silicone oil-filled cylindrical form measuring 60 mm in diameter and 120 mm in height is considered (Fig. 1). The lower plate center is the coordinate system's origin, and the vertical axis, X, is oriented upward. Each wall has a non-slip coating and is impermeable. The top and bottom walls are maintained at temperatures: Ttop > Tbottom. An incompressible Newtonian fluid called silicone oil is combined with a Fluorinert FC-75 droplet. Its physical properties do not change, with the exception of density, viscosity, and surface tension. Later on, as the linear expression in Eq. 11 shows, surface tension varies with temperature. Once a time-independent temperature distribution is obtained and the velocity is set to zero, the time-dependent movement of the droplets is released. Gravity is not taking into account, meaning zero gravity environment is considered. Ultimately, a 3D and 2D axisymmetric model is used in this work to analyze the impact of heated sidewalls caused by a continuous flux on the migration of thermocapillary droplets in a vibrated fluid. The vibration is in X direction.

Fig. 1
figure 1

Configuration scheme

Full size image

The density and viscosity thermophysical characteristics of silicone oil and Fluorinert FC-75 are comparable to those reported by Hadland et al. [25]. A gradient of interfacial tension of 3.6 × 10–5 N/m.K, is also employed. The boundary conditions for the case in Fig. 1 are as the following:

  • On the sidewalls: \(\overrightarrow{\nu }\) = \(\overrightarrow{0}\), Q = constant for x = 30 mm, x = -30mm, z = 30 mm and z = 30 mm \(\forall\) y.

  • Top side: \(\overrightarrow{\nu }\) = \(\overrightarrow{0}\), Ttop = 343 K for y = 120 mm \(\forall\) x and \(\forall\) z.

  • Bottom side: \(\overrightarrow{\nu }\) = \(\overrightarrow{0}\), Tbottom = 283 K for y = 0 mm \(\forall\) x and \(\forall\) z.

In the results, the same boundary conditions are considered, we will only modify the height and the radius of the cylinder to 60 mm and 30 mm then to 90 mm and 45 mm, respectively.

3 Computational procedure

The liquid/liquid interface was tracked using the volume of fluid (VOF) method, and equations pertaining to continuum conservation for two-phase flow are solved using Ansys-Fluent software.

Kumar et al. (2022) [3, 11, 18] claim that VOF method works incredibly well for solving issues involving droplets or bubbles in a liquid. In order to attain greater accuracy on the free surface, the geo-reconstruction scheme is employed [26,27,28]. The droplet volume fraction in the liquid phase is 1, whereas the droplet phase's volume fraction is 0. The droplet-liquid interface's motion is tracked by the cell, where αd is a number between 0 and 1. The momentum equation for the domain as a whole, for both phases, is as follows:

$$\frac{\partial }{\partial t}\;(\rho \overrightarrow{\nu })+\nabla .(\rho \overrightarrow{\nu }\overrightarrow{\nu })=-\nabla p+\nabla .[\mu (\nabla \overrightarrow{\nu }+\nabla {\overrightarrow{\nu }}^{T})]+\overrightarrow{F}+{\overrightarrow{F}}_{vib}$$
(7)

where \(\overrightarrow{v}\) is treated as the mass-averaged variable:

$$\overrightarrow{v}=\frac{{\alpha }_{d}{\rho }_{d}{\overrightarrow{v}}_{d}+{\alpha }_{L}{\rho }_{L}{\overrightarrow{v}}_{L}}{\rho }$$
(8)

\({\overrightarrow{F}}_{vib}\) is the vibration force expressed as:

$${\overrightarrow{F}}_{vib}=\rho{\overrightarrow {A}}_m\sin\left(2\pi\mathrm{ft}\right)$$
(9)

with \({\overrightarrow{A}}_{m}\) (Am,0,0) and f, bubble vibration amplitude and frequency, respectively.

The interface forces arising from the surface tension force per unit volume are represented by the symbol \(\overrightarrow{F}\) in Eq. 7. It is composed of normal force, \(\overrightarrow{{F}_{N}}\), and tangential one, \(\overrightarrow{{F}_{T}}\). \(\overrightarrow{{F}_{N}}\) is calculated using the Continuum Surface Force (CSF) model, which was introduced by Brackbill et al. [29]:

$$\overrightarrow{{F}_{N}}=\sigma \frac{\rho k\overrightarrow{n}}{\frac{1}{2}({\rho }_{L}+{\rho }_{d})}$$
(10)

For surface tension:

$$\sigma ={\sigma }_{0}+{\sigma }_{T}({T}_{0}-T)$$
(11)

where \({\sigma }_{T}\) is the surface tension coefficient and \({\sigma }_{0}\) is the surface tension at a reference temperature \({T}_{0}\).

The tangential surface tension force is defined as:

$$\overrightarrow{{F}_{T}}={-\sigma }_{T}{\nabla }_{s}T$$
(12)

The liquid temperature is represented by \(T\), the local surface curvature is represented by \(k\), and the surface normal is represented by \(\overrightarrow{n}\).

$$k=-(\nabla \widehat{n})=\frac{1}{\left|\overrightarrow{n}\right|}\left[\left(\frac{\overrightarrow{n}}{\left|\overrightarrow{n}\right|}.\nabla \right)\left|\overrightarrow{n}\right|-(\nabla .\overrightarrow{n})\right]$$
(13)

The volume droplet fraction can be obtained by solving the continuity equation for droplet-liquid interface tracking:

$$\frac{\partial }{\partial t}({\alpha }_{d}{\rho }_{d})+\nabla \cdot ({\alpha }_{d}{\rho }_{d}{\overrightarrow{v}}_{d})=0$$
(14)

In order to track the droplet-liquid interface, the continuity equation for the volume droplet fraction must be solved.

$${\alpha }_{d}+{\alpha }_{L}=1$$
(15)

where \({\alpha }_{d}\) and \({\alpha }_{L}\) represent the volume fractions of droplets and liquids, respectively. The following expressions are used to calculate the density and viscosity of each cell at the interface:

$$\rho ={\alpha }_{d}{\rho }_{d}+(1-{\alpha }_{d}){\rho }_{L}$$
(16)
$$\mu ={\alpha }_{d}{\mu }_{d}+(1-{\alpha }_{d}){\mu }_{L}$$
(17)

where density, viscosity, and volume fraction are different phases represented by \(\rho\), \(\mu\) and \({\alpha }_{d}\) respectively. The energy equation for the two phases is also calculated.

$$\frac{\partial }{\partial t}(\rho E)+\nabla .[\overrightarrow{\nu }(\rho E)+p)]=\nabla .({\kappa }_{eff}\nabla T)$$
(18)

Energy (E) and temperature (T) are mass-averaged variables in the VOF model:

$$E=\frac{{\sum }_{q=1}^{n}{\alpha }_{q}{\rho }_{q}{E}_{q}}{{\sum }_{q=1}^{n}{\alpha }_{q}{\rho }_{q}}$$
(19)

where the shared temperature and the phase's specific heat are the basis for each phase's Eq. 19, respectively. The phases also share the same properties, \(\rho\) and \({k}_{eff}\) (effective thermal conductivity).

4 Grid size dependency

To examine and ensure that the simulation results are independent of the cell density, grid independence was attained by increasing the number of grid cells from 224 to 976 along the X, Y, and Z axes. Table 1 presents a mesh size dependence study for the 3D simulation. The relationship between the droplet's travel time and distance in each of these five scenarios is depicted in Fig. 2. It should be noted that the displacement velocity used in this work is predicated on the idea that it represents the Y-direction velocity of the thermocapillary droplet flow. All 3D calculations in this study were performed using grid 3, which has a total cell of 263,424 with 472 cells per droplet.

Table 1 3D grid sensitivity check for ddrop = 10 mm
Full size table
Fig. 2
figure 2

Droplet nose ascent distance versus time (s) for five distinct grid sizes

Full size image

5 Results and discussion

First, by considering the sidewalls adiabatic, the accuracy of the current model is validated with literature. Then, the impact of increasing the lateral heat flux (Q) from 5 to 30 W and the vibration amplitude from 0.005 to 0.02 m/s2 on the thermocapillary migration of the droplet from cold to hot walls in a vibrating fluid inside a stationary cylinder, is investigated. For all the studied cases, the cylinder bottom and top are maintained at constant temperatures of 283 and 343 K, respectively. The droplet is positioned on top of the cold surface in each case by a factor of 2 × droplet diameter (d). A user-defined function (UDF) was used to relate temperature to viscosity, density, and surface tension, and another UDF was used to link the vibration frequency and amplitude to time.

5.1 Validation with literature results

The obtained results match the space experiment carried out by Xie et al. [8] qualitatively (Figs. 6 and 7). As the Marangoni number increases, the velocity of the gradient droplets tends to approach an asymptotic value of about 0.3. In a similar vein, our numerical results concur with Le et al. [24] data. The ambient temperature distribution of a moving Fluorinert FC-75 droplet for different time steps at MaT = 713.13 is plotted in Fig. 3. The interferogram and the simulated results produced by [8] show a similar distribution of results.

Fig. 3
figure 3

The well-accepted CFD comparison presents results against literature data

Full size image

As the droplet moves away from the cold bottom, the temperature difference between its surface and interior becomes significant. Because the drop surface takes longer to heat up, the surrounding liquid heats up faster, causing the liquid within the droplet to recirculate. At the droplet back, this leads to the formation of a longer thermal wake (Fig. 4). Actually, two distinct types of heat transfer can account for droplet migration. On the one hand, conduction occurs between the droplet and the host liquid. On the other hand, convection begins within the droplet.

Fig. 4
figure 4

Thermocapillary droplet trajectory toward the hotter side with adiabatic sidewalls

Full size image

After validating the model for adiabatic walls, migration behavior of a droplet at various Marangoni numbers will be studied under the influence of different vibration amplitudes and sidewalls fluxes. The idea is to study the emergence of powerful forces, such as thermocapillary and low vibration forces, that were disregarded and hidden when Earth's gravity was present, on droplet behavior in zero gravity environment.

5.2 Influence of varying frequency amplitude (Am = 0.005, 0.01, 0.015, 0.02 m/s2) and cylinder side wall heat flux (Q = 0 to 30 W) on thermocapillary droplet migration (f = 0.1 Hz)

A 5 mm diameter droplet of Fluorinert FC-75 liquid is placed in a Silicone oil (DOW-Corning DC-200 series, nominal viscosity 10 cst). The vibration frequency (f) is fixed at 0.1 Hz. The cylinder height is 60mm and its diameter is 30mm. At first, for a fixed sidewalls flux value, the vibration amplitude (Am) of the host fluid is changed from 0.005 to 0.02 m/s2. Then, for each amplitude, the sidewalls flux is varied from 0 to 30W. The thermal gradient is ∇T = 1000 K/m, which corresponds to Prandtl, Reynolds, and Marangoni numbers equal to 118, 2.64, and 312, respectively for adiabatic walls. Due to heating from the sidewalls, the thermophysical properties of the host fluid changes which leads to different values of Prandtl number and consequently different Marangoni numbers.

In Fig. 5, the flow pattern of the droplet motion is illustrated, showing the impact of heating the sidewalls and vibrating the host fluid. For a fixed sidewalls flux, a slight variation in vibration amplitude causes the droplet migration behavior to change, particularly as it approaches the top for Am = 0.005 m/s2. From a vertical translation, the droplet trajectory becomes undulated. Beyond Am = 0.01 m/s2, this latter becomes more deformed with amplitude increase. For a fixed vibration amplitude, a weak difference is observed on the droplet trajectory with high heat flux value, especially for Am < 0.02 m/s2. For Am = 0.02 m/s2, the drop does not reach the hot upper surface when Q = 30W. Instead, it stops at a certain position due to the lateral heat flow, which equalizes or rises the lateral temperature in respect to the upper surface temperature. As a result, the droplet comes to a stop and does not move sideways or upward.

Fig. 5
figure 5

Droplet migration dynamics at different values of MaT and Am for f = 0.1 Hz

Full size image

The droplet in the non-vibrating fluid takes less time to reach the hot surface (Fig. 6) regardless of the considered sidewalls flux value. With increasing vibration amplitude, the droplet motion is decelerated in all the cases. This result has already been mentioned by [30] for adiabatic sidewalls. In fact, this can be explained by the fact that vibration modifies the trajectory of the bubble from vertical translation to undulated one as observed in Fig. 5. With more undulations, the bubble has to travel additional distance in the curved path, which impacts negatively the arrival time.

Fig. 6
figure 6

Droplet migration time toward the hotter side (f = 0.1 s−1) for different vibration amplitude

Full size image

When the vibration amplitude is fixed (Fig. 7), different impacts of sidewalls flux variation on the droplet’s arrival time, are observed. For stationary fluid, the droplet moves faster as the sidewalls flux rise. This has been also found by [31] and related it to the extreme temperature difference that occurs when the sidewalls flux increase, generating a convective recirculation inside the droplet, and therefore pushes the droplet to accelerate. By adding vibration, the same effect as stationary case is obtained for Am = 0.005 m/ s2. Beyond this amplitude, the droplet reaches the top quickly when Q decreases. This can be explained by the fact that the trajectory becomes more undulated in the top with Q is higher for Am > 0.005 m/ s2 (Fig. 5). Therefore, the droplet takes more time to move up.

Fig. 7
figure 7

Droplet migration time toward the hotter side (f = 0.1 s−1) for different sidewalls fluxes

Full size image

5.3 Influence of varying cylinder height with heated sidewalls on thermocapillary droplet migration in vibrating fluid

In this section, the cylinder height is changed from 60 to 90 mm, as well as its diameter from 30 to 25mm. The top and bottom surfaces continue to have the same temperatures, which are 283 and 343 K, respectively. However, the temperature gradient inside the medium will become ∇T = 666.67 K/m instead of ∇T = 1000 K/m. The vibration frequency is still 0.1 Hz. A droplet with a diameter of 7.5 mm is released inside the cylinder at a distance of 2 × droplet diameter from the cold wall. By changing the height plus the heating due to the sidewalls flux, the properties of the fluid vary. Consequently, different Marangoni, Reynolds, and Prandtl numbers are obtained. The range of Marangoni numbers presented in the last section is from 312 to 459, while it will become from 468 to 689.5 in this section.

Figure 8 shows droplet’s behavior under different sidewalls heat fluxes and vibration amplitudes for a cylinder with 90 mm height. Compared to the cylinder with 60 mm height (Fig. 5), from a small vibration amplitude Am = 0.005 ms−2, the droplet trajectory is already undulated from Q = 0W and the number of undulations increased for higher Q. A decrease in the temperature gradient between the lower and upper surfaces causes an increase in the control of vibration and lateral flow on the droplet's behavior. For a fixed Q, the trajectory undulations are enhanced with Am increase. For Q = 30 W, the droplet does not reach the top regardless of Am. In fact, the high lateral flux heating the sidewalls is trying to equilaze the temperature while the vibration hindrances the droplet motion. Therefore, the droplet is trapped in a certain position depending on Q and Am. For a fixed Am, Q increment leads the droplet trajectory to undulate more.

Fig. 8
figure 8

Droplet dynamics at different values of sidewalls flux and frequency amplitude for a cylinder of 90 mm height at f = 0.1 s.−1

Full size image

As observed in Fig. 6, the droplet reaches quickly the top in no vibration case (Fig. 9). Regardless of Q, the droplet motion decelerates when Am is high. Obviously, it takes more time for the droplet to reach the top in a cylinder with a height of 90mm than 60mm in all cases. Augmenting the height, regardless of the internal forces, will increase the distance to cover.

Fig. 9
figure 9

Droplet migration time toward the hotter side for different Am

Full size image

For a fixed vibration amplitude, Fig. 10 shows how much time takes a droplet to reach the top under sidewalls flux variation. When there is no vibration, the droplet’s arrival time decreases with Q increment as already found for lower Marangoni numbers (Fig. 7). However, when vibration is added, the drop takes more time to arrive to the top with Q augmentation, from Am = 0.005 m / s2. This can be explained by the high number of undaltions that the droplet should cover to reach top ( Fig. 8) when Q is high.

Fig. 10
figure 10

Droplet migration time toward the hotter side for different Q

Full size image

6 Conclusions

A 3D simulation was performed using the Ansys-Fluent software to assess thermocapillary droplet migration in zero gravity. The volume of liquid (VOF) method was used to trace the liquid/liquid interface. After validating the combined CFD model with extant literature, the vibration amplitude and sidewalls heat flux were varied to investigate their effects on droplet’s dynamic and arrival time. For adiabatic sidewalls, the drop travels faster from the bottom to the top with sidewalls flux increase, while the droplet’s arrival time increase with vibration amplitude increment. This shows the importance of considering insignificant vibrations on earth that becomes very powerful in zero-gravity environment. For a vibrated fluid, depending on the height of the vessel, rising sidewalls heat flux can either accelerate or decelerate the thermocapillary droplet flow to reach the apex. Moreover, overestimating the sidewalls heat flux can have the opposite effect and cause the droplet to stop flowing.