1 Introduction

Reliability engineering is specifically referred to as a technical field that studies all kinds of failure-driven characteristics of a system. If everything went according to plan and all the requirements were satisfied, there would be no cause for complaint or failure, and as a result, there would be no need for reliability engineering. But, this is sadly not the case. Failure is almost always a part of systems. Any significant failure in the system's operation, or a series of smaller problems, could lead to a disaster that would harm human lives and damage the environment, ecosystem, and property in a way that can't be restored. Growing concern over the performance of critical systems has led researchers to develop various reliability techniques for more efficient analysis of these systems (Cai 1996a). Traditional reliability techniques rely on two assumptions: a binary-state assumption that the system can only be in one of two states: fully operating or completely failed, and a probability assumption, which means a system's reliability is measured by the probability that it will be able to carry out required tasks efficiently without any error during a certain time period (Kai Yuan et al. 1991a). Traditional reliability techniques are named "probist" by Cai (1996a), and the systems studied by it were known as "probist systems" (Cai 1996a; Kai Yuan et al. 1991a). Various researchers have applied traditional reliability techniques for the analysis of the complex systems (Jamadar et al. 2023; Kumari et al. 2019; Musa et al. 2023). However, in many systems, it is extremely challenging to estimate the correct probabilities due to presence of uncertainty in the data collected from the system. In addition, it is specifically highlighted that the probist reliability theory does not provide accurate results when the system fails very rarely or when hypothetical samples are used for result calculations. Also, the system can be present in more than two states i.e. system can work in partially failed mode. Consequently, neither the binary-state assumption nor the probability assumption can be used in all practical situations. Therefore, in order to overcome the limitations of probist theory Kai-Yuan et al., (1991c) have proposed the use of possibility and fuzzy-state assumptions as an alternative to probability and binary state assumptions. According to the possibility assumption, failure behavior of the system may be described in terms of possibility measures, and according to fuzzy-state assumption the system’s success and failure are described in terms of fuzzy states. Fuzzy states are defined by fuzzy set theory (FST) given by Zadeh (1965). Other benefits of using FST over probabilistic theory are:

  • Fuzzy theory is particularly useful in situations where the uncertainty is not easily quantifiable or does not fit well with traditional probabilistic models.

  • Fuzzy theory is beneficial when dealing with linguistic variables or qualitative data that are difficult to measure precisely. This is often the case in models that incorporate human reasoning and decision-making.

  • Fuzzy models can handle nonlinear relationships more effectively than probabilistic models.

FST is important for understanding and analyzing the reliability of industrial systems in unpredictable circumstances. FST has been extensively used for estimating the reliability of repairable systems. It provides a valuable tool for maintenance planning and decision-making. By analyzing failure data and repair times, FST can help identify potential weaknesses in a system and prioritize maintenance activities to ensure optimal performance and minimize downtime (Cai 1996a, b; Chen 1994; Kai Yuan et al. 1991a, b; Kumari et al. 2021; Mon and Cheng 1994; Verma et al. 2002). Thereafter, numerous direct and indirect fuzzy set expansions have been developed and successfully applied in the majority of real-life situations. Intuitionistic fuzzy set (IFS) theory given by Atanassov (1999), is one of the extensions of FST which assigns a non-membership and a membership degree independently in such a way that the total of the two degrees must be less than one. IFS theory is widely used for the reliability analysis of complex systems. Some of the significant contributions are mentioned below. Shu et al. (2006) did an analysis of printed circuit board assembly using expert's knowledge and experience. They utilized IFS for the analysis of the system. The integration of expert knowledge with the IFS technology allowed for a more efficient and effective evaluation of the system. Mahapatra and Roy (2009) evaluated the reliability of series and parallel systems using triangular IF numbers and their arithmetic operations. Kumar et al. (2013) evaluated the Membership function and Non-membership function reliability parameters of series and parallel systems using time-dependent IFS. Garg et al. (2013b) evaluated the reliability of engineering systems using IFS. Their study found that IFS proved to be a useful tool in assessing the reliability of complex engineering systems by considering various uncertainties and vagueness in the data. Kumar and Kaushik (2020) assessed the reliability of the AP1000 passive safety system by employing qualitative data, such as expert opinions and judgements, within the IFS environment. Utilising qualitative data was found to be a valuable method for evaluating the safety performance of the system, highlighting the significance of expert opinions in assessing intricate engineering systems such as the AP1000.

The fault tree analysis (FTA) method assumes that each event's underlying causes are random and unrelated to each other statistically. However, some frequent causes may produce relationships in event probabilities that go against the independence requirements and may increase the risk of failure. Markov models efficiently overcome this limitation. However, employing the Markov approach for analysing systems requires the computation of a substantial number of equations. PNs provide a convenient solution to all these limitations. The use of PNs permits the effective simultaneous construction of minimum cut and route sets, unlike the fault tree. Modeling a system using PNs has other advantages too, like making the overall understanding of the system better with its tools (Kumar and Aggarwal 1993). Knezevic and Odoom (2001) have combined the theory of PNs with FST and Lambda-Tau Methodology (LTM). Their strategy is based on quantitative analysis of systems utilizing the FST and LTM. Whereas, qualitative modeling of the system is done using PN, with fundamental events being represented by triangular membership functions; hence the resulting methodology was named Fuzzy Lambda-Tau Methodology (FLTM). FLTM was utilized by many researchers with the aim of finding the reliability of complex systems (Dhiman and Kumar 2022; Garg et al. 2013a; Knezevic and Odoom 2001; Sharma and Mamta 2022; Srivastava et al. 2019). FLTM has the drawback that it only considers the degree of membership for the reliability analysis of system. To overcome drawback of FLTM, researchers combined PNs theory with IFS theory and LTM, creating a method called Intuitionistic Fuzzy Lambda-Tau Methodology (IFLTM) (Garg 2013, 2014; Kushwaha et al. 2021, 2022). But it was later discovered that one critical aspect, i.e., the degree of neutrality, is missing from the IFLTM. The degree of neutrality may be observed in circumstances wherein, human perspectives result in "yes," "abstain," "no," and refuse responses. For instance, 600 people can cast a ballot in an election, and the voting results are summarized as follows: 350 voted in favor, 79 abstained from voting, 140 voted against, and 31 refused to vote. When a group votes "abstain,” it indicates they reject both “agree” and “disagree” with the candidate but still count the vote. Invalid ballots or voting absentees are both examples of group “refusal of voting" (Dutta and Ganju 2018). Thereafter, to overcome this shortcoming of IFS, the picture fuzzy set (PFS) was developed by Cuong and Kreinovich (2013, 2014). PFS takes into account the neutral, positive, and negative membership degrees of elements for a more realistic representation of human behavior. Hence, to overcome the drawbacks of FLTM and IFLTM/VLTM, the present work proposes a novel methodology known as the Picture Fuzzy Lambda-Tau Methodology (PFLTM) for assessing the behavior of complex systems under ambiguous and uncertain circumstances. The primary benefit of PFLTM is that it utilizes superior PFS for the analysis of complex systems.

Objective of the study includes the comparison of membership function of various reliability parameters obtained using proposed method with the one obtained using VLTM. Another important objective of the study is to compare the defuzzified values for different spreads \(\left(\pm 15\%,\pm 25,\pm 50\right)\) obtained by FLTM and VLTM with proposed PFLTM. Furthermore, risk analysis of the system is also done using picture fuzzy sets to overcome the drawbacks of traditional risk analysis methods and to identify the most critical component of the system. A paper mill's washing unit is used to demonstrate the suggested method. Various expressions of reliability measures like mean time to repair (MTTR), mean time between failures (MTBF), reliability, availability, and expected number of failures (ENOFs) are obtained, and there are numerical values with different spreads that are calculated and compared with crisp, FLTM, and VLTM.

The remainder of the article is structured as follows: The PN theory is introduced in Sect. 2, and the procedure for transforming the FTA model into a PN model is also given here. This section also describes the lambda-tau approach for estimating the reliability of repairable systems. Picture fuzzy sets theory is given in Sect. 3. A new method to find reliability using PNs and picture fuzzy sets is proposed in Sect. 4. An example of the washing unit of a paper mill has been taken into consideration in order to explain the suggested technique in Sect. 5. Also, this section compares the new methodology with the existing methods. Risk analysis of the washing unit is done in Sect. 6. Section 7 draws conclusions and Sect. 8 at the end contains the future scope of the study.

2 Basic concepts

2.1 Petri nets theory

Petri net (PN) is a mathematical tool developed by C.A. Petri in the early 1960s for modeling complex repairable systems. PNs are mathematical and graphical tools for defining the relationships between conditions and outcomes. It is considered powerful system modeling tool because it can express a wide range of logical relations. It may also be used to observe dynamic behavior in addition to simulation, reliability analysis, and failure monitoring. The following are some of the fundamental components of PNs: places, immediate transition, timed transition, arc, token, inhibitor arc. Figure 1 shows a simple net that includes all of the PN’s elements.

Fig. 1
figure 1

Elements of Petri Nets Model

Full size image

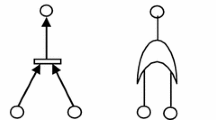
PNs are widely used by researchers for reliability analysis and failure monitoring of complex systems (Dhiman and Kumar 2022; Garg 2013, 2014; Garg et al. 2013a; Hura and Atwood 1988; Knezevic and Odoom 2001). In the discipline of reliability modelling, PNs are easier to use and outperform traditional FTA. ‘AND/OR’ logic gate operations for both “fault tree and Petri nets” are shown in Fig. 2.

Fig. 2
figure 2

‘AND/OR’ logic gate operations for fault tree and Petri nets

Full size image

2.2 Lambda-tau methodology (LMT)

LTM is a method used for quantitative analysis of the PN model repairable systems. The fundamental formulae for \(\lambda\) and \(\tau\) for components connected by ‘AND’ and ‘OR’ gates are deduced by Mishra (2012) and are shown in Table 1. These formulas might be used to derive a number of system parameters, including those given in Table 2.

Table 1 Conventional expression of Lambda-Tau methodology
Full size table
Table 2 Reliability parameters for system analysis
Full size table

3 Picture fuzzy set theory

Some basic concepts related to picture fuzzy set theory are given below:

3.1 Picture fuzzy set (PFS)

Let X be a universal set, than PFS \(\widetilde{A}\) defined on X is mathematically represented by following equation

$$\widetilde{A}=\left\{\left(x,{\mu }_{\widetilde{\text{A}}}\left(x\right), {\upeta }_{\widetilde{A}}\left(\text{x}\right),{\upnu }_{\widetilde{\text{A}}}(\text{x})\right)\vee x\in X\right\}$$
(3)

where \({\mu }_{\widetilde{\text{A}}}\left(x\right), {\upeta }_{\widetilde{A}}\left(x\right),{\upnu }_{\widetilde{\text{A}}}(x)\upepsilon [\text{0,1}]\) and \({\mu }_{\widetilde{\text{A}}}\left(x\right)\) is degree of positive membership, \({\upeta }_{\widetilde{A}}\left(x\right)\) is degree of neutral membership, \({\upnu }_{\widetilde{\text{A}}}\left(x\right)\) is degree of negative membership of \(x\) in \(\widetilde{A}\). Following are some properties of \({\mu }_{\widetilde{\text{A}}}\left(x\right), {\upeta }_{\widetilde{A}}\left(x\right),{{\vartheta }}_{\widetilde{\text{A}}}\left(x\right)\)

  1. i.

    Sum of \({\mu }_{\widetilde{\text{A}}}\left(x\right), {\upeta }_{\widetilde{A}}\left(x\right), {\upnu }_{\widetilde{\text{A}}}\left(x\right)\) is less than equal to 1

  2. ii.

    degree of refusal membership is given by \(1-\left({\mu }_{\widetilde{\text{A}}}\left(x\right)+ {\upeta }_{\widetilde{A}}\left(x\right)+{\upnu }_{\widetilde{\text{A}}}\left(x\right)\right)\)

For instance on a universal set X, if a PFS \(\widetilde{A}{\prime}s\) membership values are [0.5, 0.3, 0.1] where \({\mu }_{\widetilde{\text{A}}}\left(x\right)\) is 0.5, \({\upeta }_{\widetilde{A}}\left(x\right)\) is 0.3 and \({\upnu }_{\widetilde{\text{A}}}\left(x\right)\) is 0.1. It can be explained as, if X is the outcome of votes casted by ten individuals, then five voted in favor, three abstained from voting, one voted against, and one did not participate in the election.

3.2 α-cut of picture fuzzy set

Let \(\widetilde{A}\) is PFS on universal set X. Then α-cut of PFS \(\widetilde{A}\) is a crisp subset and is given by

$${A}^{\alpha }= \left\{x :x \in X such that {\mu }_{\widetilde{A}}\left(x\right)\ge \alpha , {1-\eta }_{\widetilde{A}}\left(x\right)\ge \alpha , 1- {\nu }_{\widetilde{A}}\left(x\right)\ge \alpha \right\}$$
(4)

where \(\alpha \in [\text{0,1}]\). That is.

$$\left. {\begin{array}{*{20}{l}} {A_{ + \;}^\alpha = \left\{ {x \in X:{\mu_{\tilde A}}\left( x \right) \geqslant \;\alpha } \right\}} \\ {A_{( \pm )}^{(1 - \alpha )} = x \in X: \in 1 - {\eta_{\tilde A}}(x)and} \\ {A_{ - \;}^{1 - \alpha } = \left\{ {x \in X:1 - {\nu_{\tilde A}}\left( x \right) \geqslant \;\alpha \;\;} \right\},} \end{array}} \right\}$$
(5)

are \(\alpha\) cut of positive, neutral, negative membership function respectively of PFS.

3.3 Triangular picture fuzzy set (TPFS)

Let \(\widetilde{A}\) be a PFS which can be represented as \(\widetilde{A}=\langle \left[\left(l,m,n\right); \mu ,\eta ,\nu \right]\rangle\), where \(l, m, n\) belongs to real numbers. Then membership function of triangular picture fuzzy number for positive, neutral, negative degrees of membership is given respectively by

$$(x)=\left\{\begin{array}{c}0; x\leq l\\ \mu \left(\frac{x-l}{m-l}\right); l\leq x\leq m\\ \mu \left(\frac{n-x}{n-m}\right); m\leq x\leq n\\ 0; n\leq x\end{array}\right.$$
(6)
$${1-\eta }_{\widetilde{A}}(x)=\left\{\begin{array}{c}0; x\leq l\\ \eta \left(\frac{x-l}{m-l}\right); l\leq x\leq m\\ \eta \left(\frac{n-x}{n-m}\right); m\leq x\leq n\\ 0; n\leq x\end{array}\right.$$
(7)
$${1-\nu }_{\widetilde{A}}(x)=\left\{\begin{array}{c}0; x\leq l\\ \nu \left(\frac{x-l}{m-l}\right); l\leq x\leq m\\ \nu \left(\frac{n-x}{n-m}\right); m\leq x\leq n\\ 0; n\leq x\end{array}\right.$$
(8)

Also α-cut of TPFS \(\widetilde{A}=\langle \left[\left(l,m,n\right); \mu ,\eta ,\nu \right]\rangle\) is given by Eq. 9 and graphically shown in Fig. 3.

Fig. 3
figure 3

α-cut of TPFS \(\widetilde{A}\)

Full size image

\({A}_{+ }^{\alpha }=\left[l+\frac{\alpha }{\mu }\left(m-l\right),n-\frac{\alpha }{\mu }\left(n-m\right)\right]{A}_{\pm }^{1-\alpha }=\left[l+\frac{\alpha }{\eta }\left(m-l\right),n-\frac{\alpha }{\eta }\left(n-m\right)\right]\),

$${A}_{- }^{1-\alpha }=\left[l+\frac{\alpha }{\nu }\left(m-l\right),n-\frac{\alpha }{\nu }\left(n-m\right)\right]$$
(9)

3.4 Arithmetic operations on two TPFSs

Consider two TPFSs \(\widetilde{A}=\langle \left[\left(l,m,n\right); {\mu }_{1},{\eta }_{1},{\nu }_{1}\right]\rangle\) and \(\widetilde{B}=\langle \left[\left(p, q, r\right); {\mu }_{2},{\eta }_{2},{\nu }_{2}\right]\rangle\) where \({0\le \mu }_{1}\le {\eta }_{1}\le {\nu }_{1}\le 1\) and \({0\le \mu }_{2}\le {\eta }_{2}\le {\nu }_{2}\le 1\). Then arithmetic operations between two TPFSs are given by equations.

  1. 1.

    \(\widetilde{A}\oplus \widetilde{B}=\langle \left[\left(l+p, m+q,n+r\right); {min(\mu }_{1},{\mu }_{2});{min(\eta }_{1},{\eta }_{2});{min(\nu }_{1},{\nu }_{2})\right]\rangle\) (10)

  2. 2.

    \(\widetilde{A}\ominus \widetilde{B}=\langle \left[\left(l-p, m-q,n-r\right); {min(\mu }_{1},{\mu }_{2});{min(\eta }_{1},{\eta }_{2});{min(\nu }_{1},{\nu }_{2})\right]\rangle\) (11)

  3. 3.

    \(\widetilde{A}\otimes \widetilde{B}\simeq \langle \left[\left(l\times p,m\times q,n\times r\right); {min(\mu }_{1},{\mu }_{2});{min(\eta }_{1},{\eta }_{2});{min(\nu }_{1},{\nu }_{2})\right]\rangle\) (12)

  4. 4.

    \(\widetilde{A}/\widetilde{B}=\langle \left[\left(l/p, m/q,n/r\right); {min(\mu }_{1},{\mu }_{2});{min(\eta }_{1},{\eta }_{2});{min(\nu }_{1},{\nu }_{2})\right]\rangle\), \(0 \notin \left[p, r\right]\) (13)

4 Proposed picture fuzzy lambda-tau methodology

A novel approach known as picture fuzzy lambda-tau methodology (PFLTM) has been proposed in the present work for the analysis of the repairable industrial systems. Fundamental assumptions of the methodology are:

  • The λ and τ of the components are constant, independent, and distributed exponentially.

  • After repairs components are considered as good as new.

  • All subsystems don't malfunction at the same time.

  • Each component has its own repair facility.

  • Repair of the component starts immediately after its failure.

First step of the methodology is to gathering data in the form of \(\lambda\) and \(\tau\) of components from multiple sources. Since, the great majority of data obtained is either out of date or were created in a variety of operational and environmental conditions hence is bound to have uncertainties and imprecision. Therefore, the obtained crisp data of \(\lambda\) and \(\tau\) is transformed into fuzzy numbers to deal with these uncertainties and imprecision. More specifically, the crisp data of \(\lambda\) and \(\tau\) is transformed into triangle picture fuzzy numbers with known spread as proposed by the design maintenance expert/system reliability analyst. Figure 4 depicts the \(\lambda\) and \(\tau\) of the ith component of a system in the form of triangle picture fuzzy numbers with equal spread 15% in both directions. In the next step of the methodology, a fault tree model of the repairable industrial system is developed based on the primary causes of failure of its subcomponents for reliability analysis. The PN model is then derived from its corresponding fault tree model, and its minimal cut sets are determined using the matrix approach (Liu and Chiou 1997). Once the triangular picture fuzzy numbers for each component and PN model of the system are obtained, the triangular picture fuzzy numbers for the \(\lambda\) and \(\tau\) of top position of PN model are obtained using the proposed PFLTM. The proposed picture fuzzy expressions (Eqs. 13–18) for the \(\lambda\) and \(\tau\) for the OR/AND transitions of PN model for triangular picture fuzzy numbers are obtained by utilizing conventional lambda-tau expression given in Table 1. For that let the \(\lambda\) and \(\tau\) be represented by triangular picture fuzzy set as \(\widetilde{{\lambda }_{i}}=\langle \left[\left({\lambda }_{i1},{\lambda }_{i2},{\lambda }_{i3}\right); {\mu }_{i},{\eta }_{i},{\nu }_{i}\right]\rangle\) and \(\widetilde{{\tau }_{i}}=\langle \left[\left({\tau }_{i1},{\tau }_{i2},{\tau }_{i3}\right); {\mu }_{i},{\eta }_{i},{\nu }_{i}\right]\rangle\)

Fig. 4
figure 4

triangle picture fuzzy numbers for \(\lambda\) and \(\tau\) of the ith component with \(\pm 15\%\) spread

Full size image

For positive membership function: Expression for AND-Transition

$$\lambda ({{\alpha }}_{\upmu })=\left\{\begin{array}{c}\left[{\prod }_{i=1}^{n}\left\{\left({\uplambda }_{\text{i}2}-{\uplambda }_{\text{i}1}\right)\frac{{{\alpha }}_{\upmu }}{{\upmu }_{\text{i}}}+{\uplambda }_{\text{i}1}\right\}\cdot {\sum }_{j=1}^{n}\left({\prod }_{\begin{array}{c}i=1\\ i\ne j\end{array}}^{n}\left\{\left({\uptau }_{\text{i}2}-{\uptau }_{\text{i}1}\right)\frac{{{\alpha }}_{\upmu }}{{\upmu }_{\text{i}}}+{\uptau }_{\text{i}1}\right\}\right)\right],\\ \left[{\prod }_{i=1}^{n}\left\{-\left({\uplambda }_{\text{i}3}-{\uplambda }_{\text{i}2}\right)\frac{{{\alpha }}_{\upmu }}{{\upmu }_{\text{i}}}+{\uplambda }_{\text{i}3}\right\}\cdot {\sum }_{j=1}^{n}\left({\prod }_{\begin{array}{c}i=1\\ i\ne j\end{array}}^{n}\left\{-\left({\uptau }_{\text{i}3}-{\uptau }_{\text{i}2}\right)\frac{{{\alpha }}_{\upmu }}{{\upmu }_{\text{i}}}+{\uptau }_{\text{i}3}\right\}\right)\right]\end{array}\right\}$$
$$\tau ({{\alpha }}_{\upmu })=\left\{\frac{\prod_{\text{i}=1}^{\text{n}}\left(\left({\uptau }_{\text{i}2}-{\uptau }_{\text{i}1}\right)\frac{{{\alpha }}_{\upmu }}{{\upmu }_{\text{i}}}+{\uptau }_{\text{i}1}\right)}{{\sum }_{j=1}^{n}\left[{\prod }_{\begin{array}{c}i=1\\ i\ne j\end{array}}^{n}\left(-\left({\uptau }_{\text{i}3}-{\uptau }_{\text{i}2}\right)\frac{{{\alpha }}_{\upmu }}{{\upmu }_{\text{i}}}+{\uptau }_{\text{i}3}\right)\right]},\frac{\prod_{\text{i}=1}^{\text{n}}\left(-\left({\uptau }_{\text{i}3}-{\uptau }_{\text{i}2}\right)\frac{{{\alpha }}_{\upmu }}{{\upmu }_{\text{i}}}+{\uptau }_{\text{i}3}\right)}{{\sum }_{j=1}^{n}\left[{\prod }_{\begin{array}{c}i=1\\ i\ne j\end{array}}^{n}\left(\left({\uptau }_{\text{i}2}-{\uptau }_{\text{i}1}\right)\frac{{{\alpha }}_{\upmu }}{{\upmu }_{\text{i}}}+{\uptau }_{\text{i}1}\right)\right]}\right\}$$
(13)

Expression for OR-Transition

$$\lambda ({{\alpha }}_{\upmu })=\left[{\sum }_{i=1}^{n}\left\{\left({\uplambda }_{\text{i}2}-{\uplambda }_{\text{i}1}\right)\frac{{{\alpha }}_{\upmu }}{{\upmu }_{\text{i}}}+{\uplambda }_{\text{i}1}\right\},\sum_{i=1}^{n}\left\{-\left({\uplambda }_{\text{i}3}-{\uplambda }_{\text{i}2}\right)\frac{{{\alpha }}_{\upmu }}{{\upmu }_{\text{i}}}+{\uplambda }_{\text{i}3}\right\}\right]$$
$$\tau ({{\alpha }}_{\upmu })=\left\{\begin{array}{c}\frac{{\sum }_{i=1}^{n}\left[\left\{\left({\uplambda }_{\text{i}2}-{\uplambda }_{\text{i}1}\right)\frac{{{\alpha }}_{\upmu }}{{\upmu }_{\text{i}}}+{\uplambda }_{\text{i}1}\right\}\cdot \left\{\left({\uptau }_{\text{i}2}-{\uptau }_{\text{i}1}\right)\frac{{{\alpha }}_{\upmu }}{{\upmu }_{\text{i}}}+{\uptau }_{\text{i}1}\right\}\right]}{{\sum }_{i=1}^{n}\left\{-\left({\uplambda }_{\text{i}3}-{\uplambda }_{\text{i}2}\right)\frac{{{\alpha }}_{\upmu }}{{\upmu }_{\text{i}}}+{\uplambda }_{\text{i}3}\right\}},\\ \frac{{\sum }_{i=1}^{n}\left[\left\{-\left({\uplambda }_{\text{i}3}-{\uplambda }_{\text{i}2}\right)\frac{{{\alpha }}_{\upmu }}{{\upmu }_{\text{i}}}+{\uplambda }_{\text{i}3}\right\}\cdot \left\{-\left({\uptau }_{\text{i}3}-{\uptau }_{\text{i}2}\right)\frac{{{\alpha }}_{\upmu }}{{\upmu }_{\text{i}}}+{\uptau }_{\text{i}3}\right\}\right]}{{\sum }_{i=1}^{n}\left\{\left({\uplambda }_{\text{i}2}-{\uplambda }_{\text{i}1}\right)\frac{{{\alpha }}_{\upmu }}{{\upmu }_{\text{i}}}+{\uplambda }_{\text{i}1}\right\}}\end{array}\right\}$$
(14)

For neutral membership function: Expression for AND-Transition

$$\lambda ({{\alpha }}_{\upeta })=\left\{\begin{array}{c}\left[{\prod }_{i=1}^{n}\left\{\left({\uplambda }_{\text{i}2}-{\uplambda }_{\text{i}1}\right)\frac{{{\alpha }}_{\upeta }}{{\upeta }_{\text{i}}}+{\uplambda }_{\text{i}1}\right\}\cdot {\sum }_{j=1}^{n}\left({\prod }_{\begin{array}{c}i=1\\ i\ne j\end{array}}^{n}\left\{\left({\uptau }_{\text{i}2}-{\uptau }_{\text{i}1}\right)\frac{{{\alpha }}_{\upeta }}{{\upeta }_{\text{i}}}+{\uptau }_{\text{i}1}\right\}\right)\right],\\ \left[{\prod }_{i=1}^{n}\left\{-\left({\uplambda }_{\text{i}3}-{\uplambda }_{\text{i}2}\right)\frac{{{\alpha }}_{\upeta }}{{\upeta }_{\text{i}}}+{\uplambda }_{\text{i}3}\right\}\cdot {\sum }_{j=1}^{n}\left({\prod }_{\begin{array}{c}i=1\\ i\ne j\end{array}}^{n}\left\{-\left({\uptau }_{\text{i}3}-{\uptau }_{\text{i}2}\right)\frac{{{\alpha }}_{\upeta }}{{\upeta }_{\text{i}}}+{\uptau }_{\text{i}3}\right\}\right)\right]\end{array}\right\}$$
$$\tau \left({{\alpha }}_{\upeta }\right)=\left\{\frac{\prod_{\text{i}=1}^{\text{n}}\left(\left({\uptau }_{\text{i}2}-{\uptau }_{\text{i}1}\right)\frac{{{\alpha }}_{\upeta }}{{\upeta }_{\text{i}}}+{\uptau }_{\text{i}1}\right)}{{\sum }_{j=1}^{n}\left[{\prod }_{\begin{array}{c}i=1\\ i\ne j\end{array}}^{n}\left(-\left({\uptau }_{\text{i}3}-{\uptau }_{\text{i}2}\right)\frac{{{\alpha }}_{\upeta }}{{\upeta }_{\text{i}}}+{\uptau }_{\text{i}3}\right)\right]},\frac{\prod_{\text{i}=1}^{\text{n}}\left(-\left({\uptau }_{\text{i}3}-{\uptau }_{\text{i}2}\right)\frac{{{\alpha }}_{\upeta }}{{\upeta }_{\text{i}}}+{\uptau }_{\text{i}3}\right)}{{\sum }_{j=1}^{n}\left[{\prod }_{\begin{array}{c}i=1\\ i\ne j\end{array}}^{n}\left(\left({\uptau }_{\text{i}2}-{\uptau }_{\text{i}1}\right)\frac{{{\alpha }}_{\upeta }}{{\upeta }_{\text{i}}}+{\uptau }_{\text{i}1}\right)\right]}\right\}$$
(15)

Expression for OR-Transition

$$\lambda ({{\alpha }}_{\upeta })=\left[{\sum }_{i=1}^{n}\left\{\left({\uplambda }_{\text{i}2}-{\uplambda }_{\text{i}1}\right)\frac{{{\alpha }}_{\upeta }}{{\upeta }_{\text{i}}}+{\uplambda }_{\text{i}1}\right\},\sum_{i=1}^{n}\left\{-\left({\uplambda }_{\text{i}3}-{\uplambda }_{\text{i}2}\right)\frac{{{\alpha }}_{\upeta }}{{\upeta }_{\text{i}}}+{\uplambda }_{\text{i}3}\right\}\right]$$
$$\tau ({{\alpha }}_{\upeta })=\left\{\begin{array}{c}\frac{{\sum }_{i=1}^{n}\left[\left\{\left({\uplambda }_{\text{i}2}-{\uplambda }_{\text{i}1}\right)\frac{{{\alpha }}_{\upeta }}{{\upeta }_{\text{i}}}+{\uplambda }_{\text{i}1}\right\}\cdot \left\{\left({\uptau }_{\text{i}2}-{\uptau }_{\text{i}1}\right)\frac{{{\alpha }}_{\upeta }}{{\upeta }_{\text{i}}}+{\uptau }_{\text{i}1}\right\}\right]}{{\sum }_{i=1}^{n}\left\{-\left({\uplambda }_{\text{i}3}-{\uplambda }_{\text{i}2}\right)\frac{{{\alpha }}_{\upeta }}{{\upeta }_{\text{i}}}+{\uplambda }_{\text{i}3}\right\}},\\ \frac{{\sum }_{i=1}^{n}\left[\left\{-\left({\uplambda }_{\text{i}3}-{\uplambda }_{\text{i}2}\right)\frac{{{\alpha }}_{\upeta }}{{\upeta }_{\text{i}}}+{\uplambda }_{\text{i}3}\right\}\cdot \left\{-\left({\uptau }_{\text{i}3}-{\uptau }_{\text{i}2}\right)\frac{{{\alpha }}_{\upeta }}{{\upeta }_{\text{i}}}+{\uptau }_{\text{i}3}\right\}\right]}{{\sum }_{i=1}^{n}\left\{\left({\uplambda }_{\text{i}2}-{\uplambda }_{\text{i}1}\right)\frac{{{\alpha }}_{\upeta }}{{\upeta }_{\text{i}}}+{\uplambda }_{\text{i}1}\right\}},\end{array}\right\}$$
(16)

For negative membership function: Expression for AND-Transition

$$\lambda ({{\alpha }}_{\upnu })=\left\{\begin{array}{c}\left[{\prod }_{i=1}^{n}\left\{\left({\uplambda }_{\text{i}2}-{\uplambda }_{\text{i}1}\right)\frac{{{\alpha }}_{\upnu }}{{\upnu }_{\text{i}}}+{\uplambda }_{\text{i}1}\right\}\cdot {\sum }_{j=1}^{n}\left({\prod }_{\begin{array}{c}i=1\\ i\ne j\end{array}}^{n}\left\{\left({\uptau }_{\text{i}2}-{\uptau }_{\text{i}1}\right)\frac{{{\alpha }}_{\upnu }}{{\upnu }_{\text{i}}}+{\uptau }_{\text{i}1}\right\}\right)\right],\\ \left[{\prod }_{i=1}^{n}\left\{-\left({\uplambda }_{\text{i}3}-{\uplambda }_{\text{i}2}\right)\frac{{{\alpha }}_{\upnu }}{{\upnu }_{\text{i}}}+{\uplambda }_{\text{i}3}\right\}\cdot {\sum }_{j=1}^{n}\left({\prod }_{\begin{array}{c}i=1\\ i\ne j\end{array}}^{n}\left\{-\left({\uptau }_{\text{i}3}-{\uptau }_{\text{i}2}\right)\frac{{{\alpha }}_{\upnu }}{{\upnu }_{\text{i}}}+{\uptau }_{\text{i}3}\right\}\right)\right]\end{array}\right\}$$
$$\tau \left({{\alpha }}_{\upnu }\right)=\left\{\frac{\prod_{\text{i}=1}^{\text{n}}\left(\left({\uptau }_{\text{i}2}-{\uptau }_{\text{i}1}\right)\frac{{{\alpha }}_{\upnu }}{{\upnu }_{\text{i}}}+{\uptau }_{\text{i}1}\right)}{{\sum }_{j=1}^{n}\left[{\prod }_{\begin{array}{c}i=1\\ i\ne j\end{array}}^{n}\left(-\left({\uptau }_{\text{i}3}-{\uptau }_{\text{i}2}\right)\frac{{{\alpha }}_{\upnu }}{{\upnu }_{\text{i}}}+{\uptau }_{\text{i}3}\right)\right]},\frac{\prod_{\text{i}=1}^{\text{n}}\left(-\left({\uptau }_{\text{i}3}-{\uptau }_{\text{i}2}\right)\frac{{{\alpha }}_{\upnu }}{{\upnu }_{\text{i}}}+{\uptau }_{\text{i}3}\right)}{{\sum }_{j=1}^{n}\left[{\prod }_{\begin{array}{c}i=1\\ i\ne j\end{array}}^{n}\left(\left({\uptau }_{\text{i}2}-{\uptau }_{\text{i}1}\right)\frac{{{\alpha }}_{\upnu }}{{\upnu }_{\text{i}}}+{\uptau }_{\text{i}1}\right)\right]}\right\}$$
(17)

Expression for OR-Transition

$$\lambda ({{\alpha }}_{\upnu })=\left[{\sum }_{i=1}^{n}\left\{\left({\uplambda }_{\text{i}2}-{\uplambda }_{\text{i}1}\right)\frac{{{\alpha }}_{\upnu }}{{\upnu }_{\text{i}}}+{\uplambda }_{\text{i}1}\right\},\sum_{i=1}^{n}\left\{-\left({\uplambda }_{\text{i}3}-{\uplambda }_{\text{i}2}\right)\frac{{{\alpha }}_{\upnu }}{{\upnu }_{\text{i}}}+{\uplambda }_{\text{i}3}\right\}\right]$$
$$\tau ({{\alpha }}_{\upnu })=\left\{\begin{array}{c}\frac{{\sum }_{i=1}^{n}\left[\left\{\left({\uplambda }_{\text{i}2}-{\uplambda }_{\text{i}1}\right)\frac{{{\alpha }}_{\upnu }}{{\upnu }_{\text{i}}}+{\uplambda }_{\text{i}1}\right\}\cdot \left\{\left({\uptau }_{\text{i}2}-{\uptau }_{\text{i}1}\right)\frac{{{\alpha }}_{\upnu }}{{\upnu }_{\text{i}}}+{\uptau }_{\text{i}1}\right\}\right]}{{\sum }_{i=1}^{n}\left\{-\left({\uplambda }_{\text{i}3}-{\uplambda }_{\text{i}2}\right)\frac{{{\alpha }}_{\upnu }}{{\upnu }_{\text{i}}}+{\uplambda }_{\text{i}3}\right\}},\\ \frac{{\sum }_{i=1}^{n}\left[\left\{-\left({\uplambda }_{\text{i}3}-{\uplambda }_{\text{i}2}\right)\frac{{{\alpha }}_{\upnu }}{{\upnu }_{\text{i}}}+{\uplambda }_{\text{i}3}\right\}\cdot \left\{-\left({\uptau }_{\text{i}3}-{\uptau }_{\text{i}2}\right)\frac{{{\alpha }}_{\upnu }}{{\upnu }_{\text{i}}}+{\uptau }_{\text{i}3}\right\}\right]}{{\sum }_{i=1}^{n}\left\{\left({\uplambda }_{\text{i}2}-{\uplambda }_{\text{i}1}\right)\frac{{{\alpha }}_{\upnu }}{{\upnu }_{\text{i}}}+{\uplambda }_{\text{i}1}\right\}},\end{array}\right\}$$
(18)

Several reliability indicators of importance, such as MTBF, reliability, ENOFs, and availability, are then determined utilizing Eqs. 13–18, minimal cuts, and formulae given in Table 2. Finally, the fuzzy output is defuzzified into a crisp value, because the majority of human or computer actions or judgements are based on binary or crisp data. Out of several defuzzification techniques, centre of gravity method of defuzzification is used here in this study. General formula for the defuzzification using alpha cut method is given below

$$Defuzzified value=\frac{{\int }_{{x}_{1}}^{{x}_{2}}x\cdot {\mu }_{\widetilde{\text{A}}}\left(x\right)\cdot dx}{{\int }_{{x}_{1}}^{{x}_{2}}{\mu }_{\widetilde{\text{A}}}\left(x\right)\cdot dx}$$
(19)

where µÃ(x) is the membership function defined on the interval \([{x}_{1},{x}_{2}]\).

5 An illustration

Kraft pulp is a dry material that can be used again to make paper. An important part of the paper making process is washing kraft pulp. The better the pulp is cleaned, the less it has to be bleached, and the less bleach used implies less is the wastage of resources. Therefore, pulp washing is an important aspect of pulp processing and, hence, of paper making. This process is used to separate the pulp from the black liquid in order to wash off residual compounds such as alkali-lignin formed during the cooking process. Prepared pulp is washed in three to four phases, and given below are four important subsystems of the washing unit (Garg 2013).

  • Filter (F): A filter is single component in the washing unit that is used to drain black liquid from prepared pulp.

  • Cleaners (C): In this subsystem, three cleaning units are placed in parallel. Each unit uses centrifugal force to clear the pulp. Any failure reduces the system's efficiency and the paper's quality.

  • Screeners (S): In this subsystem, two screener units are linked in series. These strainers are used to remove big, raw, or irregularly shaped threads from pulp. Failure of anybody will result in the entire system failing.

  • Deckers (D): In this subsystem, two decker units are connected in a parallel arrangement. Deckers are used to minimize the blackness of the pulp. When both components of the decker fail, the decker fails completely.

The following are the steps for determining the membership function of various reliability parameters:

Step 1. Data in the form of \(\lambda\) and \(\tau\) of various components has to be collected in first step from various sources. These sources include system specialists, past research, historical documents. Obtained data is given in Table 3.

Table 3 Failure rate and repair time data
Full size table

Step 2. Because the data gathered in the preceding stage from diverse sources might be imprecise, and confusing, and is gathered under a range of environmental conditions. Consequently, crisp data collected in the first stage is fuzzified into TPFNs with known and equal spreads of \(\pm 15 \%\) in left and right direction of the centre with corresponding α-cut as shown in Fig. 4.

Step 3. The PNs model of the system given in Fig. 5 is then derived from its corresponding fault tree model which is given in Fig. 6. Here “WUF” represents failure of washing unit. Minimal cut sets computed using the matrix technique are {F}, {C1, C2, C3}, {S1}, {S2} {D1, D2}. Several of the relevant reliability indicators, such as MTBF, reliability, ENOFs, and availability, are then calculated using Eqs. 13–18, minimal cuts, and formulas shown in Table 2. These parameters are calculated using PFS [0.5, 0.9, 0.7] where 0.5 is positive membership value (µ), \(\left(1-0.9=0.1\right)\) is neutral membership value (η) and \(\left(1-0.7=0.3\right)\) is negative membership value (ν). Figure 7 depicts the computed results for the mission time t = 10 h by PFLTM for \(\pm 15 \%\) spreads, along with VLTM, FLTM, and classic reliability (crisp) approach results. Whereas Table 4 and 5 Compares the reliability obtained using VLTM and proposed methods i.e. PFLTM corresponding to different membership.

Fig. 5
figure 5

PN model of paper mill’s washing unit

Full size image
Fig. 6
figure 6

Fault tree model of paper mill’s washing unit

Full size image
Fig. 7
figure 7

Membership function of reliability parameters (a) Failure rate (b) Repair time (c) MTBF (d) Reliability (e) Availability (f) ENOFs

Full size image
Table 4 Reliability achieved using the existing VLTM given by Garg 2013 and crisp
Full size table
Table 5 Reliability achieved using the proposed methodology i.e. PFLTM
Full size table

Step 4. Last step of the methodology is to find the defuzzified results of the reliability indices, as most of the decisions made by humans or machines in daily life are based on binary or crisp results. As a result, for application purposes, the fuzzified results must be converted to crisp results by the technique of defuzzification. Out of several defuzzification techniques, centre of gravity method of defuzzification is used here in this study. General formula for the defuzzification using centre of gravity method is given in Eq. 19.

5.1 Comparison and discussion

The results for a washing unit of paper plant are obtained using the crisp reliability approach, FLTM, VLTM, and the proposed method PFLTM for the different membership values. Figure 7, Tables 4, and 5 contains the obtained results and after comparing the results, the following conclusions are drawn:

  1. 1.

    The value of reliability parameters calculated using crisp methodology remains constant for all values of α. Table 4 clearly exhibits the same i.e. reliability of system is equal to 0.894488 at all α levels. Hence this methodology is appropriate when the data is exact and definite, and it does not give trusted results when vagueness is involved in the data.

  2. 2.

    The VLTM provided by Garg in (2013) is less practical since it does not take into account the degree of neutral membership values. VLTM only considers the degree of membership and non-membership, whereas the degree of hesitation or indeterminacy is simply obtained by subtracting the sum of degree of membership and non-membership from 1. This implies that, degree of neutral membership is not considered in VLTM. Table 4 shows, for example, that the degree of membership and non-membership values corresponding to reliability of the system \(r=0.902182\) are \(0.3\) and \(0.6\), respectively.There is a \(0.1\) degree of hesitation/indeterminacy that the reliability value of system is 0.902182. However, there no degree of neutral membership involved here.

  3. 3.

    Hence, the suggested technique eliminates the shortcoming of VLTM by considering 0.1 as the degree of neutral membership denoted by the red line in Fig. 7 and a” and c” in Table 5. Therefore, in PFLTM, along with positive (μ) and negative (ν), a neutral (η) membership is also considered to better capture the ambiguity present in the data. Table 5, for example, shows that the degrees of positive, negative, and neutral memberships corresponding to the reliability of the system \(r = 0.903723\) are 0.2, 0.29, and 0.41, respectively. The degree of neutral membership, i.e. 0.41 is not considered in FLTM and VLTM. Also, there is a 0.1 degree of hesitation/indeterminacy, that the reliability value of the system is 0.903723.

  4. 4.

    Table 6 contains the crisp and defuzzified values of various system parameters at different spreads, i.e., ± 15, ± 25, and ± 50. The values of these parameters have been defuzzied because it is easier for humans and machines to work with defuzzied values. The centre of gravity method given in Sect. 4 has been used to obtain the defuzzied values. Table 6 clearly shows that defuzzied values change with a change in spread, whereas crisp values don’t change with spread. Table 6 is very helpful for system analysts or decision makers in making a new maintenance plan for the system. For example, now system analysts can use the new MTBF, i.e., 93.86513873, obtained using the new PFLTM for developing newer optimized maintenance plan.

  5. 5.

    It is also observed from Table 6 that the defuzzied values of the system parameters increases or decreases with increase or decrease in the spread. This implies that the results obtained using the proposed PFLTM are conservative in nature and hence helpful to plant analysts or decision makers in getting a better idea about the plant. Thus, plant personnel can get higher profits using defuzzied results obtained by the proposed PFLTM.

Table 6 Defuzzified and Crisp values
Full size table

6 Risk analysis using picture fuzzy set

Risk analysis of a system is consideredan essential task for developing a good maintenance plan for any system. For the risk analysis of a washing unit, this study utilizes the method given by Chen and Chen (2003). The “severity of loss (\(\widetilde{{W}_{i}}\))” due to each component and the “probability of failure (\(\widetilde{{R}_{i}}\))” of each components are required. The value of \(\widetilde{{R}_{i}}\) and \(\widetilde{{W}_{i}}\) of components depends on \(\widetilde{{R}_{{i}_{j}}}\) and \(\widetilde{{W}_{{i}_{j}}}\) of their sub-components. The “probability of failure (\(\widetilde{{R}_{{i}_{j}}}\))” of any sub-component is a function of MTBF of that sub-component on the other hand the severity of loss (\(\widetilde{{W}_{{i}_{j}}}\)) depends on the MTTR of that sub-component. \(\widetilde{{R}_{{i}_{j}}}\) and \(\widetilde{{W}_{{i}_{j}}}\) of each sub-components can be represented in linguistic terms (Table 7) by using the MTBF and MTTR these sub-components. Then the “probability of failure (\(\widetilde{{R}_{i}}\))” of components is calculated in terms of their sub-components using these linguistic terms in Eq. 20 given by Chen and Chen in 2003.

$$\widetilde{{R}_{i}}= \frac{(\sum_{j=1}^{n}{\widetilde{R}}_{{i}_{j}}\otimes {\widetilde{W}}_{{i}_{j}})}{\sum_{j=1}^{n}{\widetilde{W}}_{{i}_{j}}}$$
(20)

where i = F, C, S, D and j represents number of sub-components present in each component for example for C, j = 1, 2, 3 and for S, j = 1, 2 and for D, j = 1, 2. Set of seven linguistic terms with their corresponding PFS is given in Table 7. The linguistic values given to each sub-component by two system experts E1 and E2 along with their degree of confidence (ωi) is given in Table 8. Thereafter, algorithm given by Chen and Chen in 2003 is used to obtain the \(\widetilde{{R}_{{i}_{j}}}\) of each component of washing unit.

Table 7 Linguistic terms and their corresponding picture fuzzy numbers
Full size table
Table 8 Linguistic values of \(\widetilde{{R}_{{i}_{j}}}\) and \(\widetilde{{W}_{{i}_{j}}}\) of sub-components
Full size table

Step 1. Find the \(\widetilde{{R}_{i}}\) of every component by applying Eq. 9–12 and Eq. 20 on \(\widetilde{{R}_{{i}_{j}}}\) and \(\widetilde{{W}_{{i}_{j}}}\) of each sub-component and the obtained results are as follows:

$${\widetilde{R}}_{C}= \frac{({\widetilde{R}}_{{C}_{1}}\otimes {\widetilde{W}}_{{C}_{1}})\oplus ({\widetilde{R}}_{{C}_{2}}\otimes {\widetilde{W}}_{{C}_{2}})\oplus ({\widetilde{R}}_{{C}_{3}}\otimes {\widetilde{W}}_{{C}_{3}})}{({\widetilde{W}}_{{C}_{1}}\oplus {\widetilde{W}}_{{C}_{2}}\oplus {\widetilde{W}}_{{C}_{3}})}$$
$${\widetilde{R}}_{S}= \frac{({\widetilde{R}}_{{S}_{1}}\otimes {\widetilde{W}}_{{S}_{1}})\oplus ({\widetilde{R}}_{{S}_{2}}\otimes {\widetilde{W}}_{{S}_{2}})}{({\widetilde{W}}_{{S}_{1}}\oplus {\widetilde{W}}_{{S}_{2}})}$$
$${\widetilde{R}}_{D}= \frac{({\widetilde{R}}_{{D}_{1}}\otimes {\widetilde{W}}_{{D}_{1}})\oplus ({\widetilde{R}}_{{D}_{2}}\otimes {\widetilde{W}}_{{D}_{2}})}{({\widetilde{W}}_{{D}_{1}}\oplus {\widetilde{W}}_{{D}_{2}})}$$

Step 2. Using results obtained in Step 1 and Table 7, 8 the failure probability \(\widetilde{{R}_{i}}\) of every component is:

$$\widetilde{{R}_{F}}=\{(0.105, 0.18, 0.255;0.41, 0.85, 0.58)\}$$
$$\widetilde{{R}_{C}}=\{(0.42, 0.515, 0.655;0.41, 0.875, 0.65)\}$$
$$\widetilde{{R}_{S}}=\{(0.62, 0.72, 0.835;0.45, 0.88, 0.7)\}$$
$$\widetilde{{R}_{D}}=\{(0.62, 0.72, 0.835;0.462, 0.825, 0.65)\}$$

Step 3. Using the study given by Wang et al. (2017) the score of each component is obtained and given as:

Score(\({\widetilde{R}}_{F}\)) = -0.01; Score(\({\widetilde{R}}_{C}\)) = 0.06; Score(\({\widetilde{R}}_{S}\)) = 0.15; Score(\({\widetilde{R}}_{D}\)) = 0.1125.

Greater the score, greater is the probability that component will fail. Since order of the calculated scores is Score(\({\widetilde{R}}_{S}\)) > Score(\({\widetilde{R}}_{D}\)) > Score(\({\widetilde{R}}_{C}\)) > Score(\({\widetilde{R}}_{F}\)) hence ranking order of picture fuzzy set is \({\widetilde{R}}_{S}\)>\({\widetilde{R}}_{D}\)>\({\widetilde{R}}_{C}\)>\({\widetilde{R}}_{F}\). As a result, component S has the highest failure probability, followed by D, C, and F. Hence, obtained results are very helpful to plant personals in designing better maintenance plan.

7 Conclusion

The current research paper develops a new methodology known as the picture fuzzy lambda-tau methodology for the modeling and analyzing complex systems. The paper mill's washing unit is considered here to demonstrate the proposed methodology. The proposed methodology is very helpful for qualitative and quantitative analyses of complex systems. Qualitative analysis of the system is done by obtaining its PN model whereas, for quantitative analysis the proposed PFLTM is utilized to obtain the membership function of reliability parameters such as MTBF, ENOFs, reliability, and availability. Furthermore, a systematic framework based on risk analysis has been developed to assist maintenance engineers in analysing and forecasting the behaviour of the system. The conversion of the available data into picture fuzzy numbers has greatly increased the ability of LTM for the efficient analysis the reliability of the system. Picture fuzzy set theory is used instead of fuzzy and vague set theory to deal more efficiently with imprecise and uncertain data. Therefore, the proposed methodology for reliability and risk analysis based on picture fuzzy set not only overcomes the challenges of existing methodologies but also includes domain experts' confidence levels and knowledge in a more versatile and pragmatic manner. In summary, important findings of the present study are:

  • Developed a more reliable approach to analyze the behaviour of complex systems by utilizing picture fuzzy sets, which are defined by positive, negative and neutral membership functions;

  • Calculated reliability indices, such as Mean Time Between Failures (MTBF) and Mean Time To Repair (MTTR), which are crucial for determining the maintenance requirements of complex systems;

  • A comparison is made between the membership functions of different reliability parameters produced using the proposed method and those acquired using VLTM. The results of this comparison are provided in Table 4, 5, and Fig. 7;

  • The defuzzified values of several reliability parameters for various spreads (± 15%, ± 25%, ± 50%) produced by FLTM and VLTM were compared with the proposed PFLTM;

  • Utilizing risk analysis to develop an appropriate maintenance plan to enhance system performance and minimise operational and maintenance expenses.

8 Future scope of the methodology

In future research, proposed methodology can be applied to various industries like thermal power plants, power distribution systems, battery manufacturing units, etc. This will provide a more comprehensive understanding of the reliability of complex systems and help improve maintenance strategies. Moreover, a comprehensive framework that combines metaheuristics and multi-criteria decision making (MCDM) can be created to effectively identify components that pose a risk of failure.