Impact of Gravity Variation on the Onset of Double-Diffusive Convection in a Horizontal Porous Layer with a Boundary Slab of Finite Conductivity

Abstract

The purpose of this study was to investigate the combined impact of boundary slab and gravity variance on the onset of binary convective motion in a porous layer. The lower boundary of the porous bed is subjected to a steady-state heat flux. Furthermore, the conductivity of the plate is usually different from the conductivity of the porous sheet. We considered three cases of gravity field variations: (a) linear, (b) parabolic, and (a) cubic. The analytical solutions are achieved by perturbation technique for small values of the gravity parameter, conductivity, and depth of the plate. It is obtained that the gravity parameter, depth ratio, and conductivity ratio of the plate are to hold up the beginning of convective motion. It is also found that the system is more consistent for the linear variation and more inconsistent for the cubic variation.

Introduction

Because of its various fundamental and industrial uses, Soret-driven convection in a porous matrix due to concentration and temperature gradients has been thoroughly investigated. The books (Ingham and Pop [1], Nield and Bejan [2], and Vafaï [3]) include reviews of recent developments and publications in this area.

Ouarzazi and Bois [4] investigated convective motion in a porous with temperature gradient while accounting for the Soret effect. The temperature gradient was expected to change on a regular basis over time. For the instabilities, these authors predicted two-dimensional instability levels. Sovran et al. [5] applied both linear and nonlinear perturbation theories to examine the double-diffusive convective motion in porous beds. Shevtsova et al. [6] performed double-diffusive convection by considering a binary mixture of isopropanol (10%) and water (90%).

Analysis of the convective problem with conducting boundary slabs in pure fluids was analyzed by Sparrow et al. [7] and Hurle et al. [8]. Three-dimensional finite-amplitude thermal convective motion in a fluid layer with finite conductivity boundaries was studied by Proctor [9] and Jenkins and Proctor [10]. The effect of thermal conductivity due to plates on the convective motion in a porous bed is addressed in only a few articles (Riahi [11], Gangadharaiah[12], Gangadharaiah and Ananda [13], Shivakumara et al. [14], Chaya and Gangadharaiah [15], and Rees and Mojtabi [16]).

The study of the impact of the changeable gravity effect in a porous bed is, however, very limited. Alex and Patil[17] investigated the downward gravity effect with Darcy penetrative convection in a porous bed and found that the stability of the arrangement is improved by a reduction in the gravity factor. The effect of linear gravity variance and throughflow penetrative instability in a porous bed was reported by Suma et al. [18] and Gangadharaiah et al. [19] using regular perturbation technique. Nagarathnamma et al. [20] investigated variable gravity field effects on porous layers by using Galerkin technique. Nagarathnamma et al. [21] extended the work variable gravity field effects on anisotropic porous layer by using Galerkin technique (Fig. 94.1).

Fig. 94.1

Physical configuration

Conceptual Model

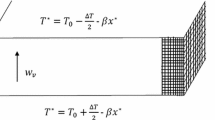
Consider an incompressible Soret horizontal porous matrix of thickness $d,$ with a solid plate at the bottom having thickness $d_{s}$ and changeable downward gravity $g\left( z \right).$ We assume that the gravity vector $\overrightarrow {g\,}$ is, $\overrightarrow {g} = - g_{0} \left( {1 + \lambda \,H\left( z \right)} \right)\,\hat{k}$.

Mathematical Formulation

Porous bed $\left( {0 \le z \le d} \right)$:

$$\nabla \cdot \overrightarrow {V} = 0$$

(94.1)

$$\frac{{\rho_{0} }}{\phi }\frac{{\partial \vec{V}}}{\partial t} = - \nabla p - \frac{\mu }{K}\vec{V} + \rho_{0} \left[ {1 - \beta \left( {T - T_{0} } \right)} \right]\,\vec{g}\left( z \right)$$

(94.2)

$$\frac{\partial T}{{\partial t}} + \left( {\overrightarrow {V} \cdot \nabla } \right)T = \nabla^{2} T$$

(94.3)

$$\frac{\partial S}{{\partial t}} + \left( {\overrightarrow {V} \cdot \nabla } \right)S = \tau \,\nabla^{2} S + \,\tilde{D}\,\nabla^{2} T$$

(94.4)

Solid layer $\left( { - d_{s} \le z \le 0\,\,} \right)$:

$$\frac{{\partial T_{s}^{{_{{}} }} }}{\partial t} = D_{s} \,\nabla^{2} T_{{s_{{}} }} .$$

(94.5)

where $\kappa$ is the thermal diffusivity, $T$ is the temperature, and $A$ is the ratio of heat capacities.

The basis steady-state solution is

$$\left( {u_{{}}^{{}} ,v,w,p,T} \right)_{{}}^{{}} = \left( {0,0,0,p_{b} (z),T_{b} (z),\;S_{b} (z)} \right)$$

(94.6)

The perturbed relation is by

$$\vec{V} = \vec{V}^{\prime } ,p = p_{b} (z) + p^{{^{\prime } }} ,T = T_{b} \left( z \right) + \theta ,S = S_{b} \left( z \right) + S^{^{\prime}}$$

(94.7)

We assume the solution is of the form

$$\left( {w,_{{}}^{{}} T,S} \right)_{{}}^{{}} = \left[ {W\left( z \right)_{{}}^{{}} ,\Theta \left( z \right)_{{}}^{{}} ,C\left( z \right)} \right]\,\,\,e^{{i\left( {lx + my} \right)}}$$

(94.8)

The linearized equations governing the perturbation are

$$\left( {D^{2} - a^{2} } \right)W - a^{2} \left( { - R_{T} \Theta + R_{S} C} \right)\left( {1 + \eta G\left( z \right)} \right) = 0$$

(94.9)

$$\left( {D^{2} - a^{2} } \right)\Theta + W = 0$$

(94.10)

$$\frac{1}{Le}\left( {D^{2} - a^{2} } \right)C + S_{r} \left( {D^{2} - a^{2} } \right)\Theta + W = 0$$

(94.11)

$$\left( {D^{2} - a^{2} } \right)\Theta_{s} = 0$$

(94.12)

The boundary conditions are:

$$W = 0\quad {\text{at}}\;z = 1.$$

(94.13)

$$D\Theta = 0 = DC\quad {\text{at}}\;z = 1.$$

(94.14)

$$W = 0\quad {\text{at}}\;z = 1.$$

(94.15)

$$DC = 0,\Theta = \Theta_{s} ,D\Theta = k_{r} D\Theta_{s}$$

(94.16)

$$D\Theta_{s} = 0\quad {\text{at}}\;z = - d_{r} .$$

(94.17)

Here, $d_{r} = {{d_{s} } \mathord{\left/ {\vphantom {{d_{s} } d}} \right. \kern-\nulldelimiterspace} d}$ is the depth ratio, $k_{r} = {{k_{s} } \mathord{\left/ {\vphantom {{k_{s} } {k_{f} }}} \right. \kern-\nulldelimiterspace} {k_{f} }}$ is the thermal conductivity ratio. Solving Eq. 94.12 using boundary conditions 16 and 17, the solid-porous interface becomes

$$D\Theta = k_{r} a\tanh \left( {a\,d_{r} } \right)\,\Theta .\quad {\text{at}}\;z = 0$$

(94.18)

Long-wavelength Asymptotic Analysis

Accordingly, the dependent variables are expanded in powers of $a^{2} \,$ in the form

$$\left( {W,\Theta ,S} \right) = \sum\limits_{i = 0}^{N} {\left( {a^{2} } \right)^{i} } \left( {W_{i} ,\Theta_{i} ,C_{i} } \right)$$

(94.19)

$$D^{2} W_{0} = 0$$

(94.20)

$$D^{2} \Theta_{0} = - W_{0}$$

(94.21)

$$D^{2} C_{0} - Le\;Sr\;D^{2} \Theta_{0} = - LeW_{0}$$

(94.22)

The boundary conditions are

$$W_{0} \left( 1 \right) = D\Theta_{0} \left( 1 \right) = DC_{0} \left( 1 \right) = 0\,\,\,\,$$

(94.23)

$$W_{0} \left( 0 \right) = D\Theta_{0} \left( 0 \right) = DC_{0} \left( 0 \right) = 0\,$$

(94.24)

Then, solutions to the above equations are

$$W_{0} = C_{0} = 0 = 0\quad {\text{and}}\;\Theta_{0} = 1$$

(94.25)

First-order equations are

$$\,D^{2} W_{1} = - \left\{ {R + \frac{{R_{s} }}{Le}} \right\}\left( {1 + \lambda G\left( z \right)} \right)$$

(94.26)

$$D^{2} \Theta_{1} = 1 - W_{1} .$$

(94.27)

$$D^{2} C_{1} - 1 + S_{r} \;Le\left( {D^{2} \Theta_{1} - 1} \right) = - LeW_{1} .$$

(94.28)

The boundary conditions are

$$W_{1} \left( 1 \right) = 0 = W_{1} \left( 0 \right)$$

(94.29)

$$D\theta_{1} \left( 0 \right) = k_{r} \,a\,\tanh \left( {a\,d_{r} } \right)\,\Theta_{0} \left( 0 \right)$$

(94.30)

The general solution of (30) is

$$W_{1} \left( {{\text{Linear}}} \right) = \left\{ {R + \frac{{R_{s} }}{Le}} \right\}\left[ {C_{1} + C_{2} z + \frac{{\lambda z^{3} }}{6} - \frac{{z^{2} }}{2}} \right]$$

(94.31)

$$W_{1} \left( {{\text{parabolic}}} \right) = \left\{ {R + \frac{{R_{s} }}{Le}} \right\}\left[ {C_{3} + C_{4} z + \frac{{\lambda z^{4} }}{12} - \frac{{z^{2} }}{2}} \right]$$

(94.32)

$$W_{1} \left( {{\text{cubic}}} \right) = \left\{ {R + \frac{{R_{s} }}{Le}} \right\}\left[ {C_{5} + C_{6} z + \frac{{\lambda z^{5} }}{20} - \frac{{z^{2} }}{2}} \right]$$

(94.33)

And solvability condition is given by

$$\int\limits_{0}^{1} {\left[ {2 + S_{r} \,Le - \left( {1 + Le} \right)\,W_{1} } \right]\,\,dz = - } k_{r} d_{r} \left( {1 + S_{r} \,Le} \right)$$

(94.34)

The expressions for $W_{1}$ are substituted into Eq. (94.34) and integrated using MATHEMATICA. The critical Rayleigh number $R^{c}$ is obtained for three different cases of variable gravity functions.

Result Analysis and Discussion

The binary fluid flow in a porous matrix in the presence of the Soret effect due to the conducting boundary slab of finite conductivity on the onset of convection is studied. The analysis takes into account three distinct forms of variations in the gravity field. Three different types of variations in the gravitational force are considered: linear, quadratic, and cubic. The gravitational force functions are as follows: $G\left( z \right) = - z$ (for linear variation), $G\left( z \right) = - z^{2}$ (for quadratic variation), and $G\left( z \right) = - z^{3}$ (for cubic variations). The influence of the gravity variation parameter, thermal conductivity ratio, depth ratio, Lewis number, and Soret on the $R^{c}$ is calculated, and outcomes are presented in Figs. 94.2, 94.3, 94.4, 94.5, 94.6, 94.7, 94.8, and 94.9.

Fig. 94.2

$W$ versus $Z$ for different values of $k_{r} \,\,{\text{and}}\,\,d_{r}$ for linear gravity field

Fig. 94.3

$W$ versus $Z$ for different values of $k_{r} \,\,{\text{and}}\,\,d_{r}$ for parabolic gravity field

Fig. 94.4

$W$ versus $Z$ for different values of $k_{r} \,\,{\text{and}}\,\,d_{r}$ for cubic gravity field

Fig. 94.5

$R_{{}}^{c}$ versus $\lambda$ with $R_{S} = 0.1 = Sr,Le = 5$ for different values of $k_{r} \,\,{\text{and}}\,\,d_{r}$ for linear gravity field

Fig. 94.6

$R_{{}}^{c}$ versus $\lambda$ with $R_{S} = 0.1 = Sr,Le = 5$ for different values of $k_{r} \,\,{\text{and}}\,\,d_{r}$ for parabolic gravity field

Fig. 94.7

$R_{{}}^{c}$ versus $\lambda$ with $\,R_{S} = 0.1 = Sr,Le = 5$ for different values of $k_{r} \,\,and\,\,d_{r}$ for cubic gravity field

Fig. 94.8

$R_{{}}^{c}$ versus $d_{r}$ with $\,R_{S} = 0.1 = Sr,Le = 5$ for different gravity field variation with $\lambda = 0.5 = d_{r} .$

Fig. 94.9

$R_{{}}^{c}$ versus $d_{r}$ with $\,R_{S} = 0.1 = Sr,Le = 5$ for different gravity field variation with $\lambda = 0.5 = k_{r} .$

Figure 94.2 depicts the eigenfunctions $W$ for different values of $k_{r}$ and $d_{r}$ for the case of linear gravity variance. It is noted that the velocity flow has maximum as the values of $k_{r}$ and $d_{r}$ increases and convection is closer in the middle of the porous bed. Similarly, from Figs. 94.3 and 94.4, we observed that with increasing $k_{r} \,\,{\text{and}}\,\,d_{r}$ and the points where the maximum value of $W\left( z \right)$ takes place is near the middle of the layer. Also noted that for the linear gravity variance, the flow is more consistent, and for cubic gravity variance, the flow is more inconsistent.

Figures 94.5 and 94.6 show the impact of $R^{c}$ with gravity effect for various values of $k_{r} \,\,{\text{and}}\,\,d_{r}$ for all types of gravity effect with $\,R_{S} = 0.1 = Sr,Le = 5$. It emphasized that with raising the value of $\lambda$, the value of $R^{c}$ also raises with higher values of $k_{r} \,\,{\text{and}}\,\,d_{r}$. Furthermore, it is observed that the system is more consistent for the linear gravity variation, while for the cubic gravity variation, the system is less stable.

Figure 94.3 depicts the variation of $R^{c}$ with $\lambda$ for various values of $k_{r}$ for all types of gravity effects with $R_{S} = 0.1 = Sr,Le = 5$. It is found that an increase in $k_{r}$ increases the $R^{c}$. In addition, it is noted that for the linear gravity change, the system is more consistent, while for the cubic gravity change, the system is less stable.

Figure 94.4 shows the variation of critical $R^{c}$ with gravity parameter for different values of the depth ratio $d_{r}$ for all three types of gravity variance with $R_{S} = 0.1 = Sr,Le = 5$. We find that an increase in $\,\,d_{r}$ increases the critical Rayleigh number since the porous-solid interface tends to be isothermal instead. In addition, it is observed that for the linear-type gravity field, the system is more consistent, while for the type cubic gravity field, the system is less stable.

Conclusions

Changeable gravity fields with height due to the conducting boundary slab of finite conductivity on the onset of binary convective motion in a porous matrix are studied. The analysis takes into account three distinct forms of variations in the gravity field. The key outcomes of the study of linear stability are defined as follows:

• The vertical velocity flow has maximum as the effect of the variable gravity parameter $\,\lambda ,$ thermal conductivity ratio $k_{r}$, and the depth ratio $d_{r}$ increases.

• As the effect of the variable gravity parameter $\,\lambda ,$ thermal conductivity ratio $k_{r}$, and the depth ratio $d_{r}$ increases, the size of the convective cells decreases.

• It is distinguished that for the linear gravity variance, the flow is more consistent, and for the cubic gravity variance, the flow is more inconsistent.