1 Introduction

The study of heat and mass transfer problem where two buoyancy driven components (heat and salt) diffuses with different rate is termed as double diffusive convection and the study of this type of problem has captivated much concentration of many researchers due to its comprehensive real life applications, see, e.g. Turner[1], Kaufman [2], Oldenburg and Pruess [3], Bear and Gillman [4], Gilman [5]. Detailed linear analysis for the double diffusive convection problem in a porous medium has been worked out by Nield [6] and in fluid layer by Baines and Gill [7]. Shir and Joseph [8] studied the double diffusive convection problem and found that, for the problem when heating is done from below however, salting is done from above then corresponding linearized system is symmetric, and thus, linear and nonlinear bounds coincide. This result was first founded by Shir and Joseph [8]. Furthermore, if both heating and salting of fluid layer is done from below then energy stability theory becomes more intricate to attain accurate results see [9, 10]. Joseph [11] established a new twist into energy stability theory. He found the idea of generalized energy theory to produce sharp nonlinear stability threshold. Mulone [12] achieved a sharp unconditional results for the double diffusive convection in a fluid layer when both heating and salting are done from below. Mulone and Rionero [13], Lombardo et al. [14] derived further sharp nonlinear stability boundaries using modified generalized energies, for a fluid layer, when heating and salting to the system are done from below. Mahajan and Tripathi [15, 16] respectively analyzed the impact of changeable viscosity and non-uniform temperature gradients on the stability of the system where both heat and mass diffusion take place.

The hypothesis of constant gravity in the pure study is not verified for wide ranging convection appearance arising in the airspace, or the mantle of the earth as the earth’s gravity field varies with the distance. In order to study the wide-ranging convection flows, it is necessary to consider the gravity field as a function of distance from the centre of earth, as identified by the Pradhan and Samal [17]. Alex et al.[18, 19] studied the impact of internal heating and changeable gravity field on the convective instability in a porous medium in the presence of inclined temperature gradient. The effect of variable gravity on the convective instability was analysed by Straughan [20] by applying linear and nonlinear analysis. The results of linear and nonlinear stability analysis are attained and compared for linearly decreasing type gravity variation function. The different types of gravity fileds are chosen to obtain its effect on the onset of Rayleigh Bénard convection problem see, Straughan [21]. Rienero and Straughan [22] also analysed the problem where gravity changes with height in a porous medium. Harfash [23] investigated the impact of gravity field and magnetic field on the convective instability in a porous medium. Later, Mahajan and Sharma [24] made an effort to check the stability by applying linear analysis technique on the convective instability of Magnetic Nano-Fluid layer. An investigation is made using simultaneous impact of variable gravity field and through flow on the stability of the system in a porous medium by Yadav [25, 26]. Recently, a very interesting problem of analyzing the gravity field impact on the stability of double diffusive system in a fluid layer where convective instability occurs due to non-uniformity in temperature and concentration gradients, is explored by Mahajan and Tripathi [27]. For more related knowledge, the researcher may call attention to the Refs. [28,29,30].

Moreover, the theory of through flow is important to manage the convective operations in geophysics, industries, and in engineering sciences etc. The impact of through flow on the Rayleigh–Bénard convection in a fluid layer was analysed by Nield [31]. The impact of through flow on the convection induced by penetration is studied by Harfash [32]. Shivkumara et al. [33] made an effort to investigated the impact of throughflow with internal heat source on convective operations in a fluid layer. Taking into consideration the work of Shivkumara [33], the combined impact of through flow and constant heat source on the double diffusive convection in anisotropic porous layer are investigated by Capone et al.[34]. In all of the studies mentioned above, the effect of throughflow with variable gravity field on convection problem (where both heat and mass diffuse) in a fluid layer has not been studied yet. The study of using combined effect of throughflow with variable gravity is very important in controlling the convection mechanism because the direction of throughflow can be taken in the direction of gravity field (throughflow inclined gravity) or in the opposite direction of gravity field (throughflow disinclined gravity). Throughflow inclined and disinclined gravity effects on the convection mechanism plays an important contribution in engineering sciences, geophysics and in hydrothermal vent systems. In the present work, the linear and energy technique are applied for double diffusive convection problem in a fluid layer with the impact of throughflow and gravity field that is non-constant. The linear analysis is applied with the help of normal mode technique while energy method is adopted to conduct the nonlinear analysis. The eigenvalue problems obtained from linear and nonlinear analysis, is solved numerically using Chebyshev pseudospectral method [35] in MATLAB. In the next section, we present a mathematical model to be studied. In Sect. 3, we introduce linear stability analysis for our system. Since the present system is not symmetric so nonlinear stability analysis gives important result thus, in Sect. 4, nonlinear stability analysis is applied using energy method. In Sect. 5, we present the results obtained using linear and nonlinear stability analysis and compare the corresponding results and conclusions are presented in Sect. 6.

2 Mathematical formulation of the problem

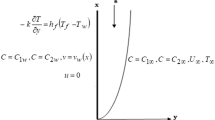
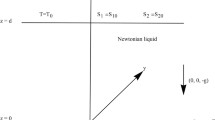
Let’s consider an incompressible fluid layer, heated and salted from below, enclosed between two parallel planes \(z = 0\) and \(z = d\) under the influence of variable gravity field \({\varvec{g}}\left( z \right)\). Let differences of the temperature and concentration are \(\Delta T = T_{1} - T_{2}\) and \(\Delta C = C_{1} - C_{2}\) respectively where \(T_{1}\), \(C_{1}\) are the temperature and concentration of lower plates respectively and \(T_{2}\), \(C_{2}\) are temperature and concentration of upper plates respectively. The fluid motion can be presented by Navier–Stokes equation.

$$ \frac{{\partial {\varvec{q}}}}{\partial t} + {\varvec{q}} \cdot \nabla {\varvec{q}} = - \frac{1}{{\rho_{0} }}\nabla p + \nu \nabla^{2} {\varvec{q}} - \left[ {1 - \alpha_{T} \left( {T - T_{0} } \right) + \alpha_{C} \left( {C - C_{0} } \right)} \right]g\left( z \right)\user2{k,} $$
(1)

The remaining governing equations are the condition of incompressibility, energy equation, and concentration equation, namely

$$ \nabla \cdot {\varvec{q}} = 0, $$
(2)
$$ \frac{\partial T}{{\partial t}} + {\varvec{q}} \cdot \nabla T = k_{T} \nabla^{2} T, $$
(3)
$$ \frac{\partial C}{{\partial t}} + {\varvec{q}} \cdot \nabla C = k_{C} \nabla^{2} C, $$
(4)

with boundary conditions

$$ \left. \begin{gathered} {\varvec{q}} = \left( {0,\,0,\,w_{0} } \right),\,\,\,\,\,z = 0,d \hfill \\ T = T_{1} ,\,C = C_{1} \,\,\,\,\,z = 0 \hfill \\ T = T_{2} ,\,C = C_{2} \,\,\,\,\,z = d \hfill \\ \end{gathered} \right\} $$
(5)

Where \(\user2{q = }\left( {u,v,w} \right)\) is the fluid velocity, denoting pressure, temperature, and concentration fields by \(p,\,T,\,C\) respectively and \(\alpha_{T} ,\,\alpha_{C} ,\,\nu ,\,k_{T} ,\,k_{C}\) by coefficient of thermal expansion, coefficient of solute expansion, dynamic viscosity, thermal diffusivity, solutal diffusivity respectively, \({\varvec{k}} = \left( {0,0,1} \right)\) is the unit vector, change in \(g\left( z \right) = \left( {1 + \varepsilon h\left( z \right)} \right)g\) denotes change in gravity field.

Let’s consider the steady state solution of (1–5) with a through flow in vertical direction of the form \({\varvec{q}} = \left( {0,0,w_{0} } \right)\), where \(w_{0}\) is the constant velocity. Now, applying the boundary conditions, we obtain the following basic state equations

$$\begin{aligned} T_{b} \left( z \right) &= T_{1} + \left( {T_{2} - T_{1} } \right)\frac{{\left( {1 - \exp \left( {\frac{{w_{0} }}{{k_{T} }}} \right)z} \right)}}{{1 - \exp \left( {\frac{{w_{0} }}{{k_{T} }}} \right)d}},\\ C_{b} \left( z \right)& = C_{1} + \left( {C_{2} - C_{1} } \right)\frac{{\left( {1 - \exp \left( {\frac{{w_{0} }}{{k_{C} }}} \right)z} \right)}}{{1 - \exp \left( {\frac{{w_{0} }}{{k_{C} }}} \right)d}},\end{aligned} $$

To assess the stability of the basic state solution, we employed perturbations as of the form

$$ {\varvec{q}} = {\varvec{q}}_{b} \left( z \right) + \user2{q^{\prime}},\,\,p = p_{b} \left( z \right) + p^{\prime}\,,\,\,\rho = \rho_{b} \left( z \right) + \rho^{\prime},\,\,T = T_{b} \left( z \right) + \theta ,\,\,C = C_{b} \left( z \right) + \phi $$

and non-dimensionalize with following scalings

$$ \left. \begin{gathered} z = dz^{ * } \,,\,\,{\varvec{q}} = \frac{{k_{T} }}{d}{\varvec{q}}^{ * } ,\,\,t = \frac{{d^{2} }}{{k_{T} }}t^{ * } \,,\,p = \frac{{\rho_{0} \nu k_{T} }}{{d^{2} }}\,p^{ * } ,\,\,\theta = \sqrt {\frac{{\Delta T\nu k_{T} }}{{\alpha_{T} gd^{3} }}} \theta^{ * } ,\,\,C = \sqrt {\frac{{\Delta C\nu k_{T}^{2} }}{{\alpha_{C} gd^{3} k_{C} }}} \phi^{ * } , \hfill \\ Le = \frac{{k_{T} }}{{k_{C} }},\,\Pr = \frac{\nu }{{k_{T} }},\,\,Ra = R^{2} = \frac{{g\alpha_{T} \Delta Td^{3} }}{{\nu k_{T} }},\,\,Rc = Rs^{2} = \frac{{g\alpha_{C} \,\Delta Cd^{3} }}{{\nu k_{C} }}\,,Q = \frac{{w_{0} d}}{{k_{T} }} \hfill \\ \end{gathered} \right\} $$
(6)

We obtain the following non-dimensional equations (after ignoring prime and asterisks)

$$ \frac{1}{\Pr }\left( {\frac{{\partial {\varvec{q}}}}{\partial t} + Q\frac{{\partial {\varvec{q}}}}{\partial z} + {\varvec{q}}.\nabla {\varvec{q}}} \right) = - \nabla p + \nabla^{2} \user2{q + }s\left( z \right)\left( {R\theta - Rs\phi } \right){\varvec{k}}, $$
(7)
$$ \nabla \cdot {\varvec{q}} = 0, $$
(8)
$$ \frac{\partial \theta }{{\partial t}} + Q\frac{\partial \theta }{{\partial z}}\user2{ + q}.\nabla \theta = \nabla^{2} \theta + Rf_{T} \left( z \right)w, $$
(9)
$$ Le\left( {\frac{\partial \phi }{{\partial t}} + Q\frac{\partial \phi }{{\partial z}}\user2{ + q}.\nabla \phi } \right) = \nabla^{2} \phi + Rsf_{C} \left( z \right)w, $$
(10)

with the perturbed boundary conditions

$$ \left. \begin{gathered} {\varvec{q}} = \left( {0,\,0,\,0} \right)\,\,\,\,z = 0,1 \hfill \\ \theta = \phi = 0,\,\,\,\,\,\,\,\,z = 0,1 \hfill \\ \end{gathered} \right\} $$
(11)

where \(\Pr\) is Prandtl number, \(Le\) is Lewis number, \(Q\) is the Peclet number, \(Ra\) is the Rayleigh number for heat, Rc is the solute Rayleigh number, \(f_{T} \left( z \right) = - \frac{d}{\Delta T}\frac{{dT_{b} }}{dz},\,f_{C} \left( z \right) = - \frac{d}{\Delta C}\frac{{dC_{b} }}{dz}\) are the non-dimensional temperature and concentration gradients respectively and \(s\left( z \right) = 1 + \varepsilon h\left( z \right)\).

3 Linear stability analysis

To proceed with the linear analysis, the nonlinear terms in Eqs. (7–10) are ignored and assuming the amplitude of the perturbations are infinitely small we take the normal mode solution in the form

$$ \left( {w,\,\theta ,\,\phi } \right) = \left[ {W(z),\,\Theta (z),\,\Phi (z)} \right]\exp \,\left[ {i\left( {a_{x} x + a_{y} y} \right) + \sigma t} \right] $$
(12)

where \(a_{x}\) and \(a_{y}\) are horizontal wave numbers and \(\sigma\) is growth rate. Now the pressure term from Eq. (7), is removed by applying \({\varvec{k}} \cdot \nabla \times \nabla \times\) Eq. (7) thus, obtain

$$ \frac{ - 1}{{\Pr }}\sigma \left( {D^{2} - a^{2} } \right)W = - \left( {D^{2} - a^{2} } \right)^{2} W + \frac{Q}{\Pr }D\left( {D^{2} - a^{2} } \right)W + a^{2} s\left( z \right)R\Theta - a^{2} s\left( z \right)Rs\Phi , $$
(13)
$$ \sigma \,\Theta = Rf_{T} \left( z \right)W - QD\Theta + \left( {D^{2} - a^{2} } \right)\Theta , $$
(14)
$$ Le\left( {\sigma \,\Phi } \right) = Rsf_{C} \left( z \right)W - LeQD\Phi + \left( {D^{2} - a^{2} } \right)\Phi $$
(15)

with boundary conditions

$$ W = DW = \Theta = \Phi = 0\;{\text{at}}\;z = 0,1 $$
(16)

Now, to solve the eigenvalue problem (13–16), we applied the Chebyshev pseudo-spectral method [35]. We first converted the domain of present problem \(\left[ {0,\,1} \right]\) into \(\left[ { - 1,1} \right]\) to match the present domain with that of Chebyshev pseudo-spectral method, applying the transformation \(z \to 2z_{1} - 1\).Thus, we obtain a system of linearized equations

$$ \frac{ - 1}{{\Pr }}\sigma \left( {4D^{2} - a^{2} } \right)W = - \left( {4D^{2} - a^{2} } \right)^{2} W + \frac{Q}{\Pr }D\left( {8D^{2} - 2a^{2} } \right)W + a^{2} s\left( {z_{1} } \right)R\Theta - a^{2} s\left( {z_{1} } \right)Rs\Phi $$
(17)
$$ \sigma \,\Theta = Rf_{T} \left( {z_{1} } \right)W - 2QD\Theta + \left( {4D^{2} - a^{2} } \right)\Theta , $$
(18)
$$ Le\left( {\sigma \,\Phi } \right) = Rsf_{C} \left( {z_{1} } \right)W - 2LeQD\Phi + \left( {4D^{2} - a^{2} } \right)\Phi $$
(19)

The boundary conditions are

$$ W = DW = \Theta = \Phi = 0\;{\text{at}}\;z = - 1,1 $$
(20)

Now, to solve the above eigenvalue problem Eqs. (17–19), we discretize the set of Eqs. (17–19) into matrix form as

$$ \sigma BX = AX, $$
(21)

where, \(X = [W\,\Theta \,\Phi ]^{T}\), \(B = \left[ {\begin{array}{*{20}c} {\frac{ - 1}{{\Pr }}\,\left( {4D^{2} - a^{2} I} \right)} & O & O \\ O & I & O \\ O & O & {LeI} \\ \end{array} } \right]\),

\(A = \left[ {\begin{array}{*{20}c} { - \left( {4D^{2} - a^{2} I} \right)^{2} + \frac{Q}{\Pr }D\left( {8D^{2} - 2a^{2} I} \right)} & {a^{2} s\left( {z_{1} } \right)RI} & { - a^{2} s\left( {z_{1} } \right)RsI} \\ {Rf_{T} \left( {z_{1} } \right)I} & {\left( {4D^{2} - a^{2} I} \right) - 2QD} & O \\ {f_{C} \left( {z_{1} } \right)RsI} & O & {\left( {4D^{2} - a^{2} I} \right) - 2LeQD} \\ \end{array} } \right]\). denoting ‘\(O\)’ and ‘I’ by the zero and identity matrices respectively. Using the boundary conditions (20) the equation (21) is now solved by applying QZ-algorithm in MATLAB. Now, the critical Rayleigh number \(Ra_{L}\) for linear theory is calculated as,

$$ Ra_{L} = \mathop {\min }\limits_{a\, > 0} R^{2} \left( a \right) $$
(22)

The matrix \(A\) of Eq. (21) above, in the absence of throughflow and gravity variation can be easily compared with Eq. (6.15) of Sect. 6.2 in Rionero [36]. So the results and conditions for the principle of exchange of stability given in Rionero [36] for the problem heated and salted from below also holds here when throughflow and gravity fields are absent. In the current problem, the inclusion of throughflow and gravity variation makes it difficult to find condition for principle of exchange of stability, however, it has been seen in the literature [see, Hill et al. [37]] that the \(\sigma\) remains real with the inclusion of throughflow; so one can argue that with the inclusion of throughflow the condition for principle of exchange of stability will not change and so the stationary convection will occur for \(Le < 1\) and convection will be oscillatory for \(1 \le Le\).

Moreover, in order to obtain the critical Rayleigh number explicitly, we take the trial function satisfying the rigid-rigid boundary condition (16) in the form, as below

$$ W = A_{1} z^{2} \left( {1 - z} \right)^{2} ,\,\Theta = A_{2} z\left( {1 - z} \right),\,\Phi = A_{3} z\left( {1 - z} \right) $$
(23)

Substituting Eq. (23) into the Eqs. (13–15) and integrating over [0,1] results in a homogeneous system, which is solved to find the Rayleigh number given by

$$ Ra = \frac{{\left( {\frac{{\sigma a^{2} }}{30\Pr } + \frac{{a^{4} }}{30} + 24} \right)\left( {2 + \frac{{a^{2} + \sigma }}{6}} \right)}}{{a^{2} F_{1} F_{2} }} + \frac{{RcF_{3} }}{{F_{2} }}\frac{{\left( {2 + \frac{{a^{2} + \sigma }}{6}} \right)}}{{\left( {2 + \frac{{a^{2} + Le\sigma }}{6}} \right)}} $$
(24)

where \(F_{1} = \int\nolimits_{0}^{1} {s\left( z \right)\left( {z - z^{2} } \right)} dz,\,F_{2} = \int\nolimits_{0}^{1} {f_{T} \left( z \right)z^{2} \left( {1 - z} \right)^{2} } dz,\,F_{3} = \int\nolimits_{0}^{1} {f_{C} \left( z \right)z^{2} \left( {1 - z} \right)^{2} } dz\).

3.1 Marginal stationary state

We put the value of \(\sigma = \sigma_{r} + i\sigma_{i}\) equal to zero, to obtain the Rayleigh number for stationary mode as

$$ Ra = R^{2} = \frac{{\left( {\frac{{a^{4} }}{30} + 24} \right)\left( {2 + \frac{{a^{2} }}{6}} \right)}}{{a^{2} F_{1} F_{2} }} + \frac{{RcF_{3} }}{{F_{2} }} $$
(25)

In the limiting case, when \(Rc = 0\), \(Q = 0,\,\varepsilon = 0\) above reduces to

$$ Ra = R^{2} = \frac{{180\left( {\frac{{a^{4} }}{30} + 24} \right)\left( {2 + \frac{{a^{2} }}{6}} \right)}}{{a^{2} }} $$
(26)

Now, by calculating the critical wave numbers using \(\frac{{dR^{2} }}{{da^{2} }} = 0\), the critical Rayleigh number comes out to be \(Ra_{L} = 1707.76\) which is the result of standard Bénard problem.

3.2 Marginal oscillatory state

In order to obtain the Rayleigh number for oscillatory mode, we apply the process as applied by Mahajan and Tripathi [38] to write

$$ Ra^{osc} = \frac{{\left( {2 + \frac{{a^{2} }}{6}} \right)\left( {\frac{{a^{4} }}{30} + 24} \right) - \frac{{\sigma_{i}^{2} a^{2} }}{180\Pr }}}{{a^{2} F_{1} F_{2} }} + \frac{{\frac{{RcF_{3} }}{{F_{2} }}\left( {2 + \frac{{a^{2} }}{6}} \right)^{2} + \frac{{Le\sigma_{i}^{2} }}{36}}}{{\left( {2 + \frac{{a^{2} }}{6}} \right)^{2} + \frac{{Le^{2} \sigma_{i}^{2} }}{36}}} $$
(27)

where oscillatory frequency is given by

$$ \sigma_{i}^{2} = \frac{36}{{Le^{2} }}\left[ {\frac{{\frac{{a^{2} RcF_{3} F_{1} }}{6}\left( {2 + \frac{{a^{2} }}{6}} \right)\left( {Le - 1} \right)}}{{\frac{{a^{2} }}{30\Pr }\left( {2 + \frac{{a^{2} }}{6}} \right) + \frac{1}{6}\left( {\frac{{a^{4} }}{30} + 24} \right)}} - \left( {2 + \frac{{a^{2} }}{6}} \right)^{2} } \right] $$
(28)

4 Nonlinear stability analysis

To solve the present problem using nonlinear stability analysis, we applied energy method [21]. Generally, the linear stability analysis gives little information about the nature of the nonlinear system since any potential growth in nonlinear terms are not taken into consideration. To analyze the nature of the nonlinear system, finite perturbations are considered and quadratic terms are not ignored. Now, to initiate the nonlinear stability analysis, Eq. (7) is multiplied by \({\varvec{q}}\), Eq. (9) is multiplied by \(\theta\) and Eq. (10) is multiplied by \(\phi\), and on integrating the resultant over the periodic cell V to obtain

$$ \frac{1}{2\Pr }\frac{d}{dt}\left\| {\varvec{q}} \right\|^{2} = - \left\| {\nabla {\varvec{q}}} \right\|^{2} + R\left\langle {s\left( z \right)\theta w} \right\rangle - Rs\left\langle {s\left( z \right)\phi w} \right\rangle $$
(29)
$$ \frac{1}{2}\frac{d}{dt}\left\| \theta \right\|^{2} = - \left\| {\nabla \theta } \right\|^{2} + R\left\langle {f_{T} (z)\theta w} \right\rangle , $$
(30)
$$ \frac{Le}{2}\frac{d}{dt}\left\| \phi \right\|^{2} = - \left\| {\nabla \phi } \right\|^{2} + Rs\left\langle {f_{C} (z)w\phi } \right\rangle , $$
(31)

where the symbols \(\left\| \cdot \right\|\) is norm and \(\left\langle \cdot \right\rangle\) is inner product on \(L^{2} \left( V \right)\). Now, adding Eq. (29–31), with the help of coupling parameters \(\left( {\lambda_{1} > 0,\,\lambda_{2} > 0} \right)\), a functional in terms of energy \(E\left( t \right)\) is constructed as

$$ E(t) = \frac{1}{2\Pr }\,\left\| {\,{\varvec{q}}\,} \right\|^{2} \, + \frac{{\lambda_{\,1} }}{2}\,\left\| {\,\theta \,} \right\|^{2} \, + \frac{{\lambda_{\,2} Le}}{2}\,\left\| {\,\phi \,} \right\|^{2} , $$
(32)

The progress of \(E\left( t \right)\) when time grows is given as

$$ \frac{dE(t)}{{dt}} = \frac{1}{2\Pr }\,\frac{d}{dt}\,\left\| {\,{\varvec{q}}\,} \right\|^{2} \, + \frac{{\lambda_{\,1} }}{2}\,\frac{d}{dt}\,\,\left\| {\,\theta \,} \right\|^{2} \, + \frac{{\lambda_{\,2} Le}}{2}\,\frac{d}{dt}\,\,\left\| {\,\phi \,} \right\|^{2} $$
(33)

Substituting Eqs. (29–31) into Eq. (33), to write

$$ \frac{d\left( E \right)}{{dt}} = I_{1} - D_{1},$$
(34)

now we have

\(\begin{gathered} I_{1} = R\left\langle {s\left( z \right)\theta w} \right\rangle - Rs\left\langle {s\left( z \right)\phi \,w} \right\rangle + \lambda_{1} R\left\langle {f_{T} (z)w\theta } \right\rangle + \lambda_{2} Rs\left\langle {f_{C} (z)w\phi } \right\rangle \hfill \\ D_{1} = \left\| {\nabla {\varvec{q}}} \right\|^{2} + \lambda_{1} \left\| {\nabla \theta \,} \right\|^{2} + \lambda_{2} \left\| {\nabla \phi \,} \right\|^{2} , \hfill \\ \end{gathered}\)

we define now \(R_{E}\) in such a way

$$ \frac{1}{{R_{E} }}\, = \,\mathop {\max }\limits_{\Omega } \frac{{I_{1} }}{{D_{1} }}, $$
(35)

where \(\Omega = \left\{ {{\varvec{q}},\theta ,\phi |{\varvec{q}},\theta ,\phi \in L^{2} \left( V \right)} \right\}\) and \({\varvec{q}},\theta ,\phi\) satisfy the boundary conditions (Eq. 11). Now, the Eqs. (34) and (35), may be written as

$$ \frac{dE\left( t \right)}{{dt}}\, \le \, - D_{1} \left( {1 - \frac{1}{{R_{E} }}} \right), $$
(36)

If \(R_{E} > 1\), then we may write \(b_{1} = \left( {1 - \frac{1}{{R_{E} }}} \right) > 0\), and further using Poincare inequality in Eq.(36), we may write the following energy inequality

$$ E(t) \le E(0)\,\exp \,\left( { - 2\pi^{2} k^{\prime}b_{1} t} \right) $$
(37)

where \(k^{\prime}\, = \min \left\{ {1,\,\Pr ,\,\frac{1}{Le}} \right\}\). Now, Eq. (37) shows exponential decay of energy function with time for all values of \(E(0)\). Now, using calculus of variation we will solve the Euler–Lagrange equation (35) using the transformation \(\theta = \frac{{\hat{\theta }}}{{\sqrt {\lambda_{1} } }}\,,\,\phi = \frac{{\hat{\phi }}}{{\sqrt {\lambda_{2} } }}\), to obtain the following system of equations

$$ 2\Pr \nabla^{2} {\varvec{q}} + R{\varvec{k}}\left( {\frac{{\Pr s\left( z \right) + \lambda_{1} f_{T} \left( z \right)}}{{\sqrt {\lambda_{1} } }}} \right)\theta - Rs{\varvec{k}}\left( {\frac{{\Pr s\left( z \right) - \lambda_{2} Le^{ - 1} f_{C} \left( z \right)}}{{\sqrt {\lambda_{2} } }}} \right)\phi = - \nabla p $$
(38)
$$ 2\nabla^{2} \theta + R\left( {\frac{{s\left( z \right)\Pr + \lambda_{1} f_{T} \left( z \right)}}{{\sqrt {\lambda_{1} } }}} \right)w = 0, $$
(39)
$$ 2\nabla^{2} \phi - LeRs\left( {\frac{{s\left( z \right)\Pr - \lambda_{2} Le^{ - 1} f_{C} \left( z \right)}}{{\sqrt {\lambda_{2} } }}} \right)w = 0, $$
(40)

denoting p as Lagrange’s multiplier and applying the curl curl on Eq. (38) and adopting the vertical component of resulting equation, to acquire

$$ 2\Pr \nabla^{4} w + \nabla_{1}^{2} R\left( {\frac{{\Pr s\left( z \right) + \lambda_{1} f_{T} \left( z \right)}}{{\sqrt {\lambda_{1} } }}} \right)\theta - \nabla_{1}^{2} Rs\left( {\frac{{\Pr s\left( z \right) - \lambda_{2} Le^{ - 1} f_{C} \left( z \right)}}{{\sqrt {\lambda_{2} } }}} \right)\phi = 0, $$
(41)

Supposing a solution showing a plane tilling in the form \(\left( {w,\theta ,\phi } \right) = \left( {W,\Theta ,\Phi } \right)\psi \left( {x,y} \right)\) that satisfy \(\left( {\nabla_{1}^{2} + a^{2} } \right)\psi = 0\), where \(\psi\) denote plane tilling function. Thus, Eqs. (39–41) can be written as

$$ 2\Pr \left( {D^{2} - a^{2} } \right)^{2} \,W - a^{2} R\,\left( {\frac{{s\left( z \right)\Pr + \lambda_{1} \,f_{T} (z)}}{{\sqrt {\lambda_{1} } }}} \right)\Theta \, + a^{2} Rs\,\left( {\frac{{\Pr s\left( z \right) - \lambda_{2} Le^{ - 1} \,f_{C} (z)}}{{\sqrt {\lambda_{2} } }}} \right)\Phi = 0,\, $$
(42)
$$ 2\left( {D^{2} - a^{2} } \right)\Theta + R\left( {\frac{{s\left( z \right)\Pr + \lambda_{1} \,f_{T} \left( z \right)}}{{\sqrt {\lambda_{1} } }}} \right)W = 0, $$
(43)
$$ 2\left( {D^{2} - a^{2} } \right)\Phi - LeRs\left( {\frac{{s\left( z \right)\Pr - \lambda_{2} Le^{ - 1} f_{C} \left( z \right)}}{{\sqrt {\lambda_{2} } }}} \right)W = 0, $$
(44)

with Eq. (16) represent an eigenvalue problem. To solve the above eigenvalue problem Eqs. (42–44) with boundary conditions (16), Chebyshev pseudospectral method is applied in MATLAB (discussed in Sect. 3). Now the critical Rayleigh number of nonlinear theory is obtained on minimizing \(R^{2}\) for fixed wave number \(a\) and maximizing for \(\left( {\lambda_{1} > 0,\,\lambda_{2} > 0\,} \right)\) thus the critical Rayleigh number \(Ra_{E}\)

$$ Ra_{E} = \mathop {\max }\limits_{{\lambda_{1\,} \lambda_{2\,} \,}} \,\mathop {\min }\limits_{a} \,R^{2} (\lambda_{1} ,\,\lambda_{2} ,\,a) $$
(45)

Now, in order to solve the eigenvalue problem (42–44) analytically, substitute Eq. (23) into the Eqs. (42–44) and integrating over [0,1] to obtain a homogeneous system, which yields to following Rayleigh number

$$ R^{2} = \frac{{8\Pr \left( {\frac{{a^{4} }}{30} + 24} \right)\left( {\frac{{a^{2} }}{6} + 2} \right)^{2} - 2a^{2} Le\left( {\frac{{a^{2} }}{6} + 2} \right)RcN_{3} N_{4} }}{{2a^{2} N_{1} N_{2} \left( {2 + \frac{{a^{2} }}{6}} \right)}} $$
(46)

where,\(N_{1} = \int\nolimits_{0}^{1} {L_{1} \left( z \right)z\left( {1 - z} \right)} dz,\,N_{2} = \int\nolimits_{0}^{1} {L_{1} \left( z \right)z^{2} \left( {1 - z} \right)^{2} } dz,\,N_{3} = \int\nolimits_{0}^{1} {L_{2} \left( z \right)z\left( {1 - z} \right)} dz,\,N_{4} = \int\nolimits_{0}^{1} {L_{2} \left( z \right)z^{2} \left( {1 - z} \right)^{2} } dz\)and \(L_{1} \left( z \right) = \left( {\frac{{s\left( z \right)\Pr + \lambda_{1} \,f_{T} (z)}}{{\sqrt {\lambda_{1} } }}} \right),\,L_{2} \left( z \right) = \left( {\frac{{s\left( z \right)\Pr - \lambda_{2} \,Le^{ - 1} f_{C} (z)}}{{\sqrt {\lambda_{2} } }}} \right)\).

Now, in the limiting case, when \(Rc = 0\), \(Q = 0,\,\varepsilon = 0\), \(N_{1}\) tends to \(\frac{1}{6}\left( {\frac{{\Pr + \lambda_{1} }}{{\sqrt {\lambda_{1} } }}} \right)\) and \(N_{2}\) tends to \(\frac{1}{30}\left( {\frac{{\Pr + \lambda_{1} }}{{\sqrt {\lambda_{1} } }}} \right)\) thus, Eq. (46) reduces in the following form

$$ R^{2} = \frac{{720\Pr \lambda_{1} \left( {\frac{{a^{4} }}{30} + 24} \right)\left( {\frac{{a^{2} }}{6} + 2} \right)}}{{a^{2} \left( {\Pr + \lambda_{1} } \right)^{2} }} $$
(47)

Now, to find the optimum value of \(R^{2}\) corresponding to \(\lambda_{1}\), we solve \(\frac{{dR^{2} }}{{d\lambda_{1} }} = 0\) which gives \(\lambda_{1} = \Pr\) and thus Eq.(47) reduces to

$$ R^{2} = \frac{{180\left( {\frac{{a^{4} }}{30} + 24} \right)\left( {\frac{{a^{2} }}{6} + 2} \right)}}{{a^{2} }} $$
(48)

The Rayleigh number in Eq. (48), shows the results of nonlinear stability analysis which is equal to the Rayleigh number obtained from linear analysis [see, Eq. (26)]. Thus, it is also clear that for a constant gravity, in absence of solute and throughflow, linear analysis accurately encapsulates the physics of convection.

5 Results and discussion section

In the present paper, the effect of throughflow on the double diffusive convection in a fluid layer with variable gravity field for heated from below and salted from below system is discussed using linear and nonlinear stability analysis. The linear analysis is applied with the help of normal mode technique however; the energy method is conducted to apply nonlinear analysis. The eigenvalue problems obtained from the linear and nonlinear stability analyses are solved using Chebyshev pseudo-spectral method. The numerical technique is checked, after solving the present problem where solute and throughflow are absent [see Table 1]. The present results show a close concurrence with the previous results.

Table 1 Comparison of present work with the study of Straughan [20], [Table 1], Straughan [21],[Table 4.4, 4.5]. The fixed parameters are \(Le = 10,\,\Pr = 10\)
Full size table

In the Fig. 1, the variation of critical Rayleigh numbers \(\left( {Ra_{L} ,\,Ra_{E} } \right)\) against solute Rayleigh number \(Rc\) is shown for the different cases of gravity variation function \(h\left( z \right)\) when the fixed parameters are \(Le = 10,\,\Pr = 10,Q = 0.5,\,\varepsilon = 0.5\). It is clear that an increase in value of the solute Rayleigh number \(Rc\) increases the critical Rayleigh number of linear theory \(\left( {Ra_{L} } \right)\) however, the critical Rayleigh number of nonlinear theory \(\left( {Ra_{E} } \right)\) remains approximately unchanged for all the assumed cases of gravity variation functions \(h\left( z \right)\).Thus, an advancement in \(Rc\) values widens the region of subcritical instability.

Fig. 1
figure 1

Critical Rayleigh numbers \(\left( {Ra_{L} ,\,Ra_{E} } \right)\) are displayed against \(Rc\). The fixed parameters are \(Le = 10,\,\Pr = 10,Q = 0.5,\,\varepsilon = 0.5\), for a \(h\left( z \right) = z\), b \(h\left( z \right) = - z\), c \(h\left( z \right) = - z^2\)

Full size image

Figure 2 express the variation of \(\left( {Ra_{L} ,\,Ra_{E} } \right)\) with gravity variation parameter \(\varepsilon\). It is deduced that the region of subcritical instability widens with the advancement in gravity variation parameter \(\varepsilon\) for the case of \(h\left( z \right) = - z,\, - z^{2}\) however, there is unnoticeable changes in the region of subcritical instability on advancing in gravity variation parameter \(\varepsilon\) for \(h\left( z \right) = z\). It is also very clear that for \(h\left( z \right) = z\), increase in the values of \(\varepsilon\) destabilizes the system, since an increase in the \(\varepsilon\) value reveals an increase in the gravity field. On the other hand, on increasing the value of \(\varepsilon\) increases the \(\left( {Ra_{L} ,\,Ra_{E} } \right)\) values for \(h\left( z \right) = - z,\, - z^{2}\) and an increase in the critical Rayleigh number values are sufficiently large for \(h\left( z \right) = - z\) when compared with the other form of \(h\left( z \right)\). Thus, \(h\left( z \right) = - z\) is the most stable profile of gravity among the other gravity profiles that we have considered.

Fig. 2
figure 2

Critical Rayleigh numbers \(\left( {Ra_{L} ,\,Ra_{E} } \right)\) are displayed against \(\varepsilon\) for the different cases of gravity variation function \(h\left( z \right)\), for a \(h\left( z \right) = z\), b \(h\left( z \right) = -z\), c \(h\left( z \right) = - z^2\). The fixed parameters are \(Le = 10,\,\Pr = 10,Q = 0.5,\,Rc = 20\)

Full size image

Figure 3 gives a visual representation of linear and nonlinear stability thresholds against \(Q\) for the different cases of \(h\left( z \right)\) and it is observed that direction of throughflow has considerable effect on the stability of the system. The positive value of \(Q\) corresponds to the throughflow in the upward direction while, the negative value of \(Q\) corresponds the throughflow in downward direction. And, for \(h\left( z \right) = z\), the convection occurs fast with increasing in \(Q\) value in the range \(Q \in \left[ { - 2,\,0} \right]\), this is because of the presence of downward throughflow, the highest value of temperature difference stagnate in that part of medium where the vertical perturbation velocity takes its largest value and thus, the rate at which energy is supplied to the disturbances is increased, and this leads to the destabilization of the system however, advancing in \(Q\) values delay the occurrence of convection in the range \(Q \in \left[ {0.5,\,2} \right]\), this is because the upward throughflow shifts the thermal gradients to the temperature boundary layer at the boundary towards which throughflow is directed and thus, large value of critical Rayleigh number is required to initiate the convection. On the other hand, for \(h\left( z \right) = - z,\, - z^{2}\) the onset of convection hastens with the increase in \(Q\) in the range \(Q \in \left[ { - 2,\, - 0.5} \right]\) however, increasing in \(Q\) values delaying the onset of convection in the range \(Q \in \left[ {0,\,2} \right]\). From the Fig. 3, it is also noticed that for \(h\left( z \right) = z\), the linear and nonlinear stability thresholds have less agreement for negative value of throughflow parameter \(Q\) in comparison of positive value of throughflow parameter \(Q\). On the other hand, for the function \(h\left( z \right) = - z,\, - z^{2}\), the thresholds have less agreement for positive values of throughflow parameter \(Q\) in comparison of negative values of throughflow parameter \(Q\). This pattern of results is approximately similar to the nature of throughflow in a porous medium [39]. As we have explained above that for increasing upward throughflow the convection is delayed and for increasing downward throughflow the onset of convection hastens but it is very interesting to notice that the effect of gravity field on the system is dominant to the effect of throughflow, which is visible in Fig. 3 i.e. on advancing the gravity field, leads to hastens the onset of convection for the small upward throughflow \(Q \in \left[ {0,\,0.5} \right]\). However, for the case when gravity field decreases with height, leads to delay the convection in the range \(Q \in \left[ { - 0.5,\,0} \right]\)(small downward throughflow). The reader may refer the work [40, 41], for more studies related to throughflow.

Fig. 3
figure 3

Critical Rayleigh numbers \(\left( {Ra_{L} ,Ra_{E} } \right)\) are displayed against throughflow parameter \(Q\). The fixed parameters are \(Le = 10,\,\Pr = 10,\,Rc = 20,\,\varepsilon = 0.5\), for a \(h\left( z \right) = z\) , b \(h\left( z \right) = - z\), c \(h\left( z \right) = - z^2\)

Full size image

Figure 4 displays the variation of critical Rayleigh numbers against Lewis number \(Le\) for the different cases of gravity variation function \(h\left( z \right)\). For each examined cases of \(h\left( z \right)\), increasing the Lewis number rapid the onset of convection however, the energy stability threshold remains constant with increasing Lewis number. It is very interesting to note that increasing the \(Rc\) values delays the onset of convection for \(Le \le 20\) but, for a value of Lewis number \(Le\) larger than a certain value, the linear instability thresholds coincide for the different values of \(Rc\).

Fig. 4
figure 4

Critical Rayleigh numbers \(\left( {Ra_{L} ,Ra_{E} } \right)\) are displayed against Lewis number \(Le\). The fixed parameters are \(Q = 0.5\,,\,\Pr = 10\,,\,\varepsilon = 0.5\), for a \(h\left( z \right) = z\), b \(h\left( z \right) = - z\), c \(h\left( z \right) = - z^2\)

Full size image

6 Conclusions

In the fluid layer, our proposal is to apply the linear and nonlinear stability analysis for the double diffusive convection problem with the effect of through flow and variable gravity field. The linear theory is performed using normal mode technique, however nonlinear stability analysis is performed using energy method. The eigenvalue problems obtained from the linear and nonlinear theories are solved using Chebyshev pseudo-spectral method in MATLAB. A comparison is made between linear and nonlinear results. The following observations are found from the investigation of the present problem. The solute Rayleigh number \(Rc\) is found to have stabilizing impact on the system for \(Le \le 20\). The system is most stable for gravity variation function \(h\left( z \right) = - z\) while the most unstable for \(h\left( z \right) = z\). For \(h\left( z \right) = z\), the thresholds have good agreement in the neighborhood of \(Q = 0.5\), however, for \(h\left( z \right) = - z,\, - z^{2}\), the thresholds have good agreement in the neighborhood of \(Q = - 0.5\). The linear instability thresholds coincide for the different values of solute Rayleigh number \(Rc\) at Lewis number \(Le\) values greater than a fixed value however, the nonlinear stability thresholds remains constant with the increase in Lewis number.