Effects of Vertical Throughflow and Variable Gravity on Hadley–Prats Flow in a Porous Medium

Abstract

The stability of convection in a horizontal porous layer which is saturated with fluid and induced by horizontal temperature gradients subjected to horizontal mass flow is investigated by means of linear and nonlinear stability analysis. The effects of variable gravity field and vertical throughflow are also considered in this analysis. The nonlinear stability analysis part has been developed via energy functional. Shooting and Runge–Kutta methods have been used to solve eigenvalue problem in both cases. Critical vertical thermal Rayleigh numbers for both linear and nonlinear analyses $R_\mathrm{L}$ and $R_\mathrm{E}$ are evaluated for different values of horizontal Rayleigh number $R_x$, horizontal Peclet number Pe, vertical Peclet number $Q_\mathrm{v}$ and variable gravity parameter $\eta$. Comparison is made between linear and nonlinear stability results. It has been observed that linear stability results are overpredicting the onset of convection compared with nonlinear theory, and hence subcritical instabilities would arise before one gets the onset of linear stability threshold.

1 Introduction

The study of buoyancy-driven flows in the porous media is vital since it has numerous applications in fields like insulation of buildings, geothermal reservoirs, and chemical reactor engineering. Natural convection in a porous layer by heating from below was first studied by Horton and Rogers (1945) and Lapwood (1948) which is known as Horton–Rogers–Lapwood (H–R–L) problem. In this study, they have investigated on a homogeneous and isotropic porous layer with uniform thickness in which Darcy law, Oberbeck-Boussinesq approximation, and local thermal equilibrium condition are valid. There are many extensions to this problem with inclusion of additional effects such as inclined temperature gradients, inclined porous layer, viscous dissipation, mass flow, local thermal non- equilibrium.

Later, Prats (1966) studied the effect of horizontal fluid flow on convection in a porous layer. Then after, Weber (1974) investigated the stability of convection induced by inclined temperature gradients assuming them as small in magnitude. This problem is more complicated than the model considered in the H–R–L problem or pure Darcy–Benard convection. In problems of this type, temperature field is assumed to vary linearly in the horizontal direction. And that non-uniformity in the horizontal temperature induces a flow into basic solution. The flow generated by these gradients is referred to as Hadley flow. Nield (1991, 1994) got rid of the limitation on horizontal temperature gradients which were to be small, and the resultant eigenvalue problem in both cases was solved by using two-term Galerkin approximation. When Hadley flow is subjected to horizontal mass flow, it leads to Hadley–Prats flow. A book by Nield and Bejan (2013) mentioned all the improvements in this area of research.

Investigation of effect of vertical throughflow is important since it gives a possibility to control the convective instability with adjustment of throughflow. This type of study has applications in packed bed reactors. Effect of throughflow in a porous medium was first studied by Wooding (1960) where the domain was semi-infinite in the vertical direction, and this study was followed by Sutton (1970) and Chen (1990). It was further extended by Nield (1998) with inclined temperature gradients by concluding that the effect of throughflow is independent of its direction when both the upper and lower boundary conditions are identical. Nield and Kuznetsov (2013) investigated throughflow on convection in a porous medium which consisted two horizontal porous layers. All the above studies are based on the Darcy flow model in which inertia and viscous dissipation effects are neglected. Barletta et al. (2010) investigated on thermal convection with effect of viscous dissipation in the energy balance and also with vertical throughflow. Khalili and Shivakumara (2003) employed Brinkman-extended Darcy model to study the effect of vertical throughflow. Rees and Bassom (2000) studied Darcy–Bénard problem where the porous layer was inclined to some angle. Brevdo and Ruderman (2009) analyzed the destabilization of transverse modes when the flow undergoes the effect of vertical throughflow. Most of the above works were concentrated only on the effect of either horizontal mass flow or vertical throughflow. But the present article aims at studying both the effects simultaneously.

When the gravity field varies with the height of the porous layer, the buoyancy force exerted by the fluid also varies. This leads to a situation where some part of the fluid layer will tendency to become stable and the remaining part unstable. Hence, in large-scale convection problems, it is essential to take account of variation of gravity with height. Alex et al. (2001) analyzed variable gravity effects on convection in isotropic porous layer with internal heat source. Later on, it was extended to anisotropic porous layer in the article by Alex and Patil (2002). Variable gravity effects was studied by Straughan (1989), Kaloni and Qiao (2001) and Harfash (2014).

Most of the above contributions are restricted to linear theory. It is a known fact that the energy method and the linear stability theory complement each other in demarking the range of parameter space in which the subcritical instabilities would arise. Nonlinear stability theory using energy functional overcomes the drawbacks in the linear stability analysis. Nonlinear analysis by energy method may be found in Straughan (2004). Homsy and Sherwood (1976) analyzed the convective instability in a porous medium confined between isothermal boundaries, using linear instability theory and nonlinear stability theory. Straughan (1989) added the effect of variable gravity field to the convection problem and examined linear and nonlinear stability analyses and observed that there is a small bandwidth where possible subcritical instabilities arise. Several researchers have studied the nonlinear stability by using the energy method. Kaloni and Qiao (1997), Qiao and Kaloni (1998), and Kaloni and Qiao (2000) extended this in various phases by including effect of inclined temperature gradients, vertical throughflow, and thermosolutal convection with horizontal mass flow, respectively. Harfash (2014) studied the convection in a fluid-saturated porous media by using linear and nonlinear analyses with the effects of internal heat source, variable gravity.

The aim of present article is to study the onset of convection with horizontal mass flow, vertical throughflow, and variable gravity effect by using linear and nonlinear stability analyses. In this discussion, Sect. 2 deals with governing equations and steady-state solution, Sects. 3 and 4 with the linear and nonlinear stability analyses, and Sect. 5 with numerical solution of the eigenvalue problems and discussion of results.

2 Mathematical Formulation

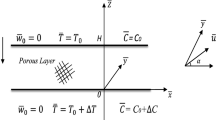
A horizontal fluid-saturated homogeneous porous layer with thickness H is considered. Cartesian system has its $z^{*}$-axis vertically upwards which opposes the direction of gravity and $x^{*}$-axis is in the direction of imposed horizontal temperature gradient $\beta$. The porous layer extends to infinity in horizontal directions, and bounded by permeable plates $z^{*}=H/2$ and $z^{*}=-H/2$. The vertical temperature difference between the plates be $\Delta T$. The schematic diagram of the problem is shown in Fig. 1. The flow in the porous medium is governed by Darcy law. Oberbeck–Boussinesq approximation is valid that means the density variations are sufficiently small to be neglected everywhere except in the body force term, and density is given by

$$\begin{aligned} {\rho _f}^{*}=\rho _0\left[ 1-\gamma _T(T^{*}-T_0)\right] , \end{aligned}$$

(1)

where $T^{*}$ is the temperature, ${\rho _f}^{*}$ is the fluid density, $\rho _0$ is the density at temperature $T_0$, and $\gamma _T$ is the volumetric thermal expansion coefficient. It is assumed that the gravity vector varies linearly with $z^{*}$ i.e.,

$$\begin{aligned} \begin{aligned} \mathbf g&=g_0 h(z^{*})\mathbf k \\&=-g_0\left( 1+\eta \frac{z^{*}}{H}\right) \mathbf k , \end{aligned} \end{aligned}$$

(2)

where $g_0$ is the constant gravitational acceleration, $\eta$ is the variable gravity coefficient, and $\mathbf k$ is the unit vector in vertical direction. The governing equations in dimensional form are

$$\begin{aligned}&\displaystyle \nabla ^{*}\,\cdot \,\mathbf v ^{*}=0, \end{aligned}$$

(3)

$$\begin{aligned}&\displaystyle \frac{\mu }{K}\mathbf v ^{*}=-\nabla ^{*}{P}^{*}+{\rho _f}^{*}\mathbf g ,\end{aligned}$$

(4)

$$\begin{aligned}&\displaystyle (\rho c)_m\frac{\partial {T^{*}}}{\partial {t^{*}}}+(\rho c_p)_f(\mathbf v ^{*}\,\cdot \,\nabla ^{*}{T^{*}})=k_m{{\nabla ^{*}}^2}T^{*}, \end{aligned}$$

(5)

where $\mathbf v ^{*} = (u^{*},v^{*},w^{*})$, $P^{*}$ are the seepage velocity and pressure, respectively. The subscripts m and f indicates to the porous medium and fluid, respectively. In addition, $\mu$, c, $k_m$, and K stand for viscosity, specific heat, thermal conductivity and permeability of the medium, respectively. It is supposed that there is a throughflow with velocity $w_\mathrm{v}$ in the vertical direction, and then the boundary conditions are in the form

$$\begin{aligned} z^{*}=\pm \frac{H}{2}:\quad w^{*}=w_v,\quad T^{*}=T_0-\frac{(\pm \Delta T)}{2}-\beta x^{*}. \end{aligned}$$

(6)

Now, the following non-dimensional variables are introduced to non-dimensionalize the governing equations (3)–(6)

$$\begin{aligned} (x,y,z)= & {} \frac{1}{H}(x^{*},y^{*},z^{*}),\quad t=\frac{\alpha _m}{\mathbf{A }{H^2}}t^{*}, \quad (u,v,w)=\mathbf{v }=\frac{H}{\alpha _m}\mathbf{v }^{*},\nonumber \\ P= & {} \frac{K(P^{*}+\rho _0\mathbf{g }z^{*})}{\mu \alpha _m},\quad T=\frac{R_z(T^{*}-T_0)}{\Delta T},\nonumber \\ \alpha _m= & {} \frac{k_m}{(\rho c_p)_f},\quad \mathbf{A }=\frac{(\rho c)_m}{(\rho c_p)_f}, \end{aligned}$$

(7)

The above scaling leads to the following non-dimensional parameters

$$\begin{aligned} Q_\mathrm{v}= & {} \frac{w_v H}{\alpha _m},\quad Pe=\frac{u_0 H}{\alpha _m},\nonumber \\ R_z= & {} \frac{\rho _0 g_0 \gamma _T KH\Delta T}{\mu \alpha _m},\quad R_x=\frac{\rho _0 g_0 \gamma _T KH^2 \beta }{\mu \alpha _m}. \end{aligned}$$

(8)

Here $Q_\mathrm{v}$, Pe are vertical and horizontal Peclet numbers and $R_z$, $R_x$ are vertical and horizontal Rayleigh numbers. The flow governing equations representing conservation of mass, momentum, and energy balance are in the form

$$\begin{aligned}&\displaystyle \nabla \,\cdot \,\mathbf v =0,\end{aligned}$$

(9)

$$\begin{aligned}&\displaystyle \mathbf v =-\nabla {P}+T(1+\eta z)\mathbf k , \end{aligned}$$

(10)

$$\begin{aligned}&\displaystyle \frac{\partial {T}}{\partial {t}}+\mathbf v \,\cdot \,\nabla {T}=\nabla ^2T. \end{aligned}$$

(11)

The corresponding boundary conditions are

$$\begin{aligned} z=\pm \frac{1}{2}:\quad w=Q_\mathrm{v},\quad T=-\frac{(\pm R_z)}{2}-R_x x. \end{aligned}$$

(12)

The basic steady-state solution $(\mathbf v _{\mathrm{s}}, P_{\mathrm{s}}, T_{\mathrm{s}})$ of Eqs. (9)–(12) are in the form

$$\begin{aligned} u_\mathrm{s}= & {} R_x\left( z+\eta \frac{z^2}{2}-\frac{\eta }{24}\right) +Pe,\quad v_\mathrm{s}=0,\quad w_\mathrm{s}=Q_\mathrm{v},\quad P_\mathrm{s}=P(x,y,z), \end{aligned}$$

(13)

$$\begin{aligned} T_{\mathrm{s}}= & {} -R_x x+Az^3+Bz^2+Cz+D-(R_z+E)\frac{(\exp (Q_\mathrm{v} z)-\cosh (Q_\mathrm{v}/2))}{F}. \end{aligned}$$

(14)

A constraint is imposed to be there is a net mass flow in the x direction, in such a way that

$$\begin{aligned} \int ^{1/2}_{-1/2} u_\mathrm{s}=Pe,\quad \int ^{1/2}_{-1/2} v_\mathrm{s}=0. \end{aligned}$$

(15)

The basic state solution is given by Eqs. (13)–(14) which is commonly referred to as Hadley–Prats flow. Vertical temperature gradient is given by

$$\begin{aligned} DT_\mathrm{s}=\frac{\hbox {d}T_\mathrm{s}}{\hbox {d}z}= {\left\{ \begin{array}{ll} - 4 G \eta z^3-12 G z^2+(G \eta -R_{x}Pe)z+(-R_z+G), &{} \text {for } Q_\mathrm{v}=0,\\ 3Az^2+2Bz+C-((R_z+E)/F)Q_\mathrm{v} \exp (Q_{v}z), &{} \text {for } Q_\mathrm{v}\ne 0. \end{array}\right. } \end{aligned}$$

where

$$\begin{aligned}&\displaystyle A=\frac{{R_x}^2 \eta }{6 Q_\mathrm{v}}, \quad B=\frac{{R_x}^2}{2}\left( \frac{\eta }{{Q_\mathrm{v}}^2}+\frac{1}{Q_\mathrm{v}}\right) ,\\&\displaystyle C=\left[ {R_x}^2\left( \frac{\eta }{{Q_\mathrm{v}}^3}+\frac{1}{{Q_\mathrm{v}}^2}-\frac{\eta }{24 Q_\mathrm{v}}\right) +\frac{R_x Pe}{Q_\mathrm{v}}\right] ,\quad D=-\frac{{R_x}^2}{8}\left( \frac{\eta }{{Q_\mathrm{v}}^2}+\frac{1}{Q_\mathrm{v}}\right) ,\\&\displaystyle E=\frac{{R_x}^2 \eta }{24 Q_\mathrm{v}}+{R_x}^2\left( \frac{\eta }{{Q_\mathrm{v}}^3}+\frac{1}{{Q_\mathrm{v}}^2}-\frac{\eta }{24 Q_\mathrm{v}}\right) +\frac{R_x Pe}{Q_\mathrm{v}},\\&\displaystyle F=2\sinh (Qv/2), \quad G=\frac{{R_x}^2}{24}. \end{aligned}$$

Now, the following perturbations to the basic solution are imposed as

$$\begin{aligned} \mathbf v =\mathbf v _\mathrm{s}+\mathbf v ^{\prime },\quad T=T_\mathrm{s}+{\theta },\quad P=P_\mathrm{s}+{p}^{\prime }. \end{aligned}$$

(16)

where the prime denotes a very small perturbation parameter. The perturbation equations are

$$\begin{aligned}&\displaystyle \nabla \cdot \mathbf v ^{\prime }=0, \end{aligned}$$

(17)

$$\begin{aligned}&\displaystyle \mathbf v ^{\prime }=-\nabla {p}^{\prime }+(1+\eta z){\theta }\mathbf k , \end{aligned}$$

(18)

$$\begin{aligned}&\displaystyle \frac{\partial {\theta }}{\partial {t}}+\mathbf v _\mathrm{s}\cdot \nabla {\theta }+\mathbf v ^{\prime }\cdot \nabla T_\mathrm{s}+\mathbf v ^{\prime }\,\cdot \,\nabla {\theta }=\nabla ^2{\theta }, \end{aligned}$$

(19)

and the corresponding boundary conditions are

$$\begin{aligned} z=\pm \frac{1}{2} :\quad w^{\prime }={\theta }=0. \end{aligned}$$

(20)

Eq. (20) represents zero perturbations on the velocity, temperature at the lower and upper plates.

Fig. 1

Sketch of the porous medium

3 Linear Stability Analysis

In order to perform the linear stability analysis, the products of perturbations are neglected in the system (17)–(19). The resultant linearized perturbation equations are subjected to small wave-like perturbations in the form

$$\begin{aligned} (u^{\prime },v^{\prime },w^{\prime },{\theta },p^{\prime })=(u(z),v(z),w(z),\theta (z),p(z))\exp i(kx+ly-\sigma t). \end{aligned}$$

(21)

where $i=\sqrt{-1}$, k, and l are wave numbers in x and y directions, respectively, and $\sigma$ is a complex growth rate parameter. On substituting Eq. (21) and eliminating u(z), v(z), and p(z), the corresponding eigenvalue problem is derived as follows

$$\begin{aligned}&\displaystyle (D^2-\alpha ^2)w+\alpha ^2 (1+\eta z)\theta =0, \end{aligned}$$

(22)

$$\begin{aligned}&\displaystyle (D^2-\alpha ^2+i\sigma -iku_{\mathrm{s}})\theta +i\frac{kR_{x}}{\alpha ^2}Dw -DT_{\mathrm{s}}w-Q_{v}D\theta =0, \end{aligned}$$

(23)

$$\begin{aligned}&\displaystyle z=\pm \frac{1}{2}{:}\quad w=\theta =0. \end{aligned}$$

(24)

where $D=\hbox {d}/\hbox {d}z$ and $\alpha =\sqrt{k^{2}+l^{2}}$ is the overall wave number. In this study, $k=0$ referred to as a longitudinal mode and $l=0$ as a transverse mode. The system of Eqs. (22)–(24) constitutes an eigenvalue problem for vertical thermal Rayleigh number $R_z$ and in this problem $R_z$ appears through the term $DT_{\mathrm{s}}$.

4 Nonlinear Stability Analysis

While carrying out the nonlinear energy stability analysis with considering all perturbations, an energy functional is defined as

$$\begin{aligned} E(t)=\frac{\xi }{2}\left\| \theta \right\| ^2, \end{aligned}$$

(25)

where $\xi$ is a coupling parameter. On multiplying Eq. (18) by $\mathbf v ^{\prime }$, Eq. (19) by $\theta$ and integrating over V by using boundary conditions and Gauss divergence theorem, the following equations are yielded

$$\begin{aligned} \left\| \mathbf v ^{\prime }\right\| ^2= & {} {<}(1+\eta z)\theta w^{\prime }{>}, \end{aligned}$$

(26)

$$\begin{aligned} \frac{1}{2}\frac{\hbox {d}}{\hbox {d}t}\left\| \theta \right\| ^2= & {} -\left\| \nabla \theta \right\| ^2-<(\mathbf v ^{\prime }\cdot \nabla T_\mathrm{s})\theta {>}. \end{aligned}$$

(27)

where V indicates periodicity cell, ${<}.{>}$ denotes integration over V, and $\left\| .\right\|$ denotes the $L^2(V)$ norm. The Eqs. (26)–(27) along with Eq. (25) can be written as

$$\begin{aligned} \frac{\hbox {d}E}{\hbox {d}t}=I-D, \end{aligned}$$

(28)

where

$$\begin{aligned} I= & {} <(1+\eta z)\theta w^{\prime }>-\xi {<}(\mathbf v ^{\prime }\cdot \nabla T_\mathrm{s})\theta {>}, \end{aligned}$$

(29)

$$\begin{aligned} D= & {} \xi \left\| \nabla \theta \right\| ^2+\left\| \mathbf v ^{\prime }\right\| ^2. \end{aligned}$$

(30)

Therefore,

$$\begin{aligned} \frac{\hbox {d}E}{\hbox {d}t}= & {} D\left( \frac{I}{D}-1\right) \nonumber \\\le & {} -D\left( 1-\max _{H}\frac{I}{D}\right) . \end{aligned}$$

(31)

where H is a set of all admissible solutions over which it is looked for maximum, further H= $(\mathbf v ^{\prime },\theta ) \in L^2(V){:}\, \nabla .\mathbf v ^{\prime }=0, \mathbf v ^{\prime }=\theta =0$ at $z=\pm \frac{1}{2}$. Eq. (28) becomes the following maximization problem

$$\begin{aligned} m= \max _{H}\frac{I}{D}, \end{aligned}$$

(32)

Eq. (31) becomes

$$\begin{aligned} \frac{\hbox {d}E}{\hbox {d}t} \le -D(1-m), \end{aligned}$$

By using Poincare inequality $\pi ^2\left\| \theta \right\| ^{2} \le \left\| \nabla \theta \right\| ^{2}$, from Eq. (31), the following inequality is arrived.

$$\begin{aligned} \frac{\hbox {d}E}{\hbox {d}t}\le -2\pi ^2(1-m)E, \end{aligned}$$

(33)

By integrating above equation, and $0<m<1$,

$$\begin{aligned} E(t) \le e^{-2\pi ^{2}(1-m)t}E(0). \end{aligned}$$

(34)

Inequality (34) shows $E(t)\rightarrow 0$ exponentially as $t\rightarrow \infty$ for $0<m<1$. In Eq. (32), assuming the critical argument $m=1$. Then the maximization problem becomes

$$\begin{aligned} \delta I-m \delta D=0. \end{aligned}$$

(35)

The associated Euler–Lagrange equations are

$$\begin{aligned}&\displaystyle (1+\eta z)\theta \mathbf k -\xi \nabla T_\mathrm{s}\theta -2\mathbf v ^{\prime }=\nabla \lambda , \end{aligned}$$

(36)

$$\begin{aligned}&\displaystyle (1+\eta z)w^{\prime }-\xi (\mathbf v ^{\prime }\cdot \nabla T_\mathrm{s})+2\xi \nabla ^2\theta =0, \end{aligned}$$

(37)

where $\lambda$ is a Lagrange multiplier which is introduced because $\mathbf v ^{\prime }$ is solenoidal. By applying curlcurl to Eq. (36) and taking third component of resulting equation, the following equation is obtained.

$$\begin{aligned} \xi DT_{\mathrm{s}}{\nabla _1}^2 \theta -(1+\eta z){\nabla _{1}}^2 \theta +2{\nabla _1}^2w^{\prime }-2\frac{\partial }{\partial z}\left( \frac{\partial u^{\prime }}{\partial x} +\frac{\partial v^{\prime }}{\partial y}\right) +\xi R_x\frac{\partial ^2 \theta }{\partial x \partial z}=0, \end{aligned}$$

(38)

where

$$\begin{aligned} {\nabla _1}^2=\frac{\partial ^2}{\partial x^2}+\frac{\partial ^2}{\partial y^2}. \end{aligned}$$

Now employing the normal modes (21) to Eqs. (37) and (38) and eliminating the variables u, v and $\lambda$, we arrived at the following equations.

$$\begin{aligned}&\displaystyle \left( D^2-\alpha ^2\right) w+\frac{1}{2}(1+\eta z)\alpha ^2 \theta +\frac{ik\xi }{2}R_{x}D\theta -\frac{\xi \alpha ^2}{2}DT_\mathrm{s}\theta =0, \end{aligned}$$

(39)

$$\begin{aligned}&\displaystyle \left( D^2-\alpha ^2\right) \theta +\frac{1}{2\xi }(1+\eta z)w+\frac{\xi }{4}{R_x}^2\theta -\frac{1}{2}DT_{\mathrm{s}}w=0, \end{aligned}$$

(40)

$$\begin{aligned}&\displaystyle z=\pm \frac{1}{2}{:}\quad w=\theta =0. \end{aligned}$$

(41)

Eqautions (39)–(41) forms an eigenvalue problem for $R_z$.

5 Results and Discussion

We look for numerical solution of eigenvalue problems (22)–(24) and (39)–(41) for linear and nonlinear cases, respectively, and $R_z$ treated as eigenvalue. Eigenvalue $R_z$ is found for given a set of input parameters $\alpha , Pe, Q_\mathrm{v}, R_x, \eta$. In order to solve the eigenvalue problems, shooting and Runge–Kutta methods are employed as given in Barletta et al. (2010). Critical Rayleigh number for both linear and nonlinear theories is as follows

$$\begin{aligned} R_{\mathrm{L}}= & {} \min _{k}\min _{l}R_{z}(k,l,R_{x},\eta ,Q_{v},Pe),\\ R_{\mathrm{E}}= & {} \max _{\xi }\min _{k}\min _{l}R_{z}(k,l,R_{x},\eta ,Q_{v},Pe,\xi ). \end{aligned}$$

Here $\xi$ is chosen optimally as given in Kaloni and Qiao (2000). In this discussion, the response of critical vertical thermal Rayleigh numbers $R_\mathrm{L}$ and $R_\mathrm{E}$ is examined for various parameters in the case of stationary longitudinal modes ($\sigma = 0$, $k = 0$) because these are the only preferred modes observed by Nield (1991). In the absence of variable gravity ($\eta =0$), the linear theory in the present problem reduces to the problem solved by Nield (1998). Table 1 a shows good agreement between Nield (1998) and the present linear theories. And also, in the absence of variable gravity, vertical throughflow ($\eta = 0, Q_\mathrm{v} = 0$), present nonlinear theory, leads to the problem in Kaloni and Qiao (1997), and this comparison is shown in Table 1. Throughout discussion, dashed lines represent the linear stability theory and solid lines represent nonlinear stability theory.

Table 1 Comparison between Nield (1998), present linear theories; Kaloni and Qiao (1997) and present nonlinear theories

Figure 2 shows the plot of critical vertical thermal Rayleigh numbers $R_\mathrm{L}$ and $R_\mathrm{E}$ versus vertical Peclet number $Q_\mathrm{v}$ for $Pe=0$ and $R_x=0$. The effect of variable- gravity parameter is displayed by comparison between $\eta =0, 1$. When $Q_\mathrm{v}> 0$ (upwardflow), the porous layer experiences hot fluid input, and hence global temperature increases. When $Q_\mathrm{v}< 0$ (downwardflow), cold fluid enters which results in the decrease in global temperature. $R_\mathrm{L}$ and $R_\mathrm{E}$ are minimum at $Q_\mathrm{v}=0$, and increases in the right and left of $Q_\mathrm{v}=0$. Increasing throughflow in both directions results in stabilizing the flow. Vertical throughflow gives a temperature distribution in which gradients are significant only in the sublayer of thickness $\epsilon$. Effective Rayleigh number is based on thickness of sublayer instead of the height of the porous layer H. So the bulk convection is confined to this sublayer only. Critical Rayleigh number depends on the order $H/\epsilon$. As vertical throughflow increases, critical Rayleigh number increases. Hence, stabilization takes place. The plot for $\eta =0$ is symmetric about $Q_\mathrm{v}=0$, and this symmetry breaks down when variable gravity is considered. For $Q_\mathrm{v}< 0$ (downwardflow), flow with $\eta =1$ is more stable than with $\eta =0$, and for $Q_\mathrm{v}> 0$ (upwardflow) flow with $\eta =0$ is more stable than with $\eta =1$. It is observed that linear and energy theories give very good agreement on critical Rayleigh numbers in absence of $Q_\mathrm{v}$. But as $Q_\mathrm{v}$ changes in both directions, the difference between the two thresholds is widened. The linear threshold is always higher than the energy threshold. This gap is referred to as subcritical region.

Fig. 2

Plot of $R_\mathrm{L}$ and $R_\mathrm{E}$ versus $Q_\mathrm{v}$ for $Pe=0, R_x=0$. Dashed lines are for linear theory and solid lines are for nonlinear theory

Figure 3 depicts the behavior of $R_\mathrm{L}$ and $R_\mathrm{E}$ versus horizontal Peclet number Pe for $R_x=0$, $Q_\mathrm{v}=0$ and $\eta =0,1$. In the absence of variable gravity ($\eta =0$), direction of horizontal mass flow (the sign of Pe) has no effect on the critical Rayleigh numbers $R_\mathrm{L}$ and $R_\mathrm{E}$, which means that graphs of $R_\mathrm{L}$ and $R_\mathrm{E}$ are symmetric about $Pe=0$. But this symmetry breaks down as soon as $\eta$ is introduced. Critical values $R_\mathrm{L}$ and $R_\mathrm{E}$ are increasing as Pe increasing from $-$20 to 0, but these critical values are decreasing as Pe increases from 0–20. For fixed $\eta$, it is noted that $R_\mathrm{L}$ in linear theory is higher than the $R_\mathrm{E}$ in energy theory. For $Pe< 0$, flow with $\eta =0$ is more unstable than that with $\eta =1$. For $Pe> 0$, flow with $\eta =1$ is more unstable than that with $\eta =0$.

Fig. 3

Graph of $R_\mathrm{L}$ and $R_\mathrm{E}$ versus Pe for $R_x=0, Q_\mathrm{v}=0$. Dashed lines are for linear theory and solid lines are for nonlinear theory

Figure 4a, b shows the plots of $R_\mathrm{L}$ and $R_\mathrm{E}$ versus horizontal thermal Rayleigh number $R_x$ for $Pe=0$ and $Q_\mathrm{v} = 1,-1$. The effect of variable gravity parameter is shown by the comparison between $\eta =0, 1$. Increasing horizontal thermal Rayleigh number stabilizes the convection pattern in the medium. The behavior of critical Rayleigh numbers is same for $Q_\mathrm{v}=1$ and $Q_\mathrm{v}=-1$. In Fig. 4a, flow with $\eta =0$ is more stable than that with $\eta =1$, whereas in Fig. 4b, reverse situation is observed.

Fig. 4

Variation of $R_\mathrm{L}$ and $R_\mathrm{E}$ versus $R_x$ for $Pe=0$. Dashed lines are for linear theory and solid lines are for nonlinear theory. (a) $Q_{v} = 1$ (b) $Q_{v} = -1$

Figure 5a, b represents variation of $R_\mathrm{L}$ and $R_\mathrm{E}$ against horizontal thermal Rayleigh number $R_x$ for $Q_\mathrm{v}=0$, $\eta = 0,1$, $Pe = 5,$ and $Pe = -5$ . When $R_{x}> 0$ and $Pe> 0$, basic temperature of fluid decreases in the average basic flow direction and when $R_{x}> 0$ and $Pe< 0$, reverse situation takes place. The behavior of critical vertical thermal Rayleigh numbers is same in both cases $Pe = 5$ and $Pe = -5$. In Fig. 5a, flow with $\eta = 0$ more stable than with $\eta =1$, where as in Fig. 5b, the flow with $\eta =1$ more stable than that with $\eta =0$. The critical value $R_\mathrm{L}$ tends to increase with increasing $R_x$, while $R_\mathrm{E}$ increases up to certain values of $R_x$ and then decreases.

Fig. 5

Plot of $R_\mathrm{L}$ and $R_\mathrm{E}$ versus $R_x$ for $Q_\mathrm{v}=0$. Dashed lines are for linear theory and solid lines are for nonlinear theory. a $Pe = 5$. b $Pe = -5$

From Figs. 4a, b, 5a, b, it is observed that for small values of $R_x$, both the linear and nonlinear thresholds have small variation in $R_\mathrm{L}$ and $R_\mathrm{E}$. But this difference between the linear and nonlinear thresholds is increased with increasing values of $R_x$. It shows that for small $R_x$ linear theory results predicts the onset of convection very well but for higher values of $R_x$, subcritical instabilities arise before having linear threshold.

Figure 6a, b shows the plots of $R_\mathrm{L}$ and $R_\mathrm{E}$ against $R_x$ for $Pe=5$, $Q_\mathrm{v}=1$ and $Q_\mathrm{v}=-1$. In the presence of both vertical and horizontal Peclet numbers $Q_\mathrm{v}$ and Pe, the behavior of critical Rayleigh numbers is different with respect to $R_x$. In Fig. 6a when $Q_{v}=1$, the flow with $\eta =0$ is more stable than that with $\eta =1$. In Fig. 6b when $Q_{v}=-1$, a different response for $R_\mathrm{L}$ is observed with $\eta$. $R_\mathrm{L}$ in the presence of $\eta$ is higher than the $R_\mathrm{L}$ in the absence of $\eta$, for small values of $R_x$, and this trend is reversed after certain values of $R_x$. Similar kind of observation is made for energy threshold. In the energy case, after certain values of $R_x$, the $R_\mathrm{E}$ decreases with $R_x$.

Fig. 6

Graph of $R_\mathrm{L}$ and $R_\mathrm{E}$ versus $R_x$. Dashed lines are for linear theory and solid lines are for nonlinear theory. a Pe = 5, $Q_{\mathrm{v}}$ = 1. b Pe = 5, $Q_{\mathrm{v}}$ = $-$1

Figure 7 shows the response of $R_\mathrm{L}$ and $R_\mathrm{E}$ versus the variable gravity parameter $\eta$ for $Q_\mathrm{v}=0,1, Pe=-10,10$. $R_\mathrm{L}$ and $R_\mathrm{E}$ are decreases as $\eta$ increases. The value of critical vertical thermal Rayleigh numbers $R_\mathrm{L}$ and $R_\mathrm{E}$ is same when $Pe=10$, $Pe=-10$ for a particular value of $Q_\mathrm{v}$. In both the linear and nonlinear cases, for small values of $\eta$, the flow with $Q_\mathrm{v}=0$ is more unstable than the flow with $Q_\mathrm{v}=1$, but for sufficiently large values of $\eta$, the situation is reversed.

Fig. 7

Variation of $R_\mathrm{L}$ and $R_\mathrm{E}$ versus $\eta$ for $R_x=0,Pe=-10,10$, $Q_\mathrm{v}=0,1$. Dashed lines are for linear theory and solid lines are for nonlinear theory

For both linear and energy stability results, it is commonly observed that linear stability results overshoot the nonlinear stability results. This is due to the reason that the nonlinear perturbations are neglected in the linear theory, and hence linear theory alone cannot define the complete picture of the stability. The linear stability theory gives instability boundary, whereas the nonlinear stability theory gives stability boundary. The subcritical instabilities arise in between both the boundaries. There is a great chance of having subcritical instabilities in the parameter space where linear stability results and energy stability results differ.

6 Conclusion

The linear and nonlinear stability analyses of Hadley–Prats flow in a porous layer induced by horizontal temperature gradients are carried out by taking variable gravity and vertical throughflow into account. The eigenvalue problems are numerically integrated using shooting and Runge–Kutta methods by treating $R_z$ as an eigenvalue. Critical thermal Rayleigh number is defined as the minimum of all $R_z$ as wave number $\alpha$ varies.

In the absence of variable gravity effect, both the vertical Peclet number $Q_\mathrm{v}$ and horizontal Peclet number Pe have symmetric nature. For some values of Peclet numbers and variable gravity parameter $\eta$, the gap between the linear and nonlinear stability boundaries increases as $R_x$ increases. The pattern of stability curves with respect to $R_x$ is same irrespective of sign of Peclet number when the other Peclet number is absent. If both the Peclet numbers are present, the pattern of the stability curve differs.