Keywords

Introduction

Mobile communication has gained popularity and brought in a revolution to the communication industry. The end to end link in cellular communication is achieved by routing the signal through a base station. The base station is generally located on top of a high rise building or at the highest point in the locality it serves. Thus, the base station is devoid of scatterers around it. Whereas, the mobile device is located at the ground level and surrounded by objects like buildings, furniture, etc. The objects around the mobile device can be considered as scatterers. The signal from the base station reaches the mobile device after being reflected, refracted and dispersed by the scatterers. The time required for the different signals to reach the mobile device depends on the path it traverses from the base station to the mobile device via the scatterers. The signal may reach the mobile device from the base station after being scattered by a single scatterer or multiple scatterers. If the signal undergoes multiple scattering before reaching the mobile device, then the power of the received signal degrades drastically and contributes negligible power to the detectable signal. Hence in this chapter, we consider a signal that reaches the mobile device after being scattered by a single scatterer.

Model Description

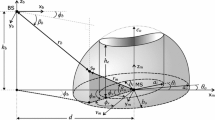
The geometrical based models are a widely used technique for modeling channels between the transmitter and receiver of wireless communication [1, 2]. In this modeling technique, as shown in Fig. 24.1, the transmitter and the receiver are separated by a distance D. The receiver is surrounded by scatterers around it inside a circle of radius R. The distance between the transmitter and the receiver (D) is considered to be much greater than the radius (R) of the scattering circle, thus justifying the use of geometric optics and representation of the waves by rays. The scatterers around the mobile device can be considered to be Gaussian or uniformly distributed depending on the environment it models. The number of scatterers does not affect the time of arrival statistics, as the time of arrival statistics is dependent on the distribution of the scatterers in the circle. But the number of scatterers should be adequately large to represent the distribution in the circle.

Fig. 24.1
figure 1

Geometrical-based model of cellular channel

Full size image

In the present work, we consider the scatterers to have a normal distribution around the mobile device. Similar work has been done before by Janaswamy in [3, 4]. The analytical approach in [3] is involved and cumbersome. In this chapter, we propose a much easier approach to find the time of arrival statistics of the signal at the mobile device. This is a more generalized approach and may be extended to any kind of scatterer distribution around the mobile device.

As mentioned earlier, we consider the scatterers to have a normal distribution around the mobile device confined in a circle of radius R. The probability density function and the cumulative density function of Gaussian distribution is given by Eqs. 24.1 and 24.2 respectively,

$$f_{X} \left( x \right) = \frac{1}{{\sqrt {2\pi \sigma^{2} } }}e^{{ - \frac{{\left( {x - \mu } \right)^{2} }}{{2\sigma^{2} }}}}$$
(24.1)
$$F_{X} \left( x \right) = \frac{1}{2}\left[ {1 + erf\left( {\frac{x - \mu }{\sigma \sqrt 2 }} \right)} \right]$$
(24.2)

where,

x :

random variable

μ :

mean value of the normal distribution

σ 2 :

variance

erf (x):

error function = \(\frac{1}{\sqrt \pi }\int_{ - x}^{x} {e^{{ - t^{2} }} dt}\)

Figure 24.2 shows a plot of the Gaussian density function. It may be observed both from the plot and Eq. 24.2 that 99.7% of the data are within the \(- 3\sigma \,\,to\,\,3\sigma\) limits. The histograms in Fig. 24.2, gives the relative number of items in the bins. The items in each bin can be assumed to be containing uniformly distributed data selected over the bin width.

Fig. 24.2
figure 2

A plot of the Gaussian density function with zero mean and unity variance

Full size image

In this chapter, we approximate the Gaussian-distributed scatterer in the scattering circle by concentric rings of uniformly distributed scatterers as shown in Fig. 24.3. The number of scatterers in a particular ring is determined by the mean, standard deviation of the Gaussian distribution and the distance of the ring from the center of the circle.

Fig. 24.3
figure 3

Concentric annular rings of scatterers

Full size image

Let us assume that the radius of the scattering circle is R and the standard deviation of the Gaussian distribution of the scatterers is \(\sigma\). If we equate the radius of the circle to \(3\sigma\), then we can make sure that 99.7% of the scatterers are within the circle of radius R. Let us assume that the circle of radius R is divided into N concentric circles of equal width, then the width of each annular ring would be \({R \mathord{\left/ {\vphantom {R N}} \right. \kern-0pt} N}\). Larger the value of N, better is the approximation. Now, we are required to put the scatterers in the annular rings in such a way that in each annular ring the scatterers are uniformly distributed whereas at the same time the scatterers should be Gaussian distributed over the circle [5]. Figure 24.3 shows the scattering circle being divided into annular rings. Correlating Figs. 24.2 and 24.3, the histogram A, B,C,…. of Fig. 24.2 corresponds to the annular rings A, B, C … of Fig. 24.3. The number of scatterers in an annular ring of Fig. 24.3 should be proportional to the area under the corresponding histogram in Fig. 24.2. The area under the histogram can be obtained by putting the lower and upper limits to the integral of Eq. 24.1. It may be noted here that the integral of Eq. 24.1 is given by the cumulative density function represented in Eq. 24.2.

The time of arrival is evaluated by calculating the time taken by the signal from the base station to reach a scatterer and then to the mobile device. The statistics of the time of arrival can be obtained after calculating the time of arrival from each scatterer. It is evident that the pattern of time of arrival statistics depends on the way the scatterers are distributed. Whereas, the actual time of arrival also depends on the separation distance between the base station and the mobile device [6].

Results and Discussion

Figure 24.4 above shows 1000 Gaussian distributed scatterers generated in a circle of radius hundred meters and at whose center the mobile device is located. The position of the scatterers is generated by using the randn function of MATLAB. This generates a set of points Gaussianly distributed over the x-axis. Then to each point, an angle is associated which is generated by using a uniform random generator which generates angles between 0 and \(2\pi\) radians.

Fig. 24.4
figure 4

Sactterers generated using Gaussian distribution directly

Full size image

Wheras Fig. 24.5 above shows one thousand scatterers generated in a circle of radius hundred meters and at whose center the mobile device is located. Here the circle is first divided into thirty annular rings of equal width. Then the scatterers are uniformly distributed in these annular rings. The total number of scatterers were considered to be thousand. The number of scatterers in each ring decreases with its distance from the center and depends on the area of the histogram it corresponds to in the Gaussian distribution.

Fig. 24.5
figure 5

Gaussian distribution of scatterers generated using annular rings with uniform distribution approach

Full size image

As the coordinates of the scatterers generated by above two methods are known, the time of arrival of the signal to the mobile from the base station placed at 500 meters away from the mobile device can be calculated. The time of arrival was calculated for the signal arriving the mobile device from each scatterer in both the cases. The probability density of the time of arrival from both the cases were then plotted, as shown in Fig. 24.6 below. It can be observed that the probability density function obtained by both the methods match each other.

Fig. 24.6
figure 6

Probability density function of time of arrival obtained by scatterers generated by Gaussian distribution and annular rings with uniform distribution

Full size image

Conclusion

The time of arrival of the signal and its statistics is an important parameter in wireless communication system. The time of arrival is one of the parameters which determine the pulse width of the communication system. In this paper, we propose an alternative way to generate the Gaussian-distributed scatterers to evaluate the time of arrival statistics between the base station and the mobile device. This method of generation divides the scattering circle into equal width annular rings. Then the scatterers are uniformly distributed in the annular rings. The number of uniformly distributed scatterers in annular rings depends on its distance from the center of the ring, the standard deviation of the Gaussian distribution it needs to replicate. This method of generation of scatterers makes the mathematical formulation for the time of arrival more tractable. The proposed method was then validated with the standard method by evaluating the time of arrival statistics by both the approaches.