Small-Scale Fading Statistics of Emerging 3-D Mobile Radio Cellular Propagation Channels

Abstract

In delivering fifth generation (5G) communication networks, the fundamental advancements in the scale of antenna arrays, density of networks, mobility of communicating nodes, size of cells, and range of frequencies necessitate the derivation of an appropriate and reliable channel model. A tunable three dimensional (3-D) geometric channel model comprehending the mobility of user terminal together with high degree of flexibility in modelling the shape, orientation, and scale of the scattering region is proposed. Characterization of Doppler spectrum, quantization of multipath dispersion in angular domain, and second order fading statistics of the radio propagation channel is presented. Mathematical expressions for joint and marginal probability density function of Doppler shift and multipath power are derived for this advanced 3-D hollow geometric scattering model. Next, an analysis on the Doppler spectrum is presented, where the impact of various physical channel parameters on its statistical characteristics is analyzed. Since, the quantification of multipath dispersion in 3-D angular domain is of vital importance for designing large scale planner antenna arrays with very high directional resolution for emerging 5G communications, therefore, a thorough analysis on the multipath shape factors (SFs) of the proposed analytical 3-D channel model is conducted. Finally, the analysis on SFs is extended for characterization of second order fading statistics of multipath channels.

1 Introduction

In the last few years, discussions and research about fifth generation (5G) standardization has gained the attention of the researchers around the world. The fourth generation (4G) systems, with some improvements and very small amount of new spectrum, has now been deployed and is getting mature; researchers are now working on “what is to be included” in 5G [1]. Some of the key things that are expected to be part of the 5G (discussed so far by the researchers) are millimeter wave (mmWave) spectrum [2], less elevated base stations (BS), small sized cells [3], ultra-densification of the network, massive multiple-input multiple-output (MIMO) [4], mobility of both ends of the communication link (Device to Device) [5, 6], new methods of allocating/re-allocating bandwidth, internet of things, and the integration of all the past and current WiFi and cellular standards to provide an omnipresent lower-latency, higher-rate experience for end users. Large scale antenna arrays are expected to be used for 5G progressively and co-phasing these arrays is one of the main challenges to make them energy efficient. When the channel changes rapidly due to mobility of either end of the communication link or due to rapid changes in the orientation of the nodes, the importance of co-phasing becomes manifold. The mobility of the communicating nodes imposes Doppler shift, which further leads to time variability in the received signal. With the increase in frequency, the effect of Doppler shift gets more pronounced [7]. So considering the high mobility, high data rates, increased number of users, and higher frequencies of the transmitted signal, it is very important to consider Doppler shift characteristics, multipath shape factors (SFs), and second order fading statistics of the radio propagation channels.

Many multipath channel models have been proposed in literature in which Doppler shift characteristics have been taken into account. Iltis et al. proposed a design for multipath channel communication systems in [8]. Characteristics of spread spectrum system design for underwater and UHF/VHF scenario have been discussed. It has been shown that best estimate of bit-error rate of the channel can be made with the accurate knowledge of the channel, Doppler and delay parameters. Expressions for the Doppler spectrum have been derived in [9] for mobile to mobile (M2M) communication scenario. Multipath three dimensional (3-D) scattering environment has been considered and dipole antennas are communicating with mobile units installed in urban areas. It has been claimed that with the accurate knowledge of multipath distribution, real time Doppler spectra can be calculated with different antenna patterns used. A general expression for the Doppler spectrum has been derived in [10] and has been shown that Doppler spectrum can be found by multiplying the average received power (for the given Doppler frequency) with probability density function (PDF) of Doppler frequency. A 3-D fading channel model is proposed in [11] and a number of functions relating power spectral density, elevation angle and PDF have been derived along with direct relation between PDF of elevation angle and power spectral density of the signal received. A geometrical model is presented in [12] in which single bounce of the multipath components from uniformly distributed scattering objects is assumed. Angle of arrival (AoA), time of arrival (ToA), and power of multipath components has been characterized. Also BS is equipped with the directional antennas to show that fading envelop correlation increases with the use of directional antenna. In [13], tapped delay line channel models have been designed for macro and microcellular environments at 5.3 GHz. Doppler spectra is seen the be changing with different taps of the designed channel models and comparisons have been made between measured and simulated results for validations of the results. Measurements using the direct sequence spread spectrum technique have been taken and compared for M2M scenario at 2.45 GHz in [14]. For each tap, different doppler spectrum has been observed. It has also been observed that changing the environment also produces different Doppler spectra. Another measurement campaign was done in Lund, Sweden at 5.2 GHz by Alexander et al. and has been presented in [15]. Mobile to fixed and M2M MIMO channels were taken into account for the measurements and path loss, power delay profile and delay Doppler spectra has been presented in M2M environment where both the mobile stations (MSs) are moving away from each other. An accurate match of the theoretical and measured Doppler shift has been observed. Doppler shift distribution of the received signal at MS has been analyzed in [16]. AoA and Doppler shift relation has been utilized to form a relation between PDFs of the Doppler spread and elevation angle. Finally, this relation between PDFs is applied to a semi spheroid model proposed in [17]. Impact of directional antennas on the Doppler spectra has been discussed in [18]. Relations between PDFs of power, Doppler shift and path distance have been derived in closed form. Also equations for marginal and joint PDFs of power, Doppler shift and elevation AoA have been derived. It has been shown that with the use of a narrow beam directional antenna at BS, the spread in the distribution of the Doppler shift can be reduced significantly. Impact of scatterer mobility on both the signals received and reflected from a scatterer have been studied and discussed in [19] named the double Doppler model. Doppler effect on the signal received at a scatterer and the scattered signal have been taken into account and thats why this model is named as double Doppler model. Analytical expressions have been compared with the measured data to validate the model. Directional antennas have been used to simulate the Doppler spectrum for vehicle to vehicle 3-D channel model in [20]. It has been shown that use of directional antennas changes the Doppler spectrum of the model as compared to the omnidirectional antennas.

Motion of the receiver in a communication system causes rapid fluctuations in the power of the received signal. This phenomena is named as small-scale fading which is caused by small wavelength changes due to change in the position of the receiver. This effect occurs due to constructive and destructive contribution of the multipath signals reaching at the receiver. These fluctuations in the power of the received signal affect the modulations schemes, equalization, diversity, error correction, and channel coding. Multipath SFs on which second order fading statistics depend are angular spread, standard deviation, angular constriction and azimuthal direction of maximum fading. These SFs are derived from PDF of AoA of the communication channel. Second order fading statistics include level crossing rate (LCR), average fade duration (AFD), autocovariance (ACV), and coherence distance (CD). Small-scale fading is characterized as a stochastic process because of its random and unpredictable nature. Relationship between narrowband fading and multipath angular spread for wireless channels has been developed in [21]. A simpler description of the multipath SFs in presence of small-scale fading is given in [22]. Geometrical relations of the SFs with AoA and fading of the channel have been derived to reduce a multipath channel with arbitrary spatial complexity to only three SFs. These SFs have been used for second order fading statistics to derive equations for LCR, AFD, ACV, and CD. 3-D multipath SFs have been derived in [23]. Directional antennas have been used and second order fading statistics have also been performed using these SFs for the derivation of AFD, LCR, and envelope correlation for 3-D Rayleigh fading channel. Second order fading statistics have been analyzed in [24]. SFs, LCR, and AFD have been derived and applied to angular distribution of multipath power of Nakagami-m channel. It has been shown that by using SFs it becomes easy, convenient and intuitive to determine the relation between the physical channel and fading characteristics. Work done in [24] has further been extended in [25] and first and second order fading statistics have been analyzed for Rician as well as Nakagami-m fading channels. Various geometric and statistical channel models have been compared on the basis of SFs in [26,27,28]. Effect of changing the Doppler spectrum on the second order fading statistics of these channels has also been analyzed. Directional antennas have been deployed on the BS and impact on the second order fading statistics has also been studied. First and second order fading statistics have been analyzed and measured by various other researchers as well [29,30,31,32]. Recently, an advanced tunable channel model for emerging communication networks is proposed in [33]. The model provides nine degrees of freedom in designing scattering regions; therefore, it delivers a good fit of analytical results on a diverse range of empirical data sets. The model however only provides analytical expression for plain AoA/ToA characteristics of the channel. Whereas, in studying time variability of the channel characteristics imposed by mobility of the communicating nodes, there is a potential scope to extend the model in [33] from plain AoA/ToA to Doppler spectrum and small-scale fading statistics.

This paper extends the tunable 3-D hollow channel model in [33, 34] for quantification of multipath spread, Doppler spectrum, and second order fading statistics. Joint and marginal analytical expressions for multipath power and Doppler shift are derived. Impact of various physical parameters of the channel on small-scale fading characteristics is also presented. Rest of the paper is organized as follows: the proposed analytical model for small-scale fading channels is explained in Sect. 2. Derivation of joint and marginal PDFs of the Doppler power spectrum are given in Sect. 3. Analysis on quantification of multipath power in 3-D angular domain is presented in Sect. 4. Second order fading statistics of the radio channel are analyzed in Sect. 5. Finally the paper is concluded in Sect. 6.

2 System Model

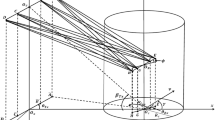
In this section, the proposed 3-D ellipsoidal model is presented. Doppler spectrum and fading statistics of the proposed 3-D model are analyzed. MS is assumed moving with velocity $v_m$ at an instantaneous distance d from BS. The BS is assumed to be fixed at height $h_b$. The effective scattering region (ESR) is modelled encompassed within the outer bounding semi-ellipsoid and inner bounding hollow elliptic cylinder. Outer bounding ellipsoid is assumed to be scalable on its major, intermediate, and minor axes which are presented by $a_o$, $b_o$, and $c_o$ and can be rotated along the azimuth with an angle $\theta _o$. Inner hollow cylinder is scalable on its major and minor axes with $a_i$ and $b_i$. Height of cylinder is fixed such that it is always greater than $c_o$ so that it hollows the outer bounding ellipsoid vertically. Also the cylinder can be rotated with an angle of $\theta _i$ on the azimuth plane. The ESR is designed tunable so that it can adapt any street or road orientation to provide the best results. Linear distance of a scattering point ($s_p$) from the BS and MS is shown by $r_b$ and $r_m$, respectively. $\beta _m$ is the elevation angle and $\phi _m$ is the azimuth angle made by $s_p$ with MS. $\phi _v$ is the azimuth angle made by the direction of motion of MS and $\phi _r$ is the azimuth angle between direction of motion of the MS and $s_p$. $\phi _b$ and $\beta _b$ are the azimuth and elevation angles respectively, between BS and $s_p$. $h_e$ is the height of cylinder for a given $\phi _m$. Scatterers are assumed to be uniformly distributed within the ESR and each scatterer is assumed to scatter a signal in all the directions with equal power. Similarly all the scattered signals received at MS are assumed to have equal power and random phases. Single bounce communication is assumed to take place and signal scattered from more than one scattering point is assumed to have negligible power [17, 35, 36]. An $s_p$ can be represented by $r_{sp}, \phi _{sp},$ and $\beta _{sp}$ in spherical coordinate system or by $x_{sp}, y_{sp},$ and $z_{sp}$ in Cartesian coordinate system. $a_o, b_o, c_o, a_i, b_i, \theta _o$, and $\theta _i$ are important geometric parameters of the channel model as they determine the size and orientation of the ESR. This high degree of freedom in geometry of ESR introduces flexibility in obtaining more diverse analytical curves for channel characteristics which helps in achieving a good fit of analytical curves on field measurement results.

Fig. 1

Proposed channel model for outdoor radio cellular communication

3 PDF of the Doppler Spectrum

In this section derivation of PDF of Doppler spectrum is presented. Azimuth angle $\phi _r$ shown in Fig. 1, is the angle between direction of MS’s motion ($\phi _v$) and the angle $\phi _m$ made by signal arriving from a certain $s_p$. Hence $\phi _r$ can be expressed as, $\phi _r = \phi _v-\phi _m$. The relationship of multipath components of the received signal with the Doppler shift can be written as,

$$\begin{aligned} f_d = f_m \cos \phi _r \cos \beta _m. \end{aligned}$$

(1)

$f_m$ given in above equation is the maximum shift in the Doppler spectrum and can be expressed as a function of carrier frequency ($f_c$), velocity of the MS (v), and velocity of light (c) as shown below,

$$\begin{aligned} f_m = \frac{v}{c}f_c. \end{aligned}$$

(2)

The normalized Doppler spread $\gamma = f_d/f_m$ can be written as,

$$\begin{aligned} \gamma = \cos \phi _r \cos \beta _m. \end{aligned}$$

(3)

The azimuth angle $\phi _m$ can be expressed as a function of direction of motion, elevation AoA, and Doppler shift as shown below,

$$\begin{aligned} \phi _m = \phi _v - \cos ^{-1}\left( \frac{\gamma }{\cos \beta _m}\right) . \end{aligned}$$

(4)

The distances of $s_p$ from BS and MS are $r_b$ and $r_m$, respectively. Total distance which the signal has to travel from BS to MS can thus be given as,

$$\begin{aligned} l = r_b + r_m. \end{aligned}$$

(5)

Parameter $r_b$ can be simplified in terms of $\beta _m$, $r_m$, and $\phi _m$ as shown below,

$$\begin{aligned} r_b = \sqrt{r_m^2+d^2+h_b^2 - 2 r_m ( d \cos \beta _m \cos \phi _m + h_b \sin \beta _m)}. \end{aligned}$$

(6)

Substituting (6) in (5) and solving for $r_m$, the equation for $r_m$ as a function of path delay and angles seen at MS can be rearranged as,

$$\begin{aligned} r_m = \frac{l^2 - d^2-h_b^2 }{2 ( l - d \cos \beta _m \cos \phi _m - h_b \sin \beta _m )}. \end{aligned}$$

(7)

Observing from MS with a given azimuth angle $\phi _m$ and at given elevation angle $\beta _m$, the distance from MS to the nearest and farthest scatterer is $r_i$ and $r_o$, respectively, given by

$$\begin{aligned} r_i= & {} \frac{1}{\cos \beta _m}\sqrt{\frac{2(a_i^2b_i^2)}{a_i^2 + b_i^2 + (b_i^2 - a_i^2 )\cos 2(\theta _i - \phi _m)}}, \end{aligned}$$

(8)

$$\begin{aligned} r_o= & {} \frac{a_ob_oc_o}{\sqrt{a_o^2b_o^2\sin ^2\beta _m+c_o^2\cos ^2\beta _m(b_o^2\cos ^2(\theta _o -\phi _m) + a_o^2\sin ^2(\theta _o - \phi _m))}}. \end{aligned}$$

(9)

Equation of joint density function $p(l,\phi _m,\beta _m)$ can be directly used here,

$$\begin{aligned} p(l,\phi _m,\beta _m) = \frac{p(r_m,\phi _m,\beta _m)}{|J(l,\phi _m,\beta _m)|}. \end{aligned}$$

(10)

The joint density function for $r_m$, $\phi _m$, and $\beta _m$ given below can be obtained as,

$$\begin{aligned} p(r_m,\phi _m,\beta _m) = f(x_m,y_m,z_m)r^2_m\cos \beta _m. \end{aligned}$$

(11)

$f(x_m,y_m,z_m)$ represents the spatial scatter density function, which is taken as uniform in this model. The Jacobian transformation used in (10) can be derived as,

$$\begin{aligned} J(l,\phi _m,\beta _m) = \left| \frac{\partial r_m}{\partial l}\right| ^{-1} = \frac{2(d\cos \beta _m\cos \phi _m+h_b\sin \beta _m-l)^2}{l^2+d^2+h_b^2-2l(d\cos \beta _m\cos \phi _m+h_b\sin \beta _m)}. \end{aligned}$$

(12)

Substituting the expressions of $p(r_m,\phi _m,\beta _m)$, $r_m$ and $J(l,\phi _m,\beta _m)$ in (10), it can be rewritten as given below,

$$\begin{aligned} p(l,\phi _m,\beta _m) = {f(x_m,y_m,z_m) } \frac{l^2 + d^2+h_b^2-2l(d \cos \beta _m \cos \phi _m + h_b \sin \beta _m)}{8sec\beta _m(d \cos \beta _m \cos \phi _m + h_b \sin \beta _m-l)^4}(l^2 - d^2-h_b^2 )^2. \end{aligned}$$

(13)

Relationship between power level $p_r$ and length of a multipath propagation path $l_p$ can be written as,

$$\begin{aligned} p_r = p_o \left( \frac{l_p}{\sqrt{d^2+h_b^2}}\right) ^{-n}. \end{aligned}$$

(14)

$p_o$ given in (14) is the power of the signal component received from LoS path, n is path loss component, $l_p$ is the propagation length of a specific multipath component from BS to MS, and $\sqrt{d^2+h_b^2}$ is the line of sight (LoS) propagation path length between BS and MS. Solving for $l_p$, the above equation can be written as,

$$\begin{aligned} l_p = \sqrt{d^2+h_b^2} \left( \frac{p_r}{p_o}\right) ^{-\frac{1}{n}}. \end{aligned}$$

(15)

Joint density function $p(p_r,\phi _m,\beta _m)$ can be derived as,

$$\begin{aligned} p(p_r,\phi _m,\beta _m) = \left. \frac{p(l_p,\phi _m,\beta _m)}{|J(l_p,\phi _m,\beta _m)|}\right| _{l_p =\sqrt{d^2+h_b^2} \left( \frac{p_r}{p_o}\right) ^{-\frac{1}{n}}}. \end{aligned}$$

(16)

The Jacobean transformation used in (16) is derived as,

$$\begin{aligned} J(l_p,\phi _m,\beta _m) = \left| \frac{\partial l_p}{\partial p_r} \right| ^{-1} = \frac{np_o}{\sqrt{d^2+h_b^2}}\left( \frac{p_r}{p_o}\right) ^{\frac{n+1}{n}}. \end{aligned}$$

(17)

Substituting the equation of $J(l_p,\phi _m,\beta _m)$ in (16) the joint density function as a function of 3-D AoA and power level, of multipath components can be shown as given below,

$$\begin{aligned} p(p_r,\phi _m,\beta _m)= & {} \displaystyle \frac{f(x_m,y_m,z_m) \cos \beta _m \big (d^2+h_b^2\big )^3 \displaystyle \bigg (\frac{p_r}{p_o}\bigg )^{\frac{-3}{n}}\displaystyle \bigg \{\bigg (\frac{p_r}{p_o}\bigg )^{\frac{2}{n}}-1\bigg \}^2 }{8np_r\bigg (\sqrt{d^2+h_b^2}-\displaystyle \bigg (\frac{p_r}{p_o}\bigg )^{\frac{1}{n}}\big (d \cos \beta _m \cos \phi _m + h_b \sin \beta _m\big )\bigg )^4}\nonumber \\&\times \left[ \sqrt{d^2+h_b^2}\bigg \{\bigg (\frac{p_r}{p_o}\bigg )^{\frac{2}{n}}+1\bigg \}-2\bigg (\frac{p_r}{p_o}\bigg )^{\frac{1}{n}}\bigg (d \cos \beta _m \cos \phi _m + h_b \sin \beta _m\bigg ) \right] . \end{aligned}$$

(18)

Joint density function $p(p_r,\gamma ,\beta _m)$ can thus be expressed as,

$$\begin{aligned} p(p_r,\gamma ,\beta _m) = \left. \frac{p(p_r,\phi _m,\beta _m)}{|J(p_r,\phi _m,\beta _m)|}\right| _{\phi _m = \phi _v-\cos ^{-1} \left( \frac{\gamma }{\cos \beta _m}\right) }. \end{aligned}$$

(19)

The Jacobean transformation for $p_r$, $\phi _m$, and $\beta _m$ can be derived as shown below,

$$\begin{aligned} J(p_r,\phi _m,\beta _m) = \left| \frac{\partial \phi _m}{\partial \gamma }\right| ^{-1} = \sqrt{\cos ^2\beta _m - \gamma ^2}. \end{aligned}$$

(20)

Substituting the expression of Jacobean transform from (20) in (19) and letting $\psi = (p_r/p_o)^{-1/n}$, joint density function of power level, Doppler spread, and elevation angle $\beta _m$ can be expressed as,

$$\begin{aligned} p(p_r,\gamma ,\beta _m)= & {} \displaystyle \sum _{i=1}^{2} \left\{ \left( \frac{(d^2+h_b^2)^3(\psi ^2-1)\psi ^{n+1}f(x_m,y_m,z_m)}{8np_o\sqrt{1-\gamma ^2sec^2\beta _m}} \right) \right. \nonumber \\&\times \left. \left( \frac{d^2+h_b^2(1+\psi ^2)-2\psi (d\cos \beta _m\cos \phi _i+h_b\sin \beta _m)}{(d\cos \beta _m\cos \phi _i+h_b\sin \beta _m-(d^2+h_b^2)\psi )^4} \right) \right\} . \end{aligned}$$

(21)

Integrating (21) over $\beta _m$ and $p_r$, respectively, gives the marginal PDF of the Doppler shift characteristics for the proposed model.

$$\begin{aligned} p(\gamma )= & {} \displaystyle \int _{0}^{\frac{\pi }{2}}\int _{p_l}^{p_u} \sum _{i=1}^{2} \left\{ \left( \frac{(d^2+h_b^2)^3(\psi ^2-1)\psi ^{n+1}f(x_m,y_m,z_m)}{8np_o\sqrt{1-\gamma ^2sec^2\beta _m}} \right) \right. \nonumber \\&\times \left. \left( \frac{d^2+h_b^2(1+\psi ^2)-2\psi (d\cos \beta _m\cos \phi _i+h_b\sin \beta _m)}{(d\cos \beta _m\cos \phi _i+h_b\sin \beta _m-(d^2+h_b^2)\psi )^4} \right) \right\} {\mathrm {d}}p_r{\mathrm {d}}\beta _m. \end{aligned}$$

(22)

$p_l$ and $p_u$ are dependant on the path lengths of the multipath components. Signal received from the longest path is assumed to have minimum power and signal coming from the shortest path holds the maximum power. When observing from the MS for a given direction ($\phi _m, \beta _m$), longest and shortest paths can be defined as follows,

$$\begin{aligned} l_{\mathrm {min}}(\phi _m,\beta _m)=\, & {} r_i + \sqrt{d^2 + (r_i\cos \beta _m)^2 - 2dr_i\cos \beta _m\cos \phi _m+(h_b - r_i\sin \beta _m)^2}, \end{aligned}$$

(23)

$$\begin{aligned} l_{\mathrm {max}}(\phi _m,\beta _m)= \,& {} r_o + \sqrt{d^2 + (r_o\cos \beta _m)^2 - 2dr_o\cos \beta _m\cos \phi _m+(h_b - r_o\sin \beta _m)^2}. \end{aligned}$$

(24)

Azimuth angle, $\phi _m$ in (23) and (24) can be eliminated using the relation given in (4). Putting these equations of $l_{\mathrm {min}}$ and $l_{\mathrm {max}}$ in (14) gives us $p_u$ and $p_l$, respectively, as shown below,

$$\begin{aligned} p_u= \,& {} p_o \left( \frac{l_{\mathrm {min}}}{\sqrt{d^2+h_b^2}}\right) ^{-n}, \end{aligned}$$

(25)

$$\begin{aligned} p_l= \,& {} p_o \left( \frac{l_{\mathrm {max}}}{\sqrt{d^2+h_b^2}}\right) ^{-n}. \end{aligned}$$

(26)

Integrating (22) over normalized Doppler shift gives the cumulative distribution function (CDF) of the Doppler spectrum as shown below,

$$\begin{aligned} F_\Gamma (\gamma ) = \int _{-1}^{\gamma }p(\Gamma ){\mathrm {d}}\Gamma . \end{aligned}$$

(27)

CDF of the received signal gives better insight of amount of received gain and the time for which the signal remains below a certain threshold level. Analytical results for Doppler shift characteristics of the proposed model are presented in Fig. 2, where the impact of various important physical parameters of the model is presented. Change in behavior of the Doppler spectrum with variation in the ratio between major ($a_o$) and intermediate ($b_o$) axes of the outer bounding ellipsoid is shown in Fig. 2a. It can be seen that as the ESR transforms from spherical to elliptical shape in azimuthal plane, the slope of CDF changes from frequency flat to frequency variant. This employs that PDF of Doppler shift transforms from flat to U shaped form. In Fig. 2b, the impact of size of inner hollow cylinder for a given $\phi _v$ is analyzed on the Doppler shift. It is evident from the figure that as the ESR becomes more hollow from inside, the PDF of Doppler shift tends to tilt more on one side (positive in this scenario) of the $\gamma$. This is because the scatterers contributing in positive and/or negative Doppler shift increase and/or decrease according to the orientation and scale of the inner bounding hollow elliptical cylinder as compared to outer bounding ellipsoid. The direction of MS’s motion ($\phi _v$) w.r.t. LoS direction has a significant impact on the Doppler shift characteristics when the geometric composition of ESR is uneven; which is shown in Fig. 2c for a specific scenario. It can be seen that when the MS moves directly towards the BS (i.e., $\phi _v = 0^{\circ }$), the scatterers contributing in positive and negative Doppler shift are even therefore the PDF is balanced U shaped. For higher values of $\phi _v$, the PDF skews towards positive or negative side depending upon the shape of the ESR.

Fig. 2

The impact of variation in a the ratio $b_o/a_o$ on the CDF, b the size of inner hollow cylinder on PDF, and c $\phi _v$ on PDF of Doppler shift characteristics

The proposed geometric channel model provides high degrees of freedom in designing the physical dimensions and orientations of the scattering region’s boundaries and therefore can be tuned to realistically model the propagation scenarios for obtaining more realistic angular statistics. The angular spread of multipath waves in a rich multipath environment highly influences the Doppler spectrum, which further determines the time variability of channel characteristics. Therefore, the proposed analytical results on Doppler spectrum are of high significance in studying the time varying characteristics of highly dynamic propagation scenarios of emerging cellular communication networks.

4 Quantification of Angular Spread

Directional characteristics of a multipath radio propagation link are of vital importance in designing antenna separation for beamforming systems in emerging radio propagation links. Therefore, quantification of multipath signals in 3-D angular domain becomes important. Various definitions for quantization of multipath angular spread are available in the literature. Multipath SFs have gained the popularity because these quantifiers are invariant under any degree of transformation and rotation in AoA statistics. Moreover, simple mathematical relationship of these SFs with second order fading statistics of the channel are another reason of their popularity. These SFs give a quick insight of the behavior of the small-scale fading phenomenon due to different propagation scenarios or by deploying different antenna patterns at the receiver.

Approach to compute the SFs in this paper has already been used by Durgin et al. [22] and Khan [37]. Multipath components received at the receiver are distributed in azimuth and elevation planes and are described by $p(\phi )$ or $p(\beta )$, respectively, where, $p(\phi )$ represents the azimuth AoA and $p(\beta )$ represents the elevation AoA. These two methods produce similar results but the approach given in [37] has been chosen because it gives the exact information of the physical dimensions of the SFs and it is more helpful in determining the directional data. Angular spread, an important SF has been derived in another form named as standard deviation. The same approach has been used by Loni et al. in [26,27,28]. $\bar{R}_n$ is the nth complex trigonometric moments of any angular distribution, i.e., for $f_\alpha$, (i.e., where $\alpha$ may be $\phi$ or $\beta$ for the azimuthal and elevational AoA), $\bar{R}_n$ will be defined as,

$$\begin{aligned} \bar{R}_n=\bar{C}_n + j\bar{S}_n, \end{aligned}$$

(28)

where

$$\begin{aligned} \bar{C}_n=\frac{1}{F_o}\sum _{0}^{2 \pi } f_i \cos (n \alpha _i), \end{aligned}$$

(29)

and

$$\begin{aligned} \bar{S}_n=\frac{1}{F_o}\sum _{0}^{2 \pi } f_i \sin (n \alpha _i), \end{aligned}$$

(30)

where $F_o = \sum _{0}^{2 \pi } f_i$. Only first two moments are used in characterization of the SFs. Magnitude of first trigonometric moment denoted by $|\bar{R}_1|$ takes values between 0 and 1. Signals received from a wider range of angles take value of 0 and close to 1 means small angular width of AoA. Measure of concentration of multipath about a single azimuthal direction is called angular spread, $\Lambda _\alpha$, and is given as below,

$$\begin{aligned} \Lambda _\alpha =\sqrt{1-|\bar{R}_1|^2}. \end{aligned}$$

(31)

The standard deviation, $\sigma _\alpha$, gives the angular energy distribution (in radians) which is given as,

$$\begin{aligned} \sigma _\alpha =\sqrt{-2\ln (|\bar{R}_1|)}. \end{aligned}$$

(32)

The other two SFs angular constriction $\gamma _\alpha$, and orientation parameter $\alpha _{MF}$, are defined by Durgin et al. in [22]. $\gamma _\alpha$ gives concentration of multipath about two directions and $\alpha _{MF}$ provides direction of maximum fading. Relation of $\gamma _\alpha$ and $\alpha _{MF}$ with trigonometric moments is given below,

$$\begin{aligned} \gamma _\alpha =\frac{|\bar{R}_2 - \bar{R}_1^2|}{1-|\bar{R}_1|^2}, \end{aligned}$$

(33)

and

$$\begin{aligned} \alpha _{MF}=\frac{1}{2}{\mathrm {phase}}\{\bar{R}_2- \bar{R}_1^2\}, \end{aligned}$$

(34)

where $\alpha$ adapts as $\phi$ for azimuth and $\beta$ for elevation angle of maximum fading.

Fig. 3

The impact of variation in the ratio between the size of outer bounding ellipsoid and inner hollow cylinder on the SFs of AoA distribution in the elevation plane observing from the MS side

In Fig. 3, the impact of variation in the ratio between the size of outer bounding ellipsoid and inner hollow cylinder on the SFs of AoA distribution in the elevation plane observing from the MS side, is shown. It can be seen that as the ESR become more hollow from inside and spherical (i.e., as the ratios $a_o/a_i = b_o/b_i$ and $b_o/a_o$ increases), angular constriction, standard deviation and direction of maximum fading also increase. However angular constriction decrease with increase in the ratios mentioned earlier.

Fig. 4

The impact of variation in the ratio $h_b/c_o$ on the angular spread of AoA distribution in azimuth and elevation planes observing from the BS side

Fig. 5

The impact of variation in the ratio $h_b/c_o$ on the angular constriction of AoA distribution in azimuth and elevation planes observing from the BS side

The impact of variations in the ratios $h_b/c_o$ and $a_o/b_o$ on angular spread and constriction observed in elevation and azimuth planes is shown in Figs. 4 and 5 when observed from the BS side. It is evident that the rate of influence of variations in the ratio $h_b/c_o$ on the angular spread and constriction decreases nonlinearly both in azimuth and elevation planes. Moreover, the difference in the plots of azimuthal angular spread and constriction taken for different values of $h_b/c_o$ reduces sharply as the geometric composition of ESR transforms from elliptical to circular shape in x–y plane. The impact of variation in the ratio between link distance d and major axis of the scattering region $a_o$ on the standard deviation and angular constriction of AoA distribution in azimuth and elevation planes, while transforming the ESR from elliptical to circular shape in x–y plane, is shown in Figs. 6 and 7, respectively. It is evident that as the ESR becomes more circular in x–y plane (i.e., $a_o$ becomes equal to $b_o$), the rate of influence of variations in $d/a_o$ on the azimuth standard deviation and constriction reduces sharply. In the elevation planes, with an increase in the link distance compared to major axis of scattering region the standard deviation decreases and angular constriction increases in both azimuth and elevation planes. Whereas, it can be observed in Figs. 6b and 7b that the transformations in the shape of the ESR along azimuth plane (i.e., variations in $b_o/a_o$) does not have any impact on elevational angular spread and constriction. Moreover, the absolute value of slope of the curves for azimuthal standard deviation and constriction w.r.t. the ratio $b_o/a_o$ decrease with an increase in the ratio $d/a_o$.

Fig. 6

The impact of variation in the ratio $d/a_o$ on the standard deviation of AoA distribution in azimuth and elevation planes observing from the BS side

Fig. 7

The impact of variation in the ratio $d/a_o$ on the angular constriction of AoA distribution in azimuth and elevation planes observing from the BS side

Fig. 8

The impact of variation in the difference between $\theta _o$ and $\theta _i$ on the a angular constriction, and b direction of maximum fading, of AoA distribution in azimuth plane observing from the MS side

The orientation of outer bounding ellipsoid and inner bounding elliptical cylinder are modeled as rotatable independently in azimuth plane w.r.t. LoS direction. The impact of change in the orientation of outer and inner bounding geometric shapes on the azimuthal constriction and direction of maximum fading observed from the MS side is shown in Fig. 8a, b, respectively. It can be seen that as the difference between $\theta _o$ and $\theta _i$ increases, the angular constriction and direction of maximum fading also increase for all values of the ratio $b_o/a_o$. Since the angular constriction is invariant under rotational transformation, therefore, the plots obtained for the scattering region’s orientation (i.e., $\theta _o-\theta _i$) taken as $+45^{\circ }$ and $-45^{\circ }$ are the same. The azimuth direction of maximum fading however carries the difference between these two directions in the results with an opposite polarity but the magnitude is observed same.

5 Second Order Fading Statistics

Multipath SFs can be used to study the fading statistics of a multipath propagation channel. These fading statistics including LCR ($N_r$), AFD ($\bar{\tau }$), ACV ($p(r,\theta )$), and CD ($D_c$) can be defined in terms of multipath SFs as given below. LCR of any random process gives useful information about the underlying process, and is widely used in many engineering fields. In channel modeling, LCR is associated with some important characteristics of the channel like handoff, AFD, fading rate, movement of MS, and the effect of diversity on fading. LCR is the count of how many times the signal crosses the threshold level ($\rho$), i.e., measurement of how rapid the fading occurs and can be defined as,

$$\begin{aligned} N_r = \sqrt{2\pi }\Lambda f_D\rho \sqrt{1+\gamma \cos (2(\phi _v-\theta _{MF}))}e^{-\rho ^2}. \end{aligned}$$

(35)

In (35), $f_D = \frac{v}{\lambda }$, where $\lambda$ is the wavelength of the radiation. AFD ($\bar{\tau }$) is the time that the signal spends below the threshold level ($\rho$) and can be defined as below,

$$\begin{aligned} \bar{\tau } = \frac{e^{-\rho ^2}-1}{\sqrt{2\pi }\Lambda f_D\rho \sqrt{1+\gamma cos(2(\phi _v-\theta _{MF}))}}. \end{aligned}$$

(36)

LCR and AFD are very important characteristics of a channel model because they determine the quality of the received signal. These two can be used together to determine the packet length of the data to be transmitted (to minimize the packet error rate while maintaining a smaller packet overhead) [38], design interleaved/noninterleaved methods of coding [39], optimize the size of the interleaver, select the depth of buffer for adaptive schemes of modulation [40], and estimate output of the communication protocols [41]. Using the LCR and AFD together the severity of fading over time of a channel model can be easily characterized. The product of the LCR and AFD, for a given $\rho$, is always a constant value given by,

$$\begin{aligned} {\mathrm {AFD}} \times {\mathrm {LCR}} = 1 - e^{-\rho ^2}. \end{aligned}$$

(37)

ACV ($\rho(r,\theta )$) is the correlation of a signal with itself at different time in space having distance r and an azimuth angle $\phi _v$. ACV can be defined as given below,

$$\begin{aligned} \rho(r,\phi _v) \approx {\mathrm {exp}}\left[ -23 \Lambda ^2 [1+\gamma (\cos 2(\phi _v-\theta _{MF}))]\left( \frac{r}{\lambda }\right) ^2\right] . \end{aligned}$$

(38)

Rate of the channel’s time variability is determined by CD. CD ($D_c$) is the distance in space over which the response of the channel is static and can be shown below,

$$\begin{aligned} D_c \approx \frac{\lambda \sqrt{\ln 2}}{\Lambda \sqrt{23[1+\gamma (\cos 2(\phi _v - \theta _{MF}))]}}. \end{aligned}$$

(39)

Fig. 9

The impact of variation in the a ratio $b_o/a_o$, b size of inner hollow cylinder, and c $\phi _v$, on the LCR

Fig. 10

The impact of variation in the a ratio $b_o/a_o$, b size of inner hollow cylinder, and c $\phi _v$, on the AFD

The impact of variation in the ratio $b_o/a_o$, size of inner hollow cylinder, and $\phi _v$ on the LCR is shown in Fig. 9a–c, respectively. It has been observed in Fig. 9a that change in the ratio between major ($a_o$) and intermediate ($b_o$) axes of the outer bounding ellipsoid effects LCR linearly. Peak of LCR is observed at $\rho = -1$, and the curves drop sharply for higher values of $\rho$. It can be seen in Fig. 9b that effect of reducing the scatterers in the local vicinity of MS is non linear. The impact of direction of MS’s motion $\phi _v$ on LCR (see Fig. 9c) is also observed as non linear.

The impact of variation in the ratio $b_o/a_o$, size of inner hollow cylinder, and $\phi _v$ on the AFD is shown in Fig. 10a–c, respectively. It can be seen in Fig. 10a that AFD increases linearly with increase in the ratio $b_o/a_o$ because of transformation of the ESR. Figure 10b shows the non linear increment in AFD with increase in the hollowness of the ESR, which means that with less number of scatterers present in the close vicinity of the MS, the fading time of the channel increases. Similar non linear increase in AFD is observed in Fig. 10c with change in the direction of motion of MS. In Figs. 11 and 12 the impact of variation in the (a) ratio $b_o/a_o$, (b) size of inner hollow cylinder, and (c) $\phi _v$ is shown on ACV, and CD, respectively. It can be seen in Fig. 11 that with increase in the distance ($r/\lambda$), ACV reduces sharply which means that as the signal travels from BS to MS, its characteristics change very fast. It has been observed in Figs. 11 and 12 that change in the azimuth geometry of the ESR (ratio $b_o/a_o$) the impact is linear both on ACV and CD, whereas the size of inner hollow cylinder and $\phi _v$ have a non linear impact on ACV and CD. It can be seen from the graphs shown that by changing the geometrical parameters of the model, it is convenient to increase/decrease the second order fading statistics parameters and hence the proposed model can take shape of any orientation of the physical scenario.

Fig. 11

The impact of variation in the a ratio $b_o/a_o$, b size of inner hollow cylinder, and c $\phi _v$, on the ACV

Fig. 12

The impact of variation in the a ratio $b_o/a_o$, b size of inner hollow cylinder, and c $\phi _v$, on the CD

6 Conclusion

Characterization of the Doppler spectrum, SFs, and second order fading statistics of the emerging land mobile radio propagation channels has been presented. Joint and marginal mathematical expressions for distribution characteristics of Doppler shift and multipath power have been derived for the advanced tunable 3-D hollow geometric scattering model. Doppler shift characteristics have been analyzed and the impact of various physical channel parameters on its statistical characteristics has been discussed. A thorough analysis on the multipath SFs of the proposed analytical 3-D channel model has been conducted. Finally, the analysis on SFs has been further extended for characterization of second order fading statistics of the dynamic and tunable radio communication channel.