Effect of Skin Impedance on Delay and Crosstalk in Lossy and Non-uniform On-Chip Interconnects

Abstract

An efficient finite-difference time-domain (FDTD) model is presented to analyse time delay and the crosstalk noise in lossy non-uniform interconnects. The complementary metal oxide semiconductor (CMOS) is used as driver for non-uniform interconnects and terminated with capacitive loads. Further, the resistive losses at high frequency due to skin effect and shrinking of interconnects are inculcated in the proposed model and analysed the high frequency effects. The improved alpha power law model represents the nonlinear behaviour of CMOS drivers, and the non-uniform interconnect is modelled including skin effect by FDTD technique. Hence, the proposed algorithm accurately estimates the crosstalk noise and delay in non-uniform interconnects at high frequencies and the results of FDTD are validated using HSPICE simulations.

1 Introduction

In recent trends, faster and compact devices need smaller interconnect length and result in performance degradation in terms of delay, noise, and crosstalk. High-speed interconnects are normally modelled with an equivalent circuit having distributed RLGC parameters. Transmission lines with frequency-dependent variables are the best suit to describe electrical characteristics of on-chip interconnect. At earlier stages of VLSI design, it is necessary that CMOS technology needs keen modelling of CMOS gate-driven interconnect structures [1]. Driving of interconnects with the CMOS driver rises frequency/time conversion problem.

Recently, the authors in [2] proposed a model to analyse crosstalk accurately but it depends on even mode and odd mode and is suitable for loss less uniform interconnects. In [3], the authors proposed FDTD algorithm for analysing transients in CMOS gate-driven lossy uniform interconnects with frequency-dependent parameters. However, it is restricted to uniform interconnects, whereas for non-uniform interconnects it is unreported. In this work, the extension of frequency-dependent parameters is incorporated for non-uniform on-chip VLSI interconnects. In high-speed interconnects, due to skin effect, the current flows near the surface of the conductors and leads to increase in effective resistance [3]. In [4, 5], the authors proposed a method to explain propagation delay for non-uniform lossy transmission lines in time (t) domain using FDTD. In this work, parameters depending on frequency are also included. However, in this model a resistive driver is connected to transmission lines and terminates using resistive loads, so this analysis is not a practical one for on-chip interconnects which are having nonlinear drivers.

In this work, an efficient method is proposed for analyzing the crosstalk of CMOS gate driven loss non uniform interconnect system. Signal integrity issues are reported due to coupling in between the interconnect lines and nonlinear behaviour of CMOS driver. Further, CMOS driver’s nonlinear behaviour is best described using improved alpha power law model and interconnects are modelled based on finite-difference time-domain (FDTD) model including frequency-dependence parameters.

2 Modelling of FDTD Algorithm for Non-uniform Lossy Interconnect System

In this section, the expressions for copper (Cu) interconnect line are developed using frequency-based skin impedance in (1) and the same is incorporated in FDTD model to find delay time and crosstalk at far end of the interconnect. The modelling part is represented below.

$$Z(z) = A_{1} (z) + B_{1} (z)\sqrt s .$$

(1)

2.1 Modelling of Non-uniform Lossy Interconnects with Frequency Dependency

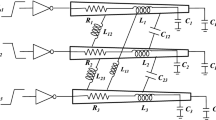
Generally, transmission line model is best suit to analyse coupled interconnect lines because both have similar RLCG distributed elements [1]. The transmission line (TL) expression with space and time dependency is modelled [7, 8] as in (2a) and (2b), and the equivalent two-coupled non-uniform lossy line is shown in Fig. 1.

Fig. 1

Non-uniform lossy interconnect line existed by CMOS nonlinear gate

$$\frac{\partial }{\partial z}v\left( {z,t} \right) + Z\left( t \right)i\left( {z,t} \right) = - l\left( z \right)\frac{\partial }{\partial z}i\left( {z,t} \right)$$

(2a)

$$\frac{\partial }{\partial z}i\left( {z,t} \right) + g\left( z \right)v\left( {z,t} \right) = - c\left( y \right)\frac{\partial }{\partial z}v\left( {z,t} \right)$$

(2b)

The internal impedance and current of the transmission line Eq. (2a) and (2b) are transformed to Laplacian domain as

$$Z\left( {z,s} \right)*i\left( {z,s} \right) = Z\left( {z,t} \right)i\left( {z,t} \right).$$

(3)

From Eq. (1) in Eq. (3),

$$L^{ - 1} \left\{ {Z\left( {z,s} \right)i\left( {z,s} \right)} \right\} = A_{1} \left( z \right)i\left( {z,t} \right) + L^{ - 1} \left\{ {\frac{{B_{1} \left( z \right)}}{\sqrt s }} \right\}*\frac{\partial }{\partial t}i\left( {z,t} \right).$$

(4)

The term (1/√s) in (4) having inverse transform as from [6] is

$$\frac{1}{{\sqrt {\pi t} }} = \frac{1}{\sqrt s }.$$

(5)

By substituting Eq. (5) in (4) gives

$$Z\left( {z,t} \right)*i\left( {z,t} \right) = \left\{ {A_{1} \left( z \right)i\left( {z,t} \right) + \left( {\frac{1}{\sqrt \pi }} \right)B_{1} \left( z \right)\int\limits_{0}^{t} {\frac{1}{\sqrt p }} \frac{\partial }{{\partial \left( {t - p} \right)}}i\left( {z,t - p} \right){\text{d}}p} \right\}.$$

(6)

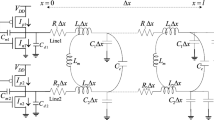
To solve lossy transmission line equations, FDTD is the most appropriate and widely used technique. By using this technique, the space position axis z is divided into equal subsections. Every adjacent V and I points are $\Delta z/2$ apart. Similarly, adjacent voltage and current time points are $\Delta t/2$ apart.

On applying finite-difference algorithm to Eq. (6) gives:

$$\int\limits_{0}^{t} {\frac{1}{\sqrt p }\frac{\partial }{\partial (t - p)}i(z,t - p){\text{d}}p = \int\limits_{0}^{t} {\frac{L(z,t - p)}{\sqrt p }{\text{d}}p} }$$

(7)

where the function $L(z,t)$ is treated as constant over the time segment ∆t. Thus, Eq. (7) becomes

$$\sum\limits_{x = 0}^{n} {\int\limits_{{\Delta t(x)}}^{{\Delta t(x + 1)}} {\frac{{L(z,(n + 1)(\Delta t - p))}}{\sqrt p }{\text{d}}p} } = \sqrt {\Delta t} \sum\limits_{x = 0}^{n} {L(z,(x + 1)\Delta t - p)P_{0} (x)} .$$

(8)

On applying finite-difference approximation to TL equations in (2a), (2b) and substituting (8) in (2a), results in (9a) and (9b) [9,10,11]

$$\begin{aligned} & l(k)\frac{{ - i_{k}^{n + 1/2} + i_{k}^{n + 3/2} }}{{\Delta t}} + \frac{{v_{k + 1}^{n + 1} }}{{\Delta z}} + A_{1} (k)\frac{{i_{k}^{n + 1/2} + i_{k}^{n + 3/2} }}{2} \\ & \quad + \frac{{B_{1} (k)}}{{\sqrt {\pi\Delta t} }}\sum\limits_{x = 0}^{n} {P_{0} (x)\left\{ {i_{k}^{n + 3/2 - x} - i_{k}^{n + 1/2 - x} } \right\} = 0} \\ \end{aligned}$$

(9a)

$$c\left( k \right)\frac{{v_{k}^{n + 1} - v_{k}^{n} }}{\Delta t} + g\left( k \right)\frac{{v_{k}^{n} + v_{k}^{n + 1} }}{\Delta t} = - \frac{{i_{k}^{n + 1/2} - i_{k - 1}^{n + 1/2} }}{\Delta z}$$

(9b)

where k = 1, 2,…., N_z. $v_{k}^{n} = v\left( {\Delta z(k - 1),\Delta t\,n} \right);i_{k}^{n} = (\Delta z\,\left( {k - \frac{1}{2}} \right),\Delta tn).$

By solving (9a) and (9b)

$$\begin{aligned} \left[ {\frac{l(k)}{{\Delta t}} + \frac{{A_{1} (k)}}{2} + \frac{{B_{1} (k)P_{0} (0)}}{{\Delta t}}} \right]i_{k}^{n + 3/2} & = \left[ {\frac{l(k)}{{\Delta t}} - \frac{{A_{1} (k)}}{2} + \frac{{B_{1} (k)P_{0} (0)}}{{\Delta t}}} \right]i_{k}^{n + 1/2} - \frac{{v_{k}^{n + 1} - v_{k}^{n + 1} }}{{\Delta z}} \\ & \quad - \frac{{B_{1} (k)P_{0} (0)}}{{\Delta t}}\sum\limits_{x = 1}^{n} {P_{0} (x)\left( {i_{k}^{n - x + 3/2} - i_{k}^{n - x + 1/2} } \right)} \\ \end{aligned}$$

(10)

$$\left[ {\frac{C(k)}{{\Delta t}} + \frac{G(k)}{2}} \right]V_{k}^{n + 1} = \left[ {\frac{C(k)}{{\Delta t}} - \frac{G(k)}{2}} \right]V_{k}^{n} - \frac{{I_{k}^{n + 1/2} - I_{k - 1}^{n + 1/2} }}{{\Delta z}}.$$

(11)

A bootstrapping method is used to solve the Eqs. (10) and (11). The interconnect line voltage and current values are assigned as zero. After applying input to the line, from Eq. (11) the voltages are evaluated based on previous voltage and current solutions; later using Eq (10), currents are evaluated in terms of present current and past voltages. The space discretization for performing the bootstrapping mechanism along the line is shown in Fig. 2.

Fig. 2

Interconnect line with space discretization along its length for implementing FDTD model

Putting k = 1 and N_Z + 1 in Eq. (11) results (12) and (13) for near- and far-end equations, respectively.

$$\left[ {\frac{c(1)}{{\Delta t}} + \frac{g(1)}{2}} \right]v_{1}^{n + 1} = \left[ {\frac{c(1)}{{\Delta t}} - \frac{g(1)}{2}} \right]v_{1}^{n} - \frac{{i_{1}^{n + 1/2} - i_{0}^{n + 1/2} }}{{\Delta z/2}}$$

(12)

$$\left[ {\frac{c(N_{z} + 1)}{{\Delta t}} + \frac{g(N_{z} + 1)}{2}} \right]v_{{N_{z} }}^{n + 1} = \left[ {\frac{c(N_{z} + 1)}{{\Delta t}} - \frac{g(N_{z} + 1)}{2}} \right] - \frac{{i_{N_{z} + 1}^{n + 1/2} - i_{N_{z}}^{n + 1/2} }}{{\Delta z/2}}.$$

(13)

The line current at near end z = 0 is $i_{0}$ and at far end z = l as $i_{N_{z}+1}$. Then, KCL expression is represented in (14) and (15), respectively.

$$i_{0} = i_{p} - i_{n} + c_{m} \left( {\frac{{{\text{d}}(v_{s}^{n} - v_{1}^{n + 1} )}}{{{\text{d}}t}}} \right) - C_{d} \frac{{{\text{d}}v_{1} }}{{{\text{d}}t}}$$

(14)

$$i_{{N_{z} + 1}} = C_{l} \frac{{\partial v_{{N_{z} + 1}} }}{\partial t}.$$

(15)

By substituting Eq. (14) and Eq. (15) in (12) and (13) yields (16) and (17), respectively. These are the expressions for line voltage and currents at any point along the interconnect lines and for k = N _a  + 1.

$$\begin{aligned} v_{1}^{n + 1} = \left[ {\frac{{c(N_{a} + 1)}}{{\Delta t}} + \frac{{g(N_{a} + 1)}}{2}} \right]^{ - 1} \left\{ {\begin{array}{*{20}l} {\left[ {\frac{{c(N_{a} + 1)}}{{\Delta t}} - \frac{{g(N_{a} + 1)}}{2}} \right]v_{1}^{n} - \frac{2}{{\Delta z}}i_{1}^{n + 1/2} } \hfill \\ { + \frac{2}{{\Delta z}}\left( {i_{p}^{n + 1/2} - i_{n}^{n + 1/2} - c_{m} \left( {\frac{{d(v_{in}^{n} - v_{1}^{n} )}}{dt}} \right) + C_{d} \left( {\frac{{dv_{1}^{n + 1/2} }}{dt}} \right)} \right)} \hfill \\ \end{array} } \right\} \hfill \\ \hfill \\ \end{aligned}$$

(16)

$$\begin{aligned} i_{k}^{n + 3/2} = \left[ {\frac{l(k)}{\Delta t} + \frac{{A_{1} (k)}}{2} + \frac{{B_{1} (k)P_{0} (0)}}{\Delta t}} \right]^{ - 1} \left\{ {\begin{array}{*{20}l} {\left[ {\frac{l(k)}{\Delta t} - \frac{{A_{1} (k)}}{2} + \frac{{B_{1} (k)P_{0} (0)}}{\Delta t}} \right]i_{k}^{n + 1/2} - \frac{{v_{k}^{n + 1} - v_{k}^{n + 1} }}{\Delta z}} \hfill \\ { - \frac{{B_{1} (k)P_{0} (0)}}{\Delta t}\sum\limits_{x = 1}^{n} {P_{0} (x)\left( {I_{k}^{n - x + 3/2} - I_{k}^{n - x + 1/2} } \right)} } \hfill \\ \end{array} } \right\}. \hfill \\ \hfill \\ \end{aligned}$$

(17)

3 Results and Discussions

In this section, the proposed FDTD model for interconnect lines is validated using HSPICE simulations for different input conditions. Consider a two-coupled non-uniform interconnects shown Fig. 1. The input excitation given as 0.9 V pulse with duty cycle of 50% and rise/fall times is 50 ps and pulse width of 300 ps.

The load capacitance (C_L) is 1fF. The interconnect line length is 1 mm, the spatial discretization of the non-uniform lines chosen to be 10 segments, and the time discretization is ∆t = 100∆tmax.

The p.u.l parameters are represented as follows:

$$l = \left[ {\begin{array}{*{20}c} {L_{1} } & {L_{12} } \\ {L_{12} } & {L_{2} } \\ \end{array} } \right]\,{\text{nH/m }}\quad c = \left[ {\begin{array}{*{20}c} {C_{1} } & {C_{12} } \\ {C_{12} } & {C_{2} } \\ \end{array} } \right] \,{\text{pF/m}}$$

$$g = \left[ {\begin{array}{*{20}c} {G_{1} } & 0 \\ 0 & {G_{2} } \\ \end{array} } \right]\,{\text{S}}/{\text{m}}\quad R = \left[ {\begin{array}{*{20}c} {R_{1} } & 0 \\ 0 & {R_{2} } \\ \end{array} } \right]\Omega /{\text{m}}$$

where $L_{1} = L_{2} = L(y) = 387/1 + \lambda (y);\,L_{m12} (y) = \lambda (y)L(y)$; $C(y) = 104.3/(1 + \lambda (y));\,C_{12} (y) = - \lambda (y)C(y)\,{\text{R}}_{1} = {\text{R}}_{2} = \, 60\,\Omega /{\text{m}}$

$$\begin{array}{*{20}l} {G_{1} = G_{2} = G(y) = 0.001/\left[ {1 - \lambda (y)} \right]} \hfill \\ {\lambda (y) = 0.25\left[ {1 + \sin (6.25\pi y + \frac{\pi }{4})} \right]} \hfill \\ \end{array} .$$

At far end of interconnect, the transient response is observed and shown in Fig. 3a–d. At near end, the transient response is shown in Fig. 4a–d. The results are validated with HSPICE simulations.

Fig. 3

Time-domain response at a port 3 in-phase, b port 4 in-phase, c port 3 out-phase, and d port 4 out-phase

Fig. 4

Time-domain response at a port 1 in-phase, b port 2 in-phase, c port 1 out-phase, and d port 2 out-phase

4 Conclusion

An efficient frequency-dependent FDTD model is developed for non-uniform lossy interconnect lines to analyse near- and far-end transient analyses for interconnects. Further, the proposed algorithm is validated using HSPICE simulation results in very good accuracy in predicting the response. The time delay analysis is done by comparing the near- and far-end interconnect time delays using FDTD, and the same is validated using HSPICE. Hence, the model is verified accurately both in predicting the timing response and delay of the on-chip interconnect lines.