Time Domain Analysis of Skin Effect in Nonuniform Interconnection Using the FDTD Technique

Abstract

During the last decades, manufacturers have opted for the miniaturization of electronic devices as an answer to high-performance equipment demand. However, Downscaling the Integrated Circuit (IC) technology has several side effects on the device’s performance. Considered one of the IC problems in the design, the skin effect impacts the IC design. In addition, high clock frequency can lead to severe Electromagnetic Compatibility (EMC) issues. The present work has used an efficient numerical method for transient analysis based on the Finite Difference Time Domain (FDTD) Method to investigate the previous phenomenon. It is used to examine the skin and incident electromagnetic field effect on the signals applied in non-uniform submicron CMOS interconnects. We have selected two research situations of non-uniform interconnects loaded by linear terminals, either in the absence or presence of an incident field. The MATLAB tool is used to implement the proposed algorithms. The outcomes are contrasted with PSPICE’s results. A close match was obtained between the two results.

1 Introduction

A variety of high-speed interconnect phenomena, including distortion, reflections, signal delay, and crosstalk, must be taken into account when designing high-frequency integrated circuits (ICs). Skin effect is also one of the previous design side effects. It is manifested in interconnections by the resistance increase of those conductors due to a current crowding electromagnetic effect in the metal conductor under high frequency [1, 2]. In addition, the nonuniform interconnections structures are frequently utilized in microwave systems and high-speed electronics. For instance, they are employed in RF and microwave circuits as filters, resonators, impedance matching, delay equalizers, analog signal processing, wave shaping, VLSI interconnects, etc. [3]. The use of high-frequency devices can cause electromagnetic compatibility (EMC) problems. EMC is a device or system’s ability to run in its electromagnetic environment without compromising its functions and without faults and vice versa. The effects of EMC are increasing in several domains, such as microelectronics, automotive, and aeronautics [4]. Several approaches have thus far been suggested to study the uniform transmission lines [5,6,7] and the nonuniform ones [8] in the absence and presence of a radiated EM wave coupling such as the finite difference quadrature [9].

The goal of this manuscript is to propose and develop a model that represents the skin effect in coupled nonuniform interconnect. The novelty of this work is due to the study of skin effect influence in presence of incident electromagnetic field and the nonuniform interconnect behavior in such an environment. Indeed, this work is dispatched as follows: Sect. 2 is reserved to the formulation of the electromagnetic coupling in nonuniform interconnections with the existence of a parasitic electromagnetic field means of the FDTD method. Section 3 of the paper provides examples of electromagnetic coupling with skin effect. The examples are presented both in the absence and presence of incident field excitation. Section 4 concludes the paper.

2 Electromagnetic Coupling of Nonuniform Interconnect Lines

On the one hand, transmission lines full-wave analysis can give greater accuracy. On the other hand, it is computationally more expensive than solving the multiconductor transmission line equations (MTL). Therefore, the MTL model is often used as a good approximation. It assumes that the parasitic field is a transverse electromagnetic (TEM) field, composed of an electric and magnetic field lying in a line axis transverse plane [10]. This section explains the modeling of the electromagnetic coupling of nonuniform interconnects suffered from skin effects and radiated by an incident field.

2.1 The FDTD Formulation for Electromagnetic Coupling

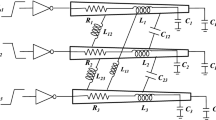
The quasi-transverse electromagnetic model is assumed to investigate and evaluate the skin effect of coupled nonuniform interconnections [10]. Thus, by applying the Kirchhoff law on the circuit shown in Fig. 1, we obtain the linked partial differential equations system shown below. (Telegrapher’s equations) [11, 12]:

$$\left\{\begin{array}{c}\frac{\partial }{\partial \mathrm{x}}V\left(\mathrm{x},\mathrm{t}\right)+Z\left(\mathrm{x},\mathrm{t}\right)I\left(\mathrm{x},\mathrm{t}\right)+L\left(\mathrm{x}\right)\frac{\partial }{\partial \mathrm{t}}I\left(\mathrm{x},\mathrm{t}\right)={\mathbf{V}}_{\mathbf{s}}\left(\mathrm{x},\mathrm{t}\right) \\ \\ \frac{\partial }{\partial \mathrm{x}}I\left(\mathrm{x},\mathrm{t}\right)+G\left(\mathrm{x}\right)I\left(\mathrm{x},\mathrm{t}\right)+C\left(\mathrm{x}\right)\frac{\partial }{\partial \mathrm{t}}V\left(\mathrm{x},\mathrm{t}\right)={\mathbf{I}}_{\mathbf{s}}\left(\mathrm{x},\mathrm{t}\right)\end{array}\right.$$

(1)

where the currents I and voltages V are written in Mx1 column vector form. The interconnect per unit parameters R, L, C and G are given by MxM matrices. V_S and I_S are representing respectively per unit length electromagnetic induced field, and are written as follows [12]:

$${\mathbf{V}}_{\mathbf{s}}\left(\mathrm{x},\mathrm{t}\right)=-\frac{\partial }{\partial \mathrm{x}}{\mathbf{E}}_{\mathbf{T}}\left(\mathrm{x},\mathrm{t}\right)+{\mathbf{E}}_{\mathbf{L}}\left(\mathrm{x},\mathrm{t}\right)$$

(2)

$${\mathbf{I}}_{\mathbf{s}}\left(\mathrm{x},\mathrm{t}\right)=-\mathbf{G}\left(\mathrm{x}\right){\mathbf{E}}_{\mathbf{T}}\left(\mathrm{x},\mathrm{t}\right)-\mathbf{C}\left(\mathrm{x}\right)\frac{\partial }{\partial \mathrm{x}}{\mathbf{E}}_{\mathbf{T}}\left(\mathrm{x},\mathrm{t}\right)$$

(3)

where I_S and V_S are expressed in Mx1 column vector. E_T and E_L are respectively the transverse and longitudinal components of the incident electric field.

The skin effect can be approximated as internal impedance that includes a resistance and an internal inductance, and we may write [10]:

$$\mathbf{Z}\left(\mathrm{x},\mathrm{t}\right)\mathbf{I}\left(\mathrm{x},\mathrm{t}\right)=\mathbf{R}\left(\mathrm{x}\right)\mathbf{I}\left(\mathrm{x},\mathrm{t}\right) +\frac{\mathbf{B}\left(\mathrm{x}\right)}{\sqrt{\pi }} {\int }_{0}^{t}\frac{1}{\sqrt{u}}\frac{\partial \mathbf{I}\left(\mathrm{x},\mathrm{t}-\mathrm{u}\right)}{\partial (t-u)}du$$

(4)

where: $\mathbf{R}\left(\mathrm{x}\right)=\frac{100}{1+K(x)}$; $\mathbf{B}\left(\mathrm{x}\right)=\frac{\sqrt{\frac{\mu }{\varepsilon }}}{2.{10}^{-6}(5+50K\left(x\right))}$; $K\left(x\right)=0.25\left[1+\mathrm{sin}\left(6.25\pi x+\frac{\pi }{4}\right)\right]$.

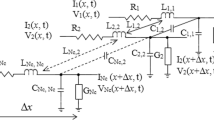
To solve Eq. (1), we used finite difference time domain (FDTD) method. This algorithm divides the time and space domains into Nt intervals and Nx cells, each with a duration of ∆t and a length of ∆x, respectively. This discretization uses Yee’s grid where the currents are determined at (t + ∆t/2) steps and (x + ∆x) positions, while the voltages are computed at (t + ∆t) steps and (x + ∆x/2) positions. To ensure the model’s stability, the spatial increment step ∆x must be smaller than the wavelength propagated on the line and ∆t must be minor to satisfy Courant-Friedrichs-Lewy condition [13].

The equations describing the recurrent voltage and current along an interconnect line are expressed:

For k = 2,3, … Nx

$${\mathrm{V}}_{\mathrm{k}}^{\mathrm{n}+1}={{A}_{4}}^{-1}\left({A}_{5}{\mathrm{V}}_{\mathrm{k}}^{\mathrm{n}}+\Delta \mathrm{x}{\mathrm{ I}}_{\mathrm{sk}}^{\mathrm{n}}+{\mathrm{I}}_{\mathrm{k}}^{\mathrm{n}+\frac{1}{2}}+{\mathrm{I}}_{\mathrm{k}+1}^{\mathrm{n}+\frac{1}{2}}\right)$$

(5)

with:

$${\mathrm{I}}_{\mathrm{sk}}^{\mathrm{n}}=\left[G\left(k\right){\mathrm{ E}}_{\mathrm{gk}}^{\mathrm{n}}+\frac{C\left(k\right)}{\Delta \mathrm{t}}\left({\mathrm{ E}}_{\mathrm{gk}}^{\mathrm{n}}-{\mathrm{ E}}_{\mathrm{gk}}^{\mathrm{n}-1}\right)\right]\left\{{A}_{\mathrm{i}}\right\}$$

(6)

For k = 1,2,3, … Nx

$$ {\text{I}}_{{\text{k}}}^{{{\text{n}} + \frac{3}{2}}} = A_{1}^{ - 1} \left( {A_{2} {\text{I}}_{{\text{k}}}^{{{\text{n}} + \frac{1}{2}}} + \Delta {\text{x V}}_{{{\text{sk}}}}^{{\text{n}}} + {\text{V}}_{{\text{k}}}^{{{\text{n}} + 1}} - {\text{V}}_{{{\text{k}} + 1}}^{{{\text{n}} + 1}} - A_{3} {\text{J}}_{{\text{k}}}^{{\text{n}}} } \right) $$

(7)

with:

$$ {\text{V}}_{{{\text{sk}}}}^{{\text{n}}} = \frac{{\left( {{\text{ E}}_{{{\text{gk}}}}^{{{\text{n}} + 1}} - {\text{ E}}_{{{\text{gk}}}}^{{\text{n}}} } \right)}}{{\Delta {\text{t}}}}.\left\{ {D_{{\text{i}}} } \right\} $$

(8)

In (8), the term ${\mathrm{J}}_{\mathrm{k}}^{\mathrm{n}}$ represents the skin effect and it is written as:

$${\mathrm{J}}_{\mathrm{k}}^{\mathrm{n}}=\sum_{{\varvec{m}}=1}^{{\varvec{n}}}{{\varvec{P}}}_{0}({\varvec{m}})\left({\mathrm{I}}_{\mathrm{k}}^{\mathrm{n}+\frac{3}{2}+\mathrm{m}}-{\mathrm{I}}_{\mathrm{k}}^{\mathrm{n}+\frac{1}{2}-\mathrm{m}}\right)$$

(9)

with A₁, A₂, A₃, A_4, and A₅ are square matrices MxM, line parameters dependent. The Mx1 column vectors A_i and D_i based on the the interconnections i^th position, the modal velocities propagated in the structure and the characteristics of the incident field.

Therefore, ${\mathrm{A}}_{1}=\mathbf{L}(\mathbf{k})\frac{\Delta \mathrm{x}}{\Delta \mathrm{t}}+\mathbf{R}(\mathbf{k})\frac{\Delta \mathrm{x}}{2}$ + $\mathbf{B}\left(\mathbf{k}\right)\frac{\Delta \mathrm{x}}{\sqrt{\uppi \Delta \mathrm{t}}}{{\varvec{P}}}_{0}\left(0\right)$;

${\mathrm{A}}_{2}=\mathbf{L}\left(\mathbf{k}\right)\frac{\Delta \mathrm{x}}{\Delta \mathrm{t}}-\mathbf{R}(\mathbf{k})\frac{\Delta \mathrm{x}}{2}$ + $\mathbf{B}\left(\mathbf{k}\right)\frac{\Delta \mathrm{x}}{\sqrt{\uppi \Delta \mathrm{t}}}{{\varvec{P}}}_{0}\left(0\right)$; ${\mathrm{A}}_{3}=\mathbf{B}\left(\mathbf{k}\right)\frac{\Delta \mathrm{x}}{\sqrt{\uppi \Delta \mathrm{t}}}$;

${\mathrm{A}}_{4}=\frac{\Delta \mathrm{x}}{\Delta \mathrm{t}}\mathbf{C}\left(\mathbf{k}\right)+\frac{\Delta \mathrm{x}}{2}\mathbf{G}(\mathbf{k}) ,$ and ${\mathrm{A}}_{5}=\frac{\Delta \mathrm{x}}{\Delta \mathrm{t}}\mathbf{C}(\mathbf{k})-\frac{\Delta \mathrm{x}}{2}\mathbf{G}(\mathbf{k})$ with ${\mathrm{E}}_{\mathrm{k}}^{\mathrm{n}}$ is the incident field at position k and time n.

The load circuits must be detailed to calculate the currents and voltages at the ends of the line structure. The following subsection describes in detail the CMOS nonlinear loads.

Fig. 1.

Equivalent circuit model of single interconnect illuminated by an incident field $\overrightarrow{\mathrm{E}}$.

2.2 The Boundary Condition

By considering Fig. 2, we obtain the following equations:

$${\mathrm{V}}_{\mathrm{g}}={\mathrm{R}}_{\mathrm{s}}{\mathrm{I}}_{\mathrm{in}}{+\mathrm{V}}_{\mathrm{in}}$$

(10)

$${\mathrm{I}}_{\mathrm{in}}+\frac{\Delta {\varvec{x}}}{2}{\mathrm{I}}_{\mathrm{s}1}={\mathrm{I}}_{1}+{\mathrm{G}}_{1}\frac{\Delta {\varvec{x}}}{2}\left({\mathrm{V}}_{\mathrm{in}}+\frac{\Delta {\varvec{x}}}{2}{\mathrm{V}}_{\mathrm{s}1}\right)+{\mathrm{C}}_{1}\frac{\Delta {\varvec{x}}}{2}\frac{\partial }{\partial \mathrm{t}}\left({\mathrm{V}}_{\mathrm{in}}+\frac{\Delta {\varvec{x}}}{2}{\mathrm{V}}_{\mathrm{s}1}\right)$$

(11)

By combining the previous equations, we get:

$${\mathrm{G}}_{\mathrm{s}}\left({\mathrm{V}}_{\mathrm{g}}-{\mathrm{V}}_{\mathrm{in}}\right)+\frac{\Delta {\varvec{x}}}{2}{\mathrm{I}}_{\mathrm{s}1}={\mathrm{I}}_{1}+{\mathrm{G}}_{1}\frac{\Delta {\varvec{x}}}{2}\left({\mathrm{V}}_{\mathrm{in}}+\frac{\Delta {\varvec{x}}}{2}{\mathrm{V}}_{\mathrm{s}1}\right)+{\mathrm{C}}_{1}\frac{\Delta {\varvec{x}}}{2}\frac{\partial {\mathrm{V}}_{\mathrm{in}}}{\partial \mathrm{t}}+{\mathrm{C}}_{1}{\left(\frac{\Delta {\varvec{x}}}{2}\right)}^{2}\frac{\partial {\mathrm{V}}_{\mathrm{s}1}}{\partial \mathrm{t}}$$

(12)

After simplification, (12) is written as:

$${\mathrm{V}}_{\mathrm{in}}^{\mathrm{n}}={\mathrm{B}}_{1}^{-1}\frac{\Delta {\varvec{x}}}{2\Delta {\varvec{t}}}\left({{\mathrm{C}}_{1}\mathrm{V}}_{\mathrm{in}}^{\mathrm{n}-1}+{{\mathrm{G}}_{\mathrm{s}}\mathrm{V}}_{\mathrm{g}}^{\mathrm{n}}-{\mathrm{I}}_{1}^{\mathrm{n}}+{{\mathrm{B}}_{2}\mathrm{E}}_{\mathrm{g}1}^{\mathrm{n}}-{{\mathrm{B}}_{3}\mathrm{E}}_{\mathrm{g}1}^{\mathrm{n}-1}+{{\mathrm{B}}_{4}\mathrm{E}}_{\mathrm{g}1}^{\mathrm{n}+1}\right)$$

(13)

where: ${B}_{1}={G}_{s}+\frac{\Delta {\varvec{x}}}{2}{C}_{1}+\frac{\Delta {\varvec{x}}}{2\Delta {\varvec{t}}}{C}_{1}$; ${B}_{2}=\frac{\Delta {\varvec{x}}}{2}\left({G}_{1}+\frac{{C}_{1}}{\Delta {\varvec{t}}}\right){A}_{1}-{\left(\frac{\Delta {\varvec{x}}}{2}\right)}^{2}\frac{{G}_{1}}{\Delta {\varvec{t}}}{D}_{1}+2{\left(\frac{\Delta {\varvec{x}}}{2\Delta {\varvec{t}}}\right)}^{2}{{C}_{1}D}_{1}$; ${B}_{3}=\frac{\Delta {\varvec{x}}}{2}\left(\frac{{C}_{1}}{\Delta {\varvec{t}}}\right){A}_{1}-{\left(\frac{\Delta {\varvec{x}}}{2}\right)}^{2}\frac{{G}_{1}}{\Delta {\varvec{t}}}{D}_{1}+{\left(\frac{\Delta {\varvec{x}}}{2\Delta {\varvec{t}}}\right)}^{2}{{C}_{1}D}_{1}$; ${B}_{4}={\left(\frac{\Delta {\varvec{x}}}{2\Delta {\varvec{t}}}\right)}^{2}{{C}_{1}D}_{1}$.

Fig. 2.

Equivalent circuit model of single interconnect illuminated by an incident field $\overrightarrow{\mathrm{E}}$.

By considering Fig. 3, we obtain the following equations:

$${\mathrm{G}}_{\mathrm{L}}{\mathrm{V}}_{\mathrm{out}}^{\mathrm{n}}={\mathrm{I}}_{\mathrm{Ndx}}^{\mathrm{n}}+\frac{\Delta {\varvec{x}}}{2}{\mathrm{I}}_{\mathrm{sNdx}}^{\mathrm{n}}-\frac{\Delta {\varvec{x}}}{2}{\mathrm{G}}_{\mathrm{Ndx}}^{\mathrm{n}}\left({\mathrm{V}}_{\mathrm{out}}^{\mathrm{n}}+{\frac{\Delta {\varvec{x}}}{2}\mathrm{V}}_{\mathrm{sNdx}}^{\mathrm{n}}\right)-\frac{\Delta {\varvec{x}}}{2}{\mathrm{C}}_{\mathrm{Ndx}}^{\mathrm{n}}\left({\mathrm{V}}_{\mathrm{out}}^{\mathrm{n}}+{\frac{\Delta {\varvec{x}}}{2}\mathrm{V}}_{\mathrm{sNdx}}^{\mathrm{n}}\right)$$

(14)

Thus, (14) can be simplified as:

$${\mathrm{V}}_{\mathrm{out}}^{\mathrm{n}}={\mathrm{F}}_{1}^{-1}\left({\mathrm{I}}_{\mathrm{Ndx}}^{\mathrm{n}}+\frac{\Delta {\varvec{x}}}{2}\frac{{\mathrm{C}}_{\mathrm{Ndx}}^{\mathrm{n}}}{\Delta {\varvec{t}}}{\mathrm{V}}_{\mathrm{out}}^{\mathrm{n}-1}+{{\mathrm{F}}_{2}\mathrm{E}}_{\mathrm{gNdx}}^{\mathrm{n}}-{{\mathrm{F}}_{3}\mathrm{E}}_{\mathrm{gNdx}}^{\mathrm{n}-1}+{{\mathrm{F}}_{4}\mathrm{E}}_{\mathrm{gNdx}}^{\mathrm{n}+1}\right)$$

(15)

where: ${F}_{1}={G}_{L}+\frac{\Delta {\varvec{x}}}{2}{C}_{Ndx}+\frac{\Delta {\varvec{x}}}{2\Delta {\varvec{t}}}{C}_{Ndx}$; ${F}_{2}\frac{\Delta {\varvec{x}}}{2}\left({G}_{Ndx}+\frac{{C}_{Ndx}}{\Delta {\varvec{t}}}\right){A}_{Ndx}-{\left(\frac{\Delta {\varvec{x}}}{2}\right)}^{2}\frac{{G}_{Ndx}}{\Delta {\varvec{t}}}{D}_{Ndx}+2{\left(\frac{\Delta {\varvec{x}}}{2\Delta {\varvec{t}}}\right)}^{2}{{C}_{Ndx}D}_{Ndx}$; ${F}_{3}=\frac{\Delta {\varvec{x}}}{2}\left(\frac{{C}_{Ndx}}{\Delta {\varvec{t}}}\right){A}_{Ndx}-{\left(\frac{\Delta {\varvec{x}}}{2}\right)}^{2}\frac{{G}_{1}}{\Delta {\varvec{t}}}{D}_{Ndx}+{\left(\frac{\Delta {\varvec{x}}}{2\Delta {\varvec{t}}}\right)}^{2}{{C}_{Ndx}D}_{Ndx}$; ${F}_{4}={\left(\frac{\Delta {\varvec{x}}}{2\Delta {\varvec{t}}}\right)}^{2}{{C}_{Ndx}D}_{Ndx}$.

Fig. 3.

Single interconnect’s equivalent circuit model illuminated by an incident field $\overrightarrow{\mathrm{E}}$.

The following section will study some cases of voltage and current implementation in MATLAB.

3 Study Cases and Discussions

3.1 Nonuniform Interconnects Loaded with Linear Circuits and the Absence of Incident Field Excitation

A trapezoidal pulse with an amplitude of 1 kV/m, rise and fall time of 100 ps, and pulse width of 0.3 ns is applied to the first line.

Fig. 4.

Two interconnects test circuit with linear loads.

We used MATLAB to implement near and far-end voltage recurrence relations. The results at the far end voltage of the first line are shown in Fig. 5-a. PSPICE tool simulation of Fig. 4 is shown in Fig. 5-b.

Fig. 5.

First line simulation, (a) MATLAB (b) PSPICE.

Similarly, we have simulated the structure and plotted second line output voltage using MATLAB (Fig. 6-a), and PSPICE (Fig. 6-b).

Fig. 6.

Second line simulation, (a) MATLAB (b) PSPICE.

In the previous figures, it has been observed that the skin effect has impacted generally the amplitude of the different voltages. For instance, the input and the output of the first line are going respectively more than 600 mV and up to 1 V (Fig. 5). The apparent fluctuations in Matlab results (Fig. 5-a) and (Fig. 6-a) and their absence in PSPICE results (Fig. 5-b) and (Fig. 6-b) are due in part to discretization in the FDTD method.

In a conclusion, we found that MATLAB outcomes match closely the industrial-level PSPICE. Thus, the accuracy of our model is proven.

3.2 Excitation by an Incident Field of Nonuniform Interconnects with Linear Loads

The following discussed study case is commonly found in reality. The growing demand for faster data transmission and processing in telecommunication systems has led to an increased interest in modeling the non-ideal effects of conductors that connect different subsystems. The second study case schematic in Fig. 7 shows two nonuniform interconnect lines, where the whole circuit is excited by an incident field of 3ns delay, with an application of a trapezoidal voltage source of 1ns delay on the first line.

Fig. 7.

Two interconnects test circuit exited by an external field $\overrightarrow{\mathrm{E}}$.

For the example given, and considering the previous parameters, we have done some MATLAB (Fig. 8.a) and PSPICE tool (Fig. 8.b) simulations.

Fig. 8.

First line simulation, (a) MATLAB (b) PSPICE.

The induced voltage at the second line input is considered as a victim and it is shown in Fig. 9.

Fig. 9.

Second line simulation, (a) MATLAB (b) PSPICE.

On the one hand, Figs. 8 and 9 have confirmed the skin effect influence on the amplitude of the various signals, for example, the input voltage of the first line is going up to 600 mV to reach 800 mV. On the other hand, sharp peaks have appeared at the output voltage which can be explained by the incident field impact.

The comparison of the results from MATLAB and PSPICE, it was observed a good agreement between them. Thus, came the conclusion of the validity of the proposed model.

4 Conclusion

The paper presents a model and simulation of nonuniform interconnect lines electromagnetic coupling affected by skin effect. The telegrapher equations and the FDTD method were employed to model the coupling. The signal propagation mode is assumed to be quasi-TEM. The validity of the algorithm is analyzed using MATLAB and PSPICE, in the absence and presence of external incident disturbances. The outcomes demonstrate a close match between MATLAB and PSPICE simulations.