Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

There has been a growing interest during the last years in the application of base isolation techniques in order to improve the earthquake resistant performance of civil structures such as buildings, bridges, nuclear reactors, etc. [8, 10, 23, 30, 33]. In fact, the potential advantages of seismic isolation and the recent advancements in isolation-system products have lead to the design and construction of an increasing number of seismically isolated structural systems. Also, seismic isolation is extensively used for seismic retrofitting of existing structures [11, 26]. One of the difficulties in the design of base-isolated structural systems is the explicit consideration of the nonlinear behavior of the isolators during the design process. Similarly, the consideration of uncertainty about the structural model and the potential variability of future ground motions is a major challenge in the analysis and design of these systems. The goal of this work is the development of a general framework for reliability based design of base-isolated systems under uncertain conditions. In particular, base-isolated building structures subject to earthquake excitation are considered in this study. A probabilistic approach is adopted for addressing the uncertainties about the structural model as well as the variability of future excitations. The uncertain earthquake excitation is modeled as a non-stationary stochastic process with uncertain model parameters. Specifically, a point-source model characterized by the moment magnitude and epicentral distance is adopted in this formulation [6]. Isolation elements composed by hysteretic devices are used for the isolation system. The hysteretic behavior of the devices is characterized by a Bouc–Wen type model [5]. The model provides general parametric hysteresis rules that gives a smooth transition of the change of stiffness as the deformation of the nonlinear elements changes. The reliability-based optimization problem is formulated as the minimization of an objective function subject to multiple design requirements including reliability constraints. First excursion probabilities are used as measures of system reliability. Such probabilities are estimated by an adaptive Markov Chain Monte Carlo procedure [4]. A sequential optimization approach based on global conservative, convex and separable approximations is implemented for solving the optimization problem [14, 18, 21]. The approach explicitly takes into account all non-linear characteristics of the structural response and it allows for a complex characterization of structural systems and excitation models. The solution of the equation of motion of the combined system (superstructure-isolation system) required during the simulation process is computed by a modified Runge–Kutta scheme of fourth-order. A numerical example is presented in order to illustrate the applicability and effectiveness of the proposed framework for reliability-based design of base-isolated buildings.

2 Reliability-Based Design Problem

The optimal design problem is defined as the identification of a vector {ϕ} of design variables that minimizes an objective function, that is

$$ \mbox{Minimize } f\bigl(\{\phi\}\bigr) $$
(10.1)

subject to design constraints

$$ h_j\bigl(\{\phi\}\bigr) \leq 0 ,\quad j=1,\ldots,n_c $$
(10.2)

and side constraints

$$ \phi_i^l \leq \phi_i \leq \phi_i^u ,\quad i=1,\ldots,n_d $$
(10.3)

The objective function is defined in terms of quantities such as initial, construction, repair, or downtime costs. On the other hand, the design constraints are given in terms of reliability constraints and/or constrains related to deterministic design requirements. In a stochastic setting the reliability constraints are usually defined in terms of failure probabilities. These probabilities provide a measure of the plausibility of the occurrence of unacceptable behavior (failure) of the system, based on the available information. The probability of failure \(P_{F_{j}}(\{\phi\})\) corresponding to a failure event F j evaluated at the design {ϕ} can be expressed in terms of the multidimensional probability integral [13, 15]

$$ P_{F_j}\bigl(\{\phi\}\bigr) = \int_{\varTheta} I_{F_j} \bigl( \{\phi\},\{\theta\}\bigr) q\bigl(\{\theta\}\bigr)\, d\{ \theta\} $$
(10.4)

where \(I_{F_{j}} ( \{\phi\},\{\theta\})\) is the indicator function for failure, which is equal to one if the system fails and zero otherwise, and {θ}, θ i , i=1,…,n u is the vector that represents the uncertain system parameters involved in the problem (structural parameters and excitation). The uncertain system parameters {θ} are modeled using a prescribed probability density function q({θ}) which incorporates available knowledge about the system. Note, that the failure probability function \(P_{F_{j}}(\{\phi\})\) accounts for the uncertainty in the system parameters as well as the uncertainties in the excitation. A model prediction error, that is, the error between the response of the actual system and the response of the model, can also be considered in the formulation [12, 31]. In this case the prediction error may be modeled probabilistically by augmenting the vector {θ} to form an uncertain parameter vector composed of both the structural and excitation model parameters as well as the model prediction-error. The failure domain \(\varOmega_{F_{j}}(\{\phi\})\) corresponding to the failure event F j evaluated at the design {ϕ} is typically described in terms of a performance function g j as

$$ \varOmega_{F_j}\bigl(\{\phi\}\bigr) = \bigl\{\{\theta\} \mid g_j\bigl( \{\phi\}, \{\theta\}\bigr) \geq 0\bigr\} $$
(10.5)

Then, the probability of failure can also be expressed as the integral of the probability density function q({θ}) over the failure domain in the form

$$ P_{F_j}\bigl(\{\phi\}\bigr) = \int_{\varOmega_{F_j}(\{\phi\})} q\bigl(\{ \theta\}\bigr) \,d\{\theta\} $$
(10.6)

With the previous notation, a reliability constraint can be written as \(h_{j}(\{\phi\}) = P_{F_{j}}(\{\phi\}) - P^{*}_{F_{j}} \leq 0\), where \(P^{*}_{F_{j}}\) is the target failure probability. The last inequality expresses the requirement that the probability of system failure must be smaller than an appropriate tolerance. It is noted that in the context of stochastic design a system that corresponds to a feasible design can not be certified with complete certainty, but with a tolerance \(P^{*}_{F_{j}}\). In other words, the system will operate safely within the pre-specified probability of failure tolerance.

3 Structural Model

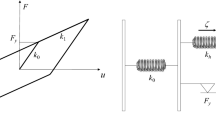
In general, base-isolated buildings are designed such that the superstructure remains elastic. Hence, the structure is modeled as a linear elastic system in the present formulation. The base and the floors are assumed to be infinitely rigid in plane. The superstructure and the base are modeled using three degrees of freedom per floor at the center of mass. Each nonlinear isolation element is modeled explicitly using the Bouc–Wen model. Let {x s (t)} be the n-th dimensional vector of displacements for the superstructure with respect to the base, and [M s ], [C s ], and [K s ] be the corresponding mass, damping and stiffness matrices. Also, let {x b (t)} be the vector of base displacements with respect to the ground and [G s ] be the matrix of earthquake influence coefficients of dimension n×3, that is, the matrix that couples the excitation components of the vector \(\{\ddot{x}_{g}(t)\}\) to the degrees of freedom of the superstructure. The schematic representation of the base-isolated structural system as well as the displacement coordinates are shown in Fig. 10.1. The equation of motion of the elastic superstructure is then expressed in the form

(10.7)

where \(\{\ddot{x}_{b}(t)\}\) is the vector of base accelerations relative to the ground. On the other hand, the equation of motion of the base can be written as

(10.8)

where [M b ] is the diagonal mass matrix of the rigid base, and {f is } is the vector containing the linear and nonlinear isolation elements forces (three components). The characterization of such forces is treated in a subsequent Section. Rewriting the previous equations, the combined equation of motion of the base-isolated structure system can be formulated in the form

(10.9)
Fig. 10.1
figure 1

Schematic representation of the base-isolated structural model

Full size image

It is noted that elastic and viscous isolation elements can also be incorporated in the isolation model. Also, the above formulation can be directly extended to more complex cases, for example, to nonlinear models for the superstructure.

4 Earthquake Excitation Model

The ground acceleration is modeled as a non-stationary stochastic process. In particular, a point-source model characterized by the moment magnitude M and epicentral distance r is considered here [3, 6]. The model is a simple, yet powerful means for simulating ground motions and it has been successfully applied in the context of earthquake engineering. The time-history of the ground acceleration for a given magnitude M and epicentral distance r is obtained by modulating a white noise sequence by an envelope function and subsequently by a ground motion spectrum through the following steps: (1) generate a discrete-time Gaussian white noise sequence \(\omega(t_{j}) = \sqrt{I/\varDelta t} \theta_{j} \), j=1,…,n T , where θ j , j=1,…,n T , are independent, identically distributed standard Gaussian random variables, I is the white noise intensity, Δt is the sampling interval, and n T is the number of time instants equal to the duration of the excitation T divided by the sampling interval; (2) the white noise sequence is modulated by an envelope function h(t,M,r) at the discrete time instants; (3) the modulated white noise sequence is transformed to the frequency domain; (4) the resulting spectrum is normalized by the square root of the average square amplitude spectrum; (5) the normalized spectrum is multiplied by a ground motion spectrum (or radiation spectrum) S(f,M,r) at discrete frequencies f l =l/T, l=1,…,n T /2; (6) the modified spectrum is transformed back to the time domain to yield the desired ground acceleration time history. Details of the characterization of the envelope function h(t,M,r) and the ground acceleration spectrum S(f,M,r) are provided in the subsequent sections. The probabilistic model for the seismic hazard at the emplacement is complemented by considering that the moment magnitude M and epicentral distance r are also uncertain. The uncertainty in moment magnitude is modeled by the Gutenberg–Richter relationship truncated on the interval [6.0,8.0], which leads to the probability density function [24]

$$ p(M) = \frac{b e^{-b M}}{{ e^{-6.0 b} - e^{-8.0 b}}} ,\quad 6.0 \leq M \leq 8.0 $$
(10.10)

where b is a regional seismicity factor. For the uncertainty in the epicentral distance r, a lognormal distribution with mean value \(\bar{r}\) (km) and standard deviation σ r (km) is used. The point source stochastic model previously described is well suited for generating the high-frequency components of the ground motion (greater than 0.1 Hz). Low-frequency components can also be introduced in the analysis by combining the above methodology with near-fault ground motion models [25].

4.1 Envelope Function

The envelope function for the ground acceleration is represented by [6, 28]

$$ h(t,M,r) = a_1 \biggl( { \frac{t}{{t_n} }} \biggr)^{a_2} e^{- a_3 ({t}/{t_n} )} $$
(10.11)

where

$$ a_2 = \frac{- 0.2 \ln(0.05)}{{1+ 0.2(\ln(0.2)-1)}} ,\qquad a_3 = \frac{a_2}{{ 0.2}} ,\qquad a_1= \biggl(\frac{e^1}{{ 0.2}} \biggr)^{a_2} $$
(10.12)

The envelope function has a peak equal to unity when t=0.2t n , and h(t,M,r)=0.05 when t=t n , with t n =2.0T gm , where T gm is the duration of ground motion, expressed as a sum of a path dependent and source dependent component \(T_{gm} = 0.05 \sqrt{r^{2} + h^{2}} + 0.5 /f_{a}\), where r is the epicentral distance, and the parameters h and f a (corner frequency) are moment dependent given by log(h)=0.15M−0.05 and log(f a )=2.181−0.496M [3]. As an example Fig. 10.2 shows the envelope function for r=20 km, and M=5 and M=7. Note that increasing the moment magnitude increases the duration of the envelope function, as expected.

Fig. 10.2
figure 2

Envelope function for epicentral distance r=20 km and moment magnitudes M=5 and M=7

Full size image

4.2 Ground Motion Spectrum

The total spectrum of the motion at a site S(f,M,r) is expressed as the product of the contribution from the earthquake source E(f,M), path P(f,r), site G(f) and type of motion I(f), i.e.

$$ S(f,M,r) = E(f,M) P(f,r) G(f) I(f) $$
(10.13)

The source component is given by

$$ E(f,M) = C M_0(M) S_a(f,M) $$
(10.14)

where C is a constant, M 0(M)=101.5M+10.7 is the seismic moment, and the factor S a is the displacement source spectrum given by [3]

$$ S_a(f,M) = \frac{1- \varepsilon}{{ 1 + ({f}/{{f_a}} )^2}} + \frac{\varepsilon}{{ 1 + ({f}/{{f_b}} )^2}} $$
(10.15)

where the corner frequencies f a and f b , and the weighting parameter ε are defined, respectively, as log(f a )=2.181−0.496M, log(f b )=2.41−0.408M, and log(ε)=0.605−0.255M. The constant C is given by \(C= U R_{\varPhi}V F / 4 \pi \rho_{s} \beta_{s}^{3} R_{0}\), where U is a unit dependent factor, R Φ is the radiation pattern, V represents the partition of total shear-wave energy into horizontal components, F is the effect of the free surface amplification, ρ s and β s are the density and shear-wave velocity in the vicinity of the source, and R 0 is a reference distance.

Next, the path effect P(f,r) which is another component of the process that affects the spectrum of motion at a particular site it is represented by functions that account for geometrical spreading and attenuation

$$ P(f,r) = Z\bigl(R(r)\bigr) e^{- \pi f R(r) / Q(f) \beta_s} $$
(10.16)

where R(r) is the radial distance from the hypocenter to the site given by \(R(r) = \sqrt{r^{2} + h^{2}}\). The attenuation quantity Q(f) is taken as Q(f)=180f 0.45 and the geometrical spreading function is selected as Z(R(r))=1/R(r) if R(r)<70.0 km and Z(R(r))=1/70.0 otherwise [3]. The modification of seismic waves by local conditions, site effect G(f), is expressed by the multiplication of a diminution function D(f) and an amplification function A(f). The diminution function accounts for the path-independent loss of high frequency in the ground motions and can be accounted for a simple filter of the form D(f)=e −0.03πf [2]. The amplification function A(f) is based on empirical curves given in [7] for generic rock sites. An average constant value equal to 2.0 is considered. Finally, the filter that controls the type of ground motion I(f) is chosen as I(f)=(2πf)2 for ground acceleration. The particular values of the different parameters of the stochastic ground acceleration model are given in Table 10.1 (see Application Problem Section). For illustration purposes Fig. 10.3 shows the ground acceleration spectrum for a nominal distance r=20 km, moment magnitudes M=5 and M=7, and model parameters given in Table 10.1. As the moment magnitude increases, the spectral amplitude increases at all frequencies, with a shift of dominant frequency content towards the lower frequency regime, as anticipated.

Fig. 10.3
figure 3

Ground acceleration spectrum for epicentral distance r=20 km and moment magnitudes M=5 and M=7

Full size image
Table 10.1 Parameters for the stochastic ground acceleration model
Full size table

5 Isolation Model

Several isolation elements can be used to model isolation systems. They include elastic, viscous, nonlinear fluid dampers, hysteretic (uniaxial or biaxial) elements for bilinear elastomeric bearings, hysteretic (uniaxial or biaxial) elements for sliding bearings, etc. Uniaxial elastomeric bearings with hysteretic behavior, such as lead rubber bearings, are considered in the present implementation. They are modeled using the Bouc–Wen model as [5]

$$ U^y \dot{z}(t)= \begin{cases} \dot{x}_b(t) [\alpha - z^{n}(t)(\gamma \operatorname{sgn}(\dot{x}_b(t) z(t)) +\beta)] & \mbox{if n is even} \\ \dot{x}_b(t) [\alpha - z^{n}(t)(\gamma \operatorname{sgn}(\dot{x}_b(t)) +\beta \operatorname{sgn}(z(t)))] & \mbox{if n is odd} \end{cases} $$
(10.17)

where z(t) is a dimensionless hysteretic variable, α, β, and γ are dimensionless quantities, U y is the yield displacement, x b (t) and \(\dot{x}_{b}(t)\) represent the base displacement and velocity, respectively, and \(\operatorname{sgn}(\cdot)\) is the sign function. The forces activated in the elastomeric isolation bearing are modeled by an elastic-viscoplastic model with strain hardening

$$ f_{is} (t) = k_p x_b(t) + c_v \dot{x}_b(t) + (k_e - k_p ) U^y z(t) $$
(10.18)

where k e is the pre-yield stiffness, k p is the post-yield stiffness, c v is the viscous damping coefficient of the elastomeric bearing, and U y is the yield displacement. If the post-yield stiffness is written as k p =α L k e , where α L is a factor which defines the extent to which the force is linear, the isolator forces can be expressed as

$$ f_{is} (t) = \alpha_L k_e x_b(t) + c_v \dot{x}_b(t) + (1- \alpha_L) k_e U^y z(t) $$
(10.19)

6 Sequential Approximate Optimization

The solution of the reliability-based optimization problem given by Eqs. (10.1)–(10.3) is obtained by transforming it into a sequence of sub-optimization problems having a simple explicit algebraic structure. Thus, the strategy is to construct successive approximate analytical sub-problems. To this end, the objective and the constraint functions are represented by using approximate functions dependent on the design variables. In particular, a hybrid form of linear, reciprocal and quadratic approximations is considered in the present formulation [14, 20, 27]. The approximate discrete sub-optimization problems take the form (k=1,2,…)

$$ \mbox{Minimize } \tilde{f}_k \bigl(\{\phi\}\bigr) $$
(10.20)

subject to

$$ \tilde{h}_{jk} \bigl(\{\phi\}\bigr) \leq 0 ,\quad j=1,\ldots,n_c $$
(10.21)

with side constraints

$$ \phi_i^l \leq \phi_i \leq \phi_i^u ,\quad i=1,\ldots,n_d $$
(10.22)

where \(\tilde{f}_{k}\) and \(\tilde{h}_{jk}\), j=1,…,n c represent the approximate objective and constraint functions at the current point {ϕ k} in the design space, respectively. The approximate objective function is obtained as

$$ \tilde{f}_k\bigl(\{\phi\}\bigr) = f_{1k}\bigl(\{\phi\} \bigr) + f_{2k}\bigl(\{\phi\}\bigr) + f_{3k}\bigl(\{\phi\} \bigr) $$
(10.23)

where f 1k ({ϕ}) is a linear function in terms of the design variables, f 2k ({ϕ}) is a linear function with respect to the reciprocal of the design variables, and f 3k ({ϕ}) is a quadratic function of the design variables. They are given by

(10.24)
(10.25)

where (i +) is the group that contains the variables for which the partial derivative of the objective function is positive at the expansion point {ϕ k}, (i −) is the group that includes the remaining variables, and χ f is a user-defined positive scalar that control the conservatism of the approximation [17, 18]. On the other hand, the constraint functions involving reliability measures (reliability constraints) are first transformed as \(h^{t}_{j} (\{\phi\})= \ln[ P_{F_{j}}(\{\phi\})]\). Then the transformed constraint functions are approximated in the form

$$ \tilde{h}_{jk}^t \bigl(\{\phi\}\bigr) = h_{j1k}^t \bigl(\{\phi\}\bigr) + h_{j2k}^t \bigl(\{\phi\}\bigr) + h_{j3k}^t \bigl(\{\phi\}\bigr) + \bar{h}^t_{jk}\bigl(\bigl\{\phi^k\bigr\}\bigr) $$
(10.26)

where

(10.27)
(10.28)
(10.29)

where \(\sum_{(i_{j}^{+})}\) and \(\sum_{(i_{j}^{-})}\) mean summation over the variables belonging to group \((i_{j}^{+})\) and \((i_{j}^{-})\), respectively, and \(\chi^{h^{t}_{j}}\) is as before a user-defined positive scalar that control the conservatism of the approximations. Group \((i_{j}^{+})\) contains the variables for which \(\partial h^{t}_{j} (\{\phi^{k}\}) / {\partial \phi_{i}}\) is positive, and group \((i_{j}^{-})\) includes the remaining variables. The same type of approximations can be applied to the deterministic constraint functions. The explicit discrete sub-optimization problems (10.20)–(10.22) are solved by standard methods that treat the problem directly in the primal design variable space such as evolution-based optimization techniques [16]. The level of effectiveness of the above sequential optimization scheme depends on the degree of convexity of the functions involved in the optimization problem. For example, if the curvatures are not too large and relatively uniform throughout the design space the proposed algorithm converges within few iterations [9, 21, 29]. For more general cases methods based on trust regions and line search methodologies may be more appropriate [1, 19, 22].

7 Reliability and Sensitivity Assessment

The characterization of the sub-optimization problems (10.20)–(10.22) requires the estimation of first excursion probabilities and their sensitivities. In order to estimate the excursion probabilities at a given design high-dimensional integrals need to be evaluated. This difficulty favors the application of Monte Carlo Simulation as fundamental approach to cope with the probability integrals. However, in most engineering applications the probability that a particular system fails is expected to be small, e.g. between 10−4–10−6. Direct Monte Carlo is robust to the type and dimension of the problem, but it is not suitable for finding small probabilities. Therefore, advanced Monte Carlo strategies are needed to reduce the computational efforts. In particular a generally applicable method, called subset simulation, is implemented in this work [4]. On the other hand, the sensitivity of the failure probability functions with respect to the design variables is estimated by an approach recently introduced in [32]. The approach is based on the approximate local representation of two different quantities. The first approximation involves the performance functions that define the failure domains while the second includes the probability of failure in terms of the maximum response levels for safe system operation. For a detailed discussion of the approach the reader is referred to [22, 32].

8 Application Problem

8.1 Description

A four-story building with a base-isolation system under earthquake motion is considered as an application problem. The plan view, as well as the dimensions for each floor are shown in Fig. 10.4. The elevation of one resistant element (A-axis) is illustrated in Fig. 10.5. Each of the four floors is supported by 80 columns of square cross section. The first floor has a height equal to 3.5 m while the other floors have a constant height equal to 3.0 m, leading to a total height of 12.5 m.

Fig. 10.4
figure 4

Plan view of the structural model

Full size image
Fig. 10.5
figure 5

Elevation view of axis A

Full size image

As previously pointed out (see Structural Model Section) each floor is represented by three degrees of freedom, i.e. two translational displacements in the direction of the x axis and y axis, and a rotational displacement. The associated active masses in the x and y direction are taken constant for the first three floors and equal to 2.50×106 kg and 1.50×106 kg for the last floor. The corresponding mass moments of inertia are taken as 2.10×109 kg⋅m2 and 1.20×109 kg⋅m2, respectively. On the other hand, the mass of the base is equal to 6.0×106 kg, and its mass moment of inertia 5.00×109 kg⋅m2. The Young’s modulus and the modal damping ratios are treated as uncertain system parameters. The Young’s modulus is modeled by a truncated normal random variable with most probable value \(\bar{E}=2.50 \times 10^{10}~\mbox{N/m}^{2}\) and coefficient of variation of 20%. Moreover, the damping ratios are modeled by independent Log-normal random variables with mean value \(\bar{\zeta}=0.03\) and coefficient of variation of 40%. The base isolation system is composed of 80 uniaxial lead rubber bearings with hysteretic behavior. The nonlinear behavior of these devices is modeled using the equations described in Sect. 5 with model parameters n=1, α=1.0, β=−0.65, γ=0.5, U y=0.5 cm, α L =0.1, k e =3×106 N/m, and c v =0.0. Figures 10.6 and 10.7 show a schematic representation of a lead rubber bearing and a typical displacement-restoring force curve of the isolation element, respectively. The structural system is excited horizontally by a ground acceleration applied in the y direction. The induced ground acceleration is characterized as in Sect. 4, with model parameters listed in Table 10.1.

Fig. 10.6
figure 6

Lead rubber bearing

Full size image
Fig. 10.7
figure 7

Typical displacement-restoring force curve of the isolation element (lead rubber bearing)

Full size image

8.2 Optimal Design Problem

The objective function f is defined as the volume of the column elements of the structural system. The design variables {ϕ} are chosen as the dimensions of the columns throughout the height, grouped in four design variables, i.e. the dimensions of the columns of each floor constitute each of the design groups. The failure event is formulated as a first passage problem during the duration of the ground acceleration. The structural responses to be controlled are the 4 interstorey drift displacements. The threshold value is chosen equal to 0.2% of the floor height for the interstorey drift displacements. Thus, the failure domains evaluated at the design {ϕ} are given by

(10.30)

where δ j (t k ,{ϕ},{θ}) is the relative displacement between the (j−1,j)-th floor evaluated at the design {ϕ}, t k are the discrete time instants, δ ∗ is the critical threshold level, and {θ} is the vector that represents the uncertain system parameters (structural parameters and excitation). Note that more than two thousand random variables are involved in the characterization of the uncertain model parameters. The reliability-based optimization problem is defined as

$$\mbox{Min } f\bigl(\{\phi\}\bigr) $$

subject to

(10.31)

Two target failure probabilities are considered: \(P^{*}_{F} = 10^{-2}\) and \(P^{*}_{F} = 10^{-4}\). The first case can be interpreted as a design problem with a moderate level of reliability while the second case corresponds to a high level of reliability. In what follows the first case will be referred as Problem 1 while the second case as Problem 2.

8.3 Results

The initial and final designs of Problems 1 and 2 are given in Table 10.2. The results of the optimization process are presented in Figs. 10.8, 10.9 and 10.10 in terms of the evolution of the objective function and failure probabilities, respectively.

Fig. 10.8
figure 8

Iteration history in terms of the objective function. Problem 1: moderate level of reliability. Problem 2: high level of reliability

Full size image
Fig. 10.9
figure 9

Iteration history in terms of the reliability constraints. Problem 1

Full size image
Fig. 10.10
figure 10

Iteration history in terms of the reliability constraints. Problem 2

Full size image
Table 10.2 Initial and final designs
Full size table

The objective function is normalized by its value at the initial design. It is observed that only a few optimization cycles are required for obtaining convergence. Moreover, most of the improvement of the objective function takes place in the first 3 iterations. It is also seen that the method generates a series of steadily improved feasible designs that move toward the optimum. The results indicate that the value of the objective function at the final design of Problem 2 is greater than the corresponding value of Problem 1. This is turn implies that the structural components (columns) at the final design of Problem 2 are bigger than the corresponding components of Problem 1, as expected. The beneficial effects of the base isolation system are shown in Table 10.3. This table shows the value of the objective function at the final designs of Problems 1 and 2 for models with and without the isolation system. The effect of the isolation system is clear from these results. The difference between the values of the objective functions is almost 40% in both Problems.

Table 10.3 Objective function value of models with and without the base isolation system
Full size table

Finally, the effect of the base isolation system can also be observed from a constraint violation viewpoint. Table 10.4 shows the probability of occurrence of the failure events associated with the final design of Problem 2 (see Table 10.2) for the case where no base isolation is considered. The probability is normalized by the target failure probability \(P^{*}_{F} = 10^{-4}\). It is seen for example that the probability of occurrence of failure event F 1 is more than 100 times greater than the target failure probability. Once again, the effect of the isolation system is evident from these results.

Table 10.4 Constraint violations
Full size table

9 Conclusions

A general framework for reliability-based design of base-isolated buildings under uncertain conditions has been presented. The reliability-based design problem is formulated as an optimization problem with a single objective function subject to multiple reliability constraints. First excursion probabilities that account for the uncertainties in the system parameters as well as in the excitation are used to characterize the system reliability. The high computational cost associated with the solution of the optimization problem is addressed by the use of approximate reliability analyses during portions of the optimization process. The proposed approach takes into account all nonlinear characteristics of the structural response in the design process and it allows for a complex characterization of structural systems and excitation models. At the same time, uncertainties in structural and excitation model parameters are considered explicitly during the design process. The numerical results and additional validation calculations highlight the beneficial effects of base-isolation systems in reducing the superstructure response. This in turn implies more robust and safer designs.