Seismic Response Prediction of Multiple Base-Isolated Structures for Monitoring

Abstract

The seismic response of multiple base-isolated structures is here evaluated through both iterative linearization and numerical solution of the nonlinear structure subjected to stochastic dynamic excitation with the purpose of predicting the behavior of a monitored system. An analytical procedure is used to determine the second-order response statistics of a simple model composed by linear superstructures posed on a common nonlinear base isolation system. The seismic excitation is modeled as a zero-mean filtered white noise and combined with the system equation of motion in an augmented state space representation. Different levels of seismic magnitudes are investigated, and preliminary results are presented here. The study furnishes insights for the design of a permanent seismic monitoring system of the four parts composing the building superstructure of the Department of Human Science at University of L’Aquila laying on a common base isolation system.

1 Introduction

Base isolation has become a popular solution to reduce seismically induced acceleration and relative displacement in buildings. Base-isolated structures reach a great number of implementations worldwide [1], and in several cases, the superstructure may consist of several parts separated by seismic or thermal joints. The prediction of seismic response of these structural systems has been simulated by a devoted numerical code in which the nonlinearities are concentrated at the base [2]. However, the approach of the problem by Monte Carlo simulations is extremely onerous. Especially when the aim is related to the reproduction of the seismic behavior of existing structures that have experienced large displacements, bringing the material in the plastic range [3]. Therefore, preliminary design criteria have been proposed for dissipative devices in adjacent structure based on the stochastic evaluation of the structural responses. Moreover, such methods have taken into account the seismic excitation modeled as a filtered white noise considering soil effects [4]. Further, performance-based optimization of nonlinear structures subject to stochastic dynamic excitation has been formulated in terms of the variance of stationary structural responses, which are obtained via equivalent linearization [5]. This approach could provide insights into the optimization of the structural design equipped by dissipative passive systems or base isolated systems. In this respect, the issue to be faced is related to a stochastic structural optimization problem. The problem has been already formulated in a more general context [6], but in recent works, it has been enriched to solve it taking into account the multi-objective nature of the engineering design problems [7]. In this chapter, the prediction of the seismic response of simplified multiple-base isolated structural model could be useful for a preliminary designing of a seismic monitoring system. A further development of the work will be to propose a relationship between the acceleration amplitude induced by environmental noise and the sensor sensitivities.

2 Problem Formulation

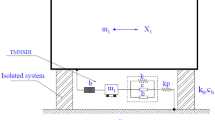
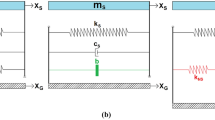
Let us consider a simple model composed by n simple oscillators modeling several separated parts of a superstructure posed on a nonlinear base isolation system (Fig. 1a). The model is suitable to evaluate the stochastic dynamic response to seismic excitation of a multiple base-isolated structure (e.g., Fig. 1b).

Fig. 1

(a) Simple model composed of linear superstructures posed on a common nonlinear base isolation system. (b) Department of Human Science buildings at L’Aquila

The equations of motion of a minimum case of two oscillators can be directly derived by D’Alambert principle as follows:

$$ {\displaystyle \begin{array}{l}{M}_1\left({\ddot{U}}_{\mathrm{b}}+{\ddot{D}}_1\right)+{C}_1{\dot{D}}_1+{K}_1{D}_1=0\\ {}{M}_2\left({\ddot{U}}_{\mathrm{b}}+{\ddot{D}}_2\right)+{C}_2{\dot{D}}_2+{K}_2{D}_2=0\\ {}{M}_{\mathrm{b}}\left({\ddot{U}}_{\mathrm{g}}+{\ddot{D}}_{\mathrm{b}}\right)+{M}_1{\ddot{D}}_1+{M}_2{\ddot{D}}_2+{C}_{\mathrm{b}}{\dot{D}}_{\mathrm{b}}+{K}_{\mathrm{b}}{D}_{\mathrm{b}}=0\end{array}} $$

(1)

Denoting L as a convenient reference length, the following set of dimensionless variables and mechanical parameters can be introduced:

$$ {\displaystyle \begin{array}{l}{u}_i=\frac{U_i}{L},\kern1em {u}_{\mathrm{b}}=\frac{U_{\mathrm{b}}}{L},\kern1em {u}_{\mathrm{g}}=\frac{U_{\mathrm{g}}}{L},\kern1em {d}_i=\frac{U_i-{U}_{\mathrm{b}}}{L},\kern1em {d}_{\mathrm{b}}=\frac{U_{\mathrm{b}}-{U}_{\mathrm{g}}}{L},\kern1em {\rho}_i=\frac{M_i}{M_{\mathrm{b}}},\\ {}{\omega}_i^2=\frac{K_i}{M_i},\kern1em {\omega}_{\mathrm{b}}^2=\frac{K_{\mathrm{b}}}{M_{\mathrm{b}}},\kern1em {\beta}_i=\frac{\omega_i}{\omega_{\mathrm{b}}},\kern1em {\xi}_i=\frac{C_i}{2\;{\omega}_i{M}_i},\kern1em {\xi}_{\mathrm{b}}=\frac{C_{\mathrm{b}}}{2\;{\omega}_{\mathrm{b}}{M}_{\mathrm{b}}},\kern1em \tau ={\omega}_{\mathrm{b}}t\end{array}} $$

(2)

where u _i, u _b, and u _g are the absolute displacements for i-th pendulum representing a part of the superstructure, base, and ground, respectively, while d _i and d _b are the relative displacements between the superstructures and base and the base and ground, respectively. The relevant parameters to describe the system dynamics are ρ _i and β _i. The first one is defined as the ratio between the mass of the i-th pendulum of the superstructure and the mass of the isolated base while the second one is the ratio between the fundamental frequency of the i-th pendulum of the superstructure and the frequency of the base isolated. The linear dimensionless equations of motion are follows:

$$ {\displaystyle \begin{array}{l}{\ddot{d}}_1+{\ddot{d}}_{\mathrm{b}}+2\;{\xi}_1\;{\beta}_1\;{\dot{d}}_1+{\beta}_1^2{d}_1=-{\ddot{u}}_{\mathrm{g}}\\ {}{\ddot{d}}_2+{\ddot{d}}_{\mathrm{b}}+2\;{\xi}_2\;{\beta}_2\;{\dot{d}}_2+{\beta}_2^2{d}_2=-{\ddot{u}}_{\mathrm{g}}\\ {}{\ddot{d}}_{\mathrm{b}}+{\rho}_1\;{\ddot{d}}_1+{\rho}_2\;{\ddot{d}}_2+2\;{\xi}_{\mathrm{b}}\;{\dot{d}}_{\mathrm{b}}+{d}_{\mathrm{b}}=-{\ddot{u}}_{\mathrm{g}}\end{array}} $$

(3)

where the dots indicate differentiation with respect to the nondimensional time τ. The dimensionless compact form is the following:

$$ \mathbf{M}\;\ddot{\mathbf{d}}+\mathbf{C}\;\dot{\mathbf{d}}+\mathbf{K}\;\mathbf{d}=-\mathbf{r}\;{\ddot{u}}_{\mathrm{g}} $$

(4)

in which M, K, and C are the mass, stiffness, and damping matrices, respectively. The vector r allocates the external forces while the vector d contains the relative displacements. All variable and parameters are as follows:

$$ {\displaystyle \begin{array}{l}\mathbf{M}=\left[\begin{array}{ccc}1& 0& 1\\ {}0& 1& 1\\ {}{\rho}_1& {\rho}_2& 1\end{array}\right],\kern1em C=\left[\begin{array}{ccc}2{\xi}_1\;{\beta}_1& 0& 0\\ {}0& 2{\xi}_2\;{\beta}_2& 0\\ {}0& 0& 2{\xi}_{\mathrm{b}}\end{array}\right],\kern1em \mathbf{K}=\left[\begin{array}{ccc}{\beta}_1^2& 0& 0\\ {}0& {\beta}_2^2& 0\\ {}0& 0& 1\end{array}\right],\\ {}\mathbf{r}=\left[\begin{array}{c}1\\ {}1\\ {}1\end{array}\right],\kern1em \mathbf{d}=\left[\begin{array}{c}{d}_1\\ {}{d}_2\\ {}{d}_{\mathrm{b}}\end{array}\right]\end{array}} $$

(5)

Considering a hysteretic behavior, the nonlinear equations of motion are given by

$$ \mathbf{M}\;\ddot{\mathbf{d}}+\mathbf{C}\;\dot{\mathbf{d}}+{\mathbf{f}}_N=-\mathbf{r}\;{\ddot{u}}_{\mathrm{g}} $$

(6)

The hysteretic component of the restoring force, f _N, is represented here by an adjunct variable, z, whose evolution is described through a Bouc–Wen model

$$ {\mathbf{f}}_N={\mathbf{K}}_{\mathrm{L}}\mathbf{d}+\left(1-\alpha \right)\mathbf{h}\;z $$

(7)

where K _L is the linear stiffness matrix, h is the allocation vector of the hysteretic component, and α is the post- to pre-yielding stiffness ratio. The matrix K _L and the vector h have the following expressions:

$$ {\mathbf{K}}_{\mathrm{L}}=\left[\begin{array}{ccc}{\beta}_1^2& 0& 0\\ {}0& {\beta}_2^2& 0\\ {}0& 0& \alpha \end{array}\right],\kern1em \mathbf{h}=\left[\begin{array}{c}0\\ {}0\\ {}1\end{array}\right] $$

(8)

The new nonlinear system is:

$$ {\displaystyle \begin{array}{l}\mathbf{M}\;\ddot{\mathbf{d}}+\mathbf{C}\;\dot{\mathbf{d}}+{\mathbf{K}}_{\mathrm{L}}\;\mathbf{d}+\left(1-\alpha \right)\;\mathbf{h}\;z=-\mathbf{r}\;{\ddot{u}}_{\mathrm{g}}\\ {}\dot{z}=-\gamma \left|{\dot{d}}_{\mathrm{b}}\right|\;z\;{\left|z\right|}^{n-1}-\beta\;{\dot{d}}_{\mathrm{b}}\;{\left|z\right|}^n+A\;{\dot{d}}_{\mathrm{b}}\end{array}} $$

(9)

where in the Bouc–Wen model, the parameters γ and β control the shape of the hysteresis loop, A the restoring force amplitude, and n the smooth transition from elastic to plastic response (for large value of n the model tends to an elasto-plastic behavior).

2.1 Stochastic Structural Response

The linear stochastic response of the system described in Eq. (4) can be calculated through the covariance matrix Γ. Moreover, defining the state vector as ${\mathbf{x}}_{\mathrm{s}}={\left[{\mathbf{d}}^{\mathrm{T}}\kern0.5em {\dot{\mathbf{d}}}^{\mathrm{T}}\right]}^{\mathrm{T}}$, Eq. (4) can be organized in the space-state formulation:

$$ {\dot{\mathbf{x}}}_{\mathrm{s}}={\mathbf{A}}_{\mathrm{s}}\;\mathbf{x}+{\mathbf{B}}_{\mathrm{s}}\;w $$

(10)

where w is a zero-mean stationary Gaussian process while the space-state matrices A and B assume the following expression:

$$ {\mathbf{A}}_{\mathrm{s}}=\left[\begin{array}{cc}{\mathbf{0}}_{3\times 3}& {\mathbf{I}}_{3\times 3}\\ {}-{\mathbf{M}}^{-1}\;\mathbf{K}& -{\mathbf{M}}^{-1}\;\mathbf{C}\end{array}\right],\kern1em {\mathbf{B}}_{\mathrm{s}}={\left[\begin{array}{cc}{\mathbf{0}}_{1\times 3}^{\mathrm{T}}& -{\mathbf{r}}^{\mathrm{T}}\end{array}\right]}^{\mathrm{T}} $$

(11)

The stationary stochastic structural responses can be obtained evaluating the covariance matrix Γ through the solution of the following Eq. (3):

$$ \mathbf{0}={\mathbf{A}}_{\mathrm{s}}\;\boldsymbol{\Gamma} +\boldsymbol{\Gamma}\;{\mathbf{A}}_{\mathrm{s}}+2\pi {\mathbf{B}}_{\mathrm{s}}\kern0.1em {\mathbf{SB}}_{\mathrm{s}} $$

(12)

which is the well-known Lyapunov equation in the unknown Γ while S is the power spectral density of the white noise. It is worth to highlight that the main diagonal of the covariance matrix consists of the expected values (variance and standard deviations) of the displacements and velocity while the mixed expected values are given by the terms out of diagonal.

The nonlinear stochastic response can be approximately determined by an equivalent linear system [4, 7] that allows to easily manage the solution to the previously introduced Lyapunov equation. Consequently, the new form of the equations of motion is follows:

$$ {\displaystyle \begin{array}{l}\mathbf{M}\;\ddot{\mathbf{d}}+\mathbf{C}\;\dot{\mathbf{d}}+{\mathbf{K}}_{\mathrm{L}}\;\mathbf{d}+\left(1-\alpha \right)\;\mathbf{h}\;z=-\mathbf{r}\;{\ddot{u}}_{\mathrm{g}}\\ {}\dot{z}+{C}_{21}\kern0.1em {\dot{d}}_{\mathrm{b}}+{K}_{22}\kern0.1em z=0\end{array}} $$

(13)

where the two coefficients C ₂₁ and K ₂₂ can be evaluated in terms of the second moments of ${\dot{d}}_{\mathrm{b}}$ and z [8]:

$$ {\displaystyle \begin{array}{l}{C}_{21}=\sqrt{\frac{2}{\pi }}\kern0.5em \left[\gamma \frac{E\;\left[{\dot{d}}_{\mathrm{b}}z\right]}{\sigma_{{\dot{d}}_{\mathrm{b}}}}+\beta\;{\sigma}_{\mathrm{z}}\right]-A\\[12pt] {}{K}_{22}=\sqrt{\frac{2}{\pi }}\kern0.5em \left[\gamma\;{\sigma}_{{\dot{d}}_{\mathrm{b}}}+\beta \frac{E\;\left[{\dot{d}}_{\mathrm{b}}z\right]}{\sigma_{\mathrm{z}}}\right]\end{array}} $$

(14)

Starting from the equivalent linear system, it is possible to define a new state-space vector as $\tilde{\mathbf{x}}={\left[\begin{array}{ccc}{\mathbf{d}}^{\mathrm{T}}& {\dot{\mathbf{d}}}^{\mathrm{T}}& z\end{array}\right]}^{\mathrm{T}}$ that brings the system to a new state-space formulation:

$$ \dot{\tilde{\mathbf{x}}}={\mathbf{A}}_{\mathrm{e}}\;\tilde{\mathbf{x}}+{\mathbf{B}}_{\mathrm{e}}\;w $$

(15)

where the new state-space matrices, A _e and B _e (where the subscript stands for equivalent linearization), assume the following form:

$$ {\mathbf{A}}_{\mathrm{e}}={\left[\begin{array}{ccc}{\mathbf{0}}_{3\times 3}& {\mathbf{I}}_{3\times 3}& {\mathbf{0}}_{3\times 1}\\ {}-{\mathbf{M}}^{-1}{\mathbf{K}}_{\mathrm{L}}& -{\mathbf{M}}^{-1}\mathbf{C}& -\left(1-\alpha \right){\mathbf{h}}_{3\times 1}\\ {}{\mathbf{0}}_{1\times 3}& {C}_{21}{\mathbf{h}}^{\mathbf{T}}& {K}_{22}\end{array}\right]}_{7\times 7},\kern1em {\mathbf{B}}_{\mathrm{e}}={\left[\begin{array}{c}{\mathbf{0}}_{3\times 1}\\ {}-{\mathbf{r}}_{3\times 1}\\ {}0\end{array}\right]}_{7\times 1} $$

(16)

Considering the fact that the coefficients C ₂₁ and K ₂₁ depend on the standard deviations, to solve the Lyapunov equation, an iterative solution is required. The iteration can start using the solution of the linear system with a stiffness equal to the pre-yielding stiffness of the nonlinear system.

The stochastic excitation can be represented as a filtered white noise (e.g., Kanai-Tajimi) that in the state space form assumes the following expression:

$$ {\displaystyle \begin{array}{l}{\dot{\mathbf{x}}}_{\mathrm{f}}={\mathbf{A}}_{\mathrm{f}}{\mathbf{x}}_{\mathrm{f}}+{\mathbf{B}}_{\mathrm{f}}w\\ {}\ddot{u}={\mathbf{C}}_{\mathrm{f}}{\mathbf{x}}_{\mathrm{f}}\end{array}} $$

(17)

where x _f is the state vector for the filter while A _f, B _f, and C _f are chosen to represent the characteristics of the excitation. In particular, combining the equations of the structural model and the ones of the loading model, a new expression of an augmented system is obtained:

$$ {\displaystyle \begin{array}{l}{\dot{\mathbf{x}}}_{\mathrm{a}}={\mathbf{A}}_{\mathrm{a}}{\mathbf{x}}_{\mathrm{a}}+{\mathbf{B}}_{\mathrm{a}}w\\ {}{\mathbf{y}}_{\mathrm{s}}={\mathbf{C}}_{\mathrm{a}}{\mathbf{x}}_{\mathrm{a}}\end{array}} $$

(18)

where

$$ {\mathbf{x}}_{\mathrm{a}}={\left(\begin{array}{cc}{\mathbf{x}}_{\mathrm{s}}^{\mathrm{T}}& {\mathbf{x}}_{\mathrm{f}}^{\mathrm{T}}\end{array}\right)}^{\mathrm{T}},\kern1em {\mathbf{A}}_{\mathrm{a}}=\left[\begin{array}{cc}{\mathbf{A}}_{\mathrm{s}}& {\mathbf{B}}_{\mathrm{s}}{\mathbf{C}}_{\mathrm{f}}\\ {}\mathbf{0}& {\mathbf{A}}_{\mathrm{f}}\end{array}\right],\kern1em {\mathbf{B}}_{\mathrm{a}}=\left[\begin{array}{c}0\\ {}{\mathbf{B}}_{\mathrm{f}}\end{array}\right],\kern1em {\mathbf{C}}_{\mathrm{a}}=\left[\begin{array}{cc}{\mathbf{C}}_{\mathrm{s}}& {\mathbf{D}}_{\mathrm{s}}{\mathbf{C}}_{\mathrm{f}}\end{array}\right] $$

(19)

In this case, the covariances of the structural responses can be determined through the solution of the following equation:

$$ {\dot{\boldsymbol{\Gamma}}}_{{\mathbf{x}}_{\mathrm{a}}}={\mathbf{A}}_{\mathrm{a}}\;{\boldsymbol{\Gamma}}_{{\mathbf{x}}_{\mathrm{a}}}+{\boldsymbol{\Gamma}}_{{\mathbf{x}}_{\mathrm{a}}}\;{\mathbf{A}}_{\mathrm{a}}+2\pi {\mathbf{B}}_{\mathrm{a}}\kern0.1em \mathbf{S}\kern0.1em {\mathbf{B}}_{\mathrm{a}} $$

(20)

In the case of direct integration, the effect of the nonstationary stochastic process could be considered multiplying the output of the filter by an envelope function e(t) [7].

3 Numerical Results

This section illustrates and describes some preliminary numerical results regarding the linear and nonlinear stochastic structural response. In particular, Fig. 2 reports the results for the linear case while Fig. 3 reports the ones with the nonlinear effects analyzed through the equivalent linearization procedure previously introduced. In the Fig. 2 have been fixed the structural parameters for the first oscillator (β ₁ = 8.33, ρ ₁ = 0.1) while in the Fig. 3 the ones of the second oscillator (β ₂ = 6.25, ρ ₂ = 0.3).

Fig. 2

Linear stochastic structural response for multiple base-isolated structures: For all cases: β ₁ = 8.33 and ρ ₁ = 0.1. Modal damping: ξ ₁ = ξ ₂ = ξ _b = 0.05. Standard deviations for first oscillator (a) and (d), second oscillator (b) and (e), base-isolated (c) and (f)

Fig. 3

Nonlinear stochastic structural response for multiple base-isolated structures: For all cases: β ₂ = 6.25 and ρ ₂ = 0.3. Modal damping: ξ ₁ = ξ ₂ = ξ _b = 0.05. Standard deviations for first oscillator (a) and (d), second oscillator (b) and (e), base-isolated (c) and (f)

Looking at the results obtained considering a linear behavior, as expected, by increasing the β ₂ parameters, a quick exponential decay of the standard deviation of the second oscillator is observed, especially for low β ₂ values (see Fig. 2b). The corresponding behavior, shown in the Fig. 2a, remains practically unchanged. The variations caused by increasing ρ ₂ are reported in the Fig. 2d, e. Such increasing seems to influence both standard deviations. However, in this case, the responses have been analyzed, preliminary, for high fixed β ₂ values, and so the variations have been visualized for a small range of the standard deviations. Some main remarks are the following: (1) in all cases, for fixed ρ-parameters, the standard deviations decrease going towards high β ₂ parameters, even if the variations are very small; (2) in Fig. 2d the value of the standard deviation seems to tend to an asymptotic value near to 0.15; (3) it is worth to highlight that in Fig. 2d, e, for all analyzed cases, local minimum (and a maximum only for β ₂ = 6.25) that could suggest the development of the design procedure is found. In the last two Fig. 2c, f, the standard deviation of the base structural response has substantially linear behavior varying the ρ ₂ parameter and unchanged varying the β ₂ parameters.

The effects of the nonlinear behavior have been evaluated increasing the value of the power spectral density of the white noise, i.e. S. In particular, as described in the previous section, the nonlinearity, introduced to describe the hysteretic component of the restoring force, directly influences the structural response of the base. This appears evident looking at the results reported in Fig. 3c, f. Indeed, for small values of the spectral intensity, the standard deviation of the base assumes a hardening behavior, reaching a minimum point for a certain value of the spectral intensity. Moreover, this particular situation occurs for increasing S-values decreasing the ρ ₁ parameter.

This makes a sense because it corresponds to a relative stiffening of the base. Imperceptible variations are observed when the β ₁ parameter is changed (see Fig. 3f). After that point, further increasing of the spectral density would seem to produce a linear increasing of the standard deviation. The standard deviations related to the relative displacements of the two oscillator seem to have a more regular behavior. Indeed, the amplitudes grow while increasing the value of the intensity and go down while decreasing both ρ ₁ and β ₁ parameters. Interesting to note that in Fig. 3d the results seem to show a point of minimum for a particular value of β ₁ with S fixed.

4 Conclusion

The work aimed at developing a simple analytical model representative of the dynamic of a multiple base-isolated structures. The evaluation of linear and nonlinear stochastic structural response could be used for both to optimize nonlinear structures equipped by dissipative devise and to select sensor sensitivities for seismic monitoring. Moreover, the application of a linearized iterative procedure permits to evaluate the stochastic stationary response avoiding the execution of very long and onerous numerical simulations. A real case study at L’Aquila will be used to verify the design procedure potentiality.