Use of active control algorithm for optimal design of base-isolated buildings against earthquakes

Abstract

This study presents a new design method that concurrently determines the stiffness and damping coefficient in a base isolation system. This design method is developed based on the similarity between the active and passive control system. Then, the stiffness and damping coefficient are derived from the linear quadratic regulator control algorithm to a single degree of freedom superstructure and formed as a function of single weighting. The best design of a base isolation system is determined by optimizing this weighting from the minimum H_∞-norm responses of base displacement and roof acceleration. A parametric study is performed to understand the influence of superstructures to the resulting optimized base isolation system. Moreover, this study also provides a numerical example to validate the optimal design of base isolation systems. The potential to design nonlinear lead-rubber bearings with added viscous dampers based on the proposed method is also investigated. As a result, the proposed method yields a high-performance base isolation system for a known superstructure.

1 Introduction

Seismic isolation is an effective means of protecting structures against earthquakes and has been widely accepted as a control strategy for structures in seismically active areas. Base isolation can reduce the transmission of ground motion to superstructures, and the main effect is to decouple the structures from ground motion by increasing the resonant period of the structure using flexible isolation elements. A detailed review of seismic isolation bearings (e.g., rubber-type and friction-type bearings) can be found in Warn and Ryan (2012). Although base shears, floor accelerations, and interstory drifts are significantly reduced, the passive base isolation intrinsically induces larger base displacements (Kelly 1999; Nagarajaiah and Ferrell 1999; Buckle et al. 2002). These large base displacements become a main concern when the isolated structure is subjected to large-amplitude, long-period, and pulse-like motion (Wongprasert and Symans 2005). This type of ground motion allows energy transferring into higher modes and subsequently results in increased interstory drifts and floor accelerations. In the design of seismic isolation systems, the large displacements at the base layer should be accommodated.

Base isolation with added damping devices is one of the solutions to mitigate the potentially large base displacements. As suggested in the Uniform Building Code (ICBO 1997), added damping devices to mitigate large base displacements under stronger maximum credible earthquake (MCE) excitation are of need (Yoshioka et al. 2002). However, excessive damping may be defective in base isolation systems. Kelly (1999) recommended to design a base isolation system that made isolation functional at the design basis earthquake (DBE) level as well as is capable of reducing the base displacements at the MCE level. Jangid and Kelly (2001) carried out a parametric study of damping effect in base isolation systems against near-fault earthquakes. For a base-isolated building, an optimal damping level can be determined to yield a minimum floor acceleration under near-fault seismic excitation. Politopoulos (2008) studied the amplification of floor accelerations in a base-isolated building and concluded that a 35% damping ratio should be considered as an upper bond for a base isolation system. Providakis (2009) also addressed that excessively designed damping level introduced large drifts in a base-isolated building against far-field earthquakes, as compared to near-fault earthquakes. Consequently, the added damping devices in a base isolation system should be appropriately designed to avoid risks of enlarging interstory drifts and floor accelerations.

In the conventional design of base-isolated buildings, the superstructure can be assumed to be a rigid body. Su et al. (1989) numerically investigated various types of base isolation systems whereby the superstructure is modeled as a rigid body. This modeling method of superstructures was proposed by Kelly (1986); however, this simplification could underestimate the floor accelerations due to the flexibility of the superstructure (Kulkarni and Jangid 2002). Moreover, Kulkarni and Jangid (2002) indicated that the assumption of rigid superstructures is valid if the natural period of superstructures is less than one-fifth of the isolation period for linear isolation systems. Alternatively, the superstructure can be modeled as a single degree-of-freedom (SDOF) structure. This simplification can be performed by the modal approach (Lin et al. 1989). The resulting base-isolated structure becomes a two degree-of-freedom (2DOF) structure. In addition, the damping matrix in the multiple degree-of-freedom (MDOF) or simplified SDOF superstructure should be properly formed. Ryan and Polanco (2008) suggested that a stiffness-proportional damping matrix used in a MDOF superstructure would better present the dynamic behavior than the Rayliegh damping matrix for base-isolated buildings. Du et al. (2002) argued the use of proportional damping for performance evaluation of base isolation systems. For more realistic evaluation, non-proportional damping should be employed in a superstructure or base-isolated building. Therefore, the simplified model of base-isolated buildings can be a 2DOF structure with a proper damping matrix.

Many researchers applied optimization algorithms to determine passive control systems for seismic protection of buildings. Liu et al. (2005) exploited performance-based heuristic and gradient-based evolutionary optimization methods to investigate the best energy dissipation device configuration for seismic protection of structures. Marano et al. (2007) developed a performance-based design method that determined the optimally viscous damper for seismically-excited buildings. In that study, the structural responses were computed in the stochastic sense, while white noise was considered as ground motions. Zou (2008) combined the cost into the optimal design of base-isolated buildings, in which the equivalent stiffness of isolation bearings and dimensions of concrete members were control variables. Marano et al. (2009) performed the genetic algorithm to optimally determine a viscous-elastic device by minimizing the covariance of structural responses, which are calculated by the Lyapunov equation. However, most of previous studies mainly focused on the optimization of damping only rather than that of both stiffness and damping in a base isolation system.

To better accommodate base displacements, a base isolation system can be added with active control devices (e.g., hydraulic actuators). These controllable devices rely on active control algorithms to deliver the control effectiveness as well as to be adaptive against a wide range of earthquakes. Kang and Yoshida (1992) explored active isolation control for buildings using the H_∞ control theory. Yang et al. (1996) experimentally explicated the sliding mode control in an active isolation system for a seismically excited building. Riley et al. (1998) implemented the fuzzy control in a hybrid sliding isolation system and experimentally investigated control performance of the actively base-isolated building. Chang et al. (2014) developed a bi-directional active isolation system with the H₂/LQG control method and experimentally verified on a laboratory-scale building using shake table testing. Indeed, the numerical and experimental results showed achievable high performance using active isolation for buildings. The power shortage during earthquakes is, however, a concern for these active isolation systems. Instead, these active control algorithms can be utilized as a tool to design passive isolation systems.

In this study, a new design procedure is developed to concurrently determine the stiffness and damping coefficient in a base isolation system by facilitating active control algorithms. First, the superstructure is assumed to be simplified from a MDOF structure with a proper damping matrix to a SDOF structure. Two individual state-space equations are established to represent both superstructure and base isolation system with interconnected dynamics. The linear quadratic regulator (LQR) control algorithm is employed to derive the isolation stiffness and damping coefficient as a function of single weighting parameter. The optimal stiffness and damping coefficient are subsequently determined by minimizing an objective function which is formed by the H_∞-norms of structural responses (i.e., the absolute roof acceleration and base displacement). A parametric study is carried out to investigate the modal properties of designed isolation systems and isolated buildings, the H_∞-norms of structural responses, and the range of the weighting parameter in terms of mass ratio between the isolation and superstructure, superstructure’s natural frequency, or superstructure’s damping ratio. Moreover, this study also provides a design example that employs the five-story, shear-type building used in Kelly et al. (1987) as the superstructure. The stiffness and damping coefficient in the base isolation system is designed in accordance with the proposed method for this superstructure. The designed stiffness and damping coefficient are further employed to comprise of nonlinear lead rubber bearings (LRB) along with linearly viscous dampers, where the LRBs are simulated by a bilinear hysteretic model (Ryan and Chopra 2004). Seismic performance of the base-isolated building is evaluated by a series of analyses and compared to the results provided in Ramallo et al. (2002). The simulation results show that the proposed method can yield an effective base isolation system to be obtained.

In Section 2 of this study, the proposed design method of base isolation systems is introduced in details. Section 3 investigates the effect of superstructure dynamics on the design of base isolation systems. Section 4 numerically evaluates the proposed design method for a five-story building and compares the results with the previous studies (Kelly et al. 1987 and Ramallo et al. 2002). Finally, Section 5 presents the conclusions of this study.

2 Problem formulation

The isolation system in a base-isolated building can be viewed as a feedback control system, which is mimicked from an actively controlled structure. Figure 1 shows the passive isolation system as a feedback control system mapping from the actively isolated building. Thus, the passive isolation system can be hypothetically designed by active control algorithms, and the resulting system is the feedback controller in Fig. 1. This study emphasizes the development of passive isolation systems based on the similarity between active and passive control.

Fig. 1

Illustration of base-isolated buildings with (a) an active isolation system and (b) a passive isolation system

2.1 Modeling of base-isolated building

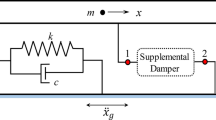
The mathematical model of a base-isolated building is assumed to be a two degree of freedom system as shown in Fig. 2. Consider the horizontal ground acceleration as ${\ddot{x}}_{\mathrm{g}}$ and the equation of motion of the system can be expressed as

$$ \mathbf{M}\left[\begin{array}{c}{\ddot{x}}_1\\ {}{\ddot{x}}_2\end{array}\right]+\mathbf{C}\left[\begin{array}{c}{\dot{x}}_1\\ {}{\dot{x}}_2\end{array}\right]+\mathbf{K}\left[\begin{array}{c}{x}_1\\ {}{x}_2\end{array}\right]=-\mathbf{M}\left[\begin{array}{c}1\\ {}1\end{array}\right]{\ddot{x}}_{\mathrm{g}} $$

(1)

where

$$ \mathbf{M}=\left[\begin{array}{cc}{m}_1& 0\\ {}0& {m}_2\end{array}\right],\mathbf{C}=\left[\begin{array}{cc}{c}_1+{c}_2& -{c}_2\\ {}-{c}_2& {c}_2\end{array}\right],\mathbf{K}=\left[\begin{array}{cc}{k}_1+{k}_2& -{k}_2\\ {}-{k}_2& {k}_2\end{array}\right] $$

Fig. 2

Schematic diagram of isolation system with SDOF superstructure

m₁. c₁, and k₁ are the mass, damping coefficient, and stiffness of the base isolation system; m₂. c₂, and k₂ are the mass, damping coefficient, and stiffness of the superstructure; x₁, ${\dot{x}}_1$, and ${\ddot{x}}_1$ are the displacement, velocity, and acceleration of the base isolation system relative to the ground; x₂. ${\dot{x}}_2$, and ${\ddot{x}}_2$ are the displacement, velocity, and acceleration of the superstructure relative to the ground.

To account for the dynamics of the superstructure, a single degree of freedom is given in the modeling instead of using the rigid-body assumption (Lin et al. 1989). Then, these two degrees of freedom are separately represented in the form of state-space equations with an absolute acceleration-force interaction such as

$$ {\displaystyle \begin{array}{l}{\dot{\mathbf{x}}}_1={\mathbf{A}}_1{\mathbf{x}}_1+{\mathbf{B}}_1{y}_c+{\mathbf{E}}_1{\ddot{x}}_{\mathrm{g}}\\ {}f={\mathbf{C}}_1{\mathbf{x}}_1\end{array}} $$

(2)

where

$$ {\mathbf{A}}_1=\left[\begin{array}{cc}0& 1\\ {}-\frac{k_1}{m_1}& -\frac{c_1}{m_1}\end{array}\right],{\mathbf{B}}_1=\left[\begin{array}{c}0\\ {}-\frac{m_2}{m_1}\end{array}\right],{\mathbf{E}}_1=\left[\begin{array}{c}0\\ {}-1\end{array}\right],{\mathbf{C}}_1=\left[{k}_2\kern0.5em {c}_2\right],{\mathbf{x}}_1=\left[\begin{array}{c}{x}_1\\ {}{\dot{x}}_1\end{array}\right] $$

and

$$ {\displaystyle \begin{array}{l}{\dot{\mathbf{x}}}_2={\mathbf{A}}_2{\mathbf{x}}_2+{\mathbf{B}}_2f+{\mathbf{E}}_2{\ddot{x}}_{\mathrm{g}}\\ {}{y}_c={\mathbf{C}}_2{\mathbf{x}}_2+{\mathbf{D}}_2f\end{array}} $$

(3)

where

$$ {\mathbf{A}}_2=\left[\begin{array}{cc}0& 1\\ {}-\frac{k_2}{m_2}& -\frac{c_2}{m_2}\end{array}\right],{\mathbf{B}}_2=\left[\begin{array}{c}0\\ {}\frac{1}{m_2}\end{array}\right],{\mathbf{E}}_2=\left[\begin{array}{c}0\\ {}-1\end{array}\right],{\mathbf{C}}_2=\left[-\frac{k_2}{m_2}\kern0.5em -\frac{c_2}{m_2}\right],{\mathbf{D}}_2=\left[\frac{1}{m_2}\right],{\mathbf{x}}_2=\left[\begin{array}{c}{x}_2\\ {}{\dot{x}}_2\end{array}\right] $$

The subscripts “1” and “2” denote the 1st and 2nd DOF representing the base isolation system in (2) and superstructure in (3), respectively. y_c is the absolute acceleration of the superstructure such as ${y}_c={\ddot{x}}_g+{\ddot{x}}_2$, while f is the force provided from the isolation system to the superstructure. As can be seen, (2) is the feedback control system of (3).

2.2 Design of Passive Control Systems Using LQR control algorithm

(2) is assumed to be a dynamic output feedback controller which is designed based on the system in (3). This dynamic output feedback controller has a similar form as an linear quadratic Gaussian controller which consists of a Kalman observer with a state feedback LQR control gain (Dyke et al. 1994). Utilizing the similarity between the dynamic output feedback controller and (2), C₁ and B₁ can be viewed as the state feedback control gain and Kalman gain. Then, an observer-based controller is presented by

$$ {\displaystyle \begin{array}{l}{\dot{\mathbf{x}}}_{\mathbf{1}}={\overline{\mathbf{A}}}_1{\mathbf{x}}_{\mathbf{1}}+\mathbf{L}{y}_c+{\mathbf{E}}_{\mathbf{2}}{\ddot{x}}_g\\ {}f={\mathbf{G}}_1{\mathbf{x}}_{\mathbf{1}}\end{array}} $$

(4)

where

$$ {\overline{\mathbf{A}}}_1=\left({\mathbf{A}}_{\mathbf{2}}+{\mathbf{B}}_{\mathbf{2}}{\mathbf{G}}_1-{\mathbf{LC}}_{\mathbf{2}}+{\mathbf{LD}}_{\mathbf{2}}{\mathbf{G}}_1\right),\mathbf{L}={\mathbf{B}}_1,{\mathbf{G}}_1={\mathbf{C}}_1 $$

G₁ and L are the state feedback control gain and Kalman gain in the dynamic output feedback controller. The resulting system matrix ${\overline{\mathbf{A}}}_1$ in (4) represents a rigid-body motion in the 1st DOF. Thus, another state feedback control gain G is designed based on the dynamics of the superstructure and derived from the LQR control algorithm to deliver the higher control authority. This control gain is determined by minimizing the control objective function (Spencer et al. 1994), given by

$$ J\left({\mathbf{x}}_2,f\right)=\underset{\tau \to \infty }{\lim}\frac{1}{\tau }E\left[{\int}_0^{\tau }{{\mathbf{x}}_2}^{\mathrm{T}}{\mathbf{Qx}}_2+{rf}^2 dt\right] $$

(5)

By solving the Riccati equation to (5), this objective function yields the control gain G as

$$ {\displaystyle \begin{array}{l}f={\mathbf{Gx}}_2\\ {}\mathbf{G}=\left[{\overline{G}}_k\kern0.5em {\overline{G}}_c\right]=\frac{1}{r}{\mathbf{B}}_2^T\mathbf{P}\\ {}{\mathbf{PA}}_2+{\mathbf{A}}_2^T\mathbf{P}+\mathbf{Q}-\frac{1}{r}{\mathbf{PB}}_2{\mathbf{B}}_2^T\mathbf{P}=0\end{array}} $$

(6)

Because of the addition state feedback control gain, the 1st-DOF system matrix in (2) has the equivalence as

$$ {\mathbf{A}}_1={\overline{\mathbf{A}}}_1+{\mathbf{B}}_{\mathbf{2}}\mathbf{G} $$

(7)

Consequently, the stiffness and damping coefficient of the base isolation system is given by

$$ {k}_1=-\frac{m_1}{m_2}{\overline{G}}_k,{c}_1=-\frac{m_1}{m_2}{\overline{G}}_c $$

(8)

(5) contains two weightings Q and r to be determined. The weighting Q can be arbitrarily assigned if Q is semi-definite. In this study, this weighting is selected by

$$ \mathbf{Q}=\left[\begin{array}{cc}q& 0\\ {}0& 0\end{array}\right] $$

(9)

where the control objective is to better mitigate the displacement of the superstructure. Therefore, the stiffness and damping coefficient of the base isolation system are derived from (6–8) and written as a function of modified weighting φ by

$$ {\displaystyle \begin{array}{l}{k}_1\left(\phi \right)=\frac{m_1}{m_2}\left(\sqrt{{k_2}^2+{m}_2^2\phi }-{k}_2\right)\\ {}{c}_1\left(\phi \right)=\frac{m_1}{m_2}\left(\sqrt{{c_2}^2+2{m}_2\left(\sqrt{{k_2}^2+{m}_2^2\phi }-{k}_2\right)}-{c}_2\right)\end{array}} $$

(10)

and

$$ \phi =\frac{q}{m_2^2r} $$

(11)

Note that the mass, damping coefficient, and stiffness of the superstructure is known, while the mass ratio between the isolation system and superstructure is predetermined. If the natural frequency and damping ratio of the superstructure is defined by ${\omega}_2\equiv \sqrt{\frac{k_2}{m_2}}$ and ${\zeta}_2\equiv \frac{c_2}{2\sqrt{k_2{m}_2}}$, then the natural frequency and damping ratio of the base isolation system is expressed by

$$ {\displaystyle \begin{array}{l}{\omega}_1\left(\phi \right)\equiv \sqrt{\frac{k_1\left(\phi \right)}{m_1}}=\sqrt{\sqrt{\omega_2^4+\phi }-{\omega}_2^2}\\ {}{\zeta}_1\left(\phi \right)\equiv \frac{c_1\left(\phi \right)}{2\sqrt{k_1{m}_1}}=\frac{\sqrt{\zeta_2^2+\frac{1}{2}\left(\sqrt{1+\frac{\phi }{\omega_2^4}}-1\right)}-{\zeta}_2}{\sqrt{\sqrt{1+\frac{\phi }{\omega_2^4}}-1}}\end{array}} $$

(12)

The objective of this study is to design a base isolation system that maintains flexibility for the base-isolated building as well as provides sufficient damping for the base displacement reduction. (10–12) are derived from the objective function in (5) which minimizes the frequency-domain energy content of the target response (i.e., the weighting on the displacement in this study) over entire frequencies in the H₂ sense (Spencer et al. 1994). However, the concern about the large base displacements during earthquakes is the instantaneous peaks. Thus, an additional objective function should be introduced in order to determine the modified weighting ϕ based on peak responses. Moreover, the design of base-isolated buildings exists a trade-off effect, that is, more reduction in base displacements may result in increased interstory drifts and floor accelerations. Therefore, the objective function to determine the modified weighting should comprise of the responses of both isolation system and superstructure.

To consider the earthquake characteristics in the modelling, the Kanai-Tajimi spectrum is employed (Constantinou and Tadjbakhsh 1985; Yoshioka et al. 2002) and given by

$$ {\displaystyle \begin{array}{l}\dot{\boldsymbol{\upeta}}={\mathbf{A}}_{\mathrm{w}}\boldsymbol{\upeta} +{\mathbf{B}}_{\mathrm{w}}w=\left[\begin{array}{cc}0& 1\\ {}-{\omega}_g^2& -2{\zeta}_g{\omega}_g\end{array}\right]\boldsymbol{\upeta} +\left[\begin{array}{c}0\\ {}1\end{array}\right]w\\ {}{\ddot{\mathbf{x}}}_g={\mathbf{C}}_{\mathrm{w}}\boldsymbol{\upeta} =\left[{\omega}_g^2\kern0.5em 2{\zeta}_g{\omega}_g\right]\boldsymbol{\upeta} \end{array}} $$

(13)

where w is scalar white noise excitation; η is the state vector for time evolution; ζ_g and ω_g are the filter parameters of the Kanai-Tajimi spectrum. The 2DOF system in (1) is then combined with the spectrum in (13) and written in the state-space representation by

$$ {\displaystyle \begin{array}{l}\dot{\mathbf{q}}={\mathbf{A}}_{\mathrm{b}}\mathbf{q}+{\mathbf{E}}_{\mathrm{b}}w\\ {}\mathbf{y}={\mathbf{C}}_{\mathrm{b}}\mathbf{q}\end{array}} $$

(14)

where

$$ {\displaystyle \begin{array}{l}{\mathbf{A}}_{\mathrm{b}}=\left[\begin{array}{cc}\mathbf{A}& {\mathbf{E}\mathbf{C}}_{\mathrm{w}}\\ {}\mathbf{0}& {\mathbf{A}}_{\mathrm{w}}\end{array}\right],{\mathbf{E}}_{\mathrm{b}}=\left[\begin{array}{c}0\\ {}{\mathbf{B}}_{\mathrm{w}}\end{array}\right],\kern0.5em \mathbf{A}=\left[\begin{array}{cc}\mathbf{0}& \mathbf{I}\\ {}-{\mathbf{M}}^{-1}\mathbf{K}& -{\mathbf{M}}^{-1}\mathbf{C}\end{array}\right],\mathbf{E}=\left[\begin{array}{c}0\\ {}-1\end{array}\right]\\ {}\mathbf{q}=\left[\begin{array}{c}\mathbf{x}\\ {}\boldsymbol{\upeta} \end{array}\right],\mathbf{x}={\left[{x}_1\kern0.5em {x}_2\kern0.5em {\dot{x}}_1\kern0.5em {\dot{x}}_2\right]}^{\mathrm{T}},\mathbf{y}=\left[\begin{array}{c}{x}_1\\ {}{\ddot{x}}_2+{\ddot{x}}_{\mathrm{g}}\end{array}\right],{\mathbf{C}}_{\mathrm{b}}=\left[\begin{array}{cccccc}1& 0& 0& 0& 0& 0\\ {}\frac{k_2}{m_2}& -\frac{k_2}{m_2}& \frac{c_2}{m_2}& -\frac{c_2}{m_2}& 0& 0\end{array}\right]\end{array}} $$

The responses considered in (14) are the displacement of the base isolation system and the absolute floor acceleration of the superstructure. To obtain the optimally modified weighting ϕ, the H_∞-norm based objective function is given by

$$ {J}_{\varphi}\left(\beta, \varphi \right)={\left(\ {\left\Vert \beta {x}_1\right\Vert}_{\infty}\right)}^2+{\left(\ {\left\Vert {\ddot{x}}_2+{\ddot{x}}_{\mathrm{g}}\right\Vert}_{\infty}\right)}^2 $$

(15)

where β is a parameter that accounts for the order of magnitude between two types of measurements. The objective function in (15) can be minimized by the gradient-based optimization method (Conn et al. 2009). Note that β can be limited to a specific range to obtain a more realistic solution. For simplicity, this study employs β = 1. Finally, the stiffness and damping coefficient in (10) are optimally determined if the solution ϕ to minimize (15) is obtained.

3 Parametric study

The proposed design method is established to concurrently determine the stiffness and damping coefficient in a base isolation system using the LQR control algorithm and H_∞-norm response minimization by (5) and (15). In this method, the dynamic properties of the superstructure are assumed to be known, while the mass of the base isolation system is predetermined. A MDOF superstructure is first reduced to a SDOF structure by the modal approach (Ramallo et al. 2002). An additional DOF is given to the base isolation system. The LQR control algorithm derives the stiffness and damping coefficient of the isolation system based on the dynamics of the SDOF superstructure. These two parameters are formed as a function of modified weighting ϕ in (10–12). Given a Kanai-Tajimi earthquake spectrum, an optimization process is subsequently performed to minimize a trade-off objective function in (15), which is formed by the H_∞-norm responses of the base-isolated building. Finally, the stiffness and damping coefficient are optimally determined for the base-isolated building. In the following, the effect of superstructure dynamics on the design of base isolation systems is parametrically studied.

The Kanai-Tajimi spectrum used in this parametric study is first presented. Four sets of earthquake records including both horizontal components are employed to generate the spectrum. These four sets of earthquake records are selected from the 1999 Chi-Chi earthquake at the stations of CHY014, CHY028, CHY088, and TCU071. These stations are assumed to be close enough to each other and can represent the far-field earthquake records. Then, these eight records are scaled to match the design spectrum using the method proposed by Lilhanand and Tseng (1988), and the damping ratio used in the design spectrum is 5%. The Kanai-Tajimi spectrum is consequently fitted by these scaled earthquake and has ω_g = 15 rad/s and ζ_g= 0.4. The fitting results of scaled earthquake records to the design spectrum and Kanai-Tajimi spectrum are shown in Fig. 3.

Fig. 3

Results of scaled earthquakes that fit (a) design spectrum and (b) Kanai-Tajimi spectrum

The effect of natural frequencies and damping ratios of superstructures is explored with the mass ratio $\frac{m_1}{m_2}$ fixed to 0.2. The natural frequencies ω₂ of superstructures range from 0.2 Hz to 3.5 Hz, while the damping ratios of superstructures ζ₂ range from 0.5% to 10%. Figure 4 exhibits the results of the parametric analysis. Note that because flexible isolation systems make the fundamental frequency of buildings away from the dominate frequency content of earthquakes, only the resulting natural frequencies and damping ratios in the 1st mode are investigated in this parametric study. A superstructure with a high natural frequency and damping ratio results in high stiffness and a low damping coefficient for the base isolation system. For a base-isolated building, a flexible superstructure results in a low natural frequency and damping ratio in the 1st mode. A stiff superstructure with a low damping ratio yields a high damping ratio in the 1st mode. A base-isolated building with a high resulting damping ratio in the 1st mode generates a low floor acceleration, while a stiff, highly damped superstructure results in a low base displacement. The modified weighting ϕ in this analysis ranges from 40 to 1.24 × 10⁵ (rad/s)⁴ which corresponds with a flexible, lightly damped superstructure to a stiff, highly damped superstructure, respectively. The variation of ϕ for a superstructure with certain stiffness is little.

Fig. 4

Effect of natural frequencies and damping ratios of superstructures: (a) natural frequencies and (b) damping ratios of isolation systems, resulting (c) natural frequencies and (d) damping ratios of base-isolated buildings in the 1st mode, H_∞-norm responses of (e) base displacements and (f) floor accelerations, and (g) modified weighting ϕ

The effect of natural frequencies ω₂ of superstructures and mass ratios $\frac{m_1}{m_2}$ is then studied as all superstructures have a fixed damping ratio ζ₂ to 5%. The natural frequencies of superstructures range from 0.2 Hz to 3.5 Hz, while the mass ratios range from 1% to 40%. Figure 5 shows the results of this parametric analysis. Note that some discontinuous points in these plots are due to the convergent issue in the optimization process to (15). (15) is a non-smooth function. When performing the gradient-based optimization algorithm, the results may be obtained from local minimums. To improve the results, the genetic algorithm or pattern search filter algorithm can be employed. As seen in this figure, a flexible, lightweight superstructure results in an isolation system with low stiffness and high damping. The resulting natural frequencies in the 1st mode for base-isolated buildings are almost proportional to the natural frequencies of superstructures. The resulting 1st-mode damping ratios of base-isolated buildings almost only depends on the mass ratios. A stiff, lightweight superstructure renders a small base displacement, while a lightweight superstructure yields a small floor acceleration. The modified weighting ϕ in this analysis ranges from 40 to 1.17 × 10⁶ (rad/s)⁴, and this weighting is mostly relevant to the natural frequencies of base isolation systems.

Fig. 5

Effect of natural frequencies of superstructures and mass ratios $\frac{m_1}{m_2}$: (a) natural frequencies and (b) damping ratios of isolation systems, resulting (c) natural frequencies and (d) damping ratios of base-isolated buildings in the 1st mode, H_∞-norm responses of (e) base displacements and (f) floor accelerations, and (g) modified weighting ϕ

The last parametric analysis discusses the effect of damping ratios ζ₂ of superstructures and mass ratios $\frac{m_1}{m_2}$as all superstructures have a fixed natural frequency ω₂ equal to 3.2 Hz. The damping ratios of superstructures range from 0.5% to 10%, while the mass ratios range from 1% to 40%. Figure 6 displays the results of this parametric analysis. A lightly-damped, lightweight superstructure produces a flexible, highly-damped isolation system. Meanwhile, a lightly-damped isolation system is generated from a highly-damped, lightweight superstructure. A lightly-damped, heavy superstructure yields a low 1st-mode natural frequency in a base-isolated building, while a lightly-damped, lightweight superstructure results in a high 1st-mode damping ratio in a base-isolated building. The base displacements and floor accelerations disproportionate to the resulting natural frequencies and damping ratios in the 1st mode of base-isolated buildings. The modified weighting ϕ in this analysis ranges from 1.57 × 10⁴ to 1.46 × 10⁶ (rad/s)⁴. A highly-damped, heavy superstructure requires a higher modified weighting in the optimization process.

Fig. 6

Effect of damping ratios of superstructures and mass ratios $\frac{m_1}{m_2}$: (a) natural frequencies and (b) damping ratios of isolation systems, resulting (c) natural frequencies and (d) damping ratios of base-isolated buildings in the 1st mode, H_∞-norm responses of (e) base displacements and (f) floor accelerations, and (g) modified weighting ϕ

To sum up, the proposed method yields reasonable base isolation systems to be obtained. For example, a base-isolated building, which has a superstructure with a 3-Hz natural frequency and a 5% damping, has a 1st-mode natural frequency and damping ratio equal to 0.41 Hz and 26% as the isolation mass is 20% of the superstructure mass. Moreover, the modified weighting ϕ is relatively irrelevant to the damping ratio of superstructures from the findings in Fig. 5-(g) and can be roughly estimated by

$$ \phi ={10}^{-0.006{\omega}_2^2+0.268{\omega}_2+1.880} $$

(16)

where ω₂ is in rad/s. When the mass ratio $\frac{m_1}{m_2}$ is between 10 and 25%, (16) yields a base isolation system with decent performance. Note that the Kanai-Tajimi spectrum is assumed to slightly affect the results in (16).

4 Numerical example

In this example, control effectiveness of the isolated buildings designed by the proposed method is evaluated and compared to the previous study (Ramallo et al. 2002). The building used in this study is a five-story, shear-type building, which was designed and analyzed by Kelly et al. (1987). In design, Ramallo et al. (2002) provided a reduced-order SDOF model for the superstructure, consisting of m₂ = 29, 485 kg, c₂ = 23.71 kN-s/m, and k₂ = 11, 912 kN/m. The example exploits this reduced-order model to design base isolation systems, while the five-story building with these base isolation systems is utilized for seismic performance evaluation.

4.1 Design of Base Isolation Systems

The mass of the base isolation systems is fixed to 6800 kg which makes $\frac{m_1}{m_2}=0.23$ same as the isolation system in Ramallo et al. 2002. The SDOF model of the superstructure yields ω₂ = 3.2 Hz and ζ₂ = 2%. With the information, the stiffness and damping coefficient of the base isolation systems can be presented as a function of ϕ by (10). In this study, four types of base isolation systems are developed for comparison, and the detailed are described in the following:

• 1. Type I: the optimal design by minimizing the objective function in (15), resulting in k₁ = 263.90 kN/m and c₁ = 54.69 kN-s/m. The optimal modified weighting ϕ is 3.29 × 10⁴ (rad/s)⁴.

• 2. Type II: the isolation system is derived from the rough design by (16), resulting in k₁ = 534.01 kN/m and c₁ = 79.93 kN-s/m. The resulting modified weighting ϕ is 6.96 × 10⁴ (rad/s)⁴.

• 3. Type III: the isolation system, which is developed by Ramallo et al. 2002, comprises of k₁ = 232 kN/m and c₁ = 3.74 kN-s/m.

• 4. Type IV: the isolation system is modified from the Type III system by increasing the damping coefficient to c₁ = 36.71 kN-s/m.

The Type I and Type II base isolation systems are designed with the Kanai-Tajimi spectrum used in the parametric study. One of good measures to assess the design of isolation systems is the effective natural frequency ω_eff and damping ratio ζ_eff, defined by

$$ {\omega}_{\mathrm{eff}}=\sqrt{\frac{k_1}{m_1+{m}_2}},{\zeta}_{\mathrm{eff}}=\frac{c_1}{2\sqrt{k_1\left({m}_1+{m}_2\right)}} $$

(17)

(17) computes the natural frequency and damping ratio with the assumption that the superstructure is a rigid body (Kelly 1986). Table 1 lists the effective natural frequencies and damping ratios and the performance indices calculated by (15) from these four types of base isolation systems. As a result, the Type I, Type II, and Type IV systems have very similar performance.

Table 1 Dynamic properties of four types of base isolation systems

4.2 Modal analysis of base-isolated five-story buildings

The first three mode shapes of the base-isolated buildings are explored and compared to each other. In this modal analysis, the natural frequencies of the Type I to Type IV isolated buildings are 0.427, 0.605, 0.400, and 0.400 Hz in the first mode and 5.466, 5.490, 5.465, and 5.464 Hz at the second mode. The damping ratios of the Type I to Type IV isolated buildings are 27.5%, 27.7%, 2.0%, and 19.7% in the first mode and 6.8%, 8.4%, 3.6%, and 5.7% in the second mode. Figure 7 shows the complex mode shapes of the superstructure relative to the base isolation and the modal amplitude of the roof to the base. As can be seen, the damping can introduce phase lags among all degrees of freedom, in particular of the third mode. The phase lags yield the maximum responses to be achieved at different times, resulting in reduced base shears for base-isolated buildings. Moreover, the modal amplitudes between the base and roof are almost the same among these four types. The design of damping coefficients therefore plays an important role of mitigating seismic responses of base-isolated buildings.

Fig. 7

Mode shapes of isolated building with Type I-Type IV isolation systems: relative mode shapes of superstructures to the base in the (a) first mode, (b) second mode, and (c) third mode and (d) modal amplitude from the roof to the base

4.3 Frequency-domain analysis

To understand the seismic effect, transfer functions calculated from the system in (14) are investigated. The Kanai-Tajimi spectrum used in this analysis is the same as the one in the parametric study. Figure 8 exhibits the base displacement and roof acceleration transfer functions of the fixed-base and base-isolated buildings. As seen in this figure, the Type I base isolation system better mitigates the roof acceleration at the first pole, while the Type II system performs a better reduction on the base displacement. Moreover, the isolation systems with higher damping would increase the high-frequency components (i.e., the components after the first pole), especially for roof accelerations.

Fig. 8

Comparison on transfer functions among the fixed-base and four base-isolated buildings: (a) base displacement and (b) roof acceleration

4.4 Time-domain dynamic analysis

In time-domain dynamic analysis, both linear and nonlinear base-isolated buildings are investigated. The linear dynamic analysis provides the validation of the optimal design for base isolation systems, while the nonlinear dynamic analysis explores the potential to utilize the optimal design result for determining the LRB parameters by (18). Furthermore, the input excitation considered in this time-domain dynamic analysis include the unscaled 1999 Chi-Chi far-field earthquake records at the stations of CHY014, CHY028, CHY088, and TCU071 and the near-fault records at the stations of TCU052, TCU065, TCU076, and TCU102. Both east-west and north-south components in these earthquake records are employed to evaluate seismic performance of these four base isolated buildings.

Fig. 9 presents the performance results of linear base-isolated buildings by observing base displacement and roof acceleration responses. Moreover, the maximum and root-mean-square (RMS) responses are investigated. As shown in this figure, the base-isolated buildings with the Type I and Type II isolation systems better decrease maximum base displacements under both far-field and near-fault excitations. In some cases, the base-isolated building with the Type III isolation system provides superior performance to reduce maximum roof accelerations under far-field excitation. When the input excitation is near-fault, the base-isolated buildings with the Type I and Type III isolation systems have a better reduction on maximum roof accelerations. In terms of RMS responses, the base-isolated buildings with the Type I and Type II isolation systems yield smaller base displacements. The base-isolated buildings with the Type I and Type IV isolation systems have quite similar performance of reducing roof accelerations, especially when subjected to near-fault earthquakes. By comparing the RMS measurements, the averaged base displacement and roof acceleration ratios of the Type I to Type II systems are 1.41 and 0.70 under far-field excitations and 1.55 and 0.77 under near-fault excitations. Meanwhile, the averaged base displacement and roof acceleration ratios of the Type I to Type IV systems are 0.79 and 1.10 under far-field excitations and 0.79 and 0.98 under near-fault excitations. Therefore, the optimally designed isolation system demonstrates the capability of reducing roof accelerations while maintaining acceptable base displacements. In addition, the rough design by using the modified weighting ϕ in (16) offers decent performance among these structures.

Fig. 9

Performance of base-isolated buildings subjected to (a) far-field earthquakes and (b) near-fault earthquakes

The potential to design LRBs using the design outcomes from the proposed method is then investigated. In simulation, the superstructure always behaves linearly. In these four isolation systems, the isolation bearings are modeled by the bilinear hysteretic curve as shown in Appendix Fig. 11. The parameters used to simulate LRBs are listed in Appendix Table 2. Moreover, the Type I, Type II, and Type IV systems require added viscous dampers with a total damping coefficient of 44.9, 66.0, and 27.5 kN-sec/m, respectively. Figure 10 presents the performance results of nonlinear base-isolated buildings in terms of base displacement and roof acceleration responses. When the base-isolated buildings are subjected to the far-field earthquakes, the Type II isolation system renders a better reduction on base displacements. All base isolation systems except for the Type III system produce base displacements within the design limit (i.e., 0.15 m). The Type I isolation system generates similar performance to the Type IV system for roof accelerations, whereas the Type I system has better performance than the Type IV system in terms of base displacements. When the base-isolated buildings are under near-fault earthquake excitation, the buildings with highly damped isolation systems (i.e., the Type I and Type II systems) yield a better reduction on base displacements. However, the isolation systems with appropriate damping coefficients, i.e., the Type I and IV systems, produce better performance on roof accelerations. Most base displacements exceed the design limit, and the Type II isolation system no longer better mitigates roof accelerations. In sum, the proposed method shows potential for designing a base isolation system with LRBs and viscous dampers. The Type I isolation system still yields a good reduction on base displacements as well as remains similar roof accelerations with the Type IV isolation system. For the far-field earthquakes, the Type II isolation system maintains a decent performance as compared to the Type I and Type II systems.

Table 2 Parameters of LRB bearings

Fig. 10

Performance of base-isolated buildings with LRBs subjected to (a) far-field earthquakes and (b) near-fault earthquakes

5 Conclusions

In this research, a new design method has been developed to concurrently determine the stiffness and damping coefficient in a base isolation system. This design method considered the superstructure as a SDOF building and included the seismic characteristics by the Kanai-Tajimi spectrum. The stiffness and damping coefficient were then formed as a function of single modified weighting, while the optimal weighting can be obtained by minimizing the H_∞-norm responses of base displacement and roof acceleration. A parametric study was carried out to investigate the effect of superstructures to the resulting isolation systems designed by the proposed method. A numerical example was provided to demonstrate the effectiveness of the proposed method for linear base isolation systems as well as to exhibit the feasibility of designing LRBs with added viscous dampers based on the optimally linear isolation system. Consequently, the proposed design method yielded a superior base isolation system that maintain roof accelerations at a lower level while producing reduced base displacements.

In this design method, the stiffness and damping coefficient in a base isolation system were obtained as a function of modified weighting in the H₂-norm sense, while the optimal weighting was then determined in the H_∞-norm sense. Thus, both energy and peak response reductions were considered in design. The parametric study showed that the optimal weighting was mostly relevant to the natural frequency of the superstructure and slightly affected by the mass ratio between the superstructure and base isolation system. A design equation was also proposed to roughly determine a weighting that yielded decent performance for the base isolation system. In numerical example, four types of base isolation systems were discussed. In the modal analysis, these four systems rendered very similar performance. The optimal isolation system (i.e., the Type I system) had a better reduction on the roof acceleration transfer function at the first pole. The linear dynamic analysis indicated that the optimal design can better decrease base displacements and roof accelerations. In the nonlinear dynamic analysis, the optimal design had quite similar performance as the results in the linear analysis. The rough design by (16) still produced descent performance that allowed users avoiding the optimization process in (15).

Appendix

1.1 Design of Lead-Rubber Bearings

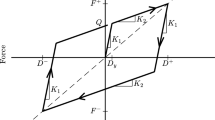
Each type of base isolation system are assumed to comprise of four LRBs. These LRBs are modeled by a bilinear hysteretic loop as illustrated in Appendix Fig. 11. In the LRB modelling, a maximum displacement D₂ should be determined in advance. The preyield to postyield stiffness ratio α is fixed to 13, while the equivalent damping ratio ζ_b is up to 5%. The equivalent stiffness in this modelling is identical to the designed stiffness k₁. If the designed damping coefficient c₁ exceeds ${\overline{c}}_1$ that the LRBs can provide, the remaining damping coefficient (i.e., ${c}_1-{\overline{c}}_1$) is realized by viscous dampers. Therefore, the preyield stiffness K_u and postyield stiffness K_d are determined by

$$ {\displaystyle \begin{array}{l}{K}_d=\frac{k_1{D}_2}{n_{\mathrm{iso}}\left({D}_2-\left(1-\alpha \right){D}_1\right)},{K}_u=\alpha {K}_d\\ {}{\zeta}_b=\frac{{\overline{c}}_1}{2\sqrt{k_1\left({m}_1+{m}_2\right)}}=\frac{4Q\left({D}_2-{D}_1\right){n}_{\mathrm{iso}}}{2\pi {k}_1{D}_2}\le 5\%,{\overline{c}}_1\le {c}_1\end{array}} $$

(18)

where n_iso is the number of LRBs used in a base isolation system. Note that (18) would result in two sets of parameters, and this study selects the set with a smaller D₁. This LRB model with D₂ = 0.15 m is then employed to perform nonlinear dynamic analysis. The LRBs used in these four types of isolation systems are listed in Appendix Table 2.

Fig. 11

Illustration of bilinear hysteretic model for modelling of lead-rubber bearing