An Optimal Data Fusion Algorithm Based on the Triple Integration of PPP-GNSS, INS and Terrestrial Ranging System

Abstract

This paper describes the integration of Locata, GNSS and INS technologies within a loosely-coupled triple integration algorithm. The conventional methods for multi-sensor integration can be classified as either centralised filtering or decentralised filtering. Centralised Kalman filtering (CKF) provides globally optimal state estimation by directly combining measurement data. However CKF system has some disadvantages such as a comparatively large computational burden and poor fault detection and isolation ability. Decentralised Kalman filtering (DKF) addresses such defects while aiming to achieve the same accuracy as a centralised filter. On the other hand global optimal filtering (GOF) can achieve a higher accuracy than the traditional CKF because it utilises more information resources than the CKF. In the information space, the information resources that can be used for estimation include the measurements, the local predictions, and the global predictions. In order to evaluate the system performance, a field experiment was conducted on a vehicle with different kinds of maneuvers, including circular motion and accelerated motion. The results indicate that: (1) GOF-based PPP-GNSS/Locata/INS integration system can provide better positioning accuracy compared with CFK and federated Kalman filtering; (2) covariance analysis shows that the GOF improves the system estimation covariance; and (3) a comparison of GOF with local filters confirms the superiority of a GOF-based triple integration system.

1 Introduction

Although Global Navigation Satellite System (GNSS) technology has been widely used to satisfy positioning and navigation requirements in many application fields, the major disadvantage of GNSS still remains: signal blockage due to obstructions, and power attenuation of the signals when operated indoors. The combination of GNSS with other sensors, such as a self-contained inertial navigation system (INS), provides an ideal position and attitude determination solution which can not only mitigate the weakness of GNSS, but also bound the INS error that otherwise would grow with time when the INS operates alone. However, the navigation accuracy provided by GNSS/INS is strongly dependent on the quality and geometry of the GNSS observations, the INS technology used, and the integration model applied.

In general, with limited GNSS availability, the navigation accuracy can only be maintained at the metre-level for no more than a few minutes even if a reasonably high quality INS is used. Many advanced fusion algorithms have been investigated to mitigate this problem however during longer GNSS outages navigation solutions may not meet the accuracy requirement of the application [1, 2].

It is possible to incorporate an auxiliary sensor system to augment GNSS/INS navigation. “Locata” is a terrestrial, radio-frequency based technology which uses a local “constellation” of signal transmitters to provide continuously time synchronised ranging signals in difficult GNSS environments, such as where there is poor satellite geometry: signal blockages in tunnels, urban canyons, and deep open-cut mines etc.

In this paper, in order to satisfy accuracy and reliability performance parameters, GNSS, based on the precise point positioning (PPP) data processing methodology, and Locata are integrated with an INS to provide robust global navigation solutions.

The fundamental challenge of integrated navigation systems is information fusion. The commonly used method is the centralised Kalman filtering (CKF) [3, 4] which ensures globally optimal state estimation by processing all sensor measurements at a central site. However, the CKF can result in a large computational burden and large data memory demands [5]. From the point of view of fault tolerance, the centralised complementary Kalman filter is not convenient to adaptively detect and isolate sensor faults, thus CKF-based navigation systems have limited reliability [6, 7].

Another approach is based on decentralised Kalman filtering (DKF), where the information from local estimators can yield global optimal or sub-optimal state estimation according to certain information fusion criteria. The advantage of this approach is that the communications load and processing demands are decreased, and the input data rates could be increased due to the use of parallel structures. Moreover, decentralised filtering leads to easy fault detection and isolation. Recently developed multi-sensor data fusion via the information space approach has shown that the global optimal filtering (GOF) can achieve a higher accuracy than the traditional CKF [8]. In order to take advantage of decentralised filtering and to improve the estimation accuracy, the GOF approach is applied in this paper. According to the information space concept, the optimal data fusion can be expressed as the projection of the state vector to all kinds of information spaces. Thus the more information resources are utilised, the better the system performance. In the information space, the measurements, the local predictions, and the global predictions are resources for the estimation process. The GOF utilises all the information resources, and hence differs from the traditional CKF and the Federated Kalman filter (FKF) that utilise only a portion of the available information resources.

In this paper GOF is applied to implement a PPP-GNSS/Locata/INS integrated navigation algorithm. This approach overcomes the disadvantages of conventional decentralised fusion by utilising all of the information resources. A decentralised estimation fusion method is established for individual integrations of PPP-GNSS and Locata with INS to independently obtain the local predictions and local estimation. The local and global information is further fused to generate the global optimal state estimation of the triple-integrated navigation system. Experimental results are presented to demonstrate the performance of the proposed method.

2 System Model and Conventional Fusion Algorithms

INS is used to establish the inertial navigation model. The system dynamic equation is described by:

$$ \dot{X}\left( t \right) = F\left( t \right)X\left( t \right) + W\left( t \right) $$

(43.1)

where $X\left( t \right)$ is the state vector of the system, $F\left( t \right)$ is the dynamic matrix of the system, $W\left( t \right)$ is the system noise. $X\left( t \right)$ is defined as:

$$ \begin{aligned} X\left( t \right) = & [\psi_{N} ,\psi_{E} ,\psi_{D} ,\delta r_{N} ,\delta r_{E} ,\delta r_{D} ,\delta v_{N} ,\delta v_{E} ,\delta v_{D} ,\varepsilon_{x} ,\varepsilon_{y} ,\varepsilon_{z} , \\ & \;\,{\nabla }_{x} ,{\nabla }_{y} ,{\nabla }_{z} ,\delta \eta_{Lx} ,\delta \eta_{Ly} ,\delta \eta_{Lz} ,\delta \eta_{Gx} ,\delta \eta_{Gy} ,\delta \eta_{Gz} ]^{T} \\ \end{aligned} $$

(43.2)

where $\left( {\psi_{N} ,\psi_{E} ,\psi_{D} } \right)$ is the attitude angle error, $\left( {\delta r_{N} ,\delta r_{E} ,\delta r_{D} } \right)$ is the position error, $\left( {\delta v_{N} ,\delta v_{E} ,\delta v_{D} } \right)$ is the velocity error, $\left( {\varepsilon_{x} ,\varepsilon_{y} ,\varepsilon_{z} } \right)$ is the gyroscope’s constant bias, $\left( {{\nabla }_{x} ,{\nabla }_{y} ,{\nabla }_{z} } \right)$ is the accelerator’s bias, $\left( {\delta \eta_{Lx} ,\delta \eta_{Ly} ,\delta \eta_{Lz} } \right)$ is the Locata lever arm components with respect to the inertial measurement unit (IMU) centre, $\left( {\delta \eta_{Gx} ,\delta \eta_{Gy} ,\delta \eta_{Gz} } \right)$ is the GNSS lever arm estimation with respect to the IMU centre.

The observation information of the integrated PPP-GNSS/Locata/INS system includes the position and velocity (PV) information from Locata and PPP-GNSS, and PV information from the INS. For centralised filtering, the measurements are described by the stacked observation vector:

$$ Z\left( t \right) = \left[ {Z_{L} ,Z_{G} } \right]^{T} = \left[ {r_{L} - r_{INS} ,v_{L} - v_{INS} ,r_{G} - r_{INS} ,v_{G} - v_{INS} } \right]^{T} $$

(43.3)

The system observation equation can be written as:

$$ Z\left( t \right) = H\left( t \right)X\left( t \right) + V\left( t \right) $$

(43.4)

where $H\left( t \right)$ and $V\left( t \right)$ are the observation matrix and observation noise of the integrated navigation system respectively.

Applying the discrete process, the system Eqs. (43.1) and (43.3) become:

$$ x\left( k \right) = F\left( k \right)x\left( {k - 1} \right) + \omega \left( k \right) $$

(43.5)

$$ z\left( k \right) = H\left( k \right)x\left( k \right) + v\left( k \right) $$

(43.6)

It is assumed that $\omega \left( k \right)$, $v\left( k \right)$ are zero-mean white sequences uncorrelated with each other, and $E\left[ {\omega \left( k \right)\omega \left( k \right)^{T} } \right] = Q\left( k \right)$, $E\left[ {v\left( k \right)v\left( k \right)^{T} } \right] = R\left( k \right)$. The initial state $x\left( 0 \right)$ is a zero-mean Gaussian random vector, $x\left( 0 \right)\sim N\left( {\bar{x}\left( 0 \right),P\left( 0 \right)} \right)$, and is independent of $\omega \left( k \right)$ and $v\left( k \right)$.

The Kalman filter algorithm is composed of time and measurement updates. The prediction of the state $\vec{x}\left( k \right)$, and its covariance matrix $\vec{P}\left( k \right)$, are obtained from the time-updating step:

$$ \vec{x}\left( k \right) = F\left( k \right)\hat{x}\left( {k - 1} \right) $$

(43.7)

$$ \vec{P}\left( k \right) = F\left( k \right)\hat{P}\left( {k - 1} \right)F^{T} \left( k \right) + Q\left( k \right) $$

(43.8)

When the measurements are available the state vector $\hat{x}\left( k \right)$ is updated as:

$$ K\left( k \right) = \vec{P}\left( k \right)H^{T} \left( k \right)\left[ {H\left( k \right)\vec{P}\left( k \right)H^{T} \left( k \right) + R\left( k \right)} \right]^{ - 1} $$

(43.9)

$$ \hat{P}\left( k \right) = \left[ {I - K\left( k \right)H\left( k \right)} \right]\vec{P}\left( k \right) $$

(43.10)

$$ \hat{x}\left( k \right) = \vec{x}\left( k \right) + K\left( k \right)\left[ {z\left( k \right) - H\left( k \right)\vec{x}\left( k \right)} \right] $$

(43.11)

where $K\left( k \right)$ is the Kalman gain, and $\hat{P}\left( k \right)$ is the covariance matrix of the state.

For a decentralised system, the sub-systems for the Locata and GNSS sensors independently observe the output of the INS. The two local filters estimate the state of the INS using the observed data. Since the two local filters share the INS navigation model, the dynamic equations of the two local systems are the same. The model of the ith (i = 1, 2) local filter is described by the following equations:

$$ x\left( k \right) = F\left( k \right)x\left( {k - 1} \right) + \omega \left( k \right) $$

(43.12)

$$ z_{i} \left( k \right) = H_{i} \left( k \right)x\left( k \right) + v_{i} \left( k \right) $$

(43.13)

where $z_{i} \left( k \right)$ is the output of the ith subsystem, and $v_{i} \left( k \right)$ is the measurement noise of the local system, which is assumed to be white noise. The covariance of the measurement noise in the local filter is defined by the general accuracy of the local Locata and PPP-GNSS solutions, which is set in this evaluation as:

$$ \begin{aligned} R_{Locata} & = diag\left({\begin{array}{*{20}c} {\left( {0.2} \right)^{2} } & {\left( {0.3} \right)^{2} } & {\left( {0.1} \right)^{2} } & {\left( {0.1} \right)^{2} } & {\left( {0.1} \right)^{2} } & {\left( {0.1} \right)^{2} } \\ \end{array} } \right) \\ R_{PPP - GNSS} & = diag\left({\begin{array}{*{20}c} {\left( {0.2} \right)^{2} } & {\left( {0.1} \right)^{2} } & {\left( {0.1} \right)^{2} } & {\left( {0.1} \right)^{2} } & {\left( {0.1} \right)^{2} } & {\left( {0.1} \right)^{2} } \\ \end{array} } \right) \\ \end{aligned} $$

Each local filter generates the optimal estimation of the local state by using the Kalman filter formulas (43.7)–(43.11).

After completing the computations of the two decentralised local filters, two local optimal state estimations $\hat{x}_{1} (k)$ and $\hat{x}_{2} (k)$ can be obtained and further fused using the global filter.

3 GOF for PPP-GNSS/Locata/INS Integrated Navigation

The multi-sensor optimal estimation is resolved in two approaches, in terms of the random vector space (RVS) approach and the information space approach [8]. In the RVS framework, the sources of information have been identified and used as the bases of the space. The estimation is mathematically described as the procedure for finding the projection of the state vector on the bases of the space. The fusion algorithm therefore describes how the global state estimate is combined by the projections and associated bases.

Differing from the RVS approach, from the point of view of the information space, optimal fusion is implemented by a series of transformations between the information spaces. The transformations map the source information vectors from the measurement information spaces to the estimate information space to produce the fused information vector. The information space approach provides a means by which the accuracies of different algorithms can be compared on a theoretical basis.

As the RVS approach is similar to the widely applied Kalman filtering forms, it is used below to discuss the nature of GOF.

Assume a linear discrete system $\hat{x}_{i} \left( {{\text{i}} = 1, 2, \ldots ,{\text{n}}} \right)$ is the unbiased estimators of the stochastic vector $x$. If $\hat{x}_{i}$ are orthogonal vectors, the estimate of $x$ can be expressed as the sum of the projection of $\hat{x}_{i}$ in a random vector space (RVS) $\Theta$ [8]:

$$ \Theta = \left\{ {\hat{x}|\hat{x} = \sum\limits_{i = 1}^{n} {C_{i} \hat{x}_{i} } } \right\} $$

(43.14)

The optimal state estimation and its covariance can be written as:

$$ \hat{x} = \hat{P}\left( {\sum\limits_{i = 1}^{n} {S_{i}^{T} \hat{P}_{i}^{ - 1} \hat{x}_{i} } } \right) $$

(43.15)

$$ \hat{P} = \left( {\sum\limits_{i = 1}^{n} {S_{i}^{T} \hat{P}_{i}^{ - 1} S_{i} } } \right)^{ - 1} $$

(43.16)

where $S_{i}$ is the mapping matrix between $\hat{x}$ and $\hat{x}_{i}$, and $\hat{x}_{i} = S_{i} \hat{x}$; $\hat{P}_{i}$ is the corresponding posteriori estimate error covariance of $\hat{x}_{i}$, which is calculated epoch by epoch to the convergence status. The initial setting of $P_{i}$ does not affect the estimate convergence, and it can be set according to the approximate accuracy of initial $x_{i} \left( 0 \right)$. It can be seen that the more information that is used, represented here as $\hat{x}_{i}$, the smaller the trace of $\hat{P}$ that is obtained. Hence the system could have improved performance.

For a better understanding, recall the Kalman filter’s measurement updating Eq. (43.11). This prediction form indicates that the state prediction is corrected when the measurement is made available. It can be rewritten in the following fusion form:

$$ \hat{x}\left( k \right) = \left[ {I - K\left( k \right)H\left( k \right)} \right]\vec{x}\left( k \right) + K\left( k \right)z\left( k \right) $$

(43.17)

It also can be regarded as the random vector space below [8]:

$$ \Theta = \left\{ {\hat{x}|\hat{x} = C_{1} \vec{x} + C_{2} \left( k \right)z} \right\} $$

(43.18)

where $C_{1} = \hat{P}\vec{P}^{ - 1}$, and $C_{2} = \hat{P}H^{T} R^{ - 1}$

The estimation $\hat{x}$ can be seen as a point or vector in the space $\Theta$, which is expressed as the projections $C_{1}$ and $C_{2}$ on the bases of $\vec{x}$ and $z$.

Similarly, the RVS of the CKF can be expanded by the measurements $z_{1}$, $z_{2}$ and the global prediction $\vec{x}$:

$$ \varTheta_{CKF} = \left\{ {\hat{x}|\hat{x} = C\vec{x} + C_{1} \left( k \right)z_{1} + C_{2} \left( k \right)z_{2} } \right\} $$

(43.19)

where $C = \hat{P}\vec{P}^{ - 1}$, $C_{1} = \hat{P}H_{1}^{T} R_{1}^{ - 1}$, $C_{2} = \hat{P}H_{2}^{T} R_{2}^{ - 1}$

An optimal multi-sensor estimation in turn requires information from the bases and the determination of the associated projections. The following random vectors in a multi-sensor system can be used as the bases [8]:

• Measurements: $z_{i} \left( k \right)$, $i = 1,2$

• Local predictions: $\vec{x}_{i} \left( k \right)$, $i = 1,2$

• Global predictions: $\vec{x}\left( k \right)$

Utilising different sources as the bases of RVS leads to different fusion algorithms. From Eq. (43.19), CKF uses global prediction and all local measurement information, FKF uses local estimates and global prediction. However, in order to ensure the same accuracy of the CKF, the local predictions of the FKF are computed from the global prediction using the so-called information-sharing principle [9, 10].

To further improve the accuracy of decentralised filtering, the GOF uses all the information sources, including the measurements, the local and global predictions to achieve global optimality, which can be represented as:

$$ \Theta = \left\{ {\hat{x}\left( k \right)|\hat{x}\left( k \right) = \sum\limits_{i = 1}^{2} {a_{i} \left( k \right)\vec{x}_{i} \left( k \right)} + \sum\limits_{i = 1}^{2} {b_{i} \left( k \right)z_{i} \left( k \right)} + c\left( k \right)\vec{x}\left( k \right)} \right\} $$

(43.20)

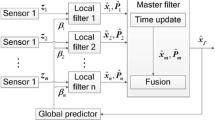
The measurements and the local predictions support local Kalman filtering fusion, thus they can be replaced by the local state estimates. The GOF configuration is shown in Fig. 43.1. The RVS of GOF in Eq. (43.20) can be rewritten as:

$$ \Theta = \left\{ {\hat{x}\left( k \right)|\hat{x}\left( k \right) = c\left( k \right)\vec{x}\left( k \right) + d_{1} \left( k \right)\hat{x}_{1} \left( k \right) + d_{2} \left( k \right)\hat{x}_{2} \left( k \right)} \right\} $$

(43.21)

where $a_{i}$, $b_{i}$, $c$, $d_{1}$ and $d_{2}$ represent the projections of the global estimate vector $\hat{x}$ on the bases.

Fig. 43.1

System configuration of GOF

In Fig. 43.1, one can see both Locata and PPP-GNSS outputs are combined with INS solution in the local filters, thus the local estimates $\hat{x}_{1}$ and $\hat{x}_{2}$ are correlated with previous feedback-INS solution, represents the previous state estimate here. On the other hand, the current global prediction is also computed from the previous global estimate. That means the two local estimates and the current global prediction are oblique to each other, not orthogonal. Therefore these three vectors need to be orthogonalised [8]. The reconstructed orthogonal global prediction and local estimates are represented as $\tilde{x}$ and $\tilde{x}_{i}$:

$$ \tilde{x}_{1} \left( k \right) = \hat{x}_{1} \left( k \right),\,\tilde{x}_{2} \left( k \right) = \hat{x}_{2} \left( k \right),\,\tilde{x}\left( k \right) = \alpha_{1} \hat{x}_{1} \left( k \right) + \alpha_{2} \hat{x}_{2} \left( k \right) + \alpha \vec{x}\left( k \right) $$

(43.22)

The corresponding covariance of reconstructed global prediction is:

$$ \tilde{P}\left( k \right) = \alpha \vec{P}\left( k \right)\alpha^{T} + \sum\limits_{i = 1}^{2} {\alpha_{i} \hat{P}_{i} \left( k \right)} \alpha_{i}^{T} + \sum\limits_{i = 1}^{2} {\alpha \tilde{P}_{i} \left( k \right)} \alpha_{i}^{T} + \sum\limits_{i = 1}^{2} {\alpha_{i} \tilde{P}_{i}^{T} \left( k \right)} \alpha^{T} $$

(43.23)

where

$$ \tilde{P}_{i} = \text{cov} \left( {\vec{x},\tilde{x}_{i} } \right) = F\left( k \right)\hat{P}\left( {k - 1} \right)F^{T} \left( k \right)\vec{P}_{i}^{ - 1} \left( k \right)\hat{P}_{i} \left( k \right) $$

(43.24)

As global prediction $\vec{x}$ and local estimates $\hat{x}_{i}$ are all unbiased estimates, the orthogonalised global prediction $\tilde{x}$ is also unbiased, hence $E\left( {\tilde{x} - x} \right) = 0$, from which one can derive:

$$ \alpha_{1} + \alpha_{2} + \alpha = I $$

(43.25)

Since the reconstructed global prediction $\tilde{x}$ and local estimation $\tilde{x}_{1}$, $\tilde{x}_{2}$ are orthogonal to each other. Thus $\text{cov} \left( {\tilde{x},\tilde{x}_{1} } \right) = 0$, $\text{cov} \left( {\tilde{x},\tilde{x}_{2} } \right) = 0$, from which one can obtains:

$$ \alpha = \left( {I - \tilde{P}_{1} \hat{P}_{1}^{ - 1} - \tilde{P}_{2} \hat{P}_{2}^{ - 1} } \right)^{ - 1} ,\,\alpha_{1} = - \alpha \tilde{P}_{1} \hat{P}_{1}^{ - 1} ,\,\alpha_{2} = - \alpha \tilde{P}_{2} \hat{P}_{2}^{ - 1} $$

(43.26)

According to the optimal state estimation Eq. (43.15) and its covariance Eq. (43.16), the optimal fused global estimation is:

$$ \hat{x}\left( k \right) = \hat{P}\left( k \right)\left[ {\tilde{P}^{ - 1} \left( k \right)\tilde{x}\left( k \right) + \hat{P}_{1}^{ - 1} \left( k \right)\hat{x}_{1} \left( k \right) + \hat{P}_{2}^{ - 1} \left( k \right)\hat{x}_{2} \left( k \right)} \right] $$

(43.27)

$$ \hat{P}\left( k \right) = \left[ {\tilde{P}^{ - 1} \left( k \right) + \hat{P}_{1}^{ - 1} \left( k \right) + \hat{P}_{2}^{ - 1} \left( k \right)} \right]^{ - 1} $$

(43.28)

4 Experiment and Analysis

The integrated test was conducted at Locata’s Numerella Test Facility (NTF), located in a rural area outside of the city of Canberra, Australia. The NTF covers an area of approximately three hundred acres and is ideally suited for real-world navigation system testing area. A number of Locata transmitters were set up to cover the NTF area. The devices that were used in the test include two Leica dual-frequency GNSS receivers (one used as the rover receiver, and the other as the base station), one H764 IMU, and one Locata rover unit. The GNSS antenna and Locata antenna were mounted with the IMU on the top of a truck. The GNSS data rates and Locata data rates were both set to 10 Hz, while the IMU’s data rate was 256 Hz. Both Locata and IMU measurements were synchronised with those from GNSS.

The PPP-GNSS and Locata solutions were post-processed independently. The initial convergence period of PPP-GNSS was excluded from this triple integration evaluation. The GNSS integer ambiguity-fixed differential carrier phase positioning solution computed by the Leica Geo Office (LGO) software was served as the ground-truth as it had a nominal accuracy of a few centimetres. The trajectory of the field test is shown in the Fig. 43.2.

Fig. 43.2

Trajectory from triple-integration system at NTF

The field test included circular motion and accelerated motion. As CKF and FKF provide solutions of the same accuracy, Fig. 43.3 shows the comparison only between the GOF and CKF solutions. Since the experiment was conducted across relatively flat terrain, a vertical constraint was applied to account for the poor vertical component observability of Locata. It can be seen that the vertical solutions of the two systems are almost the same. However in the horizontal north and east directions the GOF provides a more accurate and a smoother solution. In particular during the circular motion from 250 to 600 s, the GOF solution is obviously better. The Radial Spherical Error (MRSE) of the 3D position error is displayed in Table 43.1. The MRSE of the GOF-based triple-integration solution is 0.132 m, which is lower than that of CKF and FKF’s 0.142 m. This is an improvement of 6.4 %.

Fig. 43.3

Position comparison between CKF and GOF solutions

Table 43.1 MRSE comparison of triple-integration system and local systems

The posteriori estimate error covariance $\hat{P}\left( k \right)$ was computed. Figure 43.4 shows the square root of the converged position and velocity error covariance $\sqrt {\hat{P}\left( k \right)}$ of the CKF and GOF during the last 100 s of the test. The blue colour and red colour denote the CKF and GOF solutions respectively. The left three plots compare the position error covariance in the three direction components, and the right three plots are the corresponding velocity error covariance. It can be seen that the GOF estimate position and velocity error covariance are improved for all three directions in comparison with the results of conventional centralised filtering.

Fig. 43.4

Position and velocity precision comparison $\left( {\sqrt {\hat{P}\left( k \right)} } \right)$ between CKF and GOF during the last 100 s of the test

Further comparisons of the solutions of the local systems PPP-GNSS/INS and Locata/INS with respect to the triple-integration system are made. Figure 43.5 shows the position comparison of the two local systems with the GOF solutions. It can be seen that the triple-integration approach provides the best positioning solutions for the horizontal (north and east) direction components. From Table 43.1 it can be seen that the MRSEs of the PPP-GNSS/INS and Locata/INS solutions are 0.144 and 0.192 m respectively, while the MRSE of the GOF-based triple-integration solution is 0.132 m. This is lower than either the PPP-GNSS/INS or Locata/INS solutions.

Fig. 43.5

Position difference comparison between GOF-based triple-integration system and local systems

As in the case of Fig. 43.4, the position and velocity precisions were investigated. The square root of the a posteriori estimate error covariance was also computed. Figure 43.6 shows the comparison of the square root of the estimated covariance for the GOF-based triple-integration system and the local systems during the last 100 s of the test. The triple-integration solution is plotted in red, and those of the local systems PPP-GNSS/INS and Locata/INS are plotted in blue and green respectively. The left three plots are the comparison of the positioning error covariance in three direction components, and the right three plots illustrate the velocity error covariance. It can be seen that the GOF-based triple-integration system has the smallest estimated position and velocity error covariance.

Fig. 43.6

Position and velocity precision comparison between GOF-based triple-integration solution local PPP-GNSS/INS system solution, and local Locata/INS system solution for the last 100 s of the test

5 Concluding Remarks

This paper describes a PPP-GNSS/Locata/INS triple-integration algorithm implemented using a loosely-coupled filtering approach. Conventional centralised filtering and decentralised filtering were discussed. In order to keep the reliability character of decentralised filtering, but to improve its accuracy, the GOF algorithm was developed, based on the recently developed information space concept. The GOF utilises all the information resources, including the raw measurements, the local predictions, and the global predictions. In order to evaluate the system performance, a field experiment was conducted. The comparison between GOF, CKF and FKF triple-integration approaches indicated that the GOF approach does indeed provide the most accurate positioning solution. The a posteriori error covariance for the GOF solution is also smaller than in the case of the other two algorithms. A comparison of the GOF-based triple-integration solution with the local PPP-GNSS/INS and Locata/INS solutions shows that the GOF-based approach is superior to the alternative approaches.