Introduction

Although there will be an increasing number of Global Navigation Satellite System (GNSS) constellations deployed over the next few years, alternative navigation technologies are still of interest because of the shortcomings of GNSS, namely the weak broadcast satellite signal strengths, which makes them vulnerable to be disruption.

In some airborne applications, such as aerial mapping and aircraft landing assistance, the positioning accuracy and/or integrity cannot always be assured since a sufficient number of visible satellite cannot be guaranteed every time and everywhere. Even when satellites at low elevations are tracked, the measurements from these satellites may be contaminated by relatively high atmospheric noise (Lee 2002) or multipath. In CAT II/III aircraft precise approaching and landing, local area augmentation is suggested in order to fulfill stringent accuracy, availability, integrity and continuity requirements. GNSS is the key technology applied in such local area augmentation systems, however GNSS pseudorange-based single point positioning (SPP), or differential carrier phase GNSS (DGNSS) are unable to satisfy such requirements. The integrity of an airport-based local area augmentation system can be seriously threatened by the failure of the DGNSS systems even for short periods of time (Bartone and Graas 1997). Airport pseudolite (APL) technology has been proposed as one approach to address this problem (Lee et al. 2008; Progri and Michalson 2002). However, the challenge of time synchronization and “near-far” effects has limited the application of conventional APLs (Zumberge and Bertiger 1996; Zumberge et al. 1997). Other applications for augmented GNSS include UAV navigation, or land vehicle positioning in urban areas, where GNSS signals may suffer from interference or blockage.

A common means of overcoming such shortcomings is to use other complementary navigation technologies (Donovan et al. 2012; Du et al. 2012). Integration with an Inertial Navigation System (INS) could obviously improve the system performance. Many problems affect the use of INS, such as misalignment, scale factor non-linearity, and temperature-varying biases, and others. The accuracy of an INS will rapidly degrade with time when it operates in standalone mode. In such a case, aiding calibration provided by external sources is necessary to constrain the growth of INS time-dependent errors.

Using ground-based transmitters to augment the GNSS satellite signals is one alternative approach. “Locata” is a terrestrial radio frequency-based technology which was developed by Locata Corporation, in Australia. The fundamental principles of the Locata technology and some earlier testing results can be found in the literature (e.g., Barnes et al. 2004; Li and Rizos 2010; Choudhury et al. 2009; Jiang et al. 2013, 2014). Since Locata is a terrestrial-based system which utilizes GNSS-like signals, the navigation performance with Locata augmentation can be enhanced by virtue of the improved accuracy, availability and integrity (Jiang et al. 2015). Locata could provide stronger signals, signal strengths range from − 60 to − 105 dBm (Locata Corporation 2014), which means that Locata signals can penetrate into buildings and dense forests and provide positioning service in GNSS-denied areas. Vulnerability to signal jamming could also be considerably reduced. Locata’s GNSS-like signals could be synchronize with GNSS, thus making it relatively easy to incorporate measurements on Locata signals in order to improve “satellite” availability. As GNSS satellites can be tracked with an antenna installed on the upper surface of an aircraft, the horizontal geometry is better than the vertical geometry. As Locata is a terrestrial system, the integration of Locata and GNSS could provide better vertical geometry and improve the vertical positioning accuracy. Integrity is enhanced as the integrity warning information can be transmitted in a timely fashion. Furthermore, Locata transmitters can be installed anywhere so as to enhance availability and reliability in situations where the GNSS signals are very weak. In cooperation with Locata Corporation, researchers at the School of Civil and Environmental Engineering, University of New South Wales (UNSW), have developed a hybrid system based on the integration of GNSS, INS and Locata technology (Rizos et al. 2008).

In this study, GNSS and Locata technologies are combined with INS using either a loosely coupled or tightly coupled architecture (Wendel et al. 2006). A loosely coupled integration approach uses the solved position and velocity as the measurement inputs to the integration algorithm, which then uses them to estimate the INS errors. The tightly coupled approach is more complex. Raw pseudorange, carrier phase, and range-rate measurements from GNSS and Locata are input as measurements into the estimation filter. The benefits of the tightly coupled approach are that the system does not need a full GNSS or Locata navigation solution to aid the INS. However, the GNSS, Locata and INS are no longer operated as independent systems, and the navigation solution would only be generated at the central data fusion filter, and there is no inherent standalone GNSS or Locata solution. Moreover, since the central filter needs to handle raw pseudorange, carrier phase and range-rate measurements and INS navigation computation, the algorithms are more complex. On the other hand, the two main advantages of loosely coupled integration are simplicity and redundancy. The architecture is simple because it can be used with any INS and any GNSS/Locata user equipment, making it particularly suited for retrofit applications. Moreover, the standalone GNSS and Locata solutions are usually available, in addition to the integrated solution, which enables basic parallel solution integrity monitoring (Groves 2008). The loosely coupled approach is adopted in this research.

The core component of the multi-sensor navigation system is the data fusion algorithm. Centralized Kalman filtering (CKF) is the conventional data fusion algorithm used for combining the measurements from all local sensors into a common filter, for processing the measurements to achieve global system navigation estimation in a direct manner. However, while the CKF can achieve higher estimation accuracy it has a large communication overhead due to the high-dimensional state computation and the large data memory requirement (Gao et al. 2009). From the point of fault tolerance, CKF is not easily adapted to detect and isolate the sensor faults. The CKF system, therefore, has limited reliability (Lo et al. 2013; Li and Zhang 2010). The decentralized Kalman filtering (DKF) approach has been developed to address such shortcomings (e.g., Lo et al. 2013; Li and Zhang 2010; Li 2014). In contrast to CKF, there is no “central filtering” for the system. The measurements from the local sensors are processed in the local filters to generate local estimates, and these local estimations are then delivered to a master fusion algorithm that generates the global system solution. Since the DKF has a distributed architecture, the communication and computation burden would be decreased compared with CKF, and fault detection and isolation procedures can be more easily implemented using the popular receiver autonomous integrity monitoring (RAIM) approach, as well as other fault detection and isolation approaches (e.g., Hewitson and Wang 2006; Yang et al. 2014).

The recently developed multi-sensor data fusion algorithm based on information space, known as global optimal filtering (GOF), has been shown to achieve, in principle, a higher accuracy compared with the conventional CKF (Li 2014). From the point of view of information space, the fusion process can be described as the sum of the information vectors that are associated with the data resources of the multi-sensor system. Thus, the more information resources that are utilized, a higher system performance can be achieved. Based on this concept, the information resources are classified into three groups: local predictions, global predictions and measurements. The convention CKF and the most commonly used DKF algorithm—the federated Kalman filter (FKF)—both use local measurements and global prediction during the estimation procedure. However, the measurements and global prediction are only a subset of the available information resources. The GOF algorithm is therefore proposed so as to utilize all information resources, and it is expected that this will ensure optimal estimation performance compared with the other two data fusion algorithms.

Because of the GOF’s theoretical superiority, GOF is used instead of CKF and FKF in this research. It is also the first time that a GOF-based Locata-augmented multi-sensor navigation system is considered for an airborne application. GNSS and Locata are separately integrated with INS via the local filters, and independently generate the local information. The global prediction, local predictions and local estimations are then fused to obtain the global optimal system estimation of the airborne GNSS/Locata/INS hybrid navigation system. To evaluate the system performance, UNSW and the Locata Corporation carried out a flight trial from Bankstown Airport to Cooma Airport.

An overview of the integrated GNSS/Locata/INS system model and conventional fusion algorithms is first provided. The GOF algorithm is described in the second section, with an emphasis on the GOF’s theoretical derivation and analysis. The GOF-based GNSS/Locata/INS integration system is then discussed, comparing it to CKF- and FKF-based integration systems. Finally, the flight trial is described, including the system configuration and flight experiment design, as well as flight data analysis, followed by an evaluation of the results.

System model and conventional fusion algorithm

There are a number of ways of combining information from multiple navigation systems. The design of any integration algorithm is typically a trade-off between maximizing the accuracy and robustness of the navigation solutions, minimizing the complexity, and optimizing the processing efficiency. This section describes the integrated system model and different integration algorithms.

  1. 1.

    INS mechanism and derived dynamic model of GNSS/Locata/INS multi-sensor navigation system

To drive the integration Kalman filter system’s dynamic model, the INS error model needs to be first defined. During the last decades, considerable research has been devoted to INS error modeling (e.g., Arshal 1987; Lee et al. 1998; Goshen-Meskin and Bar-Itzhack 1992). The authors utilize the psi-angle error model in this research:

$$\delta {\dot {r}^n}=\delta {v^n} - \omega _{{en}}^{n} \times \delta {r^n}$$
$$\delta {\dot {v}^n}= - \left( {\omega _{{ie}}^{n}+\omega _{{in}}^{n}} \right) \times \delta {v^n}+\psi \times {f^n}+{\nabla ^n}+\delta {g^n}$$
(1)
$$\dot {\psi }= - \omega _{{in}}^{n} \times \psi +{\varepsilon ^n}$$

where \(\delta {r^n}\), \(\delta {v^n}\) and \(\psi\) represent the position, velocity and attitude parameters in the local navigation frame (n-frame), respectively; \(\omega _{{en}}^{n}\) is the angular-rate of the n-frame with respect to the earth-centered, earth-fixed frame (e-frame), resolved in the n-frame; \(\omega _{{ie}}^{n}\) and \(\omega _{{in}}^{n}\) are the angular-rate of the e-frame and n-frame with respect to the inertial frame (i-frame), respectively, both resolved in the n-frame; \({\nabla ^n}\) and \({\varvec{\varepsilon}^{\varvec{n}}}\) denote the error vectors of accelerometers and gyroscopes, respectively, and \(\delta {g^n}\) is the computed gravity error vector.

Thus, the system dynamic function can be written as:

$$\dot {X}(t)=F(t)X(t)+W(t)$$
(2)

where \(X(t)\) is the system state vector, \(F(t)\) is the system transition matrix relates the state and that of the previous time step, and \(W(t)\) is the process noise matrix.

The INS is normally installed in the cabin of the aircraft, the GNSS antenna is installed on the top of the aircraft to receive the satellite signals, and the Locata antenna is located on the underside of the aircraft to receive the signals from LocataLites installed on the ground. Hence the lever arm between the three systems needs to be considered. To simplify computations the positions of the GNSS and Locata antennas are both corrected to the INS reference point. As the vector length of the lever arm between GNSS/Locata antennas and the INS reference center cannot be measured. Therefore, the corresponding lever arms of GNSS-to-INS and Locata-to-INS are estimated as unknown system states. The system state vector of each epoch consists of 21 parameters, which can be written in the form of three sub-vectors: \({x_{rv\psi }}\), \({x_{\nabla \varepsilon }}\) and \({x_\eta }\) which represent the sub-vectors of navigation component, INS sensor bias component, and level arm component, respectively:

$$X(t)=\left[ {\begin{array}{*{20}{c}} {{X_{rv\psi }}}&{{X_{\nabla \varepsilon }}}&{{X_\eta }} \end{array}} \right]$$
(3)

where

$${X_{rv\psi }}=\left[ {\begin{array}{*{20}{c}} {{\psi _{\text{N}}}}&{{\psi _{\text{E}}}}&{{\psi _{\text{D}}}}&{\delta {r_{\text{N}}}}&{\delta {r_{\text{E}}}}&{\delta {r_{\text{D}}}}&{\delta {v_{\text{N}}}}&{\delta {v_{\text{E}}}}&{\delta {v_{\text{D}}}} \end{array}} \right]$$
$${X_{\nabla \varepsilon }}=\left[ {\begin{array}{*{20}{c}} {{\varepsilon _x}}&{{\varepsilon _y}}&{{\varepsilon _z}}&{{\nabla _x}}&{{\nabla _y}}&{{\nabla _z}} \end{array}} \right]$$
$${X_\eta }=\left[ {\begin{array}{*{20}{c}} {\delta {\eta _{Lx}}}&{\delta {\eta _{Ly}}}&{\delta {\eta _{Lz}}}&{\delta {\eta _{Gx}}}&{\delta {\eta _{Gy}}}&{\delta {\eta _{Gz}}} \end{array}} \right]$$

The subscripts “N”, “E”, “D” refer to the north, east, and down directions in the local geographic frame, respectively, which has its origin at the location of the navigation system; “\(x\)”, “\(y\)”, “\(z\)” refer to the front, right and down directions in the body frame (b-frame), respectively; \(L\) and \(G\) refers the Locata and GNSS, respectively; and \(\delta {\eta _ * }\) denotes the unknown GNSS and Locata lever arm parameters with respect to the INS reference point.

As for the measurement updates, the observations of the multi-sensor system are the position and velocity (PV) corrections from GNSS-to-INS and Locata-to-INS. Both GNSS and Locata provide the PV solutions that are able to correct for the INS bias. The GNSS/INS PV corrections and the Locata/INS PV corrections both need to apply the lever arm compensation due to the lever arm uncertainty mentioned above:

$$r_{*}^{n}=r_{{{\text{INS}}}}^{n}+C_{b}^{n}\eta _{*}^{b}$$
(4)
$$v_{*}^{n}=v_{{{\text{INS}}}}^{n}+\left( {\omega _{{ie}}^{n} \times +\omega _{{en}}^{n} \times } \right)C_{b}^{n}\eta _{*}^{b} - C_{b}^{n}\left( {\eta _{*}^{b} \times } \right)\omega _{{ib}}^{b}$$
(5)

where the subscript * represents the GNSS and Locata sub-systems, and \(\omega _{{ib}}^{b}\) is the angular-rate measurement obtained from the gyroscope sensors. Thus, the PV computed at the phase center of the GNSS and Locata antennas could be modified by:

$$\hat {r}_{*}^{n}=\hat {r}_{{{\text{INS}}}}^{n}+\hat {C}_{b}^{n}\eta _{{*0}}^{b} - \hat {C}_{b}^{n}\left( {\eta _{{*0}}^{b} \times } \right)\psi +\hat {C}_{b}^{n}\delta \eta _{*}^{b}$$
(6)
$$\hat {v}_{*}^{n}=\hat {v}_{{{\text{INS}}}}^{n}+\hat {C}_{b}^{n}\left( {\omega _{{ib}}^{b} \times } \right)\eta _{{0*}}^{b}+\hat {C}_{b}^{n}\left( {\omega _{{ib}}^{b} \times } \right)\delta \eta _{*}^{b} - \left[ {\left( {\hat {C}_{b}^{n}\left( {\omega _{{ib}}^{b} \times } \right)\eta _{{0*}}^{b}} \right) \times } \right]$$
(7)

where \(\eta _{{0*}}^{b}\) represents the initial estimates of the GNSS and Locata lever arms.

  1. 2.

    Measurement model of the CKF-based multi-sensor navigation system

When applying CKF, the measurements are described by the stacked observation vector:

$$Z(t)={\left[ {{Z_L},{Z_G}} \right]^{\text{T}}}={\left[ {\hat {r}_{L}^{n} - \hat {r}_{{{\text{INS}}}}^{n},\hat {v}_{L}^{n} - \hat {v}_{{{\text{INS}}}}^{n},\hat {r}_{G}^{n} - \hat {r}_{{{\text{INS}}}}^{n},\hat {v}_{G}^{n} - \hat {v}_{{{\text{INS}}}}^{n}} \right]^T}$$
(8)

The system state is estimated by a global measurement equation applied with the global stacked observation vector containing all available measurements. The system measurement equation can be described as:

$$Z(t)=H(t)X(t)+V(t)$$
(9)

where \(H(t)\) is the observation matrix, and \(V(t)\) is the measurement noise vector of the multi-sensor navigation system.

Assuming the multi-sensor navigation system is computed in the form of a discrete process, the system dynamic (2) and observation (9) can be rewritten as:

$$x(k)=F(k)x(k - 1)+\omega (k)$$
(10)
$$z(k)=H(k)x(k)+v(k)$$
(11)

where \(\omega (k)\) is the process driving noise at epoch k with covariance \(Q(k)\), and \(v(k)\) is the measurement noise at epoch k with the covariance \(R(k)\). \(\omega (k)\) and \(v(k)\) are assumed to be zero-mean white sequences that are uncorrelated with each other.

The Kalman filter algorithm can be treated as a two-step procedure: the time update step and the measurement update step. From the time update step, the state prediction \(\vec {x}(k)\) and the a priori estimate error covariance \(\vec {P}(k)\)are obtained:

$$\vec {x}(k)=F(k)\hat {x}(k - 1)$$
(12)
$$\vec {P}(k)=F(k)\hat {P}(k - 1){F^{\text{T}}}(k)+Q(k)$$
(13)

From the measurement update, the system state estimation \(\hat {x}(k)\) can be updated with the stacked measurement vectors:

$$K(k)=\vec {P}(k){H^{\text{T}}}(k){\left[ {H(k)\vec {P}(k){H^{\text{T}}}(k)+R(k)} \right]^{ - 1}}$$
(14)
$$\hat {P}(k)=\left[ {I - K(k)H(k)} \right]\vec {P}(k)$$
(15)
$$\hat {x}(k)=\vec {x}(k)+K(k)\left[ {z(k) - H(k)\vec {x}(k)} \right]$$
(16)

where \(K(k)\) is the computed Kalman filter gain and \(\hat {P}(k)\) is the a posteriori estimated error covariance.

  1. 3.

    Measurement model of the DKF-based multi-sensor navigation system

In a decentralized navigation system, the outputs of the GNSS and Locata sub-systems are individually combined with the INS output to generate the measurements of the local GNSS/INS and Locata/INS sub-systems. The two local filters independently resolve the local estimates using the measurements. As both local filters apply the INS mechanization model, the two sub-systems have the same system dynamic equation.

The \(i\)th (\(i\) = 1, 2) local filter could be written as:

$$x(k)=F(k)x(k - 1)+\omega (k)$$
(17)
$${z_i}(k)={H_i}(k)x(k)+{v_i}(k)$$
(18)

where \({z_i}(k)\) is the measurement of the \(i\)th sub-system (or sensor). Specifically:

$${z_L}(k)={\left[ {\hat {r}_{L}^{n} - \hat {r}_{{{\text{INS}}}}^{n},\hat {v}_{L}^{n} - \hat {v}_{{{\text{INS}}}}^{n}} \right]^T},\;{z_G}(k)=\left[ {\hat {r}_{G}^{n} - \hat {r}_{{{\text{INS}}}}^{n},\hat {v}_{G}^{n} - \hat {v}_{{{\text{INS}}}}^{n}} \right]$$

and \({v_i}(k)\) is the measurement noise of the sub-system, assumed to be zero-mean white noise. The measurement noise covariances of the local filters are dependent on the GNSS and Locata output accuracy.

Each local filter obtains the local estimate using the Kalman filter (12)–(16). After the processing by the decentralized local filters is completed, the local optimal state estimations \({\hat {x}_1}(k)\) and \({\hat {x}_2}(k)\) can be generated and then fused together by the global filter.

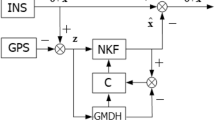
The federated Kalman filtering (FKF) is one of the most commonly used decentralized filtering algorithms in current navigation systems. The FKF was developed by Calson and Berarducci (1994) and Calson (1996). The decentralization characteristic of the FKF helps to achieve a good fault detection and isolation capability with comparatively low communications and computation burden. The basic concept of information-sharing is to achieve the optimal division between global prediction and the covariance on the local filters. Then the parallel computation architecture is implemented using local sensor observations; and finally the updated local estimations are fused via a master filter in order to provide the global estimation. The system configuration of an FKF can be seen in Fig. 1. The FKF architecture consists of several local filters and one master filter. The local filters are connected with the local sensors, and work independently of each other. The local estimation and its covariance are then sent to the master filter, and fused with the global predictor to generate the final global estimation.

Fig. 1
figure 1

System configuration of a generic FKF

Full size image

For optimal estimation (Gao et al. 2009; Li 2014), it is assumed that the linear discrete system \({\hat {x}_i}\) (i = 1,2,…,n) should have unbiased estimators of the system state vector \(x\). If \({\hat {x}_i}\) is an orthogonal vector, the optimal system estimation and its covariance can be given as:

$$\hat {x}=\hat {P}\left( {\sum\limits_{{i=1}}^{n} {S_{i}^{{\text{T}}}\hat {P}_{i}^{{ - 1}}{{\hat {x}}_i}} } \right)$$
(19)
$$\hat {P}={\left( {\sum\limits_{{i=1}}^{n} {S_{i}^{{\text{T}}}\hat {P}_{i}^{{ - 1}}{S_i}} } \right)^{ - 1}}$$
(20)

where \({S_i}\) is the mapping matrix between \(\hat {x}\) and \({\hat {x}_i}\), \({\hat {x}_i}={S_i}\hat {x}\); and \({\hat {P}_i}\) is the corresponding a posteriori estimate error covariance of \({\hat {x}_i}\), which is calculated on an epoch-by-epoch basis.

Applying this in the FKF, assume the local filters and master filter are uncorrelated, then the global estimation is:

$$P_{f}^{{ - 1}}=\sum\limits_{{i=1}}^{2} {P_{i}^{{ - 1}}} +P_{m}^{{ - 1}}$$
(21)
$$P_{f}^{{ - 1}}{\hat {x}_f}=\sum\limits_{{i=1}}^{2} {P_{i}^{{ - 1}}{{\hat {x}}_i}+} P_{m}^{{ - 1}}{\hat {x}_m}$$
(22)

where the subscript “\(i\)”, “\(m\)”, and “\(f\)”denote the local filter, master filter, and full filter, respectively. \(P_{{\text{*}}}^{{ - 1}}\) is the information matrix.

The FKF could, in theory, achieve an optimal global solution if the master filter and the local filters are independent of each other. However, in many cases, the master filter and local filter use the same dynamic model. Therefore, the master filter and the local filters are correlated with each other (Calson and Berarducci 1994; Calson 1996). Hence the FKF approach could only generate a sub-optimal global estimation. To remove the correlation, the system state estimation covariance and system processing noise covariance can be weighted by information-sharing factors:

$$\left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{{\hat {x}}_i}(k)={{\hat {x}}_f}(k)} \\ {{F_i}(k)=F(k)} \end{array}}&{i=1,2,m} \end{array}} \right.$$
(23)
$$\left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\hat {P}_{i}^{{ - 1}}(k)=\hat {P}_{f}^{{ - 1}}{\beta _i}} \\ {Q_{i}^{{ - 1}}(k)=Q_{f}^{{ - 1}}{\beta _i}} \end{array}}&{i=1,2,m} \end{array}} \right.$$
(24)

where \({\beta _i}\left( { \geqslant 0} \right)\) is the information-sharing factor such that \(\sum\nolimits_{{i=1}}^{{2,m}} {{\beta _i}=1}\).

The master filter and every local filter use the same time update procedure:

$${\vec {P}_i}(k)={F_i}(k){\hat {P}_i}(k - 1)F_{i}^{{\text{T}}}(k)+{Q_i}(k),\quad i=1,2,m$$
(25)
$${\vec {x}_i}(k)={F_i}(k){\hat {x}_i}(k - 1),\quad i=1,2,m$$
(26)

As the accelerometer and gyroscope errors are modeled as random biases, the process noise covariance is defined according to the INS sensor bias parameters:

$${Q_i}(k)={\text{diag}}\left( {{0_{1 \times 9}},\sigma _{\varepsilon }^{2},\sigma _{\varepsilon }^{2},\sigma _{\varepsilon }^{2},\sigma _{\nabla }^{2},\sigma _{\nabla }^{2},\sigma _{\nabla }^{2},{0_{1 \times 6}}} \right),\quad i=1,2,m$$
(27)

where \({\sigma _\varepsilon }\) is the gyro error variance, and \(\sigma _{\nabla }^{{}}\) is the accelerometer error variance.

The master filter and local filters use different measurement update procedures:

$${K_i}(k)={\vec {P}_i}(k)H_{i}^{{\text{T}}}(k){\left[ {{H_i}(k){{\vec {P}}_i}(k)H_{i}^{T}(k)+{R_i}(k)} \right]^{ - 1}},\quad i=1,2$$
(28)
$${\hat {P}_i}(k)=\left[ {I - {K_i}(k){H_i}(k)} \right]{\vec {P}_i}(k),\quad i=1,2$$
(29)
$${\hat {x}_i}(k)={\vec {x}_i}(k)+{K_i}(k)\left[ {{z_i}(k) - {H_i}(k){{\vec {x}}_i}(k)} \right],\quad i=1,2$$
(30)
$${\hat {P}_m}(k)={\vec {P}_m}(k)$$
(31)
$${\hat {x}_m}(k)={\vec {x}_m}(k)$$
(32)

Since the measurements of each local filter are the position and velocity corrections from GNSS or Locata, in three directions, this means the six identical components in the matrix represent the uncertainty of position and velocity solutions from GNSS and Locata. Thus, the measurement variances should be defined by the local Locata and GNSS position and velocity estimation errors. The corresponding variances are:

$${{\mathbf{R}}_{\mathbf{L}}}={\text{diag}}\left( {\begin{array}{*{20}{c}} {{{\left( {10} \right)}^2}}&{{{\left( {10} \right)}^2}}&{{{\left( {10} \right)}^2}}&{{{\left( {0.5} \right)}^2}}&{{{\left( {0.5} \right)}^2}}&{{{\left( {0.8} \right)}^2}} \end{array}} \right)$$
(33)
$${{\mathbf{R}}_{\mathbf{G}}}={\text{diag}}\left( {\begin{array}{*{20}{c}} {{{\left( 3 \right)}^2}}&{{{\left( 3 \right)}^2}}&{{{\left( 5 \right)}^2}}&{{{\left( {0.2} \right)}^2}}&{{{\left( {0.2} \right)}^2}}&{{{\left( {0.4} \right)}^2}} \end{array}} \right)$$
(34)

where the first three terms are the covariances of position (\({{\text{m}}^{\text{2}}}\)), and the last three terms are the covariances of the velocity \({\left( {{\text{m/s}}} \right)^{\text{2}}}\).

The estimated local and master filter results are then combined according to (19) and (20):

$$\hat {P}_{f}^{{ - 1}}(k)=\hat {P}_{m}^{{ - 1}}(k)+\sum\limits_{{i=1}}^{2} {\hat {P}_{i}^{{ - 1}}} (k)$$
(35)
$$\hat {x}(k)={\hat {P}_f}(k)\left[ {\hat {P}_{m}^{{ - 1}}(k){{\hat {x}}_m}(k)+\sum\limits_{{i=1}}^{2} {\hat {P}_{i}^{{ - 1}}(k){{\hat {x}}_i}(k)} } \right]$$
(36)

The global estimation and its covariance can then be then obtained, and treated as the initial input for the following estimation.

GOF-based GNSS/Locata/INS multi-sensor navigation system

The optimal data fusion algorithm is normally resolved from two concepts: the random vector space (RVS) framework and the information space framework (Li 2014). The RVS approach identifies all information sources at the first step and defines them as space bases. Then filter estimation can be achieved by determining the optimal state vector projection on the space bases. The key issue of the fusion algorithm is, therefore, how to optimally combine the projections and associated bases. As for the information space framework, the data fusion criterion generates the fused optimal estimation by making a series of transformations, and mapping the vectors from the original measurement spaces to the estimated space. In that case, the information space method can be used to evaluate the estimation performance of different algorithms.

Since the RVS approach operates in a similar way to Kalman filtering, the RVS is applied in this research to analyze the character of the GOF approach. Recall, the previously mentioned measurement update process of Kalman filter in (16); the measurement update equation can, therefore, be rewritten as the fusion of state prediction and measurements:

$$\hat {x}(k)=\left[ {I - K(k)H(k)} \right]\vec {x}(k)+K(k)z(k)$$
(37)

It also can be regarded as the random vector space (Li 2014):

$$\Theta =\left\{ {\hat {x}|\hat {x}={C_1}\vec {x}+{C_2}(k)z} \right\}$$
(38)

where \({C_1}=\hat {P}{\vec {P}^{ - 1}}\), and \({C_2}=\hat {P}{H^T}{R^{ - 1}}\).

The system estimation \(\hat {x}\) can, therefore, be treated as a point in the space \(\Theta\), obtained by projecting \({C_1}\) and \({C_2}\) onto the information bases of \(\vec {x}\) and \(z\).

Similarly, the RVS frame of the CKF algorithm can be rewritten as projecting \(C\), \({C_1}\) and \({C_2}\) on the bases of the measurements\({z_1}\) and \({z_2}\), and the global prediction \(\vec {x}\):

$${\Theta _{{\text{CKF}}}}=\left\{ {\hat {x}|\hat {x}=C\vec {x}+{C_1}(k){z_1}+{C_2}(k){z_2}} \right\}$$
(39)

where \(C=\hat {P}{\vec {P}^{ - 1}}\), \({C_1}=\hat {P}H_{1}^{T}R_{1}^{{ - 1}}\), and \({C_2}=\hat {P}H_{2}^{T}R_{2}^{{ - 1}}\). FKF similarly applies local measurements and global predictions—see (21)–(24).

According to the optimal state estimation (19) and (20), it is concluded that the more information that is utilized, shown as \({\hat {x}_i}\), the smaller the \(\hat {P}\) that is obtained, and hence the system could achieve better estimation performance. The RVS form of the optimal state estimation (19) can be expressed as the sum of the projection of \({\hat {x}_i}\) in the space \(\Theta\):

$$\Theta =\left\{ {\hat {x}|\hat {x}=\sum\limits_{{i=1}}^{n} {{C_i}{{\hat {x}}_i}} } \right\}$$
(40)

As mentioned above, a key issue of optimal data fusion estimation is determining the information bases and the associated projections. The information bases of the typical multi-sensor navigation system can be determined as:

Measurements: \({z_i}(k)\),\(i=1,2\)

Local predictions: \({\vec {x}_i}(k)\),\(i=1,2\)

Global predictions: \(\vec {x}(k)\)

Different data fusion algorithms apply different information bases under the RVS framework. The CKF and FKF estimation output could be rewritten in the RVS framework as:

$$\Theta =\left\{ {\hat {x}(k)|\hat {x}(k)=a(k)\vec {x}(k)+\sum\limits_{{i=1}}^{2} {{b_i}(k){z_i}(k)} } \right\}$$
(41)

where \(a\) and \({b_*}\) denote the projections of the global estimation vector on the global prediction space and measurements space, respectively. It can be seen that although FKF is applied in the decentralized architecture, CKF and FKF both utilize global prediction and all local measurements, which indicates that they should achieve essentially the same accuracies.

In contrast to CKF and FKF, the GOF is designed to utilize all available information bases—the local predictions, global prediction, and measurements—to achieve global optimal estimation. The GOF global estimation can be written as:

$$\Theta =\left\{ {\hat {x}(k)|\hat {x}(k)=\sum\limits_{{i=1}}^{2} {{c_i}(k){{\vec {x}}_i}(k)} +\sum\limits_{{i=1}}^{2} {{d_i}(k){z_i}(k)} +e(k)\vec {x}(k)} \right\}$$
(42)

The local predictions and the local measurements ensure filter fusion. Thus the local predictions and the measurements can be combined and rewritten as local estimates. Figure 2 shows the configuration of a GOF system. GOF estimation within the RVS framework can be represented as:

Fig. 2
figure 2

System configuration of a GOF

Full size image
$${\Theta _{}}=\left\{ {\hat {x}(k)|\hat {x}(k)=e(k)\vec {x}(k)+{f_1}(k){{\hat {x}}_1}(k)+{f_2}(k){{\hat {x}}_2}(k)} \right\}$$
(43)

where \({c_*}\), \({d_*}\), \(e\) and \({f_*}\) represent the projections of the global estimate vector \(\hat {x}\) on the different bases.

In Fig. 2 it can be seen that both the GNSS and Locata PV are used to correct INS output so as to constitute the measurement vectors in the local GNSS/INS and Locata/INS filters. The local estimates \({\hat {x}_1}\) and \({\hat {x}_2}\) are therefore both correlated with the same INS PV output, represented by the local estimations. Meanwhile, the global prediction is also achieved by processing the time update on the bases of the previous global estimation, which means that the current global prediction and the local estimates are oblique with respect to each other. Therefore, an orthogonalization process should be applied to the three vectors. The orthogonalized local estimates and global prediction are denoted as \({\tilde {x}_i}\) and \(\tilde {x}\):

$$\left\{ {\begin{array}{*{20}{c}} {{{\tilde {x}}_1}(k)={{\hat {x}}_1}(k),{{\tilde {x}}_2}(k)={{\hat {x}}_2}(k)} \\ {\tilde {x}(k)={\alpha _1}{{\hat {x}}_1}(k)+{\alpha _2}{{\hat {x}}_2}(k)+\alpha \vec {x}(k)} \end{array}} \right.$$
(44)

The covariance of the reconstructed global prediction can be written as:

$$\tilde {P}(k)=\alpha \vec {P}(k){\alpha ^{\text{T}}}+\sum\limits_{{i=1}}^{2} {{\alpha _i}{{\hat {P}}_i}(k)} \alpha _{i}^{{\text{T}}}+\sum\limits_{{i=1}}^{2} {\alpha {{\tilde {P}}_i}(k)} \alpha _{i}^{{\text{T}}}+\sum\limits_{{i=1}}^{2} {{\alpha _i}\tilde {P}_{i}^{{\text{T}}}(k)} {\alpha ^{\text{T}}}$$
(45)

where

$${\tilde {P}_i}=\operatorname{cov} (\vec {x},{\tilde {x}_i})=F(k)\hat {P}(k - 1){F^T}(k)\vec {P}_{i}^{{ - 1}}(k){\hat {P}_i}(k)$$
(46)

As the local estimate \({\hat {x}_i}\) and global prediction \(\vec {x}\) are both unbiased estimates, the orthogonalized global prediction \(\tilde {x}\) should also be unbiased. Therefore, from \(E(\tilde {x} - x)\) = 0 it can be derived that:

$${\alpha _1}+{\alpha _2}+\alpha =I$$
(47)

Since the reconstructed global prediction \(\tilde {x}\) and the local estimates \({\tilde {x}_1}\) and \({\tilde {x}_2}\) are orthogonal to each other, and thus \(\operatorname{cov} (\tilde {x},{\tilde {x}_1})=0\) and \(\operatorname{cov} (\tilde {x},{\tilde {x}_2})=0\), one obtains:

$$\left\{ {\begin{array}{*{20}{c}} {{\alpha _1}= - \alpha {{\tilde {P}}_1}\hat {P}_{1}^{{ - 1}},{\alpha _2}= - \alpha {{\tilde {P}}_2}\hat {P}_{2}^{{ - 1}}} \\ {\alpha ={{\left( {I - {{\tilde {P}}_1}\hat {P}_{1}^{{ - 1}} - {{\tilde {P}}_2}\hat {P}_{2}^{{ - 1}}} \right)}^{ - 1}}} \end{array}} \right.$$
(48)

Then the reconstructed local estimates and global prediction can be combined using (19) and (20):

$$\hat {x}(k)=\hat {P}(k)\left[ {{{\tilde {P}}^{ - 1}}(k)\tilde {x}(k)+\hat {P}_{1}^{{ - 1}}(k){{\hat {x}}_1}(k)+\hat {P}_{2}^{{ - 1}}(k){{\hat {x}}_2}(k)} \right]$$
(49)
$$\hat {P}(k)={\left[ {{{\tilde {P}}^{ - 1}}(k)+\hat {P}_{1}^{{ - 1}}(k)+\hat {P}_{2}^{{ - 1}}(k)} \right]^{ - 1}}$$
(50)

The GOF global optimal estimation and its a posteriori covariance can be then obtained, and treated as the initial input for the following estimation step.

Experiment and analysis

A flight test was conducted in the Cooma area, located in the southern part of the state of New South Wales, Australia. A LocataNet consisted of six LocataLites, which were installed near Cooma airport. According to the LotataNet positioning signal Interface Control Document (Locata Corporation 2014), the longest operating range for a LocataLite is approximately 50 km. The average distance between each LocataLite in this test was 40 km. The LocataNet, and the flight trajectory are shown in Fig. 3. The coordinates of LocataLites were pre-surveyed and obtained in the Earth-centered, Earth-fixed (ECEF) coordinate system based on the International Terrestrial Reference Frame 2008 (ITRF08) and the north–east–down (NED) coordinate system. The origin of the NED coordinate system is defined by LocataLite 3. The coordinates of the six LocataLites are listed in Table 1. In this flight experiment each LocataLite has one antenna which can transmit two signals—S1 and S6. Both signals are utilized in this research.

Fig. 3
figure 3

LocataNet configuration and aircraft trajectory for the air trial

Full size image
Table 1 Coordinates of the LocataLites (units: meters)
Full size table

The aircraft used for the flight experiment was a Beech Duchess aircraft belonging to the School of Aviation, UNSW. The devices that were used in the test included one Leica dual-frequency GPS receiver, one NovAtel SPAN-CPT GPS/INS system which can output raw INS measurements and the integrated GPS/INS solution, and two Locata receiver units. The Locata sub-system can synchronize with GPS at the first epoch, and then the Locata time system, using the 1 pulse-per-second (PPS) time reference to maintain the time system, is independent of GPS availability. All LocataLites in a LocataNet are synchronized to a master station in the network. The master LocataLite used in this trial was LocataLite 3. The performance parameters of the inertial sensors are listed in Table 2. The GPS antenna was mounted on the top of the aircraft and was used by both the SPAN-CPT and the Leica GPS receiver. The two Locata antennas were attached to the underside of the aircraft, as shown in Fig. 4. The measurements from the front antenna were processed in post-mission mode. In addition, measurements from a GPS reference station were recorded. The GPS reference station is located adjacent to LocataLite 3, marked purple in Fig. 3. Most of the distances between the trajectory and the GPS reference station were less than 5 km, and the maximum distance between the aircraft and the reference station was 19.5 km.

Table 2 Technical specifications of the INS sensors
Full size table
Fig. 4
figure 4

Experiment aircraft and antenna setup. The GPS antenna is located on the top and the Locata antennas are on the underside of the aircraft

Full size image

The gyro error standard deviation and the accelerometer error standard deviation are used to define the process noise covariance in (27).

Both the GPS and Locata data rates were set to 10 Hz. The inertial measurement rate was set to 100 Hz and synchronized with GPS time. No change was made to the ground configuration during the flight test.

Figure 5 shows the GPS and Locata observation status during the experiment period. It can be seen that the GPS observation conditions were good, with more than seven satellites available during the entire period of the trial. The elevation mask was set as 10°. Locata’s availability is not as good as that of GPS, changing frequently during the test. During some parts of the test, the number of available LocataLites was less than four.

Fig. 5
figure 5

GPS satellite (red color) and LocataLite (blue color) availability

Full size image

The GPS and Locata pseudorange and Doppler measurements were post-processed independently to obtain the PV solutions. The GPS integer ambiguity-fixed differential carrier phase positioning solution computed by the Leica Geo Office (LGO) software was used as the position ground-truth since it had a nominal accuracy of a few centimeters. The velocity and attitude reference was provided by the SPAN-CPT GPS/INS system, with stated velocity and attitude accuracy of better than 0.015 m/s and 0.06°, respectively (NovAtel Corporation 2015).

Figures 6 and 7 show the GPS and Locata PV solutions with respect to the ground-truth solution. Figure 8 shows the GPS/INS and Locata/INS position solutions with respect to the ground-truth solution. It can be seen that the quality of the Locata PV solutions is less than the GPS PV solutions. Because of the large operational area, the Locata carrier phase measurements could not be used due to the low signal strength, causing many cycle slips, and in many cases the carrier phase measurements cannot be decoded. On the other hand, Locata pseudorange measurements were more reliable, and were used to generate positioning solutions. As a result of the large operational area, the geometry and availability of LocataLites was changing quickly, and was often not ideal. For these reasons the Locata positioning accuracy is not as good as that of GPS, as can be seen in the oscillations of the Locata PV solutions.

Fig. 6
figure 6

Position comparison between Locata (blue color) and GPS (red color) solutions

Full size image
Fig. 7
figure 7

Velocity comparison between Locata (blue color) and GPS (red color) solutions

Full size image
Fig. 8
figure 8

Position comparison between Locata/INS (blue color) and GPS/INS (red color) solutions

Full size image

Figure 9 shows the dilution of precision (DOP) values for the GPS-only, Locata-only and GPS + Locata situations during the aircraft test. Both the horizontal DOP (HDOP) and vertical DOP (VDOP) were computed. It can be seen that in the case of the GPS + Locata situation the HDOPs and VDOPs are smaller than those for either GPS-only and Locata-only case. In other words, by adding signals from the Locata system, the horizontal and vertical position precision can be expected to improve.

Fig. 9
figure 9

DOP values for GPS (blue color), Locata (yellow color) and GPS + Locata (red color) situations

Full size image

Figures 10, 11 and 12 show the position, velocity and attitude performance of the CKF, FKF, and GOF multi-sensor solutions, respectively. As both CKF and FKF optimally fuse the global prediction and all local measurements, the two systems have the same accuracy, as seen from (41). The navigation systems based on CKF and FKF, therefore, show similar performance in Figs. 10, 11 and 12. Figure 10 is a plot of the comparison of the positioning results provided by each of the systems against the ground-truth trajectory generated from GPS carrier phase measurements. It can be seen that for all position and velocity estimates in the north, east and down directions, GOF provides a more accurate, and more precise (i.e., smoother) solution. In particular, when the system has abrupt errors from 550 to 700 s and 1050 to 1100 s, the GOF solution is clearly better. The root mean square (RMS) for the three components and the radial spherical error (MRSE) of the 3D position error are listed in Table 3. The MRSE of the GOF-based multi-sensor navigation solution is 10.22 m, which is lower than the 15.6 m from the CKF and FKF solutions. This is an improvement of over 30%.

Fig. 10
figure 10

Position comparison between CKF (blue color), FKF (green color) and GOF (red color) solutions

Full size image
Fig. 11
figure 11

Velocity comparison between the CKF (blue color), FKF (green color) and GOF (red color) solutions

Full size image
Fig. 12
figure 12

Attitude comparison between the CKF (blue color), FKF (green color) and GOF (red color) solutions

Full size image
Table 3 Position, velocity and attitude error statistics of the CKF, FKF and GOF solutions
Full size table

Note that the positioning performance of the Locata-augmented multi-sensor navigation system shown in Fig. 10 is not as good as the GPS/INS integration system in Fig. 8. This is because Locata’s availability and geometry are not ideal as seen Fig. 5.

Figures 11 and 12 show the velocity and attitude estimates, and comparing the results from each of the systems and the ground-truth results obtained by the SPAN-CPT system. In the case of the velocity solution there is a similar conclusion as for the position solution. The RMS values in Table 3 indicate that the velocity derived using GOF has a higher accuracy than the CKF- and FKF-derived velocities, for all three direction components. The MRSE of GOF-derived velocity is 0.31 m/s, with the improvement over the CKF and FKF velocity results being 18.4%.

The attitude component results also confirm the superiority of the GOF-based multi-sensor navigation system. From Table 3, the RMS of the roll and pitch GOF solutions is 0.05° and 0.07°, respectively, which is an improvement over the CKF and FKF solutions of 28.6 and 12.5%, respectively. The yaw solution from the three systems is worse than the roll and pitch solutions, being 0.19° for the GOF solution, and 0.24° for the CKF and FKF solutions. The improvement in the yaw GOF solution compared to the CKF and FKF solutions is more obvious, being 20.8%.

In order to further evaluate the performance of the CKF, FKF and GOF analysis approaches, a probability density function (PDF) analysis of the absolute 3D positioning differences of the three approaches was conducted. The results are shown in Fig. 13. The 3D positioning results of the three systems are displayed in histogram format using 100 bins, where each bin represents 0.5 m. Since the probability of the positioning error larger than 20 m is relatively small, the first 40 bins where the errors are smaller than 20 m are shown in the plot. It can be seen that for the GOF solutions the probability of the error being less than 5 m is higher than that of the other two approaches. The probability of the error being larger than 6 m is obviously lower than that of the other two approaches, which implies that the GOF system has a better positioning performance than the CKF and FKF approaches.

Fig. 13
figure 13

Probability density function analysis of the CKF (blue color), FKF (green color) and GOF (red color) 3D position solutions

Full size image

To evaluate the precision performance of the estimation, the a posteriori estimated covariance \(\hat {P}(k)\) of the CKF and GOF solutions was also computed. The square root of the error variance \(\sqrt {\hat {P}(k)}\) of the estimated accelerometer bias and gyroscope bias is shown in Figs. 14 and 15, respectively. To make this more obvious, only the converged period corresponding to the last 1000 s of the test has been plotted. It can be seen that for both the accelerometer bias and gyroscope bias, the error variance of GOF estimation for all three components are smaller than those of the CKF and FKF solutions.

Fig. 14
figure 14

Error variance comparison between the CKF (blue color), FKF (green color) and GOF (red color) solutions for accelerometer bias estimation

Full size image
Fig. 15
figure 15

Error variance comparison between the CKF (blue color), FKF (green color) and GOF (red color) solutions for gyroscope bias estimation

Full size image

To evaluate the reliability of the centralized filtering and decentralized filtering approaches, a GPS interference incident was simulated. A constant error of 10,000 m in position and 500 m/s in velocity was simulated. The abrupt error lasts for 10 s, added to the time period of 50–60 s in the output dataset, which simulates the GPS receiver suddenly outputting erroneous navigation solutions due to severe interference or signal jamming. Figure 16 shows the position solution comparison between the centralized filtering and decentralized filtering approaches, for the north, east and down directions. It can be seen that the centralized filtering results diverge, while the decentralized system can provide reliable positioning solutions even during the interference period. The reason is that the decentralized filter easily conducts fault-detection and fault-isolation, which assures the robustness of the navigation system, whereas for a centralized filter a sudden error is difficult to isolate.

Fig. 16
figure 16

Position solution comparison between centralized filtering approach (top plot) and decentralized filtering approach (bottom plot) with a simulated constant bias, for the north (blue color), east (green color) and down (red color) directions

Full size image

Concluding remarks

The authors describe a GNSS/Locata/INS multi-sensor navigation system implemented using a loosely coupled filtering methodology. GNSS and Locata position and velocity solutions are incorporated as measurements to estimate the INS errors. To improve the estimation process, centralized Kalman filtering (CKF), decentralized FKF and global optimal filtering (GOF) approaches were investigated. The CKF and FKF estimations are based on the global prediction and measurements, while the GOF approach utilizes all information bases: local prediction, global prediction, and measurements. In order to evaluate system performance, the three data fusion algorithms have been compared using data from a flight test conducted in Australia. A comparison of CKF, FKF, and GOF solutions verifies the theoretical conclusion—that the use of the GOF algorithm is able to improve the positioning performance. The a posteriori error variances of accelerometer and gyroscope biases for the GOF solutions are also smaller, indicating that a higher estimated precision of the parameters can be obtained using the GOF approach. To evaluate the fault-tolerant ability of the proposed system, a constant bias of 10,000 m in position and 500 m/s in velocity was simulated for a period of 10 s. The results indicate that the proposed system is not affected by the simulated failures, confirming the higher reliability and fault-tolerant capability of the proposed GOF-based GNSS/Locata/INS integration system.