Introduction

Integration of the global positioning system (GPS) with inertial navigation system (INS) is becoming increasingly popular because of the variety of high-precision navigation information that integration allows. This integration process has been investigated over recent decades for different application areas, ranging from military to agriculture applications. In the GPS/INS integrated system, the GPS provides accurate position and velocity information over longer periods, while the INS provides accurate position, velocity and attitude information in the short term. It is difficult to use GPS alone for positioning in many environments because of the system’s vulnerability to signal blockage. In contrast, an INS is a self-contained system without external signal requirements. It is clear that integration of GPS and INS can deliver enhanced performance when compared to that of the individual systems (Nassar and El-Sheimy 2006). Several strategies can be used for GPS and INS integration. In the loose integration strategy, the GPS-derived position and velocity are differenced with the corresponding INS-derived position and velocity. The integration filter then processes the position and velocity differences between the systems to estimate the error states and outputs the corrected solutions. In contrast to the loose integration strategy, both the raw GPS measurements, such as the pseudorange, carrier phase and Doppler measurements, and the INS data are processed centrally in a single common filter in the tight integration strategy. In the deep/ultra-tight integration strategy, the GPS updates are used to calibrate the INS, while the INS is used to assist the GPS receiver tracking loops during periods of interference or under degraded signal conditions.

PPP/INS integrated navigation

Recently, precise point positioning (PPP) has been developed using undifferenced carrier phase and pseudorange observations to obtain centimeter positions in static mode, after precise orbit and clock products became available (Kouba and Héroux 2001). PPP technology offered an opportunity for integrating undifferenced GPS observation with an inertial measurement unit (IMU) for precise position, velocity and attitude determination. The PPP technology could obtain the same high-grade position information as conventional differential GPS, but the PPP solution was slow to converge, requiring a period of more than 30 min. Integration of the PPP with the INS in the tightly coupled configuration would mean that resolution could be significantly improved after loss of lock (Roesler and Martell 2009). Inertially aided PPP can provide more robust positioning accuracy during global navigation satellite system (GNSS) outages (Shin and Scherzinger 2009). Partial and complete GNSS outages were simulated in an airborne survey situation to demonstrate the robustness of the system. Inertially aided PPP could navigate through the partial GPS outages without significant performance degradation. When the outage durations were <30 s, inertially aided PPP was still able to produce the decimeter-level accuracy expected of PPP technology. An integrated undifferenced GPS/microelectromechanical systems (MEMS) IMU system was developed and obtained horizontal and vertical position accuracies of 0.3 and 0.4 m, respectively (Du and Gao 2010). With assistance from the INS, cycle slip detection and repair methods with the IMU were proposed for the undifferenced GPS/MEMS INS integrated system. These methods can efficiently detect and identify cycle slips and subsequently increase the navigation accuracy of the integrated system (Du and Gao 2012). A new integrated navigation system was developed that integrated between-satellites single-difference (BSSD) PPP with a low-cost MEMS sensor-based inertial system. Decimeter-scale positioning accuracy could be achieved with undifferenced and BSSD integrated systems. However, in general, greater positioning accuracy was obtained using the BSSD integrated system (Rabbou and El-Rabbany 2015). A tight integration model of ambiguity-fixed PPP and INS is established by Liu et al. (2015). The ambiguity-fixed PPP/INS integration is able to reach stable centimeter-level positioning, and rapid re-convergence and re-fixing are achievable after a short period of GNSS outage for the PPP/INS integration.

Federated filter

The federated Kalman filter, which is based on the principle of information sharing as described by Carlson (1990), uses sensor-dedicated local filters (LFs) and a master filter (MF) to combine or fuse the local filter output. Federated filters using multiple systems such as GPS, INS and other sensors have been discussed in the literature. An adaptive determination method for the information sharing factors used in the federated Kalman filtering algorithm was proposed by Zhang et al. (2002). This approach is based on generalized eigenvalue decomposition of the covariance matrix of the estimated errors that are associated with individual sensors. In order to track weak signals and provide accurate information in GPS challenging environment, Lee (2003) proposed a GPS/INS ultra-tightly coupled system with a federated Kalman filter. Taking advantage of the parallel calculation strategy of the federated filter, Yang et al. (2004) used an integrated navigation algorithm based on local geometric adjustment outputs. This algorithm was able to avoid the correlations with the local filter. Multisensor optimal and suboptimal federated Kalman filters with two-layer fusion structures were proposed to handle problems when the estimation errors of the local subsystems were correlated (Sun 2004). The federated technology was also applied with other filters. In order to handle the information fusion problems in integrated GPS/INS/CNS (celestial navigation system) produced by the nonlinear/non-Gaussian error models, the federated unscented particle filtering (FUPF) algorithm was developed. Compared with federated unscented Kalman filtering, the FUPF technology performed more accurately in the integrated navigation system according to Hu et al. (2010). A genetic algorithm was applied by Quan and Fang (2012) to construct the adaptive federated Kalman filter model and to select the optimized information sharing factor. This new approach not only greatly enhanced the accuracy and reliability of the integrated navigation system, but also resulted in rapid convergence. In order to reduce the computational load imposed by the federated Kalman filter, Liu and Zhu (2012) proposed an expectation–maximization federated Kalman filtering (EM-FKF) algorithm for the integrated navigation system. While the federated filter can improve the computational efficiency through the information allocation factor, the adaptive information distribution ability of the federated filter is not used well.

Structure

While much research has been conducted with respect to PPP/INS integrated navigation, the focus of these research efforts is largely on navigation algorithms and system architecture. In PPP/INS integrated navigation, the carrier phase, pseudorange and Doppler measurements are introduced into the observation model, which thus increases the computational burden of the filter. Unlike previous research work, an adaptive federated filter is proposed and used in PPP/INS tightly coupled navigation in this study. The adaptive federated filter is introduced into the PPP/INS tightly coupled navigation system to realize parallel filter computing and to enhance filter adaptivity. The equivalence relationship between the federated filter and the adaptive filter is verified, which is actually the basic principle of the adaptive federated filter. After this introduction to the proposed system, an overview of the PPP observation model is given. Next, the PPP/INS tightly coupled navigation model is described, including the dynamics model and the observation model. In the following section, the adaptive federated filter is described. A subsequent section provides an overview of the PPP/INS tightly coupled navigation system, including the system’s structure and its data stream. Results are then presented and analyzed, and we conclude with a summary of the main conclusions.

Precise point positioning observation model

The traditional PPP observation model, including the pseudorange, carrier phase and Doppler measurements, can be written as (Du and Gao 2010):

$$L = \rho + c \times (dt - dt_{s} ) + d_{\text{ion}} + d_{\text{trop}} + M_{L} + \varepsilon_{L}$$
(1)
$$\varvec{\varPhi}= \rho + c \times (dt - dt_{s} ) - d_{\text{ion}} + d_{\text{trop}} + \lambda N + M_{\varvec{\varPhi}} + \varepsilon_{\varvec{\varPhi}}$$
(2)
$$\dot{\varvec{\varPhi }} = \dot{\rho } + c \times (\delta dt - \delta dt_{s} ) - \dot{d}_{\text{ion}} + \dot{d}_{\text{trop}} + \varepsilon_{{\dot{\varvec{\varPhi }}}}$$
(3)

where \(L\), \(\varvec{\varPhi}\) and \(\dot{\varvec{\varPhi }}\) are the pseudorange, carrier phase and Doppler measurements, \(\rho\) is the geometric distance as a function of the receiver and satellite coordinates, \(\dot{\rho }\) is the geometric range rate, c is the speed of light in a vacuum, \(dt_{s}\) and \(dt\) are the satellite clock error and receiver clock error, \(\delta dt_{s}\) and \(\delta dt\) are the satellite clock error drift and receiver clock error drift, \(d_{ion}\) and \(\dot{d}_{\text{ion}}\) are the first-order ionospheric delay and ionospheric delay drift, \(d_{\text{trop}}\) and \(\dot{d}_{\text{trop}}\) are the tropospheric delay and tropospheric delay drift, \(M_{L}\) and \(M_{\varvec{\varPhi}}\) are the multipath errors of the pseudorange and carrier phase measurements, and \(\varepsilon_{L}\), \(\varepsilon_{\varvec{\varPhi}}\) and \(\varepsilon_{{\dot{\varvec{\varPhi }}}}\) are a combination noise of the pseudorange, carrier phase and Doppler measurements. The tropospheric delay \(d_{\text{trop}}\) is modeled at the zenith and is mapped using a mapping function to the satellite elevation. The Niell mapping function is used in this case.

Using real-time precise GPS orbit and clock products enables the uncertainties in the satellite orbit and clock corrections to be significantly reduced. Other error sources can be eliminated by the correction model. The widely used ionospheric-free combination uses the GPS frequency dispersion property to mitigate the first-order ionospheric delay effect. The observation model of the ionospheric-free combination can be written as (Du and Gao 2010):

$$L_{\text{if}} = \frac{{f_{1}^{2} }}{{f_{1}^{2} - f_{2}^{2} }}L_{1} - \frac{{f_{2}^{2} }}{{f_{1}^{2} - f_{2}^{2} }}L_{2} = \rho + c \times (dt - dt_{s} ) + d_{\text{trop}} + M_{L} + \varepsilon_{L}$$
(4)
$$\varvec{\varPhi}_{\text{if}} = \frac{{f_{1}^{2} }}{{f_{1}^{2} - f_{2}^{2} }}\varvec{\varPhi}_{1} - \frac{{f_{2}^{2} }}{{f_{1}^{2} - f_{2}^{2} }}\varvec{\varPhi}_{2} = \rho + c \times (dt - dt_{s} ) + d_{\text{trop}} + \lambda_{1} N_{\text{if}} + M_{\varvec{\varPhi}} + \varepsilon_{\varvec{\varPhi}}$$
(5)
$$\dot{\varvec{\varPhi }}_{\text{if}} = \frac{{f_{1}^{2} }}{{f_{1}^{2} - f_{2}^{2} }}\dot{\varvec{\varPhi }}_{1} - \frac{{f_{2}^{2} }}{{f_{1}^{2} - f_{2}^{2} }}\dot{\varvec{\varPhi }}_{2} = \dot{\rho } + c \times (\delta dt - \delta dt_{s} ) + \dot{d}_{\text{trop}} + \varepsilon_{{\dot{\varvec{\varPhi }}}}$$
(6)

where the subscript if denotes the ionospheric-free combination observation.

Because the change in tropospheric delay is very slow, the tropospheric delay drift can be neglected in this case. The variables estimated here include three positional parameters, the receiver clock error, the receiver clock error drift, the zenith tropospheric delay and the ionospheric-free carrier ambiguity.

PPP/INS tightly coupled navigation model

In this research, the tightly coupled architecture is implemented in the PPP/INS integrated system. Based on real-time precise orbit and clock products, the GPS pseudorange, carrier phase and Doppler measurements and the INS-derived measurements are processed to estimate the state vector, including position, velocity and attitude. Based on the tightly coupled architecture, the error state vector is defined and the dynamics and observation models are constructed.

Dynamics model

The integrated navigation system error dynamics model used in the Kalman filter is designed based on the INS error equations. Insignificant terms are neglected in the linearization process (Titterton 2004). The psi-angle error equations of the INS in the navigation framework are given as follows (Li et al. 2014):

$$\delta {\dot{\varvec{r}}} = - {\varvec{\omega}}_{\text{en}} \times \delta {\varvec{r}} + \delta {\varvec{v}}$$
(7)
$$\delta {\dot{\varvec{v}}} = - (2{\varvec{\omega}}_{\text{ie}} + {\varvec{\omega}}_{\text{en}} ) \times \delta {\varvec{v}} - \delta {\varvec{\psi}} \times {\varvec{f}} + {\varvec{\eta}}$$
(8)
$$\delta {\dot{\mathbf{\psi }}} = - ({\varvec{\omega}}_{\text{ie}} + {\varvec{\omega}}_{\text{en}} ) \times \delta {\varvec{\psi}} + {\varvec{\varepsilon}}$$
(9)

where \(\delta {\varvec{r}}\), \(\delta {\varvec{v}}\) and \(\delta {\varvec{\psi}}\) are the position, velocity and orientation error vectors, \({\varvec{\omega}}_{en}\) is the navigation frame rate with respect to earth, and \({\varvec{\omega}}_{ie}\) is the rate of the earth with respect to the inertial frame. The system error dynamics of GPS/INS integration is obtained by expanding the accelerometer bias error vector \({\varvec{\eta}}\) and the gyro drift error vector \({\varvec{\varepsilon}}\). Both \({\varvec{\eta}}\) and \({\varvec{\varepsilon}}\) are regarded as random walk process vectors, which are modeled as follows (Titterton 2004):

$${\dot{\mathbf{\eta }}} = {\varvec{u}}_{\eta }$$
(10)
$${\dot{\mathbf{\varepsilon }}} = {\varvec{u}}_{\varepsilon }$$
(11)

where \({\varvec{u}}_{\eta }\) and \({\varvec{u}}_{\varepsilon }\) are white Gaussian noise vectors.

The receiver clock, tropospheric delay and ionospheric-free carrier ambiguity state dynamic equations can be written as (Abdel-Salam and Gao 2001):

$$\dot{d}t = \delta dt + u_{dt}$$
(12)
$$\delta \dot{d}t = u_{\delta dt}$$
(13)
$$\dot{d}_{\text{trop}} = u_{\text{trop}}$$
(14)
$$\dot{N}_{if} = 0$$
(15)

where \(u_{dt}\), \(u_{\delta dt}\) and \(u_{\text{trop}}\) are the white Gaussian noise vectors of the receiver clock error, the receiver clock error drift and the zenith tropospheric delay, respectively.

By combining (7)–(15), the system dynamics model can be generalized in a matrix and vector form:

$${\dot{\varvec{X}}} = {\varvec{FX}} + {\varvec{u}}$$
(16)

where X is the error state vector, F is the system transition matrix, and u is the process noise vector.

Observation model

The observation model in the PPP/INS tightly coupled architecture is composed of the pseudorange, carrier phase and Doppler difference vectors between the GPS observation and the INS computation value (Zhang and Gao 2008):

$${\varvec{Z}} = \left[ {\begin{array}{*{20}c} {L_{j}^{\text{GPS}} - L_{j}^{\text{INS}} } \\ {\varvec{\varPhi}_{j}^{\text{GPS}} -\varvec{\varPhi}_{j}^{\text{INS}} } \\ {\dot{\varvec{\varPhi }}_{j}^{\text{GPS}} - \dot{\varvec{\varPhi }}_{j}^{\text{INS}} } \\ \vdots \\ \end{array} } \right]$$
(17)

where \(L_{j}^{\text{GPS}}\), \(\varvec{\varPhi}_{j}^{\text{GPS}}\) and \(\dot{\varvec{\varPhi }}_{j}^{\text{GPS}}\) are the ionospheric-free pseudorange, carrier phase and Doppler measurements of the jth satellite observed by GPS, and \(L_{j}^{\text{INS}}\), \(\varvec{\varPhi}_{j}^{\text{INS}}\) and \(\dot{\varvec{\varPhi }}_{j}^{\text{INS}}\) are the ionospheric-free pseudorange, carrier phase and Doppler values of the jth satellite predicted by INS.

The generic observation equation for the Kalman filter can be written as:

$${\varvec{Z}}_{k} = {\varvec{H}}_{k} {\varvec{X}}_{k} + {\varvec{\tau}}$$
(18)

where \({\varvec{H}}_{k}\) is the observation matrix (Du and Gao 2012) and \({\varvec{\tau}}\) is the observation noise vector, which is assumed to be white Gaussian noise.

Adaptive federated filter

The most important element of the PPP/INS integrated system is a Kalman filter that fuses the measurements from GPS and the INS to obtain an optimal estimation of the system states. Based on the dynamics model and the observation model, the Kalman filter can apply the observation information to update the system states. Both the federated filter and the adaptive filters are modified Kalman filters. The federated filter can realize parallel filter computing through an information allocation factor, while the adaptive filter can eliminate the effects of the dynamics model errors using an adaptive factor. A new information allocation factor is constructed by the method that was used to compute the adaptive factor. Therefore, the new adaptive federated filter can both realize parallel filter computing and eliminate the influence of the dynamics model errors.

Kalman filter

Optimal estimates of the state vector from the Kalman filter can be attained through a combination of a time update and an observation update. The time update process of the Kalman filter is independent and is written as (Yang and Gao 2006):

$${\bar{\varvec{X}}}_{k} = {\varvec{F}}_{k,k - 1} {\hat{\varvec{X}}}_{k - 1}$$
(19)
$${\bar{\varvec{C}}}_{k} = {\varvec{F}}_{k,k - 1} {\varvec{C}}_{k - 1} {\varvec{F}}_{k,k - 1}^{\text{T}} + {\varvec{Q}}_{k - 1}$$
(20)

The observation update equation of the Kalman filter is expressed as:

$${\hat{\varvec{X}}}_{k} = {\bar{\varvec{X}}}_{k} + {\varvec{G}}_{k} \left( {{\varvec{Z}}_{k} - {\varvec{H}}_{k} {\bar{\varvec{X}}}_{k} } \right)$$
(21)
$${\varvec{G}}_{k} = {\bar{\varvec{C}}}_{k} {\varvec{H}}_{k}^{\text{T}} \left( {{\varvec{H}}_{k} {\bar{\varvec{C}}}_{k} {\varvec{H}}_{k}^{\text{T}} + {\varvec{R}}_{k} } \right)^{ - 1}$$
(22)
$${\varvec{C}}_{k} = \left( {{\varvec{I}} - {\varvec{G}}_{k} {\varvec{H}}_{k} } \right){\bar{\varvec{C}}}_{k}$$
(23)

where \({\bar{\varvec{X}}}_{k}\) is the a priori state estimation, \({\hat{\varvec{X}}}_{k}\) is the a posteriori state estimation, \({\varvec{G}}_{k}\) is the gain matrix of the Kalman filter, \({\bar{\varvec{C}}}_{k}\) is the a priori covariance matrix of the state vector, \({\varvec{C}}_{k - 1}\) is the a posteriori covariance matrix of the state vector, \({\varvec{R}}_{k}\) is the covariance matrix of the measurement noise vector, \({\varvec{Q}}_{k - 1}\) is the covariance matrix of the process noise and \({\varvec{F}}_{k,k - 1}\) is the system transition matrix from time k − 1 to time k.

In a closed-loop integration scheme, a feedback loop is used to correct the systematic errors. In this way, the INS mechanization algorithm performs simple navigation calculations under the assumption of small errors. In this case, the error states will be reset to zero after each observation update (Nassar and El-Sheimy 2006). The navigation resolution is thus expressed as:

$${\hat{\varvec{X}}}_{k} = {\bar{\varvec{C}}}_{k} {\varvec{H}}_{k}^{\text{T}} \left( {{\varvec{H}}_{k} {\bar{\varvec{C}}}_{k} {\varvec{H}}_{k}^{\text{T}} + {\varvec{R}}_{k} } \right)^{ - 1} {\varvec{Z}}_{k}$$
(24)

In a PPP/INS system working in a closed-loop configuration, estimates of the errors from the Kalman filter are introduced into the INS to correct the accelerometer bias and gyroscope drift.

Federated filter

The federated filter for the multisensor system is characterized by low computational cost, high precision and good reliability. In the PPP/INS tightly coupled navigation system, three types of independent measurements are input into the filter, which can be regarded as three sensors being integrated with the INS. Therefore, the integrated navigation system filter can be divided into a pseudorange/INS filter, a carrier phase/INS filter and a Doppler/INS filter. The federated filter can be applied in the PPP/INS tightly coupled navigation system to increase its computational efficiency. In order to reduce the computational complexity, the state equation of the local filter is the same as that of the global filter.

The dynamics model of the PPP/INS tightly coupled navigation system is expressed as shown in (16). In general, the observation equation of the ith local filter is expressed in discrete form as follows:

$${\varvec{Z}}_{ik} = {\varvec{H}}_{ik} {\varvec{X}}_{k} + {\varvec{\tau}}_{ik}$$
(25)

Suppose that the filter estimation values of the ith local filter, the master filter and the global filter are \({\hat{\varvec{X}}}_{ik}\), \({\hat{\varvec{X}}}_{mk}\) and \({\hat{\varvec{X}}}_{k}\), respectively. The corresponding weight matrices are \({\varvec{P}}_{ik}\), \({\varvec{P}}_{mk}\) and \({\varvec{P}}_{k}\), while the covariance matrices are \({\varvec{C}}_{ik}\), \({\varvec{C}}_{mk}\) and \({\varvec{C}}_{k}\).

Because the measurements are independent, the fusion resolution of the federated filter is (Quan and Fang 2012):

$${\varvec{P}}_{k} = \sum\limits_{i = 1}^{r} {{\varvec{P}}_{ik} } + {\varvec{P}}_{mk}$$
(26)
$${\hat{\varvec{X}}}_{k} = {\varvec{P}}_{k}^{ - 1} \left( {\sum\limits_{i = 1}^{r} {{\varvec{P}}_{ik} {\hat{\varvec{X}}}_{ik} + {\varvec{P}}_{mk} {\hat{\varvec{X}}}_{mk} } } \right)$$
(27)

where r is the number of local filters.

In the PPP/INS tightly coupled navigation system, the state vectors of the different local filters are all the same. Updates of the state vector and the covariance matrix are processed in the global filter. No information sharing occurs in the master filter, and as a result, \({\varvec{P}}_{mk} = {\varvec{0}}\).

Based on the principle of information conservation, the weight matrix is distributed to the local filter using the information allocation factor \(\beta_{i}\). The allocation principle is given by:

$${\varvec{P}}_{ik - 1} = \beta_{i} {\varvec{P}}_{k - 1}$$
(28)
$${\hat{\varvec{X}}}_{ik - 1} = {\hat{\varvec{X}}}_{k - 1}$$
(29)
$${\varvec{Q}}_{ik - 1}^{ - 1} = \beta_{i} {\varvec{Q}}_{k - 1}^{ - 1}$$
(30)
$$\sum\limits_{i = 1}^{r} {\beta_{i} } = 1$$
(31)

The time update process for each local filter is independent and can be written as:

$${\bar{\varvec{X}}}_{ik} = {\varvec{F}}_{k,k - 1} {\hat{\varvec{X}}}_{ik - 1}$$
(32)
$${\bar{\varvec{C}}}_{ik} = {\varvec{F}}_{k,k - 1} {\varvec{C}}_{ik - 1} {\varvec{F}}_{k,k - 1}^{\text{T}} + {\varvec{Q}}_{ik - 1}$$
(33)

The observation update equation of the local filter is expressed as:

$${\hat{\varvec{X}}}_{ik} = {\bar{\varvec{X}}}_{ik} + {\varvec{G}}_{ik} \left( {{\varvec{Z}}_{ik} - {\varvec{H}}_{ik} {\bar{\varvec{X}}}_{ik} } \right)$$
(34)
$${\varvec{G}}_{ik} = {\bar{\varvec{C}}}_{ik} {\varvec{H}}_{ik}^{\text{T}} \left( {{\varvec{H}}_{ik} {\bar{\varvec{C}}}_{ik} {\varvec{H}}_{ik}^{\text{T}} + {\varvec{R}}_{ik} } \right)^{ - 1}$$
(35)
$${\varvec{C}}_{ik} = \left( {{\varvec{I}} - {\varvec{G}}_{ik} {\varvec{H}}_{ik} } \right){\bar{\varvec{C}}}_{ik}$$
(36)

The global state estimation value and the weight matrix are obtained by fusing the local filter estimation value according to (26) and (27):

$${\varvec{P}}_{k} = \sum\limits_{i = 1}^{r} {{\varvec{P}}_{ik} }$$
(37)
$${\hat{\varvec{X}}}_{k} = {\varvec{P}}_{k}^{ - 1} \sum\limits_{{i{ = 1}}}^{r} {{\varvec{P}}_{ik} {\hat{\varvec{X}}}_{ik} }$$
(38)

The global state estimation \({\hat{\varvec{X}}}_{k}\) and the weight matrix \({\varvec{P}}_{k}\) will be distributed to each of the local filters by the information allocation factor \(\beta_{i}\) in the next filter. Figure 1 shows the federated filter architecture. In decentralized filtering, the standard Kalman filter is divided into sensor-dedicated local filters (numbered 1 to r). Operationally, these local filters work in parallel, and their solutions are periodically fused via the global filter, thus yielding a global solution. The computational load can be reduced significantly by adopting this decentralized technique. The results, however, may be locally suboptimal, but are globally optimal.

Fig. 1
figure 1

Federated filter architecture

Full size image

Adaptive filter

The adaptive factor is introduced in the adaptive filter to modify the abnormal error in the dynamics model. The adaptive filter resolution is obtained via the conditional extremum method. The extremal function can be written as (Yang and Gao 2006):

$$\Omega = {\varvec{V}}_{k}^{\text{T}} {\varvec{R}}_{k}^{ - 1} {\varvec{V}}_{k} + \alpha_{k} {\varvec{V}}_{{\bar{X}_{k} }}^{\text{T}} {\bar{\varvec{C}}}_{k}^{ - 1} {\varvec{V}}_{{\bar{X}_{k} }} - 2\lambda_{k}^{\text{T}} \left( {{\varvec{H}}_{k} {\hat{\varvec{X}}}_{k} - {\varvec{Z}}_{k} - {\varvec{V}}_{k} } \right)$$
(39)

where \({\varvec{V}}_{{\bar{X}_{k} }}\) and \({\varvec{V}}_{k}\) are the errors for the predicted state vector and the measurement vector, \({\bar{\varvec{C}}}_{k}\) and \({\varvec{R}}_{k}\) are the covariance matrices of \({\varvec{V}}_{{\bar{X}_{k} }}\) and \({\varvec{V}}_{k}\), \(\alpha_{k}\) is the adaptive factor, and \(\lambda_{k}\) is the Lagrange factor.

By calculating the minimum of (39), the adaptive filter resolution can be obtained as follows:

$$\begin{aligned} {\hat{\varvec{X}}}_{k}& = {\bar{\varvec{X}}}_{k} + \frac{ 1}{{\alpha_{k} }}{\bar{\varvec{C}}}_{k} {\varvec{H}}_{k}^{\text{T}} \left( {\frac{ 1}{{\alpha_{k} }}{\varvec{H}}_{k} {\bar{\varvec{C}}}_{k} {\varvec{H}}_{k}^{\text{T}} + {\varvec{R}}_{k} } \right)^{ - 1} \left( {{\varvec{Z}}_{k} - {\varvec{H}}_{k} {\bar{\varvec{X}}}_{k} } \right) \\ &= {\bar{\varvec{X}}}_{k} + {\bar{\varvec{G}}}_{k} \left( {{\varvec{Z}}_{k} - {\varvec{H}}_{k} {\bar{\varvec{X}}}_{k} } \right) \\ \end{aligned}$$
(40)

where \({\bar{\varvec{G}}}_{k}\) is the gain matrix of the adaptive filter.

Equivalence

The weight matrix of the state estimation value is amended in the federated local filter, and the covariance matrix is amended in the adaptive filter. The weight matrix is the inverse matrix of the covariance matrix. Based on the fact that \({\varvec{P}}_{k} = {\varvec{C}}_{k}^{ - 1}\), both sides of (28) can be processed by the inverse matrix calculation:

$${\varvec{C}}_{ik} = \frac{ 1}{{\beta_{i} }}{\varvec{C}}_{k}$$
(41)

The relation between \({\bar{\varvec{C}}}_{ik}\) and \({\bar{\varvec{C}}}_{k}\) can be obtained by substituting (41) into the right side of (33):

$$\begin{aligned} {\bar{\varvec{C}}}_{ik} &= {\varvec{F}}_{k,k - 1} {\varvec{C}}_{ik - 1} {\varvec{F}}_{k,k - 1}^{\text{T}} + {\varvec{Q}}_{ik - 1} \\ &= {\varvec{F}}_{k,k - 1} \frac{ 1}{{\beta_{i} }}{\varvec{C}}_{k - 1} {\varvec{F}}_{k,k - 1}^{\text{T}} + \frac{ 1}{{\beta_{i} }}{\varvec{Q}}_{k - 1} \\ &= \frac{ 1}{{\beta_{i} }}\left( {{\varvec{F}}_{k,k - 1} {\varvec{C}}_{k - 1} {\varvec{F}}_{k,k - 1}^{\text{T}} + {\varvec{Q}}_{k - 1} } \right) = \frac{ 1}{{\beta_{i} }}{\bar{\varvec{C}}}_{k} \\ \end{aligned}$$
(42)

The gain matrix of (35) is therefore expressed as:

$${\varvec{G}}_{ik} = \frac{ 1}{{\beta_{i} }}{\bar{\varvec{C}}}_{k} {\varvec{H}}_{ik}^{\text{T}} \left( {{\varvec{H}}_{ik} \frac{ 1}{{\beta_{i} }}{\bar{\varvec{C}}}_{k} {\varvec{H}}_{ik}^{\text{T}} + {\varvec{R}}_{ik} } \right)^{-1} = \frac{ 1}{{\beta_{i} }}{\bar{\varvec{C}}}_{k} {\varvec{H}}_{ik}^{\text{T}} \left( {\frac{ 1}{{\beta_{i} }}{\varvec{H}}_{ik} {\bar{\varvec{C}}}_{k} {\varvec{H}}_{ik}^{\text{T}} + {\varvec{R}}_{ik} } \right)^{-1}$$
(43)

If \(\alpha_{k} = \beta_{i}\), then \({\varvec{G}}_{ik}\) and \({\bar{\varvec{G}}}_{k}\) in (40) are equivalent. Therefore, the federated local filter and the adaptive filter are equivalent in form.

Adaptive federated filter

In the above demonstration, the federated local filter and adaptive filter have been shown to be equivalent in form. We therefore try to calculate the information allocation factor of the federated filter using the adaptive factor calculation method, which is used to construct the adaptive federated filter. The proposed method will increase the adaptive ability of the federated local filter.

The information allocation factor is calculated based on the predicted residuals (Yang and Gao 2006):

$$\beta_{k} = \left\{ {\begin{array}{*{20}l} 1\hfill & {\left| {\Delta V_{k} } \right| \le {\text{con}}} \hfill \\ {\frac{\text{con}}{{\left| {\Delta V_{k} } \right|}}} \hfill & {\left| {\Delta V_{k} } \right| > {\text{con}}} \hfill \\ \end{array} } \right.$$
(44)

where con is a constant, and con = 0.85–1.0. \(\Delta V_{k}\) represents the statistics constructed based on the predicted residuals \(V_{k}\), which can be expressed as (Wu and Yang 2010):

$$\Delta V_{k} = \frac{{V_{k}^{\text{T}} V_{k} }}{{{\text{tr}}({\varvec{H}}_{k} {\bar{\varvec{C}}}_{{\bar{X}_{k} }} {\varvec{H}}_{k}^{\text{T}} + {\varvec{R}}_{k} )}}$$
(45)

In order to ensure that the information allocation factor obeys the principle of information conservation, the information allocation factor in (31) is processed via a normalization calculation:

$$\beta_{ik}^{\prime } = \frac{{\beta_{ik} }}{{\sum\nolimits_{i = 1}^{r} {\beta_{ik} } }}$$
(46)

where \(\beta_{ik}^{\prime }\) is the information allocation factor of the ith local filter at time k after normalization.

PPP/INS tightly coupled navigation system

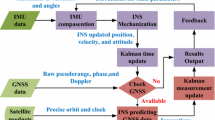
Figure 2 shows the PPP/INS tightly coupled navigation system with the adaptive federated filter. The INS mechanization algorithm derives the current position, velocity and attitude solutions from the measurements of the IMU. Using the pseudorange and Doppler measurements from the GPS receiver, the position and velocity information can also be obtained. After the quality control step, and given the ephemeris of the GPS satellites, the position and velocity from the INS mechanization algorithm are used to predict the pseudorange, carrier phase and Doppler measurement results. During prediction of the carrier phase, the float ambiguity value that resolved in the previous epoch is used. The real-time precise orbit and clock products are used to compute the precise satellite position and the clock correction. After correcting the errors in the raw GPS measurements, the corrected pseudorange, carrier phase and Doppler measurements from the undifferenced GPS are input with the INS-predicted measurements into a different local filter. The filter estimation values and the corresponding weight matrices from the pseudorange local filter, the carrier phase local filter and the Doppler local filter are fused and updated by the global filter to obtain the final position, velocity and attitude. At the same time, the filter estimation value, the information allocation factor and the corresponding weight matrix, which acts as the feedback, are imported into the local filter and will then be used in the next filter.

Fig. 2
figure 2

Proposed PPP/INS tightly coupled navigation system

Full size image

In order to test the self-navigation accuracy of the INS without GPS, a variety of simulations of INS sensors are performed during complete GPS outages. The simulation conditions are located at latitude of 37.6° north and longitude of 108.6° east. The technical parameters for the sensors are listed in Table 1. The technical parameters of system 2 are the same as those of the IMU that is used in the field test below. The technical parameters used in system 1 have values that are double those of the technical parameters of system 2, and the technical parameters of system 3 have values that are one half of those of the technical parameters of system 2. The measurements of the gyroscopes and the accelerometers are generated at a fixed frequency of 100 Hz. A positional comparison of the three systems during complete GPS outages is shown in Fig. 3. The results show that in 1 s we obtained INS self-navigation positioning accuracies of 0.347, 0.217 and 0.087 m from systems 1, 2 and 3. The navigation accuracy attained by the INS during that 1 s is much higher than that derived from the pseudorange. If GPS/INS integration frequency is higher than or equal to 1 Hz, an INS with the same or higher accuracy than system 1 can provide a more accurate initial value for PPP than the single point positioning provided by the pseudorange, which will thus improve the final filter resolution accuracy.

Table 1 Technical parameters of the three systems
Full size table
Fig. 3
figure 3

Comparison of the different INS position accuracies during complete GPS outages

Full size image

Results and discussion

Field tests were then conducted to evaluate the performance of the proposed method. The test systems comprised two Leica GPS receivers and a tactical grade IMU. One of the Leica receivers was set up as the reference station, and the other was used as the rover receiver, with its antenna located above the roof of the test vehicle. We received 1 Hz GPS data and 100 Hz INS data. The total time taken for the test was approximately 20 min. The GPS observations were processed using the GPS software GrafNav™ 8.0 in differential GPS (DGPS) mode, and the results were regarded as position and velocity references. The attitude reference was generated via the DGPS/INS integrated system using Inertial Explorer software produced by NovAtel Inc. The Inertial Explorer software used the DGPS data to update the INS errors with forward and backward filters, and this promises much greater accuracy than the proposed PPP/INS tightly coupled navigation system. The technical parameters of the IMU are given in Table 2 and are the same as those of the simulated system 2 above. The reference solution accuracy is summarized in Table 3. The trajectory of the experiment and the satellite numbers are shown in Figs. 4 and 5.

Table 2 Technical parameters of tactical grade IMU
Full size table
Table 3 Reference solution accuracy
Full size table
Fig. 4
figure 4

Field test trajectory

Full size image
Fig. 5
figure 5

Numbers of satellites

Full size image

Test one

In order to analyze the effects of the INS on the kinematic PPP, the kinematic PPP scheme without the INS (scheme 1) and the PPP/INS tightly coupled scheme (scheme 2) were both applied to process the data. New initial position is required every epoch as input to the Kalman filter for kinematic PPP. The initial position is provided by a single point positioning (SPP) with pseudoranges in scheme 1. Because the GPS sampling frequency was 1 Hz, scheme 2 can obtain a more accurate initial position using the INS resolution. Positional errors were computed with respect to the reference position to evaluate the overall performance.

Figure 6 shows the time series of the position errors in the north, east and down directions for schemes 1 and 2. These three sets of figures show that the proposed PPP/INS tightly coupled navigation system provides better navigation results. Table 4 illustrates the root-mean-square (RMS) errors and the maximum value of the position error. When compared to scheme 1, the proposed scheme 2 improves the positional accuracy in the north, east and down directions by 7.7, 7.8 and 2.3 %, respectively. The velocity in the down direction is near zero for the land vehicles. Zero setting algorithm is employed after every filter process, so the difference of position error between scheme 1 and scheme 2 is very little.

Fig. 6
figure 6

Position errors in the north (top), east (middle) and down (bottom) directions for different schemes

Full size image
Table 4 Comparison of two schemes in terms of position error
Full size table

In order to compare the performance of the above schemes under challenging urban environment conditions, two simulated partly blocked stretches of GPS satellite reception were introduced. Only three GPS satellites were observed between 400 and 500 s and between 900 and 1000 s. Because the number of satellites used is fewer than four, the single point positioning with the pseudoranges does not provide the position information, which will lead to reduced initial position accuracy.

Figure 7 shows the time series of the position errors in the north, east and down directions for schemes 1 and 2. The RMS errors and the maximum value of the position error during the GPS blockage are given in Table 5. When compared to scheme 1, the position accuracy in the north, east and down directions is improved by 65, 47 and 24 %, respectively, in scheme 2. Under the challenging positioning conditions, INS can provide great benefits to PPP because it is able to provide initial position with higher accuracy to PPP resolution.

Fig. 7
figure 7

Position errors in the north (top), east (middle) and down (bottom) directions for different schemes

Full size image
Table 5 Comparison of two schemes in terms of position error
Full size table

Test two

In order to test the efficiencies of the proposed navigation strategy and the filter method shown in Fig. 2, three calculation schemes are used: the conventional GPS/INS tightly coupled navigation system using pseudorange and Doppler measurements (scheme 1), the PPP/INS tightly coupled navigation system with the centralized Kalman filter (scheme 2), and the PPP/INS tightly coupled navigation system with the adaptive federated filter (scheme 3).

Position comparisons of the three schemes are shown in Table 6 and Fig. 8. The black line, the blue line and the red line are the solution differences with respect to the reference value for schemes 1, 2 and 3, respectively. The two lines from schemes 2 and 3 are shown to be almost perfect. The navigation results from Table 6 show that the accuracies of schemes 2 and 3 are almost of the same quality. The federated Kalman filter thus has the same level of performance as the centralized Kalman filter. From another perspective, when compared to the centralized Kalman filter, the federated Kalman filter has a clear advantage in terms of computational efficiency because it can realize parallel filter computing. Because a dynamics model without abrupt errors is used, scheme 3 does not show any adaptive advantage. When compared to scheme 1, the positional accuracies in the north, east and down directions are improved by 94, 84 and 70 %, respectively, for scheme 3. The largest position errors that occur the north, east and down directions are 5.400, 1.756 and 5.321 m, respectively, when scheme 1 is used. In contrast, the largest corresponding position errors that occur when scheme 3 is applied are 0.375, 0.350 and 1.451 m, respectively.

Table 6 Comparison of three schemes in terms of position errors
Full size table
Fig. 8
figure 8

Position errors in the north (top), east (middle) and down (bottom) directions for different schemes

Full size image

Table 7 shows the velocity improvements realized when using the proposed PPP/INS tightly coupled navigation system. Figure 9 plots the integrated system velocity errors in the north, east and down directions. In a similar manner to the position results, the accuracies of schemes 2 and 3 are again almost of the same quality. The results show that the velocity of scheme 3 can achieve accuracy levels of 0.161, 0.139 and 0.423 m/s for the north, east and down coordinate components, respectively. When compared to scheme 1, the proposed PPP/INS tightly coupled navigation system improves the velocity errors in the north, east and down directions by 24, 13 and 34 %, respectively. The improvements in the velocity errors are much smaller than the improvements in the position errors, because the velocity estimation is mainly reliant on the Doppler measurements, which are used in both scheme 1 and scheme 3.

Table 7 Comparison of three schemes in terms of velocity errors
Full size table
Fig. 9
figure 9

Velocity errors in the north (top), east (middle) and down (bottom) directions for different schemes

Full size image

The roll, pitch and yaw errors of schemes 1, 2 and 3 are shown in Table 8 and Fig. 10. Compared with scheme 1, the proposed PPP/INS tightly coupled navigation system improves the roll, pitch and yaw errors by 45, 27 and 41 %, respectively. Figure 11 shows that the PPP/INS tightly coupled navigation system achieves the required suppression of the attitude errors in scheme 1.

Table 8 Comparison of three schemes in terms of attitude errors
Full size table
Fig. 10
figure 10

Attitude errors in the roll (top), pitch (middle) and yaw (bottom) for different schemes

Full size image
Fig. 11
figure 11

Position errors in the north (top), east (middle) and down (bottom) directions for different schemes

Full size image

Test three

In order to analyze the adaptive performance of the adaptive federated filter, the non-adaptive federated filter (scheme 1) and the adaptive federated filter (scheme 2) were both applied in the PPP/INS tightly coupled navigation system. Over the entire trajectory, there is no natural gross error in the dynamics model. At the time of 736 s, a simulated gross error was thus added to the dynamics model.

Figure 11 shows the differences between the solutions of the different schemes and the reference in the north, east and down directions. The three sets of figures show that the proposed PPP/INS tightly coupled navigation system with the adaptive federated filter provides better overall navigation performance. At the time of 736 s, the position errors of scheme 1 reach −0.954, −1.885 and −0.734 m in the north, east and down directions, respectively, while the position errors of scheme 2 reach −0.197, −0.190 and −0.032 m, respectively. Compared with scheme 1, scheme 2 shows position errors at the time of 736 s in the north, east and down directions that have been reduced by 79, 90 and 96 %, respectively.

Conclusions

We present a PPP/INS tightly coupled navigation system to improve the measurement accuracy of the position, velocity and attitude parameters. At the same time, an adaptive federated filter is also proposed and is applied to the PPP/INS integrated system. Through a series of simulations, it can be proved that the federated local filter and the adaptive filter are equivalent in form. Based on that equivalence, the information allocation factor in the federated filter is constructed based on the adaptive factor, which can enable parallel filter computing and improve filter adaptive abilities.

In the standard PPP algorithm, the initial position for the Kalman filter is provided by a single point positioning (SPP) with pseudoranges, while INS resolution can be regarded as the initial position of the filter for PPP in PPP/INS tightly coupled system. The results indicate that the tactical grade INS can provide a more accurate initial position to the Kalman filter for kinematic PPP than the SPP algorithm, which will contribute to a better overall navigation performance. Compared with the standard PPP solution alone, the proposed PPP/INS tightly coupled navigation architecture accuracy in terms of the east, north and down components can be improved by 45, 47 and 24 %, respectively, during partial blockage of the GPS satellite. Additionally, when compared to a conventional GPS/INS integrated system with pseudorange and Doppler measurements, the position, velocity and attitude errors have all been reduced. The proposed adaptive federated filter can obtain the same degree of resolution as the centralized Kalman filter, and it can also realize parallel filter computing and remove the effects of dynamics model errors on the navigation accuracy. In our future work, the potential of INS for improving the PPP ambiguity convergence rate will be investigated.