Single Image Super Resolution via Neighbor Reconstruction

Abstract

Super Resolution (SR) is a complex, ill-posed problem where the aim is to construct the mapping between the low and high resolution manifolds of image patches. Anchored neighborhood regression for SR (namely A+ [15]) has shown promising results. In this paper we present a new regression-based SR algorithm that overcomes the limitations of A+ and benefits from an innovative and simple Neighbor Reconstruction Method (NRM). This is achieved by vector operations on an anchored point and its corresponding neighborhood. NRM reconstructs new patches which are closer to the anchor point in the manifold space. Our method is robust to NRM sparsely-sampled points: increasing PSNR by 0.5 dB compared to the next best method. We comprehensively validate our technique on standardised datasets and compare favourably with the state-of-the-art methods: we obtain PSNR improvement of up to 0.21 dB compared to previously-reported work.

1 Introduction

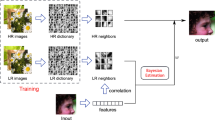
The purpose of single image super-resolution (SR) is to estimate a high resolution (HR) image from a single low resolution (LR) image. It provides a way to enhance the existing images which were generated by delayed imaging equipment or limited imaging conditions, and have been widely studied in recent years. Acquiring a HR estimation from an LR observation is an ill-posed problem and so priors of high quality images are normally relied on in the estimation process. Based on the different priors, existing single image SR methods can be broadly classified into three categories: interpolation-based methods [6, 7], reconstruction-based methods [1, 17] and example learning-based methods [2,3,4,5, 8, 14, 15, 18].

Fig. 1.

Average PSNR (dB) vs time (s) of our algorithm (NRM) compared to other SR methods. We largely improve (red) over the original example based single image super-resolution methods (blue), i.e. our NRM method is 0.21 dB better than A+ [15] and 0.91 dB better than the Global Regression (GR) [14]. Results reported on Set5 with magnification 4. (Color figure online)

Among the above mapping-based methods, neighbor embedding approaches have achieved great research interests. In [14], Timofte et al. proposed a highly efficient and effective SR algorithm called ANR, which maps the LR patches onto the HR domain using the projections learned form neighborhoods. Specifically, it relaxes the $\ell _{1}$-norm regularization commonly used in most of the neighbor embedding and sparse coding approaches [16, 17] to a $\ell _{2}$-norm regularized regression which can be solved offline and stored for each dictionary atom/anchor. This results in large speed benefits. Subsequently, those authors proposed an improved variant of the ANR method called A+ [15] that learns the regressors from the locally nearest training LR and HR patches instead of the small dictionary. It thus better utilizes the prior data to achieve improved performance. Under the framework of A+, many notable methods such as the Half Hypersphere Confinement Regression (HHCR) [11], the Patch Symmetry Collapse (PSyCo) [9] and RFL [12] were proposed.

Although the A+ method [15] has achieved great success in delivering high quality HR estimation, it has two serious limitations: First, to obtain dense sample patches, A+ needs to harvest data images with different scales repeatedly, resulting in a large amount of computation and storage; Second, even if A+ does a so-called densely harvesting, we find that these patches are still too sparse for the high dimension space.

1.1 Contributions

In this paper, we propose a novel and simple neighbor reconstruction method and extend the concept of A+ resulting in a significant improvement.

• 1. Compared with A+, our method utilizes fewer features to construct a closer neighbor and that results in a more accurate reconstruction coefficient vector $\mathbf {x}$. Specifically, we present a new neighbor reconstruction method which adds an anchor point and its corresponding neighbor features together and divides the result by a scalar to generate a much closer neighbor. Compared with the A+ method, our method requires fewer features to generate a closer neighbor set.

• 2. Meanwhile, we have also designed a new projector which has much better numerical stability to adapt to our new problem. As in A+, to obtain the low resolution reconstruction coefficient vector $\mathbf {x}$, we solve a regularized and over-completed least-squares problem detailed in Eq. (4). We present a numerically stable projector Eq. (6) to supplement our method.

• 3. In this case, by benefiting from closer neighbor we obtain a more accurate reconstruction coefficient vector $\mathbf {x}$ leading to an improvement circa 0.1–0.21 dB over A+. Moreover, with fixed memory, more anchor points can be trained leading to much better generalization. Figure 1 shows improved quantitative performance.

Fig. 2.

Illustration of sample reconstruction. (a) geometric interpretation of neighborhood reconstruction. The figure shows how to create a cosine similarity closer point $(\mathbf {f}^{t_{k}}_{l}+\mathbf {f}^{t}_{l})/c$ by using $\mathbf {f}^{t}_{l}$ and its neighbor $\mathbf {f}^{t_{k}}_{l}$. c is an adjustable parameter to make $(\mathbf {f}^{t_{k}}_{l}+\mathbf {f}^{t}_{l})/c$ be close to the intrinsic manifold, namely the solid line. In this figure, when $c=1.85$, $(\mathbf {f}^{t_{k}}_{l}+\mathbf {f}^{t}_{l})/c$ can fall on the intrinsic manifold. (b) shows how to do neighbor reconstruction process iteratively.

2 Analysis of Manifold-Based Single Image SR

We analyse in more detail the A+ technique and explain the limitations of their method. All of our analysis is based on a basic property of the manifold: if an assigned neighbor is close enough then the local manifold subspace can be well described by the observed coordinates of the neighbor. Namely, if the neighbor of aimed anchor point is close enough, we can use our coordinated points to describe the inherent property of the manifold. The well-known Local Linear Embedding (LLE) [10] was proposed based on this property and A+ method was, in turn, motivated by LLE. There are two major deficiencies of A+ method.

• 1. To harvest dense sample patches, the A+ method samples patches at different scales. If we generate dense patches with the A+ method on a large database, it is massively expensive in both computation and memory. For example, for a 91-image dataset, to obtain dense patches around the anchored point, A+ method attempts to harvest 12 times at different scales resulting in about 5 millions patches.

• 2. A simple estimation shows that the patches harvested with the A+ method are not close enough. In practice the dimension of features drawn from the low dimensional patches is around 30. We aim to find a neighbor which lies within an anchor point centred hypersphere whose radius is 0.1. Without loss of generality, supposing that features are normalized and uniformly distributed, at least $10^{30}$ features are needed to reconstruct that required neighbor while only 5 million features are used in A+.

2.1 A Manifold-Based Model

We analyse the generalisation capacity of manifold-based single image SR. Firstly, some notation is introduced. Suppose $\mathbf {p}_{h}$ are small sampled patches which are directly cropped from raw training images. $\mathbf {p}_{l}$ is downsampled patches from $\mathbf {p}_{h}$. And that $\mathbf {f}_{l}$ and $\mathbf {f}_{h}$ are normalized features extracted from $\mathbf {p}_{l}$ and $\mathbf {p}_{h}$ respectively by feature extractors, $\mathbf {f_{l}}=K_{l}(\mathbf {p_{l}})$, $NNNNNNNNNNNNnn\mathbf {f_{h}}=K_{h}(\mathbf {p_{h}})$, where $K_{l}$ and $K_{h}$ is linear feature extractors.

Further suppose that $\widehat{M}_{l}$ and $\widehat{M}_{h}$ are sampled manifolds corresponding to low-dimensional and high-dimensional feature spaces, namely, $\widehat{M}_{l}=\{\mathbf {f}^{(i)}_{l}\}^{n}_{i=1}$, $\widehat{M}_{h}=\{\mathbf {f}^{(i)}_{h}\}^{n}_{i=1}$, where n is the number of extracted features in the low-dimensional or high-dimensional feature space. Suppose $M_{l}$ and $M_{h}$ are continuous ground truth manifolds corresponding to the LR and HR feature spaces. These two manifolds are structurally similar at local subspace. The relationship between the sampled manifolds and ground truth manifolds is: ${M}_{l}=\lim _{n\rightarrow \infty }\widehat{M}_{l}$, ${M}_{h}=\lim _{n\rightarrow \infty }\widehat{M}_{h}$.

There is an important one-to-one mapping, $H(\mathbf {p}_{h})=\mathbf {f}_{l} (\in \widehat{M}_{l})$, which is a naturally formed result when we are preparing the low and high patches. In practice we firstly train an LR dictionary $\mathbf {D}_{l}$,

$$\begin{aligned} \mathbf {D}_{l},\mathbf {\alpha }^{i}=arg\min _{\mathbf {D}_{l}, \mathbf {\alpha }^{i}}\varSigma _{i}\Vert \mathbf {f}_{l}^{(i)}-\mathbf {D}_{l}\mathbf {\alpha }^{i}\Vert _{2}^{2}+\lambda ^{2}\Vert \mathbf {\alpha }^{i}\Vert _2^{2}. \end{aligned}$$

(1)

Each column of $D_{l}$ is called as an atom, $\mathbf {d}_{l}$. In A+ researchers use atoms as anchor points in $\widehat{M}_{l}$ to anchor offline projectors. Given a target low dimensional feature $\mathbf {f}_{l}^{t}$ researchers use a neighbor set of its nearest atom to reconstruct $\mathbf {f}_{l}^{t}$. This reconstruction leads to a reconstruction parameter $\mathbf {x}$. The reconstruction process can be formulated as,

$$\begin{aligned} \begin{array}{l} \mathbf {x}=\mathop {arg \min }\nolimits _{\mathbf {x}} \Vert \mathbf {f}_{l}^{t}-\mathbf {N}_{l}(\mathbf {d}_{l})\mathbf {x}\Vert _{2}^{2}+\lambda ^{2}\Vert \mathbf {x}\Vert _2^{2} \\ \end{array} \end{aligned}$$

(2)

where $\mathbf {N}_{l}(\mathbf {d}_{l})$ is a neighbor set of $\mathbf {d}_{l}$. The Eq. (2) can be solved with a closed-form,

$$\begin{aligned} \begin{array}{l} \mathbf {x}=\mathbf {P}\mathbf {f}_{l}^{t}, \\ \end{array} \end{aligned}$$

where $\mathbf {P}=(\mathbf {N}^T_{l}\mathbf {N}_{l}+\lambda ^{2}\mathbf {I})^{-1}\mathbf {N}^{T}_{l}$. Obviously for each atom its corresponding $\mathbf {P}$ can be prepared offline. With parameter $\mathbf {x}$ and the one-to-one mapping $H(\mathbf {p}_{h})=\mathbf {f}_{l} (\in \widehat{M}_{l})$ high-dimensional patch $\mathbf {p}_{l}$ can be reconstructed in the way used in LLE [10].

The SR problem in the NE framework is to construct a generalized function $G(\mathbf {f}_{l})\approx \mathbf {p}_{h} : M_{l} \rightarrow P_{h}$ where $P_{h}$ is continuous high-dimensional image patches manifold space. Referring to the former one-to-one mapping H. During testing, a given evaluation criterion is used, such as PSNR (Peak Signal to Noise Ratio), SSIM (Structural Similarity Index) and IFC (Information Fidelity Criterion), to estimate the performance of G. The estimator is,

$$\begin{aligned} C(I(G(\mathbf {f}_{l}^{(i)}))- I(\mathbf {p}_{h}^{(i)})), \end{aligned}$$

where C is a chosen image evaluation criterion, I is a patch combining function which generates final patch-combining images. And $\mathbf {f}_{l}^{(i)} \in \widehat{M}_{l}, \mathbf {p}_{h}^{(i)} \in \widehat{P}_{h}$, $\widehat{P}_{h}$ are HR patch sets harvested from the training database.

The object fun of SR is,

$$\begin{aligned} \max _{G} \sum _{i}C(I(G(\mathbf {f}_{l}^{(i)}))- I(\mathbf {p}_{h}^{(i)})). \end{aligned}$$

2.2 The Neighbor Reconstruction Method

As in A+ when we are training the function G, given a target feature $\mathbf {f}^{t}_{l}$, we want to obtain a reconstruction coefficient vector $\mathbf {x}$. Then we directly transfer the coefficient vector into HR patch space, and construct the interest $\mathbf {p}^{t}_{h}$ with one-to-one mapping H. In the HR patch space we use the coefficient vector $\mathbf {x}$ and the corresponding neighbor to reconstruct target $\mathbf {p}^{t}_{h}$. So it is crucial to choose a good neighbor. Inspired by a Euclidean theorem in plane space, namely the parallelogram axiom of vectors, we have designed a neighbor reconstruction method denoted NRM, more detailed in Fig. 2(a). Based on the cosine similarity metric we construct a closer, or more highly correlative, neighbor set for $\mathbf {f}^{t}_{l}$ which will be beneficial in generating a more accurate reconstruction coefficient $\mathbf {x}$.

Denote the neighbors $\mathbf {N}_{l}(\mathbf {d}_{l})$ of $\mathbf {f}^{t}_{l}$ as the set of vectors $[\mathbf {f}^{t_{1}}_{l}, \mathbf {f}^{t_{2}}_{l},\ldots , \mathbf {f}^{t_{k}}_{l}]$. We concatenate the central point and its corresponding neighbors together as column in the matrix $\bar{\mathbf {F}}=[\mathbf {f}^{t_{1}}_{l}, \mathbf {f}^{t_{2}}_{l},\ldots , \mathbf {f}^{t_{k}}_{l}, \mathbf {f}^{t}_{l}]$. We induce a reconstruction operator,

$$\begin{aligned} \mathbf {R}=\begin{bmatrix} \frac{1}{c}&0&\dots&0&0\\0&\frac{1}{c}&\dots&0&0\\ \vdots&\vdots&\ddots&\vdots&\vdots \\ 0&0&0&\frac{1}{c}&0\\ \frac{1}{c}&\frac{1}{c}&\frac{1}{c}&\frac{1}{c}&1 \end{bmatrix}\in \mathbb {R}^{(k+1)\times (k+1)} \end{aligned}$$

(3)

where $c ({>}1)$ is an adjustable parameter. For the jth$\,(1\le j<k+1)$ column $R_{j}$, it can generate the jth reconstructed neighbor $\frac{1}{c}\mathbf {f}^{t}_{l}\,+\,\frac{1}{c}\mathbf {f}^{t_{j}}_{l}$ by the right multiplication $\bar{\mathbf {F}}R_{j}$. For the $(k+1)$th column, it is used to preserve central point $\mathbf {f}^{t}_{l}$ for the next iteration. In NRM, reconstruction manipulation is achieved in parallel by right multiplying $\mathbf {R}$ by $\bar{\mathbf {F}}$. This manipulation can be done achieved iteratively. $\bar{\mathbf {F}}^{(r)}=\bar{\mathbf {F}}\mathbf {R}^r (r \in \{0, 1, 2, 3,\ldots , s\})$ where s is a truncation number. After operating on $\bar{\mathbf {F}}$ for s times, NRM collects $\pm \bar{\mathbf {F}}^{(r)}$ as a large set $\mathfrak {F}=\{\pm \bar{\mathbf {F}}^{(r)}\}_{r=0}^{s}$. The final step in NRM is to select k the nearest points for $\mathbf {f}^{t}_{l}$ from $\mathfrak {F}$ to replace the original neighbor set. Further details of the iterative approach are shown in Fig. 2(b).

$-1$ before $\bar{\mathbf {F}}^{(r)}$ reverse the sign, if we want to employ the parallelogram axiom of vectors to efficiently generate a closer neighbor feature, we must ensure $\mathbf {f}^{t}_{l}$ and $\mathbf {f}^{t_{j}}_{l}$ lie on the same side of the anchor. Considering the existence of antipodal points we reverse the neighbor set by multiplying a negative one ($-1$) on its features, and utilize these reversed antipodal points to generate reconstructed points.

2.3 Solving the Model

First, given a target feature $\mathbf {f}^{t}_{l}$, we employ NRM to generate a corresponding neighbor set $\mathbf {N}_{l}$. To obtain reconstruction coefficients $\mathbf {x}$ in a low resolution space, we need to solve the optimization problem,

$$\begin{aligned} \min _{\mathbf {x}}\Vert \mathbf {f}_{l}^{t}-\mathbf {N}_{l}\mathbf {x}\Vert _{2}^{2}+\lambda ^{2}\Vert \mathbf {x}\Vert _2^{2}. \end{aligned}$$

(4)

For the problem, in A+, the solution is,

$$\begin{aligned} \mathbf {x}=\mathbf {P}\mathbf {f}_{l}^{t}, \end{aligned}$$

where the projector $\mathbf {P}=(\mathbf {N}^T_{l}\mathbf {N}_{l}+\lambda ^{2}\mathbf {I})^{-1}\mathbf {N}^{T}_{l}$.

In our method, we reconstruct a closer neighbor leading to a greater condition number of $\mathbf {N}_l$. If we still apply the projector $\mathbf {P}$ which is deduced with normal equation method to obtain $\mathbf {x}$ in Eq. (4), this will lead to poor results. Because in normal equation method an inverse of matrix is needed to be computed, a large condition number will lead to a big numerical error which can be a deviation from our best results about 6 dB as shown in Fig. 3.

To regular this great condition number problem we design a new projector based on matrix QR decomposition in which we do not have to compute a inverse of matrix. Rewriting Eq. (4) in the least-squares form:

$$\begin{aligned} min \Vert \begin{bmatrix} \lambda \mathbf {I} \\ \mathbf {N}_l \end{bmatrix}_{(m+n,n)} \mathbf {x} -\begin{bmatrix} \mathbf {O} \\ \mathbf {f}_{l}^{t} \end{bmatrix}_{(m+n,1)} \Vert _{2}^{2}, \end{aligned}$$

(5)

where m is the dimension of the features in $\mathbf {N}_l$, n is the number of neighbor features, $(m \ll n)$. And $\mathbf {N}_l \in \mathbb {R}^{m\times n}, \lambda \mathbf {I}\in \mathbb {R}^{n\times n}, \mathbf {O} \in \mathbb {R}^{n\times 1}, \mathbf {f}_{l}^{t} \in \mathbb {R}^{m\times 1}$.

Applying the QR decomposition method to Eq. (5) gives:

$$\begin{aligned} \begin{bmatrix} \lambda \mathbf {I} \\ \mathbf {N}_l \end{bmatrix}_{(m+n,n)}=\mathbf {Q}\mathbf {R}, \end{aligned}$$

where $\mathbf {Q}$ is unitary, $\mathbf {R}$ is upper-triangular, $\mathbf {Q} \in \mathbb {R}^{(m+n)\times (n+m)}, \mathbf {R} \in \mathbb {R}^{(m+n)\times (n)}$.

Fig. 3.

PSNR results of proposed projector and original projector in A+. The red line shows PSNR performance of our method employing with proposed projector. The green one shows the performance of our method employing with original projector. (Color figure online)

Our problem now becomes:

$$\begin{aligned} (\mathbf {Q}\mathbf {R})\mathbf {x}={\begin{bmatrix} \mathbf {O} \\ \mathbf {f}_{l}^{t} \end{bmatrix}}_{(m+n,1)}, \end{aligned}$$

$$\begin{aligned} \mathbf {R}\mathbf {x}&=\hat{\mathbf {Q}}{\begin{bmatrix} \mathbf {O} \\ \mathbf {f}_{l}^{t} \end{bmatrix}}_{(m+n,1)}\\&={\begin{bmatrix} \hat{\mathbf {Q}}_n&\hat{\mathbf {Q}}_m \end{bmatrix}}{\begin{bmatrix} \mathbf {O} \\ \mathbf {f}_{l}^{t} \end{bmatrix}}_{(m+n,1)}\\&\Rightarrow \mathbf {R}\mathbf {x}=\hat{\mathbf {Q}}_m\mathbf {f}_{l}^{t}, \end{aligned}$$

$$\begin{aligned} \begin{array}{l} \mathbf {y}=\hat{\mathbf {Q}}_{m}\mathbf {f}_{l}^{t},\\ \mathbf {R}\mathbf {x}=\mathbf {y},\\ \end{array} \end{aligned}$$

(6)

where, $\hat{\mathbf {Q}}=\mathbf {Q}^{*}$, and $\hat{\mathbf {Q}}_m$ is the last $m$th columns of $\hat{\mathbf {Q}}$, $\mathbf {Q}^{*}$ is conjugate transpose of $\mathbf {Q}$, and $\mathbf {R}\mathbf {x}=\mathbf {y}$ can be solved by substitution method. The performance comparison between normal equation method based and our method based projector is shown in Fig. 3.

Table 1. Performance of x2, x3, and x4 magnification in terms of averaged PSNR (dB), SSIM and execution time (s) on data set Set5, Set14 and BSD100. Best results in red and runner-up in blue.

3 Experiments

We now comprehensively analyze the performance of our proposed NRM in relation to its design parameters and benchmark it in quantitative and qualitative comparison with A+ and other state-of-the-art methods.

We use the training set of images as proposed by Yang et al. [16], Timofte et al. [15] and by Zeyde et al. [17]. However we use a different way to harvest patches from these images. Timofte et al. [15] repeatedly harvested dense patches by means of image pyramid. Because NRM can group a set of dense patches by reconstruction, we employ the Augmented Data set proposed by Timofte et al. in [13], which is a more general sparse data set, and harvest it once. To compare with A+ as fairly as possible, we also trained A+ on the Augmented Data set with the same harvest configuration. However, this configuration degraded A+s quality results. So in the following we use the original configurations of A+.

Note that Set5 and Set14 contain respectively 5 and 14 commonly used images for super-resolution evaluation. B100 aka Berkeley Segmentation Dataset is the B100 data set proposed by Timofte et al. in [15]. We use the same LR path features as Zeyde et al. [17] and Timofte et al. [15].

We compare with the following six methods which share the same training data set: standard bicubic upsampling method, the efficient sparse coding method of Zeyde et al. [17], neighbor Embedding with Locally Linear Embedding (referred to as NE+LLE) [1], Adjusted Anchored Neighborhood Regression (referred to as A+) of Timofte et al. [15], Convolutional Neural Network Method (referred to as SRCNN) of Dong et al. [4] and Fast and Accurate Image Upscaling with Super-Resolution Forest (referred to as RFL) of Schulter et al. [12].

3.1 Results

In order to assess the quality of our proposed method, we tested on 3 datasets (Set5, Set14, B100) used by Timofte et al. [15] for 3 upscaling factors (x2, x3, x4) in the same CPU (Intel Core i7 4750HQ 2 GHz) and memory (8 Gb). Considering quality and time cost, we use dictionary with 4096 atoms and a neighborhood size of 2048. The method of Zeyde et al., NE+LLE, the similarity to Chang et al. [1], and A+ is set up with its common parameters. SRCNN and RFL are training on the same training data set proposed by Timofte et al. leading to a decrease compared to their best performance reported in articles. We report quantitative PSNR and (structural similarity) SSIM results, as well as running times for our bank of methods. In Table 1 we summarize the quantitative results.

In Table 1 we show the averaged PSNR, SSIM and execution times of the benchmark. NRM almost obtains the best PSNR values, around 0.12 dB higher across all scale and data set when compare to the most related algorithm A+. We also outperform some very recent methods (SRCNN and RFL) which are less competitive when trained on the same 91 images training data set. In the terms of computation time, our algorithm is very slightly slower than A+ but still faster than all other methods.

4 Conclusion

In this paper we present a new method for regression-based SR that is built on a novel neighbor reconstruction method (NRM). Via manipulations on anchored points and corresponding neighborhoods, NRM can reconstruct new points which are more closer to anchor point on the assumed manifold. Our contributions are: (1) a new sample reconstruction method with application to regression-based SR; (2) Supported by matrix QR decomposition, we design a more condition-number-stable regressor to compute effective result under closer neighborhood situation. Our results confirm the effectiveness of this approach using various accepted benchmarks, where we clearly outperform the current state-of-the-art. Finally, when the harvested samples are sparse on the manifold, NRM can still construct much closer points and perform well.