Fast Super-Resolution via Dense Local Training and Inverse Regressor Search

Abstract

Regression-based Super-Resolution (SR) addresses the upscaling problem by learning a mapping function (i.e. regressor) from the low-resolution to the high-resolution manifold. Under the locally linear assumption, this complex non-linear mapping can be properly modeled by a set of linear regressors distributed across the manifold. In such methods, most of the testing time is spent searching for the right regressor within this trained set. In this paper we propose a novel inverse-search approach for regression-based SR. Instead of performing a search from the image to the dictionary of regressors, the search is done inversely from the regressors’ dictionary to the image patches. We approximate this framework by applying spherical hashing to both image and regressors, which reduces the inverse search into computing a trained function. Additionally, we propose an improved training scheme for SR linear regressors which improves perceived and objective quality. By merging both contributions we improve speed and quality compared to the state-of-the-art.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Super resolution (SR) comprises any reconstruction technique capable of extending the resolution of a discrete signal beyond the limits of the corresponding capture device. The SR problem is by nature ill-posed, so the definition of suitable priors is critical. Over more than two decades, many of them have been proposed.

Originally, image SR methods were based on piecewise linear and smooth priors (i.e. bilinear and bicubic interpolation, respectively), resulting in fast interpolation-based algorithms. Tsai and Huang [1] showed that it was possible to reconstruct higher-resolution images by registering and fusing multiple images, thus pioneering a vast amount of approaches on multi-image SR, often called reconstruction-based SR. This idea was further refined, among others, with the introduction of iterative back-projection for improved registration by Irani and Peleg [2], although further analysis by Baker and Kanade [3] and Lin and Shum [4] showed fundamental limits on this type of SR, mainly conditioned by registration accuracy. Learning-based SR, also known as example-based, overcame some of the aforementioned limitations by avoiding the necessity of a registration process and by building the priors from image statistics. The original work by Freeman et al. [5] aims to learn from patch- or feature-based examples to produce effective magnification well beyond the practical limits of multi-image SR.

Fig. 1.

Overview of the proposed inverse-search SR: (a) Previous approaches search the 1st nearest dictionary atom for each image patch. (b) Our Proposed approach searches the k-nearest image patches for each dictionary atom.

Example-based SR approaches using dictionaries are usually divided into two categories: internal and external dictionary-based SR. The first exploits the strong self-similarity prior. This prior is learnt directly from the relationship of image patches across different scales of the input image. The opening work on this subcategory was introduced by Glasner et al. [6], presenting a powerful framework for fusing reconstruction-based and example-based SR. Further research on this category by Freedman and Fattal [7] introduced a mechanism for high-frequency transfer based on examples from a small area around each patch, thus better localizing the cross-scale self-similarity prior to the spatial neighborhood. The recent work of Yang et al. [8] further develops the idea of localizing the cross-scale self-similarity prior arriving to the in-place prior, i.e. the best match across scales is located exactly in the same position if the scale is similar enough.

External dictionary-based SR methods use other images to build their dictionaries. A representative widely used approach is the one based on sparse decomposition. The main idea behind this approach is the decomposition of each patch in the input image into a combination of a sparse subset of entries in a compact dictionary. The work of Yang et al. [9] uses an external database composed of related low and high-resolution patches to jointly learn a compact dictionary pair. During testing, each image patch is decomposed into a sparse linear combination of the entries in the low-resolution (LR) dictionary and the same weights are used to generate the high-resolution (HR) patch as a linear combination of the HR entries. Both the dictionary training and testing are costly due to the $L_{1}$ regularization term enforcing sparsity. The work of Zeyde et al. [10] extends sparse SR by proposing several algorithmic speed-ups which also improves performance. However, the bottleneck of sparsity methods still remains in the sparse decomposition.

More recently, regression-based SR has received a great deal of attention by the research community. In this case, the goal is to learn a certain mapping from the manifold of the LR patches to that of HR patches, following the manifold assumption already used in the earlier work of Chang et al. [11]. The mapping of the manifold is assumed to be locally linear and therefore several linear regressors are used and anchored to the manifold as a piecewise linearization. Although these methods are among the fastest in the state-of-the-art, searching the proper regressor takes a significant quota of the running time from within the whole SR pipeline.

In this paper we introduce the following contributions:

• 1. We propose a training scheme which noticeably improves the quality of linear regression for SR (Sect. 3.1) while keeping the same testing complexity, i.e. not increasing testing time.

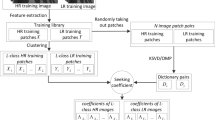
• 2. We formulate an inverse-search approach where for every regressor in the dictionary its k-Nearest Neighbors (k-NN) input image features are found (Fig. 1). Also, we provide a suitable and efficient spherical hashing framework to exploit this scheme, which greatly improves speed at little quality cost. (Section 3.2).

By merging the two contributions, we improve both in speed and quality to both the fastest and the best-performing state-of-the-art methods, as shown in the experimental results.

2 Regression-Based SR

In this section we introduce the SR problem and how example-based approaches tackle it, followed by a review of the recent state-of-the-art regression work of Timofte et al. [12] as it is closely related with the work presented in this paper. The contributions of this paper follow in Sect. 3.

2.1 Problem Statement

Super-Resolution aims to upscale images which have an unsatisfactory pixel resolution while preserving the same visual sharpness, more formally

$$\begin{aligned} X=\,\uparrow (Y)\; s.t.\;\mathcal {X}\approx \mathcal {Y}, \end{aligned}$$

(1)

where $Y$ is the input image, $X$ is the output upscaled image, $\uparrow (\cdot )$ is an upsampling operator and calligraphic font denotes the spectrum of an image.

In the literature this transformation has usually been modeled backwards as the restoration of an original image that has suffered several degradations [9]

$$\begin{aligned} Y=\,\downarrow (B(X)), \end{aligned}$$

(2)

where $B(\cdot )$ is a blurring filter and $\downarrow (\cdot )$ is a downsampling operator. The problem is usually addressed at a patch level, denoted with lower case (e.g. $y,\, x$).

The example-based SR family tackles the super-resolution problem by finding meaningful examples from which a HR counterpart is already known, namely the couple of dictionaries $D_{l}$ and $D_{h}$:

$$\begin{aligned} \min _{\beta }\left\| y-D_{l}\beta \right\| _{2}^{2}+\lambda \left\| \beta \right\| _{p}, \end{aligned}$$

(3)

where $\beta$ selects and weights the elements in the dictionary and $\lambda$ weights a possible $L{}_{p}$-norm regularization term. The $L_{p}$-norm selection and the dictionary-building process depend on the chosen priors and they further define the SR algorithm.

2.2 Anchored Neighborhood Regression

The recent work of Timofte et al. [12] is especially remarkable for its low-complexity nature which achieves orders of magnitude speed-ups while having competitive quality results compared to the state-of-the-art. They proposed a relaxation of the $L_{1}$-norm regularization commonly used in most of the Neighbor Embedding (NE) and Sparse Coding (SC) approaches, reformulating the problem as a least squares (LS) $L_{2}$-norm regularized regression, also known as Ridge Regression. While solving $L_{1}$-norm constrained minimization problems is computationally demanding, when relaxing it to a $L_{2}$-norm, a closed-form solution can be used. Their proposed minimization problem reads

$$\begin{aligned} \min _{\beta }\left\| y_{F}-N_{l}\beta \right\| _{2}^{2}+\lambda \left\| \beta \right\| _{2}, \end{aligned}$$

(4)

where $N_{l}$ is the LR neighborhood chosen to solve the problem and $y_{F}$ is a feature extracted from a LR patch. The algebraic solution is

$$\begin{aligned} \beta =(N_{l}^{T}N_{l}+\lambda I)^{-1}N_{l}^{T}y_{F}. \end{aligned}$$

(5)

The coefficients of $\beta$ are applied to the corresponding HR neighborhood $N_{h}$ to reconstruct the HR patch, i.e. $x=N_{h}\beta$. This can also be written as the matrix multiplication $x=R\, y_{F}$, where the projection matrix (i.e. regressor) is calculated as

$$\begin{aligned} R=N_{h}(N_{l}^{T}N_{l}+\lambda I)^{-1}N_{l}^{T} \end{aligned}$$

(6)

and can be computed offline, therefore moving the minimization problem from testing to training time.

They propose to use sparse dictionaries of $d_{s}$ atoms size, trained with the K-SVD algorithm [13]. A regressor $R_{j}$ is anchored to each atom $d_{j}$ in $D_{l}$, and the neighborhood $N_{l}$ in Eq. (6) is selected from a k-NN subset of $D_{l}$:

$$\begin{aligned} N_{l_{j}}=\mathrm {{\textstyle kNN}}(d_{j},\, D_{l}). \end{aligned}$$

(7)

The SR problem can be addressed by finding the NN atom $d_{j}$ of every input patch feature $y_{iF}$ and applying the associated $R_{j}$ to it. In the specific case of a neighborhood size $k=d_{s}$, only one general regressor is obtained whose neighborhood comprises all the atoms of the dictionary and consequently does not require a NN search. This case is referred in the original paper as Global Regression (GR).

2.3 Linear Regression Framework

Once the closest anchor point is found, the regression is usually applied to certain input features and aims to recover certain components of the patch. We model the linear regression framework in a general way as

$$\begin{aligned} x=\tilde{x}+R\, y_{F}, \end{aligned}$$

(8)

where $\tilde{x}$ is a coarse first approximation of the HR patch $x$. The choice of how to obtain $\tilde{x}$ requires selecting a prior on how to better approximate $x$. In the work of Yang et al. [8] they use the in-place prior as this first-approximation and Timofte et al. [12] use the bicubic interpolation assuming a smooth prior. The regressors are trained to improve the reconstruction whenever the coarse prior is not sufficient. Intuitively, for an optimal performance, the selected feature representation has to be related with the chosen first approximation $\tilde{x}$. Supporting this, [8] uses as input feature the subtraction of the low-pass filtered in-place example to the bicubic interpolation, intuitively modeling the errors of the in-place prior for the low-frequency band; and [12] uses gradient-based features, representing the high-frequency components which are likely not going to be well-reconstructed with bicubic interpolation.

3 Fast Hashing-Based Super-Resolution

In this section we present our super-resolution algorithm based on an inverse-search scheme. The section is divided into two parts representing the contributions of the paper: We first discuss the optimal training stage for linear super-resolution regressors and then introduce our hashing-based regressor selection scheme.

3.1 Training

In regression-based SR the objective of training a given regressor $R$ is to obtain a certain mapping function from LR to HR patches. From a more general perspective, LR patches form an input manifold $M$ of dimension $m$ and HR patches form a target manifold $N$ of dimension $n$. Formally, for training pairs $(y_{Fi},\, x_{i})$ with $y_{F}\in M$ and $x_{i}\in N$, we would like to infer a mapping $\varPsi :M\subseteq \mathbb {R}^{m}\rightarrow N\subseteq \mathbb {R}^{n}$.

Fig. 2.

(a) Mean euclidean distance between atoms and its neighborhood for different neighborhood sizes. (b) Quality improvement measured in PSNR (dB) for a reconstruction using ANR [12] together with our proposed training. 1024 anchor points were used for this experiment.

As we have previously seen, recent regression-based SR use linear regressors because they can be easily computed in closed form and applied as a matrix multiplication. However, the mapping $\varPsi$ is highly complex and non-linear [14]. To model the non-linearity nature of the mapping, an ensemble of regressors $\{R_{i}\}$ is trained, representing a locally linear parametrization of $\varPsi$, under the assumption that both manifolds $M$ and $N$ have a similar local geometry. We analyze the effect on the distribution of those regressors in the manifold (i.e. the anchor points) and the importance of properly choosing the $N_{l}$ in Eq. (6), concluding on a new training approach.

In the work of Timofte et al. [12], an overcomplete sparse representation is obtained from the initial LR training patches using K-SVD [13]. This new reduced dictionary $D_{l}$ is used both as anchor points to the manifold and datapoints for the regression training. In their GR, a unique regressor $R_{G}$ is trained with all elements of the dictionary, therefore accepting higher regression errors due to the single linearization of the manifold. For a more fine-tuned regression reconstruction they also propose the Anchored Neighborhood Regression (ANR), they use as anchor points $\left\{ A_{1},\ldots ,A_{d_{s}}\right\}$ the dictionary points $\left\{ D_{1},\ldots ,D_{d_{s}}\right\}$ and they build for each one of those atoms a neighborhood of $k$-NN within the same sparse dictionary $D_{l}$.

Fig. 3.

A normalized degree 3 polynomial manifold illustrating the proposed approach compared to the one in [12]. (a) Bidimensional manifold samples. (b) The manifold (blue) and the sparse representation obtained with K-SVD algorithm (green) of $8$ atoms. (c) Linear regressors (red) trained with the neighborhoods ($k=1$) obtained within the sparse dictionary, as in [12]. (d) Linear regressors (red) obtained using our proposed approach: The neighborhoods are obtained within the samples from the manifold ($k=10)$ (Color figure online).

Performing a sparse decomposition of a high number of patches efficiently compresses data in a much smaller dictionary, yielding atoms which are representative of the whole training dataset, i.e. the whole manifold. For this reason they are suitable to be used as anchor points, but also sub-optimal for the neighborhood embedding. They are sub-optimal since the necessary local condition for the linearity assumption is likely to be violated. Due to the $L_{1}$-norm reconstruction minimization imposed in sparse dictionaries, atoms in the dictionary are not close in the Euclidean space, as shown in Fig. 2(a).

This observation leads us to propose a different approach when training linear regressors for SR: Using sparse representations as anchor points to the manifold, but forming the neighborhoods with raw manifold samples (e.g. features, patches). In Fig. 2(a) we show how, by doing so, we find closer nearest neighbors and, therefore, fulfill better the local condition. Additionally, a higher number of local independent measurements is available (e.g. mean distance for 1000 neighbors in the raw-patch approach is comparable to a 40 atom neighborhood in the sparse approach) and we can control the number of k-NN selected, i.e. it is not upper-bounded by the dictionary size. We show a low-dimensional example of our proposed training scheme in Fig. 3.

Fig. 4.

Running times measured when computing $6$-bit hash codes ($6$ hyperspheres) for increasing number of queries (in logarithmic axis and without re-ranking) for single-threaded (CPU) and parallel (CPU and GPU) implementations.

In Fig. 2(b) we show the comparison of ANR [12] with both training approaches in terms of resulting image PSNR. We use the same training dataset of the original paper, and for our neighbor embedding we use the $L_{2}$-normalized raw features which are introduced in the K-SVD algorithm. We fix the dictionary size (only used as anchor points in our scheme) to 1024. By applying our training scheme we achieve substantial quality improvements, both qualitatively and quantitatively.

3.2 Inverse Search via Spherical Hashing

When aiming at a fine modeling of the mapping between LR and HR manifolds, several linear regressors have to be trained to better represent the non-linear problem. Although state-of-the art regression-based SR has already pushed forward the computational speed with regard to other dictionary-based SR [9, 10], finding the right regressor for each patch is still consuming most of the execution time. In the work of [12], most of the encoding time (i.e. time left after subtracting shared processing time, including bicubic interpolations, patch extractions, etc.) is spent in this task (i.e. ${\sim }96\,\%$ of the time).

Fig. 5.

Spherical hashing applied for the inverse search super-resolution problem. Certain hashing functions are optimized on feature patch statistics creating a set of hyperspheres intersections that are directly labeled with a hash code. In training time, regressors fill this intersections (i.e. bins) and in testing time the hashing function is applied to each patch, which will directly map it to a regressor.

The second contribution of this paper is a novel search strategy designed to benefit from the training outcome presented in Sect. 3.1, i.e. anchor points of the dictionary and their neighborhoods are obtained independently and ahead from the search structure.

In order to improve the search efficiency, search structures of sublinear complexity are often built, usually in the form of binary splits, e.g. trees, hashing schemes [15–18]. One might consider determining the search partitions with the set of anchor points, since those are the elements to retrieve. However, the small cardinality of this set leads to an imprecise partitioning due to a shortage of sampling density. We propose an inverse search scheme which consists in finding the k-ANN (Approximate Nearest Neighbor) patches within the image for every anchor point, as shown in Fig. 1. By doing so, we have a dense sampling (i.e. all training patches) at our disposal, which results in meaningful partitions.

We choose hashing techniques over tree-based methods. Hashing schemes provide low memory usage (the number of splitting functions in hashing-based structures is $O(\log _{2}(n))$ while in tree-based structures is $O(n)$, where $n$ represents the number of clusters) and are highly parallelizable.

Binary hashing techniques aim to embed high-dimensional points in binary codes, providing a compact representation of high-dimensional data. Among their vast range of applications, they can be used for efficient similarity search, including approximate nearest neighbor retrieval, since hashing codes preserve relative distances. There has recently been active research in data-dependent hashing functions opposed to hashing methods such as [17] which are data-independent. Data-dependent methods intend to better fit the hashing function to the data distribution [18, 19] through an off-line training stage.

Among the data-dependent state-of-the-arts methods, we select the Spherical Hashing algorithm of Heo et al. [16], which is able to define closed regions in $\mathbb {R}^{m}$ with as few as one splitting function. This hashing framework is useful to model the inverse search scheme and enables to benefit from substantial speed-ups by reducing the NN search into applying a precomputed function, which conveniently scales with parallel implementations, as shown in Fig. 4.

Spherical hashing differs from previous approaches by setting hyperspheres to define hashing functions on behalf of the previously used hyperplanes. A given hashing function $H(y_{F})=(h_{1}(y_{F}),\ldots ,h_{c}(y_{F}))$ maps points from $\mathbb {R}^{m}$ to a base 2 $\mathbb {N}^{c}$, i.e. $\left\{ 0,1\right\} ^{c}$. Every hashing function $h_{k}(y_{F})$ indicates whether the point $y_{F}$ is inside $k$th hypersphere, modeled for this purpose as a pivot $p_{k}\in \mathbb {R}^{m}$ and a distance threshold (i.e. radius of the hypersphere) $t_{k}\in \mathbb {R}^{+}$ as:

$$\begin{aligned} h_{k}(y_{F})={\left\{ \begin{array}{ll} 0 &{} when\, d(p_{k},y_{F})>t_{k}\\ 1 &{} when\, d(d_{k},y_{F})\le t_{k} \end{array}\right. }, \end{aligned}$$

(9)

where $d(p_{k},y_{F})$ denotes a distance metric (e.g. Euclidean distance) between two points in $\mathbb {R}^{m}$. The advantages of using hyperspheres instead of hyperplanes is the ability to define closed tighter sub-spaces in $\mathbb {R}^{m}$ as intersection of hyperspheres. An iterative optimization training process is proposed in [16] to obtain the set $\left\{ p_{k},t_{k}\right\}$, aiming a balanced partitioning of the training data and independence between hashing functions.

We perform this mentioned iterative hashing-function optimization in a set of input patch features from training images, so that $H(y_{F})$ adapts to the natural image distribution in the feature space. Our proposed spherical hashing search scheme becomes symmetrical as we can see in Fig. 5, i.e. both image and anchor points have to be labeled with binary codes. This can be intuitively understood as creating NN subspace groups (we refer them as bins), which we label with a regressor by applying the same hashing functions to the anchor points. Relating a hash code with a regressor can be done during training time.

The inverse search approach returns k-NN for each anchor point, thus not ensuring that all the input image patches have a related regressor (i.e. whenever the patch is not within the k-NN of any of the anchor points). Two solutions are proposed: (a) use a general regressor for the patches which are not in the k-NN of any anchor point or (b) use the regressor of the closest labeled hash code calculated with the spherical Hamming distance, defined by [16] as $d_{SH}(a,b)=$ $\frac{\sum (a\oplus b)}{\sum (a\wedge b)}$, where $\oplus$ is the XOR bit operation and $\wedge$ is the AND bit operation. Note that although not being guaranteed, it rarely happens that a patch is not within any of the k-NN regressors (e.g. for the selected parameter of 6 hyperspheres it never occurs). Since we have not observed significant differences in performance, we select (a) as the lowest complexity solution, although more testing on (b) is due.

In a similar way, an inverse search might also assign two or more regressors to a single patch. It is common in the literature to do a re-ranking strategy to deal with this issue [20].

Table 1. Performance of $\times 3$ and $\times 4$ magnification in terms of averaged PSNR (dB) and averaged execution time (s) on datasets Set14, Kodak and 2k.

4 Results

In this section we show experimental results of our proposed method and we compare its performance in terms of quality and execution time to other state-of-the-art recent methods. We perform extensive experiments with image resolutions ranging from $2.5$ Kpixels to $2$ Mpixels, showing the performance for classic literature testing images but additionally demonstrating how these algorithms would perform in current upscaling scenarios. We further extend the benchmark in [12] by adding to Set5 and Set14 two more datasets: the 24 image kodak dataset and 2k, which is a image set of 9 sharp images obtained from the internet with a pixel resolution of $1920\times 1080$.

Table 2. Performance of $\times 3$ and $\times 4$ magnification in terms of PSNR (dB) and execution time (s) on the Set5 dataset.

Fig. 6.

Visual qualitative assessment of $\times 3$ magnification factor for images from different datasets. From left to right and top to bottom: Original, bicubic interpolation, Global Regressor [12], Zeyde et al. [10], ANR [12] and Proposed SR. Better viewed zoomed in.

Fig. 7.

Effect of the number of spheres selected in terms of PSNR (a) and time (b).

All the experiments were run on a Intel Xeon W3690@3.47 GHz and the code of the compared methods was obtained from [12] and used with their recommended parameters. The methods compared are the sparse coding SR of Zeyde et al. [10], an implementation of the LS regressions used by Chang et al. [11] (NE + LLE), and the Non-Negative Least Squares (NE + NNLS) method of Bevilaqcua et al. [21].

The proposed algorithm is written in MATLAB with the most time-consuming stages implemented in OpenCL without further emphasis in optimization, and runs in the same CPU platform used for all methods. Our experiments use the same K-SVD sparse dictionary of 1024 used for the compared methods.

We selected bicubic as our coarse approximation $\tilde{x}$ since it does not limit the upscaling steps for super-resolution (e.g. in-place examples are only meaningful for very small magnification factors) and also the features used by Zeyde et al. [10, 12] composed by 1st and 2nd order derivative filters compressed with PCA and truncating when the feature still conserves $99.9\,\%$ of its energy. We also use a $L_{2}$-norm regularized linear regressor illustrated in Eq. (4). We build therefore on top of the regressor scheme proposed by Timofte et al. [12]. We used $6$-bit spherical hashing ($6$ hyperspheres) and the chosen neighborhood is of $1300$ k-NN. The selection of number of spheres is a trade-off between quality and speed, since when we decrease the number of hyperspheres we have more collision of regressors (i.e. more than one regressor arrives to the same bin) and due to the re-ranking process we get closer to an exact nearest neighbor search. This can be seen in Fig. 7.

In Tables 1 and  2 we show objective results of the performance in terms of PSNR (dB) and execution time (s). For both measures, our proposed algorithm is the best performing. The improvement in PSNR is more noticeable for magnification factors of 3, where we reach improvements of up to $0.3$ dB when compared to the second best-performer. In terms of running time, our algorithm has consistent speed-ups in all datasets and all scales. When compared to GR (which is the fastest of the compared methods), the speed-ups are ranging from $\times 2$ to $\times 3$, additionally with a gap in quality reconstruction. The speed-ups for ANR range from $\times 3$ to $\times 4$ and for the rest of the methods, the running times are several orders of magnitudes slower. Note that the theoretical complexity of GR is lower than that of our method since it does not perform a NN search (i.e. for similar implementations, GR should be slightly faster). Nevertheless, our parallel implementation is more efficient than the one provided by their authors [12], which mostly relies on optimized MATLAB matrix multiplication.

In Fig. 6 a visual qualitative assessment can be performed. Our method obtains more natural and sharp edges, and strongly reduces ringing. A good example of that is shown in the butterfly image.

5 Conclusions

In this paper we have presented two main contributions: An improved training stage and an efficient inverse-search approach for regression-based and, more generally, dictionary-based SR. Spherical hashing techniques have been applied in order to exploit the benefits of the inverse-search scheme. We obtain both quality improvements due to the optimal training stage and also substantial speed-ups from the low-complexity spherical hashing similarity algorithm used in the regressor selection. An exhaustive testing has been performed comparing our method with four datasets of several pixel resolutions, with different upscaling factors and with several state-of-the-art methods. Our experimental results show consistent improvements in PSNR and running times over the state-of-the-art methods included in the benchmark, positioning as the first in both measures.