1 Introduction

The primary purpose of single image super-resolution (SISR) is to restore a high-resolution (HR) image from a single low-resolution (LR) image. Since HR image contain abundant high-frequency detailed information, it can facilitate many computervision tasks. Image SR techniques has been extensively adopted to enhance the image’s resolution to overcome the limitation of low-quality imaging devices [24, 27, 29]. For example, the LR images such as positron emission tomography (PET) images [16], magnetic resonance images (MRI) [3], can be reconstructed using image SR technique to improve its resolution, leading to an improved diagnosis accuracy.

Due to it’s ill-posed characteristic, image SR still remains a challenging problem. Over the past few decades, many researchers have conducted extensive studies on SR and a large amount of methods have been proposed in the literature. These approaches can be categorized into two broad categories, interpolation-based SR methods and learning-based SR methods.

Interpolation-based SR methods [15, 20, 23, 35] use different interpolation approaches, such as nearest neighbor interpolation, bilinear and bicubic interpolation, to approximate the unknown pixels in the HR grid. Interpolation-based methods are difficult to recover lost high-frequency details due to their low-pass filtering characteristics, resulting in excessively smooth HR images. Even more, jagged artifacts tend to arise at the edges of the reconstructed HR image.

Freeman et al. [11] believed that it is possible to recover lost details in the LR image by learning from an external training set and proposed an example-based SR method. The basic idea of example-based SR method is to establish a mapping relationship between HR and LR image patches. Following Freeman’s idea, many learning-based SR methods had been proposed, which can be divided into three categories: neighborhood embedding (NE) based methods, sparse coding based methods and regression-based methods. NE SR method was presented by Chang et al. in [1], which assumes that the two manifolds in the HR and LR space have the same geometric structure, and the target LR patch can be represented by a linear combination of its neighborhood patches. NE SR method can recover a HR image with less complexity of computation, however it’s SR performance still remains great room for improvement. Li et al. [21] proposed an neighbor embedding SR method based on local preservation constraints (LPC), which explicitly emphasize the local consistency on the two manifolds, resulting in reduced blurring and artifacts. Gao et al. [12] divided the entire training set into several subsets using histogram of gradient clustering (HOG), and then, the method finds neighbors for a given patch in the corresponding subset using Robust-SL0 algorithm. Chen et al. [2] use kernel trick to learn the nonlinear mapping between LR and HR image patches. Yu et al. [38] presented an improved NE method by enlarging neighborhood range to all neighbors.

Another class of learning-based SR methods is sparse coding based methods, which was originally proposed by Yang et al. [36]. The sparse coding based SR (ScSR) method encodes the LR or HR image patches in the training set as a linear combination of a LR or HR dictionary, respectively. Under the premise that the LR and HR patches have the same sparse representation coefficients, the target HR patch for a given LR patch can be reconstructed by linearly combining the sparse representation coefficients of the given LR patch and HR dictionary. ScSR method has demonstrated it’s excellent performance and possesses robustness to noise. However, several disadvantages are still associated with ScSR. The sparse coding of LR patch is time-consuming. To speed up the sparse coding process, Zeyde et al. [39] proposed to use principal component analysis (PCA) and orthogonal matching pursuit (OMP) for LR patches sparse coding. As well, a coupled dictionary method [37], Bayesian dictionary [14] learning method had also been proposed for addressing this problem. In addition, the hypothesis that the LR and HR patches have the same sparse representation coefficients is not fully reasonable, which leads to performance drop. In [6], Dong et al. incorporate the difference of sparse coefficients between LR and HR features into the sparse coding of process LR patches.

Regression-based methods also play an essential role in learning-based methods. Kim et al. [18] first adopted the kernel ridge regression to learn the mapping relationship between LR and HR patches. The sparse solution is derived by combining kernel matching pursuit with gradient descent. To acquire sharper edge information in reconstructed HR image, Tang et al. [28] utilized multiple matrix-valued kernel regression for nonlinear mapping. In [22], the linear kernel regression is employed to establish the regression relationship between HR image and fuzzy HR image patches. Furthermore, a kernel regression method with an adaptive Gaussian kernel was proposed in [26]. To overcome over-fitting problem, Ogawa et al. [25] presented a new SR method which combines Gaussian mixture model (GMM) and partial least squares (PLS) regression. The Gaussian process regression (GPR) [13] is introduced into image SR to improve the generalization ability of regression models.

Apart from the those learning-based SR methods mentioned above, Timoft et al. [31] proposed ANR for image SR. This method combines NE method with sparse coding method, which exhibits outstanding SR performance. So far, many improved ANR variants have been proposed. With the aim of exploring the nonlinear relationship between the LR and HR spaces, Jiang et al. [17] exploited the local geometric prior to regularize the neighborhood regression, and meanwhile, the quality of reconstructed HR image is further enhanced using non-local self-similarity. In [40], MI-KSVD method is introduced into dictionary training, and the neighborhoods of a given LR patch is found according to the coherence between dictionary atoms and training samples. In [41], a modified ANR method was proposed using clustering and collaborative representation, in which the whole training set is divided into 1024 clusters using k-means clustering algorithm and each center of clustering represents an atom. In [42], Zhang et al. introduced a collaborative representation cascade (CRC) method to learn the multilayered mapping model between the LR and HR feature space.

With the continuous development of deep learning, more and more researchers have started to apply deep learning to SR reconstruction. Deep learning-based SR methods extract the high-level abstract features from LR/HR images in the train set through multiple-layer convolutional operation and nonlinear transformations, and then reconstruct a HR image by aggregating the extracted features. In 2014, Dong et al. proposed an image SR method based on deep convolutional networks (called SRCNN) [4]. After SRCNN, many deep learning models for image SR had been proposed. To speed up the convergence of SRCNN and obtain global optimal solution, Wang et al. introduced deep and shallow convolution networks [34] for image SR. Tian et al. proposed a lightweight enhanced SRCNN (LESRCNN) [30], which is more computationally frugal than SRCNN. Esmaeilzehi et al. [9] described image SR reconstruction as a three-priority optimization problem and developed an ultra-lightweight convolutional neural network for image SR. In [7], a new residual depth network called ComNet was proposed to solve image SR problem. In [8], Esmaeilzehi et al. proposed a new image restoration network, using pixel by pixel feature attention to calibrate the feature maps extracted by the network. Compared with most existing SR methods, deep learning-based image SR methods have demonstrated great advantage in performance. Though it is, the deep learning-based SR methods have a great deal of demanding on computational resource and power. In addition, the training of deep learning models are time-consuming.

Though ANR and its variants have demonstrated excellent performance, however, there sill has certain disadvantages. In ANR and it’s variants, the ridge regression is adopted to establish the relationship between the target patch and its neighbors in the LR/HR feature space. The coefficients of the ridge regression model are obtained by the least square method. The least square is not the optimal estimator because it does not take the prior distribution of the coefficients into account, which make it less robust to noise and lead to over-fitting. To address the above issues, we propose a new image SR method called B-ANR. B-ANR uses sparse Bayesian regression model to establish the mapping relationship between the LR image patch and its neighbors. The parameter’s of Bayesian regression model and its variance are obtained by maximum a posterior, which is more accurate than the least square. Since our B-ANR is derived in the probabilistic framework, it performs better in terms of generalization and robustness to noise. Experimental results verify that our approach is superior to ANR.

The remainder of this paper is organized as follows. Section 2 characterizes the details our proposed B-ANR method, Sect. 3 presents the experimental results and analysis, Sect. 4 discusses the advantages and disadvantages of the proposed method and deep learning methods, and Sect. 5 derives conclusions to conclude.

2 The Proposed Method

In this section, the proposed method is detailed explained. For the convenience of narration, we first recall the fundamentals of ANR and then explain our proposed B-ANR model.

2.1 Anchored Neighborhood Regression(ANR)

In [31], Timofte et al. introduced an ANR based SR method, which can be viewed as a combination of sparse coding method and NE SR method. ANR starts from a learned LR and HR sparse dictionary pair. ANR takes each atom \(\textbf{d}_j\) in the learned LR dictionary (via the method of [39]) as an anchor point. Then, one finds K nearest neighbors \(\varvec{N}_{l}\) for anchor \(\textbf{d}_j\) in the LR dictionary based on the correlation between the dictionary atoms. Denotes \(\varvec{N}_{l}\) as

$$\begin{aligned} \begin{aligned} \varvec{N}_{l}=\left\{ \varvec{d}_{l}^{1},\varvec{d}_{l}^{2},...,\varvec{d}_{l}^{K}\right\} \end{aligned} \end{aligned}$$
(1)

Using the same assumptions as [1], the input LR image patch \(\varvec{x}_t\) can be approximated as a linear combination of its neighbors \(\varvec{N}_l\) and the weight coefficients \(\varvec{w}\), which can be mathematically expressed as

$$\begin{aligned} \begin{aligned} \varvec{x}_t=\varvec{N}_{l}\varvec{w}+\epsilon . \end{aligned} \end{aligned}$$
(2)

In Eq. (2), the optimal coefficients \(\varvec{w}\) are found by using ridge regression, that is,

$$\begin{aligned} \begin{aligned} \min _{\varvec{w}}{\parallel \varvec{x}_{t}-\varvec{N}_{l}\varvec{w}\parallel }_{2}^{2}+\lambda {\Vert \varvec{w}\Vert }_{2} \end{aligned} \end{aligned}$$
(3)

where \(\lambda \) is a regularization parameter controlling the balance between the reconstruction error of \(\varvec{x}_t\) and the smoothness of \(\varvec{w}\). The closed algebraic solution for ridge regression problem (3) is

$$\begin{aligned} \begin{aligned} \varvec{w}=(\varvec{N}_l^{T}\varvec{N}_l+\lambda \varvec{I})^{-1}\varvec{N}_l^{T}\varvec{x}_t \end{aligned} \end{aligned}$$
(4)

Then, the HR output patch can be calculated using the same weight coefficients on HR neighborhood \(\varvec{N}_h\) as

$$\begin{aligned} \begin{aligned} \varvec{y}_t&=\varvec{N}_h\varvec{w} \end{aligned} \end{aligned}$$
(5)

where \(\varvec{y}_t\) is the HR output patch and \(\varvec{N}_h\) is the HR neighborhood corresponding to \(\varvec{N}_l\). Once the neighborhood is defined, an individual projection matrix \(\varvec{P}_j\) is calculated based on the neighborhood for each anchor \(\varvec{d}_j\) as

$$\begin{aligned} \begin{aligned} \varvec{P}_j=\varvec{N}_h(\varvec{N}_l^{T}\varvec{N}_l+\lambda \varvec{I})^{-1}\varvec{N}_l^{T}. \end{aligned} \end{aligned}$$
(6)

After building the projection matrix for each anchor \(\varvec{d}_j\), one can use the projection matrices to super-resolve a LR image. The process is described as following. First, for each input LR patch \(\varvec{x}_i\), we calculate the correlation between \(\varvec{x}_i\) and all the atoms in the LR dictionary as

$$\begin{aligned} \text {corr}_j= \langle \varvec{x}_i,\varvec{d}_j\rangle . \end{aligned}$$
(7)

Let

$$\begin{aligned} m = \max _{j} \text {corr}_j, \end{aligned}$$

then, the m-th atom in the LR dictionary is selected as the neighbor atom of the input LR patch \(\varvec{x}_i\). Then, the corresponding HR output \(\varvec{y}_i\) patch is reconstructed using the m-th projection matrix as

$$\begin{aligned} \begin{aligned} \varvec{y}_i=\varvec{P}_{m}\varvec{x}_{i}. \end{aligned} \end{aligned}$$
(8)

2.2 Bayesian Anchored Neighborhood Regression

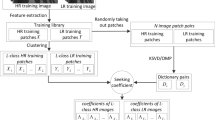
In ANR [31], ridge regression is adopted to build the relationship between the target patch and its neighbors. The coefficients of the ridge regression model are calculated by the least squares method. From a probabilistic perspective, the least squares method is equal to maximum likelihood estimation when the regression error follows a Gaussian distribution. Maximum likelihood estimation does not take the parameter prior into account, leading to less robustness to noise and over-fitting. To build an accurate model to characterize the relationship between the input image patch and its neighbors, we propose B-ANR, which introduces the prior of the weight coefficients into the regression process. Meanwhile, we estimate the model weight coefficients and it’s variance using maximum a posterior estimate method. The overall framework of the proposed B-ANR algorithm is shown in Fig. 1. The following will provide a detailed introduction to our proposed method.

Fig. 1
figure 1

The block diagram of SR algorithm proposed in this paper

Full size image

Given a target LR patch \(\varvec{x}_t\) and it’s nearest neighbors \(\varvec{N}_l\), in the ANR framework, \(\varvec{x}_t\) can be represented as

$$\begin{aligned} \begin{aligned} \varvec{x}_t=\sum _{k=1}^{K}\varvec{w}_{k}\varvec{d}_l^k+\epsilon \end{aligned} \end{aligned}$$
(9)

where \(\epsilon \) represents mean-zero Gaussian with variance \(\sigma ^2\). Let \(\varvec{w}=(\varvec{w}_1,...\varvec{w}_K)^\textrm{T}\) denote weight the coefficient matrix associated with the target patch, then, \(\varvec{x}_t\) can be written in matrix form as

$$\begin{aligned} \begin{aligned} \varvec{x}_t= \varvec{N}_{l}\varvec{w} +\epsilon . \end{aligned} \end{aligned}$$
(10)

The likelihood function of the target vector \(\varvec{x}_t\) could be expressed as

$$\begin{aligned} \begin{aligned} p(\varvec{x}_t|\varvec{w},\sigma ^2)=(2\pi )^{-N/2}\sigma ^{-N}\exp \left\{ -\frac{{\parallel \varvec{x}_t-\varvec{N}_{l}\varvec{w}\parallel }^{2}}{2\sigma ^2} \right\} \end{aligned} \end{aligned}$$
(11)

Directly estimating the weight coefficients \(\varvec{w}\) and variance \(\sigma ^2\) using maximum likelihood easily leads to over-fitting. To solve this issue, the prior distribution of \(\varvec{w}\) is incorporated into the estimation of \(\varvec{w}\). The prior distribution of \(\varvec{w}\) is assumed to be a zero-mean Gaussian distribution with variance of \(\alpha _k^{-1}\) as

$$\begin{aligned} \begin{aligned} p(\varvec{w}|\varvec{\alpha })=(2\pi )^{-K/2}\prod _{k=1}^{K}\sqrt{\alpha _k}\exp \left( -\frac{\alpha _{k}\varvec{w}_{k}^2}{2}\right) \end{aligned} \end{aligned}$$
(12)

Using the Bayesian formula, the weight coefficients posterior \(p(\varvec{w}|\varvec{x}_t,\varvec{\alpha },\sigma ^2)\) can be written as

$$\begin{aligned} p(\varvec{w}|\varvec{x}_t,\varvec{\alpha },\sigma ^2) =\frac{p(\varvec{x}_t|\varvec{w},\sigma ^2)p(\varvec{w}|\varvec{\alpha })}{p(\varvec{x}_t|\varvec{\alpha },\sigma ^2)} \end{aligned}$$
(13)

Substituting Eqs. (11) and (12) into (13), and after some manipulations, one can get

$$\begin{aligned} p(\varvec{w}|\varvec{x}_t,\varvec{\alpha },\sigma ^2) =(2\pi )^{-N/2}\left| \varvec{\Sigma } \right| ^{-\frac{1}{2}}\exp \left\{ -\frac{{\parallel \varvec{w}-\varvec{\mu }\parallel }^{2}}{2\varvec{\Sigma }} \right\} \end{aligned}$$
(14)

by ignoring the denominator of Eq. (13). In Eq. (14)

$$\begin{aligned} \varvec{\Sigma }= & {} (\varvec{A}+\sigma ^{-2}\varvec{N}_l^{T}\varvec{N}_l)^{-1} \nonumber \\ \varvec{\mu }= & {} \sigma ^{-2}\varvec{\Sigma } \varvec{N}_l^{T}\varvec{x}_t \end{aligned}$$
(15)

with \(\varvec{A}\)=diag\((\alpha _1,\alpha _2,...\alpha _k)\). The optimal weight coefficients \(\varvec{w}^*\) would be one that maximizes \(p(\varvec{w}|\varvec{x}_t,\varvec{\alpha },\sigma ^2)\), i.e.,

$$\begin{aligned} \varvec{w}^* = \arg \max _{\varvec{w}} p(\varvec{w}|\varvec{x}_t,\varvec{\alpha },\sigma ^2) \end{aligned}$$
(16)

The optimal solution of problem (15) can be obtained by taking derivation of \(p(\varvec{w}|\varvec{x}_t,\varvec{\alpha },\sigma ^2)\) with \(\varvec{w}\) setting it to zero. Since \(p(\varvec{w}|\varvec{x}_t,\varvec{\alpha },\sigma ^2)\) is a Gaussian function, therefore, the optimal solution of (15) is

$$\begin{aligned} \varvec{w}^* =\varvec{\mu }. \end{aligned}$$
(17)

However, in Eq. (17), the hyper-parameter \(\varvec{\alpha }\) and \(\sigma \) are unknown. Therefore, one should make an estimation for them. This can be done using type-II maximum marginal likelihood procedure. The marginal likelihood is

$$\begin{aligned} \begin{aligned} p(\varvec{x}_t|\varvec{\alpha },\sigma ^2)=\int {p(\varvec{x}_t|\varvec{w},\sigma ^2)p(\varvec{w}|\varvec{\alpha })}\textrm{d}\varvec{w} \end{aligned} \end{aligned}$$
(18)

or its logarithm

$$\begin{aligned} \begin{aligned} \mathcal {L}(\varvec{\alpha })=\ln p(\varvec{x}_t|\varvec{\alpha },\sigma ^2)=-\frac{1}{2}\left[ N\ln (2\pi )+\ln |\varvec{C}|+\varvec{x}_t^{T}\varvec{C}^{-1}\varvec{x}_t\right] \end{aligned} \end{aligned}$$
(19)

where

$$\begin{aligned} \begin{aligned} \varvec{C}=\sigma ^{2}\varvec{I}+\varvec{N}_{l}\varvec{A}^{-1}\varvec{N}_l^T \end{aligned} \end{aligned}$$
(20)

To improve sparsity and reduce computational requirements, we simplify Eq. (20) using the same method as in [33], updating only a single \(\alpha _i\) rather than the entire vector \(\varvec{\alpha }\) per iteration. Rewritten \(\varvec{C}\) as

$$\begin{aligned} \begin{aligned} \varvec{C}&=\sigma ^{2}\varvec{I}+\sum _{k\ne i}\alpha _k^{-1}\varvec{d}_l^{k}\varvec{d}_l^{kT}+\alpha _i^{-1}\varvec{d}_l^{i}\varvec{d}_l^{iT}\\&=\varvec{C}_{-i}+\alpha _i^{-1}\varvec{d}_l^{i}\varvec{d}_l^{iT} \end{aligned} \end{aligned}$$
(21)

where \(\varvec{C}_{-i}\) is \(\varvec{C}\) after removing the contribution of the basis vector i. Using the Woodbury identity for Eq. (21), it is possible to obtain

$$\begin{aligned} \varvec{C}^{-1}=\varvec{C}_{-i}^{-1}-\frac{\varvec{C}_{-i}^{-1}\varvec{N}_l^{i}\varvec{N}_l^{iT}\varvec{C}_{-i}^{-1}}{\alpha _i+\varvec{N}_l^{iT}\varvec{C}_{-i}^{-1}\varvec{N}_l^i} \end{aligned}$$
(22)

and using the determinant identity, we get

$$\begin{aligned} |\varvec{C}|=|\varvec{C}_{-i}||1+\alpha _i^{-1}\varvec{N}_l^{iT}\varvec{C}_{-i}^{-1}\varvec{N}_l^i| \end{aligned}$$
(23)

Substituting Eqs. (22) and (23) into (19), then \(\mathcal {L}(\varvec{\alpha })\) can be written as

$$\begin{aligned} \begin{aligned} \mathcal {L}(\varvec{\alpha })&=\mathcal {L}(\varvec{\alpha }_{-i})+\frac{1}{2}\left[ \log \alpha _i-\log (\alpha _i+s_i)+\frac{q_i^2}{\alpha _i+s_i}\right] \\&=\mathcal {L}(\varvec{\alpha }_{-i})+\ell (\alpha _i) \end{aligned} \end{aligned}$$
(24)

For the convenience of simplicity, let

$$\begin{aligned} \begin{aligned} s_i=\varvec{d}_l^{iT}\varvec{C}_{-i}^{-1}\varvec{d}_l^{i},\quad q_i=\varvec{d}_l^{iT}\varvec{C}_{-i}^{-1}\varvec{x}_t \end{aligned} \end{aligned}$$
(25)

Then, the objective function \(\mathcal {L}(\varvec{\alpha })\) function is decomposed into \(\mathcal {L}(\varvec{\alpha }_{-i})\) and \(\ell (\alpha _i)\), in which the terms in \(\alpha _i\) are now conveniently isolated. Obviously, the unique maximum value of \(\mathcal {L}(\varvec{\alpha })\) is [10]

$$\begin{aligned} \alpha _i= & {} \frac{s_i^2}{q_i^2-s_i}\quad \quad if\quad q_i^2\>s_i \nonumber \\ \alpha _i= & {} \infty \quad \quad \quad \quad if\quad q_i^2\le s_i \end{aligned}$$
(26)

From Eq. (26) we can determine which basis vectors should be included in the model and which ones should be excluded. Once hyper-parameters \(\alpha _i\) is updated using Eq. (26), the parameters \(q_i\), \(s_i\) \(\mu \) and \(\Sigma \) are updated efficiently. As in [33], \(q_i\), \(s_i\) can be updated as the following formula

$$\begin{aligned} S_i= & {} \varvec{d}_l^{iT}\varvec{B}\varvec{d}_l^i-\varvec{d}_l^{iT}\varvec{B}\varvec{N}_l\Sigma \varvec{N}_l^{T}\varvec{B}\varvec{d}_l^i \end{aligned}$$
(27)
$$\begin{aligned} Q_i= & {} \varvec{d}_l^{iT}\varvec{B}\varvec{x}_t-\varvec{d}_l^{iT}\varvec{B}\varvec{N}_l\Sigma \varvec{N}_l^{T}\varvec{B}\varvec{x}_t\end{aligned}$$
(28)
$$\begin{aligned} s_i= & {} \frac{\alpha _{i}S_i}{\alpha _i-S_i}\end{aligned}$$
(29)
$$\begin{aligned} q_i= & {} \frac{\alpha _{i}Q_{i}}{\alpha _{i}-S_{i}} \end{aligned}$$
(30)

where \(\varvec{B}=\sigma ^{-2}\varvec{I}\). Here \(\varvec{N}_l\) and \(\varvec{\Sigma }\) contain only the feature vectors currently included in the model, which is normally a very minor part of the whole K, thus reducing the computational effort considerably.

According to the nature of the marginal likelihood function, we use Eq. (26) as the decision criteria to add or delete the candidate nearest-neighbor features for maximizing the marginal likelihood objective function. In summary, the process of determining the weight coefficients \(\varvec{w}\) is shown in Algorithm 1.

In the reconstruction phase, we assume that LR space and HR space have the same geometry, so the resulting weight coefficients \(\varvec{w}\) can be used to construct the HR image. The HR image patch is calculated by using the HR neighborhood \(\varvec{N}_h\) corresponding to the LR neighborhood \(\varvec{N}_l\) and the weight coefficients \(\varvec{w}\). The SR reconstruction of the image is carried out as follows:

$$\begin{aligned} \begin{aligned} \varvec{y}_t=\varvec{N}_h\varvec{w} \end{aligned} \end{aligned}$$
(31)

where \(\varvec{y}_t\) is the HR output patch and \(\varvec{N}_h=(\varvec{d}_h^1,...\varvec{d}_h^K)\) is the HR neighborhood.

Algorithm 1
figure a

Maximum a posterior estimation of \(\varvec{w}\)

Full size image

3 Experimental Results and Analyses

To verify the validity of the proposed method, super-resolution experiments on several datasets are conducted. Meanwhile, the experimental results obtained by the method of this paper are compared with those obtained by several most advanced SR methods SR methods like Yang et al. [36], Zeyde et al. [39], ANR [31] , NE + LS, NE + LLE [1]. We use peak signal-to-noise ratio (PSNR) and structural similarity (SSIM) as evaluation criteria for measuring the performance of image reconstruction. PSNR represents the ratio of the maximum possible power of a signal to the power of the destructive noise that affects the accuracy of its representation. SSIM is a measure of similarity between two images.

3.1 Experimental Settings

Training Set Learning-based method requires a large amount of image patch pairs for training. In this paper, we use the same training set as Yang et al. [36], Zeyde et al. [39], ANR [31]. We use the images in the training set as HR images and the corresponding LR images are acquired by bicubic interpolation. We divide the HR images into HR image patches of 9 \(\times \) 9 pixel size with an overlap of 6 pixels between neighboring patches. The size of the corresponding LR image patches is set to 3 \(\times \) 3 pixels with an overlap of 2 pixels.

Testing Set To better compare with other methods, we uniformly use Set5 , Set14 and BSD100 as test sets, including 5, 14 and 100 common images, respectively. We perform bicubically interpolation on the images in the test set to obtain LR images for testing and segment the LR images into LR image patches of the same size as in the training set.

Features As the human eye is more susceptible to luminance constituents, we extract features from the luminance channel of the image patches. We use the identical features as Zeyde et al. [39] and Yang et al. [36], who started from the first- and second-order gradients of luminance and performed PCA to reduce the dimension and project the features into a low-dimensional subspace.

Since the features used in the LR patches are not reflective of absolute luminance, we subtract the mean from the luminance-based feature vector for each HR patch. When constructing the target HR image, the patches generated by the SR process are added to the average luminance value of the corresponding LR patches.

Dictionaries In our experiments, We train the dictionaries using the same external images as in Zeyde et al. [39]. For dictionary learning, we use the K-SVD/OMP learning method of Zeyde et al. [39]. To facilitate qualitative comparison with other methods, we uniformly use a dictionary of size 1024.

Neighborhoods As we are calculating weights and reconstructing them based on the neighborhood of the input patch in the dictionary, the method of neighborhood selection is important. For neighborhood selection, we choose neighborhoods on the basis of the correlation between dictionary atoms and image patches. Different sizes of neighborhoods also have different effects on performance, and when comparing methods, we choose the best neighborhood value for each method. In the learning dictionary, the best neighborhood for NN + LS is 12, for NE + LLE [1] and ANR [31] is 40, the best neighborhood chosen for our method is 80.

Table 1 Performance of different methods in terms of PSNR and SSIM per image on Set5 dateset with magnification factor \(\times \)3
Full size table
Table 2 Performance of different methods in terms of PSNR and SSIM per image on Set14 dataset with magnification factor \(\times \)3
Full size table
Table 3 Performance of different methods in terms of PSNR and SSIM at different magnifications for Set5, Set14 and BSD100 dateset
Full size table

3.2 Experimental Results

Timofte et al. [31] demonstrate that for the proper set of parameters, such as feature representation, neighborhood size, most current neighborhood embedding methods are capable of achieving a certain quality of performance. Tables 1 and 2 display the PSNR and the SSIM values for each test image at magnification factor \(\times \)3 for the Set5, Set14 and BSD100 dateset. In addition to deep learning-based SR method, it is evident that our results obtain the highest PSNR and SSIM values compared to other methods, both PSNR and SSIM have different degrees of improvement. In Table 3, we show the average PSNR and SSIM values for the amplification factors \(\times \)2,\(\times \)3,\(\times \)4 on the Set5, Set14, BSD100 datasets. With the exception of TPCNN [4], our proposed method is the best among the others in terms of quality, with an average improvement PSNR of 0.14 dB (BSD100, \(\times \)2) to 0.09 dB (Set5, \(\times \)2) over the ANR [31] method. Different amplification factors of SSIM on Set5, Set14 and BSD100 data sets have an average increase of 0.0023 compared to ANR [31].

In order to demonstrate the superior visual quality of our method compared to other methods, we compare our method with others from a visual perspective in Figs. 2, 3, 4, 5 and 6. We select ‘butterfly’ in Set 5 and ‘baboon’, ‘zebra’, ‘foreman’ and ‘pepper’ in Set 14 with the magnified \(\times \)3. From the figure it can be seen that the Bicubic interpolation method has the worst visual results, producing blurred edge information. Yang et al. [36] reconstructed HR images based on dictionary learning, which also resulted in some ringing and artefact effects. Zeyde et al. [39] used PCA dimensionality reduction to greatly reduce the computational complexity, but it did not have good information about the details of the recovered. NE+LS produces serrated edge information and annoying texture details irritating texture details. NE+LLE method can mitigate the fuzzy edges produced in [36] and [39] by the neighborhood embedding reconstruction method, but it also produces a ringing effect at the edges. ANR [31] combined with neighborhood embedding and sparse coding produced favorable image SR performance, but also did not reconstruct edge information well. In contrast, our method recovers the detail information well and yields sharp edges.

Table 4 Comparison of training time and parameter amount between deep learning methods and our method
Full size table
Fig. 2
figure 2

The visual qualitative assessment of the ‘baboon’ image is from Set5 magnified \(\times \)3

Full size image
Fig. 3
figure 3

The visual qualitative assessment of the ‘butterfly’ image is from Set5 magnified \(\times \)3

Full size image
Fig. 4
figure 4

The visual qualitative assessment of the ‘zebra’ image is from Set14 magnified \(\times \)3

Full size image
Fig. 5
figure 5

The visual qualitative assessment of the ‘foreman’ image is from Set5 magnified \(\times \)3

Full size image
Fig. 6
figure 6

The visual qualitative assessment of the ‘pepper’ image is from Set14 magnified \(\times \)3

Full size image

4 Discussion

In the example-based image SR framework, ANR method achieves the best SR performance compared with other methods using traditional machine-learning techniques. ANR method combines the advantage of sparse coding theory and neighborhood embedding. In ANR, the sparse coding is adopted to extract the feature of image patches and neighborhood embedding to build the relationship among the features. In this paper, we further improved ANR method using Bayesian regression. From theoretic viewpoint and experimental results, one can see that the SR performance of the proposed method indeed has certain improvement.

Though it is, ANR and our proposed method are still associated with some disadvantages compared with deep learning based SR methods. For example, the feature extraction ability of ANR and our proposed method is still weak in a certain extent because only the sparse representation features are utilized. However, the deep learning based methods show powerful ability in extracting the shallow and deep features of images by utilizing a series of convolutional layers. Full utilization of the shallow features and semantic features are helpful for SR performance improvement and enhancement of robustness. This is the essential reason that the deep learning based methods can achieve the breakthrough SR performance.

On the other, the model complexity and computations of deep learning based methods are very large. Because a large number of convolutional layers are involved in deep learning based models, the computation burden in model training and test is huge, therefore, massive computing power are required for most of the deep learning based SR methods. Table 4 lists the rough time required for model training and parameter amount of several deep learning based models and our proposed method. The large computations hampers the application of deep learning based SR methods in the devices with limited computing power such as smart phone and edge-devices.

If we comprehensively take the SR performance and computations into account, ANR and our proposed method are competitive to deep learning based methods.

5 Conclusions

This paper presents an image SR algorithm based Bayesian anchored neighborhood regression. So as to better suppress the noise and increase the generalization performance of SR, we consider the prior distribution of the weight coefficients, using sparse Bayesian regression model to model the mapping relationship between LR image patch and its neighbors. Qualitative comparisons with several state-of-the-art SISR methods are performed to verify the effectiveness and stability of the proposed algorithm. Additionally, we assume that the parameters obey a Gaussian prior distribution, and other probability distributions can also be assumed to verify the validity of the algorithm, which we will investigate in more detail in future work.