An integrated particle swarm optimization approach hybridizing a new self-adaptive particle swarm optimization with a modified differential evolution

Abstract

Hybridizing particle swarm optimization (PSO) with differential evolution (DE), this paper proposes an integrated PSO–DE optimizer and examines the performance of this optimizer. Firstly, a new self-adaptive PSO (SAPSO) is established to guide movements of particles in the proposed hybrid PSO. Aiming at well trade-offing the global and local search capabilities, a self-adaptive strategy is proposed to adaptively update the three main control parameters of particles in SAPSO. Since the performance of PSO heavily relies on its convergence, the convergence of SAPSO is analytically investigated and a convergence-guaranteed parameter selection rule is provided for SAPSO in this study. Subsequently, a modified self-adaptive differential evolution is presented to evolve the personal best positions of particles in the proposed hybrid PSO in order to mitigant the potential stagnation issue. Next, the performance of the proposed method is validated via 25 benchmark test functions and two real-world problems. The simulation results confirm that the proposed method performs significantly better than its peers at a confidence level of 95% over the 25 benchmarks in terms of the solution optimality. Besides, the proposed method outperforms its contenders over the majority of the 25 benchmarks with respect to the search reliability and the convergence speed. Moreover, the computational complexity of the proposed method is comparable with those of some other enhanced PSO–DE methods compared. The simulation results over the two real-world issues reveal that the proposed method dominates its competitors as far as the solution optimality is considered.

1 Introduction

Over the past few decades, inspired by modeling of social interactions among different animals, considerable amount of excellent work has been done to develop different evolutionary algorithms (EAs) in order to handle some complicated optimization problems. Particle swarm optimization (PSO) may be one of the most well-known and preferred EAs based on this concept. Thanks to its simplicity, population-based nature and promising convergence speed, PSO has been widely used in different optimization fields in recent years [1,2,3,4]. Unfortunately, the performance of the conventional PSO is unpromising owing to its difficulty in well adjusting the global and local search capabilities, as well as the high likelihood of being locked into stagnation [5]. Therefore, there exists strong necessity to overcome these two deficiencies in order to enhance the performance and widen the real-world applications of PSO. To this end, many excellent work has recently been done to improve PSO since the first proposal of the conventional PSO [6].

Because the three main control parameters, i.e., the inertia weight, the cognitive and social acceleration parameters, dramatically affect the global and local search abilities of PSO, the poor ability of the conventional PSO in adjusting the global and local search capabilities can be remedied or overcome via some advanced parameter updating rules. Motivated by this idea, the authors in [7] have proposed a linear parameter updating rule to fine-tune the three control parameters of particles in their proposed PSO. Yet, as the search behavior of PSO is highly nonlinear, it may be more flexible to trade-off such two abilities of PSO through nonlinear control parameter updating rules. To this end, many researchers have committed themselves to developing different nonlinear parameter updating strategies [8,9,10,11]. Since the three control parameters also determine the convergence of PSO and the convergence property significantly affects PSO’s performance, it is of great importance to mathematically address the convergence when enhancing PSO through nonlinear parameter updating rules. Unfortunately, the convergence properties of the proposed PSO approaches in these terrific studies [8,9,10,11] remain uncertain.

Considering the importance and impact of the convergence on the performance of PSO, some excellent researches have been dedicated to theoretically investigating the convergence of PSO. Mixing PSO with the evolutionary game theory, the authors in [12] have proposed a novel PSO approach, named evolutionary game-based particle swarm optimization (EGPSO). Despite analytically investigating the convergence of EGPSO, this method may be incapable of guaranteeing the convergence of all particles, since the convergence analysis of this method is conducted based on the deterministic model, which has neglected impacts of the stochastic nature of PSO on the convergence behaviors of particles. In our previous study [13], an improved PSO method, named self-adaptive SPSO 2011 (SASPSO 2011), was proposed. Although the convergence of SAPSO 2011 was analytically investigated, this method has been proven to be a locally convergent approach, which may hinder its applications on the large-scale and complex global optimization problems.

Besides the typical flaw noted above, the conventional PSO may also suffer from the stagnation issue when the global best memory of the swarm or the personal best experience of the particle keeps invariant [10]. Attempting to mitigant this potential issue, the authors in [14] have proposed a new version of PSO, named standard PSO 2011 (SPSO 2011). By randomly drawing a point in a hypersphere determined by the current position of the particle, a point a little “beyond” the personal best position of the particle and a point a little “beyond” the global best position of the swarm, the non-stagnation property can be achieved in SPSO 2011. However, since the three main control parameters of particles in SPSO 2011 remain invariant and there exists no difference between the social and cognitive acceleration parameters, this method may be still incapable of adaptively updating the global and local search capabilities of particles.

Since PSO belongs to the community of EAs, it is natural and reasonable that hybridizing PSO with some other EAs can be a remedy to the potential stagnation issue of PSO. As both PSO and the hybridized EA pertain to the family of EAs, integrating PSO with another EA can not only leverage advantages of two algorithms to enhance the overall perform of the mixed PSO method, but also relieve the potential stagnation of PSO. Thus, in order to avoid particles plugging into iterative stagnation, implementing different EAs to evolve the global best position of the swarm or the personal best positions of particles may be one of the most popular methods [15]. Among the currently existing hybrid PSO approaches, combining differential evolution (DE) with PSO has become one of the most preferred methods, probably thanks to the simplicity and the formidable reliability of DE [16, 17]. However, since DE is sensitive to its generation strategies and control parameters, it is of great significance to set the proper generation strategies and control parameters of DE in the context of integrating PSO with DE [16, 17].

Attempting to remedy the two aforementioned drawbacks of the conventional PSO and enhance the performance of PSO, under the background of combing PSO with DE, this paper proposes a hybrid PSO–DE approach. In order to strike a good balance between the global and local search capabilities of particles, a novel self-adaptive PSO (SAPSO) which adopts a newly established nonlinear control parameter updating rule to tune the three control parameters of particles is developed to guide movements of particles in the proposed hybrid method. Afterward, a modified self-adaptive DE (mSADE) is presented to evolve the personal best memories of particles in the proposed hybrid approach so as to overcome the potential stagnation issue. Note that since the proposed method integrates SAPSO with mSADE, it is named SAPSO–mSADE in this paper. The main works and contributions of this study can be summarized as follows:

• (1) a novel self-adaptive control parameter updating strategy is proposed to nonlinearly adapt the three main control parameters of particles in SAPSO in order to well balance the global and local search abilities of particles.

• (2) the convergence of SAPSO is theoretically studied and a parameter selection principle, sufficiently guaranteeing the convergence of SAPSO, is developed in this paper.

• (3) a ranking-based mutation operator and two different self-adaptive control parameter adaption mechanisms are presented to adjust the scaling factor and the crossover rate in the mSADE algorithm in order to release the optimization burden of the proposed SAPSO–mSADE.

The performance of the proposed method is validated through 25 benchmark test functions, as well as two real-world problems. The numerical simulation results on the 25 benchmarks confirm that: (1) The proposed method is significantly better than its peers with respect to the solution optimality over 25 test functions at the confidence level of 95%; (2) the proposed method performs superior to its contenders over the most of the 25 test functions in terms of the search reliability, as well as the convergence speed; (3) the computational complexity of the proposed method is comparable with those of some other hybrid PSO–DE approaches compared. The numerical simulation results on two real-world issues show that the proposed method performs superior to the compared methods regarding the solution optimality.

The remainder of this paper is organized as follows. Section 2 recalls the conventional PSO and the standard DE. Section 3 states SAPSO and analytically investigates the convergence property pertaining to this method. Section 5 mainly introduces the design of the SAPSO–mSADE-based optimization framework after the statement of mSADE shown in Sect. 4. The numerical simulations, analysis and comparisons of the proposed method on the 25 selected benchmarks are conducted in Sect. 6. The applications of the proposed method on two real-world problems are shown in Sect. 7. Lastly, Sect. 8 draws conclusions and shows some potential options for future work.

2 The conventional PSO and the standard DE

2.1 Review of the conventional PSO

Modeling over the collaborative behavior of bird flocking and fish schooling, Eberhart and Kennedy first proposed the conventional PSO in 1995. The original aim of this algorithm is to reproduce social interactions among individuals to handle some complicated optimization problems [18]. Each individual in the PSO file is referred to be a particle and assigned a velocity which is dynamically updated based on its own flight memory, as well as those of its companions. From the current iteration k to the next iteration $k+1$, particles update their velocities and positions in the conventional PSO as follows [18]:

$$\begin{aligned} {\mathbf {V}}^{k+1}_m &= \omega {\mathbf {V}}^k_m + c_1 r_1 \left( {\mathbf {pbest}}^k_m - {\mathbf {X}}^k_m\right) + c_2 r_2 \left( {\mathbf {gbest}}^k - {\mathbf {X}}^k_m\right) \end{aligned}$$

(1)

$$\begin{aligned} {\mathbf {X}}^{k+1}_m &= {\mathbf {X}}^k_m + {\mathbf {V}}^{k+1}_m \end{aligned}$$

(2)

where ${\mathbf {V}}^{k}_m$ and ${\mathbf {X}}^k_m$ denote the velocity and position of the mth particle at iteration k, respectively. $\omega$ is a real coefficient, standing for the inertia weight parameter. $c_1$ and $c_2$ are two positive real parameters, respectively, denoting the cognitive and social acceleration parameters. $r_1$ and $r_2$ are two random numbers uniformly distributed in [0, 1]. ${\mathbf {pbest}}^k_m$ and ${\mathbf {gbest}}^k$ represent the personal best position of the mth particle and the global best position of the swarm at iteration k, respectively.

2.2 Review of the standard DE

Each individual in the DE file is called a genome or chromosome, representing a potential solution to an optimization problem. In the standard DE, the mutation, crossover and selection operators are three key factors in determining the evolvement of each individual. After these three operators, a newly produced offspring is allowed to the next generation only if it enhances the quality of solution [19].

Focusing on diversifying the population and avoiding the potential local optimum, the mutation operator is applied to yield a trial vector ${\mathbf{T}}_{i}(k)$ through randomly changing the genetic information of three different parent individuals as follows:

$$\begin{aligned} {\mathbf{T}}_{i}(k) = {\mathbf{P}}_{i_3}(k) + {\mathbf {S}}{i} \left( {\mathbf{P}}_{i_1}(k) - {\mathbf{P}}_{i_2}(k)\right) \end{aligned}$$

(3)

where ${\mathbf {S}}{i}$ denotes the scaling vector. ${\mathbf{P}}_{i_1}(k)$, ${\mathbf{P}}_{i_2}(k)$ and ${\mathbf{P}}_{i_3}(k)$ represent three different parent individuals randomly selected from the swarm.

Following a discrete recombination manner to reassemble the genetic information of the trial vector with those of the parent vector, the crossover operator is used to produce new high-quality offsprings in some unknown solution spaces. Based on the binomial recombination, a new offspring can be yielded by the crossover operator in the standard DE as follows:

$$\begin{aligned} U_{ij}(k) = \left\{ \begin{array}{ll} T_{ij}(k),& \quad {\mathrm {if}} \ r_{ij}\le C_r \ {\mathrm {or}} \ j = j_{r}\\ P_{ij}(k), & \quad {\mathrm {otherwise}} \end{array} \right. \end{aligned}$$

(4)

where $U_{ij}(k)$ is the jth element of the new offspring ${\mathbf {U}} _i(k)$ and j ($j = 1,2,\dots , D$) denotes a specific dimension number. D is the dimension of an optimization problem. $P_{ij}$ and $T_{ij}(k)$ refer to the jth elements of ${\mathbf{P}}_i(k)$ and ${\mathbf{T}}_i(k)$, respectively. $j_{r}$ is an integer randomly generated in [1, D]. $r_{ij}$ is a random number uniformly distributed in [0, 1]. $C_r$ stands for the crossover rate.

Adopting a one-to-one spawning principle, the selection operator completes comparisons between the newly produced offspring and its father generations. The newly yielded offspring is allowed to the next generation only if it improves the solution quality, compared with its father generations. For a minimization problem, the selection operator in the standard DE can be mathematically given as follows:

$$\begin{aligned} {\mathbf {P}}_{i}(k+1) = \left\{ \begin{array}{ll} {\mathbf {U}}_i(k), & \quad {\mathrm {if}}\ f({\mathbf {U}}_i(k)) \le f({\mathbf {P}}_i(k))\\ {\mathbf {P}}_{i}(k), & \quad {\mathrm {otherwise}} \end{array} \right. \end{aligned}$$

(5)

where $f({\mathbf {U}}_i(k))$ and $f({\mathbf {P}}_i(k))$ indicate values of the cost function, that is, the fitness values of ${\mathbf {U}} _i(k)$ and ${\mathbf {P}}_i(k)$, respectively.

3 The proposed SAPSO

3.1 Modeling of the self-adaptive strategy in SAPSO

When designing a highly promising PSO-based optimizer for different optimization problems, it is essential to strike a good trade-off between the global and local search powers of PSO [7, 10, 11]. Ideally, on one hand, the global search ability needs to be promoted in the early phases of the evolutionary process, so that particles can search through the whole solution space, rather than converging toward the currently population best solution [7, 10, 11]. On the other hand, the local search power must be strengthened in the latter stages of the evolutionary process to promote particles to local search, so that the likelihood of finding the optimal solution can be enhanced [7, 10, 11].

It is well known that such two capabilities heavily depend on the three control parameters of particles. The basic philosophies regarding how different control parameters affect these two abilities of PSO can be distilled as follows: (1) A large inertia weight parameter facilitates the global search ability, while the local search capability benefits more from a small inertia weight [7, 10, 11]; (2) a large cognitive component, comparing to the social component, leads particles to search through the entire solution space and thus promotes the global search capability [7, 10, 11]; (3) comparing to the cognitive component, a large social component encourages particles to local search and consequently enhances the local search capability [7, 10, 11].

Motivated by all concerns stated above, in order to well balance the global and local search abilities of PSO, this paper first proposes a self-adaptive PSO (SAPSO). Particles in the proposed SAPSO stick to moving rules defined in the conventional PSO to update their velocities and positions as follows [18]:

$$\begin{aligned} {\mathbf {V}}^{k+1}_m &= \omega {\mathbf {V}}^k_m + c_1 r_1 \left( {\mathbf {pbest}}^k_m - {\mathbf {X}}^k_m\right) + c_2 r_2 \left( {\mathbf {gbest}}^k - {\mathbf {X}}^k_m\right) \end{aligned}$$

(6)

$$\begin{aligned} {\mathbf {X}}^{k+1}_m &= {\mathbf {X}}^k_m + {\mathbf {V}}^{k+1}_m \end{aligned}$$

(7)

where all variables in (6) and (7) have same definitions as those in (1) and (2).

For well trade-offing the global and local search abilities of particles, we propose a self-adaptive strategy to fine-tune the three control parameters of particles in SAPSO as follows:

$$\begin{aligned} \omega _{m} &= (\omega _{s} - \omega _{f})\exp \left( -\frac{\delta _\omega k}{\beta _m}\right) + \omega _{f} \end{aligned}$$

(8)

$$\begin{aligned} c_{1m} &= (c_{1s} - c_{1f}){\exp \left( -\frac{\delta _{c1} k}{ \beta _m }\right) } + c_{1f} \end{aligned}$$

(9)

$$\begin{aligned} c_{2m} &= (c_{2s} - c_{2f}) \exp \left( \frac{\delta _{c2} k}{ \beta _m }\right) + c_{2f} \end{aligned}$$

(10)

$$\begin{aligned} \delta _\omega &= \frac{\omega _{s} - \omega _{f}}{k_{\mathrm{max}}} \end{aligned}$$

(11)

$$\begin{aligned} \delta _{c1} &= \frac{c_{1s} - c_{1f}}{k_{\mathrm{max}}} \end{aligned}$$

(12)

$$\begin{aligned} \delta _{c2}&= \frac{c_{2s} - c_{2f}}{k_{\mathrm{max}}} \end{aligned}$$

(13)

$$\begin{aligned} \beta _m&= \Big |\Big |{\mathbf {gbest}}^k - {\mathbf {pbest}}_m^k\Big |\Big | \end{aligned}$$

(14)

where subscripts “s” and “f” in each variable indicate the initial and final values of the corresponding control parameter. $\beta _m$ is a positive parameter that denotes the Euclidean distance between the personal best position of the particle and the global best position of the swarm. $k_{\mathrm{max}}$ is a predefined constant parameter, indicating the maximum iteration number.

It is notable that the initial and final values of each control parameter in the proposed self-adaptive strategy are predefined based on the empirical experience of the decision makers. Here, we set that $\omega _{f} < \omega _{s}$, $c_{1s} > c_{1f}$ and $c_{2s} < c_{2f}$ in the newly developed self-adaptive strategy defined by (8)–(14). As particles exhibit nonlinear search behaviors, it is probably more suitable and flexible to balance the global and local search abilities of PSO through nonlinear control parameter updating strategies [10]. Inspired by this concern, as shown in (8)–(14), the three control parameters of particles are nonlinearly tuned by the developed self-adaptive strategy in SAPSO. Also, probably in virtue of the fast growing nature of the exponential function, it has been discovered that adjusting the control parameters of particles based on the exponential manner may enhance the convergence speed of PSO [20]. Motivated by such a discovery, in order to enhance the convergence speed of SAPSO, the three control parameters of particles in this algorithm are updated based on an exponential manner, as shown in (8)–(10) in the developed self-adaptive strategy.

3.2 Parametric analysis under the self-adaptive strategy in SAPSO

It is clearly evident from (8) to (10) that $\omega _m$ and $c_{1m}$ decrease ($c_{2m}$ increases) with the iteration number k increasing. This implies that SAPSO is more likely to strength the global search at the beginning of the evolution, based on the basic philosophies noted above. As the evolution continues, since $\omega _m$ and $c_{1m}$ become smaller, while $c_{2m}$ grows greater, the local search ability of SAPSO is probably more favored and preserved in the latter stages of the evolution.

In addition to the iteration number k, trade-offs between the global and local search capabilities of SAPSO are also adapted based on the parameter $\beta _m$. From (8) to (10), it is trivial that changes in $\omega _m$ and $c_{1m}$ become smaller, while the variation in $c_{2m}$ grows larger as $\beta _m$ increases. This implies that the global search ability of SAPSO is possibly to be more dominant in the case where the value of $\beta _m$ remains large. In contrast, for a small value of $\beta _m$, the local search ability of this algorithm can quickly dominate and take over the global search power.

Actually, it can be observed from (14) that a large value of $\beta _m$ indicates that the personal best position of the particle is far away from the global best position of the swarm. In such a case, it is logical to strengthen the global search ability of SAPSO so as to promote particles to move closer to the global best position of the swarm as quickly as possible. Contrarily, a small value of $\beta _m$ implies that the particle’s personal best position is near to the global best position of the swarm. In such a case, it is logically reasonable to facilitate the local search capability of SAPSO in order to encourage particles to search carefully in a local solution space nearby the global best solution space, so that the possibility of finding a high-quality global best solution can be increased.

On balance, via adopting the developed self-adaptive strategy defined by (8)–(14), the three control parameters of particles in SAPSO can be adaptively updated based on a manner complying with the basic philosophies in the field of PSO development. Hence, particles in the proposed SAPSO are expected to improve their capabilities in finding high-quality solutions.

3.3 Convergence analysis of SAPSO

The analytical convergence investigation of PSO aims to discover different control parameter boundaries to theoretically guarantee the convergence of PSO. Because each dimension in velocity and position vectors of the particle in SAPSO adjusts independently from the remaining in (6) and (7), without loss of generality, SAPSO can be simplified into a one-dimensional case to study its convergence. For simplicity and without loss of generality, we omit subscript “m” in each variable in (6) and (7). The one-dimensional SAPSO can be then written into a dynamic system as follows:

$$\begin{aligned} \left[ \begin{array}{c}X(k+1)\\ V(k+1)\\ \end{array}\right] = {{\left( \begin{array}{cc} 1-c & \omega \\ -c & \omega \\ \end{array}\right) }} \left[ \begin{array}{c} X(k) \\ V(k) \\ \end{array}\right] + \left[ \begin{array}{c} c \\ c \end{array}\right] P \end{aligned}$$

(15)

where

$$\begin{aligned} c&= c _1 r_1+ c_2 r_2 \end{aligned}$$

(16)

$$\begin{aligned} P&= \frac{c_1 r_1 \cdot pbest + c_2 r_2 \cdot gbest}{c} \end{aligned}$$

(17)

Based on the dynamic system theory, the characteristic equation to the dynamic system denoted by (15) is obtained as:

$$\begin{aligned} \eta ^2 - ( 1 + \omega - c ) \eta + \omega = 0 \end{aligned}$$

(18)

Then, two roots, represented by $\eta _{1,2}$, to (15) are:

$$\begin{aligned} \eta _{1,2} = \frac{1 + \omega - c \pm \sqrt{(1+\omega -c)^2-4\omega }}{2} \end{aligned}$$

(19)

According to the dynamic system theory, (15) converges iff magnitudes of its two characteristic roots are less than 1 [21]. Therefore, we have that (15) converges, iff:

$$\begin{aligned} {\mathrm {Max}} \{\left| \eta _1 \right| , \left| \eta _2 \right| \} < 1 \end{aligned}$$

(20)

From (19), it appears that $\eta _{1,2}$ can be two real or complex roots. Both these two cases are discussed separately in order to easily analyze the convergence of SAPSO.

• (a) The case where $\eta _{1,2}$ are both complex roots, represented by $\eta _{1,2}\in {\mathbb {C}}$, where ${\mathbb {C}}$ is the set of all complex numbers.

Lemma 1

For (15), it is trivial that  $\eta _{1,2} \in {\mathbb {C}}$,  iff:

$$\begin{aligned} 1 + \omega - 2 \sqrt{\omega }< c< 1 + \omega + 2 \sqrt{\omega } \end{aligned}$$

(21)

Proof

From (18), it is evident that:

$$\begin{aligned} \eta _{1,2} \in {\mathbb {C}} \Leftrightarrow (1 + \omega - c) ^2 - 4\omega < 0 \end{aligned}$$

(22)

Expanding the right-hand inequality of (22), we can easily prove that Lemma 1 holds. $\square$

Next, we will find conditions on $\omega$ and c, which can guarantee the convergence of (15) in the case where $\eta _{1,2} \in {\mathbb {C}}$. Here, recall that (15) converges if and only if ${\mathrm {Max}} \{\left| \eta _1 \right| , \left| \eta _2 \right| \} < 1$ holds.

Lemma 2

Under the situation where  $\eta _{1,2} \in {\mathbb {C}}$,  (15)  converges, iff:

$$\begin{aligned} \left\{ \begin{array}{l} 1 + \omega - 2 \sqrt{\omega }< c< 1 + \omega + 2 \sqrt{\omega } \\ 0 \le \omega <1 \end{array} \right. \end{aligned}$$

(23)

Proof

It is notable that the magnitude of any complex number H can be obtained by $\left| H \right| = \sqrt{H_{r}^2 + H_{c}^2}$, where $H_{r}$ and $H_{c}$ represent the real and imaginary parts of H, respectively. Thus, for $\eta _{1,2} \in {\mathbb {C}}$, it is clear that:

$$\begin{aligned} \begin{array}{l} {\mathrm {Max}} \{\left| \eta _1 \right| , \left| \eta _2 \right| \} = \left| \eta _1 \right| = \left| \eta _2 \right| =\sqrt{\omega } \end{array} \end{aligned}$$

(24)

Hence, for $\eta _{1,2}$, it is clear that:

$$\begin{aligned} {\mathrm {Max}} \{\left| \eta _1 \right| , \left| \eta _2 \right| \}< 1 \Leftrightarrow \sqrt{\omega } < 1 \end{aligned}$$

(25)

According to Lemma 1, for $\eta _{1,2} \in {\mathbb {C}}$, (21) must satisfy. Thereafter, considering both conditions that $\eta _{1,2} \in {\mathbb {C}}$ and ${\mathrm {Max}} \{\left| \eta _1 \right| , \left| \eta _2 \right| \} < 1$, it is trivial that, for $\eta _{1,2} \in {\mathbb {C}}$, (15) converges, iff:

$$\begin{aligned} \left\{ \begin{array}{ll} 1 + \omega - 2 \sqrt{\omega } \le c \le 1 + \omega + 2 \sqrt{\omega } \\ 0 \le \omega <1 \end{array} \right. \end{aligned}$$

(26)

This completes the proof of Lemma 2. $\square$

For $\eta _{1,2} \in {\mathbb {C}}$, the convergence region of SAPSO concerning different control parameter planes is shown in Fig.  1.

Fig. 1

The convergence region and of SAPSO for $\eta _{1,2} \in {\mathbb {C}}$. a 3-D presentation of $\omega$, c and ${\mathrm {Max}} \{\left| \eta _1 \right| , \left| \eta _2 \right| \}$, b 2-D projection of $\omega$ and c, c 2-D projection of $\omega$ and ${\mathrm {Max}} \{\left| \eta _1 \right| , \left| \eta _2 \right| \}$, d 2-D projection of c and ${\mathrm {Max}} \{\left| \eta _1 \right| , \left| \eta _2 \right| \}$

• (b) The case where $\eta _1$ and $\eta _2$ are two real roots, represented by $\eta _{1,2} \in {\mathbb {R}}$, where ${\mathbb {R}}$ denotes the real-valued domain.

Lemma 3

For  (15),  it is evident that  $\eta _{1,2} \in {\mathbb {R}}$,  iff:

$$\begin{aligned} \left. \begin{array}{l} c \in {\mathbb {R}},\quad {\mathrm{for}} \ \omega< 0\\ {\mathrm {or}} \\ c \le 1+ \omega - 2\sqrt{\omega } < 0,\quad \, {\mathrm{for}} \ \omega \ge 0 \\ {\mathrm {or}} \\ c \ge 1+ \omega + 2\sqrt{\omega }, \quad {\mathrm{for}}\, \ \omega \ge 0 \end{array} \right. \end{aligned}$$

(27)

Proof

It is trivial from (18) that:

$$\begin{aligned} \eta _{1,2} \in {\mathbb {R}} \Leftrightarrow (1 + \omega - c)^2 -4\omega \ge 0 \end{aligned}$$

(28)

Expanding the right-hand inequality of (28), we can have that c belongs to any real number, denoted as $c \in {\mathbb {R}}$ in (27), in the case where $\omega < 0$ or $c \le 1+ \omega - 2\sqrt{\omega } < 0$ or $c \ge 1+ \omega + 2\sqrt{\omega }$ in the case where $\omega >0$. Thus, this completes the proof of Lemma 3. $\square$

Next, we will find conditions on c and $\omega$ to guarantee the convergence of (15) in the case where $\eta _{1,2} \in {\mathbb {R}}$. Trivially, we can obtain from (19) and (20) that ${\mathrm {Max}} \{\left| \eta _1 \right| , \left| \eta _2 \right| \} < 1$ holds, iff:

$$\begin{aligned} -1< \frac{1 + \omega - c - \sqrt{(1+\omega -c)^2-4\omega }}{2} \le \frac{1 + \omega - c + \sqrt{(1+\omega -c)^2-4\omega }}{2} <1 \end{aligned}$$

(29)

Expanding (29) yields:

$$\begin{aligned} c - \omega -3< \pm \sqrt{(1+ \omega - c)^2-4\omega } < c - \omega + 1 \end{aligned}$$

(30)

Since $\eta _{1,2} \in {\mathbb {R}}$, it is evident that:

$$\begin{aligned} (30) \Leftrightarrow \left\{ \begin{array}{l} c - \omega -3< - \sqrt{(1+ \omega -c )^2-4\omega } \\ \sqrt{(1+\omega - c)^2-4\omega } < c - \omega + 1 \end{array} \right. \end{aligned}$$

(31)

Simplifying the right-hand inequalities in (31) produces:

$$\begin{aligned} (30) \Leftrightarrow \left\{ \begin{array}{ll} 2\omega +2 - c> 0 \\ c > 0 \end{array} \right. \end{aligned}$$

(32)

In the case where $\eta _{1,2} \in {\mathbb {R}}$, (27) must hold based on the conclusion drawn in Lemma 3. Thus, taking both conditions that $\eta _{1,2} \in {\mathbb {R}}$ and ${\mathrm {Max}}\{\left| \eta _1 \right| , \left| \eta _2 \right| \}< 1$ into account, in the case where $\eta _{1,2} \in {\mathbb {R}}$, (15) converges, iff:

$$\begin{aligned} \left\{ \begin{array}{l} 0< c< 2\omega + 2, \ -1< \omega< 0 \\ 0< c \le 1 + \omega - 2\sqrt{\omega } \ {\mathrm {or}} \ 1 + \omega + 2\sqrt{\omega } \le {{c}}< 2\omega +2, \ 0 \le \omega <1 \\ \end{array} \right. \end{aligned}$$

(33)

Figure 2 shows the convergence domain of SAPSO in the case where $\eta _{1,2} \in {\mathbb {R}}$.

Fig. 2

The convergence domain of SAPSO for $\eta _{1,2} \in {\mathbb {R}}$. a 3-D presentation of $\omega$, c and ${\mathrm {Max}} \{\left| \eta _1 \right| , \left| \eta _2 \right| \}$, b 2-D projection of $\omega$ and c, c 2-D projection of $\omega$ and ${\mathrm {Max}} \{\left| \eta _1 \right| , \left| \eta _2 \right| \}$, d 2-D projection of c and ${\mathrm {Max}} \{\left| \eta _1 \right| , \left| \eta _2 \right| \}$

Finally, combining convergence conditions of SAPSO in the cases where $\eta _{1,2} \in {\mathbb {C}}$ and $\eta _{1,2} \in {\mathbb {R}}$ together, it is conclusive that SAPSO converges, iff:

$$\begin{aligned} \left\{ \begin{array}{ll} 0< c< 2\omega + 2 \\ -1< \omega < 1 \end{array} \right. \end{aligned}$$

(34)

Since $c = c_1r_1 + c_2r_2$, the necessary and sufficient condition for the convergence of SAPSO given by (34) can be rewritten as follows:

$$\begin{aligned} \left\{ \begin{array}{l} 0< c_1r_1 + c_2r_2< 2 \omega + 2 \\ -1< \omega < 1 \end{array} \right. \end{aligned}$$

(35)

Note that the convergence condition given by (35) is the necessary and sufficient condition for the convergence of SAPSO. The real convergence domain of SAPSO is demonstrated in Fig. 3. Only if any control parameter selection of $\omega$ and c (here, $c = c_1r_1 + c_2r_2$ ) locates in the region denoted by Fig. 3b, the convergence of SAPSO can be necessarily and sufficiently guaranteed.

Fig. 3

The real convergence domain of SAPSO. a 3-D presentation of $\omega$, c and ${\mathrm {Max}} \{\left| \eta _1 \right| , \left| \eta _2 \right| \}$, b 2-D projection of $\omega$ and c, c 2-D projection of $\omega$ and ${\mathrm {Max}} \{\left| \eta _1 \right| , \left| \eta _2 \right| \}$, d 2-D projection of c and ${\mathrm {Max}} \{\left| \eta _1 \right| , \left| \eta _2 \right| \}$

3.4 The convergence-guaranteed parameter selection rule for SAPSO

Similar to the most PSO methods, the stochastic nature of SAPSO imposes difficulties on rigorously establishing an exact relationship between the stochastic nature and the convergence condition of this algorithm. Therefore, after analytically investigating the convergence of SAPSO, it is necessary to study the convergence of this method without considering its stochastic nature, so that a sufficient convergence condition can be easily discovered for this approach. To this end, followed by the proof of the following lemma, this study provides a parameter selection rule which can sufficiently guarantee the convergence of SAPSO. Note that the stochastic nature of SAPSO is attributed to existences of two random numbers $r_1$ and $r_2$ in (35).

Lemma 4

Without considering its stochastic nature, SAPSO converges, if:

$$\begin{aligned} \left\{ \begin{array}{l} 2\omega + 2> c_1 + c_2 \\ -1< \omega < 1 \\ c_1,c_2 > 0 \end{array} \right. \end{aligned}$$

(36)

Proof

As $c_1$ and $c_2$ are two positive parameters, and $r_1$ and $r_2$ are uniformly distributed in [0, 1], it is trivial that $c_1 \ge c_1r_1$ and $c_2 \ge c_2r_2$. Therefore, we have:

$$\begin{aligned} \left\{ \begin{array}{l} 2\omega + 2> c_1 + c_2 \\ -1< \omega< 1 \\ c_1,c_2 > 0 \end{array} \right. \Rightarrow \left\{ \begin{array}{l} 0< r_1c_1 + r_2c_2< 2\omega + 2 \\ -1< \omega < 1 \end{array} \right. \end{aligned}$$

(37)

Because the right-hand side inequalities in (37) denote the necessary and sufficient condition for the convergence of SAPSO, as shown in (35), the proof of Lemma 4 is completed according to the logical relationship given by (37). $\square$

It is notable that Lemma 4 provides a sufficient convergence condition for SAPSO. From this lemma, one can easily observe that the convergence of SAPSO is determined by values of the three control parameters. Also, from the developed self-adaptive strategy defined by (8)–(14), it is clear that values of these control parameters in SAPSO are decided by the initial and final values corresponding to these control parameters. This implies that the initial and final values of the three main control parameters have profound impacts on the convergence of SAPSO. Thus, as shown in Lemma 4, after obtaining a sufficient convergence condition for SAPSO, we still need to discover how to set the initial and final values of the three control parameters in the self-adaptive strategy defined by (8)–(14), so that the sufficient convergence condition given by Lemma 4 can be satisfied. To this end, a parameter selection rule regarding how to set the initial and final values of the three control parameters is provided for SAPSO in the following lemma. By adopting this parameter selection rule, the convergence of SAPSO can be sufficiently guaranteed.

Lemma 5

SAPSO sufficiently converges, if the initial and final values of the three control parameters of each particle satisfy the following conditions:

$$\begin{aligned} \left\{ \begin{array}{l} 2\omega _{f} + 2> c_{1s} + c_{1f} \\ 1> \omega _{s}> \omega _{f}> -1 \\ c_{1s} = c_{2f}> c_{1f} = c_{2s} > 0 \\ \end{array} \right. \end{aligned}$$

(38)

Proof

If $c_{1s}=c_{2f}$ and $c_{1f} = c_{2s}$, it is evident from (9), (10), (12) and (13) that $c_1 + c_2$ = $c_{1s}+c_{1f}$ for any particle at any iteration in the self-adaptive strategy proposed in SAPSO. Here, it is worth mentioning that the subscript m is omitted from each variable for simplicity. Moreover, from (8) to (10), one can easily observe that $\omega _{f} \le \omega \le \omega _{s}$, $c_{1f} \le c_{1} \le c_{1s}$ and $c_{2s} \le c_{2} \le c_{2f}$ for any particle at any iteration in the proposed self-adaptive strategy. Therefore:

$$\begin{aligned} \left\{ \begin{array}{l} 2\omega _{f} + 2> c_{1s} + c_{1f} \\ 1> \omega _{s}> \omega _{f}> -1 \\ c_{1s} = c_{2f}> c_{1f} = c_{2s}> 0 \\ \end{array} \right. \Rightarrow \left\{ \begin{array}{l} 2\omega + 2> c_1 + c_2 \\ -1< \omega < 1 \\ c_1,c_2 > 0 \end{array} \right. \end{aligned}$$

(39)

As proven in Lemma 4, because the right-hand side inequalities in (39) denote the sufficient condition for the convergence of SAPSO, the proof of Lemma 5 can be completed based on the relationship given by (39). $\square$

Since the initial and final values of the three control parameters are predefined, the convergence conditions given by (38) can be easily met via setting proper initial and final values of these control parameters. In other words, the convergence of SAPSO can be easily guaranteed through setting proper initial and final values corresponding to these control parameters in the self-adaptive strategy defined by (8)–(14). In this paper, we empirically set that $\omega _{s} = 0.9$, $\omega _{f} = 0.4$, $c_{1s} = c_{2f} = 2$ and $c_{1f} = c_{2s} = 0.1$ in the self-adaptive strategy proposed in SAPSO. Figure 4 displays the convergence position and velocity trajectories of the particle in SAPSO under this suggested parameter settings.

Fig. 4

Convergence position and velocity trajectories of the particle in SAPSO under the suggested parameter settings. a Position trajectory, b velocity trajectory

3.5 The equilibrium point of SAPSO

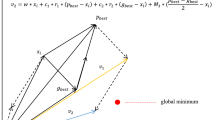
After the convergence analysis of SAPSO stated above, the remaining mission is to discover the equilibrium point, namely, to answer toward which stable point particles in SAPSO converge if the convergence condition given by (34) is met. Calculating limits on both sides of (15) produces:

$$\begin{aligned} \left\{ \begin{array}{l} \lim \limits _{k \rightarrow \infty }{X(k+1)} = \lim \limits _{k \rightarrow \infty }{X(k)} + \omega \lim \limits _{k \rightarrow \infty }{V(k)} + c \lim \limits _{k \rightarrow \infty }{(P-X(k))} \\ \lim \limits _{k \rightarrow \infty }{V(k + 1)} = \lim \limits _{k \rightarrow \infty }{X(k+1)} - \lim \limits _{k \rightarrow \infty }{X(k)} \end{array} \right. \end{aligned}$$

(40)

When each particle in SAPSO converges, it is clear that $\lim \nolimits _{k \rightarrow \infty }{X(k + 1)} = \lim \nolimits _{k \rightarrow \infty }{X(k)}$ and $\lim \nolimits _{k \rightarrow \infty }{V(k+1)} = \lim \nolimits _{k \rightarrow \infty }{V(k)}$. Therefore, after substituting these two equations into (40), the equilibrium point of SAPSO is obtained as:

$$\begin{aligned} \left\{ \begin{array}{l} \lim \limits _{k \rightarrow \infty }{X(k)} = P = \frac{c_1r_1 \cdot pbest + c_2 r_2 \cdot gbest}{c} \\ \lim \limits _{k \rightarrow \infty }{V(k )} = 0 \end{array} \right. \end{aligned}$$

(41)

where $c = c_1r_1 + c_2r_2$. pbest and gbest, respectively, denote the personal best position of the particle and the global best position of the swarm. $r_1$ and $r_2$ are two random numbers uniformly distributed in [0,1].

4 The statement of mSADE

In the developed mSADE algorithm, a ranking-based mutation operator presented in [22] is used to yield a trial vector in order to increase the chance of finding high-quality solution. Moreover, two different strategies are developed to adaptively adjust the scaling factor and the crossover rate in mSADE in order to release the burden of the optimizer. Below, the ranking-based mutation operator is first described. Then, the two self-adaptive strategies used to update the aforementioned control parameters in mSADE are detailed.

Based on the natural selection principle, since good species contain “better” genetic information, high-quality offspring can be generated by mutating those good species. Inspired by such a consideration, in order to yield “better” new offspring, a ranking-based mutation strategy is first used in mSADE. Given the size of the swarm as NP, all parent individuals are first sorted in an ascending order based on their fitness values in the ranking-based mutation strategy. Then, the rank value of each parent individual i is assigned as follows [22]:

$$\begin{aligned} RS_{i} = NP - i \end{aligned}$$

(42)

where i is the index number of the parent individual ($i=1,2,\dots , NP$).

According to the rank value assigned to each parent individual, the selection probability that each parent individual is allowed to the mutation operator is computed as:

$$\begin{aligned} SP_{i} = \frac{RS_{i}}{NP} \end{aligned}$$

(43)

After calculating the selection probability of each parent solution, three different parent individuals are selected based on the roulette wheel mechanism to participate in the mutation operator defined by (3). Following the above ranking-based strategy, the parent individuals containing “better” genetic information can be authorized to the next generation with higher possibilities, and thus, the likelihood of producing high-quality new offspring can be increased.

To adaptively adjust the crossover rate, a self-adaptive strategy is proposed in mSADE as:

$$\begin{aligned} Cr_i(k+1) = \left\{ \begin{array}{ll} Cr_i(k),& \quad {\mathrm {if}} \ f({\mathbf {U}}_i(k)) \le f({\mathbf {P}}_i(k)) \\ N(0.5,0.1),& \quad {\mathrm {otherwise}} \end{array} \right. \end{aligned}$$

(44)

where N(0.5, 0.1) denotes a number randomly produced by a normal distribution function of average 0.5 and standard deviation 0.1.

$f({\mathbf {U}}_i(k)) \le f({\mathbf {P}}_i(k))$ indicates that the current crossover rate of the ith solution has a higher chance to enhance the quality of candidate solutions at the next generation. Thus, the possibility of producing high-quality solutions can be increased by preserving the current crossover rate at the next generation. On the other way around, $f({\mathbf {U}}_i(k)) > f({\mathbf {P}}_i(k))$ implies that the chance of generating promising solutions may be lowered by applying the current crossover rate at the next generation. Therefore, changing the current crossover rate may be more suitable at the next generation in such a case. Moreover, since no additional parameter is introduced in the above self-adaptive strategy, the optimization difficulties can be decreased via this self-adaptive strategy.

For easily controlling the scaling factor, a population diversity-based mechanism is proposed to update the scaling factor in mSADE as follows:

$$\begin{aligned} S_{i,j}&= 1 - PD_{i,j}(k) \end{aligned}$$

(45)

$$\begin{aligned} PD_{i,j}(k)&= \frac{ \sum _{i=1} ^ {NP} \sqrt{E_{\mathrm{div}}}}{NP \cdot {\mathrm{max}}(\sqrt{E_{\mathrm{div}}})} \end{aligned}$$

(46)

$$\begin{aligned} E_{\mathrm{div}}&= {\sum _{j=1}^{D}\left[ P_{i,j}(k) - \overline{P}_{j}(k)\right] ^2} \end{aligned}$$

(47)

$$\begin{aligned} \overline{P}_{j}(k)&= \frac{1}{NP} \sum _{i=1} ^ {NP} P_{i,j}(k) \end{aligned}$$

(48)

where $S_{i,j}$ refers to jth element in ${\mathbf{S}}_i$. $PD_{i,j}(k)$ is the normalized diversity for the jth dimension of individual i. $\overline{P}_{j}(k)$ stands for the mean of the jth dimension over all individuals in the swarm.

Adopting the population diversity based on the mechanism defined by (45)–(48), the mutation step length, that is, ${\mathbf {S}}_i ({\mathbf{P}}_{i_1}(k) - {\mathbf{P}}_{i_2}(k))$ shown in (3), can be dynamically updated based on the difference between the diversity of each solution and the mean diversity of the population. Again, since the scaling factor in mSADE is adaptively changed based on the self-adaptive strategy defined by (45)–(48), no additional control or factor parameter is needed to update the scaling factor, which thus helps to reduce the optimization burden of mSADE.

5 The optimization framework of SAPSO–mSADE

Based on the analysis and statements shown in Sect. 3.5, it can be discovered from (41) that the position of each particle in SAPSO eventually converges toward to a stochastically weighted average of its personal best position and the global best position of the swarm in the case where the convergence condition given by (34) is satisfied. It is clear from (41) that if the particle’s personal best position equals to the global best position of the swarm [i.e., $pbest = gbest$ in (41)] and the global best position of the swarm remain unchanged, just like the most PSO algorithms, the position of each particle in SAPSO keeps invariant as the evolutionary process continues, which indicates that the stagnation issue emerges in SAPSO. Since the stagnation issue would significantly damage the search efficiency of SAPSO, there exists strong necessity to remedy or overcome this potential issue in SAPSO.

Based on the analysis noted above, in order to remedy the stagnation issue of SAPSO, there could be three candidate options: (1) only evolving the personal best position of each particle using some other EAs; (2) merely evolving the global best position of the swarm based on some other EAs; and (3) simultaneously evolving the personal best position of the particle and the global best position of the swarm via some other EAs. When remedying the stagnation issue of SAPSO following the second mentioned option, particles in SAPSO may take time to converge toward the global best position of the swarm, since the global best position of the swarm is kept evolving, which would lead the convergence speed of SAPSO to be greater than using the first option. When improving the stagnation issue of SAPSO based on the third mentioned choice, the search efficiency of SAPSO could be better than the aforementioned two options. However, since the global best position of the swarm and the personal best position of the particle need to be simultaneously evolved, this option would be the most computationally expensive among the three mentioned options.

Considering the concerns stated above, to alleviate the stagnation issue of SAPSO, this paper implements the first option mentioned above, that is, merely evolving the personal best positions of particles based on some other EAs. As an extension of this study, we may examine the feasibilities and superiorities of applying the another two aforementioned options in SAPSO in the near future. As stated previously, probably thanks to its simplicity and the formidable reliability of DE, hybridizing DE with PSO to remedy the stagnation issue could be one of the most preferred methods [15,16,17]. Thus, this paper targets the mSADE algorithm to be integrated with SAPSO and completes the design of a SAPSO–mSADE-based optimization framework in order to enhance search reliability of this framework. In the designed SAPSO–mSADE-based framework, mSADE is applied to evolve the personal best positions of particles in SAPSO at each iteration.

Here, it must be highlighted that the idea of applying DE to evolve the personal best memories of particles in PSO is not novel in this paper. Some other terrific studies adopting the same idea can be also found in [15,16,17]. Moreover, we need to call the attention of the reader that since mSADE belongs to the community of EAs, which deals with population-based computation, some other well-established EAs, such as genetic algorithm (GA) [23] and ant colony optimization algorithm (ACO) [24], to name but a few, can be also considered as potential replacements of mSADE in the developed SAPSO–mSADE-based framework to obtain similar results shown in this paper. Since both SAPSO and mSADE pertain to the family of EAs, the developed SAPSO–mSADE-based optimization framework may be more suitable for hybridizing two different EAs. This may imply that some other classical optimization methods which do not belong to the community of EAs may be unsuitable to replace mSADE in this developed optimization framework.

The pseudo-code of the SAPSO–mSADE-based optimization framework for a minimization problem is summarized in Table 1, where NP denotes the size of the swarm. This optimization framework involves two modules: the explore module represented by SAPSO and the memory module denoted by mSADE. Since the global and local search capabilities of SAPSO can be well adjusted by the newly proposed self-adaptive strategy defined by (8)–(14), particles in the explore module may be promoted to search through the entire solution space to reduce the possibility of missing promising solution areas in the early stages of the evolution. On the other hand, in the latter phases of the evolution, particles are probably encouraged to turn into local search to improve the quality of the final solution searched by the swarm. Since mSADE is a global search method which can not only encourage individuals to search on particular search space, but also encourage particles to search toward some unexplored space areas, applying the memory module denoted by mSADE to evolve the personal best memories of particles may prevent particles plugging into stagnation.

Table 1 The pseudo-code of SAPSO–mSADE

6 Numerical simulations

6.1 Descriptions of benchmark test functions

As shown in Table 2, 25 benchmark test functions issued from the literature [25,26,27] are selected to validate the efficiency of the proposed method. Based on their different characteristics, these benchmarks can be roughly divided into three categories, as shown in Table 2. The first category contains 4 high-dimensional functions ($F_1$–$F_4$) with a regular local optimal and separable variables. The second category contains 3 classical low-dimensional functions ($F_5$–$F_7$) having multiple local optimum and non-separable variables. There are 18 complex functions ($F_8$–$F_{25}$) extracted from CEC 2005 [27] involved in the last category. The global optimal solutions of these 18 complex functions are either shifted within the solution space or rotated beyond the edge of the solution space. For more details about these benchmarks, the reader is referred to [25,26,27].

Table 2 Benchmark functions (“D” is the dimension and “$\xi$” is the accuracy level)

6.2 Evaluation of the combination SAPSO and mSADE

In order to test the effectiveness of combining SAPSO with mSADE in the proposed SAPSO–mSADE, five different cases are compared for solving $F_1$, $F_2$, $F_{10}$ and $F_{23}$ shown in Table 2. In the first case, denoted as Case 1, only the conventional PSO is applied to handle these 4 selected benchmarks. In the second case, denoted by Case 2, merely the performances of the standard DE are examined over the 4 benchmarks. The third case, presented by Case 3, just investigates the performances of mSADE over these 4 selected problems. The fourth case, denoted by Case 4, only examines the performances of SAPSO over the 4 benchmarks. In the last case, denoted as Case 5, these 4 test functions are only handled by the proposed SAPSO–mSADE.

For each test function, a Monte Carlo experiment with 25 runs is conducted in each tested case. In each studied case, the size of each method is empirically set to be 40 and the maximum iteration number of each method is given as 1E+05 in each run of the Monte Carlo test. Besides, the evolution of each considered case exists only if the iteration number of each algorithm reaches the given maximum iteration number or the error of the final solution searched by an algorithm reaches a predefined accuracy level, as shown in Table 2. The simulation parameters of SAPSO–mSADE are set to be: $\omega _{s} = 0.9$ , $\omega _{f} = 0.4$, $c_{1s} = c_{2f} = 2$ and $c_{1f} = c_{2s} = 0.1$ based on the convergence analysis results shown in Sect. 3.4. For each test function, the search accuracy metric measured by $E_{\mathrm{mean}}$ is adopted to indicate the solution optimality of each method in each studied case. It is worth noting that $E_{\mathrm{mean}}$ of a given method for a test function in a multiple-run Monte Carlo experiment means the average value of the solution value searched by the method in each run of the Monte Carlo experiment [25].

The statistical results of $E_{\mathrm{mean}}$ obtained by each method for each test function are summarized in Table 3. The convergence graphs of $E_{\mathrm{mean}}$ gained by different algorithms for the 4 test functions are visualized in Fig. 5. It is apparent from Table 3 that Case 5 is followed by Case 4, Case 3, Case 2 and Case 1 in terms of $E_{\mathrm{mean}}$ for each test function. This indicates that the order obtained is SAPSO–mSADE, SAPSO, mSADE, the standard DE and the conventional PSO in terms of $E_{\mathrm{mean}}$ over these 4 benchmark problems, which, to a certain degree, can reflect the effectiveness and superiority of the hybridization SAPSO with mSADE in the proposed SAPSO–mSADE.

Fig. 5

Convergence graphs of $E_{\mathrm{mean}}$ obtained by different cases for different test functions. a$F_{1}$, b$F_{2}$, c$F_{10}$, d$F_{23}$

Table 3 Statistical results of $E_{\mathrm{mean}}$ obtained by different methods over different benchmarks (“STD” denotes the standard deviation)

6.3 Comparison of the proposed approach with some other EAs

After evaluating the effectiveness of hybridizing SAPSO with mSADE in the proposed method, the performance of the proposed method is also examined and evaluated over 25 benchmark test functions as shown in Table 2. For a rigorous evaluation, the performance of the proposed SAPSO–mSADE is compared with those of 7 well-established EAs: IDPSO [6], EGPSO [12], SPSO 2011 [14], FGIWPSO [20], HPSO-DE [28], NPSO-DE [29] and AH-DEa [30]. The simulation parameters for these compared methods are issued from their original literature and summarized in Table 4. Also, a Monte Carlo experiment with 25 runs of each method over each test function is conducted. The existence condition of each method described in Sect. 6.2 is adopted for each method over each test function in this subsection.

Apart from the solution optimality evaluated by the search accuracy metric $E_{\mathrm{mean}}$, the success rate (SR), the average number of function evaluations (NFE) and the computational burden (CB) are adopted as another three evaluation metrics in order to examine different properties of the proposed method. Here, SR stands for the percentage of trials when a method converges to the actual optimal solution with a predefined accuracy level. This metric is widely applied to measure the search reliability of a given method [25]. NFE represents the average function calls when a method converges to the actual optimal solution with a predefined accuracy level, which is used to denote the average convergence speed of a given method and calculated as $NFE = 1/N \sum _{i=1}^{N}FE_{i}$, where N denotes the total runs of a Monte Carlo experiment and $FE_{i}$ is the number of function evaluations of the ith run of the Monte Carlo experiment [25]. CB is a performance index implemented to denote the computational complexity of a given method [27].

Table 4 Simulation parameters for different compared methods

6.3.1 Evaluation of the solution optimality

After performing the Monte Carlo experiment described above, the statistical results of $E_{\mathrm{mean}}$ of different methods for each test function are summarized in Table 5. The convergence graphs of $E_{\mathrm{mean}}$ of different methods for each test function are demonstrated in “Appendix A”. From Table 5, it is clear that, with the exceptions of $F_3$, $F_7$, $F_{11}$, $F_{15}$ and $F_{20}$, the proposed method dominates its contenders in terms of $E_{\mathrm{mean}}$. Therefore, it can be intuitively inferred that the proposed method is highly competitive over the majority of the 25 test functions with respect to the solution optimality.

However, it is important to note that, based on the analysis stated above, we cannot conclusively claim that the proposed method performs superior to its competitors over the 25 test functions in terms of the solution optimality, since the average $E_{\mathrm{mean}}$ performances of different methods significantly diversify for different test functions, as shown in Table 5. In order to detect whether all the tested methods perform significantly different over the 25 test functions and highlight the significance of the average $E_{\mathrm{mean}}$ performance improvement of the proposed method over its peers, we conduct a statistical comparison detailed below.

In the statistical comparison, a ranked-based analysis is first conducted to examine the average rank of the mean $E_{\mathrm{mean}}$ performance of each method over the 25 test functions. According to simulation results reported in Table 5, the ranks of and average rank of the mean $E_{\mathrm{mean}}$ performance of each method for the 25 benchmarks are summarized in Table 6. From this table, one can note that the order of the mean $E_{\mathrm{mean}}$ performance over the 25 test functions is that the proposed method is followed by EGPSO, AH-DEa, FGIWPSO, NPSO-DE, HPSO-DE, IDPSO and SPSO 2011. From such an observation, although the proposed method is highly powerful in solving the 25 benchmark functions in terms of the solution optimality, it is still insufficient to conclude that this method preforms significantly different or even better than the other methods over these 25 test functions.

In order to detect whether all considered methods perform significantly different over the 25 test functions, the nonparametric Friedman test [31] on the average rank of the mean $E_{\mathrm{mean}}$ performance is performed at a confidence level of 95%. Because this study compares 8 methods over 25 test functions, the F-statistic value of the Friedman test equals to 2.0645 at a confidence level of 95%. Note that the F-statistic value of the Friedman test at a confidence level of $\alpha \%$ can be gained using the MATLAB command: $f{\mathrm{inv}}(\alpha , K-1, (K-1)(N-1) )$, where K and N denote the number of methods and the number of test functions, respectively. From Table 6, the obtained Friedman test value ($F_{\mathrm{score}}$) is equal to 27.8433. For the calculation of $F_{\mathrm{score}}$ of K methods over N problems, the reader is referred to [31]. Since the F-statistic value of the Friedman test is less than the $F_{\mathrm{score}}$ value, the null hypothesis that assumes each method performs equally over all considered benchmark problems can be rejected. Therefore, it allows us to conclude that the 8 methods perform significantly different at a confidence level of 95% over the 25 benchmark problems as far as the $E_{\mathrm{mean}}$ performance is concerned.

Although the nonparametric Friedman test confirms that the 8 methods are significantly different over the 25 benchmarks at the confidence level of 95%, it cannot sufficiently conclude that the proposed SAPSO–mSADE significantly dominates its peers at the same confidence level. In order to highlight the $E_{\mathrm{mean}}$ performance improvement of the proposed method over its competitors, the pairwise post hoc Bonferroni–Dunn test is conducted at the confidence level of 95% in the conducted statistical comparison. In order to detect whether or not a given method performs significantly better than another method at the confidence level of $\alpha \%$ using the hoc Bonferroni–Dunn test, one only needs to check whether the difference of the average ranks between those two methods is greater than the critical difference (CD) of the Bonferroni–Dunn test. If yes, one can claim that the given method is significantly better than its competitor at a confidence level of $\alpha \%$ [31]. Here, the value of CD can be calculated by $q_\alpha \sqrt{K(K+1)/(6N)}$ for K methods over N benchmark test functions, where $q_\alpha$ is a constant parameter [31].

Again, since this paper compares 8 methods over 25 benchmarks, the value of CD of the pairwise post hoc Bonferroni–Dunn test equals to 1.8637. Moreover, it can be easily observe from Table 6 that the differences of the average ranks between our proposed method and EGPSO, AH-DEa, FIGWPSO, NPSO-DE, HPSO-DE, IDPSO and SPSO 2011 are 2.04, 2.12, 2.68, 3.72, 3.76, 4.60 and 5.88, respectively. Since all these difference values of the average ranks between our proposed method and its peers are greater than the value of CD, we can sufficiently conclude that the proposed method performs significantly better than its contenders over the 25 benchmark test functions in terms of $E_{\mathrm{mean}}$ (i.e., the solution optimality) at a confidence level of 95%.

Table 5 Statistical results of $E_{\mathrm{mean}}$ of different methods for different benchmarks

Table 6 Rank values of $E_{\mathrm{mean}}$ results of different methods for the 25 benchmarks (“AVR.” denotes the average rank of each method over the 25 benchmarks)

6.3.2 Evaluation of search reliability

This subsection uses the performance index SR to examine the search reliability of each method. After the execution of the proposed Monte Carlo experiment, the simulation results of SR obtained by different methods over the 25 test functions are reported in Table 7. From this table, it can be seen that $F_{10}$, $F_{15}$, $F_{18}$, $F_{22}$, $F_{23}$, $F_{24}$ and $F_{25}$ can be never solved by any method considered in this study, probably due to the challenging fitness landscape of these functions. Apart from these 7 functions, the remaining 18 functions can be completely or partially solved by at least one tested method. Here, a function can be completely, partially or never solved by a method if SR of the method for the test function satisfies: $SR = 1$, $0<SR <1$ or $SR=0$, respectively.

From Table 7, it is clear that the proposed method can completely solve 11 test functions over the 18 test functions that can be completely or partially solved. Obviously, the number of test functions that can be completely solved by the proposed method is all greater than those of the other methods compared. Also, as confirmed in Table 7, the number of test functions that can be partially solved by the proposed method equals to 7, which is ranked first or second among the 8 methods in the case where the test function can be partially solved. Since SR is a performance metric used to denote the search reliability, it is conclusive that the proposed method is highly promising over the 25 benchmarks in terms of the search reliability.

The reasons why the proposed method is formidable in the search reliability may be explained by the following two facts: (1) Since the global search ability of the proposed method is promoted in the early phases of the evolution via the proposed self-adaptive strategy in SAPSO, the likelihood of missing promising solution areas can be decreased in early stages of the evolution; (2) since the personal best experience of particles in the proposed method is evolved by mSADE, particles in the proposed method can be avoided falling into stagnation as far as possible, which thus helps to strengthen the search reliability of this method.

Table 7 Simulation results of SR obtained by different methods for different test functions

6.3.3 Evaluation of the average convergence speed

The target of this subsection is to examine the mean convergence speed of each method based on the NFE performance criterion. After conducting a Monte Carlo experiment with 25 runs for each test function shown in Tables 2, 8 summarizes the simulation results of NFE obtained by different methods for different benchmarks. As shown in this table, since $F_{10}$, $F_{15}$, $F_{18}$, $F_{22}$, $F_{23}$, $F_{24}$ and $F_{25}$ can be never solved by any considered method, the NFE results of each method for these test functions equal to the given maximum iteration number.

From Table 8, it is clearly trivial that the proposed method and FGIWPSO are ranked first and second in terms of the NFE performance index, since these two approaches can, respectively, provide 13 and 4 best NFE results over the remaining 18 test functions that can be completely or partially solved. Apparently, the proposed method performs 3.25 times better than the second best algorithm, i.e., FGIWPSO, as far as the average convergence speed is concerned. Thus, it allows us to claim that the proposed method is highly powerful with respect to the average convergence speed. As stated previously, probably thanks to the fast growing nature of the exponential function, exponentially adjusting the control parameters of PSO may facilitate the convergence speed of PSO. This may interpret the potential reason why the proposed method is highly competitive in the convergence speed, since the control parameters of particles in the proposed method are exponentially adjusted.

Table 8 Simulation results of NFE obtained by different methods for different functions

6.3.4 Evaluation of the computational complexity

The computational complexity of each method is examined through the performance index computational burden (CB) [27] in this subsection. Following the procedure proposed in [27], the value of CB of a given method is calculated by $({\widehat{T}}_2 - T_{1})/{T_{0}}$, where ${\widehat{T}}_2$, $T_1$ and $T_0$, respectively, denote the computation time consumed by the corresponding mathematical operations described in [27] in seconds. The reader is referred to [27] for more information about the computation methods of ${\widehat{T}}_2$, $T_1$ and $T_0$.

In this subsection, the 30-dimensional test function $F_{10}$ as shown in Table 2 is used to investigate the computational complexities of different methods. After conducting each mathematical operation suggested in [27], the simulation results of ${\widehat{T}}_2$, $T_1$ and $T_0$ of each method are shown in Table 9. From this table, SPSO 2011 exhibits the best performance, while the proposed method is ranked sixth among the 8 methods in the computational complexity. Such observation is reasonable because the three control parameters of SPSO 2011 keep invariant and no additional computation resource is needed to update the three control parameters of this method, which thus reduces the computational complexity of this method. Since the proposed method integrates SAPSO and mSADE together, the proposed method is inevitably more computationally complicated than the non-enhanced PSO and DE methods compared.

However, it is of great importance to highlight that despite being more computationally complicated than SPSO 2011 and FGIWPSO, AH-DEa, EGPSO and IDPSO, the proposed method significantly dominates these methods in terms of the solution optimality, the search reliability and the average convergence speed, as confirmed in former contents of this section. Also, it is worth highlighting that even if the proposed method is not as promising as those non-enhanced PSO and DE methods compared, the proposed method performs better than the two enhanced PSO–DE methods, i.e., NPSO-DE and HPSO-DE in terms of the computational complexity. Therefore, considering all the concerns raised, it allows us to conclude that the proposed method is highly promising and can be considered as a vital alternative in the field of soft computation.

Table 9 Results of the computational complexities of different methods

6.4 Scalability analysis

So far, the performance of the proposed method is only validated by 25 30-dimensional test functions. However, the scalability of the proposed method on higher dimensional optimization problems remains uncertain. In order to study the scalability of the proposed method, 8 complex benchmarks $F_{18}$–$F_{25}$ shown in Table 2 are selected in a 50-dimensional case in this subsection. For rigorous validation, the performance of the proposed method is compared with those of the seven aforementioned methods.

For each 50-dimensional test function, the Monte Carlo experiment with 25 runs is conducted for each method. The maximum iteration number of each method in each run of the Monte Carlo experiment is set to be 3E+05. The evolution of each method in each run of the Monte Carlo experiment exists if the iteration number of the method reaches the given maximum iteration number or the error of the final solution searched by a method reaches a predefined accuracy level as shown in Table 2. For each test function, only the average solution optimality measured by $E_{\mathrm{mean}}$ is considered in the scalability examination in this subsection.

After executing the Monte Carlo experiment described above, the statistical results of $E_{\mathrm{mean}}$ gained by different methods over each test function are provided in Table 10. The evolution curves of $E_{\mathrm{mean}}$ obtained by different methods for these 50-dimensional problems are visualized in “Appendix B”. From Table 10, it can be found that the proposed method exhibits the best performance over the 8 large-scale test functions in terms of $E_{\mathrm{mean}}$ (i.e., the solution optimality), which, to some degrees, can reflect the scalability of the proposed method.

Table 10 The statistical results of $E_{\mathrm{mean}}$ obtained by different methods for the 50-dimensional test functions

6.5 Parameter sensitivity study

In order to gain insight on how different parameter settings affect the performance of the proposed method, this subsection investigates the sensitivity of the performance of the proposed method to different parameter settings regarding NP (population size), $\omega$ (inertia weight), $c_1$(cognitive acceleration parameter) and $c_2$ (social acceleration parameter). In the sensitivity investigation, only Functions $F_{10}$ and $F_{15}$ depicted in Table 2 are selected in this subsection. The same Monte Carlo experiment depicted in Sect. 6.2 is adopted for each parameter sensitivity study. The descriptions and simulation results of different parameter settings for these two functions are given below.

• (1) Settings of NP: Population size NP is an important parameter in PSO, which greatly influences PSO’S the performance and computation time. To investigate impacts of the population size on the performance and computation time of the proposed method, different parameter settings of NP varying from 10 to 100 are considered for the two selected test functions. The rest simulation parameters of the proposed method are remained as the same as those in Sect. 6.2.

The simulation results of $E_{\mathrm{mean}}$ and the computational burden (CB) of the proposed method over the two selected test functions are shown in Table 11. From this table, it can be observed that the average solution optimality can be improved, whereas the computational burden is significantly increased as the population size increases. Also, it can be seen from Table 11 that the performance of the average solution optimality is not promising in the case where the population size is less than 30. Besides, the improvements of the average solution optimality are insignificant in the case where the population size is greater than 50, as shown in Table 11. Since the decision makers may prefer to obtain an acceptable solution at a lower computation cost in real-world applications, we empirically set the population size of the proposed method to be 40 by compromisingly considering the solution optimality and the computation time.

Table 11 Simulation results of $E_{\mathrm{mean}}$ and CB for $F_{10}$ and $F_{15}$ under different settings of the population size

• (2) Settings of $\omega$, $c_1$ and $c_2$: Since these three control parameters play key roles in affecting the performance of the proposed method, the sensitivities of the performance of the proposed method to these parameters are investigated. Three different cases are executed to investigate the sensitivities of the performance of the proposed method to different parameter settings of $\omega$, $c_1$ and $c_2$, respectively. In the first case, the inertia weight decreases from 0.9 to 0.4. In the second case, the cognitive acceleration parameter decreases from 2 to 0.1. The third case investigates settings of the social acceleration parameter increasing from 0.1 to 2. Note that when one parameter varies in each individual case, the other two control parameters are kept as the same as those in Sect. 6.2.

Tables 12, 13 and 14 summarize simulation results of $E_{\mathrm{mean}}$ regarding different settings of $\omega$, $c_1$ and $c_2$, respectively. The corresponding fitness curves of $E_{\mathrm{mean}}$ regarding different settings of these three control parameters for $F_{10}$ and $F_{15}$ are visualized in Figs. 6 and 7, respectively. One can make an observation from Tables 12, 13 and 14 that the three main control parameters of particles can heavily affect the overall performance of the proposed method. Moreover, it is clear from these two tables that the proposed method is highly promising in terms of the solution optimality in the cases where $\omega$ and $c_1$ decrease, whereas $c_2$ increases. This observation may further help to interpret the reasons why the three control parameters of particles in the proposed SAPSO–mSADE are updated based on the self-adaptive control parameter updating rule defined by (8)–(14). It is clear from (8) to (14) that $\omega$ and $c_1$ of each particle decrease, whereas $c_2$ of each particle increases with the iteration number increasing. These variation tendencies of the three control parameters in the proposed method may imply that the global search ability of the proposed method could be enhanced in the early stages of the evolution, while the local search ability of the proposed method would be facilitated in the latter phases of the evolution, based on the discoveries found in [7, 10, 11]. When the global search abilities of particles are enhanced in the early stages of the evolution, they are more likely to be encouraged to search the entire solution space, so that the possibility of missing some high-quality solution areas would be decreased in the early evolution stages. On the other hand, when local search abilities of particles are enhanced in the latter stages of the evolution, they could be encouraged search carefully in a local region in the latter phases of the evolution, which may increase the possibility of finding the high-quality solution.

Table 12 Simulation results of $E_{\mathrm{mean}}$ for $F_{10}$ and $F_{15}$ under different settings of $\omega$

Table 13 Simulation results of $E_{\mathrm{mean}}$ for $F_{10}$ and $F_{15}$ under different settings of $c_1$

Table 14 Simulation results of $E_{\mathrm{mean}}$ for $F_{10}$ and $F_{15}$ under different settings of $c_2$

Fig. 6

Fitness curves of $E_{\mathrm{mean}}$ for $F_{10}$ under different parameter settings. a Settings of $\omega$, b settings of $c_1$, c settings of $c_2$

Fig. 7

Fitness curves of $E_{\mathrm{mean}}$ for $F_{15}$ under different parameter settings. a Settings of $\omega$, b settings of $c_1$, c settings of $c_2$

7 Applications of the proposed method on two real-world problems

Since the 25 selected benchmarks shown in Table 2 are unconstrained optimization problems, despite investigating the effectiveness and superiorities of the proposed method over the 25 benchmarks in the former contents of this paper, the feasibilities of the proposed method on some constrained optimization problems remain unknown. In order to examine the feasibilities of the proposed method on some real-world constrained optimization problems, the proposed method is tested by two real-world problems: the tension compression spring design problem and the three-bar truss design problem [13]. For a rigorous examination, the performances of the proposed method are compared with those of SPSO 2011 [14] and the bare-bone PSO (BBPSO) [25]. The needed simulation parameters of the proposed method are set to be as the same as those in Sect. 6.2. The simulation parameters of SPSO 2011 and BBPSO are referred to their corresponding literature.

Since the real optimums of these two real-world problems remain uncertain, a Monte Carlo experiment with 10 runs is conducted for each considered method on each real-world problem in order to reduce the random discrepancy. In each run of the Monte Carlo experiment, the population size and the maximum iteration number of each method are set to be 40 and 500, respectively. The evolution of each method does not exist until the iteration number of each method reaches the given maximum iteration number in each run of the Monte Carlo experiment. It is important to note that, differing from the 25 benchmarks stated above, the solution optimality of each method for each selected real-world problem is indicated by the fitness value, namely the value of the cost function of each problem, due to the uncertainties of the real optimal solutions of these two real-world problems. After conducting the described Monte Carlo experiment for each problem, the statistical results of the fitness value obtained by different methods for each studied real-world problem are reported and compared. Because the two selected real-world problems are constrained optimization problems, the adaptive relaxation method presented in [13] is adopted to deal with constraints of these two problems in this section in order to diversify solutions. For more details about these two real-world problems and the mentioned constraint tackling method, the reader is referred to [13].

After executing the Monte Carlo experiment described above, the statistical results of the fitness values obtained by different methods for the tension compression spring design problem are shown in Table 15. Table 16 exhibits the details of the best solution searched by each method for the tension compression spring design problem. The average fitness curves of different methods obtained in the Monte Carlo experiment for the tension compression spring design problem are visualized in Fig. 8. Table 17 summarizes the statistical results gained by each method for the three-bar truss design problem. The detailed information of the best solution found by each method for the three-bar truss design problem is reported in Table 18. Figure 9 displays the average fitness curves of different methods gained in the Monte Carlo experiment for the three-bar truss design problem.

From Tables 15 and 17, it is clear that the proposed method can provide the best average fitness values for these two real-world issues among the three methods. This indicates that the proposed method generally dominates the other two methods for solving these two problems in terms of the solution optimality. Moreover, it can be found from these two tables that the proposed method also provides the best performances in terms of the best and worst fitness values in the Monte Carlo experiment. Based on these analysis and comparisons, it can be inferred that the proposed method generally performs better than the other two methods with respect to the solution optimality over these two real-world problems. Besides, it can be seen from Tables 16 and 18 that the best solutions found by the three methods to these two problems are all feasible solutions since all variables of the best solutions searched by each method meet their corresponding constraints and the best solutions found by each method satisfy all constraints of these two problems. This, to some extent, can reflect the feasibilities of the three methods on these two real-world problems.

Table 15 Statistical results of the fitness value obtained by different methods for the tension compression spring design problem

Table 16 The details of the best solution searched by different methods for the tension compression spring design problem

Fig. 8

The curves of the average fitness values obtained by different methods for the tension compression spring design problem

Table 17 Statistical results of the fitness value obtained by different methods for the three-bar truss design problem

Table 18 The details of the best solution searched by different methods for the three-bar truss design problem

Fig. 9

The curves of the average fitness values obtained by different methods for the three-bar truss design problem

8 Conclusions and future work

Aiming at overcoming the typical flaws of the conventional PSO and enhancing the performance of PSO, this paper proposes an integrated PSO–DE method. Attempting to well balance the global and local search capabilities, a new SAPSO which adopts a newly established self-adaptive control updating rule to adjust the three main control parameters of particles is first developed to guide movements of particles in the proposed integrated method. Moreover, a parameter selection principle, guaranteeing the convergence of SAPSO, is provided for this algorithm after the convergence investigation of this algorithm. Besides, a mSADE algorithm is presented to evolve the personal best experience of particles in the proposed hybrid PSO method so as to mitigant the potential stagnation issue. For releasing the burden of the optimizer and diversifying solutions, a ranking-based mutation operator and two self-adaptive strategies are developed to update the scaling factor and the crossover rate in mSADE.

The performance of the proposed method is verified through 25 benchmark test functions against 7 well-known EA methods under four widely accepted performance metrics. The simulation results over the 25 benchmarks confirm that the proposed method is highly competitive in terms of the search reliability and the convergence speed. Also, the proposed method significantly dominates its peers at a confidence level of 95% over the 25 benchmarks with respect to the solution optimality. Moreover, despite being more computationally expensive than some other non-enhanced PSO methods, the computational complexity of the proposed method is comparable with those of the enhanced PSO–DE methods compared. The feasibilities and superiorities of the proposed method on real-world applications are evaluated through two real-world problems. The numerical simulation results on two real-world issues reveal that the proposed method outperforms its competitors in terms of the solution optimality. Thus, it is conclusive that the proposed method can be treated as a vital alterative in the field of evolutionary computation.

The method and results presented in this study raise some interesting issues that deserve some future study. Firstly, a convergence-guaranteed parameter selection principle can be provided for the proposed method after the second-order convergence analysis (i.e., the convergence of the variance of the particle’s position) of the proposed method. Despite studying the convergence of the proposed method to an equilibrium point, the local or global optimality of this point remains unknown, which can be considered as the second future work of this study. Thirdly, how different mutation operation models affect the performance of the proposed method can be studied. Last and but not least, the effectiveness of the proposed method can be tested by some more complicated real-world applications against some more state-of-the-art EAs.

Appendices

Appendix A

The fitness curves of $E_{\mathrm{mean}}$ of different methods for the 25 30-dimensional test functions are listed in this appendix (See Figs. 10, 11 and 12).

Fig. 10

Convergence graphs of $E_{\mathrm{mean}}$ of different PSO variants for functions $F_1$–$F_{10}$. a$F_1$, b$F_2$, c$F_3$, d$F_4$, e$F_5$, f$F_6$, g$F_7$, h$F_8$, i$F_9$, j$F_{10}$

Fig. 11

Convergence graphs of $E_{\mathrm{mean}}$ of different PSO variants for functions $F_{11}$–$F_{18}$. a$F_{11}$, b$F_{12}$, c$F_{13}$, d$F_{14}$, e$F_{15}$, f$F_{16}$, g$F_{17}$, h$F_{18}$

Fig. 12

Convergence graphs of $E_{\mathrm{mean}}$ of different PSO variants for functions $F_{19}$–$F_{25}$. a$F_{19}$, b$F_{20}$, c$F_{21}$, d$F_{22}$, e$F_{23}$, f$F_{24}$, g$F_{25}$

Appendix B

The fitness curves of $E_{\mathrm{mean}}$ of different methods for the 8 50-dimensional test functions are listed in this appendix (Fig. 13).

Fig. 13

Convergence graphs of $E_{\mathrm{mean}}$ obtained by different methods for different 50-dimensional test functions. a$F_{18}$, b$F_{19}$, c$F_{20}$, d$F_{21}$, e$F_{22}$, f$F_{23}$, g$F_{24}$, h$F_{25}$