1 Introduction to Mathematical Modelling in Cancer

Mathematical models of cancer growth and therapy have already known numerous developments and publications in the past 20 years or so. They belong to two general classes: agent-based models, ruled by stochastic rules of growth (for division, death, motion, interactions with the environment) in which the individual agents are cancer cells, and continuous models that rely on ordinary or partial differential equations, sometimes delay differential equations, whose solutions are densities of cancer cell populations. The benefits and limitations of these two respective classes of models, with examples, are discussed, e.g., in [6]. As regards anticancer treatments, the continuous version allows to take advantage of mathematical optimisation and optimal control algorithms that have been designed in this framework, originally in engineering settings. A short review of models designed with this therapeutic control vision is presented, for instance, in [2]. It is sometimes possible to obtain a continuous model starting from an agent-based one by averaging methods; alternatively, one can also develop in parallel the two types of models applied to the same biological problem and compare the predicted behaviour of the modelled cell populations, as e.g., in [5], or in a general setting, in [3].

The goal of such models of cancer growth may be to merely understand the biological phenomenon of cancer growth, by designing accurate models that are all the more relevant to describe a biological reality as they are identified and validated on biological measurements in vitro in culture dishes, in vivo on laboratory animals, or from observations (e.g., radiological images) on humans, to be confronted to theoretical growth curves depending on a priori unknown parameters (the physicist’s viewpoint). But it may also be of a different nature, to represent the effects of treatments on tumours, with the aim to optimise them. In the latter case, these effects may be described either by their molecular effects on known drug targets (keeping in mind that precision targeting is often alluring, since drugs may have unpredictable effects on non recognised targets) or by their functional effects on the possible fates of cell populations, namely proliferation, extinction, differentiation or senescence. The respective advantages of these two points of view are also discussed, with examples, in [6]. Whatever the chosen point of view, molecular or functional, the goal of these models is here clearly established as understanding and improving the efficacy of anticancer treatments (the physician’s viewpoint).

2 Drug Resistance in Cancer

2.1 The Two Main Pitfalls of Cancer Therapeutics

Unwanted toxic side effects on healthy cell populations and emergence of resistance to treatments in cancer cell populations are the two main pitfalls of cancer therapeutics in the clinic. Toxicity is always a concern for the clinician, as it limits the tolerable doses of drugs delivered to the patient, who otherwise might see his tumours eradicated, but at the expense of deadly insults to essential organs or functions (haematopoiesis, digestion, skin covering, liver function, heart function). It has lately been proposed that instead of delivering for short periods of time the maximum tolerated dose (MTD), it might be as efficient to deliver small drug doses (the so-called metronomic strategy), thus minimising toxicity, with as good results on the cancer cell population. To what extent is the immune system involved in the efficacy of this new way of designing delivery schedules is not completely clear and might depend on the anticancer drug in use [36, 37], however metronomic therapies certainly challenge the MTD strategy in both limitation of toxicity and improvement of efficacy. Note that an initial interpretation of the success of metronomic therapies was more mechanic, postulating that too high amounts of drugs destroy the blood vessels that bring the drugs to the tumour [1, 24]. It is not exclusive of the immunogenic explanation [36, 37], which proposes that giving small drug doses may reveal hidden (internalised) cancer antigens by shattering a small number of cancer cells, enough to trigger an efficient immune response towards the whole cancer cell population. Both explanations still remain to be more biologically documented—especially with respect to the immune response—mathematically modelled and tried in clinical settings; however, they address the question of toxicity in an apparently paradoxical way (“more is not necessarily better”) that is a challenge for modellers.

Drug resistance, the other major pitfall of cancer therapeutics, is a treatment efficacy limitation of another nature; it may be defined as adaptation of the target cancer cell populations to the hostile environment created by the drug. Resistance to treatments in cancer cell populations, insofar as it is not constitutive of organisms therapies apply to, but secondary, i.e., induced by treatments as a stress response. In many cases (in fact, in most cases), treatments that show remarkable initial efficacy by drastically shrinking tumours see their response decrease with time, until they become totally inefficient as tumours regrow. Furthermore, the newly growing cancer cell populations, that have become resistant to the drug in use, are out of reach for this therapy, and often for others that have not been employed (multi-drug resistance). At the molecular scale, different mechanisms have been identified, such as overexpression of drug efflux pumps (ABC transporters [14], such as the P-glycoprotein, also known as MDR1, or ABCB1), of intracellular drug processing enzymes or of DNA repair enzymes, and it has been proposed to combine cytotoxic drugs with inhibitors of these mechanisms, unfortunately eventually to no avail. As mentioned above, the molecular point of view in pharmacological treatments in principle offers a satisfying framework to perform cancer treatment optimisation, but so-called targeted therapies (i.e., that target intracellular molecular pathways), with a few exceptions, result in disappointing outcomes (see, e.g., [11, 12]).

2.2 From the Single Cancer Cell to Cancer Cell Populations

Indeed, these treatments share the same flaw, which is that they focus on a given molecular target (or on several molecular targets), considering cancer as the disease of the same single cell extended to large quantities, instead of taking into account the population of cancer cells in its diversity, which might offer a key explanation of their failure [13]. Such population diversity (or heterogeneity) is not necessarily of genetic nature but linked to epigenetic changes in the chromatin, thus reversible [31], at least on the initiation of drug resistance (mutations can come later to irreversibly establish resistance in a subclone of the cell population), and may result in differently expressed phenotypes in different cells, potentially inducing different resistance mechanisms as responses to cytotoxic stress in a population of cells bearing all the same genotype.

Introducing the population of cancer cells (indeed, the actual target of anticancer treatments) naturally sets the scenery for Darwinian evolution of cells exposed to anticancer drugs seen as an environmental selection pressure, as will be developed in the next section. This viewpoint, introduced in theoretical ecology for quite a long time already, is rather new in biology and medicine (where it has given rise to the new field of Darwinian medicine), however, does not allow to decide whether the selection is of pure Darwinian nature (selection of the fittest, cells that were already present in the population before exposure to the drug) or may involve a part of Lamarckian adaptation (no resistant cells initially present, but stochastic triggering of resistance mechanisms in a few cells for which the response to stress happens to be well adapted to resist the cytotoxic effects of the drug in use). This alternative, discussed in a mathematical setting in [5] was already the object of the biological experiment by Luria and Delbrück [23], concluding to sheer Darwinian selection. However, Luria and Delbrück’s experiment was performed not on cancer cells exposed to drugs, but on bacteria exposed to bacterium-eating viruses (phages), while human and animal cancer cells bear a genome—and epigenome, i.e., chromatin (histones)—that is by far richer than the bacterial genome, which in our case does not allow to conclude. Nevertheless, the cell population point of view clearly opens new ways to understand and overcome drug resistance in cancer.

3 Cancer as Evolutionary Disease

3.1 Evolution of Multicellularity and Cancer

Darwinian evolution (together with possible Lamarckian adaptation) of cancer—and healthy—cell populations (but healthy cell populations are in principle well controlled as regards their possibilities of phenotype evolution) must of course be considered on the short-time level of a human life or disease, but the much larger time of evolution in the course of billions of years, from unicellular organisms towards the organised and coherent forms of multicellularity represented by present animals and plants, may also shed light on cancer as evolutionary disease. Cancer is a disease of multicellular organisms, that may be defined as loss of coherence between tissues due to loss of coherence control by those genes that have been essential in the evolution towards multicellularity. In [9], it is advocated that the genes that are altered in cancer are precisely the ones that have been employed by evolution to design multicellular organisms. Indeed, evolution proceeds, as stated by Nobel prize laureate François Jacob in [18], by tinkering, i.e., it proceeds by trials and errors taking advantage of any existing material, and, as regards multicellularity, such tinkering may result in localised (in organs and physiological functions elicited by corresponding genes) fragilities, that secondarily, under environmental pressure, may be caught off guard and result in localised cancers. Such loss of coherence control, unmasking a pluripotent phenotype that is also named plasticity, may in particular be seen in the process of de-differentiation of cancer cells, i.e., adoption of a pluripotential phenotype (eventually yielding the so-called ‘cancer stem cell’, whose existence is likely to be transient [21]) making the cells that bear it, as endowed with a rich panel of non-repressed genes, able to develop a wide variety of responses to cytotoxic stress. The involvement of such failed multicellularity (i.e., unpreserved normal differentiation) control genes in revealing an ancient ‘toolkit’ of preexisting adaptations [9] still remains to be documented, but it certainly offers new ways of considering cancer as an evolutionary disease and drug resistance in cancer as an evolutionary—and adaptive—mechanism.

3.2 Heterogeneity and Plasticity in Cancer Cell Populations

Heterogeneity in cancer cell populations has been documented in advanced solid tumours as of genetic nature, with evidence of multiple branched mutations [10], but, as mentioned above, it may also consist of sheer epigenetic and reversible modifications [31] linked to enzymatic activities located on the chromatin, i.e., without mutations in the genome. However, as recently shown in [30], such fast epigenetic, non genetic, reprogramming of a sparse subpopulation of cancer cells may eventually result in a stably resistant state.

Another look at heterogeneity induced in cancer cell populations by exposure to cytotoxic drugs is presented in [35]. In this article, it is proposed that so-called cold genes that have been identified as expressed in the genome of cancer cells (multiple myeloma cells) have a very ancient origin, being conserved without changes throughout evolution from unicellularity, and may be responsible for stress response in extremely hostile and unpredictable situations (resulting from events comparable, mutatis mutandis, to the impact on animal life of the meteorite that 66 million years ago hit the Earth—creating the Chicxulub crater in Yucatán—subsequently putting an end to the dominance of dinosaurs), by possibly launching secondary expression of various resistance mechanisms. In this respect, these very ancient ‘cold genes’, elaborated in a remote past of our planet, when conditions of life were different from the present (UV radiation, acidity, low oxygen concentration in the oceans and in the atmosphere), might be the genetic toolkit of preexisting adaptations mentioned above, or part of it.

The variety of resistance mechanisms developed by cancer cell populations exposed to lethal doses of cytotoxic drugs—an extremely hostile and unpredictable situation for any cell population—has been related to what is called bet hedging in theoretical ecology. The term ‘bet hedging’ is used to qualify behaviour relying on an ensemble of traits that make a population of living individuals adaptable to an unpredictable environment, using a so-called ‘risk-spreading strategy’, that at the scale of the population may result in keeping safe only a small part of it, but a part that will be able to reconstitute the whole population, with preservation of its common genome, after such adaptation to the new environment [26]. Bet hedging in tumours has been proposed as a stochastic ‘cancer strategy’. It is also presented as “an ultimate explanation of intra-tumour heterogeneity” in chapter XVII of the book [33].

Plasticity, mentioned above about de-differentiation of cancer cells and the transient state of cancer stem cell, may be evidenced at the level of the single cell (derepression of genes that must be epigenetically repressed in physiology to produce the differentiation that yields about 200 different functional cell types in the human organism), but also at the level of the cell population, since the spreading of such pluripotent cells makes the population adaptable to environmental changes (plastic), possibly by using expression of cold genes in a tiny subpopulation and stochastic (or distributed) bet hedging of resistance phenotypes.

The plasticity—physiologically normal in highly undifferentiated cell states, close to stem cells, but totally pathological in cell populations for which a defined terminal physiological function exists—of the epigenetic landscape of a given human genome, as metaphorically proposed in [34], recently revised from a systems biology viewpoint by Sui Huang, see, e.g., [15, 16], provides another approach to plasticity and evolution of cancer, that has been, for instance, exploited to study lineage commitment in haematopoiesis by using bifurcation analysis of an ordinary differential equation model [17].

4 Continuous Mathematical Models

4.1 Phenotype-Structured Mathematical Models

The modelling framework of adaptive dynamics we present here is more likely to correspond biologically to epigenetic modifications rather than to genetic mutations, as the evolution in phenotype is in this mathematical setting always reversible (not to mention that, in the case of the application to drug resistance in cancer that we have in mind, eventual induction of emergent resistant cell clones due to mutations under drug pressure is never to be excluded in the long run). From the biologist’s point of view, we study phenotypically heterogeneous, but genetically homogeneous, cancer cell populations under stress (in particular by cytotoxic drugs).

The models considered here are all based on the so-called logistic ODE model, which we recall here. It is given by the equation

$$\displaystyle \begin{aligned}\frac{d N} {dt} = \left(r - d N \right)N, \end{aligned}$$

which describes the time-evolution of the number of cells N(t), starting from a prescribed initial condition N 0.

Coefficient r denotes the net selection rate of the cells, namely the difference between their proliferation and death rates, while the logistic term dN stands for an additional death rate proportional to the number of cells.

The underlying assumption is that competition for nutrients and space inside the population does not allow for exponential unconstrained proliferation. Mathematically, it is indeed true that if \(N_0 \leq \frac {r}{d}\), then N(t) converges increasingly toward the carrying capacity \(\frac {r}{d}\).

Let us now introduce a basic phenotype-structured model, where the quantity of interest is a number of cells n(t, x) at time t > 0, and of phenotype expression level (hereafter simply designed as phenotype) x ∈ [0, 1] standing for the resistance to a given drug. We stress that this phenotype is taken to be continuous, because, as already mentioned, it can be correlated to biological characteristics which themselves are continuous. Here, [0, 1] is taken for simplicity but multi-dimensional phenotypes can of course be considered.

The model reads

$$\displaystyle \begin{aligned} \frac{\partial n} {\partial t}(t,x) = \left(r(x) - d(x) \rho(t) \right)n(t,x), \end{aligned}$$

where \(\rho (t) := \int _0^1 n(t,x) \, dx\) is the total number of cells at time t, starting from some initial condition n 0(⋅). As before, r(x) is the net proliferation rate of cells of cells of phenotype x, while d(x)ρ(t) is the natural extension of the previous logistic term. Note that more general logistic death terms through a Kernel K can be considered, in the form \(\int _0^1 K(x,y) n(t,y) \,dy\).

The basic model described above is characterised by two main phenomena: convergence and concentration. The first one means convergence of ρ(t) towards \(\max \left (\frac {r}{d}\right )\), and concentration of the density n on the set of phenotypes where \(\frac {r}{d}\) reaches its maximum, namely \(\arg \max \left (\frac {r}{d}\right )\). This is why this class of models is extensively used in adaptive dynamics to model selection: only the cells in the fittest phenotypic states can survive, which corresponds mathematically to the convergence of n(t, ⋅) to a sum of Dirac masses located on the set \(\arg \max \left (\frac {r}{d}\right )\).

This modelling framework also extends to several populations, in which case the competition between the populations is modelled through Lotka–Volterra-like terms. Let us introduce a model of two interacting populations, which will be further developed in the next section with the modelling of chemotherapy as control terms. It is concerned with two densities of healthy and cancer cells n H(t, x) and n C(t, x) respectively, where x is again a continuous phenotype, in the application we have in mind describing the level of resistance to a given drug. The model is given by

$$\displaystyle \begin{aligned} \frac{\partial n_H} {\partial t} & = \big[r_H(x) - d_H(x) \left(a_{HH} \rho_H(t) + a_{HC} \rho_C(t)\right)\big]n_H(t,x), \end{aligned} $$
(1)
$$\displaystyle \begin{aligned} \frac{\partial n_C} {\partial t} & = \big[r_C(x) - d_C(x) \left(a_{CC} \rho_C(t) + a_{CH} \rho_H(t)\right)\big]n_C(t,x), \end{aligned} $$
(2)

where, as before, \(\rho _H(t) = \int _0^1 n_H(t,x) \, dx\), \(\rho _C(t) = \int _0^1 n_C(t,x) \, dx\). The logistic terms now incorporate an intraspecific competition term weighted by coefficients a HC and a CH. Because healthy and cancer cells compete harder within their own population than with the other population (in other words, cells belong to different ecological niches, e.g., for metabolic and energetic reasons linked in particular to respiratory oxidative phosphorylation in one case and glycolysis in the other), it is quite natural to assume

$$\displaystyle \begin{aligned} a_{HC} < a_{HH}, \; a_{CH} < a_{CC}.\end{aligned}$$

Under hypothesis (4.1), it is proved in [29] that the behaviour of (1) is again convergence and concentration, where the asymptotic values of ρ H, ρ C and the sets on which n H, n C concentrate can also be explicitly computed.

4.2 Optimal Control for Anticancer Therapeutics

Optimal control methods (reviewed in [32]) applied to models of cancer therapeutics using systems of ordinary differential equations [4, 19, 20] or of partial differential equations [29] are the appropriate tool to theoretically optimise cancer therapeutics, in particular by taking into account the inevitable emergence of drug resistance in cancer cell populations.

The built-in targets for theoretical therapeutic control that are present in the phenotype-structured PDE models we advocate here are not supposed to represent well-defined molecular effects of the drugs in use, but rather functional effects, i.e., related to cell death (cytotoxic drugs), or to proliferation in the sense of slowing down the cell division cycle without killing cells (cytostatic drugs). We propose that cell life-threatening drugs (cytotoxics) induce by far more resistance in the highly plastic cancer cell populations than drugs that only limit their growth (cytostatics), and that a rational combination of the two classes of drugs—and possibly others, adding relevant targets to the model—may be optimised to propose therapeutic control strategies to avoid the emergence of drug resistance in tumours.

We address this optimal control problem in the context of two populations, healthy and cancer as in the model is given by (1), now complemented with two types of drugs of infusion rates u 1 and u 2 for cytotoxic and cytostatic drugs, respectively. The resistance phenotype x they are endowed with is defined with respect to the cytotoxic drug pressure, and is taken to range from sensitiveness (x = 0) to resistance (x = 1). The controlled model thus reads

$$\displaystyle \begin{aligned} \begin{cases} \frac{\partial n_H} {\partial t}(t,x) & = \bigg[\frac{r_H(x)}{1+\alpha_H u_2(t)} - d_H(x) I_H(t) - \mu_C(x) u_1(t)\bigg]n_H(t,x),\\ {}\frac{\partial n_C} {\partial t}(t,x) & = \bigg[\frac{r_C(x)}{1+\alpha_C u_2(t)} - d_C(x) I_C(t) -\mu_H(x) u_1(t)\bigg]n_C(t,x), \end{cases} \end{aligned} $$
(3)

On a fixed therapeutic time-window [0, T], the optimal control problem is to choose the controls u 1 and u 2 so as to minimise the number of cancer cells ρ C(T), while satisfying the three following constraints.

  • remaining under maximum tolerated doses: \(0 \leq u_1(t) \leq u_1^{\max }\), \(0 \leq u_2(t) \leq u_2^{\max }\),

  • avoiding the emergence of too big a tumour: \(\frac {\rho _H(t)}{\rho _H(t) + \rho _C(t)} \geq \theta _{HC}\),

  • limiting unwanted adverse effects to the healthy cell population: \(\rho _H(t) \geq \theta _H \rho _H^0\).

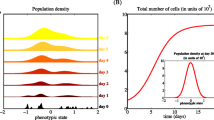
This optimal control problem is motivated by the inefficacy of using constant high doses of drugs, a strategy which on the long run violates the last two constraints. This is indeed what is observed in the simulation presented in Fig. 1: although the tumour size first decreases, it is at the expense of the cancer cell density concentrating on a resistant phenotype. The treatment becomes inefficient and relapse occurs.

Fig. 1
figure 1

What should never be done in the clinic! Simulation with u 1(t) = Cst = 3.5 and u 2(t) = Cst = 2, in time T = 10. Here \(\rho _{CS}(t) = \int _0^1 (1-x) n_C(t,x) \, dx\) is a measure of the number of sensitive cells in the cancer cell population. Constant high doses of the cytotoxic drug yield concentration of cancer cells around a resistant phenotype. The cancer cell population increases steadily while healthy cells decrease

Full size image

In [29], the previously defined optimal control problem is analysed both numerically and theoretically. As the time T increases, it is found that the optimal control strategy becomes increasingly close to a two-phase strategy.

  • The first phase is long, and only constant low doses as given, so as to saturate the second constraint. At the end of this first phase, the drug pressure has been low enough to ensure that the cancer cell density has concentrated on a sensitive phenotype.

  • The second phase is short and starts with maximum tolerated doses for both drugs, leading to a quick decrease of both cell numbers because they are efficient on a sensitive cancer cell population. Once the third constraint (on the heathy cell density) has been reached, cytostatic drugs switch to some intermediate value (which can be computed in feedback form) which allows for a further decrease of the tumour size while keeping the healthy cell number at its lower bound.

A numerical simulation of the optimal strategy is presented in Fig. 2.

Fig. 2
figure 2

Simulation of the optimal control problem for T = 60. Here, the phenotype is concentrated on a sensitive value at the end of the first delivery phase, and eventually likely more resistant—but for a very rare surviving fraction—in the cancer cell population, if one compares the curves showing ρ C(t) and ρ CS(t)∕ρ C(t) towards the end of the treatment course. Delivered at a high dose for a brief duration only, followed by a medium dose for the remaining time, the cytotoxic drug u 1(t) impinges a drastic decrease, if not total eradication, in the cancer cell population, while preserving healthy cell numbers over a predefined threshold

Full size image

For a practical implementation of the previous strategy, it is natural to repeat it in a quasi-periodic manner. One can hope that after enough cycles, the tumour will be eradicated, or at least made chronic. In order to decide when to switch from the second short phase to another cycle with a long first phase, one must identify markers for resistance. Indeed, as long as constant low doses do not violate the second constraint on the relative tumour size, they must be given to ensure that the (assumed to be plastic) tumour is becoming sensitive to the treatment again. The switch to the second phase can be led as soon as the markers indicate that the tumour has become sensitive enough again. Finally, if the healthy cells tissue is too damaged (namely the third constraint saturates), one can hope to still let the tumour decrease with a properly chosen cytotoxic drug infusion. When this is no longer possible, one must switch back to the long first phase (no infusion).

5 Future Tracks in Modelling for Cancer Therapeutics

5.1 Beyond Present Models to Optimise Cancer Therapeutics

The models of adaptive population dynamics that we have presented here, with their built-in targets for control, rely on a nonlocal Lotka–Volterra vision of cell-cell population competition. This point of view could be extended to other modes of interaction, which could be mutualistic or predator-prey like, and to an arbitrary number of cell populations. For an analysis of a mutualistic integro-differential 2 × 2 system modelling interactions between breast cancer cells and their supporting stroma (adipocytes), we refer to [27], whereas a more general Lotka–Volterra-like model for N populations is analysed in [28]. The inferred asymptotic behaviour is again convergence and concentration.

Let us now come to extensions of the integro-differential setting by considering the basis 1-dimensional model that we first mentioned. Recall first that more general logistic interaction terms can be considered. The other natural extension is to model epimutations (occurring on the relevant time-scale, which is here that of a tumour). They can either be modelled by a Laplacian, leading to

$$\displaystyle \begin{aligned} \frac{\partial n} {\partial t}(t,x) = \left(r(x) - d(x) \rho(t) \right)n(t,x) + \beta \Delta n(t,x), \end{aligned}$$

with Neumann boundary conditions, or more generally through a mutation kernel. Note that both modelling are linked at the limit through a proper rescaling of the kernel, as explained in [25].

A complementary advection term can be added, accounting for cells actively adapting to their environment, seeking for phenotype changes that make them fitter. These can be seen as stress-induced epimutations and with them the model becomes

$$\displaystyle \begin{aligned} \frac{\partial n} {\partial t}(t,x) + \frac{\partial}{\partial x} (v(x)n(t,x)) = \left(r(x) - d(x) \rho(t) \right)n(t,x) + \beta \Delta n(t,x). \end{aligned}$$

Note that in [5], the advection happens to be compulsory to observe quick enough dynamics to fit those obtained in the experiments presented in [31]. Besides, in [7], the effects of an additional advection term are rigorously studied.

A further advantage of these more general PDE models is that they are able to represent possible asymptotic coexistence of phenotypes, which is not the typical output of the integro-differential models. Moreover, whereas in [5] the agent-based model and the PDE model were treated concurrently in parallel, in [8], a general method describing the passage from the former to the latter is rigorously presented.

A final possible extension worth-mentioning is the addition of a space variable, since it is believed that the heterogeneity of a tumour varies from its periphery to its centre. This is also particularly relevant in view of optimal control through chemotherapy since drugs will efficiently access the outer rim of the tumour but less its core. For possible cancer models taking both phenotype and space into account, we refer to [22].

5.2 Need for Models with a Larger Evolutionary Perspective

From the biological part of this article, it clearly appears that the abovementioned models, sophisticated though they may be, are not enough to study in mathematical settings the evolution of multicellularity and its intrinsic failure, namely cancer, nor are they presently enough to design optimised therapeutic strategies that can overcome drug resistance in cancer. Open questions to biologists remain if one wants to make available a framework within which mathematical modelling may be designed. What are the genes that must be silenced in physiology and are re-expressed in de-differentiated cancer cells? What are the observable links between genes that are known to be essential for multicellularity and what are the genes that are altered in cancer (the same, following [9])? What models to study physiological coherence between tissues in the same organism, i.e., what sticks together in harmony the 200 different cell types of a human organism? What part of the genome bears the so-called cold genes, what part the individual signature of an organism that is transmitted throughout differentiation (the ‘self’, certainly to be related with the major histocompatibility complex, MHC), and what part the genes that are normally sequentially silenced in the history of differentiations? As regards mechanisms of drug resistance, what part of launching in a cancer cell population is deterministic (triggering cold genes) and what part is stochastic? And such list of open questions is not intended to be comprehensive.

6 Conclusion: A Challenging New Field for Mathematicians

In this short description of cancer as evolutionary disease, focusing on the question of drug resistance and its possible overcoming by optimised strategies in the clinic, we have presented what has been recently developed in the framework of mathematical modelling, that is, adaptive dynamics of cell populations represented by phenotype-structured models relying on partial differential equations, together with optimal control methods to guide their asymptotic behaviour. We have also proposed immediate tracks for future extensions of these existing models, and only sketched the scenery for future mathematical models that still lack biological answers to guide their design. We are nevertheless confident in the fast progress of cancer biology to help mathematicians design models that can be helpful in prevention, prediction and control of cancer in the clinic, provided that the right questions are posed, mathematically challenged and experimentally tackled.