Shock Reflection in Axisymmetric Internal Flows

Abstract

The flow downstream of an axisymmetric conical shock wave, with a downstream pointing apex, can be predicted by solving the Taylor-Maccoll equations. Previous research, however, has suggested that these theoretical flowfields are not fully realisable in practice, and that a Mach reflection forms towards the centreline of the flow. This phenomenon is investigated for the case where the freestream Mach number is 3.0 and the shock angle is 150$^\circ$. A range of complementary prediction techniques that include the solution to the Taylor-Maccoll equations, the method of characteristics, curved shock theory and CFD, are used to gain insight into this flow. The case where a cylindrical centrebody is placed along the axis of symmetry is studied for several values of centrebody radius that are expected to produce regular reflection at the centrebody surface. An analysis of pressure gradients suggests that the flowfield downstream of the reflected shock does not contribute to the process of transition from regular to Mach reflection at these conditions.

1 Introduction

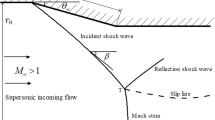
Previous theoretical analyses have shown that converging, conical, incident shocks cannot occur at a centreline of symmetry [1,2,3,4,5], and that Mach reflection of the converging shocks should occur instead. This theoretical result is supported by numerical and physical experiments [6, 7] that have shown that a conical incident shock and its regular shock reflection, near the axis of symmetry and, in particular, at the apex point, do not exist. In approaching the axis, the incident, conical, shock becomes stronger, its angle increases and a Mach reflection results; even for flows with weak incident shocks. Similar behaviour has also been shown for non-conical shocks [3, 4, 7]. It thus appears that the transition to, and the appearance of, Mach reflection is caused by the effects of shock and flow convergence near the centreline. This raises the intriguing question: How far off the centreline does the regular reflection have to be so as not to suffer the effects that force Mach reflection?

In studying shocks that converge towards the centreline, it is useful to work with shocks that maintain a constant strength (shock angle) as they approach the axis. Such conical shocks and flows can be produced from the solutions of the Taylor-Maccoll (TM) equations. Integration of the TM equations produces a streamtube, which may be viewed as a solid surface supporting the conical shock. The trailing edge of such a streamtube ends at a conical singularity. The flow between the conical shock, the singularity and the streamtube is called ‘M-flow’ [8] and is one of the four possible cases of supersonic, conically symmetric, flowfields that are bounded by a uniform flow [2]. Grozdovskii [2] identified a ‘limiting characteristic’ in the M-flow, upstream of which the flow is controlled by the surface and is conical. The downstream flow is therefore not controlled by the M-flow surface, which raises a question about the nature of the flow further towards the axis. Rylov [5] showed that centreline Mach reflection must occur since the portion of the shock downstream of the limiting characteristic must steepen continuously as it approaches the axis. Furthermore, it was shown that even a sharp expansion corner at the downstream end of the M-flow surface, producing a local Prandtl–Meyer fan (ordinarily expected to weaken the shock), cannot prevent the shock from strengthening near the centreline. The conclusion therefore is that the flow in this region cannot be conically symmetric and that centreline Mach reflection is unavoidable.

A number of M-flow features render its investigation challenging. Steepening of the incident shock occurs, primarily, close to the axis of symmetry, as compared to the entry radius of the M-flow surface. As a result, the size of the Mach disk at the axis of symmetry may be small, especially for initially weak shocks (a spectacular example of smallness is provided in [6]). The angle between the bounding rays of the theoretical M-flow (i.e., between the shock and the singularity) is relatively small, requiring high-resolution calculations to describe the incident shock angle and curvature with good accuracy.

The aim of the present study is to provide detailed quantitative analysis of an M-flow with a freestream Mach number of 3.0 and a shock angle of 150$^\circ$, referred to as M3/150. To add further insight into the issue of centreline shock reflection, the case where a cylindrical centrebody is placed along the flowfield axis is studied for several different values of centrebody radius. Results are then used to look for mechanisms that may contribute to the transition to Mach reflection. In view of the above-mentioned flow features and associated difficulties, several complementary techniques are used, which include: (1) the solution of the TM equations, (2) curved shock theory (CST) [9], (3) the method of characteristics (MOC) and (4) an adaptive unstructured inviscid time-marching finite-volume CFD code Masterix [10]. Another potentially useful tool to be considered elsewhere is a space-marching CFD code, such as the one described in [11].

2 Approaches

2.1 Theoretical Conical Flow

The TM equations are integrated by a Runge–Kutta scheme starting from the oblique shock conditions downstream of the conical incident shock. The solution yields the radial and circumferential components of Mach number in the flowfield [8]. A streamline and a C$^-$ characteristic are also traced as part of the calculation. The fact that the downstream extent of M-flow is terminated by a singularity in the TM equations means that it can never be exactly reached by numerical integration. The singularity exists where the Mach number normal to the ray is equal to $-1$, and therefore the integration process is stopped within a tolerance of $10^{-5}$ of this value. Then, due to the self-similarity of conical flows, the C$^-$ characteristic can be scaled such that it begins at the downstream end of the M-flow surface. This defines the limiting C$^-$ characteristic, as originally shown by Grozdovskii [2]. These features are shown in Fig. 1. For M3/150, it is found that the limiting characteristic intersects the shock at $y/y_1=0.384$ (where $y_1$ is the leading edge radius), and therefore the shock is expected to be of constant strength from the leading edge to this point and then to strengthen towards the axis. Only the straight portion of the shock is shown in Fig. 1 as a solid red line.

Fig. 1

Schematic for M3/150 M-flow configuration

2.2 Method of Characteristics

Calculations are conducted for the flow downstream of the limiting characteristic, where the flow must be assumed to be non-conical. The characteristics method is based on that described in [12] and is suitable for the analysis of axisymmetric rotational flows. Boundary condition data is provided by the limiting C$^-$ characteristic at the M-flow surface trailing edge, where the surface takes on infinite curvature [5], indicating a corner, so that the local flow can be modelled as a Prandtl–Meyer expansion. The M-flow shock angle of $150^\circ$ is applied at the point where the shock meets the limiting C$^-$ characteristic. Only $4.5^\circ$ of flow turning at the expansion corner (out of $\sim$$9^\circ$ flow turning required to realign the local flow with the freestream direction) is modelled. This is sufficient to take the shock close enough to the axis and generate a large enough field for cases where the shock reflects from a centrebody. The spacing between characteristics is defined to be $0.01^\circ$ at the expansion corner and $\varDelta /y_1=0.001$ along the shock. These particularly fine spacings are chosen to accurately capture gradients for CST analysis, although a convergence study has shown that the basic shock geometry is captured using much coarser spacings. Calculations are physically limited to $y/y_1=0.02$ (where the incident shock angle $\theta _\mathrm{i}=134.55^\circ$) to avoid convergence problems associated with the flow approaching sonic conditions behind the shock.

For cases that include a cylindrical centrebody, MOC analysis of the shock reflection is possible when the reflection is of regular type with supersonic flow downstream from the reflected shock. Flow calculations behind the reflected shock are driven by the centrebody geometry and the incident field. In theory, MOC can be used to analyse the reflected field for $\theta _\mathrm{i}>140.66^\circ$, which corresponds to the sonic limit of shock reflection, and occurs at a centrebody radius of $y/y_1=0.0387$. In practice however, the downstream Mach number $M_3$ must be slightly above sonic and a value of $y/y_1=0.04$ ($M_3=1.047$) is found to be the practical minimum centrebody radius at which MOC solutions could be obtained. Characteristics are distributed along the reflected shock with a spacing of $\varDelta /y_1=0.001$.

2.3 Curved Shock Theory

CST relates gradients of pressure, flow inclination and vorticity immediately upstream and downstream of a shock to the curvature of the shock itself. This includes shocks with curvatures in both the flow and flow-normal planes, such as those discussed here. The main quantities of interest are: the normalised pressure gradient $P={(\partial {p}/\partial {s})}/{{\rho }V^2}$; the streamline curvature $D=\partial {\delta }/\partial {s}$; and shock curvatures in the flow plane $S_a=\partial {\theta }/\partial {\sigma }$, and in the flow-normal plane, $S_b=-\cos \theta /y$, where s is measured along the streamline; $\sigma$ is measured along the shock; $\delta$ is the flow inclination to the x-axis; y is the distance from the symmetry axis; $\theta$ is the angle of shock inclination to the incoming velocity vector; V is the flow velocity along the streamline; $\rho$ is the density; p is the pressure. In general, two unknown quantities can be determined given all other values. Further details can be found in [9, 13].

This work applies CST in several ways. First to the incident shock, where downstream gradients of pressure, $P_2$, and flow inclination, $D_2$, are determined having input the incident shock geometry ($\theta _\mathrm{i}$, $S_{a, \mathrm{i}}$, $S_{b, \mathrm{i}}$) and the freestream conditions. Second, to the point of shock reflection from a centrebody to determine the downstream pressure gradient, $P_3$, and the reflected shock curvature, $S_{a, \mathrm{r}}$. In this case, CST is used to determine gradients downstream of the incident shock and then again to determine values downstream of the reflected shock, which allows $P_3$ and $S_{a, \mathrm{r}}$ to be found given $D_3=0$ at the cylinder surface. The third application is off-surface data for the reflected shock, where downstream gradients ($P_3$ and $D_3$) are found given the reflected shock geometry and the gradients in the incident field.

Where the incident shock is conical ($S_{a, \mathrm{i}}=0$), $P_2$ and $D_2$ can be determined based on the known shock geometry. Where the flow plane curvature of the incident shock is finite, or in cases where a reflected shock is predicted, the method for obtaining shock angles and curvatures becomes more involved. These values are provided by MOC, which predicts a discrete set of coordinates with associated shock properties as part of the solution process and requires minimal post-processing to derive the required data; extracting similar data from a CFD solution, for example, would not have been possible with the same accuracy.

2.4 CFD

The numerical CFD modelling results presented below are obtained with the Euler (inviscid, non-heat-conducting) flow model. The gas (air) is assumed to be ideal with constant specific heats (the specific heat ratio $\gamma =1.4$). An adaptive unstructured finite-volume flow solver [10] is used. The solver employs a node-centred, second order in space and time (for smooth solutions and uniform grids), MUSCL-Hancock TVD finite-volume scheme, see [14] for more details. The grid is locally adapted to solution peculiarities (e.g. shock fronts, slipstreams etc.) via an h-refinement procedure governed by a sensor based on the normalised second derivative of density. Additional uniform refinement is applied in the regions deemed essential for computational accuracy.

The geometry of the solid surface begins at the M-flow leading edge. At the M-flow trailing edge, the surface becomes parallel to the freestream direction, generating a sharp corner. The inflow boundary runs from the leading edge of the M-flow surface along the conical shock and then becomes vertical and comes to the axis (see Fig. 2). This is done to avoid accuracy issues arising from the interaction of numerically smeared shock profile with the M-flow surface. Such inaccuracies can be, in principle, reduced by grid refinement along the shock. However, very fine meshes, resulting in very small time steps, render the flow solver computationally inefficient.

Freestream conditions are used to initialise the entire computational domain for each computational run, which corresponds to instant placement of the M-flow surface into the freestream. Each computation proceeds until a steady state is reached. The mesh size for the current case includes $\sim$$1.62 \times 10^5$ grid nodes. A region of refinement is specified to begin upstream of the incident shock and end downstream of the conical singularity. Another region of refinement is specified towards the centreline to capture the region around the Mach reflection. The minimum cell width (normalised by the leading edge radius $y_1$) in both of these regions is $\sim$$1.3 \times 10^{-3}$. The minimum allowable cell width within the entire computational domain is $\sim$$6.25 \times 10^{-4}$.

3 Results

Figure 2 shows the CFD prediction of the Mach number field, with results from TM and MOC overlaid for comparison. The CFD prediction shows that incident shock steepening occurs downstream from the limiting C$^-$ characteristic. Mach reflection has occurred, with a Mach stem that appears to be approximately perpendicular to the freestream flow with a height of $y/y_1=0.027$. The subsonic streamtube (bound by the slip-surface) downstream of the Mach stem contracts as the flow re-accelerates towards sonic conditions. The end point of the TM-predicted limiting C$^-$ characteristic is located almost exactly on the CFD-predicted shock, which appears to be straight upstream of that point, in agreement with the TM theory. The MOC prediction of the shock begins to deviate slightly from the CFD prediction as it approaches the axis, although the level of agreement is generally good, with a maximum discrepancy of $x/y_1=0.003$ found at the triple point and visible only on the enlarged Fig. 2c. The disagreement may be attributed to coarser CFD grids (as compared to MOC spacings) downstream from the incident shock in the flow regions which affect the shock shape. Further grid convergence studies are required.

The MOC-predicted Mach number field as well as associated shock angle and flow plane shock curvature are shown in Figs. 3 and 4. The shock wave clearly becomes steeper with reducing y, whilst the rate at which it steepens is also found to increase as it approaches the axis. It is to be noted that the CFD/MOC-calculated incident shock, that is close to the axis, may be strong enough not to reflect regularly off an axisymmetric cylinder. Then a Mach reflection would ensue for this as well as for all smaller cylinders. As an example: the MOC calculation reached its limit at $y/y_1=0.020$ whereas CFD predicted Mach reflection with a stem radius of $y/y_1=0.027$, so that the Mach stem radius is greater than the MOC limit.

Fig. 2

CFD prediction of M3/150 (without centrebody cylinder) Mach number field with TM prediction of limiting C$^-$ characteristic (dash-dotted black line) and MOC prediction of shock position (solid black line)

Fig. 3

MOC prediction of Mach number field downstream from the incident shock and limiting C$^-$ characteristic

Fig. 4

MOC-predicted shock angle $\theta _\mathrm{i}$ and curvature $S_{a,\mathrm{i}}$ along the incident shock. Top: complete predicted shock. Bottom: focus on shock in the centreline region. TP indicates the location of CFD-predicted triple point for shock reflection from the axis of symmetry; ‘det.’, ‘son.’and ‘vN’ indicate the positions of the detachment, sonic and von-Neumann points, respectively, for shock reflection from a straight cylindrical centrebody

The effects of shock curvature on the pressure gradient $P_2$ and streamline curvature $D_2$ are shown in Fig. 5. In the region between the M-flow surface and the limiting C$^-$ characteristic, the flow is conical and the trends are explained by considering that in the direction of streamlines, conical rays become closer to one another when moving towards the axis; if the conical shock were continued towards the axis both $P_2$ and $D_2$ would approach infinity. Discontinuities in the gradient of $P_2$ and $D_2$ are found where the limiting C$^-$ characteristic meets the shock, which is where the incident shock curvature $S_{a, \mathrm{i}}$ departs from zero (see Fig. 4). The pressure gradient $P_2$ passes through zero at $y/y_1=0.173$, which separates regions of accelerating and decelerating flow downstream of the shock. This point is known as the Thomas point [9].

Fig. 5

MOC-predicted pressure gradient $P_2$ and streamline curvature $D_2$ downstream of the M3/150 incident shock. Top: complete predicted shock. Bottom: focus on shock in the centreline region. TP indicates location of CFD-predicted triple point; ‘det.’, ‘son.’and ‘vN’ indicate the position of the detachment, sonic and von-Neumann points, respectively, for shock reflection from a straight cylindrical centrebody

Fig. 6

MOC-calculated Mach number field for flow behind the reflected shocks on cylinders with $y_\mathrm{cb}/y_1=0.04, 0.08, 0.12$ (from bottom to top)

MOC predictions for cases with a centrebody cylinder are plotted in Fig. 6 and 7. Reflected shock angles are consistent with the two-shock theory of shock reflection, which is applied as part of the MOC solution. Figure 7 shows that the incident shock (in the non-conical region) is concave towards the incident flow whereas the reflected shock is convex, i.e., $S_{a, \mathrm{i}}>0$ and $S_{a, \mathrm{r}}<0$. This is in agreement with CST [9]. Mach number distributions downstream of the reflected shock show that pressure gradients in the positive x and y directions are negative. This observation is highlighted by the results in Fig. 8, where the black line shows surface pressure gradient, immediately downstream of the reflected shock, for the possible range of centrebody radius, i.e., $y_\mathrm{cb}/y_1=0.0387\rightarrow 1.0$. It shows that negative pressure gradients exist in this region for any chosen centrebody radius. Other, coloured, lines are for specific centrebody radii and include off-surface data, which confirms that negative pressure gradients continue along the reflected shock. A similar picture is found by plotting values along the centrebody surface itself, see Fig. 9. Again, the black line shows surface pressure gradient, immediately downstream of the reflected shock, for the possible range of centrebody radius. Other, coloured, lines are obtained by applying a finite difference method to surface MOC data obtained for specific cylinder radii. These curves indicate that gradients decrease significantly downstream of the shock, and although asymptotic values are difficult to determine, it seems reasonable to suggest that the gradients approach zero far from the point of shock impingement.

The reason of our particular attention to Mach number and pressure gradients behind the reflected shock is related to recent conjectures [9, 15, 16] that regular-to-Mach-reflection transition might occur not only due to reflected shock detachment by excessive flow turning, but also due to reflected shock detachment due to local flow choking. In [9], the post-shock pressure gradient is identified as the underlying cause of local choking. The above results show that the supersonic flow downstream of the reflected shock is expanding, and therefore, in the cases considered, the situation is not conducive to local choking.

Fig. 7

MOC-calculated incident, $\theta _\mathrm{i}$, and reflected, $\theta _\mathrm{r}$, shock angles. The common incident shock is shown in black. Various reflected shocks corresponding to various cylinder radii (indicated by thin black lines) are shown in colour

Fig. 8

Pressure gradient $P_3$ downstream of the reflected shock. Surface values at the reflection point for all potential values of centrebody radius are shown in black. Off-surface values for specific centrebody radii are shown in colour

Fig. 9

Surface pressure gradient $P_\mathrm{s}$ downstream of shock impingement. Values immediately downstream of reflected shock, at the reflection point, for all potential values of centrebody radius are shown in black. Downstream surface values for specific centrebody radii are shown in colour

4 Conclusions

An exploratory, analytical study is presented of the flow associated with an initially conical shock (M-flow) as the shock approaches the axis of symmetry and as it impinges on, and reflects off, coaxial cylinders of various radii. The analysis uses direct solutions of the Taylor-Maccoll equations, the method of characteristics, curved shock theory and CFD. Agreement between CFD and MOC is generally very good, with some minor discrepancies in the prediction of the shock geometry. MOC has proved to be a useful tool in terms of providing detailed shock wave data at discrete points along the shock, facilitating analysis by CST. Nonetheless, it has the obvious restriction of only being able to provide prediction in flows with regular reflections.

The pressure gradient behind the reflected shock is examined to see if it could lead to local flow choking and detachment of the reflected shock. For the Mach 3.0, 150$^\circ$ incident M-flow shock the pressure gradient is found to be negative and not conducive to local choking and termination of regular reflection. Further exploration of stronger incident shocks is warranted for situations where the Mach number behind the reflected shock is subsonic and the pressure gradient is negative so that the flow would tend towards choking.