Curved shock theory

Abstract

Curved shock theory (CST) is introduced, developed and applied to relate pressure gradients, streamline curvatures, vorticity and shock curvatures in flows with planar or axial symmetry. Explicit expressions are given, in an influence coefficient format, that relate post-shock pressure gradient, streamline curvature and vorticity to pre-shock gradients and shock curvature in steady flow. The effect of pre-shock flow divergence/convergence, on vorticity generation, is related to the transverse shock curvature. A novel derivation for the post-shock vorticity is presented that includes the effects of pre-shock flow non-uniformities. CST applicability to unsteady flows is discussed.

1 History and introduction

There is a long, albeit thin, history of research, stretching over 75 years, on curved shocks, in steady flow with bounding curved streamlines and varying pressure, from Crocco [2] and Thomas [22] to the modern treatment of Emanuel [5]. These efforts, focusing on shock curvature and the resulting flow property gradients, have been largely analytical. Crocco [2] showed that, on a curved, planarly symmetric (planar) shock wave, there is a shock angle where the streamline behind the shock is straight, irrespective of shock curvature. This location on the shock surface is called the Crocco point. Thomas [24] derived the curved shock equations for steady flow of an ideal gas with planar shocks in uniform flow. He found an expression for the curvature of the streamlines behind a curved shock. Any influence of upstream vorticity was not considered. Lin and Rubinoff [16] re-derived the equations of Crocco and Thomas to show that a normal shock can sit on a continuously curving surface only if the Mach number exceeds a certain supersonic value. Thomas [23] extended the curvature notion to higher derivatives of shock and streamline shape, giving extensive graphs of the first-derivative relations. Algebraic complexities prevented Thomas from examining higher derivatives. Today’s computerized algebra manipulators such as Matlab and Maple could be used to advance Thomas’ early efforts. Thomas [24, 25] also considered the motion of a shock attached to the leading edge of a planar, curved surface and developed total differential equations for the first, second and third approximations for the surface pressure. Truesdell [28] derived the formula for the vorticity jump across a curved shock wave, but erroneously concluded that, “when a uniform flow of any fluid breaks across a shock the pressure gradient cannot vanish on the rear side of the shock at any point where the shock is curved and oblique.” A simple physical argument shows otherwise and so does the correct theory. The shock angle and place on the shock wave where the pressure gradient vanishes is called the Thomas point. An application of curved shock theory (CST) to the propagation and decay of spherical blast waves is found in Thomas [27]. Gerber and Bartos [6] presented coefficients for the curved shock equations for determining the orientation of constant property lines behind planar and axisymmetric (axial) shocks in steady, irrotational, uniform flow of an ideal gas. Truly unsteady (i.e., non-pseudo-steady) flow and shock motion were allowed by Pant [20] in deriving gradient expressions for flow behind a moving shock. Mölder [17, 18] presented numerical results for curved shocks in regular reflection (RR) and Mach reflection (MR) at a plane wall and some results for polar streamline directions behind the triple point of Mach reflection for steady flow [19]. Pant [21] presented similar results for planar flow. Darden [3] derived the spatial derivatives of flow properties behind curved weak shocks with applications to sonic boom problems. Emanuel [5] presents a modern treatment of curved shocks based on a vector calculus approach. All of the above contributions have assumed that the gas is both thermally and calorically perfect. Hsu [11] accounted for the effects of non-equilibrium dissociation on gradient functions for flow behind a shock. Hornung [9, 10] described many interesting features of real gas effects on curved shocks and inferred real gas properties from measurements of shock curvature on plane wedges.

A whole series of papers by Truesdell [28], Hayes [7], Kanwal [14] and Emanuel [5] have treated the production of vorticity by a curved shock. Most of these make use of the equation of state and Crocco’s thermodynamic relation. Kanwal [13] shows that the jump in vorticity is independent of the energy equation and the form of the equation of state.

Most of the curved shock equation derivations such as [1] and [26], and the ones above, are for single shock curvature in a flow that is either planarly or axially symmetric. In more complex situations, such as shock reflections in axial flows, terms must be included which account for complex shock curvature since the reflected shock, facing non-uniform and rotational flow, becomes doubly curved. A reflected shock, behind a curved incident shock, has an upstream flow that is non-uniform, rotational and convergent or divergent as well. Previous derivations of CST are for a uniform upstream flow and so do not contain terms reflecting upstream vorticity, upstream flow non-uniformity and compound shock curvature.

The CST is derived and embodied in the curved shock equations, which relate shock curvature directly to the gradients of flow properties near the shock. The equations are derived by applying the Rankine–Hugoniot and Euler equations of conservation to a perfect gas, in steady flow, across a doubly curved shock wave—a shock surface that is curved in two orthogonal planes. The results, although algebraically cumbersome, are more versatile than the Method of Characteristics because they can be used in flow regions where the flow is locally subsonic; however, they are restricted to giving answers in the close proximity of the shock waves. Here the resulting expressions are explicit and exact, being presentable in an influence coefficient format that exactly and explicitly connects various input parameters to the output variables of interest. Important features of shock wave dynamics become apparent when examined by CST; features which are not present for plane shock waves. It becomes evident that many of the results that are derived for flat shocks are not applicable to curved shock waves. A well-known example of this is the detachment of a flat shock from a flat wedge and the detachment of a conical shock from a cone surface.

We present equations, and the details of their derivation, for pressure gradient, flow curvature and vorticity for flow behind a doubly curved shock in steady non-uniform flow where the upstream flow can have a pressure gradient, a streamline curvature, vorticity and can be inclined to the axis.

Fig. 1

Doubly curved shock element—red surface

2 Geometry of curved shocks

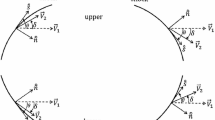
Figure 1 shows an oblique, doubly curved shock element (red) in supersonic flow separating the pre-shock state (1) from the post-shock state (2). The gas enters the shock with a velocity vector ${{\varvec{V}}}_{1}$ and leaves with a velocity vector ${{\varvec{V}}}_{2}$ (or Mach numbers $M_1$ and $M_2$). These vectors are contained in, and they define the flow plane [12]. The coordinate plane, (x, y), lies in the flow plane and x is measured in the direction of the symmetry axis. The velocity vectors are inclined at $\delta _1$ and $\delta _2$ to the x-axis so that the net flow deflection through the shock is $\delta =\delta _2 -\delta _1$. The shock has a trace $a-a$ in the flow plane that is inclined at an angle $\theta$ (the shock angle) to the incoming flow vector (Fig. 2). Distance measured along the shock trace $a-a$ is $\sigma$ and distances measured along and normal to the streamline are s and n. The shock trace $a-a$ has a curvature $S_{a} = \partial \theta _{1}/\partial \sigma$ and a radius of curvature $R_a =-1/S_a$ in the flow plane. The flow-normal plane is normal to both the flow plane and the shock surface. The shock has a trace $b-b$ in the flow-normal plane. The $b-b$ trace has a curvature $S_b$ and a radius of curvature, $R_b =-1/S_b$. In axial flow, y is an important geometric parameter that enters the analysis through $S_b = -\cos \theta _1 /y$, where y is the distance to the axis of symmetry. The pre-shock flow inclination, $\delta _{1}$, also enters through $S_b$ because $\theta _1 =\theta +\delta _1$. At the triple point, in Mach reflection, the three shocks have the same value of y but their $S_{b}$’s are different because the shock angles and pre-shock flow inclinations differ. y is also a convenient scaling parameter for normalizing the length variables. For planar flow $y \rightarrow \infty$ so that $S_{b} \rightarrow 0$. In planar flow, the length scaling parameter can be any convenient length that characterizes the flow size. Shock curvature is positive when, moving along the shock, so that the upstream is on the left, the shock angle increases. A positively curved shock is always concave towards the upstream flow.¹ Using this definition of curvature makes the results applicable to general shock surfaces with no particular degrees of symmetry, as long as the coordinate axis (x, y) is located in the flow plane. A streamline has positive curvature if the flow along it turns away from the wall, x-axis or the centre line of symmetry. The distance from the shock to the axis of symmetry is y. The geometric shock angle $\theta _1$ is distinguished from the aerodynamic shock angle $\theta$ when the pre-shock flow is diverging /converging so that $\theta _1 =\theta +\delta _1$, in which case the geometric curvature, $S_a =\frac{\partial \theta _1 }{\partial \sigma }=\frac{\partial \theta }{\partial \sigma }+\frac{\partial \delta _1 }{\partial \sigma }$ showing that $S_{a}$ is equal to the vorticity-producing term $\frac{\partial \theta }{\partial \sigma }$ only when the pre-shock flow convergence/divergence, $\delta _{1}$ is constant. A significant parameter that appears in the applications of CST is, $\varvec{\mathcal {R}}=S_a /S_b$. At any point, on the shock, its shape is completely determined by the shock angle, $\theta$ or $\theta _{1}$, and the two shock curvatures, $S_{a}$ and $S_{b}$.

Fig. 2

Shock trace $a-a$ in the flow plane

2.1 Rankine–Hugoniot and Euler equations

Across a normal shock wave, the relations expressing conservation of mass, momentum/force, energy and state are [15] (p. 56),

$$\begin{aligned}&\rho _1 V_1 = \rho _2 V_2 \end{aligned}$$

(1)

$$\begin{aligned}&p_1 +\rho _1 V_1^2 = p_2 +\rho _2 V_2^2 \end{aligned}$$

(2)

$$\begin{aligned}&C_p T_1 +V_1^2 /2 = C_p T_2 +V_2^2 /2 \end{aligned}$$

(3)

$$\begin{aligned}&\frac{p_1 }{\rho _1 T_1 } = \frac{p_2 }{\rho _2 T_2 } \end{aligned}$$

(4)

where the usual density, velocity, pressure and temperature symbols with subscript 1 refer to the flow entering the shock and the subscript 2 refers to the departing flow in Figs. 1 and 2. For an oblique (acute or obtuse) shock, the conservation equations are,

$$\begin{aligned}&\rho _1 V_{1N} = \rho _2 V_{2N} \end{aligned}$$

(5)

$$\begin{aligned}&p_1 +\rho _1 V_{1N}^2 = p_2 +\rho _2 V_{2N}^2 \end{aligned}$$

(6)

$$\begin{aligned}&\rho _1 V_{1N} V_{1T} = \rho _2 V_{2N} V_{2T} \end{aligned}$$

(7)

$$\begin{aligned}&C_p T_1 +(V_{1N}^2 +V_{1T}^2 )/2 = C_p T_2 +(V_{2N}^2 +V_{2T}^2 )/2 \end{aligned}$$

(8)

$$\begin{aligned}&\frac{p_1 }{\rho _1 T_1 } = \frac{p_2 }{\rho _2 T_2 } \end{aligned}$$

(9)

The additional subscripts N and T denote velocity components normal and tangential to the oblique shock. For the applications that follow it is important to affirm that these equations relate flow properties immediately up- and downstream of the shock surface and they apply locally to plane as well as to smoothly curving shock waves, be the shocks stationary or not, as long as velocities are measured with respect to the shock wave. Equation (7), when divided by (5), becomes $V_{1T} =V_{2T}$, however, we retain the (7) form so as to get proper coupling between derivatives when (7) is differentiated.

Away from the shock surfaces, either upstream or downstream, flow properties are governed by the Euler equations. These express the conservation of mass, momentum/force and energy in intrinsic coordinate directions along (s) and normal (n) to a streamline. For our purposes, we make the assumption that the flow is homenergic so that the stagnation enthalpy is constant along, as well as across, streamlines. Under these conditions, in the natural or intrinsic streamline coordinates [8] (p. 482), the Euler conservation equations, for steady, axial or planar flow, are,

$$\begin{aligned}&\hbox {Mass conservation:} \quad \frac{\partial }{\partial s}\rho Vy^{j}+\rho Vy^{j}\frac{\partial \delta }{\partial n}=0 \end{aligned}$$

(10)

$$\begin{aligned}&s\hbox {-momentum:} \quad \rho V\frac{\partial V}{\partial s}+\frac{\partial p}{\partial s}=0 \end{aligned}$$

(11)

$$\begin{aligned}&n\hbox {-momentum:} \quad \rho V^{2}\frac{\partial \delta }{\partial s}+\frac{\partial p}{\partial n}=0 \end{aligned}$$

(12)

$$\begin{aligned}&\hbox {Energy (homenergic flow):} \quad \frac{\partial h}{\partial s}+V\frac{\partial V}{\partial s}=0 \end{aligned}$$

(13)

$$\begin{aligned}&\frac{\partial h}{\partial n}+V\frac{\partial V}{\partial n}=0 \end{aligned}$$

(14)

$$\begin{aligned} \hbox {Vorticity is defined as},\quad \omega =V\frac{\partial \delta }{\partial s}-\frac{\partial V}{\partial n} \end{aligned}$$

(15)

In these equations, y is the normal distance from the x-axis of symmetry, $\delta$ is the inclination of the streamline from the x-axis and $h=C_p T$ is the enthalpy. The equations apply to continuous steady flow, in smooth flow regions, between the shock waves. Distance s is measured in the flow direction along the streamline and n is normal to it. j is 0 or 1 for planar or axial flow, respectively. For the present theory, the flow has to be neither planar nor axial if y is taken as the local radius of curvature of the shock trace in the plane normal to the upstream velocity vector. With this, more general definition of y, what follows is applicable to doubly curved shock waves possessing at least left–right symmetry with an identifiable y and where s and n are local (intrinsic) coordinates fixed in the flow plane at the shock. The normal coordinate n is well defined only at the shock wave but this poses no difficulties since we are concerned only with the flow immediately up- and downstream of the shock. Both (x, y) and (s, n) are in right-hand coordinate systems so that the corresponding, positive, z and t point “out-of-the page.” For axial flow, y is the distance from the shock to the axis of symmetry and it is used to normalize all distances. In planar flow, all distances are normalized by a convenient length scale that need not be specified at this stage.

For sake of algebraic neatness, we define the following variable gradients:

$$\begin{aligned}&\hbox {The normalized pressure gradient, }\quad P\equiv \frac{\partial p/\partial s}{\rho V^{2}}\\&\hbox {The streamline curvature, }\quad D\equiv \partial \delta /\partial s\\&\hbox {The normalized vorticity, }\quad \Gamma \equiv \omega /V \end{aligned}$$

and note that along a streamline in front of the shock $\left( {\frac{\partial y}{\partial s}} \right) _1 =\sin \delta _1$ and $\left( {\frac{\partial y}{\partial s}} \right) _2 =\sin \delta _2$ behind.

With these definitions, the Euler equations, (10)–(15), can be written as,

$$\begin{aligned}&\hbox {Mass:} \quad \frac{\partial \delta }{\partial n}=-(M^{2}-1)P-j\frac{\sin \delta }{y} \end{aligned}$$

(16)

$$\begin{aligned}&s\hbox {-momentum:}\quad \frac{1}{V}\frac{\partial V}{\partial s}=-\frac{1}{\rho V^{2}}\frac{\partial p}{\partial s}=-P \end{aligned}$$

(17)

$$\begin{aligned}&n\hbox {-momentum:}\quad \frac{1}{\rho V^{2}}\frac{\partial p}{\partial n}=-\frac{\partial \delta }{\partial s}=-D \end{aligned}$$

(18)

$$\begin{aligned}&\hbox {Energy:} \quad \frac{1}{\rho }\frac{\partial \rho }{\partial n}=-M^{2}\left[ {D+\left( {\gamma -1} \right) \Gamma } \right] \end{aligned}$$

(19)

$$\begin{aligned}&\frac{1}{\rho }\frac{\partial \rho }{\partial s}=M^{2}P \end{aligned}$$

(20)

$$\begin{aligned}&\hbox {Vorticity:}\quad \frac{1}{V}\frac{\partial V}{\partial n}=D-\Gamma \end{aligned}$$

(21)

where the Mach number is defined by $M^{2}=\rho V^{2}/\gamma p$.

These relations will be used to eliminate the derivatives of $\delta , V, p$ and $\rho$ on the left-hand side in favour of M, P, D and $\Gamma$, appearing on the right. In the above equations, all variables have either the subscript 1 or 2 depending on whether application is to flow on the up- or downstream side of the shock. The parameter y needs no subscript since it has the same value when states 1 and 2 are on opposite sides of the same shock. The use of j to denote flow with planar or axial symmetry will not be carried further. This parameter occurs only when multiplied by 1 / y so that its effect is obtained in calculations by assigning a very large value to y when dealing with planar flows.

2.2 The curved shock equations

Consider a segment of a doubly curved shock wave inclined at an angle $\theta$ to the freestream flow direction, as shown in Figs. 1 and 2. This aerodynamic shock angle, $\theta$, is measured in the flow plane that contains both the entering and leaving velocity vectors. This definition of shock angle is very general and makes the theory applicable to a curved shock segment at any orientation in the flow that possesses left–right symmetry. In the flow plane, the geometric curvature of the shock is $S_a =\partial \theta _1 /\partial \sigma$, where $\sigma$ is the distance, measured along the shock trace, in the flow plane, and $\theta _1 =\theta +\delta _1$ is the geometric shock angle. The curvature of the shock trace in a plane normal to the flow plane and normal to the shock surface is $S_b$. The corresponding radii of curvature are then $R_a =-1/S_a$ and $R_b =-1/S_b$. In axial flow, $y/R_b =\cos \theta _1$, so that $S_b =-\cos \theta _1 /y$, where y is the normal distance from the axis to the shock. In the flow plane, the velocity components, normal and tangential to the shock, upstream (1) and downstream (2) of the shock are,

With these substitutions, the Rankine–Hugoniot equations, (5)–(9), become:

$$\begin{aligned}&\rho _1 V_1 \sin \theta =\rho _2 V_2 \sin (\theta -\delta ) \end{aligned}$$

(26)

$$\begin{aligned}&p_1 +\rho _1 V_1^2 \sin ^{2}\theta =p_2 +\rho _2 V_2^2 \sin ^{2}(\theta -\delta ) \end{aligned}$$

(27)

$$\begin{aligned}&V_1 \cos \theta =V_2 \cos (\theta -\delta ) \end{aligned}$$

(28)

$$\begin{aligned}&V_1 V_2 \sin \theta \sin \left( {\theta -\delta } \right) =a_*^2 -\frac{\gamma -1}{\gamma +1}V_1^2 \cos ^{2}\theta \end{aligned}$$

(29)

Here $a_*^2$ is the sound speed at sonic conditions (a constant in adiabatic flow).

2.2.1 Conditions of compatibility and derivation of CST equations

If some quantity (e.g. mass flux) remains constant across a shock wave then the derivatives of this quantity, along the same direction, on either sides of the surface of the shock, must be equal. This kinematic condition is the basic premise underlying all of CST and it seems “intuitively obvious.” It is perhaps less obvious for unsteady flow—but it must still be so since we are dealing locally with quantities immediately up- and downstream of the shock discontinuity that take no time to cross the shock and it is implicit in the fact that the discontinuity conservation equations, (26)–(29), contain no time-dependent terms. This is a subtle yet essential assumption that forms the basis of CST. The same argument can be applied to higher derivatives, Thomas [24], and Kanwal [13] refers to this as “geometrical and kinematical conditions of compatibility,” attributing them to Thomas [24].

The curved shock equations are derived by taking derivatives of both sides of each of equations (26), (27) and (28) with respect to $\sigma$ (the distance along the shock) and equating these pre- and post-shock derivatives for each equation. The derivations are presented in Appendices 1, 2 and 3.

For example, taking derivatives of the left- and right-hand sides of the conservation of mass (26) produces,

$$\begin{aligned}&\rho _1 V_1 \frac{\partial \sin \theta }{\partial \sigma }+\rho _1 \sin \theta \frac{\partial V_1 }{\partial \sigma }+V_1 \sin \theta \frac{\partial \rho _1 }{\partial \sigma } \\&\quad =\rho _2 V_2 \frac{\partial }{\partial \sigma }\sin \left( {\theta -\delta } \right) +\rho _2 \sin \left( {\theta -\delta } \right) \frac{\partial V_2 }{\partial \sigma }\\&\qquad +\,V_2 \sin \left( {\theta -\delta } \right) \frac{\partial \rho _2 }{\partial \sigma } \end{aligned}$$

and similarly (not presented here) for equation (27), producing two differentiated conservation equations involving the aerodynamic shock curvature terms $\frac{\partial \sin \theta }{\partial \sigma }$ explicitly.

In front of the shock, the derivative of any quantity with respect to distance along the shock, can be expressed in terms of the two derivatives along and normal to the streamline,

$$\begin{aligned} \left( {\frac{\partial {\bullet }}{\partial \sigma }} \right) _1 =\left( {\frac{\partial {\bullet }}{\partial s}} \right) _1 \cos \theta +\left( {\frac{\partial {\bullet }}{\partial n}} \right) _1 \sin \theta \, \hbox { for } \rho , V, T \mathrm{and}~p \nonumber \\ \end{aligned}$$

(30)

Similarly, behind the shock,

$$\begin{aligned} \left( {\frac{\partial {\bullet }}{\partial \sigma }} \right) _2 =\left( {\frac{\partial {\bullet }}{\partial s}} \right) _2 \cos \left( {\theta -\delta } \right) +\left( {\frac{\partial {\bullet }}{\partial n}} \right) _2 \sin \left( {\theta -\delta } \right) \nonumber \\ \end{aligned}$$

(31)

These expressions are used to replace the $\sigma$-derivatives in the differentiated conservation equations by s and n derivatives and then replacing all derivatives $\frac{\partial {\bullet }}{\partial s}$ and $\frac{\partial {\bullet }}{\partial n}$ by expressions involving $P_{1}, D_{1}, \Gamma _1, D_{2}, P_{2}, S_{a}$, and $S_{b}$ from the Euler equations. This produces, with a few pages of algebraic manipulation, the curved shock equations,

(32)

(33)

where the coefficients A, B, E, C, G and their primed and subscripted variants (14 in all) are given by,

$$\begin{aligned}&A_1 = 2\cos \theta ((3M_1^2 -4)\sin ^{2}\theta -(\gamma -1)/2)/(\gamma +1) \nonumber \\&B_1 = 2\sin \theta ((\gamma -5)/2+(4-M_1^2 )\sin ^{2}\theta )/(\gamma +1) \nonumber \\&E_1 = -2\sin ^{3}\theta ((\gamma -1)M_1^2 +2)/(\gamma +1) \nonumber \\&A_2 = \sin \theta \cos \theta /\sin (\theta -\delta ) \end{aligned}$$

(34)

$$\begin{aligned}&B_2 = -\sin \theta \cos \theta /\cos (\theta -\delta ) \nonumber \\&C = -4\sin \theta \cos \theta /(\gamma +1) \nonumber \\&G = 4\sin ^{2}\theta \cos \theta \sin \delta _1 /[(\gamma +1)\cos \left( {\theta +\delta _1 } \right) ] \nonumber \\&\mathrm{and}\nonumber \\&A_1^{\prime } = M_1^2 \cos \delta \cos ^{2}\theta -(M_1^2 -1)\cos (2\theta +\delta )\nonumber \\&B_1^{\prime } = -\sin (2\theta +\delta )-M_1^2 \sin \delta \sin ^{2}\theta \nonumber \\&E_1^{\prime } = -(2+(\gamma -1)M_1^2 )\sin \delta \sin ^{2}\theta \nonumber \\&A_2^{\prime } = (1+(M_2^2 -2)\sin ^{2}(\theta -\delta ))\left( {\sin \theta \cos \theta } \right) {/}\nonumber \\&\left( {\sin \left( {\theta -\delta } \right) \cos \left( {\theta -\delta } \right) } \right) \\&B_2^{\prime } = -\sin (2\theta ) \nonumber \\&C^{\prime } = -\sin (2\delta )/(2\cos (\theta -\delta ))\nonumber \\&G^{\prime } = [\sin \theta \sin \delta _1 \sin \left( {\theta +\delta } \right) \nonumber \\&-\sin \theta \cos \theta \sin \delta _2 \tan (\theta -\delta )]{/}\cos (\theta +\delta _1 )\nonumber \end{aligned}$$

(35)

where,

$$\begin{aligned}&M_2^2 =\frac{\left( {\gamma +1} \right) ^{2}M_1^4 \sin ^{2}\theta -4\left( {M_1^2 \sin ^{2}\theta -1} \right) \left( {\gamma M_1^2 \sin ^{2}\theta +1} \right) }{\left[ {2\gamma M_1^2 \sin ^{2}\theta -\left( {\gamma -1} \right) } \right] \left[ {\left( {\gamma -1} \right) M_1^2 \sin ^{2}\theta +2} \right] } \nonumber \\&\hbox { and }\quad \delta =\delta _2 -\delta _1 \end{aligned}$$

(36)

The two equations (32, 33) relate shock curvature, $S_{a}$ and $S_{b}$, to streamwise pressure gradient, P,  and streamline curvature, D, on the up- and downstream sides of a shock element while accounting for any upstream vorticity, $\Gamma _1$ and flow divergence/convergence $\delta _{1}$. The equations (32, 33), together with the coefficients (34, 35), constitute the tools for analysing shock wave curvature and flow gradients on the up- (subscript 1) and downstream (subscript 2) sides of a single, curved shock wave. The derivations of the curved shock equations and their coefficients are found in Appendices 1, 2 and 3. If we assume that the freestream Mach number $(M_{1})$, the flow inclination in front of the shock $(\delta _{1})$ and the shock angle ($\theta$ or $\theta _{1}$) are known then all the coefficients can be calculated. Then, in the curved shock equations, five of the seven variables $P_{1}, D_{1}, \Gamma _{1}, D_{2}, P_{2}, S_{a}$, and $S_{b}$ must be known and the remaining two can then be calculated from the two “simultaneous” curved shock equations, (32, 33). If the coordinate system is aligned with the uniform freestream, then the shock angle, $\theta$, is measured with respect to the freestream direction and $\delta _1 =0$ so that $\delta =\delta _2$. In the derivation of the curved shock equations, the vorticity, as defined by (15), appears explicitly on both sides of the shock as $\Gamma _{1}$ and $\Gamma _{2}$, so that the vorticity is just another dependent variable along with the pressure gradient and streamline curvature and it should have its own equation alongside the two curved shock equations. However, in (32, 33), $\Gamma _{2}$ has been eliminated using the vorticity expression from Appendix 3. Various restricted forms of the curved shock equations have been presented by many authors: Crocco [2], Thomas [22] and Pant [21]. However, they have not appeared with the degree of generality that includes both upstream vorticity, ${\Gamma }_{1}$, and transverse shock curvature, $S_{b}$. Both of these are essential in application to curved shock wave reflection, both planar and axial. The detailed derivation of the curved shock equations (32, 33) and their coefficients has been verified more recently (2015) by Prof. Yancheng You and Weiqiang Han as presented in Appendices 1 and 2. The equations can be solved, yielding explicit expressions for the downstream pressure gradient and streamline curvature,

(37)

where,

$$\begin{aligned} L=A_1 P_1 +B_1 D_1 +E_1 \Gamma _1 \nonumber \\ L^{\prime }=A_1^{\prime } P_1 +B_1^{\prime } D_1 +E_1^{\prime } \Gamma _1 \end{aligned}$$

(38)

These are the most general expressions for pressure gradient and streamline curvature for flow behind a doubly curved shock, with curvatures $(S_{a}, S_{b})$, facing a non-uniform upstream flow with pressure gradient $P_{1}$, streamline curvature $D_{1}$ and vorticity ${\Gamma }_{1}$; the upstream non-uniformities being contained in the two expressions L and $L^\prime$. The upstream flow inclination, $\delta _{1}$, is contained in the two coefficients G and $G^\prime$; it embodies the effects of flow convergence/divergence in front of the shock.

Both $P_{2}$ and $D_{2}$ can be written in the influence coefficient form,

(39)

where the influence coefficients are,

$$\begin{aligned} J_p= & {} {\left( {A_1 B_2^{\prime } -A_1^{\prime } B_2 } \right) }/{\left[ {AB} \right] }\qquad K_p =-{\left( {A_1 A_2^{\prime } -A_1^{\prime } A_2 } \right) }/{\left[ {AB} \right] } \nonumber \\ J_d= & {} {\left( {B_1 B_2^{\prime } -B_1^{\prime } B_2 } \right) }/{\left[ {AB} \right] }\qquad K_d =-{\left( {B_1 A_2^{\prime } -B_1^{\prime } A_2 } \right) }/{\left[ {AB} \right] } \nonumber \\ J_g= & {} {\left( {E_1 B_2^{\prime } -E_1^{\prime } B_2 } \right) }/{\left[ {AB} \right] }\qquad K_g =-{\left( {E_1 A_2^{\prime } -E_1^{\prime } A_2 } \right) }/{\left[ {AB} \right] } \nonumber \\ J_a= & {} {\left( {B_2 C^{\prime }-B_2^{\prime } C} \right) }/{\left[ {AB} \right] }\qquad K_a =-{\left( {A_2 C^{\prime }-A_2^{\prime } C} \right) }/{\left[ {AB} \right] } \nonumber \\ J_b= & {} {\left( {B_2 G^{\prime }-B_2^{\prime } G} \right) }/{\left[ {AB} \right] }\qquad K_b =-{\left( {A_2 G^{\prime }-A_2^{\prime } G} \right) }/{\left[ {AB} \right] }\nonumber \\ \end{aligned}$$

(40)

and where $\left[ {AB} \right] =A_2 B_2^{\prime } -A_2^{\prime } B_2$.

In most aeronautical applications, the freestream is uniform so that $P_{1} = D_{1}={\Gamma }_{1}= \delta _{1} = 0$ and $L = L^{\prime } = 0$, and (39) then simplify to,

$$\begin{aligned} P_{2}= & {} J_a S_a + J_b S_b \end{aligned}$$

(41)

$$\begin{aligned} D_{2}= & {} K_a S_a + K_b S_b \end{aligned}$$

(42)

Fig. 3

Influence coefficients for pressure gradient

Fig. 4

Influence coefficients for streamline curvature

The influence coefficient equations show explicitly how each of $P_{2}$ and $D_{2}$ are determined by the upstream quantities and the shock curvatures where the shock properties $(M_{1}, \theta )$ determine the influence coefficients. The influence of pre-shock flow convergence/divergence, as expressed by $\delta _1$, is unfortunately not as explicit, being embedded in $J_{a}, J_{b}$ and $K_{a}, K_{b}$, through the coefficients $C, C^{\prime }, G, G^{\prime }$. Figure 3 shows the influence coefficients for the post-shock pressure gradient, $P_2$ for both an acute and obtuse shock facing a Mach 3 air flow.² The blue curve shows that for weak shocks the pre-shock pressure gradient is amplified in the same sense by a factor of about 4, whereas for a strong shock the incoming gradient is amplified by as much as 40 with a sense reversal.³ At some intermediate values of shock angle of about 72$^\circ$ and (180$^\circ$–72$^\circ$), the incoming pressure gradient has no influence on the post-shock gradient. The green curve shows that a pre-shock flow curvature, $D_1$, causes an unlike sense contribution to the post-shock pressure gradient for the acute shock and a like sense contribution for the obtuse shock. Upstream vorticity’s contribution (red curve) to post-shock pressure gradient is in the opposite sense to the pre-shock flow curvature’s but otherwise similar. The contribution of the flow-plane curvature, $S_a$, to the pressure gradient is shown by the cyan-coloured curve. The effect is similar to that of pre-shock pressure gradient; sense reversal occurring near a shock angle of 76$^\circ$ and (180$^\circ$–76$^\circ$). The black curve shows the influence of the lateral shock curvature, $S_b$, on the post-shock pressure gradient when there is no flow divergence/convergence in front of the shock. There can be, however, a change in divergence/convergence as represented by $\frac{\partial \delta _1 }{\partial \sigma }$, contributing to $S_{b}$. This becomes more apparent in the derivation of (47), below.

Fig. 5

Diverging flow in front of curved, axial shock element. Flow divergence angle is $\delta _1$. Geometric shock angle is $\theta _1$. $R_{b}$ is transverse shock radius of curvature

Figure 4 depicts the influence coefficients for the pre-shock and shock curvature terms affecting the post-shock flow curvature, $D_2$. The blue curve shows that a positive pre-shock pressure gradient contributes negatively to post-shock curvature for a weak acute shock and positively to a strong acute shock. The effect is anti-symmetric for an obtuse shock. The green curve shows that the pre-shock flow curvature causes a positive contribution to the post-shock curvature for weak shocks and a negative contribution for strong shocks, acute as well as obtuse. The contribution of pre-shock vorticity (red curve) is similar except with an opposite sense. Cyan and black curves show the anti-symmetric effects of the two shock curvatures $S_a$ and $S_b$. The $J_{a}$ curve crosses the horizontal axis at the Crocco point, where the flow curvature behind the shock vanishes.

The two graphs, Figs. 3 and 4, are either symmetric or anti-symmetric for acute and obtuse shocks. This is because the freestream has been set to be parallel to the axis of symmetry $(\delta _1 =0)$. A finite value of $\delta _1$ has no effect in planar flow, however in axial flow, it leads to pre-shock flow convergence or divergence effects through the $\sin \delta _1 /y$-term in (16).

For all examples, involving an oblique shock element, we first need to solve the Rankine–Hugoniot equations (26)–(29) to obtain one of $M_{2}, \theta$, and $\delta$ in terms of the other two and the upstream conditions. These are required to calculate the coefficients of the curved shock equations (32, 33). For shocks facing a uniform upstream, all terms on the left-hand sides of the two curved shock equations are zero. So is G, on the right-hand side, if we choose to align the freestream with the x-axis, for then $\delta _1 =0$. This is not the case when the equations are applied to the reflected shock in the shock reflection process below, for then the flow in front of the reflected shock is inclined towards the axis and it is also non-uniform (with curvature and pressure gradient) and rotational, as produced by a curved incident shock.

2.2.2 Vorticity behind the shock

When applying CST to RR and MR, the post-shock vorticity, in region (2), behind the incident shock, is required as input to the curvature calculations of the reflected shock when a curved incident shock has created vorticity in front of the reflected shock.

For a uniform upstream flow, the vorticity behind a curved shock, as given by Truesdell [28], Hayes [7] and more recently by Emanuel [4] is,

$$\begin{aligned} \omega _2 =V_1 \frac{\rho _2 }{\rho _1 }\left( {1-\frac{\rho _1 }{\rho _2 }} \right) ^{2}\cos \theta \frac{\partial \theta }{\partial \sigma } \end{aligned}$$

(43)

The derivation of this relation uses the Crocco relation between vorticity and entropy and assumes a uniform upstream flow. The normalized version of (43) is,

$$\begin{aligned} \Gamma _2 =\frac{\omega _2 }{V_2 }=\frac{V_1 }{V_2 }\frac{\rho _2 }{\rho _1 }\left( {1-\frac{\rho _1 }{\rho _2 }} \right) ^{2}\cos \theta \frac{\partial \theta }{\partial \sigma } \end{aligned}$$

(44)

This equation gives the normalized vorticity in front of a reflected shock (in region 2) as produced by a curved incident shock. Equation (44) can be further simplified to,

$$\begin{aligned} \Gamma _2 =\frac{2\sin ^{2}\delta }{\sin (2\theta )\sin (\theta -\delta )}\frac{\partial \theta }{\partial \sigma } \end{aligned}$$

(45)

This equation gives the normalized vorticity behind an acute or obtuse shock, in region 2, where $\frac{\partial \theta }{\partial \sigma }$ is the change of the aerodynamic shock angle with distance along the shock. This change in the aerodynamic shock angle is due to the curvature of the shock, in the flow plane, $S_{a}$, and any divergence/convergence of the pre-shock flow. This becomes apparent if one considers the relation, $\theta _1 =\theta +\delta _1$ (Fig. 2) and its shock-wise derivative $\frac{\partial \theta _1 }{\partial \sigma }=\frac{\partial \theta }{\partial \sigma }+\frac{\partial \delta _1 }{\partial \sigma }$ so that $\frac{\partial \theta }{\partial \sigma }=S_a -\frac{\partial \delta _1 }{\partial \sigma }$, where $\frac{\partial \delta _1 }{\partial \sigma }$ expresses the change, along the shock, of the divergence/convergence angle in the pre-shock flow, so that,

$$\begin{aligned} \Gamma _2 =\frac{2\sin ^{2}\delta }{\sin (2\theta )\sin (\theta -\delta )}\left[ {S_a -\frac{\partial \delta _1 }{\partial \sigma }} \right] \end{aligned}$$

(46)

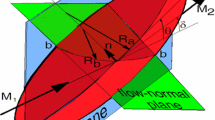
This equation gives the vorticity behind a shock that has a geometric curvature, $S_{a}$, in the flow plane and a pre-shock, shock-wise, change of divergence, $\frac{\partial \delta _1 }{\partial \sigma }$. Otherwise, for this equation, the pre-shock flow is uniform, i.e., there is no pressure gradient, no streamline curvature and no vorticity in the pre-shock flow. It now remains to show what the effect of $S_b$ is when there is a change in pre-shock divergence, $\frac{\partial \delta _1 }{\partial \sigma }$, along the shock. Figure 5 shows the flow plane trace of a curved axial shock element $a-a$ (red) on a symmetry axis $x-x$. At the point s, on the shock element, the shock makes an angle $\theta _1$ with $x-x$. The transverse radius of shock curvature is $R_{b}$ and the pre-shock flow approaches at an angle $\delta _1$ so that the angle between the shock and the pre-shock flow is $\theta _1 -\delta _1$. The infinitesimal shock segment $\hbox {d}\sigma$ (blue) subtends an angle $\hbox {d}\delta _1$ at the axis. From geometry: $\hbox {d}\delta _1 =\hbox {d}\sigma \sin \left( {\theta _1 -\delta _1 } \right) /r$ and $\tan \theta _1 =R_b /w$. The law of sines, $\sin (\pi -\theta _1 )/r=\sin \delta _1 /w$, is used to eliminate the lengths r and w to give,

$$\begin{aligned} \frac{\partial \delta _1 }{\partial \sigma }=-\frac{\sin \delta _1 \sin \left( {\theta _1 -\delta _1 } \right) }{\cos \theta _1 }S_b \end{aligned}$$

(47)

Equation (46) can then be written,

$$\begin{aligned} \Gamma _2 =\frac{2\sin ^{2}\delta }{\sin (2\theta )\sin (\theta -\delta )}\left[ {S_a +\frac{\sin \delta _1 \sin \left( {\theta _1 -\delta _1 } \right) }{\cos \theta _1 }S_b } \right] \end{aligned}$$

(48)

The coefficients multiplying $S_a$ and $S_b$, respectively, are simplified versions of the influence coefficients $I_{a}$ and $I_{b}$ derived in Appendix 3. The purely geometric relation between $S_b$ and $\frac{\partial \delta _1 }{\partial \sigma }$ in  (47), shows that $S_b$ is a measure of the vorticity generating term $\frac{\partial \delta _1 }{\partial \sigma }$ and it explains the appearance of $S_b$, in the influence coefficient equation for vorticity, when the flow is diverging/converging in front of the shock. Note that if the pre-shock flow is divergent then it would, most likely, have a pressure gradient. This gradient has its own effect on the post-shock vorticity through the influence coefficient $I_{p}$ in Appendix 3. The pressure gradient effect is not included in (43)–(46), (48). The same is true for any pre-shock flow curvature and vorticity. For a Mach wave and a normal shock, for which $\delta =0$, (46) shows that no vorticity can be produced by the curvature of either one of these waves. The level of generality in (46) is sufficient for the study of RR and MR in a uniform and parallel freestream flow. If, however, the vorticity value is desired behind the reflected shock (in region 3), then a more general expression is required which includes the pre-shock pressure gradient, curvature, divergence and vorticity. This is so also if the freestream is non-uniform.

The derivation of the equation for vorticity, behind a curved shock, in non-uniform pre-shock flow (including divergence), is contained in Appendix 3.

3 Application to three-dimensional flows and to unsteady flows

A flow plane is defined as containing the pre- and post-shock flow vectors. A smooth three-dimensional shock has to have two such vectors at every point on its surface and it would therefore have a flow plane. The curvature of the trace that the shock makes in the flow plane is $S_{a}$. A flow-normal plane, that is normal to the flow plane as well as the shock, has a shock trace with a curvature $S_{b}$. Thus there are, generally, two definable shock curvatures, $S_{a}$ and $S_{b}$, of the traces that the 3D shock makes in the two planes and there are no apparent restrictions on the dimensionality of the shock. The Rankine–Hugoniot equations apply and the shock appears to be locally two-dimensional. This makes it tempting to assert that CST, as derived, is applicable to three-dimensional shock waves. However, as pointed out by G. Emanuel (private communication), the Euler equations (10)–(15) apply on an osculating plane that contains the curved post-shock streamline and this osculating plane, generally, veers away from the flow plane in the post-shock flow so that the CST applies only when the flow plane and the osculating plane are co-planar, i.e., the angle, $\upomega$, between them is zero. This angle is given by tan $\upomega = - (\partial p/\partial b)/(\partial p/\partial s)$ [5], where the two partial derivatives are of the pressure gradients in the flow plane and the flow-normal plane. The flow-normal pressure gradient is zero when the shock-trace curvature in the flow-normal plane is constant, i.e., $\partial S_{b}/\partial b = 0$. This occurs at a meridional plane of symmetry in three-dimensional flow, if such a symmetry plane exists. For example, a shape with an elliptic cross section, at zero angle of attack, produces a surrounding flow that has two orthogonal, meridional planes of symmetry, both planes containing the symmetry axis. In this case, the flow plane, the osculating plane and a symmetry plane are co-planar and the CST applies wherever the shock intersects these planes. Thus, there are such lines of symmetry, on three-dimensional shocks, where CST does apply. At other points, on the shock, it does not.

The Euler equations (10)–(15), as used in the derivations of the CST, do not contain any time-dependent terms so that CST does not apply to unsteady flows, in general. However, when the flows are self-similar⁴ in the (S, N) coordinate system, where $S = s/t$ and $N = n/t$, and the Euler equations are written in the (S, N) system so that they do not contain t explicitly, then CST applies. Such self-similar flows occur, in “pseudo-steady” flow, when a flat shock moves over a plane wedge or over a cone or when a flat shock turns around a sharp corner.

4 Conclusions

The CST relates shock curvatures and flow divergence/convergence, in both planar and axial flow, to vorticity and to pressure gradient and streamline curvature at the shock surface. The theory allows non-uniform flow both up- and downstream of a doubly curved shock surface. The effect of pre-shock flow divergence/convergence, on vorticity generation, is related to the transverse shock curvature. A novel derivation for post-shock vorticity includes effects of pre-shock flow non-uniformities, including flow divergence. Expressions for flow gradients are made explicit in an influence coefficient form.

Appendices

Appendix 1. Derivation of the curved shock equation (32)

For nomenclature and methodology refer to Sect. 2.

The pressure ratio across an oblique shock is given by,

$$\begin{aligned}&\frac{p_2 }{p_1 } = \frac{2\gamma }{\gamma +1}M_1^2 \text {sin}^{2}\theta -\frac{\gamma -1}{\gamma +1}\\&\frac{p_2 }{p_1 } = \frac{2\gamma }{\gamma +1}\frac{\rho _1 V_1^2 }{\gamma p_1 }\text {sin}^{2}\theta -\frac{\gamma -1}{\gamma +1}\\&\left( {\gamma +1} \right) p_2 = 2\rho _1 V_1^2 \text {sin}^{2}\theta -\left( {\gamma -1} \right) p_1 \end{aligned}$$

Taking derivatives of both sides with respect to distance along the shock, $\sigma$,

$$\begin{aligned} \left( {\gamma +1} \right) \frac{\partial p_2 }{\partial \sigma }= & {} 2\rho _1 V_1^2 \frac{\partial \text {sin}^{2}\theta }{\partial \sigma }+2\rho _1 \text {sin}^{2}\theta \frac{\partial V_1^2 }{\partial \sigma }\\&+2V_1^2 \text {sin}^{2}\theta \frac{\partial \rho _1 }{\partial \sigma }-\left( {\gamma -1} \right) \frac{\partial p_1 }{\partial \sigma } \end{aligned}$$

Changing $\sigma$ derivatives to s and n derivatives,

$$\begin{aligned}&\left( {\gamma +1} \right) \left[ {\frac{\partial p_2 }{\partial s}\text {cos}\left( {\theta -\delta } \right) +\frac{\partial p_2 }{\partial n}\text {sin}\left( {\theta -\delta } \right) } \right] \nonumber \\&\quad =4\text {sin}\theta \text {cos}\theta \rho _1 V_1^2 \frac{\partial \theta }{\partial \sigma }\nonumber \\&\qquad +\,4V_1 \rho _1 \text {sin}^{2}\theta \left( {\frac{\partial V_1 }{\partial s}\text {cos}\theta +\frac{\partial V_1 }{\partial n}\text {sin}\theta } \right) \nonumber \\&\qquad +\,2V_1^2 \text {sin}^{2}\theta \left( {\frac{\partial \rho _1 }{\partial s}\text {cos}\theta +\frac{\partial \rho _1 }{\partial n}\text {sin}\theta } \right) \nonumber \\&\qquad -\,\left( {\gamma -1} \right) \left( {\frac{\partial p_1 }{\partial s}\text {cos}\theta +\frac{\partial p_1 }{\partial n}\text {sin}\theta } \right) \end{aligned}$$

(49)

Derivatives $\frac{\partial \theta }{\partial \sigma },\frac{\partial {\bullet }}{\partial \hbox {s}}$ and $\frac{\partial {\bullet }}{\partial \hbox {n}}$ can be expressed as:

$$\begin{aligned}&\frac{\partial p_1 }{\partial \hbox {s}}=P_1 \rho _1 V_1^2 \quad \quad \frac{\partial p_2 }{\partial \hbox {s}}=P_2 \rho _2 V_2^2\\&\frac{\partial p_1 }{\partial \hbox {n}}=-D_1 \rho _1 V_1^2 \quad \quad \frac{\partial p_2 }{\partial \hbox {n}}=-D_2 \rho _2 V_2^2\\&\frac{\partial V_1 }{\partial \hbox {s}}=-P_1 V_1 \quad \quad \frac{\partial V_1 }{\partial \hbox {n}}=V_1 \left( {D_1 -\Gamma _1 } \right) \\&\frac{\partial \rho _1 }{\partial \hbox {s}}=\rho _1 M_1^2 P_1 \quad \quad \frac{\partial \rho _1 }{\partial \hbox {n}}=-\rho _1 M_1^2 \left[ {D_1 +\left( {\gamma -1} \right) \Gamma _1 } \right] \\&\frac{\partial \theta }{\partial \sigma }=S_a +\left( {M_1^2 -1} \right) \text {sin}\theta P_1 -\text {cos}\theta D_1 +\frac{\text {sin}\theta \text {sin}\delta _1 }{y} \end{aligned}$$

With these substitutions (49) becomes,

$$\begin{aligned}&\left( {\gamma +1} \right) \left[ {P_2 \rho _2 V_2^2 \text {cos}\left( {\theta -\delta } \right) -D_2 \rho _2 V_2^2 \text {sin}\left( {\theta -\delta } \right) } \right] \nonumber \\&\quad =4\text {sin}\theta \text {cos}\theta \rho _1 V_1^2 \left[ S_a +\left( {M_1^2 -1} \right) \text {sin}\theta P_1\right. \nonumber \\&\left. \qquad -\,\text {cos}\theta D_1 +\frac{\text {sin}\theta \text {sin}\delta _1 }{y} \right] \nonumber \\&\qquad +\,4V_1 \rho _1 \text {sin}^{2}\theta \left[ {-P_1 V_1 \text {cos}\theta +V_1 \left( {D_1 -\Gamma _1 } \right) \text {sin}\theta } \right] \nonumber \\&\qquad +\,2V_1^2 \text {sin}^{2}\theta \left\{ \rho _1 M_1^2 P_1 \text {cos}\theta \right. \nonumber \\&\qquad \left. -\,\rho _1 M_1^2 \left[ {D_1 +\left( {\gamma -1} \right) \Gamma _1 } \right] \text {sin}\theta \right\} \nonumber \\&\qquad -\,\left( {\gamma -1} \right) \left( {P_1 \rho _1 V_1^2 \text {cos}\theta -D_1 \rho _1 V_1^2 \text {sin}\theta } \right) \end{aligned}$$

(50)

Replacing $\frac{1}{y} \hbox { by}-\frac{S_b }{\text {cos}\theta _1 } \left( {\frac{1}{y}=-\frac{S_b }{\text {cos}\theta _1 }} \right)$, (50) becomes,

$$\begin{aligned}&\left( {\gamma +1} \right) \left[ {P_2 \rho _2 V_2^2 \text {cos}\left( {\theta -\delta } \right) -D_2 \rho _2 V_2^2 \text {sin}\left( {\theta -\delta } \right) } \right] \\&\quad =4\text {sin}\theta \text {cos}\theta \rho _1 V_1^2 \left[ S_a +\left( {M_1^2 -1} \right) \text {sin}\theta P_1\right. \\&\left. \qquad -\,\text {cos}\theta D_1 -\frac{S_b \text {sin}\theta \text {sin}\delta _1 }{\text {cos}\theta _1 } \right] \\&\qquad +\,4V_1 \rho _1 \text {sin}^{2}\theta \left[ {-P_1 V_1 \text {cos}\theta +V_1 \left( {D_1 -\Gamma _1 } \right) \text {sin}\theta } \right] \\&\qquad +\,2V_1^2 \text {sin}^{2}\theta \left\{ \rho _1 M_1^2 P_1 \text {cos}\theta \right. \\&\left. \qquad -\,\rho _1 M_1^2 \left[ {D_1 +\left( {\gamma -1} \right) \Gamma _1 } \right] \text {sin}\theta \right\} \\&\qquad -\,\left( {\gamma -1} \right) \left( {P_1 \rho _1 V_1^2 \text {cos}\theta -D_1 \rho _1 V_1^2 \text {sin}\theta } \right) \end{aligned}$$

Collecting terms,

$$\begin{aligned}&\left[ -4\rho _1 V_1^2 \left( {M_1^2 -1} \right) \text {sin}^{2}\theta \text {cos}\theta +4\rho _1 V_1^2 \text {sin}^{2}\theta \text {cos}\theta \right. \\&\left. \quad \quad -\,2\rho _1 V_1^2 M_1^2 \text {sin}^{2}\theta \text {cos}\theta +\left( {\gamma -1} \right) \rho _1 V_1^2 \text {cos}\theta \right] P_1 \\&\quad \quad +\,\left[ 4\rho _1 V_1^2 \text {sin}\theta \text {cos}^{2}\theta -4\rho _1 V_1^2 \text {sin}^{3}\theta \right. \\&\quad \quad \left. +\,2\rho _1 V_1^2 M_1^2 \text {sin}^{3}\theta -\left( {\gamma -1} \right) \rho _1 V_1^2 \text {sin}\theta \right] D_1 \\&\quad \quad +\,\left[ {4\rho _1 V_1^2 \text {sin}^{3}\theta +2\left( {\gamma -1} \right) \rho _1 V_1^2 M_1^2 \text {sin}^{3}\theta } \right] \Gamma _1 \\&\quad =\left[ {-\left( {\gamma +1} \right) \rho _2 V_2^2 \text {cos}\left( {\theta -\delta } \right) } \right] P_2\\&\quad \quad +\,\left[ {\left( {\gamma +1} \right) \rho _2 V_2^2 \text {sin}\left( {\theta -\delta } \right) } \right] D_2 \\&\quad \quad +\,\left( {4\rho _1 V_1^2 \text {sin}\theta \text {cos}\theta } \right) S_a \\&\quad \quad +\left[ {-\frac{4\rho _1 V_1^2 \text {sin}^{2}\theta \text {cos}\theta \text {sin}\delta _1 }{\text {cos}\theta _1 }} \right] S_b \end{aligned}$$

Dividing through by $\rho _1 V_1^2$,

$$\begin{aligned}&\left[ -4\left( {M_1^2 -1} \right) \text {sin}^{2}\theta \text {cos}\theta +4\text {sin}^{2}\theta \text {cos}\theta \right. \\&\left. \quad -\,2M_1^2 \text {sin}^{2}\theta \text {cos}\theta +\left( {\gamma -1} \right) \text {cos}\theta \right] P_1 \\&\quad +\,\left[ {4\text {sin}\theta \text {cos}^{2}\theta -4\text {sin}^{3}\theta +2M_1^2 \text {sin}^{3}\theta -\left( {\gamma -1} \right) \text {sin}\theta } \right] D_1 \\&\quad +\,\left[ {4\text {sin}^{3}\theta +2\left( {\gamma -1} \right) M_1^2 \text {sin}^{3}\theta } \right] \Gamma _1 \\&\,=\left[ {-\left( {\gamma +1} \right) \frac{\text {sin}\theta \text {cos}\theta }{\text {sin}\left( {\theta -\delta } \right) }} \right] P_2\\&\quad +\,\left[ {\left( {\gamma +1} \right) \frac{\text {sin}\theta \text {cos}\theta }{\text {cos}\left( {\theta -\delta } \right) }} \right] D_2 +\left( {4\text {sin}\theta \text {cos}\theta } \right) S_a \\&\quad +\,\left[ {-\frac{4\text {sin}^{2}\theta \text {cos}\theta \text {sin}\delta _1 }{\text {cos}\theta _1 }} \right] S_b \end{aligned}$$

Thus, the curved shock equation (32),

$$\begin{aligned} A_1 P_1 +B_1 D_1 +E_1 \Gamma _1 =A_2 P_2 +B_2 D_2 +CS_a +GS_b \end{aligned}$$

has the coefficients $A_{1}, B_{1}, E_{1}, A_{2}, B_{2}, C$, and G, given by,

$$\begin{aligned} A_1= & {} \frac{4\left( {M_1^2 -1} \right) \text {sin}^{2}\theta \text {cos}\theta -4\text {sin}^{2}\theta \text {cos}\theta +2M_1^2 \text {sin}^{2}\theta \text {cos}\theta -\left( {\gamma -1} \right) \text {cos}\theta }{\gamma +1}\\= & {} \frac{2\text {cos}\theta \left[ {\left( {3M_1^2 -4} \right) \text {sin}^{2}\theta -\left( {\gamma -1} \right) /2} \right] }{\gamma +1}\\ B_1= & {} \frac{-4\text {sin}\theta \text {cos}^{2}\theta +4\text {sin}^{3}\theta -2M_1^2 \text {sin}^{3}\theta +\left( {\gamma -1} \right) \text {sin}\theta }{\gamma +1}\\= & {} \frac{4\text {sin}\theta \left( {\text {sin}^{2}\theta -1} \right) +4\text {sin}^{3}\theta -2M_1^2 \text {sin}^{3}\theta +\left( {\gamma -1} \right) \text {sin}\theta }{\gamma +1}\\= & {} \frac{2\text {sin}\theta \left[ {\left( {\gamma -5} \right) /2+\left( {4-M_1^2 } \right) \text {sin}^{2}\theta } \right] }{\gamma +1}\\ E_1= & {} \frac{-4\text {sin}^{3}\theta -2\left( {\gamma -1} \right) M_1^2 \text {sin}^{3}\theta }{\gamma +1}\\= & {} -\frac{2\text {sin}^{3}\theta \left[ {2+\left( {\gamma -1} \right) M_1^2 } \right] }{\gamma +1}\\ A_2= & {} \frac{\text {sin}\theta \text {cos}\theta }{\text {sin} \left( {\theta -\delta } \right) }\\ B_2= & {} -\frac{\text {sin}\theta \text {cos}\theta }{\text {cos}\left( {\theta -\delta } \right) }\\ \hbox {C}= & {} -\frac{4\text {sin}\theta \text {cos}\theta }{\gamma +1}\\ \hbox {G}= & {} \frac{4\text {sin}^{2}\theta \text {cos}\theta \text {sin}\delta _1 }{\left( {\gamma +1} \right) \text {cos}\theta _1 } \end{aligned}$$

These coefficients can be further simplified by dividing all of them through by $\text {sin}\theta$.

Appendix 2. Derivation of the curved shock equation (33)

Starting from (26), (27) and (28),

$$\begin{aligned}&p_1 +\rho _1 V_1^2 \text {sin}^{2}\theta = p_2 +\rho _2 V_2^2 \text {sin}^{2}\left( {\theta -\delta } \right) \\&p_1 -p_2 = \rho _1 V_1^2 \text {sin}\theta \text {cos}\theta \tan \left( {\theta -\delta } \right) -\rho _1 V_1^2 \text {sin}^{2}\theta \end{aligned}$$

Taking derivatives of both sides with respect to $\sigma$,

$$\begin{aligned} \frac{\partial p_1 }{\partial \sigma }-\frac{\partial p_2 }{\partial \sigma }= & {} \rho _1 V_1^2 \text {sin}\theta \text {cos}\theta \frac{\partial \tan \left( {\theta -\delta } \right) }{\partial \sigma }\\&+\,\rho _1 V_1^2 \text {sin}\theta \tan \left( {\theta -\delta } \right) \frac{\partial \text {cos}\theta }{\partial \sigma } \\&+\,\rho _1 V_1^2 \text {cos}\theta \tan \left( {\theta -\delta } \right) \frac{\partial \text {sin}\theta }{\partial \sigma }\\&+\,\rho _1 \text {sin}\theta \text {cos}\theta \tan \left( {\theta -\delta } \right) \frac{\partial V_1^2 }{\partial \sigma } \\&+\,V_1^2 \text {sin}\theta \text {cos}\theta \tan \left( {\theta -\delta } \right) \frac{\partial \rho _1 }{\partial \sigma }\\&-\rho _1 V_1^2 \frac{\partial \text {sin}^{2}\theta }{\partial \sigma }\\&-\,\rho _1 \text {sin}^{2}\theta \frac{\partial V_1^2 }{\partial \sigma }-V_1^2 \text {sin}^{2}\theta \frac{\partial \rho _1 }{\partial \sigma } \\ \end{aligned}$$

Changing to s and n derivatives,

$$\begin{aligned}&\left( {\frac{\partial p_1 }{\partial s}\text {cos}\theta +\frac{\partial p_1 }{\partial n}\text {sin}\theta } \right) \nonumber \\&\quad \quad -\,\left[ {\frac{\partial p_2 }{\partial s}\text {cos}\left( {\theta -\delta } \right) +\frac{\partial p_2 }{\partial n}\text {sin}\left( {\theta -\delta } \right) } \right] \nonumber \\&\quad \,=\rho _1 V_1^2 \text {sin}\theta \text {cos}\theta \frac{1}{\text {cos}^{2}\left( {\theta -\delta } \right) }\frac{\partial \left( {\theta -\delta } \right) }{\partial \sigma }\nonumber \\&\quad \quad -\,\rho _1 V_1^2 \text {sin}^{2}\theta \tan \left( {\theta -\delta } \right) \frac{\partial \theta }{\partial \sigma } \nonumber \\&\quad \quad +\,\rho _1 V_1^2 \text {cos}^{2}\theta \tan \left( {\theta -\delta } \right) \frac{\partial \theta }{\partial \sigma }\nonumber \\&\quad \quad +\,2\rho _1 V_1 \text {sin}\theta \text {cos}\theta \tan \left( {\theta -\delta } \right) \left( {\frac{\partial V_1 }{\partial s}\text {cos}\theta +\frac{\partial V_1 }{\partial n}\text {sin}\theta } \right) \nonumber \\&\quad \quad +\,V_1^2 \text {sin}\theta \text {cos}\theta \tan \left( {\theta -\delta } \right) \left( {\frac{\partial \rho _1 }{\partial s}\text {cos}\theta +\frac{\partial \rho _1 }{\partial n}\text {sin}\theta } \right) \nonumber \\&\quad \quad -2\text {sin}\theta \text {cos}\theta \rho _1 V_1^2 \frac{\partial \theta }{\partial \sigma } \nonumber \\&\quad \quad -2\rho _1 V_1 \text {sin}^{2}\theta \left( {\frac{\partial V_1 }{\partial s}\text {cos}\theta +\frac{\partial V_1 }{\partial n}\text {sin}\theta } \right) \nonumber \\&\quad \quad -V_1^2 \text {sin}^{2}\theta \left( {\frac{\partial \rho _1 }{\partial s}\text {cos}\theta +\frac{\partial \rho _1 }{\partial n}\text {sin}\theta } \right) \end{aligned}$$

(51)

Derivatives $\frac{\partial \theta }{\partial \sigma },\frac{\partial \left( {\theta -\delta } \right) }{\partial \sigma },\frac{\partial {\bullet }}{\partial {s}}$ and $\frac{\partial {\bullet }}{\partial {n}}$ can be expressed as,

$$\begin{aligned}&\frac{\partial p_1 }{\partial {s}}=P_1 \rho _1 V_1^2 \quad \quad \frac{\partial p_2 }{\partial {s}}=P_2 \rho _2 V_2^2\\&\frac{\partial p_1 }{\partial {n}}=-D_1 \rho _1 V_1^2 \quad \quad \frac{\partial p_2 }{\partial {n}}=-D_2 \rho _2 V_2^2\\&\frac{\partial V_1 }{\partial {s}}=-P_1 V_1 \quad \quad \frac{\partial V_1 }{\partial {n}}=V_1 \left( {D_1 -\Gamma _1 } \right) \\&\frac{\partial \rho _1 }{\partial {s}}=\rho _1 M_1^2 P_1 \quad \quad \frac{\partial \rho _1 }{\partial {n}}=-\rho _1 M_1^2 \left[ {D_1 +\left( {\gamma -1} \right) \Gamma _1 } \right] \\&\frac{\partial \theta }{\partial \sigma }=S_a +\left( {M_1^2 -1} \right) \text {sin}\theta P_1 -\text {cos}\theta D_1 +\frac{\text {sin}\theta \text {sin}\delta _1 }{y}\\&\frac{\partial \left( {\theta -\delta } \right) }{\partial \sigma }=S_a +\left( {M_2^2 -1} \right) \text {sin} \left( {\theta -\delta } \right) P_2 -\text {cos} \left( {\theta -\delta } \right) D_2\\&\qquad +\,\frac{\text {sin} \left( {\theta -\delta } \right) \text {sin}\delta _2 }{y} \end{aligned}$$

So (51) becomes,

$$\begin{aligned}&\left( {\rho _1 V_1^2 P_1 \text {cos}\theta -\rho _1 V_1^2 D_1 \text {sin}\theta } \right) \nonumber \\&\quad \quad -\,\left[ {\rho _2 V_2^2 P_2 \text {cos}\left( {\theta -\delta } \right) -\rho _2 V_2^2 D_2 \text {sin}\left( {\theta -\delta } \right) } \right] \nonumber \\&\quad =\frac{\rho _1 V_1^2 \text {sin}\theta \text {cos}\theta }{\text {cos}^{2}\left( {\theta -\delta } \right) }\left[ S_a +\left( {M_2^2 -1} \right) \text {sin} \left( {\theta -\delta } \right) P_2\right. \nonumber \\&\left. \quad \quad -\text {cos} \left( {\theta -\delta } \right) D_2 +\frac{\text {sin} \left( {\theta -\delta } \right) \text {sin}\delta _2 }{y} \right] \nonumber \\&\quad \quad +\,\left[ \rho _1 V_1^2 \text {cos}^{2}\theta \tan \left( {\theta -\delta } \right) -\rho _1 V_1^2 \text {sin}^{2}\theta \tan \left( {\theta -\delta } \right) \right. \nonumber \\&\left. \qquad -2\rho _1 V_1^2 \text {sin}\theta \text {cos}\theta \right] \left[ S_a +\left( {M_1^2 -1} \right) \text {sin}\theta P_1\right. \nonumber \\&\left. \qquad -\text {cos}\theta D_1 +\frac{\text {sin}\theta \text {sin}\delta _1 }{y} \right] \nonumber \\&\quad \quad +\,\left[ {2\rho _1 V_1 \text {sin}\theta \text {cos}\theta \tan \left( {\theta -\delta } \right) -2\rho _1 V_1 \text {sin}^{2}\theta } \right] \nonumber \\&\quad \quad \times \,\left[ {-P_1 V_1 \text {cos}\theta +V_1 \left( {D_1 -\Gamma _1 } \right) \text {sin}\theta } \right] \nonumber \\&\quad \quad +\,\left[ {V_1^2 \text {sin}\theta \text {cos}\theta \tan \left( {\theta -\delta } \right) -V_1^2 \text {sin}^{2}\theta } \right] \nonumber \\&\quad \quad \times \,\left\{ {\rho _1 M_1^2 P_1 \text {cos}\theta -\rho _1 M_1^2 \left[ {D_1 +\left( {\gamma -1} \right) \Gamma _1 } \right] \text {sin}\theta } \right\} \nonumber \\ \end{aligned}$$

(52)

Replacing $\frac{1}{y}\hbox { by }-\frac{S_b }{\text {cos}\theta _1 }$, (52) becomes,

$$\begin{aligned}&\left[ {\frac{\text {sin}\theta \text {cos}\theta }{\text {sin}\left( {\theta -\delta } \right) }P_2 -\frac{\text {sin}\theta \text {cos}\theta }{\text {cos}\left( {\theta -\delta } \right) }D_2 } \right] \\&\quad \,=\frac{\text {sin}\theta \text {cos}\theta }{\text {cos}^{2}\left( {\theta -\delta } \right) }\left[ S_a +\left( {M_2^2 -1} \right) \text {sin} \left( {\theta -\delta } \right) P_2\right. \\&\quad \left. \quad -\text {cos} \left( {\theta -\delta } \right) D_2 -\frac{S_b \text {sin} \left( {\theta -\delta } \right) \text {sin}\delta _2 }{\text {cos}\theta _1 } \right] \\&\quad \quad +\,\left[ {\text {cos}^{2}\theta \tan \left( {\theta -\delta } \right) -\text {sin}^{2}\theta \tan \left( {\theta -\delta } \right) -2\text {sin}\theta \text {cos}\theta } \right] \\&\quad \quad \times \,\left[ {S_a +\left( {M_1^2 -1} \right) \text {sin}\theta P_1 -\text {cos}\theta D_1 -\frac{S_b \text {sin}\theta \text {sin}\delta _1 }{\text {cos}\theta _1 }} \right] \\&\quad \quad +\,\left[ {2\text {sin}\theta \text {cos}\theta \tan \left( {\theta -\delta } \right) -2\text {sin}^{2}\theta } \right] \\&\qquad \times \,\left[ {-P_1 \text {cos}\theta +\left( {D_1 -\Gamma _1 } \right) \text {sin}\theta } \right] \\&\quad \quad +\,\left[ {\text {sin}\theta \text {cos}\theta \tan \left( {\theta -\delta } \right) -\text {sin}^{2}\theta } \right] \left\{ M_1^2 P_1 \text {cos}\theta \right. \\&\left. \qquad -M_1^2 \left[ {D_1 +\left( {\gamma -1} \right) \Gamma _1 } \right] \text {sin}\theta \right\} \end{aligned}$$

Collecting terms,

$$\begin{aligned}&\left\{ \text {cos}\theta \text {cos}\left( {\theta -\delta } \right) -\left( {M_1^2 -1} \right) \text {sin}\theta \left[ \text {cos}^{2}\theta \text {sin}\left( {\theta -\delta } \right) \right. \right. \\&\left. \left. \quad \quad -\text {sin}^{2}\theta \text {sin}\left( {\theta -\delta } \right) -2\text {sin}\theta \text {cos}\theta \text {cos}\left( {\theta -\delta } \right) \right] \right. \\&\left. \quad \quad +\,\text {cos}\theta \left[ {2\text {sin}\theta \text {cos}\theta \text {sin}\left( {\theta -\delta } \right) -2\text {sin}^{2}\theta \text {cos}\left( {\theta -\delta } \right) } \right] \right. \\&\left. \quad \quad -\,\!M_1^2 \text {cos}\theta \left[ {\text {sin}\theta \text {cos}\theta \text {sin}\left( {\theta -\delta } \right) -\text {sin}^{2}\theta \text {cos}\left( {\theta -\delta } \right) } \right] \right\} P_1 \\&\quad \qquad +\,\left\{ -\text {sin}\theta \text {cos}\left( {\theta -\delta } \right) +\text {cos}\theta \left[ \text {cos}^{2}\theta \text {sin}\left( {\theta -\delta } \right) \right. \right. \\&\left. \left. \qquad -\text {sin}^{2}\theta \text {sin}\left( {\theta -\delta } \right) -2\text {sin}\theta \text {cos}\theta \text {cos}\left( {\theta -\delta } \right) \right] \right. \\&\left. \quad \quad -\text {sin}\theta \left[ {2\text {sin}\theta \text {cos}\theta \text {sin}\left( {\theta -\delta } \right) -2\text {sin}^{2}\theta \text {cos}\left( {\theta -\delta } \right) } \right] \right. \\&\left. \quad \quad +\,\!M_1^2 \text {sin}\theta \left[ {\text {sin}\theta \text {cos}\theta \text {sin}\left( {\theta -\delta } \right) -\text {sin}^{2}\theta \text {cos}\left( {\theta -\delta } \right) } \right] \right\} D_1 \\&\quad \quad +\,\left\{ \text {sin}\theta \left[ {2\text {sin}\theta \text {cos}\theta \text {sin}\left( {\theta -\delta } \right) -2\text {sin}^{2}\theta \text {cos}\left( {\theta -\delta } \right) } \right] \right. \\&\quad \,\,\,\, \left. +\,\left( {\gamma -1} \right) M_1^2 \text {sin}\theta \left[ \text {sin}\theta \text {cos}\theta \text {sin}\left( {\theta -\delta } \right) \right. \right. \\&\left. \left. \quad \,\,\,\, -\text {sin}^{2}\theta \text {cos}\left( {\theta -\delta } \right) \right] \right\} \Gamma _1 \end{aligned}$$

$$\begin{aligned}&\,=\left[ \frac{\text {sin}\theta \text {cos}\theta \text {cos}\left( {\theta -\delta } \right) }{\text {sin}\left( {\theta -\delta } \right) }\right. \\&\left. \quad +\,\frac{\text {sin}\theta \text {cos}\theta }{\text {cos}\left( {\theta -\delta } \right) }\left( {M_2^2 -1} \right) \text {sin} \left( {\theta -\delta } \right) \right] P_2\\&\quad +\,\left[ {-2\text {sin}\theta \text {cos}\theta } \right] D_2 \\&\quad +\,\left[ \frac{\text {sin}\theta \text {cos}\theta }{\text {cos}\left( {\theta -\delta } \right) }+\text {cos}^{2}\theta \text {sin}\left( {\theta -\delta } \right) -\text {sin}^{2}\theta \text {sin}\left( {\theta -\delta } \right) \right. \\&\left. \quad -2\text {sin}\theta \text {cos}\theta \text {cos}\left( {\theta -\delta } \right) \right] S_a \\&\quad +\,\left\{ -\frac{\text {sin}\theta \text {cos}\theta }{\text {cos}\left( {\theta -\delta } \right) }\frac{\text {sin} \left( {\theta -\delta } \right) \text {sin}\delta _2 }{\text {cos}\theta _1 }\right. \\&\left. \quad -\,\frac{\text {sin}\theta \text {sin}\delta _1 }{\text {cos}\theta _1 }\left[ \text {cos}^{2}\theta \text {sin}\left( {\theta -\delta } \right) -\text {sin}^{2}\theta \text {sin}\left( {\theta -\delta } \right) \right. \right. \\&\left. \left. \quad -2\text {sin}\theta \text {cos}\theta \text {cos}\left( {\theta -\delta } \right) \right] \right\} S_b \end{aligned}$$

The curved shock equation (33),

$$\begin{aligned} A_1^{\prime } P_1 +B_1^{\prime } D_1 +E_1^{\prime } \Gamma _1 =A_2^{\prime } P_2 +B_2^{\prime } D_2 +{C}^{\prime }S_{a} +G^{\prime }S_{b} \end{aligned}$$

where the coefficients $A_1^{\prime }, B_1^{\prime }, E_{1}^{\prime }, A_2^{\prime }, B_2^{\prime },{C}^{\prime },G^{\prime }$ are given by,

$$\begin{aligned} A_1^{\prime }= & {} \text {cos}\theta \text {cos}\left( {\theta -\delta } \right) -\left( {M_1^2 -1} \right) \text {sin}\theta \left[ \text {cos}^{2}\theta \text {sin}\left( {\theta -\delta } \right) \right. \\&\left. -\text {sin}^{2}\theta \text {sin}\left( {\theta -\delta } \right) -2\text {sin}\theta \text {cos}\theta \text {cos}\left( {\theta -\delta } \right) \right] \\&+\,\text {cos}\theta \left[ {2\text {sin}\theta \text {cos}\theta \text {sin}\left( {\theta -\delta } \right) -2\text {sin}^{2}\theta \text {cos}\left( {\theta -\delta } \right) } \right] \\&-\,M_1^2 \text {cos}\theta \left[ {\text {sin}\theta \text {cos}\theta \text {sin}\left( {\theta -\delta } \right) -\text {sin}^{2}\theta \text {cos}\left( {\theta -\delta } \right) } \right] \\= & {} \text {cos}\theta \text {cos}\left( {\theta -\delta } \right) +\left( {M_1^2 -1} \right) \text {sin}\theta \text {sin}\left( {\theta +\delta } \right) \\&+\,M_1^2 \text {sin}\theta \text {cos}\theta \text {sin}\delta -2\text {sin}\theta \text {cos}\theta \text {sin}\delta \\= & {} \text {cos}\theta \left( {\text {cos}\theta \text {cos}\delta +\text {sin}\theta \text {sin}\delta } \right) \\&+\,\left( {M_1^2 -1} \right) \text {sin}\theta \left( {\text {sin}\theta \text {cos}\delta +\text {sin}\delta \text {cos}\theta } \right) \\&+\,M_1^2 \text {sin}\theta \text {cos}\theta \text {sin}\delta -2\text {sin}\theta \text {cos}\theta \text {sin}\delta \\= & {} 2M_1^2 \text {sin}\theta \text {cos}\theta \text {sin}\delta -2\text {sin}\theta \text {cos}\theta \text {sin}\delta \\&+\,M_1^2 \text {sin}^{2}\theta \text {cos}\delta +\text {cos}^{2}\theta \text {cos}\delta -\text {cos}\delta \text {sin}^{2}\theta \\= & {} \left( {M_1^2 -1} \right) \text {sin}2\theta \text {sin}\delta +\left( {M_1^2 -1} \right) \text {sin}^{2}\theta \text {cos}\delta \\&+\,\left( {M_1^2 -1} \right) \text {cos}^{2}\theta \text {cos}\delta -\left( {M_1^2 -1} \right) \text {cos}^{2}\theta \text {cos}\delta \\&+\,\text {cos}^{2}\theta \text {cos}\delta \\= & {} M_1^2 \text {cos}^{2}\theta \text {cos}\delta -\left( {M_1^2 -1} \right) \text {cos}\left( {2\theta +\delta } \right) \\ B_1^{\prime }= & {} -\text {sin}\theta \text {cos}\left( {\theta -\delta } \right) +\text {cos}\theta \left[ \text {cos}^{2}\theta \text {sin}\left( {\theta -\delta } \right) \right. \\&\left. -\text {sin}^{2}\theta \text {sin}\left( {\theta -\delta } \right) -2\text {sin}\theta \text {cos}\theta \text {cos}\left( {\theta -\delta } \right) \right] \\&-\text {sin}\theta \left[ {2\text {sin}\theta \text {cos}\theta \text {sin}\left( {\theta -\delta } \right) -2\text {sin}^{2}\theta \text {cos}\left( {\theta -\delta } \right) } \right] \\&+\,\!M_1^2 \text {sin}\theta \left[ {\text {sin}\theta \text {cos}\theta \text {sin}\left( {\theta -\delta } \right) -\text {sin}^{2}\theta \text {cos}\left( {\theta -\delta } \right) } \right] \\= & {} -\text {sin}\theta \text {cos}\left( {\theta -\delta } \right) -\text {cos}\theta \text {sin}\left( {\theta +\delta } \right) \\&+\,2\text {sin}^{2}\theta \text {sin}\delta -M_1^2 \text {sin}^{2}\theta \text {sin}\delta \\= & {} -\text {sin}\left( {2\theta +\delta } \right) -M_1^2 \text {sin}^{2}\theta \text {sin}\delta \end{aligned}$$

$$\begin{aligned} E_1^{\prime }= & {} \text {sin}\theta \left[ {2\text {sin}\theta \text {cos}\theta \text {sin}\left( {\theta -\delta } \right) -2\text {sin}^{2}\theta \text {cos}\left( {\theta -\delta } \right) } \right] \\&+\,\left( {\gamma -1} \right) M_1^2 \text {sin}\theta \left[ \text {sin}\theta \text {cos}\theta \text {sin}\left( {\theta -\delta } \right) \right. \\&\left. -\,\text {sin}^{2}\theta \text {cos}\left( {\theta -\delta } \right) \right] \\= & {} -\left[ {2+\left( {\gamma -1} \right) M_1^2 } \right] \text {sin}\delta \text {sin}^{2}\theta \\ A_2^{\prime }= & {} \frac{\text {sin}\theta \text {cos}\theta \text {cos}\left( {\theta -\delta } \right) }{\text {sin}\left( {\theta -\delta } \right) }+\frac{\text {sin}\theta \text {cos}\theta }{\text {cos}\left( {\theta -\delta } \right) }\left( {M_2^2 -1} \right) \text {sin} \left( {\theta -\delta } \right) \\= & {} \frac{\text {sin}\theta \text {cos}\theta \text {cos}^{2}\left( {\theta -\delta } \right) +\text {sin}\theta \text {cos}\theta \left( {M_2^2 -1} \right) \text {sin}^{2}\left( {\theta -\delta } \right) }{\text {sin}\left( {\theta -\delta } \right) \text {cos}\left( {\theta -\delta } \right) }\\= & {} \frac{\left[ {1+\left( {M_2^2 -2} \right) \text {sin}^{2}\left( {\theta -\delta } \right) } \right] \text {sin}\theta \text {cos}\theta }{\text {sin}\left( {\theta -\delta } \right) \text {cos}\left( {\theta -\delta } \right) } \end{aligned}$$

$$\begin{aligned} B_2^{\prime }= & {} -2\text {sin}\theta \text {cos}\theta =-\text {sin}\left( {2\theta } \right) \\ C^{\prime }= & {} \frac{{\text {sin}\theta \text {cos}\theta }}{{\text {cos}\left( {\theta - \delta } \right) }} + \text {cos}^{2} \theta {\text {sin}}\left( {\theta - \delta } \right) - \text {sin}^{2} \theta {\text {sin}}\left( {\theta - \delta } \right) \\&- 2\text {sin}\theta \text {cos}\theta \text {cos}\left( {\theta - \delta } \right) \\= & {} \frac{{\text {sin}\theta \text {cos}\theta + \text {cos}2\theta {\text {sin}}\left( {\theta - \delta } \right) \text {cos}\left( {\theta - \delta } \right) - \text {sin}2\theta \text {cos}^{2} \left( {\theta - \delta } \right) }}{{\text {cos}\left( {\theta - \delta } \right) }}\\= & {} \frac{{\text {sin}\theta \text {cos}\theta - \text {sin}\left( {\theta + \delta } \right) \text {cos}\left( {\theta - \delta } \right) }}{{\text {cos}\left( {\theta - \delta } \right) }}\\= & {} \frac{{ - \text {sin}\left( {2\delta } \right) }}{{2\text {cos}\left( {\theta - \delta } \right) }}\\ G^{\prime }= & {} - \frac{{\text {sin}\theta \text {cos}\theta }}{{\text {cos}\left( {\theta - \delta } \right) }}\frac{{\text {sin} \left( {\theta - \delta } \right) \text {sin}\delta _{2} }}{{\text {cos}\theta _{1} }}\\&-\,\frac{\text {sin}\theta \text {sin}\delta _1 }{\text {cos}\theta _1 }\left[ \text {cos}^{2}\theta \text {sin}\left( {\theta -\delta } \right) -\text {sin}^{2}\theta \text {sin}\left( {\theta -\delta } \right) \right. \\&\left. -\,2\text {sin}\theta \text {cos}\theta \text {cos}\left( {\theta -\delta } \right) \right] \\= & {} -\frac{\text {sin}\theta \text {cos}\theta \tan \left( {\theta -\delta } \right) \text {sin}\delta _2 }{\text {cos}\theta _1 }+\frac{\text {sin}\left( {\theta +\delta } \right) \text {sin}\theta \text {sin}\delta _1 }{\text {cos}\theta _1 }\\= & {} -\frac{\text {sin}\theta \text {cos}\theta \tan \left( {\theta -\delta } \right) \text {sin}\delta _2 -\text {sin}\left( {\theta +\delta } \right) \text {sin}\theta \text {sin}\delta _1 }{\text {cos}\theta _1 } \end{aligned}$$

Appendix 3. Derivation of the equation for vorticity behind a curved shock

Although the effect of pre-shock vorticity on the post-shock flow curvature and pressure gradient is included in the curved shock equations (32, 33), the post-shock vorticity does not appear explicitly. For example, when applying CST to RR and MR, the post-shock vorticity, in region (2), behind the incident shock, is required as input to the curvature calculations of the reflected shock when a curved incident shock has created vorticity in front of the reflected shock.

The vorticity behind a curved shock, as given by Truesdell [28], and more recently by Emanuel [4] is,

$$\begin{aligned} \omega _2 =V_1 \frac{\rho _2 }{\rho _1 }\left( {1-\frac{\rho _1 }{\rho _2 }} \right) ^{2}\cos \theta \times \frac{\partial \theta }{\partial \sigma } \end{aligned}$$

(53)

The derivation of this equation uses the Crocco relation between vorticity and entropy and assumes a uniform upstream flow. The normalized version of (53) is,

$$\begin{aligned} \Gamma _2 =\frac{\omega _2 }{V_2 }=\frac{V_1 }{V_2 }\frac{\rho _2 }{\rho _1 }\left( {1-\frac{\rho _1 }{\rho _2 }} \right) ^{2}\cos \theta \times \frac{\partial \theta }{\partial \sigma } \end{aligned}$$

(54)

Equation (54) can be further simplified using the oblique shock relations:

$$\begin{aligned} \Gamma _2 =\frac{2\sin ^{2}\delta }{\sin (2\theta )\sin (\theta -\delta )}\frac{\partial \theta }{\partial \sigma } \end{aligned}$$

(55)

This equation gives the normalized vorticity behind an acute or obtuse shock with aerodynamic curvature $\frac{\partial \theta }{\partial \sigma }$ when the upstream flow is uniform and irrotational. The aerodynamic curvature consists of the geometric curvature and the pre-shock flow divergence/convergence according to $\frac{\partial \theta }{\partial \sigma }=\frac{\partial \theta _1 }{\partial \sigma }-\frac{\partial \delta _1 }{\partial \sigma }$.

We seek an expression for vorticity behind a doubly curved shock for a shock that faces a flow that is curved, has a pressure gradient, is vorticial and is converging or diverging towards or away from the line of symmetry—altogether a very high degree of generality. As for the previous derivations, the flow is steady and of a calorically and thermally perfect gas. Results apply directly to flows that possess axial and planar symmetry and with some considerations of symmetry also to curved shock elements in three-dimensional flow. As for $P_{2}$ and $D_{2}$ derivations, we derive the rational as well as the influence coefficient forms of the vorticity equation. The derivation is based on the shock-tangential momentum equation, the Euler equations and the definition of vorticity for the upstream (subscript 1) and downstream (subscript 2) flows. The following Euler relations are used to eliminate derivatives of velocity in favour of expressions containing streamwise pressure gradient, streamline curvature and normalized vorticity,

$$\begin{aligned} \begin{aligned}&\frac{1}{V_1 }\left( {\frac{\partial V}{\partial s}} \right) _1 =-P_1 \qquad \frac{1}{V_1 }\left( {\frac{\partial V}{\partial n}} \right) _1 =D_1 -\Gamma _1 \\&\frac{1}{V_2 }\left( {\frac{\partial V}{\partial s}} \right) _2 =-P_{2} \qquad \frac{1}{V_2 }\left( {\frac{\partial V}{\partial n}} \right) _2 =D_2 -\Gamma _2 \end{aligned} \end{aligned}$$

(56)

The geometric shock angle is $\theta _1 =\theta +\delta _1$. Taking derivatives of $\theta _1$ with respect to $\sigma$ gives the geometric shock curvature in the flow plane, $S_a$,

$$\begin{aligned} S_a =\frac{\partial \theta _1 }{\partial \sigma }=\frac{\partial \theta }{\partial \sigma }+\frac{\partial \delta _1 }{\partial \sigma } \end{aligned}$$

(57)

This can be written,

$$\begin{aligned} S_a =\frac{\partial \theta }{\partial \sigma }+\cos \theta \frac{\partial \delta _1 }{\partial s}+\sin \theta \frac{\partial \delta _1 }{\partial n} \end{aligned}$$

(58)

But

$$\begin{aligned} \frac{\partial \delta _1 }{\partial s}=D_1 \hbox { and }\frac{\partial \delta _1 }{\partial n}=-\left( {M_1^2 -1} \right) P_1 -\sin \delta _1 /y \end{aligned}$$

(59)

So that,

$$\begin{aligned} \frac{\partial \theta }{\partial \sigma }=S_a +\left( {M_1 ^{2}-1} \right) \sin \theta P_1 -\cos \theta D_1 +\sin \theta \sin \delta _1 /y\nonumber \\ \end{aligned}$$

(60)

Similarly, starting from $\theta -\delta =\theta _1 -\delta _2$ gives,

$$\begin{aligned} \frac{\partial \left( {\theta -\delta } \right) }{\partial \sigma }= & {} S_a +\left( {M_2 ^{2}-1} \right) \sin \left( {\theta -\delta } \right) P_2 -\cos \left( {\theta -\delta } \right) D_2\nonumber \\&+\sin \left( {\theta -\delta } \right) \sin \delta _2 /y \end{aligned}$$

(61)

In these equations $\delta _1$ and $\delta _2$ are the geometric flow inclinations in front of and behind the shock. $\delta =\delta _2 -\delta _1$ is the flow deflection through the shock and $\theta$ is the corresponding aerodynamic shock angle. $\theta _1$ is the geometric (physical) shock inclination. All inclinations are measured from the axis of symmetry, in the flow plane. For axial flow, y is the perpendicular distance from the shock to the axis of symmetry or, more generally, the radius of curvature of the shock trace in the transverse plane. For planar flow $y\rightarrow \infty$. Equations (11) and (15) are needed in the derivation of the vorticity equation. The derivation follows.

The momentum equation tangential to the shock is,

$$\begin{aligned} V_1 \cos \theta =V_2 \cos \left( {\theta -\delta } \right) . \end{aligned}$$

(62)

Taking derivatives of both sides of this equation with respect to the distance $\sigma$ along the shock gives,

$$\begin{aligned} V_1 \frac{\partial \cos \theta }{\partial \sigma }\,+\,\cos \theta \frac{\partial V_1 }{\partial \sigma }\,=\,V_2 \frac{\partial \cos \left( {\theta -\delta } \right) }{\partial \sigma }\,+\,\cos \left( {\theta -\delta } \right) \frac{\partial V_2 }{\partial \sigma } \end{aligned}$$

Dividing through by $V_{1}$ and using equations (56) and (59) gives,

$$\begin{aligned}&\sin \theta \frac{\partial \theta }{\partial \sigma }-\cos \theta \left[ {\cos \theta \frac{1}{V_1 }\left( {\frac{\partial V}{\partial s}} \right) _1 +\sin \theta \frac{1}{V_1 }\left( {\frac{\partial V}{\partial n}} \right) _1 } \right] \nonumber \\&\quad =\frac{V_2 }{V_1 }\left[ {\sin \left( {\theta -\delta } \right) \frac{\partial \left( {\theta -\delta } \right) }{\partial \sigma }} \right] \nonumber \\&\qquad -\cos \left( {\theta -\delta } \right) \frac{V_2 }{V_1 }\left[ \cos \left( {\theta -\delta } \right) \frac{1}{V_2 }\left( {\frac{\partial V}{\partial s}} \right) _2\right. \nonumber \\&\left. \qquad +\sin \left( {\theta -\delta } \right) \frac{1}{V_2 }\left( {\frac{\partial V}{\partial n}} \right) _2 \right] \end{aligned}$$

(63)

Using (11) and (15) to replace the velocity and angle derivatives and replacing $V_2 /V_1$ by $\cos \theta {/}\cos \left( {\theta -\delta } \right)$ gives,

$$\begin{aligned}&\sin \theta \left[ {S_a +\left( {M_1^2 -1} \right) \sin \theta P_1 -\cos \theta D_1 +\sin \theta \sin \delta _1 /y} \right] \nonumber \\&\qquad +\cos ^{2}\theta P_1 -\cos \theta \sin \theta \left\{ {D_1 -\Gamma _1 } \right\} \nonumber \\&\quad =\cos \theta \tan \left( {\theta -\delta } \right) \left[ S_a +\left( {M_2^2 -1} \right) \sin \left( {\theta -\delta } \right) P_2\right. \nonumber \\&\left. \qquad -\cos \left( {\theta -\delta } \right) D_2 +\sin \left( {\theta -\delta } \right) \sin \delta _2 /y \right] \nonumber \\&\qquad -\cos \theta \left[ {-\cos \left( {\theta -\delta } \right) P_2 +\sin \left( {\theta -\delta } \right) \left\{ {D_2 -\Gamma _2 } \right\} } \right] \nonumber \\ \end{aligned}$$

(64)

Dividing through by $\cos \theta$ and collecting coefficients of the physical variables $P_{1}, D_{1}$ etc. results in the vorticity equation,

(65)

where,

$$\begin{aligned} \begin{aligned}&{A}_1^{\prime \prime } = \left( {M_1^2 -1} \right) \tan \theta \sin \theta +\cos \theta \\&{B}_1^{\prime \prime } = -2\sin \theta \\&\Gamma _1 :{E}_1^{\prime \prime } = \sin \theta \\&{A}_2^{\prime \prime } = \left( {M_2^2 -1} \right) \tan \left( {\theta -\delta } \right) \sin \left( {\theta -\delta } \right) +\cos \left( {\theta -\delta } \right) \\&{B}_2^{\prime \prime } = -2\sin \left( {\theta -\delta } \right) \\&\Gamma _2 :{E}_2^{\prime \prime } = \sin \left( {\theta -\delta } \right) \\&{C}^{\prime \prime } = \tan \left( {\theta -\delta } \right) -\tan \theta \\&{G}^{\prime \prime } = -{F}^{\prime \prime }{/}\cos \left( {\theta +\delta _1 } \right) \\&{F}^{\prime \prime } = \tan \left( {\theta -\delta } \right) \sin \left( {\theta -\delta } \right) \sin \delta _2 -\sin \theta \tan \theta \sin \delta _1 \end{aligned} \end{aligned}$$

(66)

Equation (65) can now be written as,

$$\begin{aligned} {L}^{\prime \prime }={A}_2^{\prime \prime } P_2 +{B}_2^{\prime \prime } D_2 +{E}_2^{\prime \prime } \Gamma _2 +{C}^{\prime \prime } S_a +{G}^{\prime \prime } S_b \end{aligned}$$

(67)

or,

$$\begin{aligned} L^{\prime \prime } =A_2^{\prime \prime } P_2 +B_2^{\prime \prime } D_2 +E_2^{\prime \prime } \Gamma _2 +C^{\prime \prime } S_a +F^{\prime \prime }/y \end{aligned}$$

(68)

where,

$$\begin{aligned} L^{\prime \prime }=A_1^{\prime \prime } P_1 +B_1^{\prime \prime } D_1 +E_1^{\prime \prime } \Gamma _1 \end{aligned}$$

(69)

Either one of the equations (67) or (68) can be used to solve for the post-shock vorticity, $\Gamma _2$, in terms of the other variables. The two equations differ in their last terms depending on whether the transverse curvature of the shock is specified by $S_b$ or y—a choice determined by the problem at hand. $S_b$ and y are themselves interchangeable through $S_b =-\cos \left( {\theta +\delta _1 } \right) {/}y$. Choosing (67) and solving (65) for $\Gamma _2$ gives the desired expression for the downstream vorticity,

(70)

This is the generalized vorticity equation in a rational form for ${\Gamma }_{2}$, the normalized vorticity behind a curved shock facing non-uniform, divergent flow. Together with equations (39), it forms three equations for the three unknowns $P_2, D_2$ and $\Gamma _2$ so as to completely define the non-uniform post-shock flow. For a uniform upstream, (70) reduces to,

$$\begin{aligned} \Gamma _2 =\left[ {\frac{{C}^{\prime \prime }}{{E}_2^{\prime \prime } }+\frac{\left[ {BC} \right] }{\left[ {AB} \right] }\frac{{A}_2^{\prime \prime } }{{E}_2^{\prime \prime }}-\frac{\left[ {AC} \right] }{\left[ {AB} \right] }\frac{{B}_2^{\prime \prime } }{{E}_2^{\prime \prime } }} \right] S_a \end{aligned}$$

(71)

The coefficient multiplying $S_{a}$ is identical to the coefficient of $S_{a}=\partial \theta /\partial \sigma$ in (55). Fortunately $P_2$ and $D_2$ are decoupled from $\Gamma _2$, leading to explicit solutions for all unknowns. $P_2$ and $D_2$, appearing in the equations (65) and (70), are found from the two curved shock equations (37) and (38) which are repeated here:

$$\begin{aligned} P_2&=\frac{B_2 \left( {C^{\prime } S_a +G^{\prime } S_b -L^{\prime }} \right) -B_2^{\prime } \left( {CS_a +GS_b -L} \right) }{A_2 B_2^{\prime } -A_2^{\prime } B_2 } \nonumber \\ D_2&=-\frac{A_2 \left( {C^{\prime } S_a +G^{\prime } S_b -L^{\prime }} \right) -A_2^{\prime } \left( {CS_a +GS_b -L} \right) }{A_2 B_2^{\prime } -A_2^{\prime } B_2 } \end{aligned}$$

(72)

where the L-terms above are given by,

$$\begin{aligned} L&=A_1 P_1 +B_1 D_1 +E_1 \Gamma _1 \nonumber \\ L^{\prime }&=A_1^{\prime } P_1 +B_1^{\prime } D_1 +E_1^{\prime } \Gamma _1 \end{aligned}$$

(73)

Note that L and $L^{\prime }$ contain the upstream gradients and that G and $G^{\prime }$ contain the upstream flow inclination $\delta _1$. Substituting $P_2$ and $D_2$ from (72) into (70) and collecting terms of the upstream gradients and the shock curvatures gives the influence coefficient form of the vorticity equation (70),

$$\begin{aligned} \Gamma _2 =I_p P_1 +I_d D_1 +I_g \Gamma _1 +I_a S_a +I_b S_b \end{aligned}$$

(74)

where the I-coefficients, each multiplying their respective variables, appear in the full equation for $\Gamma _2$ as shown below,

$$\begin{aligned} \Gamma _2= & {} \left\{ \left[ {AB} \right] A_1^{\prime \prime } +\left( {B_2 A_1^{\prime } -B_2^{\prime } A_1 } \right) A_2^{\prime \prime }\right. \nonumber \\&\left. -\left( {A_2 A_1^{\prime } -A_2^{\prime } A_1 } \right) B_2^{\prime \prime } \right\} {/}\left\{ {\left[ {AB} \right] E_2^{\prime \prime } } \right\} P_1 \nonumber \\&+\left\{ \left[ {AB} \right] B_1^{\prime \prime } +\left( {B_2 B_{1}^{\prime } -B_2^{\prime } B_1 } \right) A_2^{\prime \prime }\right. \nonumber \\&\left. -\left( {A_2 B_1^{\prime } -A_2^{\prime } B_1 } \right) B_2^{\prime \prime } \right\} {/}\left\{ {\left[ {AB} \right] E_2^{\prime \prime }} \right\} D_1 \nonumber \\&+\left\{ \left[ {AB} \right] E_1^{\prime \prime } +\left( {B_2 E_1^{\prime } -B_2^{\prime } E_1 } \right) A_2^{\prime \prime }\right. \nonumber \\&\left. -\left( {A_2 E_1^{\prime } -A_2^{\prime } E_1 } \right) B_2^{\prime \prime } \right\} {/}\left\{ {\left[ {AB} \right] E_2^{\prime \prime } } \right\} \Gamma _1 \nonumber \\&-\left\{ \left[ {AB} \right] C^{\prime \prime }+\left( {B_2 C^{\prime }-B_2^{\prime } C} \right) A_2^{\prime \prime }\right. \nonumber \\&\left. -\left( {A_2 C^{\prime }-A_2^{\prime } C} \right) B_2^{\prime \prime } \right\} {/}\left\{ {\left[ {AB} \right] E_2^{\prime \prime } } \right\} S_a \nonumber \\&-\left\{ \left[ {AB} \right] G^{\prime \prime }+\left( {B_2 G^{\prime }-B_2^{\prime } G} \right) A_2^{\prime \prime }\right. \nonumber \\&\left. -\left( {A_2 G^{\prime }-A_2^{\prime } G} \right) B_2^{\prime \prime } \right\} {/}\left\{ {\left[ {AB} \right] E_2^{\prime \prime } } \right\} S_b \end{aligned}$$

(75)

Fig. 6

Influence coefficients for vorticity behind the shock as by (74)

Fig. 7

Plot of the $I_{\mathrm{b}}$ influence coefficient against shock angle with the pre-shock flow divergence angle as parameter

The unprimed and single-primed coefficients, $A\ldots G$, are listed as equations (34, 35); the double-primed are in (66). Equation (75) shows clearly what the role is of each upstream non-uniformity $P_1, D_1$ and $\Gamma _1$ and of the shock curvatures $S_a$ and $S_b$ in determining the downstream vorticity, $\Gamma _2$. Note that the above derivation for vorticity does not need Crocco’s thermodynamic relation between vorticity and entropy gradient, and that the resulting equations account for upstream flow non-uniformity and vorticity as well as flow divergence. Derivation of the vorticity equation parallels those for the pressure gradient and streamline curvature but it is quite a bit simpler. The use of j to denote planar or axial symmetry has been dropped since the equations are uniformly valid for both geometries. For axial flow, y is the radius of the shock’s curvature in the transverse plane, so that the flow is sensitive to dimensionality through the parameter y. In the calculations for planar flow, y is set to a very large number. Figure 6 depicts the influence coefficients for vorticity plotted against shock angle. The blue curve shows the influence of pre-shock pressure gradient $P_1$, and we see that a positive pressure gradient causes a positive vorticity contribution for an acute shock and a negative contribution for an obtuse shock. The green curve shows that a positive pre-shock flow curvature, $D_1$ produces a positive contribution to vorticity. The red curve is for the effect of pre-shock vorticity itself. At the Mach wave limits, the influence coefficient has a value of 1, predicting that vorticity passes through Mach waves unchanged. All other curves are at zero so, at Mach wave conditions, there is no vorticity production due to pre-shock gradients or Mach wave curvatures. Stronger shocks tend to amplify and reverse the direction of vorticity. The cyan curve shows that positive vorticity is produced by a positive flow-plane shock curvature, $S_a$, for an acute shock and negative vorticity is produced by a positively curving obtuse shock. The black curve is for the effect of the transverse shock curvature, $S_b$, and it shows that the influence coefficient for the transverse curvature is identically zero. This confirms the fact that the shock produces vorticity only by its flow-plane curvature and not by the transverse curvature so that flow behind a conical shock is irrotational. For flows with no pre-shock divergence/convergence, the $I_b S_b$ term can be dropped from equations (74) and (75) since $I_{b}$ is identically zero.

The situation becomes complicated when the pre-shock flow is diverging. The role played by flow divergence $\delta _1$ and transverse shock curvature $S_b$ is interactive and has to be carefully considered. From what we know of the behaviour of vorticity, it seems incorrect that post-shock vorticity is a function of the cross-stream curvature, $S_b$, as evident from the last term of (75). So we examine the influence coefficient for $S_b$,

$$\begin{aligned} \hbox { I}_b= & {} -\left\{ \left[ {AB} \right] G^{\prime \prime }+\left( {B_2 G^{\prime }-B_2^{\prime } G} \right) A_2^{\prime \prime }\right. \nonumber \\&\left. -\left( {A_2 G^{\prime }-A_2^{\prime } G} \right) B_2^{\prime \prime } \right\} /\left\{ {\left[ {AB} \right] E_2^{\prime \prime } } \right\} \end{aligned}$$

(76)

In particular its numerator,

$$\begin{aligned} \hbox { N}_b = \left[ {AB} \right] G^{\prime \prime }+\left( {B_2 G^{\prime }-B_2^{\prime } G} \right) A_2^{\prime \prime } -\left( {A_2 G^{\prime }-A_2^{\prime } G} \right) B_2^{\prime \prime }\nonumber \\ \end{aligned}$$

(77)

must be zero when $\delta _1$ is zero. The black curve in Fig. 6 shows that it is indeed so. Note that $\delta _1$ is contained in $G^{\prime }$ and $G^{\prime \prime }$ only and not in G. This requires that the part of $\hbox {N}_{b}$, not containing $\delta _1$ equals zero, i.e.,

$$\begin{aligned} A_{2}^{{\prime }} B_{2}^{{\prime \prime }} -B_{2}^{{\prime }} A_{2}^{{\prime \prime }} =0 \end{aligned}$$

(78)

This has proven that there is no influence on post-shock vorticity from $S_b$ when there is no pre-shock divergence. The proof of this is straightforward, with four lines of algebra, so that, without loss of generality, the influence coefficient for $S_{b}$ can be simplified to,

$$\begin{aligned} I_b = -\left\{ {\left[ {AB} \right] G^{\prime \prime }+\left( {B_2 G^{\prime }} \right) A_2^{\prime \prime } -\left( {A_2 G^{\prime }} \right) B_2^{\prime \prime } } \right\} /\left\{ {\left[ {AB} \right] E_2^{\prime \prime } } \right\} \nonumber \\ \end{aligned}$$

(79)

$I_{b}$ from this equation is plotted in Fig. 7, against the shock angle, for Mach 3, with the divergence angle $\delta _1$ ($^\circ$) as parameter. Actually it is $I_{\mathrm{b}}\times S_{\mathrm{b}}\times y$ because $I_{\mathrm{b}}$ by itself goes to infinity when $\cos \left( {\theta +\delta _1 } \right)$ goes to zero and it gets hard to display. Note that $\cos \left( {\theta +\delta _1 } \right) = -S_{b}\times y$. The green line is for $\delta _1 = 0$, black curves are for positive $\delta _1$ increasing by 10$^\circ$ away from the zero line to 50. Red curves are for negative $\delta _1$ decreasing by 10$^\circ$ to −50$^\circ$.