1 Introduction

The behavior of a planar shock wave reflected from a concave cavity has been the subject of numerous previous investigations. Sturtevant and Kulkarny [1] performed experiments and theoretical analyses on planar shock waves, which underwent focusing in three different shape reflectors. They noticed that the wave front is dominated by the nonlinear interaction of the incident shock and the reflected waves participating in the focusing process. Izumi et al. [2] have studied the effect of incident shock strength and shape by a parabolic reflector on shock focusing processes experimentally and numerically. They concluded that in their case the shock focusing occurred when two triple points from Mach reflection of the incident shock met on the center axis. The focusing patterns were classified and discussed. Kowalczyk et al. [3] investigated the process of shock wave focusing in a rarefied noble gas by solving the Boltzmann equation. Teng et al. [4] carried out a numerical study of toroidal shock wave focusing. Multiple focal points with strong supersonic jets were observed. Skews et al. [5] and Paton et al. [6] experimentally and numerically studied the behavior of a conical shock wave imploding asymmetrically. Complex patterns and instabilities were observed and analyzed. Hosseini and Takayama [7] carried out an experiment to investigate the focusing of a toroidal shock wave in a compact vertical tube. They found that the pressure ratio during implosion is much higher than that of a comparable shock reflection in two space dimensions. Eliasson et al. [8–10] experimentally and numerically investigated the polygonal shock wave focusing created by various geometrical shapes. Mach configurations and the type of reflected shock waves were discussed. Furthermore, the light emission from the focusing point was observed. A comprehensive analysis of flow features was obtained by Skews and Kleine [11] and Skews et al. [12] who used high-speed digital cameras to record shock wave focusing in cylindrical and parabolic cavities. The details of waves reflected from a curved wall, the forming of a gas dynamic focus and the development of jet effects and instabilities were demonstrated and discussed. Bond et al. [13] studied a planar shock wave propagating into a 2D linearly convergent geometry. The differences between distributed and compact reflections were discussed. Skews et al. [14] adopted an ultra-fast high-resolution camera to study the shock focusing in a cylindrical cavity and found a number of new features, which improved the understanding of the shock focusing mechanisms. Numerical simulations were carried out by MacLucas and Skews [15] to study the effects of cavity depth, entrance shape and incoming shock strength on shock-induced pressure distributions. In a purely numerical study, Jung [16] used the wave propagation algorithm and a Cartesian embedded boundary method successfully to obtain reasonable results of planar shock focusing in a circular reflector. Recently, shearing interferometry and direction-indicating color schlieren have been used by MacLucas et al. [17] to study the wave interaction in a concave cavity, thereby demonstrating the benefit of using this type of equipment for analysis of highly transient two-dimensional flow fields.

An important application of shock focusing is the initiation of detonation waves in reactive gaseous media. The reliable high-frequency initiation of detonation waves is crucial for designing a pulse detonation engine (PDE), a novel propulsion concept for hypersonic flight. Levin et al. [18] report a new design for a PDE based on shock-induced combustion ignition, which utilizes shock wave focusing and a resonator concept with a 24–25 \(\mathrm {kHz}\) operational frequency.

The self-ignition phenomenon at a shock focusing point in lean hydrogen–air mixture has been investigated by Gelfand et al. [19]. Two-dimensional wedges, semi-cylindrical and parabolic cavities were used as reflectors in their experiment. The position of detonation initiation and its resulting propagation speed were discussed. Bartenev et al. [20] considered the initiation of detonations by focusing shock waves and two different initiation mechanisms were discovered. Achasov and Penyazkov [21] studied the initiation of detonations in reactive gaseous mixtures by shock focusing and resulting jetting by means of numerical simulation. Jackson and Shepherd [22] investigated the effectiveness of imploding shock waves for initiating a detonation in stoichiometric ethylene- and propane–oxygen–nitrogen mixtures. A variety of shock strengths and mixture sensitivities were tested in order to find the critical conditions for detonation initiation.

Fig. 1
figure 1

Sketch of shock tube and test section. (1 Shock tube; 2 dump tank; 3 test section; 4 window; 5, 6 pressure transducer)

Full size image
Fig. 2
figure 2

Sketch of the test section (all numbers in millimeters)

Full size image

To investigate the character of shock wave focusing in a concave cavity of a PDE, an incident planar shock is first divided into two parts by an obstacle in the center axis of the test section. The two shocks then enter symmetric cavities and focus into a single apex. Numerical calculations have been carried out in order to provide a better understanding of the phenomena observed in the experiments. Beside a qualitative description of the experimental results, the paper presents a quantitative analysis of the various shock reflection types that are occurring during the shock focusing phase based on the numerical calculations.

2 Experimental apparatus

2.1 Shock tube

The experiment was carried out in a standard conventional rectangular steel shock tube, as shown in Fig. 1. The shock tube consists of a 6-m-long driver section and an 8-m-long driven section. Both inner cross sections had a rectangular shape of \(80 ~\mathrm {mm}\times 130~\mathrm {mm}\) width. Two pressure transducers (PCB Inc., \(525~\mathrm {mV/psi}\), resonant frequency \(500~\mathrm {kHz}\)) were installed \(0.66~\mathrm {m}\) apart and 0.3 m ahead the entry of the test section to record the arrival time of the shock wave, as shown in Fig. 2. The uncertainty of Mach number is less than 1 %. The diameter of the pressure transducer was \(5.6~\mathrm {mm}\). At the end of the shock tube was a cylindrical dump tank with an inner diameter of 800 and \(1500~\mathrm {mm}\) length, which was used to hold and encapsulate the test section. This dump tank was equipped with two K9 quartz glass windows of diameter \(300~\mathrm {mm}\).

2.2 Test section

The test section consists of two components: a cavity and a wing-shaped obstacle. The straight part of the cavity has an inner cross section of identical size as the shock tube. A cylindrical segment and its tangent planes constitute the cavity surface. The tangent planes directly connect to the straight tube. A further PCB pressure transducer for recording pressure history is installed at the cavity apex. The half attack angle of the straight segment of the obstacle is \(22.5{}^\circ \) and it transitions smoothly to zero with a spherical radius of \(240~\mathrm {mm}\). Other dimensions of the test section configuration are given in Fig. 2. Note that for the preliminary tests reported here, the obstacle has a prototypical shape but it is not optimized in any respect. It will be modified according to the experimental results in further studies.

2.3 Flow visualization

A traditional schlieren system was used to visualize the flow. Flow field images were recorded using a high-speed digital camera (Phantom V310). The frame rate was \(27{,}000~\mathrm {fps}\) with an exposure time per frame of \(1.02~\mathrm {\upmu s}\) and the resolution of the image was \(320\times 240\) pixels. The light source was a continuous bi-Xenon Corporation lamp.

3 Numerical methods

To obtain deeper insight into the experiments, the Cartesian shock-capturing solver system AMROC V2.0 [23] within the freely available Virtual Test Facility software [24] was adopted. A variety of discretizations are implemented in AMROC, and in this study we have utilized a WENO method with third-order accuracy in space and time. Detailed descriptions of WENO methods in AMROC, including verification and validation simulations, can be found in [25] and [26] and are therefore omitted here. We ignore viscous effects and numerically solve the two-dimensional Euler equations [27]. The operating gas was air, which was treated here as a polytropic ideal gas.

3.1 Level set methods and adaptive mesh refinement

The consideration of geometrically complex boundaries in AMROC is achieved in a discretization-independent way by a level set technique. A scalar level set function is employed to map the geometrically complex boundary onto a Cartesian grid which stores the signed distance to the boundary. Based on the signed distance information, reflective wall boundary conditions are constructed in cells adjacent to the boundary but deemed outside of the fluid domain before the Cartesian discretization is employed to compute the next time step. A detailed description of the algorithm including necessary inter- and extrapolation operations is given in [28].

To mitigate inaccuracies from the Cartesian boundary approximation, typical for the level set approach, AMROC allows the application of the block-structured adaptive mesh refinement (AMR) method after Berger and Colella [29]. The AMR method adopts a patch-wise mesh refinement strategy instead of replacing individual cells by finer ones. Cells flagged by user-defined error indicators are then clustered into rectangular boxes by a special algorithm, cf. [23]. Time step refinement by the same factor as the spatial refinement ensures that the stability condition of the explicit WENO method is in principle satisfied on all refinement levels.

Note that the AMROC software was applied with the exact same computational techniques and WENO discretization by Bond et al. [13] for simulating a converging shock wave in two and three space dimensions focused by two wedges of slightly different angle. Excellent agreement between numerical predictions and experimental results was obtained, which motivated its application for the slightly more complex cavity geometry used here.

3.2 Computational domain and boundary conditions

The computational domain used had a length of 0.4 m and a height of 0.064 m. Only half of the physical domain was calculated due to the symmetry of the flow. The base level grid had \(800\times 128\) cells and three additional levels, each refined by a factor of 2, were applied to obtain high resolution of the discontinuities, as can be seen in Figs. 3 and 5. The adaptation along discontinuities is achieved by evaluating density gradients multiplied by the local step size in all directions, more details can be found in [28].

Fig. 3
figure 3

Levels of grid refinement (shown by color) and visualization of the initial conditions

Full size image

The finest grid resolution was \(0.0625~\mathrm {mm}\). The air at rest inside the computational domain was initiated as \(p_0=101{,}325~\mathrm {Pa}\), \(T_0=300~\mathrm {K}\) and \(p_0=8820~\mathrm {Pa}\), \(T_0=300~\mathrm {K}\) for incident shock Mach numbers of 1.4 and 2.1, respectively. The incident shock was positioned near the left boundary and the state variables left of the shock front are computed from the normal shock relations to obtain the required incident Mach number. The left boundary condition was set as inflow boundary using the same incident state and other boundaries are set as slip wall. To check the grid independence, the calculations were performed with three different base grids (400 \(\times \) 64, 800 \(\times \)128, 1600 \(\times \) 256). The refinement level was chosen in a way that the finest grid had the same size for all three base grids. The shock structure including shock position, reflection type and slip line position is the same in Fig. 4. The second configuration (800 \(\times \) 128) was adopted as it runs fastest on our computer.

Fig. 4
figure 4

Shock structure at 614.8 \(\upmu \)s with \(M_0=1.4\). a Base grid is \(400\times 64\) with refinement level of \(2\times 2\times 4\). b Base grid is \(800\times 128\) with refinement level of \(2\times 2\times 2\). c Base grid is \(1600\times 256\) with refinement level of \(2\times 2\)

Full size image

4 Results and discussion

4.1 Incident shock reflected from side walls

As the planar shock wave is impacting on the obstacle in the test section, it is reflected from the obstacle surface and produces two leading shocks moving forward and a circular reflected shock wave moving backward. In the present test, the incident shock Mach numbers were 1.4 and 2.1 and the reflected shock configurations are typical single Mach reflections at this stage. The initial planar shock wave is split into two shocks as shown in Fig. 5. The reflected wave and slip line were sharply resolved and the AMR algorithm reduced the number of grid cells substantially.

Fig. 5
figure 5

Leading shock reflected from obstacle with incident shock \(M_0=1.4\) (upper graphic color plot of density; lower graphic refinement levels depicted by color)

Full size image
Fig. 6
figure 6

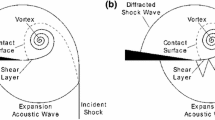
Visualization of the shock wave focusing configuration for incident Mach number \(M_0=1.4\) (left experimental schlieren photo, right numerical schlieren image). Time interval between snapshots is \(37.04~\mathrm {\upmu s}\). LS leading shock, R reflected shock, SL slip line, M Mach stem, V vortex, N node, BS bow shock, J jet, S shock. The reflection types in region (1) and (2) (the fourth subplot) are used as sample data to do shock polar analyses in Table 1 and Fig. 11

Full size image

4.2 Incident shock Mach number of 1.4

Figure 6 shows the processes of shock wave focusing with incident shock Mach number of 1.4, comparing schlieren visualizations from the experiment and the numerical simulation directly. It is apparent that the numerical prediction is consistent with the experiment, beside some minor unwanted flow asymmetries in the experiment. The reflected shock R undergoes several reflections between the test section inner wall and the obstacle surface, which can be seen in Fig. 6a, b. This continuously enhances the leading shock wave as it propagates into the cavity. The leading shock LS diffracts at the corner of the obstacle and a circular diffraction shock is formed, which can be seen in Fig. 6c. The reflected shock wave R and the slip line SL are clearly present in both experimental and numerical results. When the leading shock meets the circular part of the cavity wall, its reflected shock R is bent away from it. The configuration of the reflected shock R is shown in Fig. 6d. This flow feature is similar to the planar shock directly reflected from a cylindrical cavity. However, this reflected shock is a combination of two shock waves. One shock is the ensemble of compression waves arising from the disturbance of the cylindrical wall. The other is a reflected shock that follows the leading shock front. The two shocks meet in the point N and merge into a single reflected wave. Although the Mach stem M is indistinguishable in the experimental photo, the numerical result confirms its existence. This observation is in accordance with Skews and Kleine’s [11] results. The circular diffracted shocks develop into the bow shock BS and regularly reflect from one another. Vortex V at the corner is large enough to be seen in this frame. Figure 6e shows the shock wave configuration after focusing. The reflected shock consists of two separate shocks rather than a single shock wave, as normally observed when a planar shock is reflected from a cavity. The incident angle of the bow shock is much smaller than in a head-on collision in the usual case. As a consequence, the focusing shock is rather weak and lags behind the reflected shock R. The bow shock BS and the terminated reflected shock R are partially merged near the wall. A jet induced by shock focusing is present in both experimental and numerical results. In the final frame, the terminated shock has caught up with the bow shock and has apparently merged into a single shock wave propagating backwards, which is shown in Fig. 6f. The jetting is more visible than in the previous frame.

Fig. 7
figure 7

Pressure history at cavity apex in numerical simulation (left) and experiment (right); incident shock of \(M_0=1.4\)

Full size image

The pressure history at the apex of the cavity wall with incident shock Mach number of 1.4 is shown in Fig. 7. The measured maximum pressure at the apex is \(1.39~\mathrm {MPa}\) in the experiment and \(1.74~\mathrm {MPa}\) in the numerical calculation. The difference is about 25.2 % relative to the experimental result. This difference can be expected from the imperfect focusing in the experiment, as seen in Fig. 6c. An additional reason is that the pressure transducer records only a spatially averaged pressure and its sampling response frequency is limited. Note also that the used pressure transducer has originally been designed to capture a step signal, for instance, the arrival of a shock wave, which explains the comparably large variation in measured data points.

Fig. 8
figure 8

Color plot of pressure during the occurrence of the pressure maximum in the numerical simulation; incident shock of \(M_0=1.4\)

Full size image

Note that the pressure maximum at the wall is smaller than the eventual focusing maximum pressure point, which is located slightly inwards. This issue can be inferred from the computational depiction of Fig. 8. The focusing point is about \(1.3~\mathrm {mm}\) away from the cavity apex on the central axis. The high pressure zone is produced by the collision of triple points, which is in agreement with numerous previous observations [2, 12]. The length of the Mach stem (M in Fig. 6d) indicates the distance of the focusing point away from the wall. When the incident Mach number and the geometric configuration are varied, the location of the focus point will change accordingly. As a result, it is difficult to accurately predict the position of the maximal focusing pressure.

4.3 Incident shock Mach number of 2.1

Figure 9 shows the processes of shock focusing with an incident shock Mach number of 2.1. The main features are similar to the case discussed above. The leading shock is reflected several times from the aisle walls, similar to the previous case with smaller incident Mach number. In Fig. 9a, the leading shock LS and its reflected shock R can easily be identified. The bow shocks BS are a result of the diffraction of the leading shock waves at the corner and regularly reflect from one another, as shown also in Fig. 9b. However, the reflected shock R is weaker than in the previous case and no compression waves can be identified in this frame. As a consequence, the reflected shock forms a closed shock after focusing, as visualized in Fig. 9c. This is different from the previous case, where reflected shocks are separately propagating backwards, cf. Fig. 6e. Although the incident shock is stronger now, the reflected shock from the cavity wall is much weaker than in the previous case with \(M_0=1.4\). In the case \(M_0=2.1\), the closed shock CS is strong enough to catch up with the terminated reflected shock R, which is similar to a planar shock reflected from a cylindrical cavity as discussed by Skews and Kleine [11]. The flow field is more unstable and a jet induced by the focusing is stronger than in the previous case. The closed shock CS expands and is split into two shocks by the corner vortex. Then the split shock catches up with the bow shock and merges into a single anomalous shock S, as shown in Fig. 9d.

Fig. 9
figure 9

Visualization of the shock wave focusing configuration for incident Mach number \(M_0=2.1\) (left experimental schlieren photo, right numerical schlieren image). Time interval between snapshots is again \(37.04~\mathrm {\upmu s}\). LS leading shock, R reflected shock, M Mach stem, V vortex, BS bow shock, CS closed shock, J jet, S shock. The regular reflection in rectangle (the second subplot) is used as sample data to do shock polar analyses in Table 1 and Fig. 11. a t = 374.1 \(\upmu \)s; b t = 411.1 \(\upmu \)s; c t = 448.2 \(\upmu \)s; d t = 485.2 \(\upmu \)s

Full size image

5 Shock polar analyses

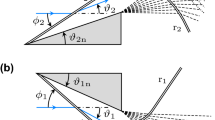
There are several types of shock wave reflection patterns present both in the experiment and the simulations. Just from the schlieren photos and computer-generated graphics alone, it is not always possible to distinguish the type of shock wave reflection pattern unambiguously. Yet, with the help of the high-resolution numerical simulations, a detailed and quantitative shock transition analysis and pattern classification is possible. For this purpose, we have numerically created a shock reflection transition boundary diagram for a polytropic gas with \( \gamma = 1.4\) following Ben-Dor [30] for varying inflow Mach number. Given an oblique shock, whose Mach number and shock angle are known, the reflection type can be analytically determined. Using a sketch of a generic double Mach reflection in Fig. 10 to identify the key pattern regions, we briefly recall the transition criteria between different Mach reflection patterns according to [30] for

Fig. 10
figure 10

Sketch of a generic double Mach reflection of shock wave impinging on a wedge with angle \(\theta _w\) (T primary triple point, R reflection point, i incident shock, m Mach reflection, r reflected shock, s slip line, \(T'\) secondary triple point, \(m', r', s'\) Mach stem, reflected shock, slip line of triple point configuration around \(T'\))

Full size image

the benefit of the reader: If the Mach number (with respect to the reflection point R) behind the oblique shock, in the region marked (1), satisfies \(M_1^R<1\), there is no reflection (NR). If the Mach number in the region marked (2) (with respect to the reflection point R) behind the reflected shock satisfies \(M_2^R>1\), the reflection type is a regular reflection (RR). In all other cases, it is a Mach reflection (MR) (note that weak Mach reflection is not considered here), which can be further divided into a single Mach reflection (SMR), a transitional Mach reflection (TMR), a double Mach reflection (DMR), and other minor reflection types that are not present in this study. If the Mach number (with respect to the primary triple point T) of the flow behind the reflected shock satisfies \(M_2^T<1\), the reflection type is an SMR, otherwise it is a TMR or a DMR. If the Mach number (with respect to the secondary triple point \(\mathrm{T}'\)) behind the reflected shock satisfied \(M_2^{T'}<1\), the reflection type is a TMR, otherwise it is a DMR.

To reliably determine the inflow Mach number \(M_0\) for a given shock reflection pattern in the frame of reference of the primary triple point T, we apply a computational technique explained in depth in [31]. By tracking the maximum vorticity over time, highly resolved triple point trajectories are obtained onto which the schlieren image of the respective triple point pattern is overlaid. In the resulting image, the angle \(\phi \) between triple point trajectory and incident shock, which corresponds to \(\theta _w+\chi \) in Fig. 10, can be measured with high accuracy. Picking then pressure values \(p_0\) and \(p_1\) in the vicinity of T, in front and behind the incident shock, respectively, and using the oblique shock relations, the inflow Mach number \(M_0\) in state (0) in the frame of reference of the triple point T can be obtained. For a polytropic gas, the oblique shock relations yield across the incident shock the well-known relation [27]

$$\begin{aligned} \frac{p_1}{p_0} = \frac{2\gamma }{\gamma +1}\left( M_0^2 \sin ^2\phi -1\right) +1, \end{aligned}$$
(1)

which is easily transformed into a direct expression for the inflow Mach number normal to the incident shock \(M_s\):

$$\begin{aligned} M_s=M_0\sin \phi =\sqrt{\frac{\gamma +1}{2\gamma }\left( \frac{p_1}{p_0}-1\right) +1} \end{aligned}$$
(2)

In Table 1, the required values to calculate \(M_s\) from (2) are provided for some characteristic snapshots. Note that \(\phi ^c\) is the complementary angle of \(\phi \), defined as \(\phi ^c=90^\circ -\phi \). Since the variation in \(p_1\) is typically around \(1\%\), we find an error bound of \(\sim \)0.1 % in determining \(M_s\) from (2) and the error in measuring \(\phi \) is \(\sim \) \(0.5^\circ \).

Table 1 Values for the data points given in the transition diagram Fig. 11
Full size table
Fig. 11
figure 11

Mach reflection transition domain diagram for air at \(T_0=300~\mathrm {K}\) modeled as polytropic gas with \(\gamma =1.4\). (Open symbols and solid line are for the \(M_0=1.4\) case with \(101{,}325~\mathrm {Pa}\), closed symbols and dash line are for the \(M_0=2.1\) case with \(p_0=8820~\mathrm {Pa}\). Note that the error in \(M_s\) is \(\sim \)0.1 % and the error in the angle \(\phi ^{c}\) is \(\sim \) \(0.5^\circ \)

Full size image
Fig. 12
figure 12

Single Mach reflection for \(M_0=1.4\), \(t=123.7~\upmu \mathrm {s}\) (left) and \(M_0=2.1\), \(t=88.78~\upmu \mathrm {s}\) (right). Obtained by superimposing a greyscale map of the magnitude of the density gradient and the trajectory of the triple point

Full size image
Fig. 13
figure 13

Single Mach reflection for \(M_0=1.4\), \(t=529.6~\upmu \mathrm {s}\) (left) and transitional Mach reflection for \(M_0=2.1\), \(t=340.7~\upmu \mathrm {s}\) (right). Obtained by superimposing a greyscale map of the magnitude of the density gradient and the trajectory of the triple point

Full size image

Plotting the points from Table 1 into a transition diagram in the \(M_s-\phi ^{c}\) domain, given in Fig. 11, shows that the SMR type occurs most frequently in the case of the previously discussed experiments. Figure 12 shows two standard SMR configurations with incident shock Mach number \(M_0=1.4\) and \(M_0=2.1\), with \(\phi ^c=31.9\) and \(\phi ^c=34.1\), respectively. Although the wedge is curved, the triple point trajectories remain straight in these cases. Following this method, additionally the reflection configurations from Figs. 6, 9 and 13 are plotted in Fig. 11. The regular reflections in Figs. 6d and 9b are very close to the transition boundary. With the increase of the shock angle, these regular reflections transition to SMR patterns very quickly, as observed in the computations.

Beside RR and SMR, TMR patterns are also present, which is shown in Fig. 13. A TMR is stronger than an SMR, but weaker than a DMR. In a TMR configuration, the secondary triple point is not fully developed. The most important distinction between an SMR and a TMR is that the latter has an almost straight segment in the reflection shock and a rolling up slip line, which indicates that it is a stronger reflection. Just looking at the triple point patterns of Fig. 13, the TMR and SMR patterns can hardly be distinguished, which illustrates the benefit of utilizing the described quantitative post-processing technique.

6 Conclusions

Experiments and numerical simulations were performed in order to investigate the process of a planar shock wave focusing in a cavity, where the incident shock is diffracted by an obstacle. The numerical calculations achieve a high resolution of the discontinuities and the computational results agree very well with experimental schlieren photos. Complex shock–shock, shock–wall and shock–vortex interactions are resolved. Mach reflection theory for a polytropic gas in combination with high-resolution computational results has been applied successfully to identify Mach reflection patterns around triple points that occur during shock focusing.

Similarities and differences between the present work and previous works on shock focusing in a cavity without an obstacle have been discussed. Experiments and simulations show that a closed shock is not always formed after the incident shock wave has focused in the cavity. Further studies are needed to investigate the influence of the obstacle geometry and different incident shock strengths on the focusing behavior.