Vertical Motion Control of Crane Without Load Position Information Using Nonlinear Control Theory

Abstract

When a load is lifted by a crane system, the load position may be unexpectedly vertically vibrated due to the elasticity of the rope. This problem reduces the system stability and load positioning accuracy. To resolve this actual problem, this paper describes a model for studying the dynamic behavior of the offshore crane system such that a control system design method is introduced to occupy desirable performance. The obtained model allows evaluating the fluctuations of the load arising from the elasticity of the rope. In addition, the rope is modeled as a mass-damper-spring system, and the winch as the main actuator coefficients are identified via experiments and simulation. Especially, in this paper, the authors design a control system in which winch a rotation angle and a rope tension are used to make control signals without load position information. In the real plants, the load position cannot be accurately measured because the load type is various and other environmental constraints. Considering these facts, the controller design based on input-output feedback linearization theory is presented which can handle the effect of the elasticity of the rope and track the load target trajectory. Besides that, for comparison study, a full order observer is designed to estimate unknown states. Finally, the experimental results show that the proposed method can successfully make something good control performance.

1 Introduction

As well known, an offshore crane system is an omnipresent system which provides indispensable heavy lifting capabilities in a wide range of ocean industrial fields. And an offshore crane system is widely used as a successful offshore system. It is also a dangerous offshore system which has several failure modes. For an example, the accurate load positioning is a challenging issue for the offshore crane operation because the load position is hard to be judged, especially when the load position is controlled under affecting by some external disturbances, such as a rope extension variation due to the elasticity of the rope. Therefore, the issue for improving the offshore crane operating performance is a very important fact.

Many researchers have been concentrated on studying sway control in the horizontal motion of the rotary crane [1,2,3]. Just a few significant efforts dealt with such kind of vertical load vibration which can find in some lifting machines such as elevators [4] and heavy load lifting cranes [5]. However, the controller design concepts in these papers are so complex such that it cannot be applied to the real system. Furthermore, these papers assumed that a rope is not flexible, although a rope is flexible and the rope characteristics have spring characteristics. Moon et al. [6] showed that the rope parameters are presented as spring stiffness, damping constant and mass of rope which are time-varying. Therefore, to guarantee the highest performance of load position control, the load position in the vertical motion should be considered in careful.

In this paper, the authors describe the model of crane system by considering the affecting facts such as rope extension which is illustrated by the elasticity of the rope.

Therefore, the proposed model in this paper is a nonlinear system including time-varying parameters which are carefully treated in modeling and controller design process. Especially, the authors make a crane model and design the controller for controlling vertical motion without load position information. In the real plant, it is not easy to measure the load position directly due to irregular types and other reasons.

Based on the real work conditions, the authors design robust vertical motion control system by introducing nonlinear control approach. As well known in nonlinear control theory, the input-output feedback linearization theory is chosen to build up a full control system to get the highest performance. Furthermore, introducing a full state observer system, some unknown states are estimated and used for comparison study. The experimental results are presented in Sect. 4 to evaluate the effectiveness of the proposed controller design concept.

2 Mathematical Model

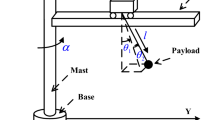
In this study, the authors assume that the offshore crane system is modeled as a rigid body system. Moreover, considering load lifting in the vertical direction, the rope elasticity is modeled as a mass-damper-spring system. Next, the winch model as the main actuator is identified and approximated via simulations and experiments.

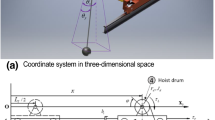
To take the necessary dynamic information for designing control system, the encoder for measuring the winch rotation angle and the load cell for measuring the rope extension made from the elasticity of the rope are installed in. Only these two sensing signals are used to calculate the control signals. The load distance sensor appeared in Fig. 1 is not used for actual control but for comparing study.

Fig. 1.

The configuration of the offshore crane model.

Based on the Newton/Euler method, the differential equation of load motion dynamics in the vertical direction is presented under considering the elasticity of the rope as shown in Eq. (1).

$$ m\ddot{Z}_{p} + d\dot{\Delta }L + k\Delta L = 0 $$

(1)

where $\Delta L$ denotes the rope extension due to the elasticity of the rope, $Z_{p}$ denotes the load position, $m$ denotes the equivalent mass, $d$ and $k$ denote the damping coefficient and spring stiffness of the rope, respectively.

In the Eq. (1), the load position $Z_{p}$ is derived in detail as follows:

$$ Z_{p} = Z_{w} +\Delta L + L_{0} $$

(2)

where $L_{0}$ is the initial rope length from the winch to the load, and $Z_{w}$ is the rope length released from the winch.

According to Moon et al. [6], the mass $m_{r}$, damping constant $d$ and the spring stiffness $k$ of the rope are time-varying, and strongly depend on the rope length variation. Then these parameters are calculated and approximated as follows:

$$ k = \frac{{e_{r} A_{r} }}{{\left( {Z_{w} + L_{0} } \right)}},\,d = \frac{{\beta A_{r} }}{{\left( {Z_{w} + L_{0} } \right)}},\,m_{r} = m_{unit} \left( {Z_{w} + L_{0} } \right) $$

(3)

where $m_{unit}$ denotes the mass per meter unit of the rope length. $A_{r}$ denotes the wire rope cross section. $\beta$ denotes the wire rope constant of damping. $e_{r}$ denotes the wire rope modulus of elasticity.

If the rope is wound or released by the winch system, the mass of rope $m_{r}$ is not constant but time-varying parameter. The authors assume that the mass of rope is divided into two equal parts. One of them is lumped to the equivalent mass $m$, and another part is lumped to the winch. However, the authors design and build an offshore crane model based on the assumption that the crane is operated in a short distance. Therefore, the equivalent mass $m$ is approximated and presented as follows:

$$ m = m_{L} + \frac{1}{2}m_{unit} \left( {Z_{w} + L_{0} } \right) \simeq m_{L} + \frac{1}{2}m_{unit} L_{0} $$

(4)

As previously mentioned, the winch system is the main actuator which can lift up or down the load in the vertical direction. Without loss of generousness, the dynamics of the winch system is described as follows:

$$ J_{w} \ddot{Z}_{w} + d_{w} \dot{Z}_{w} + k_{w} Z_{w} = T_{in} - r_{w} T_{dis} $$

(5)

where $T_{in} = \eta v$ is defined as the torque of the winch system, and $T_{dis} = k\Delta L$ is a disturbance torque made from load moving. $\eta$ denotes the multiplier constant, and $v$ is the input voltage to the winch. $J_{w} ,\,d_{w} ,\,k_{w}$ and $r_{w}$ are disturbance force which affects the winch system, inertia moment, damping coefficient, spring coefficient and radius of the winch, respectively.

3 Controller Design

By defining the states as ${\mathbf{x}} = \left[ {\begin{array}{*{20}c} {x_{1} } & {x_{2} } & {x_{3} } & {x_{4} } \\ \end{array} } \right]^{T} = \left[ {\begin{array}{*{20}c} {Z_{w} } & {\dot{Z}_{w} } & {\Delta L} & {{\dot{\Delta }}L} \\ \end{array} } \right]^{T}$, input as $v$, and output as $y = Z_{p}$, then the system can be written in the state-space form as follows:

$$ \left\{ {\begin{array}{*{20}c} {{\dot{\mathbf{x}}} = A_{(x)} + B_{(x)} v} \\ {y = C_{(x)} } \\ \end{array} } \right. $$

(6)

where $x_{1}$ denotes the rope length released from the winch, $x_{2}$ denotes the velocity of $x_{1}$, $x_{3}$ denotes the rope extension, $x_{4}$ denotes derivative of $x_{3}$. Then,

$$ A_{(x)} = \left[ {\begin{array}{*{20}c} {x_{2} } \\ { - \frac{{k_{w} }}{{J_{w} }}x_{1} - \frac{{d_{w} }}{{J_{w} }}x_{2} - \frac{{r_{w} }}{{J_{w} }}\frac{{e_{r} A_{r} }}{{\left( {x_{1} + L_{0} } \right)}}x_{3} } \\ {x_{4} } \\ {\frac{{k_{w} }}{{J_{w} }}x_{1} + \frac{{d_{w} }}{{J_{w} }}x_{2} + \left( {\frac{{r_{w} }}{{J_{w} }}\frac{{e_{r} A_{r} }}{{\left( {x_{1} + L_{0} } \right)}} - \frac{{e_{r} A_{r} }}{{\left( {x_{1} + L_{0} } \right)\left( {m_{L} + \frac{1}{2}m_{unit} L_{0} } \right)}}} \right)x_{3} - \frac{{\beta A_{r} }}{{\left( {x_{1} + L_{0} } \right)\left( {m_{L} + \frac{1}{2}m_{unit} L_{0} } \right)}}x_{4} } \\ \end{array} } \right] $$

(7)

$$ B_{(x)} = \left[ {\begin{array}{*{20}c} 0 & {\frac{\eta }{{J_{w} }}} & 0 & { - \frac{\eta }{{J_{w} }}} \\ \end{array} } \right]^{T} $$

(8)

$$ C_{(x)} = x_{1} + x_{3} + L_{0} $$

(9)

As the first step of the controller design based on the input/output feedback linearization theory, the output relative degree $r$ is defined by following conditions:

$$ \left\{ {\begin{array}{*{20}c} {L_{{B_{(x)} }} L_{{A_{(x)} }}^{i} C_{\left( x \right)} = 0} \\ {L_{{B_{(x)} }} L_{{A_{(x)} }}^{r - 1} C_{\left( x \right)} \ne 0} \\ \end{array} } \right.\quad \begin{array}{*{20}c} {\forall i = 0,1, \ldots ,r - 2} \\ {\forall x\,{ \in }\,{\mathbb{R}}^{n} } \\ \end{array} $$

(10)

where $L_{{A_{(x)} }} C_{\left( x \right)}$ and $L_{{B_{(x)} }} C_{\left( x \right)}$ are called as the Lie Derivative of $A_{(x)}$ and $B_{(x)}$ with respect to $C_{(x)}$, respectively.

Following the conditions in Eq. (10), the first-order and second-order derivative of $y$ are not dependent on the control input $v$. However, the control input $v$ appears in the equation of the third-order derivative $\dddot y$ with non-zero coefficient, since $L_{{B_{(x)} }} L_{{A_{(x)} }}^{2} C_{(x)} \ne 0$ as follows:

$$ \dddot y = \frac{{\partial \left( {L_{{A_{(x)} }}^{2} C_{(x)} } \right)}}{\partial x}\left[ {A_{\left( x \right)} + B_{\left( x \right)} v} \right] = L_{{A_{(x)} }}^{3} C_{(x)} + L_{{B_{(x)} }} L_{{A_{(x)} }}^{2} C_{(x)} v $$

(11)

Thus, the relative degree of the system is 3. The foregoing equation shows clearly that the system is input/output feedback linearization, because the input-output feedback linearization control:

$$ v = \frac{{ - L_{{A_{(x)} }}^{3} C_{\left( x \right)} + u}}{{L_{{B_{(x)} }} L_{{A_{(x)} }}^{2} C_{\left( x \right)} }} $$

(12)

where the trajectory tracking control law $u$ given by:

$$ u = \dddot y_{ref} - k_{0} e_{error} - k_{1} \dot{e}_{error} - k_{2} \ddot{e}_{error} $$

(13)

and $e_{error} = y_{ref} - y$, $y_{ref}$ denotes the target trajectory, input $k_{0} ,k_{1}$ and $k_{2}$ are state feedback gains which can be designed by using any linear control design technique, such as the LQR method or pole placement method, etc.

However, the parameters affected by rope length are hardly measured such as wire rope damping constant $\beta$ and wire rope modulus of elasticity $e_{r}$.

To deal with these conditions and demonstrate the effect of the elasticity of the rope, the authors assume that the damping constant of the rope ($d = \beta A_{r} /\left( {x_{1} + L_{0} } \right)$) can be neglected. Then, to represent the spring stiffness of the rope ($k = e_{r} A_{r} /\left( {x_{1} + L_{0} } \right)$), the spring with stiffness constant $k_{r}$ and the mass constant $m_{spring}$ is inserted between the load and the end of the rope as shown in Figs. 1 and 2. Then, to estimate the spring extension and load position, the authors use the load cell which is placed above the inserted spring as shown in Fig. 2. As previously mentioned, in this study, the load cell is used to estimate the load position and displacement for control. The distance sensing information is not used for control but evaluating and comparing the results.

Fig. 2.

The experimental apparatus with sensing system.

With the assumptions and Eq. (4), the equivalent mass is recalculated as follows:

$$ m = m_{L} + \frac{1}{2}m_{unit} L_{0} + m_{loadcell} + m_{spring} $$

(14)

In the result, the nonlinear system in Eq. (6) can be described as a linear system. Following the controller design process is given in Eqs. (10)–(13), the control input is obtained as follows:

$$ v = \frac{{\frac{{k_{r} }}{m}\left( {\frac{{k_{w} }}{{J_{w} }}Z_{w} + \frac{{d_{w} }}{{J_{w} }}\dot{Z}_{w} + \left( {\frac{{r_{w} k_{r} }}{{J_{w} }} - \frac{{k_{r} }}{m}} \right)\Delta_{L} } \right) + \ddddot y_{ref} - k_{0} e_{error} - k_{1} \dot{e}_{error} - k_{2} \ddot{e}_{error} - k_{3} \dddot e_{error} }}{{\frac{{k_{r} }}{m}\frac{\eta }{{J_{w} }}}} $$

(15)

The spring extension $\Delta L$ can be estimated by using the signal from load cell as follows:

$$ \Delta L = \frac{{T_{loadcell} - \left( {m_{spring} + m_{L} } \right)g}}{{k_{r} }} $$

(16)

where $T_{loadcell}$ is the tension force, $g$ is the gravitational constant.

However, an observer is introduced to estimate the some dynamic parameters such as load position and load position variation, etc. Because it is difficult to insert the load cell sensor to the real system and impossible to measure the load motions due to the irregular types of the loads.

Anyway, the authors consider that only the winch rotation angle is obtained using the encoder. It means that the others except winch rotation angle should be estimated by the estimation method. Then, the introduced observer structure is shown in Fig. 3.

Fig. 3.

Observer structure.

With the actual system described in Eq. (6) and the new output ($C_{1} = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ \end{array} } \right]$), the observer is described as follows:

$$ \left\{ {\begin{array}{*{20}c} {{\mathbf{\dot{\hat{x}}}} = \left[ {\begin{array}{*{20}c} 0 & 1 & 0 & 0 \\ { - \frac{{k_{w} }}{{J_{w} }}} & { - \frac{{d_{w} }}{{J_{w} }}} & { - \frac{{r_{w} k_{r} }}{{J_{w} }}} & 0 \\ 0 & 0 & 0 & 1 \\ {\frac{{k_{w} }}{{J_{w} }}} & {\frac{{d_{w} }}{{J_{w} }}} & {\left( {\frac{{r_{w} k_{r} }}{{J_{w} }} - \frac{{k_{r} }}{m}} \right)} & 0 \\ \end{array} } \right]{\hat{\mathbf{x}}} + \left[ {\begin{array}{*{20}c} 0 \\ {\frac{\eta }{{J_{w} }}} \\ 0 \\ { - \frac{\eta }{{J_{w} }}} \\ \end{array} } \right]v + L\left( {y - \hat{y}} \right)} \\ {\hat{y} = \hat{x}_{1} } \\ \end{array} } \right. $$

(17)

where ${\hat{\mathbf{x}}} = \left[ {\begin{array}{*{20}c} {Z_{w} } & {\dot{Z}_{w} } & {{\hat{\Delta }}L} & {{\dot{\hat{\Delta }}}L} \\ \end{array} } \right]^{T}$, $y = x_{1} = Z_{w}$ and $L$ is the $\left[ {1{ \times }4} \right]$ gain matrix for the observer. The gain matrix of the observer can be computed by any methods such as pole placement method, LQR method, etc.

4 Experimental Results

4.1 Parameters of Motor-Winch System

The parameters $J_{w} ,d_{w} ,k_{w} ,\eta$ are identified using the Matlab Identification Toolbox software. As the first step, a chirp signal $v(t)$ of frequency variations (from 0.05 Hz to 1 Hz in 40 s with 2 volts amplitude) is used to excite the motor-winch system. For this, the output is defined as the winch displacement $Z_{w}$.

Based on the obtained experimental data, we can identify the system parameters by specifying poles and zeros using the Matlab Identification Toolbox. Then the fitting ratio between experimental result and simulation result is shown in Fig. 4 and Table 1.

Fig. 4.

Simulation results for linear models and experiment results.

Table 1. The fitting ratio of various motor-winch models for a real plant.

In the results, the authors choose the second order transfer function as a model based on the data shown in Table 1. Then, the identified model is obtained as follows:

$$ \frac{{z_{w} }}{v} = \frac{0.65}{{s^{2} + 5.369s + 0.007986}} $$

(18)

4.2 Experimental Data Acquisition

A modeling of the crane system has been completed. Then, for the experiment, the real-time control using Labview Language and the data acquisition program using National Instrument PCI 6259 card is implemented. The load position data is collected to evaluate the control performance by using the distance sensor. As mentioned before, the real position data obtained from the load cell is not used in the real control experiment. The specification of experimental apparatus is described in Table 2.

Table 2. The specification of the experimental apparatus.

4.3 The Relationship Between the Load Position and Rope Tension Force

As previously mentioned, in this study, the authors assume that the real load position information (displacement) is not used for control. Instead of that, we use the rope tension force and estimate the load position using it. Therefore, we need to check whether this method is useful or not.

Here the experiment results are shown in Fig. 5 to illustrate the relationship between the load position measured by the distance sensor and the rope tension force measured by the load cell. In the experiment, the winch system is not operated but exposed to disturbances ($Z_{w} = 0$). In Fig. 5, in 0[sec]–3[sec] time range, the load is in the initial position without no external force. But in 3[sec]–4[sec], the load is pulled down by external force and freed from it. By using this method, the time responses are obtained and the test results are shown the figure where the solid line is the real tension force measured by the load cell and the dashed line is estimated load position. This result means that we can estimate the load position from the rope tension force.

Fig. 5.

The relationship between a load position and measured force.

4.4 Experimental Results

Then the effectiveness of proposed control method is evaluated by PID and Observer-based control method. Here, the target trajectories are given by the step type and the impulse type with a specified slew rate. In the proposed method, the feedback gains are calculated as $k_{0} = 3000,k_{1} = 3800,k_{2} = 1050$ and $k_{3} = 10$ based on the LQR method. Finally, the observer gains are also calculated as $L_{0} = 1,L_{1} = 500,L_{2} = - 60$ and $L_{3} = - 10$ based on the pole placement method. Besides that, the parameters of PID controller are chosen as $K_{P} = 0.0436556,K_{I} = 0.002356435$ and $K_{d} = - 0.00379$.

Experimental results for the step type reference input are shown in Figs. 6 and 7. Figure 6 shows the control inputs of PID controller, proposed controller, and observer based control method, respectively. The load position responses for the step reference input (dash-dotted black line) are shown in Fig. 7. As we can see, the output of PID controller (dashed-gray line) cannot track the reference target. Also, the observer based control method cannot give good tracking performance (blue-solid line). Especially, in the steady state, the vibrated motion is appeared. It is clear that this result comes from rare dynamics information. However, the output of the proposed controller (red-solid line) can track the reference target well.

Fig. 6.

Control inputs in case of step type reference trajectory input.

Fig. 7.

Load position responses for the step reference trajectory input.

As the second try, the system responses for the ramp type reference with slew rate 50[mm/s] are shown in Figs. 8 and 9. Figure 8 shows the control inputs using PID, proposed controller and observer based control method. The load position responses for the ramp type reference input (dash-dotted black line) are shown in Fig. 9.

Fig. 8.

Control inputs in case of ramp type reference trajectory input.

Fig. 9.

Control responses for the ramp type reference trajectory input.

As we can see in Fig. 9, we can find out more improved transient responses for all control methods. However, by comparing experimental results, it is clear that the similar control performances are obtained.

5 Conclusions

The paper proposed a nonlinear control strategy for controlling the load position of a crane system under effecting of the elasticity of the rope. The novelty of this research is the load motion control system design method in which the load displacement is not measured but estimated from rope tension information measured by the load cell. In the real work environment, it is impossible to use the measurement system for measuring the load motions in direct due to the many reasons. It means that the proposed control method is useful and effective one such that it might be useful tool for real application.